iterativealgorithms.ppsx
Download as PPSX, PDF0 likes13 views
The document discusses parallelizing iterative image reconstruction algorithms on multi-core systems. It analyzes ART, MLEM, and MAPEM algorithms run sequentially and in parallel. Results show MLEM achieves best PSNR values while MAPEM requires fewer iterations than MLEM and ART for large images. Parallelizing the algorithms via OpenMP yields speedups of up to 7x compared to sequential versions by distributing reconstruction tasks across multiple cores.
![• C++ omp is used in this research work.
• Environmental Variable
• OMP_DYNAMIC
• OMP_NUM_THREADS
• OMP_NUM_THREADS=num_threads
• OMP_SCHEDULE
• Directive
• #pragma omp name_of_directives[clause]
• Parallel
• Used to denote a region to be executed in parallel
• If(exp)
• Shared(list)
• Reduction(operator:list)
• for
OpenMP](https://image.slidesharecdn.com/iterativealgorithms-220622022303-003299ed/85/iterativealgorithms-ppsx-7-320.jpg)
iterativealgorithms.ppsx
- 1. Iterative Image Reconstruction Algorithms on a Multi-core system based on PSNR optimization 30.06.2020
- 2. • Image Reconstruction Technique is suitable for identifying the disease based on scanned image. • Reconstructing an Image using Projection displays good quality images • To improve the accuracy level for medical applications, iterative algorithms such as ART, MLEM and MAPEM are implemented for limited number of angles. • The number of iterations are optimized • It is found that all three systems suffers from high computation time. • To reduce reconstruction time a parallel computation method is proposed. • To prove the parallel computing performance Amdahl’s Law is used. Objective
- 3. • Analytical • Filtered Back Projection (FBP) • Iterative • Algebraic Reconstruction Technique (ART) • Solving a linear system of equations iteratively • Statistical Reconstruction Technique • Weighted Least Square • Likelihood based iterative Expectation Maximization • Maximum Likelihood Expectation Maximization • Maximum A Posteriori Expectation Maximization Introduction
- 4. Introduction • Estimated Image – Image acquired using projection • Computed Projection and Measured projections are compared • If discrepancy occurs back projection is applied to form updated image • Updated image will be considered as Estimated Image during next iteration • Iteration will be repeated till the discrepancies has been reduced. • Depending on data size and number of iterations the reconstruction time will be more. • To reduce the reconstruction time parallel computing is introduced.
- 5. • Serial Computing • Problem is broken into number of instructions • Instructions are executed sequentially one after other • Parallel Computing • Problem is divided into sub problems • Each Sub problem is broken into number of instructions • Instructions are executed sequentially under a processor • Implemented with many computers generally referred as parallel computers or multi-core processors • Programming Languages, Operating System, Parallel algorithm and compiler that support parallel programming Parallel Computing
- 6. • The multiprocessor can be distributed system or shared memory. • Distributed System • Designed by placing the components on different networked computers • The coordination and communication is done by passing message to one another • Shared Memory • Multiprocessor that has more than one processor inside a single computer itself • Each processor is treated as Thread • Thread reads, writes and processes on data concurrently using common memory • Data, Task and Pipeline are the categories of parallel computing • API used to implement parallel programs are Open Multi-Processing (OMP) and Message Passing Interface (MPI) • MPI – Distributed Systems • OMP – Shared Memory Parallel Computing
- 7. • C++ omp is used in this research work. • Environmental Variable • OMP_DYNAMIC • OMP_NUM_THREADS • OMP_NUM_THREADS=num_threads • OMP_SCHEDULE • Directive • #pragma omp name_of_directives[clause] • Parallel • Used to denote a region to be executed in parallel • If(exp) • Shared(list) • Reduction(operator:list) • for OpenMP
- 8. • Amdahl’s Law • statement of the maximum theoretical speed-up you can ever hope to achieve. S(n) = ts/tp • Quinn’s Notation Speedup and Efficiency time execution Parallel time execution Sequential Speedup f n f f p S 1 / ) 1 ( 1 ) (
- 9. Algebraic Reconstruction Techniques (ART) • In the image reconstruction process, the linear system problems are effectively solved by using one of the iterative methods called ART technique. • ART is a Linear Equation Ax=b • The continuous two dimensional function is an infinite number of projections • The image function f(x,y) is derived based on the finite number of points fj j= 1, 2, . . ., N.
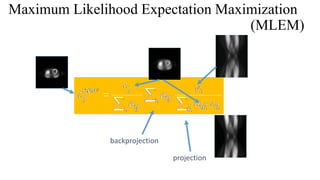
- 10. • An Object Model, System Model, Statistical Model, Cost function and algorithm are the five components of Statistical reconstruction methods. • Weighted Least Square and Likelihood are two group of existing Statistical algorithms. • Expectation Maximization algorithm is generally used category under Likelihood groups. • Each iteration has two steps of actions. One is Expectation normally known as E-step and other is M-Step called as Maximization step. • The MLEM refers to the fact that there is an expectation step that uses current estimates of the unknowns to perform the reconstruction, followed by a maximum likelihood step to update the estimates. Maximum Likelihood Expectation Maximization (MLEM)
- 11. projection backprojection Maximum Likelihood Expectation Maximization (MLEM)
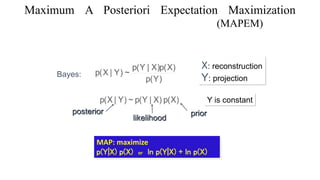
- 12. Maximum A Posteriori Expectation Maximization (MAPEM) • MAPEM is introduced with a prior knowledge as a constraint that favors convergence of the expectation maximization algorithm process called as regularization • The prior is usually chosen to penalize the noisy images. • The goal of the required criterion is simultaneously maximized which leads to a scheme called One Step Late (OSL) algorithm. • The priori term is the derivative of an energy function chosen to enforce smoothing. • At the initial condition the reconstruction method guesses the estimate value that resembles the internal structure, by feeding projection data as input.
- 13. Y is constant posterior likelihood prior X: reconstruction Y: projection Bayes: MAP: maximize p(Y|X) p(X) or ln p(Y|X) + ln p(X) Maximum A Posteriori Expectation Maximization (MAPEM)
- 14. • E-Step Procedure: Estimates the expectation of the missing value i.e. unlabeled class information. This step corresponds to performing classification of each unlabeled document. Probability distribution is calculated using current parameter. • M-Step Procedure: Calculates the maximum likelihood parameters for the current estimate of the complete data. Maximum A Posteriori Expectation Maximization (MAPEM)
- 15. Dataset • Phantom imaging is specially designed object to evaluate, analyze and tune performance of devices • The research has used Shepp Logan Phantom as dataset • It serves as the model of a human head in the development and testing of image reconstruction algorithms 256 X 256
- 16. Sinogram • The sinogram for the considered image set is obtained using the radon function in Matlab. • Radon function produces the raw data that is sinogram of the given image in the specified angles. • The projections are obtained at 180, 150, 120, 90 and 60 angles for the study 60 90 120 150 180
- 17. ART • W, v, p, numIter are the input parameters used • W – Weighted matrix size is size of image x size of projections • v – Vector that hold the size of the output image • p – projection data • numIter – number of Iterations • retV – output parameter used to store the value of the reconstructed pixel values. • Initially the cell density fj = 0 is assumed for blank and fj = 1 for gray screen. • The calculated projection is compared with the measured projection. • If both are equal for all cells and all samples then that is the image obtained at first iteration. • ART is repeatedly done for the specified numIter for all projections p. m m m m m m m m w w w p w f f f ) 1 ( ) 1 ( ) (
- 18. pART • The OpenMP directive #pragma omp parallel creates a multicore environment • The omp_set_num_threads is used to set the number of cores. • 1, 2, 4 or 8 numbers of cores can be opted. • Instead of parallelizing the whole art algorithm just reconstructing region alone has been parallelized. • So as to know the improved time complexity
- 19. MLEM • With the projection data obtained and the Initial guess of the estimate MLEM algorithm is passed as input to reconstruct an image. • MLEM is an iterative reconstruction method based on statistical data and the required iterations have been optimized based on the PSNR value. • This is done by calling MEX function • Time taken to reconstruct an image is noted
- 20. pMLEM • The iterative statistical pMLEM algorithm implemented under the multi-core is considered as parallel version. • Similar steps exist as in sequential version. • MLEM for calculating each pixel value for each projection is done in parallel by calling the MEX function • In the MEX function the number of cores are set to 2, 4 or 8 using the OMP_SET_NUM_THREAD (num_thread) function • Time taken to reconstruct an image is noted
- 21. MAPEM • The algorithm initially reads the projection data, apply E-step and M- step and update the vector. • The E-step, calculates the maximum likelihood based on true value. • The M-step update the values using the value obtained from the E-step to estimate the parameters. • Time taken to reconstruct an image is noted
- 22. pMAPEM • The parallel version of MAPEM implementd on a multi-core environment is termed as pMAPEM. • Same as the sequential operation, but with the help of OpenMP the operation will be functioned in multiple processes. • . In this method the operation will be done in parallel to reduce the time complexity. • At the end the master thread collects all the values from worker thread and updates the value • Time taken to reconstruct an image is noted
- 23. Results
- 24. Results Algorithm 10 12 15 20 30 ART 158 142 124 46 24 MLEM 59 40 51 40 69 MAPEM 61 39 45 29 61 Optimized Number of Iterations
- 25. Results PSNR Algorithm PSNR 10 12 15 20 30 ART 69.3787 69.5936 70.676 70.3131 71.0605 pART 69.3787 69.5936 70.676 70.3131 71.0605 MLEM 69.5807 69.7042 70.5335 70.4742 71.0236 pMLEM 69.5807 69.7042 70.5335 70.4742 71.0236 MAPEM 69.5812 69.7039 70.251 70.3148 71.0151 pMAPEM 69.5812 69.7039 70.251 70.3148 71.0151
- 26. Results Time Taken to Reconstruct an Image Algorithm Cores 10 12 15 20 30 ART 1 1609.1 1699.73 1889.8 918.3131 723.983 pART 2 1118.1 972.613 1365.52 658.447 524.681 4 905.076 866.0894 943.866 444.67 314.839 8 683.986 470.454 557.619 273.9013 195.646 MLEM 1 522.894 462.973 750.215 709.861 2134.4 pMLEM 2 508.943 341.971 743.438 766.535 1987.55 4 375.436 266.157 435.619 550.758 1304.25 8 200.919 179.447 264.467 485.687 797.848 MAPEM 1 726.522 532.309 727.098 532.317 771.465 pMAPEM 2 502.087 332.341 502.65 332.347 463.192 4 398.953 297.146 399.495 297.143 447.483 8 198.488 145.926 199.045 145.934 259.513
- 27. Result
- 28. Results Speed up Calculation Algorithm Cores 10 12 15 20 30 ART 1 1 1 1 1 1 2 1.19581 1.54942 1.54023 1.75870 1.78459 4 1.22511 2.8198 3.15109 2.93728 3.39847 8 1.57189 6.13920 6.11620 7.18971 7.21240 MLEM 1 1 1 1 1 1 2 1.20794 1.73988 1.70430 1.63692 1.61799 4 1.21839 2.38677 2.26052 2.16825 2.17675 8 1.2495 3.14354 3.08499 3.15482 2.89362 MAPEM 1 1 1 1 1 1 2 1.27736 1.97445 1.99581 1.98687 1.99471 4 1.51692 3.91267 3.95574 3.8835 3.91221 8 1.6212 7.50019 7.74031 7.91742 7.71174
- 29. Results
- 30. Summary • The performance measure of MAPEM compared to MLEM and ART • The iterations required to reconstruct an image is lesser than MLEM and higher than ART for small size of images. • The MAPEM and MLEM algorithms results in minimum iteration than ART for large size of images. • MLEM algorithm results better PSNR values compared to MAPEM and ART. • The reconstruction process shows a constant speedup • The applications designed using pART, pMLEM and pMAPEM in this research study shows more promising result.