Benginning Calculus Lecture notes 1 - functions
- 1. Beginning Calculus -Real-Valued Functions - Shahrizal Shamsuddin Norashiqin Mohd Idrus Department of Mathematics, FSMT - UPSI (LECTURE SLIDES SERIES) VillaRINO DoMath, FSMT-UPSI (D0) Real-Valued Functions 1 / 18
- 2. Functions Increasing and Decreasing Functions New Functions From Old Transformations of Functions Important Functions Learning Outcomes Determine the existence of limits of functions Compute the limits of functions Determine the continuity of functions. Connect the idea of limits and continuity of functions. VillaRINO DoMath, FSMT-UPSI (D0) Real-Valued Functions 2 / 18
- 3. Functions Increasing and Decreasing Functions New Functions From Old Transformations of Functions Important Functions Functions De…nition 1 Let X and Y be any two nonempty sets. A function f from X to Y is a rule that assigns each element x 2 X to a unique element y 2 Y . f : X ! Y f (x) = y, x 2 X, y 2 Y x y X Y f VillaRINO DoMath, FSMT-UPSI (D0) Real-Valued Functions 3 / 18
- 4. Functions Increasing and Decreasing Functions New Functions From Old Transformations of Functions Important Functions Domain and Range f (x) = y, x 2 X, y 2 Y Remark 1 x 2 X is called the independent variable, and y 2 Y is the dependent variable. The set X is called the domain of f . The set Y is called the codomain of f . The range of f is the set fy 2 Y j y = f (x) , for some x 2 Xg . The graph of f = f(x, f (x) j x 2 X)g VillaRINO DoMath, FSMT-UPSI (D0) Real-Valued Functions 4 / 18
- 5. Functions Increasing and Decreasing Functions New Functions From Old Transformations of Functions Important Functions Monotonic Functions De…nition 2 Let f be a function on an interval I R (a) f is called monotonic increasing (nondecreasing) on I if f (x1) f (x2) x1 < x2; x1, x2 2 I (1) (b) f is called monotonic decreasing (nonincreasing) on I if f (x1) f (x2) x1 < x2; x1, x2 2 I (2) VillaRINO DoMath, FSMT-UPSI (D0) Real-Valued Functions 5 / 18
- 6. Functions Increasing and Decreasing Functions New Functions From Old Transformations of Functions Important Functions Strictly Increasing and Decreasing Functions De…nition 3 Let f be a function on an interval I R. (a) f is called strictly increasing on I if f (x1) < f (x2) x1 < x2; x1, x2 2 I (3) (b) f is called strictly decreasing on I if f (x1) > f (x2) x1 < x2; x1, x2 2 I (4) Example y x-1-5 2 5 D ecreasing Increasing Constant VillaRINO DoMath, FSMT-UPSI (D0) Real-Valued Functions 6 / 18
- 7. Functions Increasing and Decreasing Functions New Functions From Old Transformations of Functions Important Functions Example Each of the functions f , g, h in the table below is increasing, but each increases in a di¤erent way. Match each function with its possible graph. x f (x) g (x) h (t) 1 23 10 2.2 2 24 20 2.5 3 26 20 2.8 4 29 37 3.1 5 33 44 3.4 6 38 50 3.7 (a) (b) (c) VillaRINO DoMath, FSMT-UPSI (D0) Real-Valued Functions 7 / 18
- 8. Functions Increasing and Decreasing Functions New Functions From Old Transformations of Functions Important Functions Algebra of Functions De…nition 4 Given two functions f and g. De…ne f + g, f g, f g, and f g as follows (a) (f + g) (x) = f (x) + g (x) . (b) (f g) (x) = f (x) g (x) . (c) (f g) (x) = f (x) g (x) . (d) f g (x) = f (x) g (x) , g (x) 6= 0. VillaRINO DoMath, FSMT-UPSI (D0) Real-Valued Functions 8 / 18
- 9. Functions Increasing and Decreasing Functions New Functions From Old Transformations of Functions Important Functions Composition of Functions De…nition 5 Let f : X ! Y 0 and g : Y ! Z be functions. De…ne a new function g f : X ! Z as follows: (g f ) (x) = g (f (x)) , 8x 2 X (5) The function g f is called the composition of f and g. VillaRINO DoMath, FSMT-UPSI (D0) Real-Valued Functions 9 / 18
- 10. Functions Increasing and Decreasing Functions New Functions From Old Transformations of Functions Important Functions Inverse of Functions De…nition 6 Let f : X ! Y be a one-to-one correspondence function. Then f has an inverse f 1 and, f 1 (y) = x , y = f (x) x 2 X, y 2 Y (6) VillaRINO DoMath, FSMT-UPSI (D0) Real-Valued Functions 10 / 18
- 11. Functions Increasing and Decreasing Functions New Functions From Old Transformations of Functions Important Functions Even and Odd Functions De…nition 7 For any function f , (a) f is called an even function if f ( x) = f (x) , for all x in the domain. (b) f is called an odd function if f ( x) = f (x) , for all x in the domain. VillaRINO DoMath, FSMT-UPSI (D0) Real-Valued Functions 11 / 18
- 12. Functions Increasing and Decreasing Functions New Functions From Old Transformations of Functions Important Functions Example f (x) = x2 and g (x) = ex2 are examples of even functions; h (x) = x3 and l (x) = x1/3 are examples of odd functions. y x (-x, y) (x, y) y x (-x, -y) (x, y) y x (x, -y) (x, y) VillaRINO DoMath, FSMT-UPSI (D0) Real-Valued Functions 12 / 18
- 13. Functions Increasing and Decreasing Functions New Functions From Old Transformations of Functions Important Functions Re‡ecting De…nition 8 Let y = f (x). Then, (a) the re‡ection of the graph of y = f (x) in the x axis is the graph of y = f (x) . (b) the re‡ection of the graph of y = f (x) in the y axis is the graph of y = f ( x) . VillaRINO DoMath, FSMT-UPSI (D0) Real-Valued Functions 13 / 18
- 14. Functions Increasing and Decreasing Functions New Functions From Old Transformations of Functions Important Functions Example The re‡ection of f (x) = x2 in the x axis is the graph of f (x) = x2. -4 -2 2 4 -20 -10 10 20 x y f(x) g(x) = -f(x) VillaRINO DoMath, FSMT-UPSI (D0) Real-Valued Functions 14 / 18
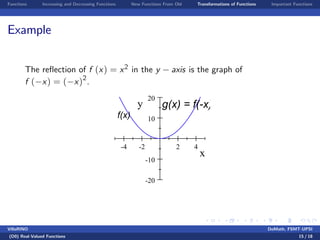
- 15. Functions Increasing and Decreasing Functions New Functions From Old Transformations of Functions Important Functions Example The re‡ection of f (x) = x2 in the y axis is the graph of f ( x) = ( x)2 . -4 -2 2 4 -20 -10 10 20 x y g(x) = f(-x) f(x) VillaRINO DoMath, FSMT-UPSI (D0) Real-Valued Functions 15 / 18
- 16. Functions Increasing and Decreasing Functions New Functions From Old Transformations of Functions Important Functions Shifting De…nition 9 Let c > 0 is any constant. Vertical and horizontal shifts in the graph of y = f (x) are represented as follows: (a) Vertical shift c units upward: g (x) = f (x) + c; (b) Vertical shift c units downward: g (x) = f (x) c; (c) Horizontal shift c units to the right: g (x) = f (x c) (d) Horizontal shift c units to the left: g (x) = f (x + c) VillaRINO DoMath, FSMT-UPSI (D0) Real-Valued Functions 16 / 18
- 17. Functions Increasing and Decreasing Functions New Functions From Old Transformations of Functions Important Functions Example Let f (x) = x3. Then the graph of a function: g (x) = x3 + 3 = f (x) + 3 is obtained by shifting the graph of f (x) = x3, 3 unit upward. -4 -2 2 4 -4 -2 2 4 x y f(x) g(x) = f(x)+3 g (x) = x3 3 = f (x) 3 is obtained by shifting the graph of f (x) = x3, 3 unit downward. 4y f(x)VillaRINO DoMath, FSMT-UPSI (D0) Real-Valued Functions 17 / 18
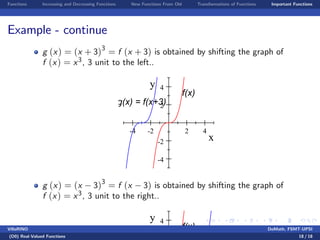
- 18. Functions Increasing and Decreasing Functions New Functions From Old Transformations of Functions Important Functions Example - continue g (x) = (x + 3)3 = f (x + 3) is obtained by shifting the graph of f (x) = x3, 3 unit to the left.. -4 -2 2 4 -4 -2 2 4 x y f(x) g(x) = f(x+3) g (x) = (x 3)3 = f (x 3) is obtained by shifting the graph of f (x) = x3, 3 unit to the right.. 4y f(x)VillaRINO DoMath, FSMT-UPSI (D0) Real-Valued Functions 18 / 18