Lecture-2-Relational-Algebra-and-SQL-Advanced-DataBase-Theory-MS.pdf

Advanced Database Theory
Lecture 2: Relational Algebra-I
MS Semester-III
Dr. Syed Asad Raza Kazmi
Computer Science Department
GC University Lahore
February 13, 2017

Relational Database Schemas
Relational Algebra
Relation Schemas and Relational Database Schemas
Relation Schemas and Relational Database Schemas
• A k-ary relation schema
R(A1, A2, . . . , AK ) is a set {A1, A2, . . . , Ak }
of k attributes.
• COURSE(course-no, course-name, term, instructor, room, time)
• CITY-INFO(name, state, population)
Thus, a k-ary relation schema is a blueprint, a template for some k-ary relation.
• An instance of a relation schema is a relation conforming to the schema
(arities match; also, in DBMS, data types of attributes match).
• A relational database schema is a set of relation schemas
Ri (A1, A2, . . . , Ak )
for 1 ⩽ i ⩽ m.
• A relational database instance of a relational schema is a set of relations Ri each
of which is an instance of the relation schema
Ri , 1 ⩽ i ⩽ m.
Dr. Syed Asad Raza Kazmi Advanced Database Theory

Relational Algebra
Relational Database Schemas - Examples
Example 1 (Relational Database Schemas - Examples)
• BANKING relational database schema with relation schemas
• CHECKING-ACCOUNT(branch, acc-no, cust-id, balance)
• SAVINGS-ACCOUNT(branch, acc-no, cust-id, balance)
• CUSTOMER(cust-id, name, address, phone, email)
• . . .
• UNIVERSITY relational database schema with relation schemas
• STUDENT(student-id, student-name, major, status)
• FACULTY(faculty-id, faculty-name, dpt, title, salary)
• COURSE(course-no, course-name, term, instructor)
• ENROLLS(student-id, course-no, term)
• . . .

Relational Algebra
Schemas vs. Instances
Keep in mind that there is a clear distinction between
• relation schemas and instances of relation schemas and between
• relational database schemas and relational database instances.
Syntactic Notion:
.
• Relation Schema
.
• Relational Database Schema
Semantic Notion
(discrete mathematics notion)
• Instance of a relation schema (i.e., a
relation)
• Relational database instance (i.e., a
database)

Relational Algebra
Programming Languages Paradigms
Programming Languages Paradigms
There are two main paradigms of programming languages: imperative (or
procedural) languages and declarative languages.
1 Imperative (Procedural) Languages: programs are expressed by specifying
how the task is to be accomplished (sequence of operations).
Example 2
FORTRAN, C,...
2 Declarative Languages: programs are expressed by specifying what has to
be accomplished (as opposed to how).
Example 3
LISP (functional programming), PROLOG (logic programming),...

Relational Algebra
Query Languages for the Relational Data Model
Query Languages for the Relational Data Model
Codd introduced two different query languages for the relational data model:
1 Relational Algebra, which is a procedural language.
• It is an algebraic formalism in which queries are expressed by applying a
sequence of operations to relations.
2 Relational Calculus, which is a declarative language.
• It is a logical formalism in which queries are expressed as formulas of
first-order logic.
Codd’s Theorem:
Relational Algebra and Relational Calculus are essentially equivalent in
terms of expressive power.
(but what does this really mean?)

Relational Algebra
Declarative vs Procedural
• In our queries, we ask what we want to see in the output.
• But we do not say how we want to get this output.
• Thus, query languages are declarative: they specify what is needed in the
output, but do not say how to get it.
• Database system figures out how to get the result, and gives it to the user.
• Database system operates internally with different, procedural languages,
which specify how to get the result.

Relational Algebra
Declarative vs Procedural: example
Declarative vs Procedural: example

Relational Algebra
Declarative vs Procedural: another example
Declarative vs Procedural: another example

Relational Algebra
• Theoretical languages:
1 Declarative: relational calculus, rule-based queries
2 Procedural: relational algebra
• Practical languages: mix of both, but mostly one uses declarative features.

Relational Algebra
Why Study the Relational Model?
Why Study the Relational Model?
• Most widely used model.
• Vendors: IBM, Informix, Microsoft, Oracle, Sybase, etc.
• “Legacy systems” in older models
• E.G., IBMs IMS
• Recent competitor: object-oriented model
• ObjectStore, Versant, Ontos
• A synthesis emerging: object-relational model
• Informix Universal Server, UniSQL, O2, Oracle, DB2

Relational Algebra
Relational Database: Definitions
Relational Database: Definitions
• Relational database: a set of relations
• Relation: made up of 2 parts:
1 Instance : a table, with rows and columns.
# Rows = cardinality, # fields = degree / arity.
2 Schema : specifies name of relation, plus name and type of each column.
Example 4
Students(sid: string, name: string, login: string, age: integer, gpa: real).
• Can think of a relation as a set of rows or tuples
(i.e., all rows are distinct).

Relational Algebra
Example Instance of Students Relation
Example Instance of Students Relation
• Cardinality = 3, degree = 5, all rows distinct
• Do all columns in a relation instance have to be distinct?

Relational Algebra
Relations and Attributes
Figure 1: Anatomy of Relation

Relational Algebra
Relation Film
Figure 2: Relational Model

Relational Algebra
Terminology
Terminology
attributes distinct columns in a relation. Each attribute has a associated
domain.
cardinality number of rows in a table
degree number of columns in a table
domain a set of different values with the same property types (”data type”).
The NULL value is possible if not explicitly stated otherwise.
relation a table (visual view) with a unique name. a two dimensional,
inhomogeneous matrix (mathematical view). The ordering of tuples
in a relation is important.
schema schema of a relation refers to the permanent characteristics of a
relation
tuple the set of values in a row. Those values are instances of the
attribute domain.

Relational Algebra
Tabular Representation
Tabular Representation
The table
A B C
1 3 2
1 4 1
2 4 2
2 3 1
is shorthand for the following set of tuples:







{A : 1, B : 3, C : 2},
{A : 1, B : 4, C : 1},
{A : 2, B : 4, C : 2},
{A : 2, B : 3, C : 1}







.

Relational Algebra
Notation
Notation
• Every tuple is a total function from a set of attributes to the set of
constants.
• Therefore, if t = {A : 1, B : 3, C : 2},
then t(B) = 3 and t[{A, C}] = {A : 1, C : 2}.
• Note that t(B) is a constant, and t[{A, C}] a tuple.
• In database theory, we often omit curly brackets ({}) and union symbols (∪)
in the notation of sets. For example, if A, B, C, D are attributes and
X = {A, B}, then XCD denotes the set {A, B, C, D}.

Relational Algebra
Algebraic Operators
Algebraic Operators
• Unary operators: Select, Project, Rename
• Binary operators: Join, Union, Difference
• Unary operators take in a single relation; binary operators take in two
relations.
NOTE
Every operator returns a single relation.

Relational Algebra
Algebraic Operators Symbols
Algebraic Operators Symbols
σ selection
π projection
∪ union
− difference
× cartesian product
ρ rename
./ join
n left semi join
o right semi join
∩ intersection
÷ division

Relational Algebra
Relational Algebra
Definition 5 (Relational Algebra)
Relation Algebra is a procedural relationally complete language. A language that
can define any relation definable in relational calculus is relationally complete.
Using this algebra we perform set operations on relations.

Relational Algebra
Relations: terminology
Relations: terminology
• Degree of a relation: how long the tuples are, or how many columns the table has
• In the first example (name,email) degree of the relation is 2
• In the second example (name,email,telephone) degree of the relation is 3
• Often relations of degree 2 are called binary, relations of degree 3 are called
ternary etc.
• Cardinality of the relation: how many different tuples are there, or how many different
rows the table has.
Example-1
This is a relation between people and email
addresses
NAME Email
Hameed ham@gcu.edu.pk
Ali ali@gcu.edu.pk
Baber bab@gcu.edu.pk
Example-2
This is a relation between people, email
addresses and phone numbers
NAME Email Phone
Hameed ham@gcu.edu.pk 123456
Ali ali@gcu.edu.pk 4567843
Baber bab@gcu.edu.pk 0336245

Relational Algebra
Relations
Relations
• Each value in the first column is a name, each value in the second column is
an email address.
• In general, each column has a
domain a set from which all possible values can come
Example-1
This is a relation between people and email addresses
NAME Email
Ali ali@gcu.edu.pk

Relational Algebra
Relational Model:
Data Manipulation
Data Manipulation
• Data is represented as relations.
• Manipulation of data (query and update operations) corresponds to
operations on relations
• Relational algebra describes those operations. They take relations as
arguments and produce new relations.
• Think of numbers and corresponding operators +, −, or booleans and
corresponding operators &, |, ! (and, or, not).
• Relational algebra contains two kinds of operators: common set-theoretic
ones and operators specific to relations
(for example projecting on one of the columns).

Relational Algebra
Union
Union
• Standard set-theoretic definition of union:
A ∪ B = {x : x ∈ A or x ∈ B}
Example
{a, b, c} ∪ {a, d, e} = {a, b, c, d, e}
• For relations, we want the result to be a relation again: a set
R ⊆ D1 × D2 × · · · × Dn
for some n and domains D1, D2, . . . , Dn
(or, in other words, a proper table, with each column associated with a single
domain of values).
• So we require in order to take a union of relations R and S that R and S have the
same number of columns and that corresponding columns have the same domains.

Relational Algebra
Union-compatible relations
Definition 6 (Union-compatible relations)
Two relations R and S are union-compatible if they have the same number of
columns and corresponding columns have the same domains.

Relational Algebra
Example: not union-compatible
not union-compatible
Example-1
This is a relation between people and email
addresses
NAME Email
Ali ali@gcu.edu.pk
Example-2
This is a relation between people, email
addresses and phone numbers
NAME Email Phone
Hameed ham@gcu.edu.pk 123456
Ali ali@gcu.edu.pk 4567843
Baber bab@gcu.edu.pk 0336245
different number of columns

Relational Algebra
Example: not union-compatible
not union-compatible
Example-1
NAME Email
Ali ali@gcu.edu.pk
Example-2
NAME DOB
Hameed 1984
Ali 1983
Baber 1990
different domains for the second column

Relational Algebra
Example: union-compatible
union-compatible
Example-1
NAME DOB
Aleena 1987
Fatima 1994
Marium 1995
Example-2
NAME DOB
Hameed 1984
Ali 1983
Baber 1990
union-compatible: Same number of Column and having same type

Relational Algebra
Union of two relations
Union of two relations
• Let R and S be two union-compatible relations. Then their union R ∪ S is a
relation which contains tuples from both relations:
R ∪ S = {x : x ∈ R or x ∈ S}.
NOTE
• Note that union is a partial operation on relations: it is only defined for
some (compatible) relations, not for all of them.
• Similar to division for numbers (result of division by 0 is not defined).

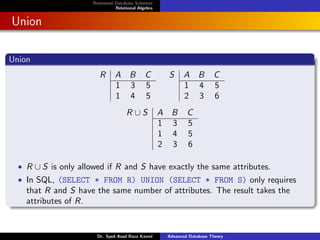
Relational Algebra
Union
Union
R A B C
1 3 5
1 4 5
S A B C
1 4 5
2 3 6
R ∪ S A B C
1 3 5
1 4 5
2 3 6
• R ∪ S is only allowed if R and S have exactly the same attributes.
• In SQL, (SELECT * FROM R) UNION (SELECT * FROM S) only requires
that R and S have the same number of attributes. The result takes the
attributes of R.

Relational Algebra
Difference of Two Relations
Difference of Two Relations
Let R and S be two union-compatible relations. Then their difference R - S is a
relation which contains tuples which are in R but not in S:
R − S = {x : x ∈ R and x 6∈ S}.
NOTE
Note that difference is also a partial operation on relations.

Relational Algebra
Difference
Difference
R A B C
1 3 5
1 4 5
S A B C
1 4 5
2 3 6
R − S A B C
1 3 5
• R − S is only allowed if R and S have exactly the same attributes.
• In SQL, (SELECT * FROM R) MINUS (SELECT * FROM S) only requires
that R and S have the same number of attributes. The result takes the
attributes of R.

Relational Algebra
Intersection of two relations
Intersection of Two Relations
Let R and S be two union-compatible relations. Then their intersection a relation
R ∩ S which contains tuples which are both in R and S:
R ∩ S = {x : x ∈ R and x ∈ S}
NOTE
1 Note that intersection is also a partial operation on relations.
2 Set-intersection is defined in terms of set-difference:
r ∩ s = r − (r − s)
3 Thus, set-intersection must follow the same compatibility rules as
set-difference: same arity, corresponding domains.

Relational Algebra
Cartesian Product
Definition 7 (Cartesian Product)
1 Cartesian product is a total operation on relations.
2 Usual set theoretic definition of product:
R × S = {< x, y >: x ∈ R, y ∈ S}
Example 8
Under the standard definition, if
< Cheese, 1.34 >∈ R and < Soap, 1.00 >∈ S
then
<< Cheese, 1.34 >, < Soap, 1.00 >>∈ R × S
(the result is a pair of tuples).

Relational Algebra
Extended Cartesian product
Extended Cartesian product
• Extended Cartesian product flattens the result in a 4-element tuple:
< Cheese, 1.34, Soap, 1.00 >
Definition 9 (Extended Cartesian Product of Relations)
Let R be a relation with column domains {A1, . . . , An} and
S a relation with column domains {B1, . . . , Bm}
Then their Extended Cartesian product R × S is a relation
R × S = {< c1, . . . , cn, cn+1, . . . , cn+m >:< c1, . . . , cn >∈ R, < cn+1, . . . , cn+m >∈ S}

Relational Algebra
Example

Relational Algebra
The Projection Operator
The Projection Operator
Motivation:
It is often the case that, given a table R, one wants to:
• Rearrange the order of the columns
• Suppress some columns
• Do both of the above.
Fact
Fact: The Projection Operation is tailored for this task

Relational Algebra
Projection

Relational Algebra
Projection
Projection
Let R be a relation with n columns, and X is a set of column identifiers (at the
moment, we will use numbers, but later we will give then names, like Email, or
Telephone). Then projection of R on X is a new relation
πX (R)
which only has columns from X.
Example 10
For example,
π1,2(R)
is a table with only the 1st and 2nd columns from R.

Relational Algebra
Projection
Definition 11 (Projection)
The projection is an operation to reduce a relation containing containing only
specified columns. All duplicate result tuples will be removed.
Projection Syntax
project <source relation name>
over <list of attribute names>
giving <result relation name>
The list of attribute names shall be given as comma separated list.

Relational Algebra
Project
Project
R A B C
1 3 1
1 3 2
1 4 3
1 4 4
2 3 5
π{A,B}(R) A B
1 3
1 4
2 3
• Since relations are sets, duplicates are removed.
• Note that SELECT A, B FROM R in SQL does not remove duplicates.

Relational Algebra
Selection
Selection
• Chooses tuples that satisfy some condition
• σc (R) : only leaves tuples t for which c(t) is true
• Conditions: conjunctions of
1 R.A = R.A0
-two attributes are equal
2 R.A = constant the value of an attribute is a given constant
Same as above but with 6= instead of =
Example 12
• Movies.Actor=Movies.Director
Movies.Actor 6= Nicholson
Movies.Actor=Movies.Director ∧ Movies.Actor=Nicholson
• Provides the user with a view of data by hiding tuples that do not satisfy the
condition the user wants.

Relational Algebra
Selection

Relational Algebra
Select
Select
R A B C
1 3 2
1 4 1
2 4 2
2 3 1
σA=“1”(R) A B C
1 3 2
1 4 1
σA=C (R) A B C
1 4 1
2 4 2
• This is like SELECT * FROM R WHERE A="1" in SQL.

Relational Algebra
Combining Selection and Projection

Relational Algebra
PROJECT Operation Properties
PROJECT Operation Properties
• The number of tuples in the result of projection
π<list>(R)
is always less or equal to the number of tuples in R
• If the list of attributes includes a key of R, then the number of tuples in the
result of PROJECT is equal to the number of tuples in R
• PROJECT is not commutative
π<list1>(π<list2>(R)) = π<list1>(R)
as long as < list2 > contains the attributes in < list1 >

Relational Algebra
References I
• Slides of Relational Databases, Logic, and Complexity by Phokion G. Kolaitis; University of California, Santa Cruz & IBM Research-Almaden
• Foundations of Databases Relational Query Languages; Slides from Werner Nutt, Thomas Eiter and Leonid Libkin
• Foundation of Database by Serge Abiteboul, Richard Hull, Victor Vianu

After all... tomorrow is another day.
(Scarlett O’Hara, “Gone with the Wind”)

Lecture-2-Relational-Algebra-and-SQL-Advanced-DataBase-Theory-MS.pdf

More Related Content

Similar to Lecture-2-Relational-Algebra-and-SQL-Advanced-DataBase-Theory-MS.pdf (20)

More from ssuserf86fba (16)

Recently uploaded (20)

Lecture-2-Relational-Algebra-and-SQL-Advanced-DataBase-Theory-MS.pdf