Lecture5 kernel svm

Lecture 5: SVM as a kernel machine
Stéphane Canu
stephane.canu@litislab.eu
Sao Paulo 2014
March 4, 2014

Plan
1 Kernel machines
Non sparse kernel machines
sparse kernel machines: SVM
SVM: variations on a theme
Sparse kernel machines for regression: SVR

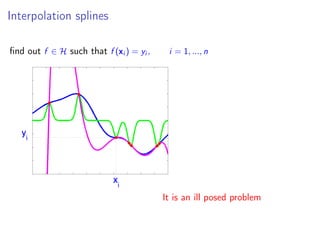
Interpolation splines
ﬁnd out f ∈ H such that f (xi ) = yi , i = 1, ..., n
It is an ill posed problem

Interpolation splines: minimum norm interpolation
min
f ∈H
1
2 f 2
H
such that f (xi ) = yi , i = 1, ..., n
The lagrangian (αi Lagrange multipliers)
L(f , α) =
1
2
f 2
−
n
i=1
αi f (xi ) − yi

min
f ∈H
1
2 f 2
H
L(f , α) =
1
2
f 2
−
n
i=1
αi f (xi ) − yi
optimality for f : f L(f , α) = 0 ⇔ f (x) =
n
i=1
αi k(xi , x)

min
f ∈H
1
2 f 2
H
L(f , α) =
1
2
f 2
−
n
i=1
αi f (xi ) − yi
optimality for f : f L(f , α) = 0 ⇔ f (x) =
n
i=1
αi k(xi , x)
dual formulation (remove f from the lagrangian):
Q(α) = −
1
2
n
i=1
n
j=1
αi αj k(xi , xj ) +
n
i=1
αi yi solution: max
α∈IRn
Q(α)
Kα = y

Representer theorem
Theorem (Representer theorem)
Let H be a RKHS with kernel k(s, t). Let be a function from X to IR
(loss function) and Φ a non decreasing function from IR to IR. If there
exists a function f ∗minimizing:
f ∗
= argmin
f ∈H
n
i=1
yi , f (xi ) + Φ f 2
H
then there exists a vector α ∈ IRn
such that:
f ∗
(x) =
n
i=1
αi k(x, xi )
it can be generalized to the semi parametric case: +
m
j=1 βj φj (x)

Elements of a proof
1 Hs = span{k(., x1), ..., k(., xi ), ..., k(., xn)}
2 orthogonal decomposition: H = Hs ⊕ H⊥ ⇒ ∀f ∈ H; f = fs + f⊥
3 pointwise evaluation decomposition
f (xi ) = fs(xi ) + f⊥(xi )
= fs(.), k(., xi ) H + f⊥(.), k(., xi ) H
=0
= fs(xi )
4 norm decomposition f 2
H = fs
2
H + f⊥
2
H
≥0
≥ fs
2
H
5 decompose the global cost
n
i=1
yi , f (xi ) + Φ f 2
H =
n
i=1
yi , fs(xi ) + Φ fs
2
H + f⊥
2
H
≥
n
i=1
yi , fs(xi ) + Φ fs
2
H
6 argmin
f ∈H
= argmin
f ∈Hs
.

Smooting splines
introducing the error (the slack) ξ = f (xi ) − yi
(S)



min
f ∈H
1
2 f 2
H + 1
2λ
n
i=1
ξ2
i
such that f (xi ) = yi + ξi , i = 1, n
three equivalent deﬁnitions
(S ) min
f ∈H
1
2
n
i=1
f (xi ) − yi
2
+
λ
2
f 2
H



min
f ∈H
1
2
f 2
H
such that
n
i=1
f (xi ) − yi
2
≤ C



min
f ∈H
n
i=1
f (xi ) − yi
2
such that f 2
H ≤ C
using the representer theorem
(S ) min
α∈IRn
1
2
Kα − y 2
+
λ
2
α Kα
solution: (S) ⇔ (S ) ⇔ (S ) ⇔ (K + λI)α = y
= ridge regression:
min
α∈IRn
1
2
Kα − y 2
+
λ
2
α α

Kernel logistic regression
inspiration: the Bayes rule
D(x) = sign f (x) + α0 =⇒ log IP(Y =1|x)
IP(Y =−1|x) = f (x) + α0
probabilities:
IP(Y = 1|x) =
expf (x)+α0
1 + expf (x)+α0
IP(Y = −1|x) =
1
1 + expf (x)+α0
Rademacher distribution
L(xi , yi , f , α0) = IP(Y = 1|xi )
yi +1
2 (1 − IP(Y = 1|xi ))
1−yi
2
penalized likelihood
J(f , α0) = −
n
i=1
log L(xi , yi , f , α0) +
λ
2
f 2
H
=
n
i=1
log 1 + exp−yi (f (xi )+α0)
+
λ
2
f 2
H

Kernel logistic regression (2)
(R)



min
f ∈H
1
2 f 2
H + 1
λ
n
i=1
log 1 + exp−ξi
with ξi = yi (f (xi ) + α0) , i = 1, n
Representer theorem
J(α, α0) = 1I log 1I + expdiag(y)Kα+α0y
+
λ
2
α Kα
gradient vector anf Hessian matrix:
αJ(α, α0) = K y − (2p − 1I) + λKα
HαJ(α, α0) = Kdiag p(1I − p) K + λK
solve the problem using Newton iterations
αnew
= αold
+ Kdiag p(1I − p) K + λK
−1
K y − (2p − 1I) + λα

Let’s summarize
pros
Universality
from H to IRn
using the representer theorem
no (explicit) curse of dimensionality
splines O(n3) (can be reduced to O(n2))
logistic regression O(kn3) (can be reduced to O(kn2)
no scalability!
sparsity comes to the rescue!

Roadmap
1 Kernel machines
Non sparse kernel machines
sparse kernel machines: SVM
SVM: variations on a theme
Sparse kernel machines for regression: SVR
Stéphane Canu (INSA Rouen - LITIS) March 4, 2014 11 / 38

SVM in a RKHS: the separable case (no noise)



max
f ,b
m
with yi f (xi ) + b ≥ m
and f 2
H = 1
⇔
min
f ,b
1
2 f 2
H
with yi f (xi ) + b ≥ 1
3 ways to represent function f
f (x)
in the RKHS H
=
d
j=1
wj φj (x)
d features
=
n
i=1
αi yi k(x, xi )
n data points
min
w,b
1
2 w 2
IRd = 1
2 w w
with yi w φ(xi ) + b ≥ 1
⇔
min
α,b
1
2 α Kα
with yi α K(:, i) + b ≥ 1

using relevant features...
a data point becomes a function x −→ k(x, •)

Representer theorem for SVM
min
f ,b
1
2 f 2
H
with yi f (xi ) + b ≥ 1
Lagrangian
L(f , b, α) =
1
2
f 2
H −
n
i=1
αi yi (f (xi ) + b) − 1 α ≥ 0
optimility condition: f L(f , b, α) = 0 ⇔ f (x) =
n
i=1
αi yi k(xi , x)
Eliminate f from L:



f 2
H =
n
i=1
n
j=1
αi αj yi yj k(xi , xj )
n
i=1
αi yi f (xi ) =
n
i=1
n
j=1
αi αj yi yj k(xi , xj )
Q(b, α) = −
1
2
n
i=1
n
j=1
αi αj yi yj k(xi , xj ) −
n
i=1
αi yi b − 1

Dual formulation for SVM
the intermediate function
Q(b, α) = −
1
2
n
i=1
n
j=1
αi αj yi yj k(xi , xj ) − b
n
i=1
αi yi +
n
i=1
αi
max
α
min
b
Q(b, α)
b can be seen as the Lagrange multiplier of the following (balanced)
constaint n
i=1 αi yi = 0 which is also the optimality KKT condition on b
Dual formulation



max
α∈IRn
−1
2
n
i=1
n
j=1
αi αj yi yj k(xi , xj ) +
n
i=1
αi
such that
n
i=1
αi yi = 0
and 0 ≤ αi , i = 1, n

SVM dual formulation
Dual formulation



max
α∈IRn
−1
2
n
i=1
n
j=1
αi αj yi yj k(xi , xj ) +
n
i=1
αi
with
n
i=1
αi yi = 0 and 0 ≤ αi , i = 1, n
The dual formulation gives a quadratic program (QP)
min
α∈IRn
1
2 α Gα − I1 α
with α y = 0 and 0 ≤ α
with Gij = yi yj k(xi , xj )
with the linear kernel f (x) =
n
i=1 αi yi (x xi ) =
d
j=1 βj xj
when d is small wrt. n primal may be interesting.

the general case: C-SVM
Primal formulation
(P)



min
f ∈H,b,ξ∈IRn
1
2 f 2
+ C
p
n
i=1
ξp
i
such that yi f (xi ) + b ≥ 1 − ξi , ξi ≥ 0, i = 1, n
C is the regularization path parameter (to be tuned)
p = 1 , L1 SVM
max
α∈IRn
−1
2 α Gα + α 1I
such that α y = 0 and 0 ≤ αi ≤ C i = 1, n
p = 2, L2 SVM
max
α∈IRn
−1
2 α G + 1
C I α + α 1I
such that α y = 0 and 0 ≤ αi i = 1, n
the regularization path: is the set of solutions α(C) when C varies

Data groups: illustration
f (x) =
n
i=1
αi k(x, xi )
D(x) = sign f (x) + b
useless data important data suspicious data
well classiﬁed support
α = 0 0 < α < C α = C

The importance of being support
f (x) =
n
i=1
αi yi k(xi , x)
data
point
α
constraint
value
set
xi useless αi = 0 yi f (xi ) + b > 1 I0
xi support 0 < αi < C yi f (xi ) + b = 1 Iα
xi suspicious αi = C yi f (xi ) + b < 1 IC
Table: When a data point is « support » it lies exactly on the margin.
here lies the eﬃciency of the algorithm (and its complexity)!
sparsity: αi = 0

The active set method for SVM (1)



min
α∈IRn
1
2 α Gα − α 1I
such that α y = 0 i = 1, n
and 0 ≤ αi i = 1, n



Gα − 1I − β + by = 0
α y = 0
0 ≤ αi i = 1, n
0 ≤ βi i = 1, n
αi βi = 0 i = 1, n
αa
0
− − + b
1
1
0
β0
ya
y0
=
0
0
G α − −1I β + b y = 0
Ga
Gi G0
Gi
(1) Gaαa − 1Ia + bya = 0
(2) Gi αa − 1I0 − β0 + by0 = 0
1 solve (1) (ﬁnd α together with b)
2 if α < 0 move it from Iα to I0
goto 1
3 else solve (2)
if β < 0 move it from I0 to Iα
goto 1

The active set method for SVM (2)
Function (α, b, Iα) ←Solve_QP_Active_Set(G, y)
% Solve minα 1/2α Gα − 1I α
% s.t. 0 ≤ α and y α = 0
(Iα, I0, α) ← initialization
while The_optimal_is_not_reached do
(α, b) ← solve
Gaαa − 1Ia + bya
ya αa
= 0
if ∃i ∈ Iα such that αi < 0 then
α ← projection( αa, α)
move i from Iα to I0
else if ∃j ∈ I0 such that βj < 0 then
use β0 = y0(Ki αa + b1I0) − 1I0
move j from I0 to Iα
else
The_optimal_is_not_reached ← FALSE
end if
end while
α
αold
αnew
Projection step of the active
constraints algorithm
d = alpha - alphaold;
alpha = alpha + t * d;
Caching Strategy
Save space and computing time by computing only the needed parts of kernel matrix G

Two more ways to derivate SVM
Using the hinge loss
min
f ∈H,b∈IR
1
p
n
i=1
max 0, 1 − yi (f (xi ) + b)
p
+
1
2C
f 2
Minimizing the distance between the convex hulls



min
α
u − v 2
H
with u(x) =
{i|yi =1}
αi k(xi , x), v(x) =
{i|yi =−1}
αi k(xi , x)
and
{i|yi =1}
αi = 1,
{i|yi =−1}
αi = 1, 0 ≤ αi i = 1, n
f (x) =
2
u − v 2
H
u(x) − v(x) and b =
u 2
H − v 2
H
u − v 2
H

Regularization path for SVM
min
f ∈H
n
i=1
max(1 − yi f (xi ), 0) +
λo
2
f 2
H
Iα is the set of support vectors s.t. yi f (xi ) = 1;
∂f J(f ) =
i∈Iα
γi yi K(xi , •) −
i∈I1
yi K(xi , •) + λo f (•) with γi ∈ ∂H(1) =] − 1, 0[

Regularization path for SVM
min
f ∈H
n
i=1
max(1 − yi f (xi ), 0) +
λo
2
f 2
H
Iα is the set of support vectors s.t. yi f (xi ) = 1;
∂f J(f ) =
i∈Iα
γi yi K(xi , •) −
i∈I1
yi K(xi , •) + λo f (•) with γi ∈ ∂H(1) =] − 1, 0[
Let λn a value close enough to λo to keep the sets I0, Iα and IC unchanged
In particular at point xj ∈ Iα (fo(xj ) = fn(xj ) = yj ) : ∂f J(f )(xj ) = 0
i∈Iα
γioyi K(xi , xj ) = i∈I1
yi K(xi , xj ) − λo yj
i∈Iα
γinyi K(xi , xj ) = i∈I1
yi K(xi , xj ) − λn yj
G(γn − γo) = (λo − λn)y avec Gij = yi K(xi , xj )
γn = γo + (λo − λn)w
w = (G)−1
y

Example of regularization path
γi ∈] − 1, 0[ yi γi ∈] − 1, −1[ λ =
1
C
γi = − 1
C αi ; performing together estimation and data selection

How to choose and P to get linear regularization path?
the path is piecewise linear ⇔
one is piecewise quadratic
and the other is piecewise linear
the convex case [Rosset & Zhu, 07]
min
β∈IRd
(β) + λP(β)
1 piecewise linearity: lim
ε→0
β(λ + ε) − β(λ)
ε
= constant
2 optimality
(β(λ)) + λ P(β(λ)) = 0
(β(λ + ε)) + (λ + ε) P(β(λ + ε)) = 0
3 Taylor expension
lim
ε→0
β(λ + ε) − β(λ)
ε
= 2
(β(λ)) + λ 2
P(β(λ))
−1
P(β(λ))
2
(β(λ)) = constant and 2
P(β(λ)) = 0

Problems with Piecewise linear regularization path
L P regression classiﬁcation clustering
L2 L1 Lasso/LARS L1 L2 SVM PCA L1
L1 L2 SVR SVM OC SVM
L1 L1 L1 LAD L1 SVM
Danzig Selector
Table: example of piecewise linear regularization path algorithms.
P : Lp =
d
j=1
|βj |p
L : Lp : |f (x) − y|p
hinge (yf (x) − 1)p
+
ε-insensitive
0 if |f (x) − y| < ε
|f (x) − y| − ε else
Huber’s loss:
|f (x) − y|2 if |f (x) − y| < t
2t|f (x) − y| − t2 else

SVM with non symmetric costs
problem in the primal



min
f ∈H,b,ξ∈IRn
1
2 f 2
H + C+
{i|yi =1}
ξp
i + C−
{i|yi =−1}
ξp
i
with yi f (xi ) + b ≥ 1 − ξi , ξi ≥ 0, i = 1, n
for p = 1 the dual formulation is the following:
max
α∈IRn
−1
2 α Gα + α 1I
with α y = 0 and 0 ≤ αi ≤ C+
or C−
i = 1, n

ν-SVM and other formulations...
ν ∈ [0, 1]
(ν)



min
f ,b,ξ,m
1
2 f 2
H + 1
np
n
i=1
ξp
i − νm
with yi f (xi ) + b ≥ m − ξi , i = 1, n,
and m ≥ 0, ξi ≥ 0, i = 1, n,
for p = 1 the dual formulation is:



max
α∈IRn
−1
2 α Gα
with α y = 0 et 0 ≤ αi ≤ 1
n i = 1, n
and ν ≤ α 1I
C = 1
m

Generalized SVM
min
f ∈H,b∈IR
n
i=1
max 0, 1 − yi (f (xi ) + b) +
1
C
ϕ(f ) ϕ convex
in particular ϕ(f ) = f p
p with p = 1 leads to L1 SVM.



min
α∈IRn,b,ξ
1I β + C1I ξ
with yi
n
j=1
αj k(xi , xj ) + b ≥ 1 − ξi ,
and −βi ≤ αi ≤ βi , ξi ≥ 0, i = 1, n
with β = |α|. the dual is:



max
γ,δ,δ∗∈IR3n
1I γ
with y γ = 0, δi + δ∗
i = 1
n
j=1 γj k(xi , xj ) = δi − δ∗
i , i = 1, n
and 0 ≤ δi , 0 ≤ δ∗
i , 0 ≤ γi ≤ C, i = 1, n
Mangassarian, 2001

K-Lasso (Kernel Basis pursuit)
The Kernel Lasso
(S1) min
α∈IRn
1
2 Kα − y 2
+ λ
n
i=1
|αi |
Typical parametric quadratic program (pQP) with αi = 0
Piecewise linear regularization path
The dual:
(D1)
min
α
1
2 Kα 2
such that K (Kα − y) ≤ t
The K-Danzig selector can be treated the same way
require to compute K K - no more function f !

Support vector regression (SVR)
Lasso’s dual adaptation:
min
α
1
2 Kα 2
s. t. K (Kα − y) ≤ t
min
f ∈H
1
2 f 2
H
s. t. |f (xi ) − yi | ≤ t, i = 1, n
The support vector regression introduce slack variables
(SVR)
min
f ∈H
1
2 f 2
H + C |ξi |
such that |f (xi ) − yi | ≤ t + ξi 0 ≤ ξi i = 1, n
a typical multi parametric quadratic program (mpQP)
piecewise linear regularization path
α(C, t) = α(C0, t0) + (
1
C
−
1
C0
)u +
1
C0
(t − t0)v
2d Pareto’s front (the tube width and the regularity)

Support vector regression illustration
0 1 2 3 4 5 6 7 8
−1
−0.8
−0.6
−0.4
−0.2
0
0.2
0.4
0.6
0.8
1
Support Vector Machine Regression
x
y
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5
−1.5
−1
−0.5
0
0.5
1
1.5
Support Vector Machine Regression
x
y
C large C small
there exists other formulations such as LP SVR...

SVM reduction (reduced set method))
objective: compile the model
f (x) =
ns
i=1
αi k(xi , x), ns n, ns too big
compiled model as the solution of: g(x) =
nc
i=1
βi k(zi , x), nc ns
β, zi and c are tuned by minimizing:
min
β,zi
g − f 2
H
where
min
β,zi
g − f 2
H = α Kx α + β Kz β − 2α Kxz β
some authors advice 0, 03 ≤ nc
ns
≤ 0, 1
solve it by using use (stochastic) gradient (its a RBF problem)
Burges 1996, Ozuna 1997, Romdhani 2001

logistic regression and the import vector machine
Logistic regression is NON sparse
kernalize it using the dictionary strategy
Algorithm:
ﬁnd the solution of the KLR using only a subset S of the data
build S iteratively using active constraint approach
this trick brings sparsity
it estimates probability
it can naturally be generalized to the multiclass case
eﬃcent when uses:
a few import vectors
component-wise update procedure
extention using L1 KLR
Zhu & Hastie, 01 ; Keerthi et. al., 02

Historical perspective on kernel machines
statistics
1960 Parzen, Nadaraya Watson
1970 Splines
1980 Kernels: Silverman, Hardle...
1990 sparsity: Donoho (pursuit),
Tibshirani (Lasso)...
Statistical learning
1985 Neural networks:
non linear - universal
structural complexity
non convex optimization
1992 Vapnik et. al.
theory - regularization -
consistancy
convexity - Linearity
Kernel - universality
sparsity
results: MNIST

what’s new since 1995
Applications
kernlisation w x → f , k(x, .) H
kernel engineering
sturtured outputs
applications: image, text, signal, bio-info...
Optimization
dual: mloss.org
regularization path
approximation
primal
Statistic
proofs and bounds
model selection
span bound
multikernel: tuning (k and σ)

challenges: towards tough learning
the size eﬀect
ready to use: automatization
adaptative: on line context aware
beyond kenrels
Automatic and adaptive model selection
variable selection
kernel tuning (k et σ)
hyperparametres: C, duality gap, λ
IP change
Theory
non positive kernels
a more general representer theorem

biblio: kernel-machines.org
John Shawe-Taylor and Nello Cristianini Kernel Methods for Pattern Analysis, Cambridge
University Press, 2004
Bernhard Schölkopf and Alex Smola. Learning with Kernels. MIT Press, Cambridge, MA,
2002.
Trevor Hastie, Robert Tibshirani and Jerome Friedman, The Elements of Statistical
Learning:. Data Mining, Inference, and Prediction, springer, 2001
Léon Bottou, Olivier Chapelle, Dennis DeCoste and Jason Weston Large-Scale Kernel
Machines (Neural Information Processing, MIT press 2007
Olivier Chapelle, Bernhard Scholkopf and Alexander Zien, Semi-supervised Learning, MIT
press 2006
Vladimir Vapnik. Estimation of Dependences Based on Empirical Data. Springer Verlag,
2006, 2nd edition.
Vladimir Vapnik. The Nature of Statistical Learning Theory. Springer, 1995.
Grace Wahba. Spline Models for Observational Data. SIAM CBMS-NSF Regional
Conference Series in Applied Mathematics vol. 59, Philadelphia, 1990
Alain Berlinet and Christine Thomas-Agnan, Reproducing Kernel Hilbert Spaces in
Probability and Statistics,Kluwer Academic Publishers, 2003
Marc Atteia et Jean Gaches , Approximation Hilbertienne - Splines, Ondelettes, Fractales,
PUG, 1999

Lecture5 kernel svm

More Related Content

What's hot (20)

Viewers also liked (10)

Similar to Lecture5 kernel svm (19)

Lecture5 kernel svm