Lecture7 data structure(tree)
- 1. Lecture 7 Tree (Data Structure) Abdisalam Issa-Salwe Taibah University College of Computer Science & Engineering Computer Science Department Outline Binary trees Binary search trees AVL trees B trees Applications 2 1
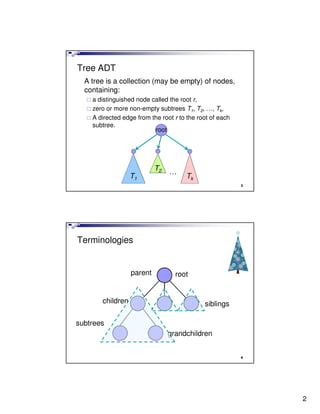
- 2. Tree ADT A tree is a collection (may be empty) of nodes, containing: a distinguished node called the root r, zero or more non-empty subtrees T1, T2, …, Tk, A directed edge from the root r to the root of each subtree. root T2 … T1 Tk 3 Terminologies parent root children siblings subtrees grandchildren 4 2
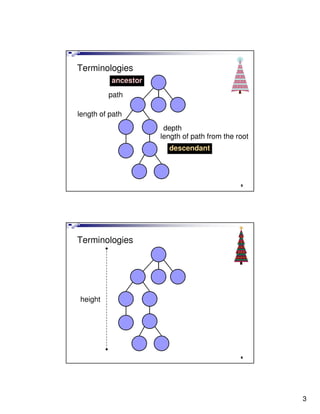
- 3. Terminologies ancestor path length of path depth length of path from the root descendant 5 Terminologies height 6 3
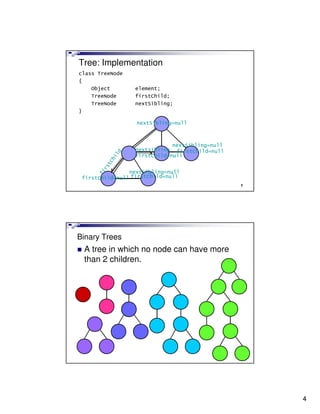
- 4. Tree: Implementation class TreeNode { Object element; TreeNode firstChild; TreeNode nextSibling; } nextSibling=null nextSibling=null nextsibling firstChild=null firstChild=null nextSibling=null firstChild=null firstChild=null 7 Binary Trees A tree in which no node can have more than 2 children. 8 4
- 5. Binary Tree: Implementation Class BinaryNode { 3 Object element; BinaryNode left; BinaryNode right; } 5 node.element=3 node.left=node node.right=node 9 node.element=9 node.element=5 node.left=null node.left=node node.right=null node.right=null 9 Binary Tree: Implementation class BinaryNode { // Constructors BinaryNode ( Comparable theElement ) { this ( theElement, null, null); } BinaryNode (Comparable theElement, BinaryNode lt, BinaryNode rt) { element = theElement; left = lt; right = rt; } // Friendly data; accessible by other package routines Comparable element; // The data in the node BinaryNode left; // Left child BinaryNode right; // Right child 10 } 5
- 6. Binary Search Trees Properties of a binary search tree T 1. T is a binary tree. 2. For each node n in T, whose left subtree is Tl and right subtree is Tr, • the item in each node in Tl is smaller than the item in n. • the item in each node in Tr is larger than the item in n. 11 Example 8 3 11 2 4 9 12 1 6 5 7 12 6
- 7. Binary Search Trees public class BinarySearchTree { public BinarySearchTree( ) { root = null; } public void insert( Comparable x ) { root = insert( x, root ); } public void remove( Comparable x ) { root = remove( x, root ); } public Comparable find( Comparable x ) { return elementAt( find( x, root ) ); } public void makeEmpty( ) { root = null; } ... private BinaryNode root; } 13 FIND 8 Find 6 < 3 11 > 2 4 9 12 > 1 6 5 7 14 7
- 8. Method find private BinaryNode find ( Comparable x, BinaryNode t ) { if( t == null ) return null; if( x.compareTo( t.element ) < 0 ) return find( x, t.left ); else if( x.compareTo( t.element ) > 0 ) return find( x, t.right ); else return t; // Match } 15 INSERT 10 8 Insert 10 > 3 11 < 2 4 9 12 1 6 10 5 7 16 8
- 9. Method insert private BinaryNode insert ( Comparable x, BinaryNode t ) { if( t == null ) t = new BinaryNode( x, null, null ); else if( x.compareTo( t.element ) < 0 ) t.left = insert( x, t.left ); else if( x.compareTo( t.element ) > 0 ) t.right = insert( x, t.right ); else ; // Duplicate; do nothing return t; } 17 FindMax, FindMin 8 3 11 2 4 9 12 max min 1 6 5 7 18 9
- 10. Methods findMin & findMax private BinaryNode findMin( BinaryNode t ) { if( t == null ) return null; else if( t.left == null ) return t; return findMin( t.left ); } private BinaryNode findMax( BinaryNode t ) { if( t != null ) while( t.right != null ) t = t.right; return t; } 19 REMOVE Remove 7 11 3 13 2 7 12 14 1 5 9 4 6 10 20 10
- 11. REMOVE Remove 7 11 3 13 2 7 12 14 1 9 8 10 21 REMOVE Remove 7 11 3 13 2 7 12 14 1 5 4 6 22 11
- 12. Method Remove private BinaryNode remove(Comparable x,BinaryNode t) { if(t == null) return t; // Item not found;do nothing if( x.compareTo(t.element) < 0 ) t.left = remove(x, t.left); else if ( x.compareTo(t.element) > 0 ) t.right = remove(x, t.right); else if (t.left!=null && t.right!=null) // 2 child { t.element = findMin(t.right).element; t.right = remove(t.element, t.right); } else t = (t.left != null) ? t.left : t.right; return t; } 23 AVL Trees An AVL tree is a binary search tree with a balance condition. A self-balancing binary search tree. AVL tree is named after G.M. Adelson- Velskii and E.M. Landis. Balance condition For every node in the tree, the height of the left & right subtrees can differ by at most 1. 24 12
- 13. AVL Trees (cont…) The balance factor of a node is the height of its left subtree minus the height of its right subtree (sometimes opposite) and a node with balance factor 1, 0, or −1 is considered balanced. A node with any other balance factor is considered unbalanced and requires rebalancing the tree. The balance factor is either stored directly at each node or computed from the heights of the subtrees. 25 AVL Trees 11 11 3 13 3 13 2 7 12 14 2 7 12 14 1 5 8 1 5 not AVL tree AVL tree 4 6 26 13
- 14. Single Right Rotation k2 k1 k1 Zh k2 Yh Xh+1 Yh Zh Xh+1 27 Single Left Rotation k2 k1 k1 Xh k2 Yh Zh+1 Zh+1 Xh Yh 28 14
- 15. Height of AVL Tree If N is the number of nodes in an AVL tree, the height of the tree, h(N), is approximately 1.44 log(N+2)-.328. 29 Inorder Traversal + (a – (b * (c / d))) + (e – f) - - a * e f b / c d 30 15
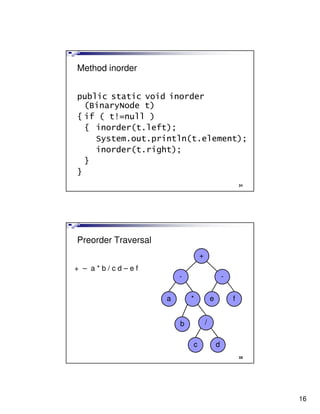
- 16. Method inorder public static void inorder (BinaryNode t) { if ( t!=null ) { inorder(t.left); System.out.println(t.element); inorder(t.right); } } 31 Preorder Traversal + + – a*b/cd–ef - - a * e f b / c d 32 16
- 17. Method preorder public static void preorder (BinaryNode t) { if ( t!=null ) { System.out.println(t.element); inorder(t.left); inorder(t.right); } } 33 Postorder Traversal + abcd/*–ef–+ - - a * e f b / c d 34 17
- 18. Method postorder public static void postorder (BinaryNode t) { if ( t!=null ) { inorder(t.left); inorder(t.right); System.out.println(t.element); } } 35 B tree N-ary tree Increase the breadth of trees to decrease the height Used for indexing of large amount of data (stored in disk) 36 18
- 19. B tree (cont…) Unlike a binary-tree, each node of a b-tree may have a variable number of keys and children. The keys are stored in non-decreasing order. Each key has an associated child that is the root of a subtree containing all nodes with keys less than or equal to the key but greater than the preceeding key. A node also has an additional rightmost child that is the root for a subtree containing all keys greater than any keys in the node. 37 Example 12 52 78 4 8 83 91 05 19 26 37 46 60 69 168 279 79 85 93 11 13 20 27 38 49 54 61 70 80 86 95 12 14 21 28 44 50 56 62 71 81 90 97 17 22 31 45 57 66 76 82 98 19 26 35 59 67 77 83 99 60 38 19
- 20. B tree (cont…) A b-tree has a minumum number of allowable children for each node known as the minimization factor. If t is this minimization factor, every node must have at least t - 1 keys. Under certain circumstances, the root node is allowed to violate this property by having fewer than t - 1 keys. Every node may have at most 2t - 1 keys or, equivalently, 2t children. 39 Height of B-Tree For n greater than or equal to one, the height of an n-key b-tree T of height h with a minimum degree t greater than or equal to 2, 40 20
- 21. Properties of B Trees For an M-ary B tree: The root has up to M children. Non-leaf nodes store up to M-1 keys, and have between M/2 and M children, except the root. All data items are stored at leaves. All leaves have to same depth, and store between L/2 and L data items. 41 Search Search for 66 12 52 78 4 8 83 91 05 19 26 37 46 60 69 168 279 79 85 93 11 13 20 27 38 49 54 61 70 80 86 95 12 14 21 28 44 50 56 62 71 81 90 97 17 22 31 45 57 66 76 82 98 19 26 35 59 67 77 83 99 60 42 21
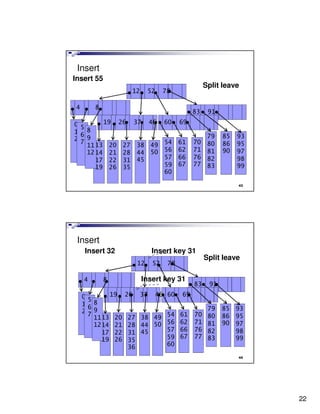
- 22. Insert Insert 55 Split leave 12 52 78 4 8 83 91 05 19 26 37 46 60 69 16 8 27 9 79 85 93 54 61 70 80 86 95 11 13 20 27 38 49 12 14 21 28 44 50 56 62 71 81 90 97 17 22 31 45 57 66 76 82 98 19 26 35 59 67 77 83 99 60 43 Insert Insert 32 Insert key 31 Split leave 12 52 78 4 8 Insert key 31 83 91 05 19 26 37 46 60 69 168 279 79 85 93 11 13 20 27 38 49 54 61 70 80 86 95 12 14 21 28 44 50 56 62 71 81 90 97 17 22 31 45 57 66 76 82 98 19 26 59 67 77 83 99 35 36 60 44 22
- 23. B+ tree B+ tree or B plus tree is a type of tree which represents sorted data in a way that allows for efficient insertion, retrieval and removal of records, each of which is identified by a key. It is a dynamic, multilevel index, with maximum and minimum bounds on the number of keys in each index segment (usually called a "block" or "node"). In a B+ tree, in contrast to a B-tree, all records are stored at the leaf level of the tree; only keys are stored in interior nodes. 45 B+ tree (cont…) The primary value of a B+ tree is in storing data for efficient retrieval in a block- oriented storage context — in particular, file systems. This is primarily because unlike binary search trees, B+ trees have very high fanout (typically on the order of 100 or more), which reduces the number of I/O operations required to find an element in the tree. 46 23
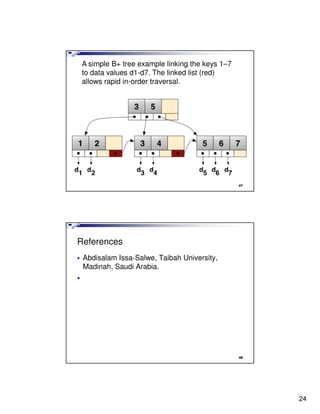
- 24. A simple B+ tree example linking the keys 1–7 to data values d1-d7. The linked list (red) allows rapid in-order traversal. 47 References Abdisalam Issa-Salwe, Taibah University, Madinah, Saudi Arabia. 48 24