Lecture9 multi kernel_svm

Lecture 9: Multi Kernel SVM
Stéphane Canu
stephane.canu@litislab.eu
Sao Paulo 2014
April 16, 2014

Roadmap
1 Tuning the kernel: MKL
The multiple kernel problem
Sparse kernel machines for regression: SVR
SimpleMKL: the multiple kernel solution

Standard Learning with Kernels
User
Learning Machine
kernel k data
f
http://www.cs.nyu.edu/~mohri/icml2011-tutorial/tutorial-icml2011-2.pdf
Stéphane Canu (INSA Rouen - LITIS) April 16, 2014 3 / 21

Learning Kernel framework
User
Learning Machine
kernel
family
km
data
f , k(., .)

from SVM
SVM: single kernel k
f (x) =
n
i=1
αi k (x, xi ) + b
=
http://www.nowozin.net/sebastian/talks/ICCV-2009-LPbeta.pdf

from SVM → to Multiple Kernel Learning (MKL)
MKL: set of M kernels k1, . . . , km, . . . , kM
learn classier and combination weights
can be cast as a convex optimization problem
f (x) =
n
i=1
αi
M
m=1
dm km(x, xi ) + b
M
m=1
dm = 1 and 0 ≤ dm
=

from SVM → to Multiple Kernel Learning (MKL)
MKL: set of M kernels k1, . . . , km, . . . , kM
learn classier and combination weights
can be cast as a convex optimization problem
f (x) =
n
i=1
αi
M
m=1
dm km(x, xi ) + b
M
m=1
dm = 1 and 0 ≤ dm
=
n
i=1
αi K(x, xi ) + b with K(x, xi ) =
M
m=1
dm km(x, xi )

Multiple Kernel
The model
f (x) =
n
i=1
αi
M
m=1
dmkm(x, xi ) + b,
M
m=1
dm = 1 and 0 ≤ dm
Given M kernel functions k1, . . . , kM that are potentially well suited for a
given problem, ﬁnd a positive linear combination of these kernels such that
the resulting kernel k is “optimal”
k(x, x ) =
M
m=1
dmkm(x, x ), with dm ≥ 0,
m
dm = 1
Learning together
The kernel coeﬃcients dm and the SVM parameters αi , b.

Multiple Kernel: illustration

Multiple Kernel Strategies
Wrapper method (Weston et al., 2000; Chapelle et al., 2002)
solve SVM
gradient descent on dm on criterion:
margin criterion
span criterion
Kernel Learning & Feature Selection
use Kernels as dictionary
Embedded Multi Kernel Learning (MKL)

Multiple Kernel functional Learning
The problem (for given C)
min
f ∈H,b,ξ,d
1
2
f 2
H + C
i
ξi
with yi f (xi ) + b ≥ 1 + ξi ; ξi ≥ 0 ∀i
M
m=1
dm = 1 , dm ≥ 0 ∀m ,
f =
m
fm and k(x, x ) =
M
m=1
dmkm(x, x ), with dm ≥ 0
The functional framework
H =
M
m=1
Hm f , g Hm
=
1
dm
f , g Hm

The problem (for given C)
min
{fm},b,ξ,d
1
2 m
1
dm
fm
2
Hm
+ C
i
ξi
with yi
m
fm(xi ) + b ≥ 1 + ξi ; ξi ≥ 0 ∀i
m
dm = 1 , dm ≥ 0 ∀m ,
Treated as a bi-level optimization task
min
d∈IRM



min
{fm},b,ξ
1
2 m
1
dm
fm
2
Hm
+ C
i
ξi
with yi
m
fm(xi ) + b ≥ 1 + ξi ; ξi ≥ 0 ∀i
s.t.
m
dm = 1 , dm ≥ 0 ∀m ,

Multiple Kernel representer theorem and dual
The Lagrangian:
L =
1
2 m
1
dm
fm
2
Hm
+ C
i
ξi −
i
αi yi
m
fm(xi ) + b − 1 − ξi −
i
βi ξi
Associated KKT stationarity conditions:
mL = 0 ⇔
1
dm
fm(•) =
n
i=1
αi yi km(•, xi ) m = 1, M
Representer theorem
f (•) =
m
fm(•) =
n
i=1
αi yi
m
dmkm(•, xi )
K(•,xi )
We have a standard SVM problem with respect to function f and kernel K.

Multiple Kernel Algorithm
Use a Reduced Gradient Algorithm1
min
d∈IRM
J(d)
s.t.
m
dm = 1 , dm ≥ 0 ∀m ,
SimpleMKL algorithm
set dm = 1
M for m = 1, . . . , M
while stopping criterion not met do
compute J(d) using an QP solver with K = m dmKm
compute ∂J
∂dm
, and projected gradient as a descent direction D
γ ← compute optimal stepsize
d ← d + γD
end while
−→ Improvement reported using the Hessian
1
Rakotomamonjy et al. JMLR 08

Computing the reduced gradient
At the optimal the primal cost = dual cost
1
2 m
1
dm
fm
2
Hm
+ C
i
ξi
primal cost
=
1
2
α Gα − e α
dual cost
with G = m dmGm where Gm,ij = km(xi , xj )
Dual cost is easier for the gradient
dm J(d) =
1
2
α Gmα
Reduce (or project) to check the constraints m dm = 1 → m Dm = 0
Dm = dm
J(d) − d1
J(d) and D1 = −
M
m=2
Dm

Complexity
For each iteration:
SVM training: O(nnsv + n3
sv).
Inverting Ksv,sv is O(n3
sv), but might already be available as a
by-product of the SVM training.
Computing H: O(Mn2
sv)
Finding d: O(M3).
The number of iterations is usually less than 10.
−→ When M < nsv, computing d is not more expensive than QP.

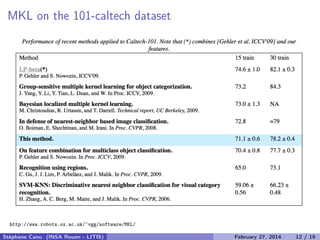
MKL on the 101-caltech dataset
http://www.robots.ox.ac.uk/~vgg/software/MKL/

Support vector regression (SVR)
the t-insensitive loss
min
f ∈H
1
2 f 2
H
with |f (xi ) − yi | ≤ t, i = 1, n
The support vector regression introduce slack variables
(SVR)
min
f ∈H
1
2 f 2
H + C |ξi |
with |f (xi ) − yi | ≤ t + ξi 0 ≤ ξi i = 1, n
a typical multi parametric quadratic program (mpQP)
piecewise linear regularization path
α(C, t) = α(C0, t0) + (
1
C
−
1
C0
)u +
1
C0
(t − t0)v
2d Pareto’s front (the tube width and the regularity)

Support vector regression illustration
0 1 2 3 4 5 6 7 8
−1
−0.8
−0.6
−0.4
−0.2
0
0.2
0.4
0.6
0.8
1
Support Vector Machine Regression
x
y
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5
−1.5
−1
−0.5
0
0.5
1
1.5
Support Vector Machine Regression
x
y
C large C small
there exists other formulations such as LP SVR...

Multiple Kernel Learning for regression
The problem (for given C and t)
min
{fm},b,ξ,d
1
2 m
1
dm
fm
2
Hm
+ C
i
ξi
s.t.
m
fm(xi ) + b − yi ≤ t + ξi ∀iξi ≥ 0 ∀i
m
dm = 1 , dm ≥ 0 ∀m ,
regularization formulation
min
{fm},b,d
1
2 m
1
dm
fm
2
Hm
+ C
i
max(
m
fm(xi ) + b − yi − t, 0)
m
dm = 1 , dm ≥ 0 ∀m ,
Equivalently
min
m},b,ξ,d
i
max
m
fm(xi ) + b − yi − t, 0 +
1
2C m
1
dm
fm
2
Hm
+ µ
m
|dm|

The problem (for given C and t)
min
{fm},b,ξ,d
1
2 m
1
dm
fm
2
Hm
+ C
i
ξi
s.t.
m
fm(xi ) + b − yi ≤ t + ξi ∀iξi ≥ 0 ∀i
m
dm = 1 , dm ≥ 0 ∀m ,
Treated as a bi-level optimization task
min
d∈IRM



min
{fm},b,ξ
1
2 m
1
dm
fm
2
Hm
+ C
i
ξi
s.t.
m
fm(xi ) + b − yi ≥ t + ξi ∀i
ξi ≥ 0 ∀i
s.t.
m
dm = 1 , dm ≥ 0 ∀m ,

Multiple Kernel experiments
0 0.2 0.4 0.6 0.8 1
−1
−0.5
0
0.5
1
LinChirp
0 0.2 0.4 0.6 0.8 1
−2
−1
0
1
2
x
0 0.2 0.4 0.6 0.8 1
0.2
0.4
0.6
0.8
1
Wave
0 0.2 0.4 0.6 0.8 1
0
0.5
1
x
0 0.2 0.4 0.6 0.8 1
0.2
0.4
0.6
0.8
1
Blocks
0 0.2 0.4 0.6 0.8 1
0
0.2
0.4
0.6
0.8
x
0 0.2 0.4 0.6 0.8 1
0.2
0.4
0.6
0.8
1
Spikes
0 0.2 0.4 0.6 0.8 1
0
0.5
1
x
Single Kernel Kernel Dil Kernel Dil-Trans
Data Set Norm. MSE (%) #Kernel Norm. MSE #Kernel Norm. MSE
LinChirp 1.46 ± 0.28 7.0 1.00 ± 0.15 21.5 0.92 ± 0.20
Wave 0.98 ± 0.06 5.5 0.73 ± 0.10 20.6 0.79 ± 0.07
Blocks 1.96 ± 0.14 6.0 2.11 ± 0.12 19.4 1.94 ± 0.13
Spike 6.85 ± 0.68 6.1 6.97 ± 0.84 12.8 5.58 ± 0.84
Table: Normalized Mean Square error averaged over 20 runs.

Conclusion on multiple kernel (MKL)
MKL: Kernel tuning, variable selection. . .
extention to classification and one class SVM
SVM KM: an efficient Matlab toolbox (available at MLOSS)2
Multiple Kernels for Image Classification: Software and Experiments
on Caltech-1013
new trend: Multi kernel, Multi task and ∞ number of kernels
2
http://mloss.org/software/view/33/
3

Bibliography
A. Rakotomamonjy, F. Bach, S. Canu & Y. Grandvalet. SimpleMKL. J.
Mach. Learn. Res. 2008, 9:2491–2521.
M. Gönen & E. Alpaydin Multiple kernel learning algorithms. J. Mach.
Learn. Res. 2008;12:2211-2268.

Lecture9 multi kernel_svm

More Related Content

What's hot (20)

Viewers also liked (20)

Similar to Lecture9 multi kernel_svm (20)

Recently uploaded (20)

Lecture9 multi kernel_svm