Modul clustering data mining modul clustering
Download as DOC, PDF0 likes1,434 views
Analisis cluster adalah teknik data mining untuk mengelompokkan objek berdasarkan kesamaan karakteristik, dengan tujuan mempermudah analisis dan interpretasi data. Teknik ini sering digunakan dalam pemasaran untuk segmentasi pasar, memahami perilaku pelanggan, dan mengidentifikasi peluang produk baru. Prosedur analisis meliputi pemilihan ukuran jarak dan metode pengelompokan, seperti metode hierarkis dan divisif, dengan berbagai teknik pengukuran jarak yang dapat diterapkan.
![k
ì1,
if
í
2 2
6) Minkowski
= [ - p ]1
D(X, Y) p
p = 1 (absolute metric)
p = 2 (euclidian metric)
7) Chi-Square
å Xi Yi
8) Phi-Square
D(X, Y) =
å ( Xi
-E ( EX ( i X) i ))
+ å ( Yi
-E ( EY ( i Y) i ))
1 æ (Xi - E(Xi))2 (Yi - E(Yi))2 ö
9) Hamming
D(X, Y) = ç å n è E(Xi)
+ å ÷
E(Yi) ø
D(P,Q) = åd (X pk .X qk )
k =1
Dimana : d (Xpk , X
qk
)=
X pk ¹ X qk
î0, lainnya
2.5 Teknik – Teknik dalam Analisis Cluster](https://image.slidesharecdn.com/modulclusteringdatamining-modulclustering-141126100754-conversion-gate01/85/Modul-clustering-data-mining-modul-clustering-4-320.jpg)
Modul clustering data mining modul clustering
- 1. CLUSTERING 1 Clustering Concept Analisis cluster merupakan salah satu teknik data mining yang bertujuan untuk mengidentifikasi sekelompok obyek yang mempunyai kemiripan karakteristik tertentu yang dapat dipisahkan dengan kelompok obyek lainnya, sehingga obyek yang berada dalam kelompok yang sama relatif lebih homogen daripada obyek yang berada pada kelompok yang berbeda. Jumlah kelompok yang dapat diidentifikasi tergantung pada banyak dan variasi data obyek. Tujuan dari pengelompokan sekumpulan data obyek ke dalam beberapa kelompok yang mempunyai karakteristik tertentu dan dapat dibedakan satu sama lainnya adalah untuk analisis dan interpretasi lebih lanjut sesuai dengan tujuan penelitian yang dilakukan. Model yang diambil diasumsikan bahwa data yang dapat digunakan adalah data yang berupa data interval, frekuensi dan biner. Set data obyek harus mempunyai peubah dengan tipe yang sejenis tidak campur antara tipe yang satu dengan lainnya. 2.2 Tujuan Analisis Cluster Analisis cluster dapat diterapkan pada bidang apa saja. Namun pemakaian teknik ini lebih familiar pada bidang pemasaran karena memang salah satu kegiatan yang
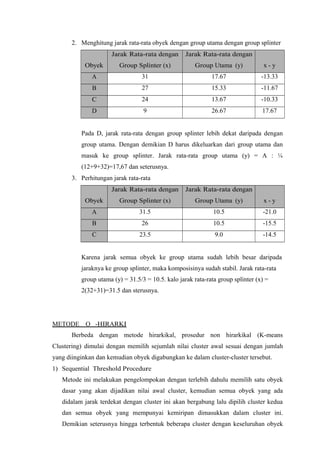
- 2. dilakukan dalam pemasaran adalah pengelompokan, yang disebut segmentasi pasar. Tujuan analisis cluster di dalam pemasaran adalah sebagai berikut : 1. Membuat segmen pasar (segmenting the market) Pelanggan atau pembeli sering diklasterkan berdasarkan manfaat atau keuntungan yang diperoleh dari pembelian barang. Setiap cluster akan terdiri dari pelanggan/pembeli yang relatif homogen, dinyatakan dalam manfaat yang dicari. 2. Memahami perilaku pembeli Analisis cluster digunakan untuk mengenali/mengidentifikasi kelompok pembeli yang homogen/relatif homogen. Kemudian perilaku dalam untuk setiap kelompok perlu dikaji secara terpisah. Responden (pembeli) dikelompokkan didasarkan pada self-reported importance yang terkait pada setiap faktor pilihan yang digunakan untuk memilih toko atau mall di mana para pembeli membeli barang yang dibutuhkan. 3. Mengenali peluang produk baru Dengan mengklasterkan merk dan produk, competitive set di dalam pasar bisa ditentukan. Merek di dalam klaster yang sama bersaing sengit satu sama lain, daripada merek dari klaster lain. 4. Mereduksi data. Analisis cluster digunakan sebagai suatu alat mereduksi data secara umum, untuk mengembangkan klaster atau sub-group dari data yang mudah dikelola dari kumpulan data asli, secara individual. 2.3 Prosedur Analisis Cluster Rumuskan Masalah Pilih Ukuran Jarak Pilih Prosedur Peng-cluster-an Penentuan Banyaknya Cluster Profilisasi Customer Menentukan segmentasi Pasar
- 3. Secara umum proses dimulai dengan merumuskan masalah pengklasteran dengan mendefinisikan variabel-variabel yang dipergunakan untuk dasar pengklasteran/pembentukan klaster. Kemudian pengambilan p pengukuran peubah pada n obyek pengamatan. Data tersebut dijadikan matriks data mentah berukuran m x p. Matrik tersebut ditransformasikan ke dalam bentuk matriks similaritas (kemiripan) berupa n x n yang dihitung berdasarkan pasangan-pasangan obyek p peubah. Konsep dasar pengukuran analisis cluster adalah konsep pengukuran jarak (distance) dan kesamaan (similarity). Distance adalah ukuran tentang jarak pisah antar obyek sedangkan similarity adalah ukuran kedekatan. Konsep ini penting karena pengelompokan pada analisis cluster didasarkan pada kedekatan. Pengukuran jarak (distance type measure) digunakan untuk data-data yang bersifat matriks, sedangkan pengukuran kesesuaian (matching type measure) digunakan untuk data-data yang bersifat kualitatif. 2.4 Teknik Pengukuran Jarak 1) Euclidean Distance Merupakan ukuran jarak antara dua item X dan Y. D(X, Y) = å (Xi - Yi) 2 2) Squared Euclidean Distance Merupakan ukuran jarak antara dua item X dan Y. D(X, Y) = å (Xi - Yi) 2 3) Pearson Correlation Korelasi antara vektor nilai : S(X, Y) = åZ xZi yi (N - 1) di mana Zxi adalah nilai x yang telah distandarkan untuk item ke-i dan N adalah jumlah itemnya. 4) Chebychev 5) Block D(X, Y) = maxi Xi - Yi D(X, Y) = å Xi - Yi
- 4. k ì1, if í 2 2 6) Minkowski = [ - p ]1 D(X, Y) p p = 1 (absolute metric) p = 2 (euclidian metric) 7) Chi-Square å Xi Yi 8) Phi-Square D(X, Y) = å ( Xi -E ( EX ( i X) i )) + å ( Yi -E ( EY ( i Y) i )) 1 æ (Xi - E(Xi))2 (Yi - E(Yi))2 ö 9) Hamming D(X, Y) = ç å n è E(Xi) + å ÷ E(Yi) ø D(P,Q) = åd (X pk .X qk ) k =1 Dimana : d (Xpk , X qk )= X pk ¹ X qk î0, lainnya 2.5 Teknik – Teknik dalam Analisis Cluster
- 5. M ETO D E H I R A R K I Teknik hirarki (hierarchical methods) adalah teknik clustering membentuk kontruksi hirarki atau berdasarkan tingkatan tertentu seperti struktur pohon (struktur pertandingan). Dengan demikian proses pengelompokkannya dilakukan secara bertingkat atau bertahap. Hasil dari pengelompokan ini dapat disajikan dalam bentuk dendogram. Metode-metode yang digunakan dalam teknik hirarki: 1) Agglomerative Methods Metode ini dimulai dengan kenyatan bahwa setiap obyek membentuk clusternya masing-masing. Kemudian dua obyek dengan jarak terdekat bergabung. Selanjutnya obyek ketiga akan bergabung dengan cluster yang ada atau bersama obyek lain dan membentuk cluster baru. Hal ini tetap memperhitungkan jarak kedekatan antar obyek. Proses akan berlanjut hingga akhirnya terbentuk satu cluster yang terdiri dari keseluruhan obyek. Ada beberapa teknik dalam Agglomerative methods yaitu: a) S in g le link a g e ( n ea r e st n e i g hbor m e thods) Metode ini menggunakan prinsip jarak minimum yang diawali dengan mencari dua obyek terdekat dan keduanya membentuk cluster yang pertama. Pada langkah selanjutnya terdapat dua kemungkinan, yaitu : · obyek ketiga akan bergabung dengan cluster yang telah terbentuk, atau · dua obyek lainnya akan membentu cluster baru. Proses ini akan berlanjut sampai akhirnya terbentuk cluster tunggal. Pada metode ini jarak antar cluster didefinisikan sebagai jarak terdekat antar anggotanya. Contoh : Terdapat matriks jarak antara 5 buah obyek, yaitu : A B C D E A 0.0 1.0 5.0 6.0 8.0 B 1.0 0.0 3.0 8.0 7.0 C 5.0 3.0 0.0 4.0 6.0 D 6.0 8.0 4.0 0.0 2.0 E 8.0 7.0 6.0 2.0 0.0 Langkah penyelesaiannya : 1. Mencari obyek dengan jarak minimum A dan B mempunyai jarak terdekat, yaitu 1.0 maka obyek A dan A bergabung menjadi satu cluster.
- 6. 2. Menghitung jarak antara cluster AB dengan obyek lainnya. D(AB)C = min {dAC, dBC}= dBC = 3.0 D(AB)D = min {dAD, dBD}= dAD = 6.0 D(AB)E = min {dAE, dBE}= dBE = 7.0 Dengan demikian terbentu matriks jarak yang baru AB C D E AB 0.0 3.0 6.0 7.0 C 3.0 0.0 4.0 6.0 D 6.0 4.0 0.0 2.0 E 7.0 6.0 2.0 0.0 3. Mencari obyek dengan jarak terdekat D dan E mempunyai jarak yang terdekat yaitu 2.0 maka obyek D dan E bergabung menjadi satu cluster. 4. menghitung jarak antara cluster dengan obyek lainnya. D(AB)C = 3.0 D(AB)(DE) = min {dAD, dAE, dBD, dBE} = dAD = 6.0 D(DE)C = min {dCD, dCE} = dCD = 4.0 5. Mencari jarak terdekat antara cluster dengan obyek dan diperoleh obyek C bergabung dengan cluster AB 6. Pada langkah yang terakhir, cluster ABC bergabung dengan DE sehingga terbentuk cluster tunggal. b) Complete linkage (furthest neighbor methods) Metode ini merupakan kebalikan dari pendekatan yang digunakan pada single linkage. Prinsip jarak yang digunakan adalah jarak terjauh antar obyek. Contoh : Terdapat matriks jarak antara lima buah obyek yaitu : A B C D E A 0.0 1.0 5.0 6.0 8.0 B 1.0 0.0 3.0 8.0 7.0 C 5.0 3.0 0.0 4.0 6.0 D 6.0 8.0 4.0 0.0 2.0 E 8.0 7.0 6.0 2.0 0.0
- 7. Langkah penyelesaiannya : 1. Mencari obyek dengan jarak minimum A dan B mempunyai jarak terdekat yaitu 1.0 maka obyek A dan B bergabung menjadi satu cluster. 2. Menghitung jarak antara cluster AB dengan obyek lainnya. D(AB)C = max {dAC, dBC}= dAC = 5.0 D(AB)D = max {dAD, dBD}= dBD = 8.0 D(AB)E = max {dAE, dBE}= dAE = 8.0 Dengan demikian terbentuk matriks jarak yang baru AB C D E AB 0.0 5.0 8.0 8.0 C 5.0 0.0 4.0 6.0 D 8.0 4.0 0.0 2.0 E 8.0 6.0 2.0 0.0 3. Mencari obyek dengan jarak terdekat. D dan E mempunyai jarak terdekat yaitu 2.0 maka obyek D dan E bergabung menjadi satu cluster 4. Menghitung jarak antar cluster dengan obyek lainnya. D(AB)C = 5.0 D(AB)(DE) = max {dAD, dAE, dBD, dBE} = dAE = dBD = 8.0 D(DE)C = max {dCD, dCE} = dCE = 6.0 5. Maka terbentuklah matriks jarak yang baru, yaitu : AB C DE AB 0.0 5.0 8.0 C 5.0 0.0 6.0 DE 8.0 6.0 0.0 6. Mencari jarak terdekat antara cluster dengan obyek dan diperoleh obyek C bergabung dengan cluster AB
- 8. 7. Pada langkah yang terakhir cluster ABC bergabung dengan DE sehingga terbentuk cluster tunggal. c) Average linkage methods ( between groups methods) Metode ini mengikuti prosedur yang sama dengan kedua metode sebelumnya. Prinsip ukuran jarak yang digunakan adalah jarak rata-rata antar tiap pasangan obyek yang mungkin. Contoh : Terdapat matriks jarak antara 5 buah obyek, yaitu : A B C D E A 0.0 1.0 5.0 6.0 8.0 B 1.0 0.0 3.0 8.0 7.0 C 5.0 3.0 0.0 4.0 6.0 D 6.0 8.0 4.0 0.0 2.0 E 8.0 7.0 6.0 2.0 0.0 Langkah penyelesaiannya : 1. Mencari obyek dengan jarak minimum A dan B mempunyai jarak terdekat, yaitu 1,0 maka obyek A dan B bergabung menjadi satu cluster. 2. Menghitung jarak antara cluster AB dengan obyek lainnya d(AB)C = max {dAC, dBC} = dAC = 5,0 d(AB)D = max {dAD, dBD} = dBD = 8,0 d(AB)E = max {dAE, dBE} = dAE = 8,0 Dengan demikian terbentuk matriks jarak yang baru : AB C D E AB 0.0 5.0 8.0 8.0 C 5.0 0.0 4.0 6.0 D 8.0 4.0 0.0 2.0 E 8.0 6.0 2.0 0.0
- 9. 3. Mencari obyek dengan jarak terdekat. D dan E mempunyai jarak terdekat, yaitu 2,0 maka obyek D dan E bergabung menjadi satu cluster. 4. Menghitung jarak antara cluster dengan obyek lainnya. d(AB)C = 4,0 d(AB)(DE) = 1/2{dAD, dAE, dBD, dBE} = 7,25 d(DE)C = 1/2{dCD, dCE,} = dCE = 5,00 Maka terbentuklah matrik jarak yang baru, yaitu : AB 0.0 4.0 7.25 C 4.0 0.0 5.00 DE 7.25 5.0 0.00 5. Mencari jarak terdekat antara cluster dengan obyek dan diperoleh obyek C bergabung dengan clster AB. 6. Pada langkah yang terakhir, cluster ABC bergabung dengan DE sehingga terbentuk cluster tunggal. d) Ward’s error sum of squares methods Ward mengajukan suatu metode pembentukan cluster yang didasari oleh hilangnya informasi akibat penggabungan obyek menjadi cluster. Hal ini diukur dengan jumlah total dari deviasi kuadrat pada mean cluster untuk tiap observasi. Error sum of squares (ESS) digunakan sebagai fungsi obyektif. Dua obyek akan digabungkan apabila mempunyai fungsi obyektif terkecil diantara kemungkinan yang ada. ESS = å AB C DE å X 2 ij - 1 n ( X )2 å j ij Dengan Xij adalah nilai untuk obyek ke-i pada cluster ke-j. e) Within groups methods f) Median methods g) Centroid methods
- 10. 2) Divisive Methods Metode divisive berlawanan dengan metode agglomerative. Metode ini pertama-tama diawali dengan satu cluster besar yang mencakup semua observasi (obyek). Selanjutnya obyek yang mempunyai ketidakmiripan yang cukup besar akan dipisahkan sehingga membentuk cluster yang lebih kecil. Pemisahan ini dilanjutkan sehingga mencapai sejumlah cluster yang diinginkan. a) Splinter average distance methods Metode ini didasarkan pada perhitungan jarak rata-rata masing-masing obyek dengan obyek pada grup splinter dan jarak rata-rata obyek tersebut dengan obyek lain pada grupnya. Proses tersebut dimulai dengan memisahkan obyek dengan jarak terjauh sehingga terbentuklan dua group. Kemudian dibandingkan dengan jarak rata-rata masing-masing obyek dengan group splinter dengan groupnya sendiri. Apabila suatu obyek mempunyai jarak yang lebih dekat ke group splinter daripada ke groupnya sendiri, maka obyek tersebut haruslah dikeluarkan dari groupnya dan dipisahkan ke group splinter. Apabila komposisinya sudah stabil, yaitu jarak suatu obyek ke groupnya selalu lebih kecil daripada jarak obyek itu ke group splinter, maka proses berhenti dan dilanjutkan dengan tahap pemisahan dalam group. Contoh : Terdapat matriks jarak antara 5 buah obyek, yaitu : A B C D E A 0 12 9 32 31 B 12 0 9 25 27 C 9 9 0 23 24 D 32 25 23 0 9 E 31 27 24 9 0 Perhitungan : 1. Menghitung jarak rata-rata antar obyek A = ¼ (12+9+32+31) = 21 D = ¼ (32+25+23+9) = 22.25 B = ¼ (12+9+25+27) = 18.25 E = ¼ (31+27+24+9) = 22.75 C = ¼ (9+9+23+24) = 16.25 Terlihat bahwa E mempunyai nilai jarak terjauh, yaitu 22.75, maka E dipisahkan dari group utama dan membentuk group splinter.
- 11. 2. Menghitung jarak rata-rata obyek dengan group utama dengan group splinter Obyek Jarak Rata-rata dengan Group Splinter (x) Jarak Rata-rata dengan Group Utama (y) x - y A 31 17.67 -13.33 B 27 15.33 -11.67 C 24 13.67 -10.33 D 9 26.67 17.67 Pada D, jarak rata-rata dengan group splinter lebih dekat daripada dengan group utama. Dengan demikian D harus dikeluarkan dari group utama dan masuk ke group splinter. Jarak rata-rata group utama (y) = A : ¼ (12+9+32)=17,67 dan seterusnya. 3. Perhitungan jarak rata-rata Obyek Jarak Rata-rata dengan Group Splinter (x) Jarak Rata-rata dengan Group Utama (y) x - y A 31.5 10.5 -21.0 B 26 10.5 -15.5 C 23.5 9.0 -14.5 Karena jarak semua obyek ke group utama sudah lebih besar daripada jaraknya ke group splinter, maka komposisinya sudah stabil. Jarak rata-rata group utama (y) = 31.5/3 = 10.5. kalo jarak rata-rata group splinter (x) = 2(32+31)=31.5 dan sterusnya. M ETO D E O - H I R A R K I Berbeda dengan metode hirarkikal, prosedur non hirarkikal (K-means Clustering) dimulai dengan memilih sejumlah nilai cluster awal sesuai dengan jumlah yang diinginkan dan kemudian obyek digabungkan ke dalam cluster-cluster tersebut. 1) Sequential Threshold Procedure Metode ini melakukan pengelompokan dengan terlebih dahulu memilih satu obyek dasar yang akan dijadikan nilai awal cluster, kemudian semua obyek yang ada didalam jarak terdekat dengan cluster ini akan bergabung lalu dipilih cluster kedua dan semua obyek yang mempunyai kemiripan dimasukkan dalam cluster ini. Demikian seterusnya hingga terbentuk beberapa cluster dengan keseluruhan obyek
- 12. didalamnya.
- 13. 2) Parallel Threshold Prosedure Secara prinsip sama dengan prosedur sequential threshold, hanya saja dilakukan pemilihan terhadap beberapa obyek awal cluster sekaligus dan kemudian melakukan penggabungan obyek ke dalamnya secara bersamaan. 3) Optimizing Merupakan pengembangan dari kedua metode diatas dengan melakukan optimasi pada penempatan obyek yang ditukar untuk cluster lainnya dengan pertimbangan krteria optimasi. Teknik partisi (Partitioning Methods) mencakup : · K-Means Clustering · Methods based on the trace Prosedur analisis cluster K-means digunakan untuk mengelompokkan sejumlah kasus besar yang lebih dari 200 dengan lebih efisien. Metode ini berdasarkan nearest centroid sorting, yaitu pengelompokan berdasarkan jarak terkecil antara kasus dengan pusat dari cluster. Teknik ini membutuhkan jumlah cluster yang ditentukan terlebih dahulu oleh pemakai. Untuk tujuan tersebut dapat menggunakan analisis hierarkikal dalam menentukan jumlah cluster. Teknik ini juga dapat digunakan untuk menempatkan data baru untuk dikelompokkan ke dalam cluster terdekat. Agar hasil cluster dapat digunakan dengan baik, maka sebaiknya dilakukan tahapan interpretasi dan validasi. Yang perlu diperhatikan pada tahapan interpretasi adalah karakteristik yang membedakan masing-masing cluster sehingga kita dapat memberikan label pada masing-masing cluster tersebut. Dengan demikian perlu kiranya dispesifikasikan kriteria-kriteria yang mendasari kelompok-kelompok yang telah terbentuk. Pada tahap validasi dilakukan pengujian terhadap cluster yang telah terbentuk. Uji yang dapat dilakukan antara lain dengan membandingkan hasil yang telah diperoleh dengan algoritma yang berbeda. Sebagai contoh, apabila pertama kali kita menggunakan algoritma hierarkikal, maka kemudian dicoba dengan menggunakan algoritma nonhierarkikal dan kemudian dilihat apakah hasilnya mirip atau tidak. Dengan demikian kita sudah melakukan pengujian terhadap cluster yang kita bentuk.