Prim's Algorithm on minimum spanning tree

Prim's Algorithm
on minimum spanning tree

Submitted by:
Abdullah Al Mamun (Oronno)
Department of Computer Science & Engineering,
University of Dhaka.
2nd Year, Session: 2006-07

What is Minimum Spanning Tree?
• Given a connected, undirected graph, a
spanning tree of that graph is a subgraph
which is a tree and connects all the
vertices together.
• A single graph can have many different
spanning trees.
• A minimum spanning tree is then
a spanning tree with weight less
than or equal to the weight of
every other spanning tree.

graph G

Spanning Tree from Graph G
2 2

4 3 4 5

1 1 1

Algorithm for finding
Minimum Spanning Tree

• The Prim's Algorithm
• Kruskal's Algorithm
• Baruvka's Algorithm

About Prim’s Algorithm
The algorithm was discovered in 1930 by
mathematician Vojtech Jarnik and later independently
by computer scientist Robert C. Prim in 1957.
The algorithm continuously increases the size of a
tree starting with a single vertex until it spans all the
vertices.
Prim's algorithm is faster on dense
graphs.
Prim's algorithm runs in O(n*n)
But the running time can be reduce
using a simple binary heap data structure
and an adjacency list representation

• Prim's algorithm for finding a minimal
spanning tree parallels closely the depth-
and breadth-first traversal algorithms. Just
as these algorithms maintained a closed
list of nodes and the paths leading to
them, Prim's algorithm maintains a closed
list of nodes and the edges that link them
into the minimal spanning tree.
• Whereas the depth-first algorithm used a
stack as its data structure to maintain the
list of open nodes and the breadth-first
traversal used a queue, Prim's uses a
priority queue.

Let’s see an example to
understand
Prim’s Algorithm.

Lets….
 At first we declare an array named: closed list.

 And consider the open list as a priority queue
with min-heap.
 Adding a node and its edge to the closed list
indicates that we have found an edge that links
the node into the minimal spanning
tree. As a node is added to the
closed list, its successors
(immediately adjacent nodes)
are examined and added to a
priority queue of open nodes.

Total Cost: 0

Open List: d
Close List:

Total Cost: 0

Open List: a, f, e, b
Close List: d

Total Cost: 5

Open List: f, e, b
Close List: d, a

Total Cost: 11

Open List: b, e, g
Close List: d, a, f

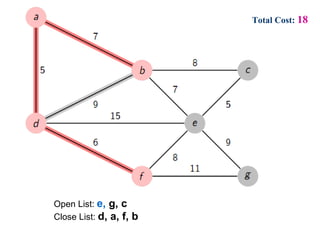
Total Cost: 18

Open List: e, g, c
Close List: d, a, f, b

Total Cost: 25

Open List: c, g
Close List: d, a, f, b, e

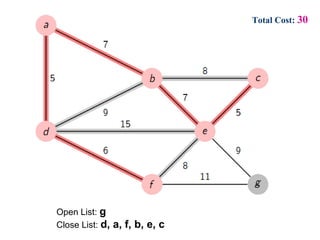
Total Cost: 30

Open List: g
Close List: d, a, f, b, e, c

Total Cost: 39

Open List:
Close List: d, a, f, b, e, c

PSEUDO-CODE FOR PRIM'S
ALGORITHM
 Designate one node as the start node
 Add the start node to the priority queue of open nodes.
 WHILE (there are still nodes to be added to the closed list)
{
Remove a node from priority queue of open nodes, designate it as current
node.
IF (the current node is not already in the closed list)
{
IF the node is not the first node removed from the priority queue, add the
minimal edge connecting it with a closed node to the minimal spanning
tree.
Add the current node to the closed list.
FOR each successor of current node
IF (the successor is not already in the closed list OR the successor is
now connected to a closed node by an edge of lesser weight than
before)
Add that successor to the priority queue of open nodes;
}
}

Sample C++ Implementation
• void prim(graph &g, vert s) { • int minvertex(graph &g, int *d) {
• int v;
• int dist[g.num_nodes];
• int vert[g.num_nodes]; • for (i = 0; i < g.num_nodes; i++)
• if (g.is_marked(i, UNVISITED)) {
• for (int i = 0; i < g.num_nodes; i++) { • v = i; break;
• dist[i] = INFINITY; • }

• dist[s.number()] = 0; • for (i = 0; i < g.num_nodes; i++)
• if ((g.is_marked(i, UNVISITED)) && (dist[i] <
dist[v])) v = i;
• for (i = 0; i < g.num_nodes; i++) {
• vert v = minvertex(g, dist);
• return (v);
• }
• g.mark(v, VISITED);
• if (v != s) add_edge_to_MST(vert[v], v);
• if (dist[v] == INFINITY) return;

• for (edge w = g.first_edge; g.is_edge(w), w = g.next_edge(w)) {
• if (dist[g.first_vert(w)] = g.weight(w)) {
• dist[g.second_vert(w)] = g.weight(w);
• vert[g.second_vert(w)] = v;
• }
• }
• }
• }

Complexity Analysis
Minimum edge weight data Time complexity (total)
structure

adjacency matrix, searching O(V*V)

binary heap and adjacency O((V + E) log(V)) = O(E
list log(V))

Fibonacci heap and O(E + V log(V))
adjacency list

Application
 One practical application of a MST would be in the design of a
network. For instance, a group of individuals, who are
separated by varying distances, wish to be connected together
in a telephone network. Because the cost between two terminal
is different, if we want to reduce our expenses, Prim's
Algorithm is a way to solve it
 Connect all computers in a computer science building using
least amount of cable.
 A less obvious application is that the minimum spanning tree
can be used to approximately solve the traveling salesman
problem. A convenient formal way of defining this problem is
to find the shortest path that visits each point at least once.
 Another useful application of MST would be finding airline
routes. The vertices of the graph would represent cities, and
the edges would represent routes between the cities.
Obviously, the further one has to travel, the more it will cost,
so MST can be applied to optimize airline routes by finding
the least costly paths with no cycles.

Reference
Book:
Introduction to Algorithm
By: Thomas H. Cormen
Website:
• mathworld.wolfram.com
• www-b2.is.tokushima-u.ac.jp/suuri/Prim.shtml
• www.cprogramming.com/tutorial/
computersciencetheory/mst.html
• en.wikipedia.org/wiki/Prim's_algorithm
• www.unf.edu/~wkloster/foundations/
PrimApplet/PrimApplet.htm

Thank you for being with me…

Any question?????

Prim's Algorithm on minimum spanning tree

More Related Content

What's hot (20)

Similar to Prim's Algorithm on minimum spanning tree (20)

Recently uploaded (20)

Prim's Algorithm on minimum spanning tree