Probabilistic data structures. Part 3. Frequency
- 1. tech talk @ ferret Andrii Gakhov PROBABILISTIC DATA STRUCTURES ALL YOU WANTED TO KNOW BUT WERE AFRAID TO ASK PART 3: FREQUENCY
- 2. FREQUENCY Agenda: ▸ Count-Min Sketch ▸ Majority Algorithm ▸ Misra-Gries Algorithm
- 3. • To estimate number of times an element occurs in a set THE PROBLEM
- 5. COUNT-MIN SKETCH • proposed by G. Cormode and S. Muthukrishnan in 2003 • CM Sketch is a sublinear space data structure that supports: • add element to the structure • count number of times the element has been added (frequency) • Count-Min Sketch is described by 2 parameters: • m - number of buckets (independent from n, but much smaller) • k - number of different hash functions, that map to 1…m (usually, k is much smaller than m) • required fixed space: m*k counters and k hash functions
- 6. COUNT-MIN SKETCH: ALGORITHM • Count-Min Sketch is simply an matrix of counters (initially all 0), where each row corresponds to a hash function hi, i=1…k • To add element into the sketch - calculate all k hash functions increment counters in positions [i, hi(element)], i=1…k +1 +1 +1 +1 +1 h1 h2 hk 1 2 3 m x h1(x) h2(x) hk(x) … … …
- 7. COUNT-MIN SKETCH: ALGORITHM • Because of soft collisions, we have k estimations of the true frequency of the element, but because we never decrement counter it can only overestimate, not underestimate. • To get frequency of the element we calculate all k hash functions and return the minimal value of the counters in positions [i, hi(element)], i=1…k. • Time needed to add element or return its frequency is a fixed constant O(k), assuming that every hash function can be evaluated in a constant time.
- 8. COUNT-MIN SKETCH: EXAMPLE • Consider Count-Min Sketch with 16 columns (m=16) • Consider 2 hash functions (k=2): h1 is MurmurHash3 and h2 is Fowler-Noll-Vo (to calculate the appropriate index, we divide result by mod 16) • Add element to the structure: “berlin” h1(“berlin”) = 4, h2(“berlin”) = 12 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 01 2 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 01 2 0
- 9. COUNT-MIN SKETCH: EXAMPLE • Add element “berlin” 5 more times (so, 6 in total): • Add element “bernau”: h1(“bernau”) = 4, h2(“bernau”) = 4 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 0 0 0 0 0 0 0 0 0 0 0 0 6 0 0 0 0 0 0 0 6 0 0 0 0 0 0 0 0 0 0 01 2 0 • Add element “paris”: h1(“paris”) = 11, h2(“paris”) = 4 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 0 0 0 0 1 0 0 0 0 0 0 0 6 0 0 0 0 0 0 0 7 0 0 0 0 0 0 0 0 0 0 01 2 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 0 0 0 0 2 0 0 0 0 0 0 0 6 0 0 0 0 0 0 0 7 0 0 0 0 0 0 1 0 0 0 01 2 0
- 10. COUNT-MIN SKETCH: EXAMPLE • Get frequency for element: “london”: h1(“london”) = 7, h2(“london”) = 4 freq(“london”) = min (0, 2) = 0 • Get frequency for element: “berlin”: h1(“berlin”) = 4, h2(“berlin”) = 12 freq(“berlin”) = min (7, 6) = 6 • Get frequency for element: “warsaw”: h1(“warsaw”) = 4, h2(“warsaw”) = 12 freq(“warsaw”) = min (7, 6) = 6 !!! due to hash collision 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 0 0 0 0 2 0 0 0 0 0 0 0 6 0 0 0 0 0 0 0 7 0 0 0 0 0 0 1 0 0 0 01 2 0
- 11. COUNT-MIN SKETCH: PROPERTIES • Count-Min Sketch only returns overestimates of true frequency counts, never underestimates • To achieve a target error probability of δ, we need k ≥ ln 1/δ. • for δ around 1%, k = 5 is good enough • Count-Min Sketch is essentially the same data structure as the Counting Bloom filters. The difference is followed from the usage: • Count-Min Sketch has a sublinear number of cells, related to the desired approximation quality of the sketch • Counting Bloom filter is sized to match the number of elements in the set
- 12. COUNT-MIN SKETCH: APPLICATIONS • AT&T has used Count-Min Sketch in network switches to perform analyses on network traffic using limited memory • At Google, a precursor of the count-min sketch (called the “count sketch”) has been implemented on top of their MapReduce parallel processing infrastructure • Implemented as a part of Algebird library from Twitter
- 13. COUNT-MIN SKETCH: PYTHON • https://github.com/rafacarrascosa/countminsketch CountMinSketch is a minimalistic Count-min Sketch in pure Python • https://github.com/farsightsec/fsisketch FSI Sketch a disk-backed implementation of the Count- Min Sketch algorithm
- 14. COUNT-MIN SKETCH: READ MORE • http://dimacs.rutgers.edu/~graham/pubs/papers/cm- latin.pdf • http://dimacs.rutgers.edu/~graham/pubs/papers/ cmencyc.pdf • http://dimacs.rutgers.edu/~graham/pubs/papers/ cmsoft.pdf • http://theory.stanford.edu/~tim/s15/l/l2.pdf • http://www.cs.dartmouth.edu/~ac/Teach/CS49-Fall11/ Notes/lecnotes.pdf
- 15. • To find a single element that occurs strictly more than n / 2 times n - number of elements in a set MAJORITY PROBLEM
- 16. MAJORITY PROBLEM • Mostly a toy problem, but it let us better understand the frequency problems for data streams • Majority problem has been formulated as a research problem by J Strother Moore in the Journal of Algorithms in 1981. • It’s possible that such element does not exists • It could be at most one majority element in the set • If such element exists, it will be equal to the median. So, the Naïve linear-time solution - compute the median of the set • Problem: it requires multiple pass through the stream
- 17. MAJORITY PROBLEM • The Boyer-Moore Majority Vote Algorithm has been invented by Bob Boyer and J Strother Moore in 1980 to solve the Majority Problem in a single pass through the data stream. • The similar solution was independently proposed by Michael J. Fischer and Steven L. Salzberg in 1982.This is the most popular algorithm for undergraduate classes due to its simplicity. • An important pre-requirement is that the majority element actually exists, without it the output of the algorithm will be an arbitrary element of the data stream. • Algorithm requires only 1 left-to-right pass! • The Data structure for the Majority Algorithm just a pair of an integer counter and monitored element current
- 18. MAJORITY ALGORITHM: ALGORITHM • Initialise counter with 1 and current with the first element from the left • Going from left to right: • If counter equals to 0, then take the current element as the current and set counter to 1 • if counter isn’t 0, then increase counter by 1 if the element equals to current or decrease counter by 1 otherwise • The last current is the majority element (if counter bigger that 0) Intuition: each element that contains a non-majority-value can only “cancel out” one copy of the majority value. Since more than n/2 of the elements contain the majority value, there is guaranteed to be a copy of it left standing at the end of the algorithm.
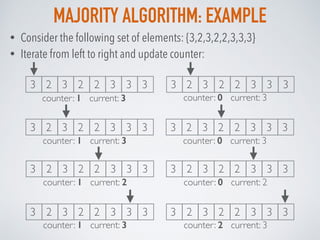
- 19. MAJORITY ALGORITHM: EXAMPLE • Consider the following set of elements: {3,2,3,2,2,3,3,3} • Iterate from left to right and update counter: 3 2 3 2 2 3 3 3 counter: 1 current: 3 3 2 3 2 2 3 3 3 counter: 1 current: 3 3 2 3 2 2 3 3 3 counter: 0 current: 3 3 2 3 2 2 3 3 3 counter: 0 current: 3 3 2 3 2 2 3 3 3 counter: 1 current: 2 3 2 3 2 2 3 3 3 counter: 0 current: 2 3 2 3 2 2 3 3 3 counter: 1 current: 3 3 2 3 2 2 3 3 3 counter: 2 current: 3
- 20. MAJORITY: READ MORE • https://courses.cs.washington.edu/courses/cse522/14sp/ lectures/lect04.pdf • http://theory.stanford.edu/~tim/s16/l/l2.pdf
- 21. • To find elements that occurs more than n / k times (n >> k) * also known as k-frequency-estimation HEAVY HITTERS PROBLEM
- 22. • There are not more than k such values • The majority problem is a particular case of the heavy hitters problem • k ≈ 2 − δ for a small value δ > 0 • with the additional promise that a majority element exists • Theorem: There is no algorithm that solves the heavy hitters problems in one pass while using a sublinear amount of auxiliary space • ε-approximate heavy hitters (ε-HH) problem: • every value that occurs at least n/k times is in the list • every value in the list occurs at least n/k − εn times in the set • ε-HH can be solved with Count-Min Sketch as well, but we consider Misra-Gries / Frequent algorithm here … HEAVY HITTERS PROBLEM
- 24. MISRA-GRIES / FREQUENT ALGORITHM • A generalisation of the Majority Algorithm to track multiple frequent items, known as Frequent Algorithm, was proposed by Erik D. Demaine, et al. in 2002. • After some time it was discovered that the Frequent algorithm actually the same as the algorithm that was published by Jayadev Misra and David Gries in 1982, known now as Misra-Gries Algorithm • The trick is to run the Majority algorithm, but with many counters instead of 1 • The time cost of the algorithm is dominated by the O(1) dictionary operations per update, and the cost of decrementing counts
- 25. MISRA-GRIES: ALGORITHM The Data structure for Misra-Gries algorithm consists of 2 arrays: • an array of k-1 frequency counters C (all 0) and k-1 locations X* (empty set) For every element xi in the set: • If xi is already in X* at some index j: • increase its corresponding frequency counter by 1: C[j] = C[j] + 1 • If xi not in X*: • If size of X* less than k (so, there is free space in the top): • append xi to X* at index j • set the corresponding frequency counter C[j] =1 • else If X* is already full: • decrement all frequency counters by 1: C[j] = C[j] - 1, j=1..k-1 • remove such elements from X* whose counters are 0. Top k-1 frequent elements : X*[j] with frequency estimations C[j], j=1..k-1
- 26. MISRA-GRIES:EXAMPLE 0 0C: X*: • Step 1: {3,2,1,2,2,3,1,3} Element {3} isn’t in X* already and X* isn’t full, so we add it at position 0 and set C[0] = 1 • Step 2: {3,2,1,2,2,3,1,3} Element {2} isn’t in X* already and X* isn’t full, so we add it at position 1 and set C[1] = 1 1 0C: X*: 3 • Consider the following set of elements: {3,2,1,2,2,3,1,3}, n= 8 • We need to find top 2 elements in the set that appears at least n/3 times. 1 1 2 C: X*: 3
- 27. MISRA-GRIES:EXAMPLE • Step 3: {3,2,1,2,2,3,1,3} Element {1} isn’t in X* already, but X* is full, so decrement all counters and remove elements that have counters less then 1: • Step 4: {3,2,1,2,2,3,1,3} Element {2} isn’t in X* already and X* isn’t full, so we add it at position 0 and set C[0] = 1 0 0C: X*: 1 0C: X*: 2 • Step 5: {3,2,1,2,2,3,1,3} Element {2} is in X* at position 0, so we increase its counter C[0] = C[0] + 1 = 2 2 0C: X*: 2
- 28. MISRA-GRIES:EXAMPLE • Step 6: {3,2,1,2,2,3,1,3} Element {3} isn’t in X* already and X* isn’t full, so we append {3} at position 1 and set its counter to 1: C[1] = 1 • Step 7: {3,2,1,2,2,3,1,3} Element {1} isn’t in X* already, but X* is full, so decrement all counters and remove elements that have 0 as the counters values: 2 1 3 C: X*: 2 1 0C: X*: 2 • Step 8: {3,2,1,2,2,3,1,3} Element {3} isn’t in X* already and X* isn’t full, so we append {3} at position 1 and set its counter to 1: C[1] = 1 2 1 3 C: X*: 2 Top 2 elements
- 29. MISRA-GRIES: PROPERTIES • The algorithm identifies at most k-1 candidates without any probabilistic approach. • It's still open question how to process such updates quickly, or particularly, how to decrement and release several counters simultaneously. • For instance, it was proposed to use doubly linked list of counters and store only the differences between same-value counter’s groups and use. With such data structure each counter no longer needs to store a value, but rather its group and its monitored element.
- 30. MISRA-GRIES: READ MORE • https://courses.cs.washington.edu/courses/cse522/14sp/ lectures/lect04.pdf • http://dimacs.rutgers.edu/~graham/pubs/papers/ encalgs-mg.pdf • http://drops.dagstuhl.de/opus/volltexte/2016/5773/pdf/ 3.pdf • http://theory.stanford.edu/~tim/s16/l/l2.pdf
- 31. ▸ @gakhov ▸ linkedin.com/in/gakhov ▸ www.datacrucis.com THANK YOU






![COUNT-MIN SKETCH: ALGORITHM
• Count-Min Sketch is simply an matrix of counters (initially all 0), where each row
corresponds to a hash function hi, i=1…k
• To add element into the sketch - calculate all k hash functions increment
counters in positions [i, hi(element)], i=1…k
+1
+1
+1
+1
+1
h1
h2
hk
1 2 3 m
x
h1(x)
h2(x)
hk(x)
… …
…](https://image.slidesharecdn.com/probabilisticdatastructurespart3-160923061849/85/Probabilistic-data-structures-Part-3-Frequency-6-320.jpg)
![COUNT-MIN SKETCH: ALGORITHM
• Because of soft collisions, we have k estimations of the true
frequency of the element, but because we never decrement
counter it can only overestimate, not underestimate.
• To get frequency of the element we calculate all k hash
functions and return the minimal value of the counters in
positions [i, hi(element)], i=1…k.
• Time needed to add element or return its frequency is a fixed
constant O(k), assuming that every hash function can be
evaluated in a constant time.](https://image.slidesharecdn.com/probabilisticdatastructurespart3-160923061849/85/Probabilistic-data-structures-Part-3-Frequency-7-320.jpg)
















![MISRA-GRIES: ALGORITHM
The Data structure for Misra-Gries algorithm consists of 2 arrays:
• an array of k-1 frequency counters C (all 0) and k-1 locations X* (empty set)
For every element xi in the set:
• If xi is already in X* at some index j:
• increase its corresponding frequency counter by 1: C[j] = C[j] + 1
• If xi not in X*:
• If size of X* less than k (so, there is free space in the top):
• append xi to X* at index j
• set the corresponding frequency counter C[j] =1
• else If X* is already full:
• decrement all frequency counters by 1: C[j] = C[j] - 1, j=1..k-1
• remove such elements from X* whose counters are 0.
Top k-1 frequent elements : X*[j] with frequency estimations C[j], j=1..k-1](https://image.slidesharecdn.com/probabilisticdatastructurespart3-160923061849/85/Probabilistic-data-structures-Part-3-Frequency-25-320.jpg)
![MISRA-GRIES:EXAMPLE
0 0C:
X*:
• Step 1: {3,2,1,2,2,3,1,3}
Element {3} isn’t in X* already and X* isn’t full, so we add it at position 0 and set C[0] = 1
• Step 2: {3,2,1,2,2,3,1,3}
Element {2} isn’t in X* already and X* isn’t full, so we add it at position 1 and set C[1] = 1
1 0C:
X*: 3
• Consider the following set of elements: {3,2,1,2,2,3,1,3}, n= 8
• We need to find top 2 elements in the set that appears at least n/3 times.
1 1
2
C:
X*: 3](https://image.slidesharecdn.com/probabilisticdatastructurespart3-160923061849/85/Probabilistic-data-structures-Part-3-Frequency-26-320.jpg)
![MISRA-GRIES:EXAMPLE
• Step 3: {3,2,1,2,2,3,1,3}
Element {1} isn’t in X* already, but X* is full, so decrement all counters and remove
elements that have counters less then 1:
• Step 4: {3,2,1,2,2,3,1,3}
Element {2} isn’t in X* already and X* isn’t full, so we add it at position 0 and set C[0] = 1
0 0C:
X*:
1 0C:
X*: 2
• Step 5: {3,2,1,2,2,3,1,3}
Element {2} is in X* at position 0, so we increase its counter C[0] = C[0] + 1 = 2
2 0C:
X*: 2](https://image.slidesharecdn.com/probabilisticdatastructurespart3-160923061849/85/Probabilistic-data-structures-Part-3-Frequency-27-320.jpg)
![MISRA-GRIES:EXAMPLE
• Step 6: {3,2,1,2,2,3,1,3}
Element {3} isn’t in X* already and X* isn’t full, so we append {3} at position 1 and set
its counter to 1: C[1] = 1
• Step 7: {3,2,1,2,2,3,1,3}
Element {1} isn’t in X* already, but X* is full, so decrement all counters and remove
elements that have 0 as the counters values:
2 1
3
C:
X*: 2
1 0C:
X*: 2
• Step 8: {3,2,1,2,2,3,1,3}
Element {3} isn’t in X* already and X* isn’t full, so we append {3} at position 1 and set
its counter to 1: C[1] = 1
2 1
3
C:
X*: 2
Top 2 elements](https://image.slidesharecdn.com/probabilisticdatastructurespart3-160923061849/85/Probabilistic-data-structures-Part-3-Frequency-28-320.jpg)


