Randomized algorithms all pairs shortest path

Randomized
Algorithms: All Pairs
Shortest Path
Instructor: Dr. S. N. Hashemi
Lecturer: Mohammad Akbarizadeh
m.akbarizadeh@aut.ac.ir

Outline
● Deterministic Algorithms
○ Single Source Shortest Path
■ Dijkstra
■ Bellman-Ford
○ All Pairs Shortest path
■ Floyd-Warshall
● Randomized Algorithm
○ All Pair Distance problem
○ Boolean Product Witness Matrix
○ All Pair Shortest Path
● Comparison
2

Deterministic Algorithms
Single Source Shortest Path

Question
Q: How to solve the single source shortest path problem if the given graph is unweighted?
What is the time complexity?
4

Question
Q: How to solve the single source shortest path problem if the given graph is unweighted?
What is the time complexity?
A: We can easily apply BFS to the graph and solve it in O(V+E)
5

Dijkstra Algorithm
● Given a graph and a source vertex, find shortest paths from source to all vertices in the
given graph
● Dijkstra is a greedy algorithm for finding the shortest path from a node which ends in
having a tree with the lowest total cost (similar algorithms: Prim, Kruskal)
● It can be applied to both directed and undirected graph
● Dijkstra doesn’t work for Graphs with negative weight edges
● Time complexity: O(V2)
6

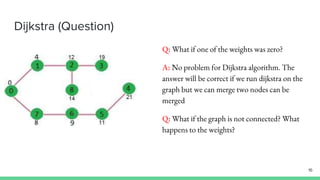
Dijkstra (example)
Graph = {(0,1)=4, (0,7)=8, (1,2)=8, (1,7)=11,
(7,8)=7, (7,6)=1, (2,3)=7, (2,5)=4, (2,8)=2,
(8,6)=6, (6,5)=2, (3,4)=9, (3,5)=14, (5,4)=10}
Distance = {INF, INF, INF, INF, INF, INF,
INF, INF, INF}
Prev = {UND, UND, UND, UND, UND,
UND, UND, UND, UND}
Q = {0, 1, 2, 3, 4, 5, 6, 7, 8}
8

Dijkstra (example)
Graph = {(0,1)=4, (0,7)=8, (1,2)=8, (1,7)=11,
(7,8)=7, (7,6)=1, (2,3)=7, (2,5)=4, (2,8)=2,
(8,6)=6, (6,5)=2, (3,4)=9, (3,5)=14, (5,4)=10}
Distance = {0, 4, INF, INF, INF, INF, INF, 8,
INF}
Prev = {UND, 0, UND, UND, UND, UND,
UND, 0, UND}
Q = {1, 2, 3, 4, 5, 6, 7, 8}
9

Dijkstra (example)
Graph = {(0,1)=4, (0,7)=8, (1,2)=8, (1,7)=11,
(7,8)=7, (7,6)=1, (2,3)=7, (2,5)=4, (2,8)=2,
(8,6)=6, (6,5)=2, (3,4)=9, (3,5)=14, (5,4)=10}
Distance = {0, 4, 12, INF, INF, INF, INF, 8,
INF}
Prev = {UND, 0, 1, UND, UND, UND,
UND, 0, UND}
Q = {2, 3, 4, 5, 6, 7, 8}
10

Dijkstra (example)
Graph = {(0,1)=4, (0,7)=8, (1,2)=8, (1,7)=11,
(7,8)=7, (7,6)=1, (2,3)=7, (2,5)=4, (2,8)=2,
(8,6)=6, (6,5)=2, (3,4)=9, (3,5)=14, (5,4)=10}
Distance = {0, 4, 12, INF, INF, INF, 9, 8, 15}
Prev = {UND, 0, 1, UND, UND, UND, 7, 0,
7}
Q = {2, 3, 4, 5, 6, 8}
11

Dijkstra (example)
Graph = {(0,1)=4, (0,7)=8, (1,2)=8, (1,7)=11,
(7,8)=7, (7,6)=1, (2,3)=7, (2,5)=4, (2,8)=2,
(8,6)=6, (6,5)=2, (3,4)=9, (3,5)=14, (5,4)=10}
Distance = {0, 4, 12, INF, INF, 11, 9, 8, 15}
Prev = {UND, 0, 1, UND, UND, 6, 7, 0, 6}
Q = {2, 3, 4, 5, 8}
12

Dijkstra (example)
Graph = {(0,1)=4, (0,7)=8, (1,2)=8, (1,7)=11,
(7,8)=7, (7,6)=1, (2,3)=7, (2,5)=4, (2,8)=2,
(8,6)=6, (6,5)=2, (3,4)=9, (3,5)=14, (5,4)=10}
Distance = {0, 4, 12, 19, 21, 11, 9, 8, 14}
Prev = {UND, 0, 1, 2, 5, 6, 7, 0, 2}
Q = {}
13

Dijkstra (Question)
Q: What if one of the weights was zero?
14

Dijkstra (Question)
A: No problem for Dijkstra algorithm. The
answer will be correct if we run dijkstra on the
graph but we can merge two nodes can be
merged
15

Dijkstra (Question)
merged
Q: What if the graph is not connected? What
happens to the weights?
16

Dijkstra (Question)
merged
Q: What if the graph is not connected? What
happens to the weights?
A: Nodes that are not reachable from the
source will have INF value and the algorithm
will not proceed 17

Bellman-Ford Algorithm
● Given a graph and a source vertex src in graph, find shortest paths from src to all
vertices in the given graph.
● This algorithm works with graphs having negative weight edges
● Greedy algorithm but simpler than Dijkstra and uses relaxation like Dijkstra
● It relaxes all the edges at most |V|-1 times until it finds the answer (no change happens
after update)
● Time complexity: O(VE)
18

Bellman-Ford Algorithm (pseudocode)
19

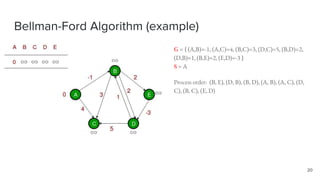
Bellman-Ford Algorithm (example)
20
G = { (A,B)=-1, (A,C)=4, (B,C)=3, (D,C)=5, (B,D)=2,
(D,B)=1, (B,E)=2, (E,D)=-3 }
S = A
Process order: (B, E), (D, B), (B, D), (A, B), (A, C), (D,
C), (B, C), (E, D)

21
G = { (A,B)=-1, (A,C)=4, (B,C)=3, (D,C)=5, (B,D)=2,
(D,B)=1, (B,E)=2, (E,D)=-3 }
S = A
C), (B, C), (E, D)

22
G = { (A,B)=-1, (A,C)=4, (B,C)=3, (D,C)=5, (B,D)=2,
(D,B)=1, (B,E)=2, (E,D)=-3 }
S = A
C), (B, C), (E, D)

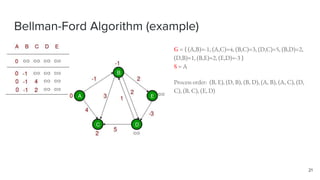
Bellman-Ford Algorithm (Question)
23
Q = What happens if (B,D)=-2 and (D,B)=-1 ?

24
Q = What happens if (B,D)=-2 and (D,B)=-1 ?
A = The algorithm gets stuck in a loop and updates the
weights until it reaches the end of the algorithm
(Algorithm won't work in this situation)
C), (B, C), (E, D)

25
Q = When does the worst case scenario happens? What
is the worst case scenario for this algorithm?

26
Q = When does the worst case scenario happens? What
is the worst case scenario for this algorithm?
A = When we a complete graph like K5 we will have
V(V-1)/2 edges which have to processed V times, which
has O(V3) time complexity

Deterministic Algorithms
All Pairs Shortest Path

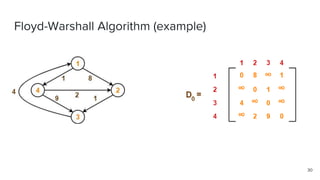
Floyd-Warshall Algorithm
● Given a graph, finds the shortest paths from all vertices to all other vertices
● Uses Dynamic Programming to solve the problem
● Edge weights can be negative (but no negative cycles) and graph can be directed
● Time complexity: O(V3)
28

Floyd-Warshall Algorithm (pseudocode)
29

Floyd-Warshall Algorithm (example)
30

31

32

33

34

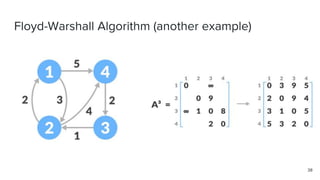
Floyd-Warshall Algorithm (another example)
35

36

37

38

39

Randomized Algorithm
● A Las Vegas algorithm is a randomized algorithm that always gives the correct result but
gambles with resources.
● Monte Carlo simulations are a broad class of algorithms that use repeated random
sampling to obtain numerical results.
○ Monte Carlo simulations are typically used to simulate the behaviour of other systems.
○ Monte Carlo algorithms, on the other hand, are randomized algorithms whose output may be incorrect with
a certain, typically small, probability.
41

How to solve APSP problem using Randomized
algorithms?
● We will show that the problem of computing all-pairs shortest path is reducible, via a
randomized reduction, to the problem of multiplying two integer matrices
● First we solve the easier version of problem for unweighted graph and then get to solve the
weighted graph
42

All Pair Distance Problem

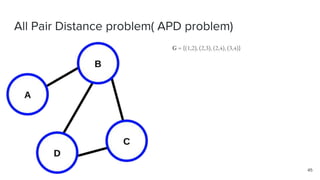
All Pair Distance problem( APD problem)
● Given an unweighted graph G and its adjacency matrix A, compute the distance
matrix D
● Let G’(V,E’) be a graph obtained from G(V,E) by placing an edge between every pair of
vertices i≠j ∊V that are at distance 1 or 2 in G
● The graph G is a subgraph of G’, and we could view G’ as the square of the graph G
● Lemma 1: If we compute Z=A2, then there is path of length 2 in G between pair of
vertices i and j if and only if Zij>0. Further, the value of Zij indicates the number of distinct
length 2 paths between i and j
● If we compute Z=A3, we can obtain if there is a path of length 3 between i and j in G if and
only if Zij>0
44

45
G = {(1,2), (2,3), (2,4), (3,4)}

46
G = {(1,2), (2,3), (2,4), (3,4)}
A = [[ 0, 1, 0, 0],
[ 1, 0, 1, 1],
[0, 1, 0, 1],
[0, 1, 1, 0]]

47
G = {(1,2), (2,3), (2,4), (3,4)}
A = [[ 0, 1, 0, 0],
[ 1, 0, 1, 1],
[0, 1, 0, 1],
[0, 1, 1, 0]]
A2= [[1, 0, 1, 1],
[0, 3, 1, 1],
[1, 1, 2, 1],
[1, 1, 1, 2]]

● If given graph G with adjacency matrix A and distance matrix D and we compute Z=G2
with adjacency matrix A’ and distance matrix D’
● To ensure A’ has a zero diagonal, we compute it by setting A’
ij=1 if and only if i≠j and at
least one of A’
ij or Aij is non-zero
● We can observe G’ is complete if and only if G has diameter at most 2, where diameter of a
graph is the maximum shortest path length over all pairs of vertices
● is there any way we could compute D’ from D?
48

● Observation: if G has a diameter at most 2, then G’ is complete and in D=2A’-A
● This can be obtained from A and A’ in time O(n2)
● Lemma 2: consider any pair of vertices i,j ∊V
○ If Dij is even then Dij=2D’
ij
○ If Dij is odd then Dij=2D’
ij - 1
● By using this lemma we can recursively compute distance matrix of graph G from distance
matrix of graph G’
● But how can we compute the parities of the shortest path lengths?
49

● Lemma 3: consider any pair of distinct vertices i and j in G
○ For any neighbor k of i, Dij- 1 ≤ Dkj ≤ Dij+ 1
○ There exists a neighbor k of i such that Dkj = Dij - 1
● Now using this lemma we can have a structural property to compute the parities of the
shortest path lengths
● Lemma 4: consider any pair of distinct vertices i and j in G:
○ If Dij is even, then D’
kj ≥ D’
ij for every neighbor k of i in G
○ If Dij is odd, then D’
kj ≤ D’
ij for every neighbor k of i in G. moreover, there exists a neighbor k of i in G such
that D’
kj < D’
ij
50

● Let Γ(i) denote the set of neighbors of i in G and d(i) be the degree of i. Note that A’
ii=d(i)
● By summing the inequalities in lemma 4 over the neighbors of vertex i we can obtain the
following result:
● Lemma 5: consider any pair of distinct vertices i and j in G:
○ Dij is even if and only if ∑k∊Γ(i) D’
kj ≥ D’
ijd(i)
○ Dij is odd if and only if ∑k∊Γ(i) D’
kj < D’
ijd(i)
● In this lemma matrix multiplication is used to compute:
○ ∑k∊Γ(i) D’
kj= ∑n
k=1 Aik D’
kj = Sij
51

52

53
● The APD algorithm computes the distance matrix for an n-vertex graph G in time
O(MM(n) log n) using integer matrix multiplication
● MM(n) indicates matrix multiplication of square matrices with length n
● The ordinary matrix multiplication algorithm has time complexity of O(n3) and currently
the best time complexity has time complexity O(n2.373)

Boolean Product Witness Matrix(BPWM)

55
● Suppose A and B are n*n boolean(0,1) matrices and P=AB is their product under boolean
matrix multiplication
● A witness for Pij is an index k∊{1, ..., n} such that Aik = Bkj = 1
● Observe that Pij=1 if and only if it has some witness k
● A Boolean Product Witness Matrix(BPWM) for P is an integer matrix W such that each
entry Wij contains a witness k for Pij if any, and is 0 if there is no such witness
● There could be as many as n witnesses for each entry in p
● The integer matrix multiplication of A and B, treating their entries as the integer 0 and 1,
yields a matrix C whose entry Cij corresponds exactly to the number of witnesses for
boolean matrix entry Pij

56
G = {(1,2), (1,6), (2,3), (2,4), (2,5), (2,6), (3,4), (4,5),
(5,6)}
A =[[0, 1, 0, 0, 0, 1],
[1, 0, 1, 1, 1, 1],
[0, 1, 0, 1, 0, 0],
[0, 1, 1, 0, 1, 0],
[0, 1, 0, 1, 0, 1],
[1, 1, 0, 0, 1, 0]]
A2=[[2, 1, 1, 1, 2, 1],
[1, 5, 1, 2, 2, 2],
[1, 1, 2, 1, 2, 1],
[1, 2, 1, 3, 1, 2],
[2, 2, 2, 1, 3, 1],
[1, 2, 1, 2, 1, 3]]

57
● If there is a unique witness for each vertex there is no problem with BPWM but if there are
many witnesses we can use some randomness
● Lemma 6: suppose an urn contains n balls of which w are white, and n-w are black.
Consider choosing r balls at random(without replacement), where n/2 ≤ wr ≤ n then:
○ PR[exactly one white ball is chosen] ≥ 1/2e

58
Consider we have n=100 balls
W = 4 balls are white
n/2 <= 4r <=n
50 <= 4r <= 100
13 <=r <= 25

60
● So what is the usage of this usage?
● Assume we have set R which contains unique witness for Pij
● R is represented as incidence vector that has Rk=1 for k∈R and Rk=0 for k∉R
● Let AR be the matrix obtained from A by setting AR
ik=kRkAik
● Let BR be the matrix obtained from B by setting BR
kj=RkBkj
● So if the entry Pij has a unique witness in the set R, corresponding entry in the integer
matrix multiplication of AR and BR is the index of this unique witness

61
● A key point is that the product of AR and BR yields witnesses for all entries in P that have a
unique witness in R
● By lemma 6 there is a constant probability that a random set R of size r has a unique
witness for an entry in P with w witness where n/2r ≤ w ≤ n/r
● Repeating this for O(log n) independent choices of R makes it extremely unlikely that
witnesses are not identified for such entries in P
● Combining the thoughts above results the following algorithm

62

63
● The BPWM algorithm is Las Vegas algorithm for BPWM problem with expected
running time O(MM(n) log2 n)
● Now we use APD and BPWM algorithm to solve APSP problem

All Pair Shortest Path

All Pair Shortest Path(randomized)
65
● We define a successor matrix S for an n-vertex graph G is and n*n matrix such that Sij is the
index k of a neighbor of vertex i that lies on a shortest path from i to j
● Fact: The successor entry for Sij=k iff
○ Dij=d
○ Dik=1
○ Dkj=d-1
○ Aik=1
● Let Bd denote the n*n boolean matrix in which Bd
kj=1 iff Dkj=d-1
● We can compute Bd from D in O(n2) time
● The problem is that this process must be repeated for n different values of d, leading to
super-cubic algorithm which is not good!

66

67
● The APSP computes the successor matrix for and n-vertex graph G in expected time
O(MM(n) log2n)

Comparison
Deterministic algorithms:
Dijkstra+Johnson: O(EV + V2 log V)
Floyd–Warshall algorithm: O(V3)
Randomized Algorithm:
APSP: O(n2.373 log2 n)
69

References
1. Prof. Eric Price, CS 388R Randomized Algorithms, Fall 2019, University of Texas ( available at :
https://www.cs.utexas.edu/~ecprice/courses/randomized/ )
2. David Karger. 6.856J Randomized Algorithms. Fall 2002. Massachusetts Institute of Technology: MIT OpenCourseWare (
available at : https://ocw.mit.edu/courses/electrical-engineering-and-computer-science/6-856j-randomized-algorithms-fall-
2002/index.htm )
3. Motwani, R., & Raghavan, P. (1995). Randomized Algorithms. Cambridge: Cambridge University Press.
doi:10.1017/CBO9780511814075
4. https://en.wikipedia.org/wiki/Shortest_path_problem#Single-source_shortest_paths
5. https://www.geeksforgeeks.org/dijkstras-shortest-path-algorithm-greedy-algo-7/
6. https://en.wikipedia.org/wiki/Dijkstra%27s_algorithm
7. https://www.youtube.com/watch?v=FtN3BYH2Zes
8. https://www.youtube.com/watch?v=oNI0rf2P9gE
9. https://www.youtube.com/watch?v=XB4MIexjvY0
10. https://www.geeksforgeeks.org/bellman-ford-algorithm-dp-23/
11. https://stackoverflow.com/questions/49460439/can-dijkstras-algorithm-work-on-a-graph-with-weights-of-0
12. https://www.programiz.com/dsa/bellman-ford-algorithm
70

References
12. Algorithms course notes, University of Illinois,(available at: https://jeffe.cs.illinois.edu/teaching/algorithms/book/09-
apsp.pdf )
13. https://www.gatevidyalay.com/floyd-warshall-algorithm-shortest-path-algorithm/
14. https://www.programiz.com/dsa/floyd-warshall-algorithm
15. https://yourbasic.org/algorithms/las-vegas/
16. (44) Lec 26: All pair shortest path-I - YouTube
17. (44) Lec 27: All pair shortest path-II - YouTube
71

exercises
1. Prover lemma 4 and 6
2. Explain and prove time complexity of APD and BPWM algorithm
3. (Bonus) Implement this algorithm and compare its performance with deterministic
algorithms on multiple graphs with different sizes of V and E
72

Randomized algorithms all pairs shortest path

More Related Content

What's hot (20)

Similar to Randomized algorithms all pairs shortest path (20)

Recently uploaded (20)

Randomized algorithms all pairs shortest path