Reducing computational complexity of Mathematical functions using FPGA

Reducing Computational complexity of Mathematical
functions using FPGA
Neha Gour, M.Tech. (VLSI Design)
Department of Electronics, Banasthali University
Guided by:
Prof. Arup Banerjee
RRCAT, Indore

Outline
Introduction
Motivation
Conventional Processor vs. FPGA
Basic skeleton of project
Work carried out
I. Optimization Directives
II. Addition of Fixed Point Numbers
III. Addition of Floating Point Numbers
IV. Matrix Multiplication using Integer Numbers
Result and Discussion
2

Introduction
• Analysis of complex algorithm demand for less execution time and low storage space.
• Computationally intensive applications such as machine learning, weather forecasting, big data,
computational biology etc.
• Require a lot of computation time to execute, because usually the task is sequentially simulated.
3

Motivation
• To reduce the computation time and make system efficient using concept of parallelism.
• Parallel processing through FPGA is one possible solution to reduce execution time.
• Objective of this work is to improve the execution time of mathematical functions using
optimization directives such as loop pipeline and loop unrolling.
4

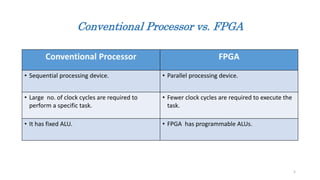
Conventional Processor vs. FPGA
Conventional Processor FPGA
• Sequential processing device. • Parallel processing device.
• Large no. of clock cycles are required to
perform a specific task.
• Fewer clock cycles are required to execute the
task.
• It has fixed ALU. • FPGA has programmable ALUs.
5

Overview of an FPGA
6
 2-D array of logic blocks with electrically programmable interconnections.
 User can configure
I. Interconnection between logic blocks,
II. The function of each block.
Figure: Basic structure of FPGA

Look Up
Tables
7
Basic Skeleton of the Project
High-Level language
(C-program)
LUT 1
LUT 2
LUT 3
* Parallel processing through FPGA is implemented using High-Level Synthesis(HLS).

Work Carried Out
8
C-Language
APPLYING DIRECTIVES
I. LOOP PIPELINE
II. LOOP UNROLL
FPGA
Fig. Basic Block diagram of design
NOTE: HLS is done by Vivado HLS(2017.2) software. Hardware implementation is done using Artix-7 FPGA.

1. Sequential loop
9
A[5]
B[5]
DATA
1
2
3
4
5
1
2
3
4
5
+
+
+
+
+
C[0]
C[1]
C[2]
C[4]
C[3]
For(i=0; i<5; i++)
{
C[i]=A[i]+ B[i];
}

I. Optimization Directives
1. Loop unrolling
• Loop unrolling is a directive that exploits the parallelism between loop iteration.
• It creates multiple copies of the loop body and adjust the loop iteration counter accordingly.
• Directive command: #pragma HLS UNROLL factor = <INTEGER>.
Unrolled loop
For( i=0;i<5; i++){
C[i]=A[i]+B[i];
C[i+1]=A[i+1]+B[i+1];
.
.
.
C[i+4]=A[i+4]+B[i+4]
}
10

cont..
DATA
11
A[5]
B[5]
1
2
3
4
5
1
2
3
4
5
+
C[0]
+
+
C[1]
C[2]
+
C[3]
+ C[4]

2. Loop Pipelining
• Loop pipelining allows the operation in a loop to be implemented in a concurrent manner.
• In pipelining the next iteration of loop can start before current iteration is finished.
• Directive command: #pragma HLS PIPELINE initiation interval(II)* = <INTEGER>.
12
*Initiation Interval (II) is the number of clock cycles between the start times of consecutive loop iterations.

cont..
13
A[5]
B[5]
1
2
3
4
5
1
2
3
4
5
+
+
+
+
+
C[0]
C[1]
C[2]
C[3]
C[4]
DATA

II. Addition of Fixed-Point Numbers
1. Sequential loop
int i, int A[i], int B[i], int C[i];
For(i=0; i<8; i++) {
C[i]=A[i]+ B[i];
}
14Fig. Fixed point addition simulation result of sequential process

2. Loop Pipelining
15Fig. Fixed point addition simulation result after applying pipelining
For(i=0; i<8; i++)
{
#pragma HLS pipeline II=1;
C[i]=A[i]+ B[i];
}

3. Loop Unrolling
16Fig. Fixed point addition simulation result after applying unrolling
For(i =0; i<8; i ++) {
C[i]=A[i]+ B[i];
C[i+1]=A[i+1]+ B[i+1];
.
.
.
C[i+7]=A[i+7]+ B[i+7];
}

Hardware Realization of Fixed-Point Addition
1. Sequential loop
17
State 1 State 2
State 3
RESET
EXIT CONDITION
OPERATION
EXIT=1
EXIT=0

2. Loop pipelining
18
State 1 State 2
State 3
RESET
EXIT CONDITION
OPERATION
EXIT=0
EXIT=1

3. Loop unrolling
19
State
1
State
2
RESET
EXIT
OPERATION
PARAMETERS Sequential Pipeline Unroll
Loop latency 17 10 1
LUTs 50 67 117
I/O ports 142 187 468
Comparison of computational optimization Directive of fixed-point addition

III. Addition of Floating Point Numbers
• For the addition and multiplication of floating point numbers we have to use floating point IPs.
• Numbers written in scientific notation have three components
20
Exponent Mantissa
Sign
31 30 23
8 bits
22 0
23 bits1bit
Single precision format(32 bit)

Floating-point Addition Block diagram(IP)
21

1. Sequential loop
int i, float A[i], float B[i], float C[i];
For(i=0; i<8; i++;) {
C[i]=A[i]+ B[i];
}
22
Fig. Floating point addition simulation result of sequential process

2. Loop Pipelining
23
Fig. Floating point addition simulation result after applying pipelining
3. Loop Unrolling
Fig. Floating point addition simulation result after applying unrolling

Hardware Realization of Floating-Point Addition
1. Sequential loop
24
State 1 State 2
State 8 State 7 State 6
State
5
State 4State 3
State
9
RESET
EXIT =0
EXIT
CONDITION
EXIT =1

2. Loop pipelining
OPERATION
RESET
EXIT =0
EXIT =1
State 1 State 2
State 3

26
3. Loop Unrolling
State 1 State 2
State 3
RESET
State 4

27
PARAMETER Sequential Pipeline Unroll
LUTs 272 326 1771
I/O ports 104 205 708
DSP48E 2 2 16
Comparison of computational optimization Directive of
floating-point addition

IV. Matrix multiplication using integer numbers
• Algorithm of Matrix multiplication
start
Read a[3][3],b[3][3]
For i=0 to 2
For j=0 to 2
For k=0 to 2
rows
C[i][j] += A[i][k] * B[k][j];
columns
product
* Sequential implementation of above code will take 79 clock cycles for completion. 28

29
1. Sequential implementation of matrix multiplication
Fig. Matrix multiplication simulation result by conventional method

Matrix multiplication with integer numbers Block
diagram(IP)
30

31
PARAMETER Sequential Pipelining Unrolling
LUTs 142 282 367
I/O ports 41 58 270
DSP48E 1 2 6
Comparison of computational optimization Directive of
Matrix multiplication

Results and Conclusion
• Applications of optimization directives have explored to reduce execution time.
• Loop Pipelining and loop unrolling of fixed-point addition show the reduction in delay by approx.
28% and 71%, and increase in hardware by 14% and 68% respectively, as compared to sequential.
• Experimental results demonstrate that, pipelining and unrolling of floating-point addition show
the reduction in delay by 72% and 91%, and increase in hardware 2 times and 5 times
respectively, as compared to sequential processing. DSP48E increased by 16 from 2 slices
compared to the conventional.
• Loop Pipelining and loop unrolling of matrix multiplication with integer entries show the
reduction in delay by approx. 73% and 87%, and increase in hardware by 30% and nearly 75%
respectively, as compared to sequential. In addition increase in DSP48E slices is also observed.
• Simulation results show that proposed design has reduced time complexity for mathematical
functions.
32

References
[1] Bob Z., ”Introduction to FPGA design” . Embedded system conference Europe.1999 classes 304-
314.
[2] James H., “Floating Point Design with Vivado HLS XAP599 (v1.0)” September 20, 2012
[3] Spyridon G., John E., “Overview of High-Level Synthesis tool”. Topical workshop on electronics for
particle physics. 2010
[4] Sumit G., Rajesh G., Nikhil D. D., Alexandru N., “SPARK: A Parallelization approach to the High-
Level Synthesis of Digital Circuit”. 2004, Springer Science US.
[5] Mohsen E., “Reducing system power and cost with Artix-7 FPGAs” . Xilinx, Artix-7, 2012:7:1-2.
33

Acknowledgement
• I would like to thank my project coordinator Prof. Arup Banerjee, who gave me the opportunity
to do this wonderful project.
• I would like to convey my sincere thanks and deepest regards to Dr. Srivathsan Vasudevan and
Dr. Satya S. Bulusu of IIT Indore for technical discussions and guidance for this work.
34

Reducing computational complexity of Mathematical functions using FPGA

More Related Content

What's hot (19)

Similar to Reducing computational complexity of Mathematical functions using FPGA (20)

Recently uploaded (20)

Reducing computational complexity of Mathematical functions using FPGA