![多項式あてはめ
今日は多項式あてはめを例にベイズ推定を説明
データ：N個 (ti, xi)
モデル：
パラメータ：ai, b
[1] https://www.r-bloggers.com/fitting-polynomial-regression-in-r/
データにフィットする
ような多項式を求める
目的：](https://image.slidesharecdn.com/bayespoly-171015115636/85/-4-320.jpg)
![ガウスノイズモデル
データにフィットする
ような確率分布を求める
確率的なモデルで多項式を表現してみる
データ：N個 (ti, xi)
モデル：
パラメータ：
[1] https://www.r-bloggers.com/fitting-polynomial-regression-in-r/
目的：](https://image.slidesharecdn.com/bayespoly-171015115636/85/-9-320.jpg)
多項式あてはめで眺めるベイズ推定 ~今日からきみもベイジアン~
- 2. 自己紹介 ・情報系 M2 ・研究：グラフィカルモデルの推定手法 ・twitter : @tanutarou730 ・mastodon : tanutarou@mathtod.online ・ベイズ見習い
- 4. 多項式あてはめ 今日は多項式あてはめを例にベイズ推定を説明 データ：N個 (ti, xi) モデル： パラメータ：ai, b [1] https://www.r-bloggers.com/fitting-polynomial-regression-in-r/ データにフィットする ような多項式を求める 目的：
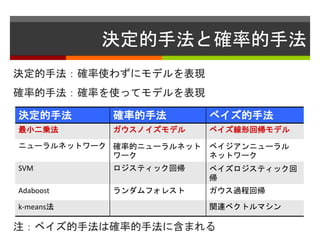
- 5. 決定的手法と確率的手法 決定的手法：確率使わずにモデルを表現 確率的手法：確率を使ってモデルを表現 注：ベイズ的手法は確率的手法に含まれる 決定的手法 確率的手法 ベイズ的手法 最小二乗法 ガウスノイズモデル ベイズ線形回帰モデル ニューラルネットワーク 確率的ニューラルネット ワーク ベイジアンニューラル ネットワーク SVM ロジスティック回帰 ベイズロジスティック回 帰 Adaboost ランダムフォレスト ガウス過程回帰 k-means法 関連ベクトルマシン
- 6. 今日の流れ 今日はこの拡張を順番に行っていき、ベイズ推定と は何かについてみていく Edwardによる実装 (Jupyter notebook)： https://gist.github.com/tanutarou/309cd8c0c725224d96526f25c20d3262 最小二乗法 ガウスノイズモデル ベイズ線形回帰モデル 決定的手法 確率的手法 ベイズ的手法
- 9. ガウスノイズモデル データにフィットする ような確率分布を求める 確率的なモデルで多項式を表現してみる データ：N個 (ti, xi) モデル： パラメータ： [1] https://www.r-bloggers.com/fitting-polynomial-regression-in-r/ 目的：