The Suitcase Case
0 likes1,188 views
The document presents a study on linear regression analysis to understand the sales performance of a luggage company, highlighting how the number of stores influences sales. It addresses inquiries regarding expected sales from various store counts and the implications for potential expansion into Brazil. Results indicate that areas with more stores tend to generate higher sales, with a regression model explaining about 73.2% of sales variability based on store numbers.
The Suitcase Case
- 1. The Suitcase Case An introduction to linear regression Anthony J. Evans Professor of Economics, ESCP Europe www.anthonyjevans.com (cc) Anthony J. Evans 2019 | http://creativecommons.org/licenses/by-nc-sa/3.0/
- 2. Introduction The world’s best luggage company are a pioneer of durable and stylish travel. Their distinctive suitcases are a hand made luxury product but following strong sales over the last few years the global financial crisis has had a noticeable impact. Senior management are interested in developing better analytical tools, to use data from across their main locations and understand what’s driving their sales. You need to answer the following questions: 1. The board suspect that the country manager for Poland is underperforming. Based on the entire data set how many sales would you expect a location with 14 stores to generate? 2. The board are interested in expanding into Brazil and are targeting sales of 10,000 cases within the first year. They are willing to invest in 8 stores – is this enough? 3. How strong are stores as a predictor of sales? Download data set from: http://www.anthonyjevans.com/cases/ 2
- 3. Table 1 Y X Observation Sales Stores 1 15,678 30 2 16,758 22 3 4,895 8 4 5,786 9 5 12,323 16 6 9,870 10 7 5,436 8 8 6,754 7 9 7,863 9 10 4,659 8 11 7,861 10 12 4,787 11 13 5,567 14 14 4,538 10 15 7,859 8 16 5,489 6 17 3,436 6 18 5,359 7 19 2,023 6 20 1,434 5 21 1,764 5 3
- 4. Graph 1 0 2,000 4,000 6,000 8,000 10,000 12,000 14,000 16,000 18,000 20,000 0 5 10 15 20 25 30 35 Sales Stores A simple scatter plot suggests that there is a relationship between stores and sales. Sites with more stores have higher sales 4
- 5. 0 2,000 4,000 6,000 8,000 10,000 12,000 14,000 16,000 18,000 20,000 0 5 10 15 20 25 30 35 Sales Stores The standard linear equation bxay += a = Intercept The value of y when x=0 b = Slope/gradient The amount by which y changes when x increases by one unit Coefficients a b y x 5
- 6. Simple model • Regression analysis is the study of the relationship between one variable (the dependent variable, Y) and one or more other variables (independent variables, X) with a view to estimating and/or predicting the average value of the dependent variable (Y) in terms of known (or fixed) values of the independent ones (X) – We accumulate independent variables (X) to explain a dependent variable (Y) • Fitting a line to data means drawing a line that comes as close as possible to the points, providing a compact description of how X explains Y • In our case we are using changes in stores (X) to explain changes in sales (Y) 6
- 7. Ordinary Least Squares: Introduction • Ordinary Least Squares (OLS) is a systematic method to construct the regression line • Since we wish to predict Y from X, we want a line that is as close as possible to the points in the vertical direction • We fit a line based on our past observations, in the expectation that they will help us predict future events • We have observations that give the real value of Y, and our regression line makes a prediction of Y (Y*). • We want to minimise the residual: Residual = observed value – predicted value 7An alternative method is to find an average no. of sales per store and multiply by 14. Since OLS will exaggerate the deviations it is a different method and therefore provides different results.
- 8. 0 2,000 4,000 6,000 8,000 10,000 12,000 14,000 16,000 18,000 20,000 0 5 10 15 20 25 30 35 Sales Stores Graph 2 y e1 Y* (fitted value) Y (actual value) x e2 8 e3
- 9. Ordinary Least Squares: Process • Take each observation (• ) and measure the deviation between the actual value (Y) and the fitted value (Y*) = (e1, e2, e3) • Every observation has a corresponding e – e2: squaring e will get rid of negative values, and give more weight to larger deviations – å e2: summing e2 takes into account all deviations – minå e2: make the fitted model as tight as possible to the sampled data by finding the minimum of the summed and squared values • Ordinary least squares (OLS) is a method of finding a* and b* such that the sum of squared residuals (å e2) is minimised 9 min $ 𝑒&
- 10. y = 584.83x + 685.74 R² = 0.7455 0 2,000 4,000 6,000 8,000 10,000 12,000 14,000 16,000 18,000 20,000 0 5 10 15 20 25 30 35 Sales Stores Graph 3 Commands • Chart > Add Trendline… • Format Trendline > Options – Display equation on chart – Display R-squared value on chart 10
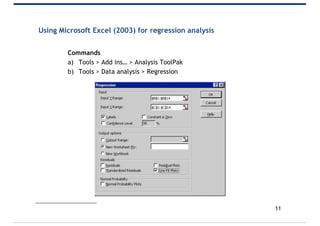
- 11. Using Microsoft Excel (2003) for regression analysis Commands a) Tools > Add ins… > Analysis ToolPak b) Tools > Data analysis > Regression 11
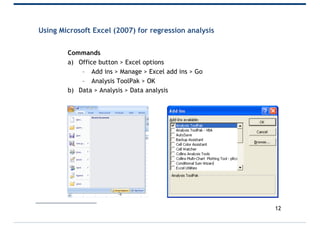
- 12. Using Microsoft Excel (2007) for regression analysis Commands a) Office button > Excel options – Add ins > Manage > Excel add ins > Go – Analysis ToolPak > OK b) Data > Analysis > Data analysis 12
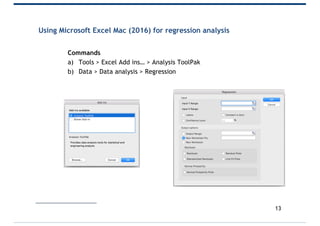
- 13. Using Microsoft Excel Mac (2016) for regression analysis Commands a) Tools > Excel Add ins… > Analysis ToolPak b) Data > Data analysis > Regression 13
- 14. Output 14 𝑦 = 𝑎 + 𝑏𝑥 s𝑎𝑙𝑒𝑠 = 𝑎 + 𝑏(𝑠𝑡𝑜𝑟𝑒𝑠) s𝑎𝑙𝑒𝑠 = 685.74 + 584.83(𝑠𝑡𝑜𝑟𝑒𝑠) ANOVA stands for “Analysis of Variance” which tests whether the means of different groups are equal. We do not need to use it for our purposes.
- 15. 1. The board suspect that the country manager for Poland is underperforming. Based on the entire data set how many sales would you expect a location with 14 stores to generate? 15 𝑦 = 685.74 + 584.83𝑥 𝑦 = 685.74 + 584.83(14) 𝑦 = 8,873
- 16. 2. The board are interested in expanding into Brazil and are targeting sales of 10,000 cases within the first year. They are willing to invest in 8 stores – is this enough? 16 𝑦 = 685.74 + 584.83𝑥 10,000 = 685.74 + 584.83𝑥 10,000 − 685.74 584.83 = 𝑥 ∴ 𝑥 = 16
- 17. Table 2 – a recap on how we generated a and b 17 Table 2 Y X Ŷ Ŷ-Y (Ŷ-Y)^2 Sales Stores Fitted Residual MSE 15,678 30 18,231 -2,552.64 6,515,971 16,758 22 13,552 3,206.00 10,278,436 4,895 8 5,364 -469.38 220,318 5,786 9 5,949 -163.21 26,638 12,323 16 10,043 2,279.98 5,198,309 9,870 10 6,534 3,335.96 11,128,629 5,436 8 5,364 71.62 5,129 6,754 7 4,780 1,974.45 3,898,453 7,863 9 5,949 1,913.79 3,662,592 4,659 8 5,364 -705.38 497,561 7,861 10 6,534 1,326.96 1,760,823 4,787 11 7,119 -2,331.87 5,437,618 5,567 14 8,873 -3,306.36 10,932,016 4,538 10 6,534 -1,996.04 3,984,176 7,859 8 5,364 2,494.62 6,223,129 5,489 6 4,195 1,294.28 1,675,161 3,436 6 4,195 -758.72 575,656 5,359 7 4,780 579.45 335,762 2,023 6 4,195 -2,171.72 4,716,368 1,434 5 3,610 -2,175.89 4,734,497 1,764 5 3,610 -1,845.89 3,407,310 Residual mean Mean Squared Error Y=685.74+584.83X 0.00 4,057,836
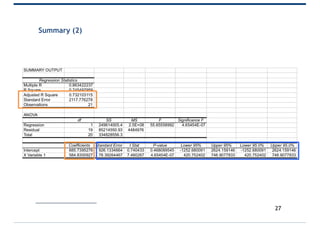
- 18. Multiple R • r is a measure of the index of co-relation between two variables • Correlation – A number between -1 and +1 that indicates if two variables are linearly related – If r = 1 there is a perfectly positive relationship – If r = -1 there is a perfectly negative relationship – If r = 0 there is no (linear) relationship • If we only have a single independent variable R-squared will be equal to the square of the correlation between the dependent and independent variable. – In our case Multiple R = 0.863 and R-squared = 0.745 • We can also find r doing correlation analysis 18
- 19. R-squared • r2 is the most commonly used goodness of fit for a regression line • It measures the proportion or percentage of the total variation in Y explained by the regression model • Hence 0 < r2 < 1 and the higher r2 the better – If r2 = 0 then there is no relationship between X and Y – If r2 = 1 then △X = △Y 19If we are comparing ice cream sales and wearing shorts we can imagine that r is high (more X = more Y) but r2 is low (△X /= △Y). Remember that correlation doesn’t mean causation!
- 20. Adjusted R-squared • Adjusted r2 is a more precise measure of r2 since it takes into account the number of independent variables in the model • It only increases if a new variable improves the model 20 𝑟& = 1 − 𝑆𝐸& 𝑠& Note: here we’re using the SE of the error terms and the s of the dependent variable (Y)
- 21. Standard error • The standard error is 2,117 – this is our estimate of the standard deviation of the residual error terms (i.e. how close the points are to the regression line) • If these errors are normally distributed – 68% of errors are within ± SE of the line – 95% of errors are within ± 2SE of the line – 99.7% of errors are within ± 3SE of the line • The lower the SE the better the fit • The SE gives an absolute measure of fit, r2 is a relative measure • r2 tells us how well the model does compared to our next best alternative – the values of Y 21Note: the standard error is the same unit of measurement as the dependent variable (Y). Notice that the standard error is ≈ the square root of the mean squared error.
- 22. Table 3 – calculation for adjusted r2 Y X Ŷ Sales Stores Fitted 15,678 30 18,231 16,758 22 13,552 4,895 8 5,364 5,786 9 5,949 12,323 16 10,043 9,870 10 6,534 5,436 8 5,364 6,754 7 4,780 7,863 9 5,949 4,659 8 5,364 7,861 10 6,534 4,787 11 7,119 5,567 14 8,873 4,538 10 6,534 7,859 8 5,364 5,489 6 4,195 3,436 6 4,195 5,359 7 4,780 2,023 6 4,195 1,434 5 3,610 1,764 5 3,610 Mean 6,673.29 StDev 4,091.63 22 𝑟& = 1 − 𝑆𝐸& 𝑠& 𝑟& = 1 − 2117& 4091& 𝑟& = 1 − 4,481,689 16,736,281 𝑟& = 1 − 0.268 𝑟& = 0.732
- 23. 3. How strong are stores as a predictor of sales? Adjusted r2 = 0.732 According to our model 73.2% of sales are determined by the number of stores 26.8% of sales are determined by other factors, which can be factored into our model to create a more robust picture 23
- 24. Summary 24
- 25. Solutions 1. The board suspect that the country manager for Poland is underperforming. Based on the entire data set how many sales would you expect a location with 14 stores to generate? – 8,873 cases (compared to 5,567) 2. The board are interested in expanding into Brazil and are targeting sales of 10,000 cases within the first few years. They are willing to invest in 8 stores – is this enough? – No! They need around 16 stores 3. How strong are stores as a predictor of sales? – They explain over 70% 25
- 26. Discussion questions • Issues of outliers – should we remove Germany? • Omitted variables – Marketing budget • Dangers of extrapolation – can we make estimates outside the range in which the data was constructed? • How can we improve on the model? – GDP per capita – No. of business trips per year 26
- 27. Summary (2) 27
- 28. Appendix The Excel output also gives the standard errors of the coefficients (given in brackets) t Stat • The estimated coefficient divided by the standard error • The distance between b and 0 (measured in units of the standard errors • It’s how many standard errors the estimate is from 0 P value • The probability of seeing a t stat that big (or bigger) if β = 0 • There is a 0.00000046 chance of a t stat bigger than 7.46 The t stat is large (and the p value small) so we are confident that β > 0, i.e. that the number of stores have a positive effect on sales We may wish to perform a test against a more reasonable hypothesis (e.g. β = 500) Note: we use a t-stat instead of a z score because of the low sample size, but the intuition is identical 28 (926) (78.39) 𝑦 = 685.74 + 584.83𝑥