Galios: Python Programming
6 likes2,264 views
The document is a tutorial on programming with Python for Galois fields. It discusses how to import the FField class to work with Galois fields in Python, create a Galois field GF(2^3), represent elements as polynomials and coefficients, convert between representations, and perform addition and multiplication operations on elements in the field. Examples of Python code are provided to demonstrate working with Galois fields, obtaining polynomial and coefficient representations of elements, and using the FField class methods to operate on elements in the field.
![1.6 Result of example2.py
Fig2: Result of example2.py
1.7 Conversion from co-efficient of polynomial to element
The coefficient(list) of the polynomial can be converted to the element(integer)
F.ConvertListToElement(list)
Returns: integer
Note: the value of a lies between 0 to 2n − 1
Following example named “example3.py” shows how do we use python programming language to convert
co-efficient of a polynomial to element over a galois field.
1 # example3.py
2 import sys
3 sys.path.append(’./Field’)
4 import ffield
5
6 # Create the field GF(2ˆ3)
7 F = ffield.FField(3)
8
9 # Converting list into the element
10 print "List: [0,0,0,0], Element: " + str(F.ConvertListToElement([0,0,0,0]))
11 print "List: [0,0,0,0], Element: " + str(F.ConvertListToElement([0,0,0,1]))
12 print "List: [0,0,0,0], Element: " + str(F.ConvertListToElement([0,0,1,0]))
13 print "List: [0,0,0,0], Element: " + str(F.ConvertListToElement([0,0,1,1]))
14 print "List: [0,0,0,0], Element: " + str(F.ConvertListToElement([0,1,0,0]))
15 print "List: [0,0,0,0], Element: " + str(F.ConvertListToElement([0,1,0,1]))
16 print "List: [0,0,0,0], Element: " + str(F.ConvertListToElement([0,1,1,0]))
17 print "List: [0,0,0,0], Element: " + str(F.ConvertListToElement([0,1,1,1]))
18
19 # Next method to convert
20 print F.ConvertListToElement(F.ShowCoefficients(0))
21 print F.ConvertListToElement(F.ShowCoefficients(7))
4](https://image.slidesharecdn.com/tutorial-120206002235-phpapp01/85/Galios-Python-Programming-4-320.jpg)
Galios: Python Programming
- 1. Tutorial on Programming with Python: Galois Field Kishoj Bajracharya Asian Institute of Technology June 20, 2011 Contents 1 Galois Field 2 1.1 To import class FField for Galois Field . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2 1.2 To Create Galois Field . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2 1.3 Polynomial Representation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2 1.4 Result of example1.py . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3 1.5 Co-efficient of Polynomial Representation . . . . . . . . . . . . . . . . . . . . . . . . . . . 3 1.6 Result of example2.py . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4 1.7 Conversion from co-efficient of polynomial to element . . . . . . . . . . . . . . . . . . . . 4 1.8 Result of example3.py . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5 2 Operation Over Galois Field 5 2.1 Addition Operation over Galois Field . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5 2.2 Result of example4.py . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6 2.3 Multiplication Operation over Galois Field . . . . . . . . . . . . . . . . . . . . . . . . . . . 6 2.4 Result of example5.py . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7 2.5 Operations over Galois Field: Another Approach . . . . . . . . . . . . . . . . . . . . . . . 7 2.6 Result of example6.py . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8 1
- 2. 1 Galois Field 1.1 To import class FField for Galois Field 1. Browse the URI http://www.mit.edu/˜emin/source_code/py_ecc and see the latest release of the file “py ecc-1-4.tar.gz” and download it. 2. Extract it and keep all the files in a separate folder named “Field”. 3. Use the import command to use the class FField from the file name “ffield.py” import sys sys.path.append(‘./Field’) import ffield 1.2 To Create Galois Field To create the Galois field F = GF (2n ) F = ffield.FField(n) Create the field GF (23 ) F = ffield.FField(3) 1.3 Polynomial Representation The polynomial representation of any number a can be obtained using following codes F.ShowPolynomial(a) Returns: string Note: the value of a lies between 0 to 2n − 1 Following example named “example1.py” shows how do we use python programming language to get poly- nomial from galois field. 1 # example1.py 2 import sys 3 sys.path.append(’./Field’) 4 import ffield 5 6 # Create the field GF(2ˆ3) 7 F = ffield.FField(3) 8 9 # Show the polynomial representation from 0-2ˆ3-1 i.e. 0-7 10 print ’For 0, polynomial: ’ + F.ShowPolynomial(0) 11 print ’For 1, polynomial: ’ + F.ShowPolynomial(1) 12 print ’For 2, polynomial: ’ + F.ShowPolynomial(2) 13 print ’For 3, polynomial: ’ + F.ShowPolynomial(3) 14 print ’For 4, polynomial: ’ + F.ShowPolynomial(4) 15 print ’For 5, polynomial: ’ + F.ShowPolynomial(5) 16 print ’For 6, polynomial: ’ + F.ShowPolynomial(6) 17 print ’For 7, polynomial: ’ + F.ShowPolynomial(7) 2
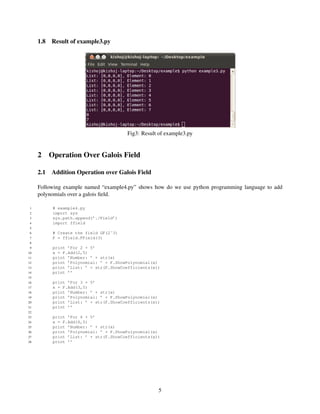
- 3. 1.4 Result of example1.py Fig1: Result of example1.py 1.5 Co-efficient of Polynomial Representation The coefficient of the polynomial representation of any number a can be obtained using following codes F.ShowCoefficients(a) Returns: list Note: the value of a lies between 0 to 2n − 1 Following example named “example2.py” shows how do we use python programming language to get the co-efficient of a polynomial from galois field. 1 # example2.py 2 import sys 3 sys.path.append(’./Field’) 4 import ffield 5 6 # Create the field GF(2ˆ3) 7 F = ffield.FField(3) 8 9 # Show the coefficient of the coefficient of polynomial representation of a,b,c,d,e,f,g,h 10 print ’For 0, coefficient of polynomial: ’ + str(F.ShowCoefficients(0)) 11 print ’For 1, coefficient of polynomial: ’ + str(F.ShowCoefficients(1)) 12 print ’For 2, coefficient of polynomial: ’ + str(F.ShowCoefficients(2)) 13 print ’For 3, coefficient of polynomial: ’ + str(F.ShowCoefficients(3)) 14 print ’For 4, coefficient of polynomial: ’ + str(F.ShowCoefficients(4)) 15 print ’For 5, coefficient of polynomial: ’ + str(F.ShowCoefficients(5)) 16 print ’For 6, coefficient of polynomial: ’ + str(F.ShowCoefficients(6)) 17 print ’For 7, coefficient of polynomial: ’ + str(F.ShowCoefficients(7)) 3
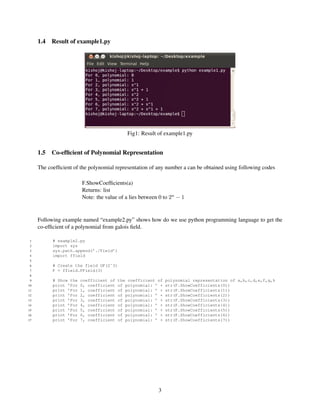
- 4. 1.6 Result of example2.py Fig2: Result of example2.py 1.7 Conversion from co-efficient of polynomial to element The coefficient(list) of the polynomial can be converted to the element(integer) F.ConvertListToElement(list) Returns: integer Note: the value of a lies between 0 to 2n − 1 Following example named “example3.py” shows how do we use python programming language to convert co-efficient of a polynomial to element over a galois field. 1 # example3.py 2 import sys 3 sys.path.append(’./Field’) 4 import ffield 5 6 # Create the field GF(2ˆ3) 7 F = ffield.FField(3) 8 9 # Converting list into the element 10 print "List: [0,0,0,0], Element: " + str(F.ConvertListToElement([0,0,0,0])) 11 print "List: [0,0,0,0], Element: " + str(F.ConvertListToElement([0,0,0,1])) 12 print "List: [0,0,0,0], Element: " + str(F.ConvertListToElement([0,0,1,0])) 13 print "List: [0,0,0,0], Element: " + str(F.ConvertListToElement([0,0,1,1])) 14 print "List: [0,0,0,0], Element: " + str(F.ConvertListToElement([0,1,0,0])) 15 print "List: [0,0,0,0], Element: " + str(F.ConvertListToElement([0,1,0,1])) 16 print "List: [0,0,0,0], Element: " + str(F.ConvertListToElement([0,1,1,0])) 17 print "List: [0,0,0,0], Element: " + str(F.ConvertListToElement([0,1,1,1])) 18 19 # Next method to convert 20 print F.ConvertListToElement(F.ShowCoefficients(0)) 21 print F.ConvertListToElement(F.ShowCoefficients(7)) 4
- 5. 1.8 Result of example3.py Fig3: Result of example3.py 2 Operation Over Galois Field 2.1 Addition Operation over Galois Field Following example named “example4.py” shows how do we use python programming language to add polynomials over a galois field. 1 # example4.py 2 import sys 3 sys.path.append(’./Field’) 4 import ffield 5 6 # Create the field GF(2ˆ3) 7 F = ffield.FField(3) 8 9 print ’For 2 + 5’ 10 x = F.Add(2,5) 11 print ’Number: ’ + str(x) 12 print ’Polynomial: ’ + F.ShowPolynomial(x) 13 print ’List: ’ + str(F.ShowCoefficients(x)) 14 print ’’ 15 16 print ’For 3 + 5’ 17 x = F.Add(3,5) 18 print ’Number: ’ + str(x) 19 print ’Polynomial: ’ + F.ShowPolynomial(x) 20 print ’List: ’ + str(F.ShowCoefficients(x)) 21 print ’’ 22 23 print ’For 6 + 5’ 24 x = F.Add(6,5) 25 print ’Number: ’ + str(x) 26 print ’Polynomial: ’ + F.ShowPolynomial(x) 27 print ’List: ’ + str(F.ShowCoefficients(x)) 28 print ’’ 5
- 6. 2.2 Result of example4.py Fig4: Result of example4.py 2.3 Multiplication Operation over Galois Field Following example named “example5.py” shows how do we use python programming language to multiply polynomials over a galois field. 1 # example5.py 2 import sys 3 sys.path.append(’./Field’) 4 import ffield 5 6 # Create the field GF(2ˆ3) 7 F = ffield.FField(3) 8 9 print ’For 2 * 5’ 10 x = F.Multiply(2,5) 11 print ’Number: ’ + str(x) 12 print ’Polynomial: ’ + F.ShowPolynomial(x) 13 print ’List: ’ + str(F.ShowCoefficients(x)) 14 print ’’ 15 16 print ’For 3 * 5’ 17 x = F.Multiply(3,5) 18 print ’Number: ’ + str(x) 19 print ’Polynomial: ’ + F.ShowPolynomial(x) 20 print ’List: ’ + str(F.ShowCoefficients(x)) 21 print ’’ 22 23 print ’For 6 * 5’ 24 x = F.Multiply(6,5) 25 print ’Number: ’ + str(x) 26 print ’Polynomial: ’ + F.ShowPolynomial(x) 27 print ’List: ’ + str(F.ShowCoefficients(x)) 28 print ’’ 6
- 7. 2.4 Result of example5.py Fig5: Result of example5.py 2.5 Operations over Galois Field: Another Approach Following example named “example6.py” shows how do we use python programming language to add and multiply polynomials over a galois field by another approach. 1 # example6.py 2 import sys 3 sys.path.append(’./Field’) 4 import ffield 5 6 # Create the field GF(2ˆ3) 7 F = ffield.FField(3) #GF(2ˆ3) 8 9 a = ffield.FElement(F,0) 10 b = ffield.FElement(F,1) 11 c = ffield.FElement(F,2) 12 d = ffield.FElement(F,3) 13 e = ffield.FElement(F,4) 14 f = ffield.FElement(F,5) 15 g = ffield.FElement(F,6) 16 h = ffield.FElement(F,7) 17 18 # Operation in a Galois Field: 19 # Addition Operation 20 p = c + f 21 print p 22 p = d + f 23 print p 24 p = g + f 25 print p 26 print ’’ 27 28 # Multiplication Operation 29 q = c * f 30 print q 31 q = d * f 7
- 8. 32 print q 33 q = g * f 34 print q 2.6 Result of example6.py Fig6: Result of example6.py 8