08 3312 c
- 1. Universidad de San Carlos de Guatemala Facultad de Ingeniería Escuela de Ingeniería Civil ANÁLISIS, CÁLCULO Y COMPARACIÓN DE CARGAS SÍSMICAS APLICANDO LOS CÓDIGOS AGIES NR-3:2000, IBC2009/ASCE-05 Y EUROCODE 8 ENV 1998-1-1, PARA UNA ESTRUCTURA DE CONCRETO REFORZADO José Ernesto Martínez Mendoza Asesorado por el Ing. Diego Velásquez Jofre Guatemala, octubre de 2011
- 2. UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA ANÁLISIS, CÁLCULO Y COMPARACIÓN DE CARGAS SÍSMICAS APLICANDO LOS CÓDIGOS AGIES NR-3:2000, IBC2009/ASCE-05 Y EUROCODE 8 ENV 1998-1-1, PARA UNA ESTRUCTURA DE CONCRETO REFORZADO TRABAJO DE GRADUACIÓN PRESENTADO A LA JUNTA DIRECTIVA DE LA FACULTAD DE INGENIERÍA POR JOSÉ ERNESTO MARTÍNEZ MENDOZA ASESORADO POR EL ING. DIEGO VELÁSQUEZ JOFRE AL CONFERÍRSELE EL TÍTULO DE INGENIERO CIVIL GUATEMALA, OCTUBRE DE 2011
- 3. UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA NÓMINA DE JUNTA DIRECTIVA DECANO Ing. Murphy Olympo Paiz Recinos VOCAL I Ing. Alfredo Enrique Beber Aceituno VOCAL II Ing. Pedro Antonio Aguilar Polanco VOCAL III Ing. Miguel Ángel Dávila Calderón VOCAL IV Br. Juan Carlos Molina Jiménez VOCAL V Br. Mario Maldonado Muralles SECRETARIO Ing. Hugo Humberto Rivera Pérez TRIBUNAL QUE PRACTICÓ EXAMEN GENERAL PRIVADO DECANO Ing. Murphy Olympo Paiz Recinos EXAMINADOR Ing. Juan Carlos Linares Cruz EXAMINADOR Ing. Luis Manuel Sandoval Mendoza EXAMINADORA Inga. María del Mar Girón Cordón SECRETARIO Ing. Hugo Humberto Rivera Pérez
- 4. HONORABLE TRIBUNAL EXAMINADOR En cumplimiento con los preceptos que establece la ley de la Universidad de San Carlos de Guatemala, presento a su consideración mi trabajo de graduación titulado: ANÁLIsIs, cÁLcuLo y corurpARAcóN DE cARGAS sísurcAs ApLrcANDo Los cÓorcos AGIES NR3:2000, lBc2009rAscE-05 Y EUROCODE I ENV 1998-l-1, PARA UNA ESTRUCTURA DE GONGRETO REFORZADO Tema que me fuera asignado por la Dirección de la Escuela de lngeniería Civil, con fecha 13 de julio de 2010. José
- 5. Dleeo VeIÁsQUEz JoFRE INceNrgno Clvrt- Colec¡¿oo 8866 Weimar, 16 de agosto de2011. lngeniero Ronald Estuardo Galindo Cabrera Coordinador del Área de Estructuras Escuela de Ingeniería Civil Facultad de Ingeniería Universidad de San Carlos de Guatemala Presente, lngeniero Galindo Cabrera: Luego de un cordial saludo, sírvame la presente para hacer de su conocimiento que el trabajo de graduación titulado: "ANÁL|S|S, CÁLCULO y COMPARACIÓN DE CARGAS SÍSMICAS APLICANDO LOS CÓDIGOS AGIES NR-3:2000, |BC2009/ASCE-05 Y EUROCODE I ENV 1998-1-1, PARA UNA ESTRUCTURA DE CONCRETO REFORZADO", elaborado por el estudiante de lngeniería Civil, José Ernesto Martínez Mendoza, ha sido finalizado a saüsfacción y revisado por mi persona. ¡ Sin otro particular y deseándole éxitos en sus actividades, me despido. Muy atentamente, "IDYENSEÑADATODOS" Diego Velásqusr Jofre Ingeniao Clvll Colegiado No, 8866 Diego V Jofre .jofre@uni-weimar.de Email : dvelasq ue zjolr e@daad-al umni. de Tnün¡NgEN, DEUTScHI-AND
- 6. UNvensrDAD DE SaN C¡,nros DE Guarsr4ere FncuLreo oe INceNTERfA Escuele or lNcexmnln Cryu. www.ingenieria-usac.edu.gt Guatemala, 2 de septiembre de 201I Ingeniero Hugo Leonel Montenegro Franco Director Escuela Ingeniería Civil Facultad de Ingeniería Universidad de San Carlos Estimado Ingeniero Montenegro. Le informo que he revisado el trabajo de graduación ¿NÁl,lSIS, CÁLCULO Y COMPARACIÓN DE CARGAS SÍSVTTCAS APLICANDO LOS CÓUTCOS AGIES NR-3:2000, IBC2009/ASCE-05 Y EUROCODE I ENV 1998-1-1, PARA UNA ESTRUCTURA DE CONCRETO REFORZADO, desarrollado por el estudiante de Ingeniería Civil José Ernesto Martínez Mendoz4 quien contó con la asesoría del Ing. Diego Velásquez Jofre.. Considero este trabajo bien desarrollado y representa un aporte para' la comunidad del área y habiendo cumplido con los objetivos del referido trabajo doy mi aprobación al mismo solicitando darle el trárnite respectivo. Atentamente, IDYENSEÑADATODOS /bbdeb. Más & /30 4*t de Tntu¡b Académtuo y Mejon Coatinua
- 7. UMvenslDAD DE Seu C¡nros DE Gu¡,reu¡rr¿ FeculrRo oe lNcnxmnle Escuele DE INGENIenTa, Crvr www.ingenieria-usac.edu.gt El director de lq Escuela de Ingenbrío Civil, despr¡es de conocer el dictomen d¿l Ing. Diego Vekísquez Jofre y del trefe del Deportqmento de Estructuras, Ing. Ronald Estuordo Golindo Cab¡wra, ol trohjo de graduoción delesh¡dionte José Ernesto Afiortírez lUlendozs, titulodo, ÁNÁLISIS, CA-eUtO y COAAPARAC¡óM DE CAR6A5 5Í5'MC AS APLTCANDO LOS CóDI6O5 A6IE5 NR-3:2@O, TBC?AW/ASCE-05 y EUROCODE 8 ENV 1998-l-1, PARA UNA ESTRUCTURA DE CONCRETO REFORZADO. ds por este medio st oproboción o dicho trobojo. 6.rstemola, ocfubre de ?Otl. /bbdeb. 6nnr rE ilffin 0$t DIRECTOR M¿ís & /,Y ñ*r de Tnba¡b Académico y Me.¡bn Contiaua
- 8. Universidad de $an *arlos D* üuatsmala F¿¡cult*d de lng*nieria D*canalo /' Ref. üTü.38ü.2ü1 1 E¡ Decanc de la Facultad de lngeniería de la Universidad de San #arfos de Guaternala, lu*gn de conccer Ía fiprüba*isn pür parte del Directcr de la Fscuela de; lngenler:ía üivil, al trahajn'de $raduación titUIAdO AS¡ÁLBI$, :CÁLCULü Y COMPARASIOT'I 'SE-'CARGAS $í$rifircA$ .' ÁplrcAruno Lg$ , 'téue*s AGIE$ NR-g:E*ss, tBc2s$gj.e$cE-05 Y ÉuRsGüpE s ENV, ts$s-t-{, pARA {.JfrlA ESTRUCTURA DE CONCRETO REFORZADCI, Preser}tado por eI estudiante universitario Jcs¿$ Hrnesto Martínes Mendona, autoriza la impre*igft det.mism*. 't' ,' ''t' '. ' ' IMPRíMASE" üuatenrala, *ctuhre de 2ü11 lr,,c
- 9. ACTO QUE DEDICO A: Dios Por permitirme alcanzar este objetivo que será una herramienta para servirle. Mis padres Odily Antonieta Mendoza Flores y Luis Rodrigo Martínez, por su amor incondicional, apoyo y estímulo para lograr mis metas. Mis hermanos Rodrigo Alberto y Sergio Rolando, por su ilimitada ayuda a lo largo de mi vida. Mis tíos Por sus oraciones, sabios consejos y apoyo, especialmente a Ana Josefa, Aura Violeta, Edgar Danilo Mendoza y Lucrecia Martínez, por su gran cariño y constancia. Mis abuelos José Rodrigo Martínez, Marina Alicia Flores y María Albertina España, por sus oraciones, cariño y por compartir su sabiduría conmigo. Mis padrinos Julio Bonilla y Mirta de Bonilla Mis primos Douglas y Lorena Tejeda
- 10. Mis casas de Al bicentenario Colegio San José de los Infantes y a estudios la tricentenaria Universidad de San Carlos de Guatemala, por enseñarme el camino para formarme como profesional y como persona. Mi país Guatemala.
- 11. AGRADECIMIENTOS A: Dios Por darme la vida y permitirme obtener el título de Ingeniero Civil. Mi asesor Ing. Diego Velásquez Jofre, por su valiosa colaboración en este trabajo y principalmente por su apoyo incondicional. Mis amigos y Quienes han compartido conmigo las etapas más compañeros importantes de mi vida y hemos buscado juntos esta meta. Ccgroup En especial a Ing. Roberto Arango e Ing. Elías Arango por permitirme llenar mis días de conocimiento y nuevas experiencias y así poder crecer en la vida profesional. Arminda Herrera Por depositar su confianza y apoyarme desde el inicio de este camino.
- 13. I ÍNDICE GENERAL ÍNDICE DE ILUSTRACIONES…………………………………………………. XI LISTA DE SÍMBOLOS………………………………………………………… . XV GLOSARIO………………………………………………………………………. XIX RESUMEN……………………………………………………………………… XXIII OBJETIVOS…………………………………………………………………….. XXV INTRODUCCIÓN……………………………………………………………… . XXVII 1. FUNDAMENTOS PRINCIPALES DE SISMOLOGÍA ................................... 1 1.1. Sismología.......................................................................................... 1 1.2. Origen de los sismos .......................................................................... 2 1.2.1. Estructura interna de la Tierra............................................... 2 1.3. Diferencias entre sismo y terremoto .................................................. 4 1.3.1. Sismo ................................................................................... 4 1.4. Movimientos del suelo ....................................................................... 5 1.4.1. Ondas sísmicas.................................................................... 5 1.5. Placas tectónicas............................................................................... 8 1.5.1. Interacción entre las placas tectónicas ................................ 9 1.6. Fallas tectónicas.............................................................................. 11 1.6.1. Tipos de fallas.................................................................... 11 1.7. Marco tectónico para Guatemala..................................................... 12 1.7.1. Placas tectónicas en la que se encuentra Guatemala ....... 12
- 14. II 1.7.2. Zonas sísmicas...................................................................14 1.7.3. Importancia del estudio de los sismos ................................15 1.8. Consideraciones generales de diseño de fuerzas sísmicas.............16 1.8.1. Efecto de sismo en edificios ...............................................16 1.8.2. Fuerzas sísmicas................................................................16 1.8.3. Cortante basal ....................................................................17 1.8.4. Cargas muertas ..................................................................18 1.8.5. Cargas vivas.......................................................................18 1.9. Sistemas estructurales básicos.........................................................19 1.9.1. Sistema de cajón E1...........................................................19 1.9.2. Sistema de marcos E2........................................................20 1.9.3. Sistema de marcos ordinarios E2-1....................................20 1.9.4. Sistema de marcos especiales E2-2...................................20 1.9.5. Sistema combinado de muros y marcos E3........................20 1.9.6. Sistema dual de muros y marcos........................................20 1.10. Regularidad estructural ....................................................................21 1.10.1. Criterio de regularidad en planta.........................................21 1.10.2. Criterio de regularidad en elevación ...................................22 2.1. Zonificación sísmica y caracterización de sitio en Guatemala .........25 2.2. Sismicidad y nivel de protección ......................................................26 2.2.1. Índice de sismicidad ...........................................................26 2.3. Requisitos de sitio ............................................................................27 2.3.1. Clasificación de sitio ...........................................................28
- 15. III 2.4. Niveles de intensidad sísmica ......................................................... 31 2.4.1. Sismo básico...................................................................... 32 2.4.2. Sismo de servicio............................................................... 33 2.4.3. Sismo extremo ................................................................... 33 2.5. Parámetros de sismoresistencia....................................................... 34 2.5.1. Factor de reducción de respuesta sísmica para el estado límite de cedencia................................................... 34 2.5.2. Factor genérico de reducción de respuesta sísmica .......... 34 2.5.3. Factor de calidad sismorresistente..................................... 34 2.6. Cortante basal estático equivalente.................................................. 37 2.6.1. Limitaciones de método de carga estática equivalente...... 37 2.6.2. Expresión básica para el estado límite de servicio............. 38 2.6.3. Expresión básica para el estado límite de cedencia .......... 38 2.6.4. Peso Ws ............................................................................. 39 2.6.5. Coeficiente sísmico del estado límite de servicio (Css)....... 39 2.6.6. Coeficiente sísmico del estado límite de cedencia (Cs)...... 39 2.6.7. Período de vibración T ....................................................... 40 2.6.8. Distribución vertical de las fuerzas sísmicas...................... 42 2.6.9. Distribución horizontal de las fuerzas sísmicas.................. 43 2.6.10. Excentricidad accidental..................................................... 43 2.6.11. Amplificación dinámica....................................................... 44 2.6.12. Dirección de las fuerzas estáticas equivalentes................. 44 2.6.13. Volteo................................................................................. 45
- 16. IV 2.6.14. Cálculo de desplazamientos laterales por sismo ...............45 2.6.15. Desplazamientos laterales de estado límite servicio .........45 2.6.16. Desplazamientos laterales del estado límite de cedencia ............................................................................46 2.6.17. Cálculo de derivas sísmicas ..............................................46 2.7. Cortante basal método de análisis modal espectral..........................47 2.7.1. Número de modos de vibración participantes....................48 2.7.2. Períodos de vibración ........................................................48 2.7.3. Cortante modal en la base.................................................48 2.7.4. Coeficiente sísmico para el estado límite de servicio ........49 2.7.5. Coeficiente sísmico para el estado límite de cedencia ......49 2.7.6. Factor de participación modal............................................50 2.7.7. Fuerzas modales ...............................................................50 2.7.8. Derivas de los pisos...........................................................51 2.7.9. Cálculo de acciones sísmicas para diseño ........................52 3. ANÁLISIS DE CORTANTE BASAL MEDIANTE INTERNATIONAL BUILDING CODE 2009(IBC-2009/ASCE-05)..............................................55 3.1. Alcances del Código (IBC-2009/ASCE-05) .......................................55 3.2. Clasificación de sitio para el diseño sísmico .....................................55 3.2.1. Parámetros asignados de aceleración................................57 3.2.2. Coeficientes de sitio y parámetros del espectro de aceleración máxima de respuesta para sismos..................57
- 17. V 3.2.3. Parámetros de diseño de aceleración de respuesta espectral........................................................... 58 3.2.4. Diseño del espectro de respuesta....................................... 59 3.2.5. Espectro de respuesta (MCE)............................................. 61 3.3. Factor de importancia y categoría de ocupación .............................. 61 3.3.1. Factor de importancia ......................................................... 61 3.3.2. Categorías de ocupación .................................................... 62 3.3.3. Categoría de diseño sísmico............................................... 65 3.4. Procedimiento de fuerza lateral equivalente..................................... 67 3.4.1. Esfuerzo cortante en la base............................................... 67 3.4.2. Cálculo del coeficiente de respuesta sísmica...................... 67 3.5. Determinación de período ................................................................ 69 3.5.1. Período fundamental........................................................... 70 3.6. Distribución vertical de las fuerzas sísmicas .................................... 71 3.7. Distribución horizontal de las fuerzas ............................................... 72 4. ANÁLISIS DE CORTANTE BASAL MEDIANTE EUROCÓDIGO 8 ENV 1998-1-1 ................................................................ 73 4.1. Principios básicos para la concepción del proyecto ......................... 73 4.1.1. Características de los edificios sismorresistente................. 73 4.2. Condiciones del suelo...................................................................... 74 4.2.1. Generalidades..................................................................... 74 4.2.2. Clasificación de las condiciones del suelo .......................... 74
- 18. VI 4.3. Acción sísmica ..................................................................................75 4.3.1. Zonas sísmicas....................................................................75 4.3.2. Representación básica de la acción sísmica .......................76 4.3.3. Espectro elástico de respuesta............................................77 4.3.4. Desplazamiento máximo del suelo ......................................80 4.3.5. Espectro de cálculo para análisis lineal ...............................81 4.3.6. Representaciones alternativas de la acción sísmica ...........83 4.3.7. Acelerogramas de cálculo....................................................83 4.3.8. Acelerogramas artificiales....................................................83 4.3.9 Categorías de ocupación y de importancia..........................85 4.4. Análisis estructural ............................................................................86 4.4.1. Análisis modal espectral simplificado ..................................86 4.4.2. Esfuerzo cortante en la base ...............................................87 4.4.3. Distribución de las fuerzas sísmicas horizontales................88 4.4.4. Solicitaciones de torsión ......................................................89 4.4.5. Componentes de cargas verticales......................................90 4.4.6. Análisis del desplazamiento.................................................90 5. CÁLCULO ESTRUCTURAL DE CARGAS SÍSMICAS ................................91 5.1. Modelo de la estructura.....................................................................91 5.1.1. Vista de planta de la estructura ...........................................91 5.1.2. Vista de elevación de la estructura......................................92 5.2. Criterios de predimensionamiento de elementos estructurales.........93 5.2.1. Predimensionamiento de losa..............................................93
- 19. VII 5.2.2. Predimensionamiento de viga............................................. 94 5.2.3. Predimensionamiento de columna...................................... 95 5.2.4. Predimensionamiento de zapata....................................... 100 5.3. Peso total de la estructura............................................................. 101 5.3.1. Carga viva......................................................................... 101 5.3.2. Carga muerta .................................................................... 101 5.4. Cálculo de cortante basal mediante AGIES NR-3:2000 ................. 107 5.4.1. Generalidades................................................................... 107 5.4.2. Cálculo de funciones de amplificación dinámica D(T)....... 107 5.4.3. Factor de reducción de respuesta sísmica........................ 108 5.4.4. Cálculo del período fundamental de la estructura T.......... 115 5.4.5. Cálculo de sismos de diseño............................................. 116 5.4.6. Cálculo de cortante basal del estado límite servicio.......... 118 5.4.7. Cálculo de cortante basal del estado límite cedencia ....... 119 5.4.8. Distribución de cargas verticales....................................... 121 5.4.9. Resultados finales de cálculo cortante basal .................... 126 AGIES NR- 3:2000............................................................ 126 5.4.10. Esquema de distribución de cargas horizontales.............. 127 5.5. Cálculo de cortante basal mediante IBC-2009/ASCE-05................ 129 5.5.1. Generalidades................................................................... 129 5.5.2. Cálculo de coeficientes de sitio Fa y Fv.............................. 129 5.5.3. Cálculo de sismo máximo espectral considerado SMS y SM1 ...................................................... 130
- 20. VIII 5.5.4. Cálculo de sismo de diseño SDS y SD1 ...............................130 5.5.5. Categoría de ocupación.....................................................130 5.5.6. Cálculo del período fundamental .......................................131 5.5.7. Diseño del espectro de respuesta .....................................131 5.5.8. Cálculo de coeficiente de respuesta sísmica.....................132 5.5.9. Cálculo de cortante basal ..................................................133 5.5.10. Distribución de cargas verticales .......................................134 5.5.11. Resultados finales de cálculo cortante basal.....................136 IBC-2009/ASCE-5..............................................................136 5.5.12. Esquema de distribución de cargas horizontales...............137 5.6. Cálculo de cortante basal mediante eurocódigo 8 ..........................139 5.6.1. Generalidades ...................................................................139 5.6.2. Cálculo del período fundamental de la estructura..............139 5.6.3. Cálculo del espectro elástico de respuesta........................139 5.6.4. Cálculo espectro para análisis lineal..................................140 5.6.5. Cálculo de cortante basal ..................................................141 5.6.6. Resultados finales de cálculo del cortante basal eurocódigo 8......................................................................145 5.6.7. Esquema de distribución de cargas horizontales...............146 6. COMPARACIÓN DE RESULTADOS ........................................................149 6.1. Resultados del cortante basal en la estructura ...............................149 6.2. Tabla de resultados de la distribución de cargas horizontales........150 niveles superiores ...........................................................................150
- 21. IX 6.3. Comparación del período de vibración de la estructura.................. 151 6.4. Comparación analítica de cortante en la base de la estructura ...... 152 6.4.1. IBC 2009/ASCE-05 con AGIES NR-3:2000 ...................... 152 6.4.2. IBC 2009/ASCE-05 con eurocódigo 8 ENV 1998-1-1:1994 .......................................................... 153 6.4.3. AGIES NR-3:2000 con eurocódigo 8 ENV 1998-1-1:1994 .......................................................... 153 6.5. Comparación de fuerzas horizontales ............................................ 154 6.5.1. IBC 2009/ASCE-05 con AGIES NR-3:2000 ...................... 154 6.5.2. IBC 2009/ASCE-05 con Eurocódigo 8 ENV 1998-1-1:1994 .......................................................... 155 6.5.3. AGIES NR-3:2000 con Eurocódigo 8 ENV 1998-1-1:1994 .......................................................... 156 6.6. Comparación de fuerzas verticales ................................................ 157 6.6.1. Comparación con AGIES NR-3:2000, IBC 2009 Eurocódigo 8 ENV 1998-1-1:1994 .................................... 157 CONCLUSIONES ........................................................................................... 159 RECOMENDACIONES................................................................................... 161 BIBLIOGRAFÍA............................................................................................... 163 APÉNDICE...................................................................................................... 165
- 22. X
- 23. XI ÍNDICE DE ILUSTRACIONES FIGURAS 1. Esquema de las principales capas que componen la Tierra ......................2 2. Esquema de la corteza terrestre.................................................................3 3. Ondas primarias .........................................................................................5 4. Ondas secundarias.....................................................................................6 5. Ondas superficiales....................................................................................7 6. Placas tectónicas........................................................................................8 7. Modelos de interacción entre placas tectónicas .........................................9 8. Esquema de los desplazamientos de las placas tectónicas .....................10 9. Tipos de fallas tectónicas .........................................................................11 10. Mapa tectónico para Guatemala...............................................................13 11. Mapa de fallas geológicas superficiales en Guatemala............................14 12. Irregularidad en planta..............................................................................22 13. Irregularidad en elevación ........................................................................23 14. Mapa de ubicación de zonas sísmicas.....................................................24 15. Función de amplificación dinámica para perfil del suelo S1......................28
- 24. XII 16. Función de amplificación dinámica para perfil del suelo S2...................... 29 17. Función de amplificación dinámica para perfil del suelo S3...................... 30 18. Diseño del espectro de respuesta............................................................ 57 19. Espectro elástico de respuesta ................................................................ 76 20. Vista en planta de la estructura................................................................ 91 21. Vista en elevación edificio A..................................................................... 92 22. Sección predimensionada de viga ........................................................... 94 23. Área tributaria en columnas ..................................................................... 95 24. Planta del área tributaria de la columna crítica ........................................ 96 25. Predimensionamiento de zapata............................................................ 100 26. Planta ashurada..................................................................................... 112 27. Ubicación del centro de masa y centro de rigidez.................................. 113 28. Distribución de fuerzas horizontales edificio Ax ..................................... 127 29. Distribución de fuerzas horizontales edificio Ay...................................... 127 30. Distribución de fuerzas horizontales edificio Bx...................................... 128 31. Distribución de fuerzas horizontales edificio By...................................... 128 32. Distribución de fuerzas horizontales edificio Ax...................................... 137 33. Distribución de fuerzas horizontales edificio Ay...................................... 137 34. Distribución de fuerzas horizontales edificio Bx...................................... 138 35. Distribución de fuerzas horizontales edificio By...................................... 138
- 25. XIII 36. Distribución de fuerzas horizontales edificio Ax .....................................146 37. Distribución de fuerzas horizontales edificio Ay ......................................147 38. Distribución de fuerzas horizontales edificio Bx ......................................147 39. Distribución de fuerzas horizontales edificio By ......................................148 TABLAS I. Cargas vivas en edificaciones ............................................................18 II. Aceleraciones máximas efectivas para el sismo...............................25 III. Valor de los períodos TA y TB para distintos perfiles del suelo..........27 IV. Funciones de ampliación dinámica...................................................27 V. Funciones de ampliación dinámica...................................................34 VI. Factor genérico de reducción de respuesta sismica.........................35 VII. Número de tramos q1........................................................................36 VIII. Reducción de desplazamientos laterales .........................................45 IX. Clasificación de Sitio de IBC-2009/ASCE-05......................................56 X. Coeficientes de sitio Fa .....................................................................58 XI. Coeficientes de sitio Fv .....................................................................59 XII. Factores de Importancia IBC-2009/ASCE-05 ...................................62
- 26. XIV XII. Categorías de Ocupación IBC-2009/ASCE-05..................................62 XIV. Categoría de diseño sísmico a corto plazo .......................................65 XVII. Factor de modificación de respuesta (R)...........................................69 XVIII. Valores de Ct y x...............................................................................70 XIX. Valores de coeficiente K....................................................................72 XX. Espectro elástico de respuesta eurocódigo 8....................................77 XXI. Valores de kd1 y kd2 ...........................................................................79 XXII. Parámetros espectro elástico de respuesta ......................................81 XXIII. Valores de kd1 y kd2 ...........................................................................82 XXIV. Duración (Ts) de la parte estacionaria de los acelerogramas..............84 XXV. Categorías de ocupación e importancia eurocódigo 8 ......................85 XXVI. Integración de cargas sobre columna crítica.....................................98 XXVII. Integración de Peso de edificio A......................................................104 XXVIII. Integración de Peso de edificio B......................................................106 XXIX. Factor de calidad sismorresistente....................................................109 XXXI. Factor de calidad sismorresistente eje Bx) ..........................................110 XXXII. Factor de calidad sismorresistente eje BY .........................................110 XXXIII. Relación Ap/Ad .................................................................................113 XXXIV. Alturas de piso ..................................................................................115
- 27. XV XXXV. Carga vertical para edificio A en eje X...............................................121 XXXVI. Carga vertical para edificio A en eje Y...............................................122 XXXVII. Carga vertical para edificio B en eje X y Y.........................................124 XXXVIII. Resultados de cortante basal ..............................................................126 XXXIX. Carga vertical para edificio A en eje X y Y.........................................134 XL. Carga vertical para edificio B en eje X y Y.........................................135 XLI. Resultados de cortante basal ............................................................136 XLII. Carga horizontal para edificio A en eje X y Y ....................................142 XLIII. Carga horizontal para edificio B en eje X y Y ....................................144 XLIV. Resultados de cortante basal en ejes X y Y ........................................145 XLV. Resultados de cortante basal ............................................................149 XLVI. Cargas horizontales por nivel ............................................................150 XLVII. Períodos de vibración........................................................................151 XLVIII. Parámetros de diseño sismorresistente.............................................152
- 28. XVI
- 29. XVII LISTA DE SÍMBOLOS Símbolo Significado ag Aceleración de cálculo del terreno S1 Aceleración espectral de diseño para período de 1 seg (AGIES NR-3:2000) SD1 Aceleración espectral de diseño para período de 1 seg (IBC-2009/ASCE-05) SDS Aceleración espectral de diseño para períodos cortos Ss Aceleración espectral de sitio para períodos cortos SM1 Aceleración espectral máxima para período de 1 seg SMS Aceleración espectral máxima para períodos cortos Ao Aceleración máxima efectiva del suelo hN Altura del edificio Ad Área de la losa A Área del elemento hX Altura del nivel x Ap Área perimetral de la losa CV Carga viva
- 30. XVIII CM Centro de masa de la estructura CR Centro de rigidez de la estructura Fv Coeficiente del lugar para período de 1 seg Fa Coeficiente del sitio para períodos cortos CSm Coeficiente modal de diseño sísmico Cs Coeficiente sísmico de diseño Css Coeficiente sísmico para el estado límite de servicio VB Cortante basal estático equivalente VBS Cortante basal para el límite de servicio Fj Cortante de cedencia Fjs Cortante de servicio Sa Demanda sísmica de diseño dg Desplazamiento máximo del suelo β0 Factor de amplificación de la aceleración espectral D(T) Factor de amplificación dinámica Q Factor de calidad de la estructura que establece las cualidades de la estructuración de un edificio q Factor de comportamiento n Factor de corrección del amortiguamiento CVj Factor de distribución de cortante basal
- 31. XIX Cvx Factor de distribución vertical I Factor de importancia de la estructura R Factor de reducción de respuesta sísmica Ro Factor genérico de reducción de respuesta sísmica V Fuerza cortante basal q1 Índice de calidad de número de tramos de la estructura q3 Índice de calidad que depende de la regularidad en planta de la estructura q2 Índice de calidad que depende del número de ejes estructurales de la estructura Io Índice de sismicidad TB, TC Límites del tramo de aceleración espectral constante L Longitud de la estructura N Número de niveles Se(T) Ordenada del espectro elástico de respuesta S Perfil del suelo Pcol Peso propio de la columna Plosa Peso propio de la losa Pviga Peso propio de la viga Ptot Peso total de los elementos estructurales
- 32. XX TL Período de transición para período largo Ta, TE Período empírico de vibración de la estructura Wßm Peso efectivo de la estructura Sa(T) Sismo básico de diseño Sf(T) Sismo de servicio de diseño Su(T) Sismo severo de diseño T Período de vibración de la estructura TD Valor definido en inicio de tramo de desplazamiento constante del espectro
- 33. XXI GLOSARIO Aceleración Reducción de la aceleración pico o la aceleración máxima efectiva máxima absoluta del suelo obtenida durante un sismo. Centro de masa Centro o punto de simetría de la masa de una planta estructural. Centro de rigidez Centro o punto de simetría de la rigidez de los elementos verticales de una estructura. Clase de sitio Los suelos se dividen en clases, según sus características generales, con énfasis en las propiedades que se pueden ver, sentir o medir. Coeficiente sísmico Define el porcentaje del peso total de la estructura que se debe considerar como cortante actuante en su base con fines de diseño. Concreto armado Elemento homogéneo compuesto por cemento, arena, piedrín, agua y reforzado con acero. Cortante basal Fuerza cortante al nivel de la base de la estructura, originada por las fuerzas sísmicas. Diseño sísmico Son los criterios sísmicos que se utilizan para contrarrestar las fuerzas sísmicas en una estructura.
- 34. XXII Espectro de Se define como un gráfico de la respuesta máxima y aceleración es (expresada en términos de desplazamiento, velo- máxima cidad y aceleración. Espectro sísmico Gráfica normalizada con respecto al perfil del suelo y de amplificación al período de vibración, sucede cuando la estructura dinámica es excitada por un movimiento sísmico. Fluencia o El límite de fluencia o esfuerzo de cedencia, es cedencia el esfuerzo después del cual, el material empieza a sufrir deformaciones permanentes. Índice de Medida relativa de severidad esperada del sismo en sismicidad una localidad. Período de Tiempo para una oscilación completa de un cuerpo vibración elástico, vibrando en un modo dado de vibración libre. Es el recíproco de la frecuencia. Período empírico Período de vibración que toma en cuenta únicamente las propiedades geométricas de la estructura. Tramo Claro libre entre soportes consecutivos de un eje o marco estructural. Sismología Ciencia que se utiliza para estudiar la Tierra y en especial el fenómeno de los sismos.
- 35. XXIII RESUMEN En el presente trabajo de graduación se determinan los valores de las cargas sísmicas que actúan en una estructura de concreto reforzado durante su período de vida útil. Se realizó entonces un análisis, cálculo y comparación de las cargas sísmicas actuantes, fue elaborado utilizando diferentes códigos de diseño estructural. Específicamente los códigos AGIES NR-3:2000, IBC2009/ASCE-05 Y EUROCODE 8 ENV 1998-1-1. En el primer capítulo se analizan los conceptos básicos necesarios para determinar la fuerza sísmica que se aplica a una estructura; las condiciones de suelo, períodos de vibración, configuración estructural, categorías de importancia, ocupación y el peso de la estructura. En el segundo capítulo se describen los procedimientos para el cálculo de diseño estructural, iniciando con un predimensionamiento de la estructura; vigas, columnas, losas, zapatas. Se determinó el peso de la estructura, se establecieron las condiciones del sitio donde se ubicará el proyecto, para realizar los cálculos correspondientes. Finalmente se procedió a calcular el cortante basal, utilizando los códigos AGIES NR-3:2000, IBC2009/ASCE-05 Y EUROCODE 8 ENV 1998-1-1. En el tercer capítulo se describen los resultados obtenidos con el objetivo de realizar una comparación de los mismos. Se analizaron las diferencias de resultados entre los códigos utilizados y se determinó con qué código el cálculo de cortante basal es similar al calculado con la norma guatemalteca.
- 36. XXIV
- 37. XXV OBJETIVOS General Elaborar una guía de análisis, cálculo y comparación de cargas sísmicas utilizando los códigos AGIES NR-3:2000, IBC2009/ASCE-05 Y EUROCODE 8 ENV 1998-1-1, para una estructura de concreto reforzado. Específicos 1. Conocer los criterios generales de diseño sismorresistente que deben aplicarse en las edificaciones, tomando en cuenta los códigos AGIES NR- 3:2000, IBC2009/ASCE-05 Y EUROCODE 8 ENV 1998-1-1. 2. Complementar los estudios realizados por los alumnos de pregrado de Ingeniería Civil, en especial de la Facultad de Ingeniería de la Universidad de San Carlos de Guatemala sobre cargas sísmicas que afectan una edificación de concreto reforzado. 3. Que el estudiante aprenda a utilizar los códigos para la determinación de cargas sísmicas que afectan las estructuras y el código del ACI para el predimensionamiento de las mismas. 4. Determinar un algoritmo sencillo de los pasos a seguir para realizar el cálculo de las fuerzas sísmicas, utilizando el AGIES NR3:2000, IBC 2009/ASCE-05 y Eurocódigo 8.
- 38. XXVI 5. Analizar los parámetros que se utilizan en cada código de diseño estructural, debido a que en los mismos se utilizan diferentes metodologías para el cálculo de la carga sísmica.
- 39. XXVII INTRODUCCIÓN Guatemala es un país propenso a actividad sísmica constante, debido a que está ubicada entre la convergencia de tres placas tectónicas (Norteamérica, Caribe y de Cocos), que ha generado una cantidad considerable de fallas geológicas y volcanes. Esta amenaza sísmica obliga al ingeniero estructural a aplicar en su trabajo de diseño, códigos estructurales vigentes. La correcta aplicación de los mismos incide en un apropiado comportamiento de la estructura al momento de ocurrir cualquier evento sísmico. En Guatemala, debido a la carencia de un código nacional estructural obligatorio, los ingenieros civiles calculistas e ingenieros estructurales, se ven en la necesidad de aplicar en su trabajo de diseño códigos internacionales. La única norma que existe en Guatemala, es la publicada por la Asociación Guatemalteca de Ingeniería Estructural y Sísmica (AGIES), pero ésta es únicamente una norma recomendada. El presente trabajo de graduación tiene como objetivo, brindarle al estudiante de ingeniería civil una guía de parámetros en tres diferentes códigos de diseño estructural, que permitan posteriormente analizar y facilitar los correspondientes cálculos y comparaciones de cada código. También pretende servir de complemento al contenido de los cursos teóricos del área de estructuras de la carrera de Ingeniería Civil, debido a que en un semestre el tiempo es limitado para desarrollar cálculos de carga sísmica con diversos códigos de diseño.
- 40. XXVIII Cada código es distinto y posee diferentes metodologías de cálculo.
- 41. 1 1. FUNDAMENTOS PRINCIPALES DE SISMOLOGÍA 1.1. Sismología La Sismología es una de las ramas de la Geofísica que se utiliza para estudiar La Tierra y en especial el fenómeno de los sismos. La Sismología utiliza el registro del movimiento del suelo producido por un sismo para estudiar el origen y propagación de la onda sísmica. Por su origen, los sismos se clasifican en naturales o artificiales. Los sismos naturales son los producidos por fallas geológicas (tectónicas), la actividad volcánica y en menor importancia por agentes meteorológicos tales como el oleaje del mar. Los sismos artificiales son los producidos por la actividad del hombre, entre los principales están las explosiones para la exploración minera, explosiones nucleares, microsismicidad producida por fábricas y el tránsito de vehículos pesados. La Sismología implica la observación de las vibraciones naturales del suelo y de las señales sísmicas generadas de forma artificial, con demasiadas ramificaciones teóricas y prácticas. Como rama de la Geofísica, la sismología ha aportado contribuciones esenciales a la comprensión de la tectónica de placas, la estructura del interior de la Tierra y la predicción de sismos. La ingeniería sísmica tiene un carácter de aplicación, se define como la parte de la mecánica aplicada dedicada al estudio del comportamiento de las estructuras bajo las cargas producidas por el movimiento del suelo, así como el análisis y diseño de las mismas.
- 42. 2 Para lograr sus objetivos la ingeniería sísmica utiliza los resultados proporcionados por la sismología, especialmente los que se emplean en la definición numérica de la acción sísmica. 1.2. Origen de los sismos Para comprender el origen de los sismos, es necesario conocer la estructura interna del planeta, la cual está establecida por tres capas: Núcleo Manto Corteza 1.2.1. Estructura interna de la Tierra La Tierra está formada por tres capas concéntricas: corteza, manto y núcleo, con propiedades físicas distintas. Estas capas han podido ser detectadas y definidas, a partir del estudio de los registros del movimiento de su superficie y más concretamente por el estudio de los sismos. Figura 1. Principales capas que componen la Tierra Fuente: http://www.insivumeh.gob.gt/geofisica/indice%20sismo.htm#estructurainternadelatierra. 18 Noviembre 2010.
- 43. 3 Entre las principales capas que componen la Tierra se enlista las siguientes: 1.2.1.1. Núcleo Con un radio de 3 470 Km, está constituido por su núcleo interior formado por hierro, su consistencia es sólida y su temperatura es de 4300°C y su núcleo exterior está formado por hierro fundido, mezclado con pequeñas cantidades de níquel, sulfuros y silicio, su consistencia es líquida y su temperatura es de 3700°C. 1.2.1.2. Manto Con un espesor de 2 900 Km, se divide en manto interior, manto exterior y una zona de transición; el manto está conformado por: magnesio, hierro, aluminio, silicio y oxígeno. Su temperatura es de 100°C. 1.2.1.3. Corteza o litósfera Es la capa exterior de la Tierra, es de elevada rigidez formada por roca, se sabe que es de espesor variable y que en algunos casos puede ser de 60 Km. En los continentes las formaciones son graníticas y basálticas en los fondos oceánicos. Figura 2. Corteza terrestre Fuente: VALDIVIA, Luis Alva. Propiedades geofísicas de la Tierra. p. 13.
- 44. 4 1.3. Diferencias entre sismo y terremoto En ambos casos se utilizan para describir un movimiento brusco en la corteza terrestre producido por el contacto entre placas tectónicas, pero el primero hace referencia a un evento sísmico sin haberse producido daños materiales, y el segundo a un evento sísmico que causa pérdidas de vida y daños materiales. 1.3.1. Sismo Movimiento brusco y errático de la superficie terrestre. Las vibraciones no poseen una trayectoria específica y pueden presentarse en cualquier dirección. Existen tres clases de movimientos sísmicos: tectónicos, volcánicos y artificiales. Los primeros son producto de la tensión de las placas tectónicas, con su zona de conflicto, que son áreas cercanas a su frontera. Los volcánicos anuncian la cercanía de erupciones y raramente son destructivos. Los sismos artificiales son producto de las actividades humanas en el subsuelo. De las tres clases de movimientos, la más importante es la de origen tectónico, debido a que la misma libera el 75% de la energía sísmica del planeta. 1.3.1.1. Movimientos sísmicos Las placas de la corteza terrestre están sometidas a tensiones. En la zona de roce (falla), la tensión es muy alta, y a veces, supera a la fuerza de sujeción entre las placas. Entonces, las placas se mueven violentamente provocando ondulaciones y liberando una enorme cantidad de energía. A este proceso se le llama movimiento sísmico. La intensidad o magnitud de un sismo en la escala
- 45. 5 de Richter representa la energía liberada y se mide en forma logarítmica, del uno al nueve. 1.4. Movimientos del suelo Los movimientos del suelo durante un sismo se manifiestan básicamente en forma de ondas, en donde la corteza terrestre funciona como un medio sólido elástico continuo que transmite la energía irradiada desde el epicentro en todas las direcciones de dicho punto de inicio. 1.4.1. Ondas sísmicas La deformación de los materiales rocosos produce distintos tipos de ondas sísmicas. Un deslizamiento súbito a lo largo de una falla, produce ondas primarias, longitudinales o de compresión (ondas P) y ondas secundarias denominadas transversales (ondas S). 1.4.1.1. Ondas longitudinales Son las que en el movimiento de vibración de las partículas, se produce en la misma dirección de propagación. Estas ondas también se les conocen como ondas de compresión y dilatación o de condensación; en sismología se les conoce como ondas primarias, por ser de las primeras que son registradas en los sismos. Éstas son las que se utilizan en prospección sísmica de reflexión y de refracción para el estudio del subsuelo.
- 46. 6 Figura 3. Ondas primarias Fuente: VIVES, Vinces. Horizonte 1: Historia y Geografía. p. 296. 1.4.1.2. Ondas transversales Ondas en las que el movimiento de vibración de las partículas se produce en la dirección perpendicular a la dirección de propagación. También se les llama ondas de corte o cizalla que en sismología se les conoce como ondas secundarias, son las segundas en registrarse en un estudio sísmico. Pueden ser verticales (SV) y horizontales (SH). Figura 4. Ondas secundarias Fuente: VIVES, Vinces. Horizonte 1: Historia y Geografía. p. 296.
- 47. 7 Las ondas superficiales son las que se propagan en la superficie libre de un medio elástico y se distinguen dos tipos principales: ondas Rayleigh (LR) y ondas Love (LL). 1.4.1.3. Ondas Rayleigh Son una combinación de las ondas longitudinales y transversales. En ellas las vibraciones de las partículas se efectúan en un plano perpendicular a la superficie, a la dirección de propagación; siendo su movimiento elíptico y retrogrado. 1.4.1.4. Ondas Love Al igual que las ondas Rayleigh, también son una combinación de las ondas longitudinales y transversales en las que el desplazamiento de las partículas es únicamente horizontal y perpendicular a la dirección de propagación. Estas ondas se propagan en un medio que está limitado en su parte superior por una superficie reflectora ideal, tal como la discontinuidad suelo-aire y en su parte inferior por un medio en el que la velocidad de las ondas transversales es mayor que en el primero. Figura 5. Ondas superficiales Fuente: VIVES, Vinces. Horizonte 1: Historia y Geografía. p. 296.
- 48. 8 1.5. Placas tectónicas Según la teoría de la tectónica de placas, la corteza terrestre está compuesta al menos por una docena de placas rígidas (unas mayores y otras menores) que se mueven y presionan con distintas direcciones. Estos bloques descansan sobre una capa de roca caliente y flexible llamada astenósfera, que fluye lentamente a modo de alquitrán caliente. Los geólogos todavía no han determinado con exactitud cómo interactúan estas dos supercapas, pero las teorías más vanguardistas afirman que el movimiento del material espeso y fundido de la astenósfera fuerza a las placas superiores a moverse, hundirse o levantarse. El concepto básico de la teoría de la tectónica de placas es simple: el calor asciende. El aire caliente asciende por encima del aire frio y las corrientes de agua caliente flotan por encima de las de agua fría, el mismo principio se aplica a las rocas calientes que están debajo de la superficie terrestre: el material fundido de la astenósfera o magma se desplaza hacia arriba; mientras que la materia fría y endurecida se hunde cada vez más hacia al fondo dentro del manto. La roca que se hunde finalmente alcanza las elevadas temperaturas de la astenósfera inferior, se calienta y comienza a ascender otra vez. Figura 6. Placas tectónicas Fuente: http://earthquake.usgs.gov/learn/topics/?topicID=30. Sistema sismológico de Estados Unidos
- 49. 9 1.5.1. Interacción entre las placas tectónicas Los modelos de interacción entre las placas tectónicas se describe mediante a la figura 7: Figura 7. Modelos de interacción entre placas tectónicas Fuente: BARBAT, Alex H. Cálculo sísmico de las estructuras. p. 4. 1.5.1.1. Subducción Ocurre cerca de las islas donde dos placas de similar espesor entran en contacto entre sí. 1.5.1.2. Deslizamiento Se produce cuando entran en contacto dos placas oceánicas o bien una continental y una oceánica.
- 50. 10 1.5.1.3. Extrusión Este fenómeno ocurre cuando hacen contacto dos placas tectónicas delgadas que se desplazan en direcciones opuestas, por ejemplo, el contacto de dos placas del fondo del océano. 1.5.1.4. Acrecencia Tiene lugar cuando hay un impacto leve entre una placa oceánica y una continental; los movimientos de las placas están asociados con la energía calorífica que se concentra bajo la litosfera. En las zonas de extrusión aparece una nueva corteza, mientras en las zonas de subducción las placas que penetran por debajo se funden por efecto del calor desarrollado en la interacción entre placas bajo condiciones de presión elevada, dando lugar al magma. Por ello los volcanes activos se sitúan frecuentemente en zonas de subducción. Figura 8. Esquema de los desplazamientos de las placas tectónicas Fuente: Insivumeh.http://www.insivumeh.gob.gt/geofisica/indice%20sismo.html.
- 51. 11 1.6. Fallas tectónicas Una roca se comporta elásticamente mientras las deformaciones producidas por el esfuerzo aplicado sean relativamente pequeñas. Si el esfuerzo aplicado es tan fuerte que produce deformaciones demasiado grandes, la roca se rompe y se dice que falla, esta ruptura es súbita y ocurre a lo largo de planos llamados planos de falla o simplemente fallas tectónicas. Figura 9. Tipos de fallas tectónicas Fuente: BARBAT, Alex H. Cálculo Sísmico de las Estructuras. p. 15. 1.6.1. Tipos de fallas Los tipos de fallas tectónicas más importantes son las siguientes: 1.6.1.1. Falla normal Corresponde a las zonas donde la corteza terrestre está en extensión, uno de los dos bloques de la falla se desliza hacia abajo.
- 52. 12 1.6.1.2. Falla invertida Corresponden a las zonas en compresión, existen dos casos: 1.6.1.2.1. Deslizamiento hacia abajo Una de las dos porciones de corteza que están en contacto penetra bajo la otra que en general es una placa continental. 1.6.1.2.2. Deslizamiento hacia arriba Una de las placas se desliza hacia arriba de la otra. 1.6.1.3. Falla de deslizamiento Implica deslizamientos horizontales entre los dos bordes de la falla. 1.7. Marco tectónico para Guatemala 1.7.1. Placas tectónicas en la que se encuentra Guatemala Guatemala es un país que se encuentra en constante amenaza sísmica, el territorio nacional está repartido en tres placas tectónicas: Norteamérica, Caribe y de Cocos. Los movimientos relativos entre éstas determinan los principales rasgos topográficos del país y la distribución de los sismos y volcanes. El contacto entre las placas de Norteamérica y Caribe es de tipo transcurrente; su manifestación en la superficie son las fallas de Chixoy-Polochic y Motagua.
- 53. 13 Figura 10. Mapa tectónico para Guatemala Fuente: http://www.insivumeh.gob.gt/geofisica/indice%20sismo.htm#marcotectónicapara Guatemala. El contacto entre las placas de Cocos y del Caribe es de tipo convergente en el cual la placa de Cocos se introduce por debajo de la placa del Caribe (fenómeno conocido como subducción). Este proceso da origen a una gran cantidad de sismos y formación de volcanes. El contacto entre estas dos placas está aproximadamente a 50 Km frente a las costas del Océano Pacífico. A su vez, estos dos procesos generan deformaciones al interior de la placa del Caribe produciendo fallamientos secundarios como: Jalpatagua, Mixco, Santa Catarina Pínula, Motagua, etc.; Como se observa en la figura 11.
- 54. 14 Figura 11. Mapa esquemático de fallas geológicas superficiales en Guatemala Fuente: BOHNENBERGER, Bonis, S. Geología General República de Guatemala, p. 45. 1.7.2. Zonas sísmicas Las principales zonas sísmicas del mundo coinciden con los contornos de las placas tectónicas y con la posición de los volcanes activos de la Tierra; esto se debe al hecho de que la causa de los sismos y de las erupciones volcánicas está fuertemente relacionada con el proceso tectónico del planeta.
- 55. 15 Al analizar las regiones sísmicas se deben definir dos conceptos importantes, la intensidad sísmica que mide los efectos de los sismos en el entorno y particularmente sobre las estructuras. La sismicidad se define como la frecuencia de ocurrencia de fenómenos sísmicos por unidad de área incluyendo al mismo tiempo, cierta información de la energía sísmica liberada. 1.7.3. Importancia del estudio de los sismos El estudio de los sismos es útil para prevenir y disminuir los daños que estos producirán, aun cuando no es posible saber cuándo y dónde ocurrirá el próximo sismo, se tiene la seguridad y certeza de que ocurrirá de nuevo según lo demuestra la evidencia geológica, los registros históricos y la información instrumental sismológica. Para disminuir los daños que producen los sismos la forma más eficaz y económica ante cualquier tipo de amenaza es la prevención. Las medidas preventivas contemplan una gran cantidad de acciones entre las que se puede mencionar: educación a nivel escolar, códigos o normas de construcción, uso adecuado del suelo y sus recursos, planes de emergencia, etc. Se puede apreciar que ésta es una tarea multidisciplinaria que involucra a toda la sociedad. El papel de las ciencias de la Tierra entre ellas, la Sismología su función es estudiar el fenómeno natural e identificar los factores que pueden producir daños en determinado lugar. Esto último se conoce como evaluación de la amenaza o peligro, que en el caso de los sismos se denomina evaluación de la amenaza sísmica.
- 56. 16 1.8. Consideraciones generales de diseño de fuerzas sísmicas 1.8.1. Efecto de sismo en edificios Durante un sismo el suelo se mueve en toda dirección. Los efectos que producen más daños en las estructuras son los movimientos paralelos a la superficie del suelo (en dirección horizontal), debido a que las estructuras se diseñan rutinariamente para resistir cargas verticales de gravedad. Es así, que para fines de diseño el efecto mayor de un sismo, por lo general, se considera en función de una fuerza horizontal. 1.8.2. Fuerzas sísmicas Las cargas sísmicas son generadas por diversos factores; entre ellos se puede mencionar: la carga muerta del edificio, las propiedades de suelo, configuración estructural, categorías de ocupación e importancia. Al considerar la aplicación de las fuerzas sísmicas se observa cada una de las partes del edificio y se considera un porcentaje de su peso como una fuerza horizontal. El peso de la estructura horizontal en realidad se encuentra distribuida sobre todo su plano, generalmente se puede tratar de manera similar a la condición de carga de borde producida por el viento. Para determinar la carga sísmica se consideran todos los elementos que están permanentemente unidos a la estructura. Los ductos, dispositivos de iluminación, instalaciones hidráulicas, sanitarias, etc., que contribuyen la carga muerta total para calcular la carga sísmica.
- 57. 17 1.8.3. Cortante basal La fuerza total horizontal calculada como el cortante basal (V) se debe distribuir, tanto vertical como horizontalmente entre los elementos del sistema resistente a cargas laterales. Esto comienza con una consideración de la distribución real de la masa del edificio, la que esencialmente genera las fuerzas de inercia reales. Los cálculos del cortante basal (V) depende de: Condiciones del suelo en el sitio. Proximidad a las fuentes potenciales de la actividad sísmica. Probabilidad de movimientos sísmicos significativos. El período fundamental (natural) de vibración de la estructura cuando se somete a cargas dinámicas. Peso de la estructura. La fuerza sísmica total en la base del edificio (cortante basal), se calcula por medio del espectro de diseño (aceleración de respuesta de la edificación según su período de vibración), y el peso total de la edificación. La manera como responde el edificio a la aceleración inducida por el sismo determina la repartición de las fuerzas sísmicas, tanto en la altura como en cada uno de los elementos estructurales que la conforman.
- 58. 18 1.8.4. Cargas muertas Éstas comprenden todas las cargas de elementos permanentes de la construcción, incluyendo la estructura en sí: pisos, rellenos, cielos, vidrieras, tabiques fijos, equipo permanente rígidamente anclado. Las fuerzas netas de pre-esfuerzo, también se consideran como cargas muertas. 1.8.5. Cargas vivas Son las que resultan por el uso y la ocupación de la edificación; los agentes que producen estas cargas no están rígidamente sujetos a la estructura. Este tipo de carga incluye, pero no está limitada a los ocupantes en sí, el mobiliario y su contenido, así como el equipo no fijo. Tabla I. Cargas vivas en edificaciones Tipo de ocupación o uso W v (kg / m 2 ) P v (kg) Vivienda Oficina Hospitales - encamamiento y habitaciones Hospitales - servicios médicos y laboratorio Hoteles - alas de habitaciones Hoteles - servicios y áreas públicas 200 250 200 350 200 500 0 800 0 800 0 800 Escaleras privadas Escaleras públicas o de escape Balcones, cornisas y marquesinas Áreas de salida y / o escape Vestíbulos públicos Plazas y áreas públicas a nivel de calle 300 500 300 500 500 500 150 150 0 0 0 800
- 59. 19 Continuación tabla I. Aulas y escuelas Bibliotecas Áreas de lectura Depósito de libros 200 200 600 400 400 800 Almacenes: Minoristas Mayoristas 350 500 800 1200 Bodegas: Cargas livianas Cargas pesadas 600 1200 800 1200 Fábricas: Cargas livianas Cargas pesadas 400 600 800 1200 Fuente: Normas estructurales de diseño recomendadas para la República de Guatemala, AGIES NR-2: 2000, p. 28-29. 1.9. Sistemas estructurales básicos La estructura de una edificación se clasifica, para este trabajo de graduación, conforme a la Norma AGIES NR: 3-2000. Cada estructura o cada parte significativa de la misma se clasificarán en cada dirección de análisis, independientemente, en una de cinco posibles familias E1 a E5. En caso de no ser posible clasificarla o en caso de duda se clasifica como E6, u otro tipo. 1.9.1. Sistema de cajón E1 Es un sistema estructural integrado con muros estructurales que soportan toda o casi toda la carga vertical y las fuerzas sísmicas son soportadas por los propios muros estructurales.
- 60. 20 1.9.2. Sistema de marcos E2 Sistema estructural integrado con marcos especiales resistentes a flexión que soportan la carga vertical y además todas las solicitaciones sísmicas. Todos los marcos deben estar unidos por diafragmas horizontales. 1.9.3. Sistema de marcos ordinarios E2-1 Es un sistema E2 en el que los marcos deben cumplir únicamente requisitos sismorresistentes fundamentales. 1.9.4. Sistema de marcos especiales E2-2 Sistema en el que los marcos deben cumplir un número de requisitos adicionales a los especificados para marcos ordinarios con el objeto de incrementar su confiabilidad y su capacidad post-elástica. 1.9.5. Sistema combinado de muros y marcos E3 Constituido por un marco espacial esencialmente completo que soporta la carga vertical. La totalidad de las solicitaciones sísmicas deben ser resistidas con muros estructurales o marcos arriostrados. 1.9.6. Sistema dual de muros y marcos Constituido con un marco espacial esencialmente completo que soporta la carga vertical. Las solicitaciones sísmicas resisten en muros estructurales incorporados en algunos de los marcos o al incluir marcos arriostrados. Los marcos deben estar unidos por diafragmas horizontales y deben resistir las
- 61. 21 solicitaciones sísmicas en proporción a su rigidez relativa, tomando en cuenta la interacción entre muros y marcos. Los marcos especiales deben resistir por sí mismos el 25% de las solicitaciones sísmicas especificadas, cuando en el modelo estructural se anula la rigidez lateral de los muros (pero no rigidez axial) y la rigidez de las riostras. 1.10. Regularidad estructural A efectos de un proyecto sismorresistente, las estructuras de los edificios se clasifican como regulares y no regulares. Por lo mismo, es conveniente considerar criterios adecuados en regularidad de planta y elevación. 1.10.1. Criterio de regularidad en planta Algunos aspectos de la configuración en planta del edificio, propician una respuesta sísmica poco conveniente y deben evitarse. Entre estos aspectos destaca la asimetría de la planta, la cual tiende a provocar vibraciones torsionales del edificio. Una posible solución a los problemas de plantas asimétricas es la subdivisión del edificio en cuerpos independientes y regulares mediante juntas de construcción (juntas sísmicas). Causas de problemas de comportamiento: Configuración en planta Asimetría en planta Configuración en altura Discontinuidad de elementos verticales
- 62. 22 Concentraciones de masa en pisos Interacción entre elementos estructurales y no estructurales Figura 12. Irregularidad en planta Fuente: DIEZ, Gloria. Diseño estructural en arquitectura. p. 17. 1.10.2. Criterio de regularidad en elevación Factores como sencillez, regularidad y simetría en la elevación del edificio, para evitar que se produzcan concentraciones de esfuerzos en ciertos pisos o amplificaciones de la vibración en las partes superiores del mismo. Particularmente críticas son las reducciones bruscas en la parte superior del edificio, donde el cambio drástico de rigidez tienden a producir el fenómeno de chicoteo con una gran amplificación en la punta.
- 63. 23 Figura 13. Irregularidad en elevación Fuente: DIEZ, Gloria. Diseño estructural en arquitectura. p. 17.
- 64. 24
- 65. 25 2. ANÁLISIS DE CORTANTE BASAL (AGIES NR-3:2000) 2.1. Zonificación sísmica y caracterización de sitio en Guatemala Guatemala está dividida en cuatro zonas sísmicas, el nivel más bajo se asigna a la mitad Nororiental del país. El área mostrada en la figura 14, cubre 30% del país, así como Belice; las otras dos terceras partes del país se dividen en las tres zonas adicionales, las cuales aumentan en intensidad a medida que se acercan al Océano Pacifico. El mapa refleja las dos zonas sismológicas más importantes en Guatemala, la falla del Motagua-Polochic y la zona de Subducción. Figura 14. Mapa de ubicación de zonas sísmicas Fuente: Normas de seguridad estructural de diseño recomendadas para la República de Guatemala, AGIES NR-2: 2000. p. 14.
- 66. 26 Tabla II. Aceleraciones máximas efectivas para el sismo básico y para el sismo frecuente Zona Sísmica Io Ao Af Observaciones 2 2 0.15g 0.015g Cuando sea necesario interpolar hacerlo sobre líneas Norte - Sur. 3 3 0.15 a 0.40g 0.015 a 0.15g 4.1 4 0.40g 0.15 a 0.20g 4.2 4 0.40g 0.20g Fuente: Normas Estructurales de diseño recomendadas para la república de Guatemala, AGIES NR-2: 2000. p. 12. 2.2. Sismicidad y nivel de protección 2.2.1. Índice de sismicidad El índice de sismicidad (Io) es una medida relativa de la severidad esperada del sismo en una localidad. Incide sobre el nivel de protección sísmica que se requiere para diseñar edificaciones. Para efecto de las Normas AGIES NR-3:2000, el territorio de Guatemala se divide en macrozonas caracterizadas por su índice de sismicidad que varía de Io = 2 a Io = 4. La distribución geográfica del índice de sismicidad se especifica en la figura 14, mapa base de macrozonificación sísmica de la República de Guatemala. Adicionalmente las Normas AGIES NR-3:2000 requieren la aplicación de un índice de sismicidad Io = 5 a nivel de microzona para tener en cuenta en condiciones localizadas. El índice Io = 5 indica que se deben tomar precauciones especiales en vista de efectos sísmicos potencialmente severos.
- 67. 27 2.3. Requisitos de sitio Se establecen tres tipos de suelo: suave (S3 ), mediano (S2 ) y suelo duro o roca (S1 ) en términos de profundidad de los estratos, propiedades geofísicas y composición. En lugares donde las propiedades del suelo no son conocidas con suficiente detalle para determinar el tipo de perfil de suelo se utiliza el caso más crítico, ya sea del perfil de suelo mediano o del perfil de suelo suave. En primer lugar, se define un criterio básico y se da el criterio de microzonificación mediante la definición de zonas de precaución diferente, de acuerdo a las principales características de la topografía de la ciudad de Guatemala y otros centros urbanos de importancia. Se hace énfasis en la identificación de la inestabilidad de terrenos con pendiente, fallos en tierra debidos a falla y licuefacción. Se dan previsiones especiales para los sitios a ser utilizados para facilidades a los que se le asigna un índice de sismicidad de Io = 5, considerado el nivel más alto.
- 68. 28 2.3.1. Clasificación de sitio Para establecer el espectro del sismo de diseño, se definen tres perfiles de suelo: Tabla III. Valor de los períodos TA y TB para distintos perfiles del suelo Perfil del suelo S1 S2 S3 TA 0.12 0.12 0.12 TB 0.4 0.6 1 Fuente: Normas estructurales de diseño recomendadas para la República de Guatemala, AGIES NR-2: 2000. p. 14. Tabla IV. Funciones de ampliación dinámica Función de amplificación dinámica Cuando T < TA D(T) = 1.0 + 1.5 T / TA Cuando 0 <T <TB D(T) = 2.5 Cuando T ≥ TB D(T) = 2.5 (TB / T )0.67 Fuente: Normas estructurales de diseño recomendadas para la República de Guatemala, AGIES NR-2: 2000. p. 14. 2.3.1.1. Perfil de suelo S1 Este perfil de suelo satisface cualquiera de las siguientes condiciones: Roca de cualquier clase: material que puede caracterizarse por velocidades de onda de corte mayores que 800 m/s.
- 69. 29 Suelo rígido cuyo basamento rocoso está a menos de 50 metros de profundidad y constituido por cenizas volcánicas, arenas y gravas densas o arcillas firmes. Figura 15. Función de amplificación dinámica para perfil del suelo S1, con 5% de amortiguamiento crítico Fuente: Normas estructurales de diseño recomendadas para la República de Guatemala, AGIES NR-2: 2000. p. 13. 2.3.1.2. Perfil de suelo S2 Este perfil de suelo satisface cualquiera de las siguientes condiciones: Suelo firme cuyo basamento rocoso está a más de 50 metros de profundidad y cuyos depósitos son cenizas volcánicas, suelos granulares densos, limos densos o arcillas firmes. En general, suelos firmes y estables cuyos, perfiles no clasifican como S1 ni como S3.
- 70. 30 Figura 16. Función de amplificación dinámica para perfil del suelo S2, con 5 % de amortiguamiento crítico Fuente: Normas estructurales de diseño recomendadas para la República de Guatemala, AGIES NR-2: 2000. p. 13. 2.3.1.3. Perfil de suelo S3 Este perfil satisface cualquiera de las siguientes condiciones: Depósitos de más de 10 metros de espesor de cenizas, arenas o limos desde sueltos hasta de densidad media. Depósitos entre 10 y 20 metros de espesor de arcillas blandas o semiblandas con o sin estratos arenosos intermedios. Perfiles de suelo donde la velocidad de onda de corte del depósito es menor que 200 m/s. En caso de duda se tomará el resultado más crítico de suponer perfil S2 y S3.
- 71. 31 Figura 17. Función de amplificación dinámica para perfil del suelo S3, con 5 % de amortiguamiento crítico Fuente: Normas estructurales de diseño recomendadas para la República de Guatemala, AGIES NR-2: 2000. p. 13. 2.4. Niveles de intensidad sísmica Se consideran tres niveles de intensidad sísmica en la Norma AGIES NR-3:2000: frecuente, severo y extremo. El nivel correspondiente a sismo severo corresponde al inciso 2.4.3 al nivel de la base. El sismo frecuente es asignado a un nivel de aceleración más bajo en cada zona sísmica. El sismo extremo se define finalmente, como el evento que producirá un 30% de incremento en los niveles de aceleración pico con respecto al caso severo.
- 72. 32 2.4.1. Sismo básico El sismo básico para el estado límite de cedencia se define como un sismo que tiene un 90 por ciento de probabilidad de no ser excedido en un período de 50 años. El espectro de diseño para el estado límite de cedencia se calcula a partir de: Cuyos términos se definen a continuación en la tabla V Tabla V. Funciones de ampliación dinámica Sa (T) Representa la respuesta sísmica máxima de un oscilador elástico de un grado de libertad. Esta función expresada como fracción de la aceleración de la gravedad. Ao Es una medida de la aceleración máxima efectiva del suelo correspondiente al sismo básico de diseño. El valor de este parámetro se específica en la figura 14 y en la tabla II. A menos que se indique explícitamente, el valor del parámetro (Ao ) para microzonas con índice de sismicidad Io = 5 no necesita ser mayor que el valor para Io = 4. T Es el período de vibración del oscilador y representa al período fundamental de vibración de la estructura o al período de alguno de sus modos de vibración, según el método requerido para el análisis. D(T) Representa la amplificación dinámica de la respuesta máxima del oscilador elástico de un grado de libertad. Es función del parámetro (T): esta función depende del tipo de perfil del suelo en el sitio de construcción. Fuente: Normas estructurales de diseño recomendadas para la República de Guatemala, AGIES NR-2: 2000. p. 9.
- 73. 33 2.4.2. Sismo de servicio Llamado también sismo frecuente, se define como un sismo que tiene una alta probabilidad de ocurrencia durante la vida útil de la estructura. El espectro correspondiente al sismo de servicio se calcula con la siguiente ecuación: onde Af Es una medida de la aceleración máxima del suelo producida por el sismo frecuente o de servicio. El valor de este parámetro se especifica en tabla II. 2.4.3. Sismo extremo Es el que tiene la máxima intensidad que puede ocurrir en el sitio. Como una guía general, el espectro de este sismo puede calcularse de acuerdo a: onde Ku(T) Factor de modificación que calibra la función D(T) para tomar en cuenta el amortiguamiento post-elástico, que ocurriría durante las severas incursiones al intervalo post-elástico de la estructura producidas por el sismo extremo.
- 74. 34 2.5. Parámetros de sismoresistencia 2.5.1. Factor de reducción de respuesta sísmica para el estado límite de cedencia El factor de reducción de respuesta sísmica (R) se utiliza para reducir la respuesta elástica de un sistema de un grado de libertad a una respuesta post-elástica: onde Ro Es el factor genérico de reducción de respuesta descrito en el inciso 2.5.2. Q Es un factor específico de calidad sismorresistente 2.5.2. Factor genérico de reducción de respuesta sísmica Este factor (Ro), depende de las características genéricas del sistema estructural seleccionado por el diseñador y de los materiales constructivos a utilizar. El valor numérico de (Ro), se especifica en la tabla VI. 2.5.3. Factor de calidad sismorresistente El factor de calidad sismorresistente (Q) evalúa el comportamiento de la edificación, como resultado de las variaciones hechas por el diseñador a una determinada configuración estructural. Se específica para cada proyecto en particular y para cada dirección de análisis. Su valor numérico se integrará para cada dirección de análisis mediante la siguiente ecuación: ∑
- 75. 35 Si el valor de (Q) baja a menos de 0.80 en cualquier dirección de análisis, deberá modificarse el proyecto, de forma que el factor (Q) alcance a ser por lo menos 0.80. Los índices de calidad (q); se obtienen conforme a lo descrito en el inciso 2.5.3.1 y según lo establecido en la tabla VII. Tabla VI. Factor genérico de reducción de respuesta sísmica (Ro) por capacidad post-elástica (ductilidad) de la estructura SISTEMA ESTRUCTÚRAL (Ver inciso 1.5) SISTEMA VERTICAL SISMORRESISTENTE FACTOR Ro (Ver inciso 2.5.2) E1. SISTEMA DE CAJÓN Con muros estructurales: De mampostería reforzada De concreto reforzado De mampostería sin refuerzo De mampostería reforzada interiormente Con marcos arriostrados 2.5 3.5 1.0 1.7 3.0 E2. SISTEMA DE MARCOS E2.1 marcos ordinarios E2.2 marcos espaciales De acero estructural De concreto reforzado De acero estructural De concreto reforzado 3.5 1.7 5.5 5.0 E3. SISTEMA COMBINADO DE MUROS Y MARCOS Con muros de mampostería reforzada Con muros de concreto reforzado 3.5 4.5
- 76. 36 Continuación tabla VI. E4. SISTEMA DUAL DE MUROS Y MARCOS Con muros de mampostería reforzada Con muros de concreto reforzado Con marcos arriostrados en vez de muros Arriostres ordinarios 3.5 5.5 3.5 E5. PÉNDULO INVERTIDO De concreto reforzado Confinado Ordinario De estructura de acero Con detalles ordinarios Con detalles sísmicos De estructura de madera 2.0 No usar 1.0 2.0 2.5 Fuente: Normas estructurales de diseño recomendadas para la República de Guatemala, AGIES NR-3: 2000. p. 5. 2.5.3.1. Número de tramos (q1) El número de tramos se describe en la tabla VII. Tabla VII. Número de tramos q1 Número de tramos Requisito Índice q1 4 o más Tramo menor > 0,75 tramo mayor Tramo menor < 0,45 tramo mayor +2,5 +1,5 3 tramos Tramo menor > 0,75 tramo mayor Tramo menor < 0,45 tramo mayor +1,5 0,0 2 tramos Tramo menor > 0,70 tramo mayor Tramo menor < 0,45 tramo mayor 0,0 -2,5
- 77. 37 Continuación tabla VII. 1 tramo -------- -3,0 Ningún tramo Es estructura tipo E5 - Fuente: Normas estructurales de diseño recomendadas para la República de Guatemala, AGIES NR-3: 2000, numeral 1.6.1.1. p. 14. Si los marcos en una dirección dada tienen diferentes índices, el índice (q) será el promedio aritmético de los índices de cada marco en esa dirección del análisis. 2.6. Cortante basal estático equivalente 2.6.1. Limitaciones del método de la carga estática equivalente Se puede utilizar el método de análisis de la carga estática equivalente, si la estructura cumple con los criterios que se dan a continuación: La altura entre la base y el del nivel más alto de la estructura no exceda a 15 m. El período fundamental de vibración que no exceda a 0,45 segundos. La estructura satisface los requisitos de regularidad horizontal, vertical y tenga un período fundamental de vibración menor que 2,0 segundos.
- 78. 38 2.6.2. Expresión básica para el estado límite de servicio Para el estado de límite de servicio las deformaciones de la estructura no deben causar daño, ni pérdida de funcionalidad a la estructura o a sus partes. El edificio se considera fijo a la base y se verifica que los desplazamientos laterales permanezcan dentro del intervalo elástico en cada dirección de análisis, bajo la aplicación del cortante basal estático equivalente para el estado límite de servicio (VBs) dado por la siguiente ecuación: onde Ws Es el peso de la estructura Css Es el coeficiente sísmico para el estado límite de servicio. 2.6.3. Expresión básica para el estado límite de cedencia El edificio se considera fijo en la base y se diseña en cada dirección de análisis para resistir, como mínimo, el cortante basal estático equivalente para el estado límite de cedencia (VB) de acuerdo con la siguiente ecuación: C onde Ws Es el peso de la estructura Cs Es el coeficiente sísmico de diseño
- 79. 39 2.6.4. Peso Ws El peso (Ws) incluirá, como mínimo, la carga muerta total de la edificación; en almacenes o bodegas, se incluirá como mínimo un 25% de la carga viva. Las masas líquidas que no sobrepasen el 5% del peso total de la edificación se añadirán simplemente al peso (Ws). 2.6.5. Coeficiente sísmico para el estado límite de servicio (Css) El coeficiente sísmico, para verificar que las deformaciones de los distintos elementos de la estructura permanezcan dentro del intervalo elástico en cada dirección de análisis se calcula de la siguiente manera: onde Sf (T) Es la demanda sísmica correspondiente al sismo de servicio (sismo frecuente), para una estructura con período (T). T Es el período fundamental de vibración de la estructura. 2.6.6. Coeficiente sísmico para el estado límite de cedencia (Cs) El coeficiente sísmico de diseño (Cs) en cada dirección de análisis se calcula de la siguiente manera: C a T
- 80. 40 onde R Es el factor de reducción de respuesta sísmica. Sa (T) Es la demanda sísmica de diseño para una estructura con período (T). 2.6.7. Período de vibración T Es el período fundamental de vibración de la estructura. Al período (T), puede asignársele el valor genérico empírico (TE), de acuerdo con el inciso 2.6.7.2. Si el período T se calcula analíticamente y resulta ser mayor que 1.2TE, se utilizará este último valor para calcular la demanda sísmica por el método de la carga estática equivalente. 2.6.7.1. Período de vibración mediante fórmula analítica El período fundamental de vibración en la dirección considerada (T), se calcula por medio del método de Rayleigh, de acuerdo con la siguiente ecuación: √ ∑ ∑ onde Wi Peso para sismo del nivel (i). u¡ Desplazamiento lateral del centro de masa del nivel (i). Estos desplazamientos laterales se pueden calcular ignorando los efectos de torsión.
- 81. 41 Fi Fuerza estática equivalente para el nivel (i). g Aceleración debida a la gravedad. Se puede tomar como 9.81 m/s2 . 2.6.7.2. Período empírico TE El período fundamental de vibración de una estructura se puede estimar en forma genérica igualado a un período empírico (TE). Para edificios en general: √ Para sistemas estructurales del tipo E2 puede utilizarse: onde KT 0,061, para marcos de concreto. KT 0,085, para marcos de acero. hn Es la altura total del edificio (en metros), desde la base o nivel del suelo; la base es el primer nivel de la edificación restringido de vibrar libremente. L Es la distancia entre los ejes estructurales extremos en la dirección de análisis, medida en metros.
- 82. 42 2.6.8. Distribución vertical de las fuerzas sísmicas El cortante basal de servicio (VBs) y el cortante basal de cedencia (VB) se distribuirán a lo alto del edificio, de acuerdo con las siguientes ecuaciones respectivamente: ∑ onde Fjs Es el cortante de servicio en el nivel (js) de la edificación. Fj Es el cortante de cedencia en el nivel (j) de la edificación. k valor de 1 para T < 0.5 seg, 0.75 + 0.5 (Ts) para T > 0.5 seg. Wi Es el peso asignado al nivel (i) de la edificación. Wj Es el peso asignado al nivel (j) de la edificación. hi Es la altura en metros del nivel (i) sobre la base de la edificación. hj Es la altura en metros del nivel (j) sobre la base de la edificación; la base es el primer nivel de la edificación restringido de vibrar libremente. Cvj Es el porcentaje del fuerza total del peso de la estructura que se le aplicara a cada nivel.
- 83. 43 2.6.9. Distribución horizontal de las fuerzas sísmicas La fuerza sísmica (Vi) acumulada desde arriba hasta el nivel (i), se distribuirá a los diversos miembros verticales del sistema sismorresistente que están en el piso debajo del nivel (i), tomando en cuenta las rigideces relativas de esos miembros verticales y las del diafragma en el nivel (i). 2.6.10. Excentricidad accidental Si en planta los niveles de una estructura fueren perfectamente simétricos, se deberá considerar una excentricidad accidental para la aplicación de las fuerzas de inercia. Esta excentricidad accidental se medirá desde el centro de masa nominal y se determinará de la siguiente forma: Para fuerzas aplicadas en una dirección paralela a los ejes ortogonales principales de la estructura, la excentricidad será igual a ± 0.1 veces la dimensión en planta de la estructura perpendicularmente a la dirección de la fuerza. Para fuerzas aplicadas en otras direcciones, la excentricidad accidental se puede suponer que se localiza sobre el contorno de una elipse con semiejes iguales a la excentricidad especificada para las direcciones ortogonales.
- 84. 44 2.6.11. Amplificación dinámica Para fines de diseño, el momento torsional definido en el inciso 2.6.9 será igual a la fuerza cortante de entrepiso multiplicada por la excentricidad que para cada marco resulte más desfavorable. Además, se deberá multiplicar dicha excentricidad por un factor de 1.5 para tomar en cuenta los efectos dinámicos e investigar cuál de las siguientes combinaciones resultan más desfavorables: 1.5e ± 0.1b ó e ± 0.1b. Siendo (e) la excentricidad nominal en planta del entrepiso y (b) la dimensión de la planta medida en la dirección de (e). Finalmente la excentricidad en cada dirección de análisis, no se tomará menor que la mitad del máximo valor de (e), calculado para los entrepisos que se hallan abajo del que se considera, ni se tomará el momento torsionante de ese entrepiso menor que la mitad del máximo calculado para los entrepisos que están arriba del considerado. 2.6.12. Dirección de las fuerzas estáticas equivalentes Para edificios con sistemas sismorresistentes en dos direcciones perpendiculares, se puede asumir que las fuerzas estáticas equivalentes actúan separadamente a lo largo de estas dos direcciones horizontales. Para otro tipo de edificios se deberá considerar diferentes direcciones para la aplicación de las fuerzas estáticas, equivalentes de tal manera, que produzcan el efecto más desfavorable en cualquier elemento estructural.
- 85. 45 2.6.13. Volteo Toda edificación se diseña para resistir los efectos de volteo causado por las fuerzas sísmicas (especificadas en el inciso 2.6.8). 2.6.14. Cálculo de desplazamientos laterales por sismo 2.6.14.1. Reducción de desplazamientos laterales Los desplazamientos laterales y las derivas sísmicas de una estructura, que se obtienen mediante un análisis elástico se podrán reducir multiplicándolas por un factor de escala, de acuerdo con el siguiente criterio: Tabla VIII. Reducción de desplazamientos laterales (a) Para edificios con tendencia a la formación de un piso débil 1.00 (b) Para otro tipo de edificios: Con seis o más niveles Con menos de seis niveles, se podrá interpolar entre 1.0 para edificios de un solo nivel y 0.85 para edificios de seis niveles. 0.85 Fuente: Normas estructurales de diseño recomendadas para la República de Guatemala, AGIES NR-3: 2000. p. 30. 2.6.15. Desplazamientos laterales del estado límite de servicio Para el cálculo de los desplazamientos laterales el estado límite de servicio tomará en consideración cualquier causa que provoque una desviación en el comportamiento elástico lineal.
- 86. 46 2.6.16. Desplazamientos laterales del estado límite de cedencia Los desplazamientos laterales post-elásticos (do) en cada nivel de la estructura se calculan de acuerdo con las ecuaciones: si T = TA si T < TA onde dy Desplazamiento nominal obtenido del análisis estático equivalente Ro Factor genérico de reducción de respuesta sísmica TA Período especificado en la tabla III T Período fundamental de vibración de la estructura 2.6.17. Cálculo de derivas sísmicas 2.6.17.1. Deriva sísmica para el estado límite de servicio Las derivas sísmicas elásticas entre niveles adyacentes (Δs), se definen como la diferencia entre los desplazamientos laterales elásticos de un nivel en particular (i) y el nivel inmediato inferior a él (i-1): e e
- 87. 47 onde ei Desplazamiento lateral elástico en el nivel (i). ei-1 Desplazamiento lateral elástico en el nivel inmediato inferior (i-1) 2.6.17.2. Deriva sísmica para el estado de cedencia Las derivas sísmicas de diseño entre niveles adyacentes (Δ , se definen como la diferencia entre los desplazamientos laterales post-elásticos de un nivel en particular (i) y el nivel inmediato inferior a este (i-1): o o onde oi Desplazamiento lateral post-elástico en el nivel (i) producido por el sismo oi-1 Desplazamiento lateral post-elástico en el nivel inmediato inferior (i-1) 2.7. Cortante basal método de análisis modal espectral El método de análisis modal espectral puede ser usado para ambos estados de límite, es decir para el estado límite de servicio y para el estado límite de cedencia. Este método tiene aplicación general, tanto para las estructuras que deben analizarse por métodos dinámicos.
- 88. 48 2.7.1. Número de modos de vibración participantes En el análisis se deberán incluir un número suficiente de modos de vibración que aseguren que el 90% o más de la masa están participando en la dirección de análisis bajo consideración. 2.7.2. Períodos de vibración Los períodos de vibración del edificio se calculan por métodos reconocidos en ingeniería estructural para la condición de base empotrada, usando las masas y rigideces del sistema sismorresistente. 2.7.3. Cortante modal en la base La parte del cortante basal que contribuye en la fuerza sísmica para el estado límite de servicio (VBsm), o para el estado límite último (VBm), se calcula de acuerdo con las siguientes ecuaciones respectivamente: onde Cssm El coeficiente sísmico para el estado límite de servicio. CSm El coeficiente sísmico para el estado límite último, también llamado coeficiente sísmico de diseño. Wßm El peso efectivo que participa en el modo (m) de vibración.
- 89. 49 2.7.4. Coeficiente sísmico para el estado límite de servicio El coeficiente sísmico modal para el estado límite de servicio (Cssm), se calcula mediante la siguiente ecuación: Sf (Tm) Es la demanda sísmica producida por el sismo de servicio. 2.7.5. Coeficiente sísmico para el estado límite de cedencia El coeficiente sísmico modal de diseño para el estado límite de cedencia (Csm), se calcula mediante la siguiente ecuación: onde Sa(Tm) es la demanda sísmica de diseño dada por el inciso 2.4.1 de acuerdo al sismo de diseño. R es el factor de reducción de respuesta sísmica para el estado límite de cedencia.
- 90. 50 2.7.6. Factor de participación modal Es la parte del peso de la estructura (Wßm) que participa con cada modo de vibración. Se calcula mediante la siguiente ecuación: ∑ ∑ onde øi,m Es la amplitud relativa del desplazamiento en el nivel (i) de la estructura. Wi Es el peso propio del nivel del edificio. 2.7.7. Fuerzas modales Serán calculadas independientemente para cada modo de vibración obteniéndose un juego de resultados por modo. La fuerza modal equivalente de servicio (Fsi,m) y de diseño (Fi,m) en el nivel (i), se calcula mediante las siguientes ecuaciones, respectivamente: ∑
- 91. 51 onde Wi Es el peso propio del nivel del edificio. øi,m Es la amplitud relativa del desplazamiento en el nivel (i) de la estructura cuando vibra en el modo (m). Se obtiene de los resultados del análisis modal. 2.7.8. Derivas de los pisos 2.7.8.1. Derivas modales para el estado límite de servicio La deriva modal de servicio (Δs i,m) en el piso (i), será calculada como la diferencia entre los desplazamientos modales elásticos (dy), del nivel (i) y el nivel (i-1): Donde el desplazamiento a la fluencia (dy i,m) se obtiene de los resultados del análisis modal utilizando la siguiente ecuación: onde Desplazamiento del nivel (i) G gravedad Wi Es el peso del nivel Fi,m Fuerza que se induce a cada nivel Tm Período de vibración de respuesta espectral
- 92. 52 2.7.8.2. Deriva modal para el estado límite de cedencia La deriva modal de diseño (Δ i,m) en el piso (i) para el modo (m), será calculada como la diferencia entre los desplazamientos modales post-elásticos (do i,m) del nivel (i) y el nivel (i-1). La deflexión modal post-elástica (do i,m), en cada nivel se calcula mediante las ecuaciones: si T < TA onde Ro Factor genérico de reducción de respuesta sísmica TA Período de vibración 2.7.9. Cálculo de acciones sísmicas para diseño 2.7.9.1. Distribución del cortante horizontal y torsión Para cada modo independiente. Se distribuirá las fuerzas modales de los pisos a los diversos marcos de la estructura. 2.7.9.2. Cortes y momentos modales en los marcos Los cortantes, los momentos y cargas axiales de volteo en los elementos de los marcos de la estructura, debido a las demandas sísmicas asignadas. Se pueden calcular por métodos lineales elásticos para cada modo de vibración.
- 93. 53 2.7.9.3. Resultados finales del análisis modal Los valores finales de cortantes, momentos, cargas axiales de volteo, desplazamientos laterales y derivas serán calculados combinando los distintos valores modales. 2.7.9.4. Prevención de resultados distorsionados La combinación de los cortantes basales modales (VBcomb) no deberá ser menor que un cortante basal estático equivalente (VB), utilizando un período T = 1.4 TE (si es que se usa el período empírico), de lo contrario todos los resultados del análisis modal se incrementarán proporcionalmente multiplicándolos por el siguiente factor (CBasal):
- 94. 54
- 95. 55 3. ANÁLISIS DE CORTANTE BASAL MEDIANTE INTERNATIONAL BUILDING CODE 2009 (IBC-2009/ASCE-05) 3.1. Alcances del Código (IBC-2009/ASCE-05) En este código se establecen requisitos mínimos estructurales de cargas para el uso en el diseño estructural y la construcción de edificios. Se incluyen cargas mínimas de diseño, así como metodologías de diseño. También se proporcionan cargas mínimas de diseño (vivas, muertas, viento, lluvia, inundaciones y sismos, así como combinaciones de cargas). Este código se basa en estándares reconocidos a nivel mundial. Un elemento fundamental en el desarrollo del mismo fue la publicación de Cargas mínimas de diseño para edificios y otras estructuras (ASCE-05) de la Sociedad Americana de Ingeniería Civil, la cual hace mención de las necesidades estructurales de diseño que deben considerarse para hacer frente de una manera satisfactoria a las condiciones sísmicas del sitio y propiedades del suelo. 3.2. Clasificación de sitio para el diseño sísmico El sitio se basa en las propiedades del suelo, debe ser clasificado como sitio de clase A, B, C, D, E o F de acuerdo con la tabla IX. En lugares donde las propiedades del suelo no son conocidas o no se tenga suficiente información del lugar, se determinará como clase de sitio D.
- 96. 56 Tabla IX. Clasificación de sitio Clase de Sitio Nombre del Perfil del Suelo Velocidades de onda cortante del suelo (VS), (mt/s) Resistencia estándar a la penetración, N Resistencia al corte del suelo sin escurrir (su) A Roca dura Vs > 1,524 N/A N/A B Roca 762 < Vs ≤ 1,524 N/A N/A C Suelo muy denso o roca suave 365 < Vs ≤ 762 N > 50 Su ≥ 2,000 D Perfil de suelo denso 182 < Vs ≤ 365 15 ≤ N ≤ 50 1,000 ≤ Su ≤2,000 E Perfil de suelo suave 182 < Vs N < 15 Su < 1,000 F --------------- Cualquier perfil con más de 10 pies del suelo con las características siguientes: 1. Índice de plasticidad IP 20, 2. Contenido de humedad (w) 40% G --------------- Cualquier perfil que contenga suelos que tengan una o más de las siguientes características: 1. Suelos vulnerables a la posible falla o colapso, bajo cargas sísmicas como suelos licuables, rápida y alta sensibilidad de arcillas. 2. Suelos que sean arcillas altamente orgánicas (H >3 metros, donde H = espesor del suelo). 3. Arcillas de muy alta plasticidad (H > 7.50 metros con índice de plasticidad IP > 75). 4. Arcillas rígidas de espesor suave/medio (H > 36 metros). Fuente: International Building Code 2009 (IBC-2009). p. 341.
- 97. 57 3.2.1. Parámetros asignados de aceleración Los parámetros del espectro de aceleración de respuesta (Ss) y (S1) se considera de 0,2 y 1,0 segundo respectivamente. Estos factores se obtienen mediante a los mapas de aceleración espectral que se establecen en las Figuras 1613.5 del código IBC-2009. 3.2.2. Coeficientes de sitio y parámetros del espectro de aceleración máxima de respuesta para sismos El espectro máximo de aceleración de respuesta se considera para períodos cortos (SMS) y para períodos de 1 seg (SM1), se calcula por medio de las siguientes ecuaciones: Los cálculos se adaptan a las propiedades de la clase de sitio de acuerdo con la tabla IX. onde Fa Coeficiente de sitio que se define en la tabla X. Fv Coeficiente de sitio que se define en la tabla XI. SS Aceleración espectral asignada a períodos cortos. S1 Aceleración espectral considerada a un período de 1 seg.
- 98. 58 3.2.3. Parámetros de diseño de aceleración de respuesta espectral El diseño del espectro de aceleración de respuesta para períodos cortos (SDS) y para períodos de 1 seg (SD1), se determina de acuerdo con las siguientes ecuaciones: onde SMS Espectro de aceleración máxima de respuesta considerada para períodos cortos. SM1 Espectro de aceleración máxima de respuesta considerada para períodos de 1 seg. Tabla X. Coeficientes de sitio Fa Clase de Sitio Parámetros máximos recomendados de aceleración de respuesta espectral asignados para sismo en un período corto de vibración Ss ≤ 0,25 Ss = 0,5 Ss = 0,75 Ss = 1,0 Ss ≥ 1,25 A 0,8 0,8 0,8 0,8 0,8 B 1,0 1,0 1,0 1,0 1,0 C 1,2 1,2 1,1 1,0 1,0 D 1,6 1,4 1,2 1,1 1,0 E 2,5 1,7 1,2 0,9 0,9 Fuente: International Building Code (IBC-2009/ASCE-05). p. 341.
- 99. 59 Tabla XI. Coeficientes de sitio Fv Clase de Sitio Parámetros máximos recomendados de aceleración de respuesta espectral asignados para sismo en un período largo de vibración S1 ≤ 0,1 S1 = 0,2 S1 = 0,3 S1 = 0,4 S1 ≥ 0,5 A 0,8 0,8 0,8 0,8 0,8 B 1,0 1,0 1,0 1,0 1,0 C 1,7 1,6 1,5 1,4 1,3 D 2,4 2,0 1,8 1,6 1,5 E 3,5 3,2 2,8 2,4 2,4 Fuente: International Building Code (IBC-2009/ASCE-05). p. 341. 3.2.4. Diseño del espectro de respuesta Cuando un diseño de espectro de respuesta sea requerido por un análisis dinámico por este Código IBC-2009/ASCE-05, los procedimientos del movimiento sísmico sitio-específicos no serán utilizados, en tanto la curva de diseño del espectro de respuesta se desarrolla como se indica en la figura 18. Para períodos T menores a To, el diseño del espectro de aceleración de respuesta Sa, se determina por medio de la siguiente ecuación: ( )
- 100. 60 Para períodos T que sea mayor o igual a (To) y menor o igual que (Ts), el diseño del espectro de aceleración de respuesta (Sa), se toma el valor de SDS. Figura 18. Diseño de espectro de respuesta Fuente: Minimum Design Loads for building and other structures (ASCE -05). p. 115. Para períodos T mayores a (Ts) y menores o iguales que (TL), el diseño del espectro de aceleración de respuesta (Sa), se determina mediante la siguiente ecuación: Para períodos (T) mayores a (TL), (Sa) se determina por la siguiente ecuación:
- 101. 61 onde SDS Parámetros de aceleración de respuesta espectral de diseño en períodos cortos. SD1 Parámetros de aceleración de respuesta espectral de diseño en períodos de 1 seg. T Período fundamental de la estructura. To TS TL Período de transición período-largo (s), depende de la ubicación del lugar y de las propiedades de la clase de suelo, como se indica en la Figura 22-15 del código ASCE-5. 3.2.5. Espectro de respuesta (MCE) En caso de que se requiera de un espectro de respuesta (MCE), se obtiene multiplicando el diseño del espectro de respuesta por un factor de 1,50. 3.3. Factor de importancia y categoría de ocupación 3.3.1. Factor de importancia El factor de importancia (I) se asigna dependiendo de la ocupación e importancia de la estructura y se calcula de acuerdo como se indica en la tabla XII y en la categoría de ocupación según lo especificado en la tabla XIII.
- 102. 62 Tabla XII. Factores de importancia Categorías de 0cupación I I o II 1,0 III 1,25 IV 1,5 Fuente: Mínimum Design Loads for building and other structures (ASCE-05). p. 116. 3.3.2. Categorías de ocupación Para el propósito de diseño de estructuras resistentes a sismos, cada una de las estructuras se asigna en una de las categorías de ocupación especificadas en la tabla XIII: Tabla XIII. Categorías de ocupación Naturaleza de la ocupación Categoría Edificios y construcciones que representan un riesgo bajo, para la vida humana en caso de colapso: Instalaciones de almacenamiento. Instalaciones temporales. Instalaciones agrícolas. Bodegas I Edificios y otras estructuras, que no clasifiquen en las categorías de ocupación I, III y IV. II
- 103. 63 Continuación tabla XIII. Edificios y otras construcciones que representan un peligro considerable para la vida humana en el caso de colapso: Edificios y otras construcciones donde se congregan más de 300 personas en un área. Edificios y otras estructuras con capacidad superior a 500 para las universidades o centros de educación de adultos. Establecimientos de salud con capacidad de 50 personas. Cárceles y centros de detención. Complejos deportivos, residenciales Hoteles Fábricas Bibliotecas Oficinas Salones de reunión Edificios y otras construcciones, no incluidos en la categoría de ocupación IV, con potencial de causar un impacto económico sustancial, incluyendo la alteración de la vida civil día a día en el caso de colapso: Central de generación de eléctrica. Instalaciones de tratamiento de aguas pluviales y residuales. III
- 104. 64 Continuación tabla XIII. Edificios y otras estructuras designadas como instalaciones esenciales: Hospitales, centros de atención de salud e instalaciones de emergencia médica. Estaciones de bomberos, policías y parqueos para vehículos de emergencia. Instalaciones designadas para refugio de emergencia, en caso de desastres naturales (terremotos, inundaciones, etc.). Instalaciones designadas para la preparación de emergencias, centros de comunicación, centros de operaciones y otras instalaciones necesarias para responder en caso de emergencias. Centrales de generación eléctricas y otras instalaciones de utilidad pública requerida en caso de emergencia. Estructuras auxiliares (torres de comunicación, tanques de almacenamiento de combustible, subestación eléctrica, tanques de almacenamiento de agua) necesarias para el funcionamiento de las estructuras de ocupación categoría IV durante una emergencia. Torres de control, centros de control de tráfico aéreo, aviones y hangares de emergencia. Edificios y otras construcciones, con funciones críticas de la defensa nacional. IV Fuente: Minimum Design Loads for building and other structures (ASCE-05). p. 3.
- 105. 65 Tabla XIV. Categoría de diseño sísmico de aceleración de respuesta basado en el período de corto plazo Valores de SDS Categorías de Ocupación I o II III IV SDS < 0,167 A A A 0, 67 ≤ SDS < 0,33 B B C 0,33 ≤ SDS < 0,50 C C D 0,50 ≤ SDS D D D Fuente: Minimum Design Loads for building and other structures (ASCE -05). p. 116. Tabla XV. Categoría de diseño sísmico de aceleración de respuesta basado en el período de 1 seg. Valores de SD1 Categorías de ocupación I o II III IV SD1 < 0,067 A A A 0,067 ≤ SD1 < 0,133 B B C 0,133 ≤ SD1 < 0,20 C C D 0,20 ≤ SD1 D D D Fuente: Minimum Design Loads for building and other structures (ASCE -05). p. 116. 3.3.3. Categoría de diseño sísmico La categoría de diseño sísmico se asigna de acuerdo con la información obtenida de la tabla XIV. Las categorías de ocupación I, II, o III se asigna a estructuras que se encuentren situadas entre los parámetros de diseño del espectro de aceleración de respuesta en períodos de 1 seg, cuando S1 es mayor o igual a 0,75; se determina a esta estructura como categoría de diseño sísmico tipo E.
- 106. 66 La categoría de ocupación IV se asigna a las estructuras que se localizan dentro de los parámetros de diseño del espectro de aceleración de respuesta en períodos de 1 seg. Cuando S1 es mayor o igual a 0,75, se asigna a la estructura como categoría de diseño sísmico tipo F. Se asigna en una de las categorías de diseño sísmico a todas las estructuras que están en función de su categoría de ocupación y de los parámetros de diseño del espectro de aceleración de respuesta SDS y SD1, que se determina de acuerdo con el inciso 3.2.5. Cuando S1 es menor a 0,75, se permite que la categoría de diseño sísmico sea determinado conforme a lo especificado en la Tabla XIV, solamente cuando se satisfaga las siguientes condiciones: En cada una de las dos direcciones ortogonales, la aproximación del período fundamental de la estructura (Ta), es menor a (0,8 T). En cada una de las dos direcciones ortogonales, el período fundamental de la estructura se utiliza para calcular la derivada de desplazamiento del nivel del edificio siempre y cuando sea inferior a (Ts). Cs se utiliza para determinar el coeficiente de respuesta sísmica.
- 107. 67 3.4. Procedimiento de fuerza lateral equivalente 3.4.1. Esfuerzo cortante en la base El cortante basal de la estructura (V), para cada una de las direcciones principales se determina mediante la siguiente ecuación: onde CS Coeficiente de respuesta sísmica. W Peso total del edificio. 3.4.2. Cálculo del coeficiente de respuesta sísmica El coeficiente de respuesta sísmica (Cs) se determina de acuerdo con la siguiente ecuación: ( ) onde SDS Diseño del espectro de aceleración de respuesta del período corto determinado a partir del inciso 3.2.5. R Factor de modificación de respuesta. I Factor de ocupación e importancia.
- 108. 68 El valor de Cs calculado anteriormente, es necesario que no supere los límites de acuerdo con las siguientes ecuaciones: ( ) ( ) Cs no debe ser inferior a: Cs = 0.01 Además, estructuras localizadas donde S1 es igual o superior a 0,60g y Cs no deberá ser menor a; en el caso de Guatemala se trabajará con una aceleración de 0,40g: ( ) Tabla XVI. Coeficiente para límite superior en un período calculado Parámetro de diseño de aceleración de respuesta espectral en 1 s, SD1 Coeficiente Cu 0,40 1,4 0.30 1,4 0,20 1,5 0,15 1,6 0,10 1,7 Fuente: Minimum Design Loads for building and other structures (ASCE -05). p. 129.
- 109. 69 Tabla XVII. Factor de modificación de respuesta (R) Sistemas de marcos estructurales Factor de modificación de respuesta (R) Estructuras especiales de concreto armado con muros de corte 8 Estructuras ordinarias de concreto armado con muros de corte 8 Fuente: Minimum Design Loads for building and other structures (ASCE -05). p. 136. SD1 Parámetros de diseño de aceleración de respuesta espectral en períodos de 1 seg, determinado de acuerdo con el inciso 3.2.5. T Período fundamental de la estructura definido en el inciso 3.5.1. TL Período transición a largo plazo (s) determinado en el inciso 3.2.6. S1 Parámetros asignados de aceleración máxima de respuesta espectral recomendados de acuerdo con el inciso 3.2.5. 3.5. Determinación de período El período fundamental de la estructura (T), en la dirección en cuestión se establece utilizando las propiedades estructurales y las características de deformación de los elementos resistentes en el análisis. El período fundamental de la estructura (T), no debe exceder el producto del coeficiente del límite superior en el período calculado (Cu) conforme a la Tabla XVII y del período fundamental aproximado (Ta).
- 110. 70 3.5.1. Período fundamental El período fundamental de la estructura se aproxima de acuerdo a la siguiente ecuación y relacionado con los datos especificados en la Tabla XVIII: Tabla XVIII. Valores de Ct y x del período fundamental Tipo de estructura Ct x Marcos de acero 0,028 (0,0724)a 0,8 Marcos de concreto 0,016 (0,0466)a 0,9 Marcos de acero excéntricamente arriostrados 0,03 (0,0731)a 0,75 Otros sistemas estructurales 0,02 (0,0488)a 0,75 Fuente: Minimum Design Loads for building and other structures (ASCE-05). p. 129. onde hn Es la altura en pies por encima de la base hasta el nivel más alto de la estructura. Ct, x Coeficientes determinados de conformidad con la tabla XVIII. Alternativamente, se permite determinar la aproximación del período fundamental (Ta), únicamente para estructuras que no exceda los 12 pisos de
- 111. 71 altura; se podrá utilizar la siguiente ecuación: en la que la fuerza-resistencia sísmica del sistema consista en su totalidad en concreto armado o acero y sea de una configuración estructural de marcos resistentes a momento y la altura del piso debe de ser al menos 10 metros: onde N Es el número de niveles del edificio. 3.6. Distribución vertical de las fuerzas sísmicas La fuerza lateral sísmica (Fx) inducida en cualquier nivel se calcula mediante la siguiente ecuación: Cvx se determina mediante la siguiente ecuacion: ∑ onde Cvx Factor de distribución vertical. V Fuerza total de diseño lateral o cortante basal. wi, wx Parte del peso efectivo total sísmico de la estructura (W). hi y hx Es la altura (piés o metros) desde la base hasta el nivel (i o x). k Exponente relacionado con el período fundamental de la estructura según lo especificado en la tabla XIX.
- 112. 72 Tabla XIX. Valores de Coeficiente K Rangos del período fundamental de la estructura para determinar coeficiente K Coeficiente K Para toda estructura con un período de ≤ 0,5 seg. 1 Para toda estructura con un período de ≥ 2,5 seg. 2 Para toda estructura que oscila entre un período 0,5 y 2.5 s, k se determina por interpolación lineal entre 1 y 2. Fuente: Minimum Design Loads for building and other structures (ASCE-05). p. 129. 3.7. Distribución horizontal de las fuerzas El diseño sísmico del esfuerzo cortante en cualquier nivel del edificio (Vx), se determina a partir de la siguiente ecuación: ∑ Donde Fi es la fuerza sísmica cortante (V) inducida en cada nivel.
- 113. 73 4. ANÁLISIS DE CORTANTE BASAL MEDIANTE EUROCÓDIGO 8 ENV 1998-1-1 4.1. Principios básicos para la concepción del proyecto La posible ocurrencia de sismos debe ser un aspecto importante a tener en cuenta para la concepción del proyecto de un edificio en una zona sísmica. Este aspecto debe considerarse en las etapas iníciales en el desarrollo del proyecto de un edificio, posibilitando el logro de un sistema estructural, que dentro de costos aceptables, satisfaga los requisitos fundamentales establecidos en el eurocódigo 8. 4.1.1. Características de los edificios sismorresistente La peligrosidad sísmica se tendrá en consideración en las etapas iníciales de la concepción del proyecto de un edificio. Los principios guía que rigen conceptualmente un proyecto sismorresistente son: Simplicidad estructural Uniformidad y simetría Resistencia, rigidez bidireccional y a torsión Cimentación adecuada
- 114. 74 4.2. Condiciones del suelo El eurocódigo establece llevar a cabo los estudios apropiados con el fin de clasificar el tipo de suelo de acuerdo a las condiciones del mismo. 4.2.1. Generalidades Para estructuras de pequeña importancia (I ≤ ,0) en zonas de baja sismicidad, pueden omitirse los estudios necesarios para determinar la clase de suelo. En este caso y en ausencia de información más precisa del sitio, la acción sísmica puede determinarse suponiendo las condiciones del suelo de acuerdo con la clase B de suelo. 4.2.2. Clasificación de las condiciones del suelo En general, la influencia de las condiciones del suelo sobre la acción sísmica se debe tener en cuenta mediante la consideración de tres diferentes clases de suelo A, B y C que se describen por los siguientes perfiles estratigráficos: 4.2.2.1. Clase de suelo A Roca u otra formación geológica caracterizada por una velocidad de la onda transversal (Vs) de 800 m/s, incluyendo como máximo 5 metros del material más débil de la superficie. Depósitos compactos de arena, grava o arcilla consolidada, de, al menos, varias decenas de metros de espesor, caracterizados por un incremento gradual de las propiedades mecánicas con la profundidad y por valores de (Vs) de 400 m/s a una profundidad de 10 metros.
- 115. 75 4.2.2.2. Clase de suelo B Depósitos profundos de arenas de densidad media, gravas o arcillas de consistencia media, con espesores desde algunas decenas a muchos centenares de metros, caracterizados por valores de (Vs), de 200 m/s a 10 metros de profundidad, que se incrementan hasta 350 m/s, por lo menos, a una profundidad de 50 metros. 4.2.2.3. Clase de suelo C Depósitos de suelo no cohesivo, con o sin algunas capas de suelo de débil cohesión, caracterizados por valores de (Vs) inferiores a 200 m/s en los 20 metros más superficiales. 4.3. Acción sísmica 4.3.1. Zonas sísmicas Por definición, la peligrosidad sísmica dentro de cada zona se puede suponer constante. Para la mayoría de aplicaciones del eurocódigo, la peligrosidad se describe en términos de un único parámetro, por el valor de (ag) de la máxima aceleración efectiva del suelo en roca o suelo consolidado, la cual a partir de ahora se llamará (aceleración de cálculo del suelo). El concepto de (máxima aceleración efectiva del suelo) es una aproximación para compensar la inadecuación, por lo general, del pico o valor máximo real para describir el potencial de daño del movimiento del suelo en términos de aceleración máxima y/o de velocidad inducida a las estructuras.
- 116. 76 En general (ag) tiende a coincidir con el máximo valor real para sismos de magnitud moderada a alta procedentes de distancias medias a largas, los cuales se caracterizan (en suelo firme) por un espectro ancho de frecuencias y aproximadamente uniforme, mientras que el valor de (ag) será más o menos reducido en relación con el máximo real para sismos próximos y de baja magnitud. La aceleración de cálculo del suelo seleccionada para cada zona sísmica por el eurocódigo, corresponde a un período de retorno de 475 años. A este período de retorno se le asigna un factor de importancia (I) igual a 1.0. Las zonas sísmicas con una aceleración de cálculo del suelo (ag) no mayor a (0.10 * g) son zonas de baja sismicidad, para las cuales y para ciertos tipos o categorías de estructuras pueden utilizarse métodos de cálculo sismorresistente reducidos o simplificados. 4.3.2. Representación básica de la acción sísmica El movimiento sísmico en un punto dado de la superficie se representa generalmente por un espectro elástico de respuesta de la aceleración del suelo. La acción sísmica horizontal se describe mediante dos componentes ortogonales, considerados independientes y los representados por el mismo espectro de respuesta. A no ser que estudios específicos indiquen lo contrario, la componente vertical de la acción sísmica debe representarse por el espectro de respuesta, tal como se define para la acción sísmica horizontal, pero con las ordenadas reducidas de la siguiente manera:
- 117. 77 Para períodos de vibración (T) menores de 0,15 seg, se multiplican las ordenadas por un factor de 0,70. Para períodos de vibración (T) mayores de 0,50 seg, se multiplican las ordenadas por un factor de 0,50. Para períodos de vibración (T) entre 0,15 y 0,50 seg, se utilizará interpolación lineal. 4.3.3. Espectro elástico de respuesta El espectro elástico de respuesta Se (T) para el período de retorno de referencia se define por las descritas en la tabla XX. Tabla XX. Espectro elástico de respuesta 0 ≤ T ≤ TB [ ] TB ≤ T ≤ TC TC ≤ T ≤ TD [ ] TD ≤ T [ ] [ ] Fuente: Normas estructurales de diseño recomendadas para la Unión Europea, Eurocódigo 8, parte 1-1. p. 19.
- 118. 78 onde Se (T) Ordenada del espectro elástico de respuesta. T Período de vibración de un sistema lineal con un grado de libertad. ag Aceleración de cálculo del terreno, para el período de retorno de referencia. β0 Factor de amplificación de la aceleración espectral para un amortiguamiento viscoso del 5%. TB, TC Límites del tramo de aceleración espectral constante. TD Valor que define el comienzo del tramo de desplazamiento constante del espectro. k1, k2 Exponentes que definen la forma del espectro para un período de vibración mayor de TC, TD respectivamente. S Parámetro del suelo. n Factor de corrección del amortiguamiento, con valor de referencia n = 1 para un amortiguamiento viscoso del 5%.
- 119. 79 Figura 19. Espectro elástico de respuesta Fuente: Normas estructurales de diseño recomendadas para la Unión Europea, Eurocódigo 8, parte 1-1. p. 20. Para la tre cla e de uelo A, , C, lo valore de lo parámetro β0, TB, TC, TD, K1, k2 y S, se especifican en la tabla XXI: Tabla XXI. Valores de los parámetros que describen el espectro elástico de respuesta Clase de S β0 k1 k2 TB (S) TC (S) TD (S) Suelo A 1,0 2,5 1,0 2,0 0,10 0,40 3,0 B 1,0 2,5 1,0 2,0 0,15 0,60 3,0 C 0,9 2,5 1,0 2,0 0,20 0,80 3,0 Fuente: Normas estructurales de diseño recomendadas para la Unión Europea, Eurocódigo 8, parte 1-1. p. 20.
- 120. 80 Estos valores han sido seleccionados para que las ordenadas del espectro elástico de respuesta tengan probabilidad de excelencia uniforme para todos los períodos (espectro de probabilidad uniforme), igual al 50%. Pueden ser necesarios estudios especiales para la definición de la acción sísmica en lugares con condiciones de suelo que no correspondan a ninguna de las tres clases de suelo A, B o C. El valor del factor de corrección del amortiguamiento n, puede determinarse por la expresión: √ Donde £ es el valor de la razón de amortiguamiento viscoso de la estructura expresada en porcentaje (porcentaje de amortiguamiento crítico). Si para estudios especiales tiene que considerarse una razón de amortiguamiento viscoso diferente del 5%. 4.3.4. Desplazamiento máximo del suelo Sin estudios especiales basados en la información disponible e indiquen lo contrario, el valor (dg) del desplazamiento máximo del suelo puede estimarse por medio de la siguiente ecuación: Con los valores de ag, S, TC, TD definidos en la tabla XXI.
- 121. 81 4.3.5. Espectro de cálculo para análisis lineal La capacidad de los sistemas estructurales para resistir las fuerzas sísmicas en el rango no lineal permite generalmente proyectarlos para fuerzas menores que las que corresponde a una respuesta elástica lineal. Los valores del factor de comportamiento (q), en el que también influye que el amortiguamiento viscoso sea diferente del 5%, están dados para los diversos materiales y sistemas estructurales. Para el período de retorno de referencia, el espectro de cálculo Sd (T), normalizado para la aceleración de la gravedad (g), se define mediante a la tabla XX: Tabla XXII. Espectro de cálculo para análisis lineal 0 ≤ T ≤ TB [ ( )] TB ≤ T ≤ TC TC ≤ T ≤ TD [ ] TD ≤ T [ ] [ ] Fuente: Normas estructurales de diseño recomendadas para la Unión Europea, Eurocódigo 8, parte 1-1. p. 21.
- 122. 82 onde Sd (T) Ordenada del espectro de cálculo, normalizada al valor de g α Cociente entre la aceleración del suelo de cálculo (ag) y de la aceleración de gravedad, g (α ag/g). q Factor de comportamiento. kd1, kd2 Exponentes que influyen en la forma del espectro de cálculo para un período de vibración mayor que TC, TD respectivamente. Para el cálculo del factor q viene dado por la aceleración de suelo vertical y horizontal αh/ αv = 1,3, este factor se utiliza para una estructura de concreto reforzado, entonces q viene dado de q = 3 αh/ αv. Lo valore de lo parámetro β0, TB, TC, TD, S se dan en tabla XXI, los valores de los parámetros kd1 y kd2, se especifican en la tabla XXIII. Tabla XXIII. Valores de kd1 y kd2 Clase de kd1 kd2 Suelo A 2/3 5/3 B 2/3 5/3 C 2/3 5/3 Fuente: Normas estructurales de diseño recomendadas para la Unión Europea, Eurocódigo 8, parte 1-1. p. 22.
- 123. 83 El espectro de cálculo definido anteriormente, no se aplica a proyectos de estructuras que contengan aislamiento en la base o sistemas de disipación de energía. 4.3.6. Representaciones alternativas de la acción sísmica 4.3.6.1. Representación del espectro de potencia El movimiento sísmico consiste en tres procesos aleatorios independientes, actuando simultáneamente a lo largo de dos ejes (x,y) horizontales ortogonales, y del eje vertical (z), estando además este proceso escalado apropiadamente. 4.3.7. Acelerogramas de cálculo El movimiento sísmico, también puede representarse por medio de registros temporales de la aceleración del suelo y magnitudes relacionadas (velocidad y desplazamiento). Cuando se requiera un modelo espacial, el movimiento sísmico constará de tres acelerogramas actuando simultáneamente. El mismo acelerograma no se puede utilizar al mismo tiempo en las dos direcciones horizontales. 4.3.8. Acelerogramas artificiales Los acelerogramas artificiales serán generados de forma que coincidan con el espectro elástico de respuesta. La duración de los acelerogramas será consistente con la magnitud y con las demás características relevantes del sismo que influyen en la determinación de (ag).
- 124. 84 Cuando no se disponga de datos específicos, la duración mínima (Ts), de la parte estacionaria de los acelerogramas para las zonas epicentrales debe correlacionarse con el valor de I * α = (I * ag/g) tal como se indica en la tabla XXIV. Tabla XXIV. Duración (Ts) de la parte estacionaria de los acelerogramas generados con una función de para (I * α) zonas epicentrales I * α 0,10 0,20 0,30 0,40 Ts 10 s 15 s 20 s 25 s Fuente: Normas estructurales de diseño recomendadas para la Unión Europea, Eurocódigo 8, parte 1-1. p. 23. Se utiliza un número suficiente de acelerogramas para obtener una medida (media y varianza) estadísticamente estable de los valores de interés de la respuesta. El contenido en frecuencia y amplitud de los acelerogramas se elegirá de forma que con su uso se obtenga en un nivel de fiabilidad del mismo orden de magnitud del que implicaría el uso del espectro elástico de respuesta. Se considera que se cumple el párrafo anterior, si se cumplen las siguientes condiciones: Se emplea un mínimo de 5 acelerogramas. La media de los valores de la respuesta espectral de la aceleración para el período cero (calculada a partir de cada uno de los acelerogramas) no es menor que el valor de (ag * S) para el lugar en cuestión. Para el rango de períodos del espectro elástico de respuesta entre (TB) y (TC) para el lugar en cuestión, el promedio de los valores del espectro medio
- 125. 85 obtenido a partir de todos los acelerogramas (calculadas con un numero apropiado de períodos de control) no será inferior al valor de (ag * S * β0) del espectro elástico de respuesta. 4.3.10. Categorías de ocupación y de importancia 4.3.10.1. Factores de importancia y de comportamiento Los edificios se clasifican por lo general, atendiendo a cuatro categorías de importancia que dependen del tamaño del edificio, de su valor e importancia para la seguridad pública y de la posibilidad de pérdidas de vidas en caso de colapso. Las categorías de importancia se caracterizan por diferentes factores de importancia (I): Tabla XXV. Categorías de ocupación y factores de importancia Categoría de importancia Edificios Factor de importancia (I) I Edificios cuya integridad durante los sismos es de vital importancia para la protección civil, por ejemplo, hospitales, parques de bomberos, centrales eléctricas, etc. 1,4
- 126. 86 Continuación tabla XXV. II Edificios cuya resistencia al sismo es de importancia a la vista de las consecuencias asociadas con su colapso, por ejemplo, colegios, salas de reunión, instituciones culturales, etc. 1,2 III Edificios corrientes que no pertenecen a las categorías anteriores. 1,0 IV Edificios de importancia mínima para la seguridad pública, por ejemplo, edificios agrícolas, entre otros. 0,8 Fuente: Normas estructurales de diseño recomendadas para la Unión Europea, Eurocódigo 8, parte 1-2. p. 25. 4.4. Análisis estructural 4.4.1. Análisis modal espectral simplificado Este tipo de análisis puede aplicarse a los edificios que se pueden analizar mediante dos modelos planos y cuya respuesta no está significativamente afectada por las contribuciones de los modos superiores de vibración. Se considera estos requisitos los edificios que cumplen los criterios de regularidad en planta y elevación según lo especificado en el inciso 1.10 de este documento.
- 127. 87 Tienen períodos fundamentales de vibración (T1) en las dos direcciones principales, inferiores a los siguientes valores: Donde TC es el período de aceleración espectral constante. 4.4.2. Esfuerzo cortante en la base El cortante basal (V), para cada una de las direcciones principales se calcula mediante la siguiente ecuación: onde Sd (T1) Ordenada del espectro de cálculo para el período (T1) de acuerdo con en el inciso 4.3.6. T1 Período fundamental de vibración de la estructura. WT Peso total del edificio. A efectos de determinar los períodos fundamentales de vibración (T1) de los dos modelos planos del edificio se pueden utilizar expresiones aproximadas basadas en métodos de la dinámica estructural.
- 128. 88 4.4.3. Distribución de las fuerzas sísmicas horizontales Las solicitaciones de origen sísmico se determinarán aplicando para los dos modelos planos, fuerzas horizontales (Fi), a las masas de cada una de las plantas del edificio. Las fuerzas se determinarán suponiendo la masa total de la estructura como una masa representativa del modo fundamental de vibración, siendo asi: ∑ onde Fi Fuerza horizontal actuando en la planta i. V Cortante basal de acuerdo con la inciso 3.3. si, sj Desplazamientos de las masas mi, mj en la deformada del modo fundamental. Wi, Wj Pesos de las masas mi, mj Cuando la deformada correspondiente al modo fundamental se aproxime mediante desplazamientos horizontales variables linealmente con la altura, las fuerzas horizontales (Fi) vienen dadas por: ∑
- 129. 89 onde zi, zj Alturas de las masas mi, mj respecto al nivel de aplicación de la acción sísmica (cimentación). Las fuerzas horizontales (Fi), determinadas anteriormente, se distribuirán entre el sistema resistente de cargas laterales, suponiendo plantas rígidas, es decir, proporcionalmente a las rigideces de aquellas. 4.4.4. Solicitaciones de torsión En el caso de distribución simétrica de la rigidez lateral y de la masa; si no se aplica un método más exacto en lo que respecta a las solicitaciones accidentales de torsión que pueden tenerse en cuenta, aumentando en cada uno de los elementos resistentes las solicitaciones de origen sísmico, evaluadas de acuerdo a un factor dado por onde x Es la distancia del elemento que se considera al centro del edificio, medida perpendicularmente a la dirección de la acción sísmica considerada. Lc Es la distancia entre los dos elementos resistentes de la carga lateral más externos, medidos de la forma anterior.
- 130. 90 4.4.5. Componentes de cargas verticales La componente vertical de la acción sísmica, tal como se define en el inciso 4.3.2 (a, b y c), se tendrá en cuenta en los siguientes casos: Componentes estructurales horizontales o casi horizontales con luces de 20 o más metros. Voladizos horizontales o casi horizontales. En general, el análisis para determinar las solicitaciones debidas a la componente vertical de la acción sísmica puede realizarse mediante un modelo parcial de la estructura. 4.4.6. Análisis del desplazamiento El desplazamiento inducido por la acción sísmica de cálculo se determinará en función de la deformación elástica del sistema estructural mediante a la siguiente expresión: onde ds Desplazamiento de un punto del sistema estructural, inducido por la acción sísmica del cálculo. qd Es el factor de comportamiento para el desplazamiento. de Es el desplazamiento del punto considerado del sistema estructural I Es el factor de importancia tabla XXV.
- 131. 91 5. CÁLCULO ESTRUCTURAL DE CARGAS SÍSMICAS 5.1. Modelo de la estructura El modelo de la Figura 21 muestra la estructura de un edificio de seis niveles. El edificio será utilizado específicamente para oficinas y se encontrará localizado en la Ciudad de Guatemala, estará compuesto por un sistema estructural de marcos de concreto reforzado, es simétrico tanto en planta como en elevación. 5.1.1. Vista de planta de la estructura Figura 20. Vista en planta Fuente: elaboración propia.
- 132. 92 5.1.2. Vista de elevación de la estructura A continuación se puede apreciar una vista en elevación de ambos edificios: Figura 21. Vista en elevación de edificio A Fuente: elaboración propia. Figura 22. Vista en elevación edificio B Fuente: elaboración propia.
- 133. 93 5.2. Criterios de predimensionamiento de elementos estructurales En este inciso se propondrá secciones de elementos estructurales, para iniciar el proceso de diseño estructural. En la parte final del diseño se tendrá que verificar si las mismas cumplen los requisitos de funcionalidad necesarios. 5.2.1. Predimensionamiento de losa Debido a la simetría del edificio se analiza una parte, ya que la estructura cuenta con losas de 6.00 m x 3.50 m, debido a que su relación a/b > 0.5, indica que es una losa con refuerzo en dos sentidos. Para calcular el espesor se considera la losa en condición crítica, por lo que se aplica las siguientes ecuaciones según como se establece en el Código ACI-318-2005: ( ) de la y lb longitud de la luz libre en las direcciones corta y larga, respectivamente. P y t Perímetro de la losa y espesor de la losa respectivamente. Para efectos de este trabajo de graduación se utilizará una losa para todos los niveles con un espesor de 12 cms.
- 134. 94 5.2.2. Predimensionamiento de viga Para calcular el peralte (h) de las vigas se recomienda una relación de 6 a 8 cm de peralte (h) por metro lineal de la luz total y u a ch (b) de ⅓ a ½ de (h): ( ) ( ⁄ ⁄ ) Utilizando este criterio, para determinar el peralte (h) de las vigas; aplicándolas sobre el claro más grande de 6.00 m, se obtiene: Por razones prácticas la sección de viga propuesta se aproxima a: Figura 23. Sección predimensionada de la viga Fuente: elaboración propia.
- 135. 95 5.2.3. Predimensionamiento de columna Se propone calcular el área gruesa de las columnas a través de la relación: ∑ ( ) de ac eg aci de ca ga a ia debida a ea ibu a ia de a c u a c ica g ea b u a de a ecci de a c u a c ica e i e cia i a a a c e i de c c e Figura 24. Área tributaria de columnas Fuente: SIC GARCÍA, Ángel. Guía teórica y práctica del curso de concreto armado 2. p. 203.
- 136. 96 Para efectos de este trabajo de graduación se utilizará la columna más crítica del edificio B, se realiza el cálculo de las áreas que tributan a la columna como se indica en la Figura 25: Figura 25. Planta del área tributaria de la columna crítica ( ) ( ) Fuente: elaboración propia. Con el propósito de predimensionar la columna se selecciona la que se encuentra expuesta a las condiciones más críticas de carga vertical. Se procede a realizar un cálculo sencillo que se realiza de la siguiente manera: Se realiza el cálculo del peso de cada elemento estructural en kg/m2 y se determina el área de cada uno de ellos en m2 . En el caso de la losa se obtiene: ⁄ ⁄
- 137. 97 La integración de cargas para la viga se calcula ⁄ ⁄ Para el caso de las columnas se realiza el siguiente cálculo: ⁄ ⁄ Respecto a los tabiques se calcula de la siguiente manera, para realizar la integración de cargas en la columna: ⁄ ⁄ Se utiliza la altura de muro de 1,50 metros debido a que llevará ventanas en la parte superior para iluminación de la edificación.
- 138. 98 Al referirse al repello, cernido e instalaciones se utiliza un peso específico de 25 kg/m2 , también se le asignará un valor de sobrecarga a la estructura de 100 kg/m2 , estos valores se asumieron de acuerdo a la tabla I de este documento. Tabla XXVI. Integración de cargas sobre columna crítica Sexto nivel Peso (kg/m 2 ) Área (m 2 ) Pact (kg) Losa 288 15,75 4536,00 Vigas 1080 2,00 2160,00 Repello + cernido 25 15,75 393,75 Tabiques 320 12,00 3840,00 Instalaciones 25 15,75 393,75 Sobrecarga 100 15,75 1575,00 Pac1 12 898,50 Quinto nivel Peso (kg/m 2 ) Área (m 2 ) Pact (kg) Losa 288 15,75 4536,00 Vigas 1080 2,00 2160,00 Repello + cernido 25 15,75 393,75 Tabiques 320 12,00 3840,00 Instalaciones 25 15,75 393,75 Sobrecarga 100 15,75 1575,00 Columna superior 1200 1,75 2100,00 Pac2 14 998,50
- 139. 99 Continuación tabla XXVI. Cuarto, Tercero y Segundo nivel Peso (kg/m 2 ) Área (m 2 ) Pact (kg) Losa 288 15,75 4536,00 Vigas 1080 2,00 2160,00 Repello + cernido 25 15,75 393,75 Tabiques 320 12,00 3840,00 Instalaciones 25 15,75 393,75 Sobrecarga 100 15,75 1575,00 Columna superior 1200 1,87 2244,00 Pac3,4,5 15 142,50 Primer nivel Peso (kg/m 2 ) Área (m 2 ) Pact (kg) Losa 288 15,75 4536,00 Vigas 1080 2,00 2160,00 Repello + cernido 25 15,75 393,75 Tabiques 320 12,00 3840,00 Instalaciones 25 15,75 393,75 Sobrecarga 100 15,75 1575,00 Columna superior 1200 3,50 4200,00 Pac6 17 098,50 Fuente: elaboración propia. ( )
- 140. 100 Para determinar el área gruesa de la sección de la columna se necesita conocer la resistencia máxima del concreto, por lo que se utilizará una resistencia de f´c = 280 kg /cm2 . Se utiliza una columna de sección cuadrada, sus dimensiones se obtienen con resolver la raíz cuadrada al área bruta (Ag): ad de c u a √( ) Se utilizará en los seis niveles columnas cuadradas 50 cms por 50 cms. 5.2.4. Predimensionamiento de zapata Figura 26. Propuesta de zapata Fuente: elaboración propia. ue c
- 141. 101 Zapata cuadrada √ √ Se utilizarán zapatas cuadradas de 2,10 m por 2,10 m. 5.3. Peso total de la estructura 5.3.1. Carga viva De conformidad con la tabla I y según lo establecido en el inciso 5.1 se determina la carga viva para el edificio CV = 250 kg/m2 , entonces se procede a calcular la carga de la siguiente manera: 5.3.2. Carga muerta 5.3.2.1 Integración de cargas para edificio A Cálculo del peso de primer nivel:
- 142. 102 ∑ ( ) ∑ ( ) Cálculo del peso de segundo, tercero y cuarto nivel: ∑ ( ) ∑ ( )
- 143. 103 Cálculo del peso de quinto nivel ∑ ( ) ∑ ( ) Cálculo del peso de sexto nivel ∑ ( ) ∑ ( )
- 144. 104 Tabla XXVII. Integración de peso de edificio A Peso de edificio A Nivel Wlosas Wvigas Wcol Wmuro Wcim Winst Wtotal (kg) 1 108 864 29 529,36 187 200 157 290 112 320 9450 612 879,00 2 108 864 29 529,36 90 675 132 641 0 9450 357 991,50 3 108 864 29 529,36 90 675 132 641 0 9450 357 991,50 4 108 864 29 529,36 90 675 132 641 0 9450 357 991,50 5 108 864 29 529,36 76 050 111 248 0 9450 343 366,50 6 108 864 29 529,36 35 100 51 345 0 9450 302 416,50 WtotalA 2 332 636,50 Fuente: elaboración propia. 5.3.2.1. Integración de cargas para edificio B Cálculo del peso de primer nivel: ∑ ( ) ∑ ( )
- 145. 105 Cálculo del peso de segundo, tercero y cuarto nivel: ∑ ( ) ∑ ( ) Cálculo del peso de quinto nivel ∑ ( ) ∑ ( )
- 146. 106 Cálculo del peso de sexto nivel ∑ ( ) ∑ ( ) Tabla XXVIII. Integración de peso de edificio B Peso de edificio B Nivel Wlosas Wvigas Wcol Wmuro Wcim Winst Wtotal (kg) 1 81 648 25 719,12 144 000 119 070,0 69 984 9450 457 047,00 2 81 648 25 719,12 69 750 65 913,8 0 9450 259 656,75 3 81 648 25 719,12 69 750 65 913,8 0 9450 259 656,75 4 81 648 25 719,12 69 750 65 913,8 0 9450 259 656,75 5 81 648 25 719,12 58 500 55 282,5 0 9450 237 775,50 6 81 648 25 719,12 27 000 25 515,0 0 9450 176 508,50 WtotalB 1 650 301,25 Fuente: elaboración propia.
- 147. 107 5.4. Cálculo de cortante basal mediante AGIES NR-3:2000 5.4.1. Generalidades El edificio estará ubicado en la ciudad de Guatemala éste se encontrará en una zona sísmica 4 y con un índice de sismicidad de I = 4 según la Norma AGIES NR-3:2000. El tipo de suelo donde se cimentará la estructura se definirá como un tipo de suelo mediano (S2). 5.4.2. Cálculo de funciones de amplificación dinámica D(T) De acuerdo con las especificaciones del inciso 5.4.1 se definen los valores de (Ta) y (Tb) establecidos de conformidad con la tabla III: Con los valores obtenidos de (Ta) y (Tb) se procede a calcular la función de amplificación dinámica D(T) de acuerdo a la tabla IV. Edificio A: Para eje X: e ce ( ) ( ⁄ ) ( ⁄ ) Para eje Y: e ce ( )
- 148. 108 Edificio B: Para eje X: e ce ( ) Para eje Y: e ce ( ) ( ⁄ ) ( ⁄ ) En donde T es el período fundamental de la estructura. 5.4.3. Factor de reducción de respuesta sísmica El factor de reducción de respuesta sísmica se calcula de acuerdo con el inciso 2.5.1 y en la tabla VI, tomando el valor de Ro para una estructura de marcos de concreto especiales. 5.4.3.1. Factor de calidad sismorresistente ∑ ( ) ( ) ( ) ( )
- 149. 109 Tabla XXIX. Factor de calidad sismorresistente eje Ax Edificio AX, eje X Eje No. de tramos Tramo mínimo Tramo máximo Rel. minimo/máximo q1x A 2 3,5 7 0,5 1,66 B 2 3,5 7 0,5 1,66 C 2 3,5 7 0,5 1,66 D 2 3,5 7 0,5 1,66 F 2 3,5 7 0,5 1,66 G 2 3,5 7 0,5 1,66 H 2 3,5 7 0,5 1,66 I 2 3,5 7 0,5 1,66 J 2 3,5 7 0,5 1,66 K 2 3,5 7 0,5 1,66 M 2 3,5 7 0,5 1,66 N 2 3,5 7 0,5 1,66 Fuente: elaboración propia. Para los ejes Ax la relación Tmin/Tmax= 0,5, según la tabla VII está entre 0,45 y 0,75 para 4 o más tramos, entonces hay que interpolar para encontrar el valor de qx1= 1,66. Tabla XXX. Factor de calidad sismorresistente eje AY Edificio AY, eje Y Eje No. de tramos Tramo mínimo Tramo máximo Rel. T mínimo/T máximo q1y 1 12 3 3 1 0 2 12 3 3 1 0 3 12 3 3 1 0 Fuente: elaboración propia. Para el eje Ay la relación Tmin/Tmax= 1,0 > 0,7, con lo cual q1y = 0.
- 150. 110 Tabla XXXI. Factor de calidad sismorresistente eje Bx Edificio BX Eje No. de tramos Tramo mínimo Tramo máximo Rel. T mínimo/T máximo q1x K 9 3,5 3,5 1 0 L 9 3,5 3,5 1 0 N 9 3,5 3,5 1 0 Fuente: elaboración propia. Para el eje Bx la relación Tmin/Tmax= 1.0 > 0.7, con lo cual q1x = 0. Tabla XXXII. Factor de calidad sismorresistente eje BY Edificio BY Eje No. de tramos Tramo mínimo Tramo máximo Rel. T mínimo/T máximo q1y 4 2 3 6 0,5 1,5 5 2 3 6 0,5 1,5 6 2 3 6 0,5 1,5 7 2 3 6 0,5 1,5 8 2 3 6 0,5 1,5 9 2 3 6 0,5 1,5 10 2 3 6 0,5 1,5 11 2 3 6 0,5 1,5 12 2 3 6 0,5 1,5 13 2 3 6 0,5 1,5 Fuente: elaboración propia. Para los ejes By la relación Tmin/Tmax= 0,5, según la tabla VII está entre 0,45 y 0,75 para 4 o más tramos, entonces hay que interpolar para encontrar el valor de qy1= 1,66.
- 151. 111 5.4.3.2. Cálculo de q2 En dirección Ax y By, la estructura tiene 3 ejes, por lo tanto, en la Tabla 1.6.1.2 de la Norma AGIES NR-3: 2000 se tiene que si una estructura tiene 3 ejes estructurales en una dirección, el valor de q2 es: difici difici En la dirección Y, la estructura tiene 13 ejes estructurales. Cuando la estructura tiene 5 o más ejes estructurales en una dirección, el valor de q2y es: difici En la dirección X, la estructura tiene 10 ejes estructurales. Cuando se tiene que la estructura tiene 5 o más ejes estructurales en una dirección, el valor de q2y es: difici
- 152. 112 5.4.3.3. Regularidad en planta Para el edificio analizado se puede observar que todas las plantas son simétricas, por consiguiente solamente se analizarán las losas. Figura 27. Planta Ashurada Fuente: elaboración propia. El área real del diafragma es el área ashurada que se muestra en la figura 27, los agujeros que se muestran en la planta (espacios sin ashurar) son los agujeros interiores dentro del diafragma que servirán para la circulación vertical del edificio. Se determina el área perimetral y el área del diafragma de la siguiente manera:
- 153. 113 Tabla XXXIII. Relación Ap/Ad Edificio Área Perimetral Área agujeros Área real del diafragma Relación Ap/Ad A (36,00*10,50)=378,00 m2 (7,0*6,0)= 42,00 m2 Ap-Aa= 378,00-42,00= 336,00 m2 378/336 = 1,12 B (31,50*9,00)= 283,50 m2 (0*0)= 0 m2 Ap-Aa= 283,50-0= 283,50 m2 283,5/283,5=1,00 Fuente: elaboración propia. Se puede observar que el área del diafragma no afecta las fuerzas laterales en la estructura, la relación Ap/Ad es menor a 1,25, por lo tanto cumple con los requisitos establecidos en la Norma AGIES NR-3:2000 e indica que es una planta regular, se toma un valor para el índice de calidad de: Figura 28. Ubicación del centro de masa y centro de rigidez Fuente: elaboración propia.
- 154. 114 Gráficamente en la planta de la figura 28 de la estructura se puede observar que por simetría el centro de masa, medido con respecto al eje de referencia X, está en el centro de la planta, ya que las columnas, muros, vigas y losas están distribuidas simétricamente. Si la estructura no fuera simétrica se calcularía según sea el caso; entonces el centro de masa del edificio A está ubicado en el eje X a 5,25 metros y para el eje Y a 18 metros de distancia y para el edificio B está ubicado en el eje X a 15.75 metros y para el eje Y a 4,50 metros de distancia. 5.4.3.4. Excentricidad en planta Si se cumple con el inciso 2,5 en cada uno de los pisos se le asigna un índice de calidad en cada dirección de análisis: 5.4.3.5. Regularidad vertical Se debe chequear la regularidad vertical de la estructura en todos sus niveles para determinar el índice de calidad sismorresistente q6, tomando en cuenta las consideraciones especificadas en AGIES NR-3:2000:
- 155. 115 Tabla XXXIV. Alturas de piso Altura de piso edificio A Nivel Altura h por nivel L1 L2 Relación L1/L2 Relación h/L1 1 4,00 36,00 10,50 3,43 0,11 2 7,75 36,00 10,50 3,43 0,22 3 11,50 36,00 10,50 3,43 0,32 4 15,25 36,00 10,50 3,43 0,42 5 18,75 36,00 10,50 3,43 0,52 6 21,75 36,00 10,50 3,43 0,60 Altura de piso edificio B Nivel Altura h por nivel L1 L2 Relación L1/L2 Relación h/L1 1 4,00 31,50 9,00 3,50 0,13 2 7,75 31,50 9,00 3,50 0,25 3 11.50 31,50 9,00 3,50 0,37 4 15,25 31,50 9,00 3,50 0,48 5 18,75 31,50 9,00 3,50 0,60 6 21,75 31,50 9,00 3,50 0,69 Fuente: elaboración propia. Por la simetría que se observa en elevación y los cálculos realizados se establece para esta estructura regular en elevación un índice de calidad sismorresistente q6: 5.4.4. Cálculo del período fundamental de la estructura T Se realiza el cálculo del período fundamental de la estructura en los dos sentidos tanto en el eje X como en el Y:
- 156. 116 5.4.4.1. Período fundamental en sentido X Según AGIES NR-3:2000, para edificios en general el período empírico de vibración se calcula de la siguiente manera: difici √ √ difici √ √ 5.4.4.2. Período fundamental en sentido Y Según AGIES NR-3:2000, para edificios en general el período empírico de vibración se calcula de la siguiente manera: difici √ √ difici √ √ 5.4.5. Cálculo de sismos de diseño Por encontrarse la edificación en una zona sísmica 4, para los sismos de diseño se establecerá una Ao de 0.40 g para los cálculos correspondientes y los resultados obtenidos de la función de amplificación dinámica D(T) en el inciso 5.4.2, se calculan los sismos de diseño de la siguiente manera:
- 157. 117 5.4.5.1. Sismo básico Para ejes X y Y de edificio A: ( ) ( ) ( ) ( ) Para ejes X y Y de edificio B: ( ) ( ) ( ) ( ) 5.4.5.2. Sismo frecuente Para eje X y Y de edificio A: ( ) ( ) ( ) ( ) Para eje X y Y de edificio B: ( ) ( ) ( ) ( )
- 158. 118 5.4.6. Cálculo de cortante basal para el estado límite de servicio En el cálculo del cortante basal se considera el peso efectivo para la fuerza sísmica el 100% de la carga muerta + el 25% de la carga viva, calculándose de la siguiente manera: 5.4.6.1. Cálculo de cortante basal edificio A El cortante basal del edificio A en los ejes X y Y, se calcula de acuerdo a las siguientes ecuaciones: 5.4.6.2 Cálculo de cortante basal edificio B El cortante basal del edificio B en los ejes X y Y, se calcula de acuerdo a las siguientes ecuaciones:
- 159. 119 5.4.6.3. Cálculo de coeficiente sísmico Edificio A ( ) ( ) Edificio B ( ) ( ) El cortante basal estático equivalente es calculado a partir del coeficiente sísmico para el estado límite de servicio, solamente es necesario para revisar la acción de carga vertical y no para el diseño de la estructura. 5.4.7. Cálculo de cortante basal para el estado límite de cedencia En el cálculo del cortante basal se considera el peso efectivo para la fuerza sísmica el 100% de la carga muerta + el 25% de la carga viva, calculándose de la siguiente manera:
- 160. 120 5.4.7.1. Cálculo de cortante basal edificio A El cortante basal del edificio A en los ejes X y Y, se calcula de acuerdo a las siguientes ecuaciones: 5.4.7.2. Cálculo de cortante basal edificio B El cortante basal del edificio B en los ejes X y Y, se calcula de acuerdo a las siguientes ecuaciones: 5.4.7.3. Cálculo de coeficiente sísmico difici ( ) ( ) difici ( ) ( )
- 161. 121 5.4.8. Distribución de cargas verticales Tabla XXXV. Carga vertical para edificio A en eje X Nivel Peso (ton) Altura h (mts) hk (mts) Wh k 1 612,90 4,00 4,00 2 451,50 2 371,15 7,75 7,75 2 875,50 3 371,15 11,50 11,50 4 268,23 4 371,15 15,25 15,25 5 660,04 5 343,40 18,75 18,75 6 438,75 6 302,40 21,75 21,75 6 577,20 28 271,22 Fuente: elaboración propia. El valor de k se toma de 1 porque el período de la estructura es menor a 0.55. ∑ Para el estado límite de servicio la distribución vertical se conforma de la siguiente manera:
- 162. 122 Tabla XXXVI. Carga vertical para edificio A en eje Y Nivel Peso (ton) Altura h (mts) hk (mts) Whk 1 612,90 4,00 4,00 2 451,50 2 371,15 7,75 7,75 2 875,50 3 371,15 11,50 11,50 4 268,23 4 371,15 15,25 15,25 5 660,04 5 343,40 18,75 18,75 6 438,75 6 302,40 21,75 21,75 6 577,20 ∑ WhK 28 271,22 Fuente: elaboración propia. El valor de k se toma el valor de 0,75 + 0,5T por ser el período mayor a 0,55, para este caso 1,09. Entonces el factor Cvj para cada nivel del edificio A en sentido Y se calcula por medio de la siguiente ecuación: ∑
- 163. 123 Para el estado límite de servicio la distribución vertical se conforma de la siguiente manera: Para el estado límite de cedencia la distribución vertical se calcula de la siguiente manera: Eje X Eje Y Para verificar los datos anteriormente obtenidos, se puede hacer una comprobación: la sumatoria de todas las fuerzas verticales en todos los niveles debe ser igual al cortante basal:
- 164. 124 Tabla XXXVII. Carga vertical para edificio B en eje X y Y Nivel Peso (ton) Altura h (mts) hk (mts) Whk 1 457,04 4,00 4,00 1 828,16 2 259,65 7,75 7,75 2 012,28 3 259,65 11,50 11,50 2 985,86 4 259,65 15,25 15,25 3 959,66 5 237,77 18,75 18,75 4 458.18 6 176,50 21,75 21,75 3 838,87 19 083,00 Fuente: elaboración propia. El valor de k se toma de 1 porque el período de la estructura es menor a 0,55, según como se especifica en el inciso 2.6.8, se considerara los mismos coeficientes tanto en X como en Y ya que el coeficiente k tiene el mismo valor, se puede verificar en el inciso 5.4.8.1.
- 165. 125 Para el estado límite de servicio la distribución vertical se conforma de la siguiente manera: Eje X Eje Y Para el estado límite de cedencia la distribución vertical se calcula de la siguiente manera: Eje X Eje Y
- 166. 126 5.4.9. Resultados finales de cálculo cortante basal AGIES NR- 3:2000 Los resultados obtenidos mediante los cálculos realizados con AGIES NR- 3:2000 se describen de la siguiente manera: Tabla XXXVIII. Resultados de cortante basal Cortante basal en edificio A Cortante Basal eje X (ton) Cortante Basal eje Y (ton) Nivel 346,40 ton 371,15 ton Primero 31,17 33,40 Segundo 38,10 40,82 Tercero 55,42 59,38 Cuarto 72,74 77,94 Quinto 83,13 89,07 Sexto 65,81 70,51 Cortante basal en edificio B Cortante Basal eje X (ton) Cortante Basal eje Y (ton) Nivel 263,50 ton 228,35 ton Primero 23,71 20,55 Segundo 26,35 22,83 Tercero 42,16 36,53 Cuarto 55,33 47,95 Quinto 60,65 52,52 Sexto 50,06 43,48 Fuente: elaboración propia.
- 167. 127 5.4.10. Esquema de distribución de cargas horizontales Figura 29. Distribución de fuerzas horizontales edificio Ax Fuente: elaboración propia. Figura 30. Distribución de fuerzas horizontales edificio Ay Fuente: elaboración propia.
- 168. 128 Figura 31. Distribución de fuerzas horizontales edificio Bx Fuente: elaboración propia. Figura 32. Distribución de fuerzas horizontales edificio By Fuente: elaboración propia.
- 169. 129 5.5. Cálculo de cortante basal mediante IBC-2009/ASCE-05 5.5.1. Generalidades En este caso se procede a calcular las cargas sísmicas con las mismas condiciones que se han establecido anteriormente. Los factores de SS y S1 se calculan mediante los mapas de aceleración espectral, como se indica en la Figura 1613.5 del código IBC-2009, las propiedades del tipo de suelo donde se encontrará la estructura: para este caso se utilizará el suelo tipo D como se establece en la tabla IX. 5.5.2. Cálculo de coeficientes de sitio Fa y Fv En Guatemala, por encontrarse en una región sísmica se consideran valores similares a los propuestos en los mapas de aceleración espectral, como se aprecia en la figura 1613.5 del Código IBC-2009 que hacen referencia a las características de suelo de los Estados Unidos, para poder adaptar y realizar los cálculos correspondientes es necesario tomar valores similares a las condiciones de suelo que hay entre los dos países. Para efecto de este estudio se tomarán en cuenta los valores de California por la similitud que hay con Guatemala, por encontrarse en una región altamente sísmica, por lo tanto SS se definirá con el valor de 1,50 g y para el valor de S1 será de 0,61 g, dentro del intervalo de contorno sísmico. Los valores de los coeficientes de sitio Fa y Fv que dependen del tipo de suelo y de los datos obtenidos de SS y S1, se calcula mediante a la información que se encuentran en las tablas X y XI:
- 170. 130 5.5.3. Cálculo de sismo máximo espectral considerado SMS y SM1 El cálculo del espectro de sismo máximo considerado se procede a calcular de la siguiente manera: 5.5.4. Cálculo de sismo de diseño SDS y SD1 El cálculo del sismo de diseño equivale a las dos terceras partes del espectro de sismo máximo considerado: 5.5.5. Categoría de ocupación Para efectos del Código IBC-2009/ASCE-05 se establece que cada estructura debe pertenecer a una de las categorías de diseño, dependiendo del espectro de sismo de diseño SDS y SD1. Por lo tanto para el espectro de diseño SDS y SD1 se considera como una categoría de ocupación tipo D, esta categoría se establece según se indica en las tablas XIV y XV.
- 171. 131 5.5.6. Cálculo del período fundamental El período fundamental se calcula a partir de la tabla XVIII, dependiendo del sistema estructural y de la altura medida del edificio (en pies): Para analizar el período fundamental se observan los valores de la tabla XVI y se procede a calcular el coeficiente para el límite superior para el período calculado anteriormente. Para este caso se tiene un factor de 1,40 porque SD1 es mayor a 0,40, entonces se obtiene el siguiente valor: 5.5.7. Diseño del espectro de respuesta En los mapas de aceleración espectral como se indica en la figura 22-15 del Código ASCE-5 se obtienen los siguientes valores:
- 172. 132 Para efectos de este documento y con las características que el Código IBC- 2009/ASCE-5 contiene, se buscó una igualdad entre las propiedades del análisis sísmico entre Estados Unidos y Guatemala, de tal forma que se utilizaron las propiedades de suelo y las especificaciones que se consideran en el estado de California. Para este estado se considera un período de transición TL como se indica en las ecuaciones anteriormente. Estas consideraciones se toman en cuenta para el diseño del espectro de respuesta. 5.5.8. Cálculo de coeficiente de respuesta sísmica El coeficiente de respuesta sísmica se calcula a través del espectro de sismo de diseño SDS, del factor de modificación de respuesta descrito en la tabla XVII y del factor de importancia que se indica en la tabla XII, de la siguiente manera: ( ) ( ) El valor de TL es de 8 seg, entonces según se establece en el inciso 3.4.2 que T < TL, se calcula el CSmax que se utiliza para el diseño del cortante basal: ( ) ( )
- 173. 133 5.5.9. Cálculo de cortante basal En el cálculo del cortante basal se considera el peso efectivo para la fuerza sísmica el 100% de la carga muerta + el 25% de la carga viva, calculándose de la siguiente manera: 5.5.9.1. Cálculo de cortante basal edificio A El cortante basal del edificio A en los ejes X y Y, se calcula de acuerdo a las siguientes ecuaciones: 5.5.9.2. Cálculo de cortante basal edificio B El cortante basal del edificio B en los ejes X y Y, se calcula de acuerdo a las siguientes ecuaciones:
- 174. 134 5.5.10. Distribución de cargas verticales Tabla XXXIX. Carga vertical para edificio A en eje X y Y Nivel Peso (ton) Altura h (mts) hk (mts) Wh k 1 612,90 4,00 6,23 3 818,36 2 371,15 7,75 14,92 5 537,55 3 371,15 11,50 25,12 9 323,28 4 371,15 15,25 36,46 13 532,12 5 343,40 18,75 47,90 16 448,86 6 302,40 21,75 58,27 17 620,84 66 281,00 Fuente: elaboración propia. El valor de k se calcula por interpolación lineal según se indica en la tabla XIX, por lo que k=1,32. Cálculo de las fuerzas sísmicas que se aplican a cada nivel de la estructura:
- 175. 135 Tabla XL. Carga vertical para edificio B en eje X y Y Nivel Peso (ton) Altura h (mts) hk (mts) Wh k 1 457,04 4,00 6,23 2 847,35 2 259,65 7,75 14,92 3 873,98 3 259,65 11,50 25,12 6 522,40 4 259,65 15,25 36,46 9 466,84 5 237,77 18,75 47,90 11 389,20 6 176,50 21,75 58,27 10 284,65 44 384,43 Fuente: elaboración propia. El valor de k se calcula por interpolación lineal según se indica en la tabla XIX, por lo que k=1,32. Cálculo de las fuerzas sísmicas que se aplican a cada nivel de la estructura:
- 176. 136 5.5.11. Resultados finales de cálculo cortante basal IBC-2009/ASCE-5 Los resultados obtenidos mediante los cálculos realizados con IBC- 2009/ASCE-5 se describen de la siguiente manera: Tabla XLI. Resultados de cortante basal Cortante basal en edificio A Cortante basal eje X (ton) Cortante basal eje Y (ton) Nivel ton ton Primero 17,81 17,81 Segundo 26,72 26,72 Tercero 44,53 44,53 Cuarto 65,32 65,32 Quinto 77,19 77,19 Sexto 65,32 65,32 Cortante basal en edificio B Cortante Basal eje X (ton) Cortante Basal eje Y (ton) Nivel ton ton Primero 14,75 14,75 Segundo 18,97 18,97 Tercero 31,62 31,62 Cuarto 44,26 44,26 Quinto 52,70 52,70 Sexto 48,48 48,48 Fuente: elaboración propia.
- 177. 137 5.5.12. Esquema de distribución de cargas horizontales Figura 33. Distribución de fuerzas horizontales edificio Ax Fuente: elaboración propia. Figura 34. Distribución de fuerzas horizontales edificio Ay Fuente: elaboración propia.
- 178. 138 Figura 35. Distribución de fuerzas horizontales edificio Bx Fuente: elaboración propia. Figura 36. Distribución de fuerzas horizontales edificio By Fuente: elaboración propia.
- 179. 139 5.6. Cálculo de cortante basal mediante eurocódigo 8 5.6.1. Generalidades Para efectos de la norma eurocódigo 8, se procede a calcular las fuerzas sísmicas con las mismas condiciones establecidas anteriormente, tanto como para la norma AGIES NR-3: 2000 y para el código IBC- 2009/ASCE- 5. 5.6.2. Cálculo del período fundamental de la estructura El cálculo del período fundamental se determina de la siguiente manera: ⁄ ⁄ A continuación se observa que en el cálculo del período fundamental de la estructura cumple con la siguiente condición, por lo tanto se procede a hacer un análisis lineal para el cálculo del cortante basal. 5.6.3. Cálculo del espectro elástico de respuesta Para las condiciones de sitio en las que se encuentra Guatemala, asumiremos un valor de aceleración máxima de suelo de 0,40 g, basado en la información obtenida en la Norma AGIES NR-3 2000 y en la Tabla II de este documento.
- 180. 140 Los factores de suelo, corrección de amortiguamiento, de amplificación de la aceleración espectral y de los períodos de vibración son obtenidos mediante la Tabla XX, y el espectro se calcula de la siguiente manera: ( ) [ ] [ ] Para el espectro elástico de respuesta se reduce en sus ordenadas por un factor que depende del período de vibración de la estructura como se indica en el inciso 4.3.2. En este caso por ser el período de vibración mayor a 0.50 segundos, el factor que le corresponde es de 0.50. ( ) En el caso de las cargas sísmicas es similar al procedimiento establecido en la Norma AGIES NR-3 2000 para el límite de estado de servicio, ya que solamente es necesario para revisar la acción de carga vertical y no para el diseño de la estructura. 5.6.4. Cálculo espectro para análisis lineal En el cálculo del espectro se debe determinar mediante el cociente entre la aceleración del suelo y de la aceleración de la gravedad para proceder a determinar el espectro para el análisis lineal:
- 181. 141 Siendo : Espectro de respuesta 1 Espectro de respuesta 2 Regiones con alta sismicidad Regiones con baja sismicidad El espectro se calcula de la siguiente manera, tomando los valores específicos establecidos en la tabla XXII: ( ) [ ] [ ] ⁄ Para un sistema estructural de marcos rígidos de concreto armado se utiliza un factor de (q) igual a: 5.6.5. Cálculo de cortante basal En el cálculo del cortante basal se considera el peso efectivo para la fuerza sísmica el 100% de la carga muerta + el 25% de la carga viva, calculándose de la siguiente manera: ( )
- 182. 142 5.6.5.1. Cálculo de cortante basal edificio A El cortante basal del edificio A en los ejes X y Y, se calcula de acuerdo a las siguientes ecuaciones: Las cargas sísmicas que se inducen a cada nivel se calculan de la siguiente manera: Tabla XLII. Carga horizontal para edificio A en eje X y Y Nivel Peso (ton) Altura h (mts) Wh 1 612,90 4,00 2451,50 2 371,15 7,75 2875,50 3 371,15 11,50 4268,23 4 371,15 15,25 5660,04 5 343,40 18,75 6438,75 6 302,40 21,75 6577,20 28 271,22 Fuente: elaboración propia.
- 183. 143 La distribución de fuerzas verticales se calcula para los ejes X y Y debido a que el cortante de basal, peso del nivel es el mismo para los dos sentidos: La sumatoria de todas las fuerzas verticales en todos los niveles debe ser igual al cortante basal: 5.6.6.2. Cálculo del cortante basal edificio B El cortante basal del edificio B en los ejes X y Y, se calcula de acuerdo a las siguientes ecuaciones:
- 184. 144 Tabla XLIII. Carga vertical para edificio B en eje X y Y Nivel Peso (ton) Altura h (mts) Wh 1 457,04 4,00 1828,16 2 259,65 7,75 2012,28 3 259,65 11,50 2985,86 4 259,65 15,25 3959,66 5 237,77 18,75 4458,18 6 176,50 21,75 3838,87 19 083,00 Fuente: elaboración propia. La distribución de fuerzas verticales se calcula para los ejes X y Y debido a que el cortante de basal, peso del nivel es el mismo para los dos sentidos:
- 185. 145 La sumatoria de todas las fuerzas verticales en todos los niveles debe ser igual al cortante basal: 5.5.6. Resultados finales de cálculo del cortante basal eurocódigo 8 Los resultados obtenidos mediante los cálculos realizados con eurocódigo 8 se describen de la siguiente manera: Tabla XLIV. Resultados de cortante basal en ejes X y Y Cortante basal en edificio A Cortante basal eje X (ton) Cortante basal eje Y (ton) Nivel Primero 31,76 31,76 Segundo 36,40 36,40 Tercero 55,42 55,42 Cuarto 72,74 72,74 Quinto 79,67 79,67 Sexto 69,28 69,28
- 186. 146 Continuación tabla XLIV. Cortante basal en edificio B Cortante basal eje X (ton) Cortante basal eje Y (ton) Nivel Primero 22,13 22,13 Segundo 27,05 27,05 Tercero 39,34 39,34 Cuarto 51,64 51,64 Quinto 59,02 59,02 Sexto 46,72 46,72 Fuente: elaboración propia. 5.5.7. Esquema de distribución de cargas horizontales Figura 37. Distribución de fuerzas horizontales edificio Ax Fuente: elaboración propia.
- 187. 147 Figura 38. Distribución de fuerzas horizontales edificio Ay Fuente: elaboración propia. Figura 39. Distribución de fuerzas horizontales edificio Bx Fuente: elaboración propia.
- 188. 148 Figura 40. Distribución de fuerzas horizontales edificio By Fuente: elaboración propia.
- 189. 149 6. COMPARACIÓN DE RESULTADOS 6.1. Resultados del cortante basal en la estructura A continuación se presentan los resultados obtenidos por los cálculos realizados anteriormente del cortante basal: Tabla XLV. Resultados de cortante basal en la estructura Cortante basal en edificio A Código Cortante Basal eje X (ton) Cortante Basal eje Y (ton) AGIES NR-3:2000 346,40 371,15 IBC 2009/ASCE-05 296,92 296,92 Eurocódigo 8 346,41 346,41 Cortante basal en edificio B Código Cortante basal eje X (ton) Cortante basal eje Y (ton) AGIES NR-3:2000 263,50 228,35 IBC 2009/ASCE-05 210,80 210,80 Eurocódigo 8 245,92 245,92 Fuente: elaboración propia.
- 190. 150 6.2. Tabla de resultados de la distribución de cargas horizontales en niveles superiores A continuación se presentan los resultados obtenidos por los cálculos realizados anteriormente de la distribución de cargas horizontales en los diferentes niveles del edificio: Tabla XLVI. Cargas horizontales por nivel Cargas horizontales por nivel en edificio A Código AGIES NR-3:2000 IBC 2009/ASCE-05 Eurocódigo 8 Nivel X Y X Y X Y Primero 31,17 33,40 17,81 17,81 31,76 31,76 Segundo 38,10 40,82 26,72 26,72 36,40 36,40 Tercero 55,42 59,38 44,53 44,53 55,42 55,42 Cuarto 72,74 77,94 65,32 65,32 72,74 72,74 Quinto 83,13 89,07 77,19 77,19 79,67 79,67 Sexto 65,81 70,51 65,32 65,32 69,28 69,28 Cargas horizontales por nivel en edificio B Código AGIES NR-3:2000 IBC 2009/ASCE-05 Eurocódigo 8 Nivel X Y X Y X Y Primero 23,71 20,55 14,75 14,75 22,13 22,13 Segundo 26,35 22,83 18,97 18,97 27,05 27,05 Tercero 42,16 36,53 31,62 31,62 39,34 39,34 Cuarto 55,33 47,95 44,26 44,26 51,64 51,64 Quinto 60,60 52,52 52,70 52,70 59,02 59,02 Sexto 50,06 43,48 48,48 48,48 46,72 46,72 Fuente: elaboración propia.
- 191. 151 6.3. Comparación del período de vibración de la estructura Se realiza la comparación de los diferentes resultados de los períodos de vibración del edificio en cada uno de los códigos: Tabla XLVII. Periodos de vibración con IBC 2009/ASCE-05, AGIES NR- 3:2000 y eurocódigo 8 Período de vibración en edificio A Código Período eje X (seg) Período eje Y (seg) AGIES NR-3:2000 0,68 0,38 IBC 2009/ASCE-05 0,83 0,83 Eurocódigo 8 0,83 0,83 Período de vibración en edificio B Codigo Período eje X (seg) Período eje Y (seg) AGIES NR-3:2000 0,40 0,74 IBC 2009/ASCE-05 0,83 0,83 Eurocodigo 8 0,83 0,83 Fuente: elaboración propia.
- 192. 152 6.4. Comparación analítica de cortante en la base de la estructura En la siguiente tabla se muestran los parámetros utilizados en el diseño sismorresistente para cada uno de los códigos de diseño estructural: Tabla XLVIII. Parámetros de diseño sismorresistente Parámetros de diseño sismorresistente Código/ Parámetros AGIES NR-3:2000 IBC 2009/ASCE-05 Eurocódigo 8 X Y X Y X Y Tipo de Suelo S2 D B Período 0,68 0,38 0,83 0,83 0,83 0,83 R 6,6 6,72 8 8 8 8 Fa 0 0 1 1 0 0 Fv 0 0 1,5 1,5 0 0 Ss 0,92 g 0,92 g 1,50 g 1,50 g 0,40 g 0,40 g S1 1,00 g 1,00 g 0,61 g 0,61 g 0,36 g 0,36 g TL 0 0 8 seg 8 seg 0 0 I 1,25 1,25 1,25 1,25 1,25 1,25 Cs edificio A 0,14 0,15 0,12 0,12 0,14 0,14 Cs edificio B 0,15 0,13 0,12 0,12 0,14 0,14 Fuente: elaboración propia. 6.4.1. IBC 2009/ASCE-05 con AGIES NR-3:2000 La comparación del cortante basal en ambos códigos difiere dentro del 15% al 25%. Esta diferencia se debe a que en cada código se utilizan diversos parámetros de diseño sismorresistente. En el IBC 2009/ASCE-05 se utilizan parámetros de suelo similares al estado de California de Estados Unidos con el fin de adaptar las mismas condiciones de suelo en Guatemala.
- 193. 153 La diferencia dentro los períodos de vibración es notoria debido a que en IBC 2009/ASCE-05 para calcular este período solo se toma como referencia la altura del edificio mientras que en AGIES NR-3:2000 se considera tanto la altura como la longitud de la estructura. 6.4.2. IBC 2009/ASCE-05 con eurocódigo 8 ENV 1998-1-1:1994 Los resultados del cortante basal se mantuvieron dentro del rango del 10% al 15%. El eurocódigo calcula el cortante basal mediante un espectro de respuesta en donde intervienen diversos factores. Los factores que intervienen en el cálculo de las cargas sísmicas en el eurocódigo son las condiciones del suelo, período de vibración, aceleración del suelo, aceleración espectral. Aunque se utilizan diferentes tipos de factores el resultado del cortante basal oscila dentro del rango anteriormente mencionado. 6.4.3. AGIES NR-3:2000 con eurocódigo 8 ENV 1998-1-1:1994 Los resultados entre estos códigos son similares debido a que los resultados oscilan dentro del rango del 12% al 15% del porcentaje del peso de la estructura. Son condiciones totalmente diferentes pero los criterios que se utilizan en estos códigos de diseño estructural siguen la misma línea de diseño sísmico que conforman los espectros de respuesta sísmica.
- 194. 154 6.5. Comparación de fuerzas horizontales Se realiza una comparación gráfica con el fin de analizar las fuerzas horizontales que se inducen a cada nivel y así poder comprenderse de una mejor manera. 6.5.1. IBC 2009/ASCE-05 con AGIES NR-3:2000 0 20 40 60 80 100 1 2 3 4 5 6 CORTANTEBASAL(TON) No. NIVEL DE EDIFICIO Cortante basal vrs. altura del edificio AGIES NR-3:2000 X IBC 2009/ASCE-05 X 0 50 100 1 2 3 4 5 6 CORTANTEBASAL(TON) No. NIVEL DE EDIFICIO Cortante basal vrs. altura del edificio AGIES NR-3:2000 Y IBC 2009/ASCE-05 Y
- 195. 155 6.5.2. IBC 2009/ASCE-05 con Eurocódigo 8 ENV 1998-1-1:1994 0 10 20 30 40 50 60 70 80 1 2 3 4 5 6 CORTANTEBASAL(TON) No. NIVEL DE EDIFICIO Cortante basal vrs. altura del edificio IBC 2009/ASCE-05 X Eurocodigo 8 X 0 10 20 30 40 50 60 70 80 1 2 3 4 5 6 CORTANTEBASAL No. NIVEL DE EDIFICIO Cortante basal vrs. altura del edificio IBC 2009/ASCE-05 Y Eurocodigo 8 Y
- 196. 156 6.5.3. AGIES NR-3:2000 con Eurocódigo 8 ENV 1998-1-1:1994 0 20 40 60 80 100 1 2 3 4 5 6 CORTANTEBASAL(TON) No. NIVEL DE EDIFICIO cortante Basal vrs. altura del edificio AGIES NR-3:2000 X Eurocodigo 8 X 0 20 40 60 80 100 1 2 3 4 5 6 CORTANTEBASAL(TON) No. NIVEL DE EDIFICIO Cortante basal vrs. altura del edificio AGIES NR-3:2000 Y Eurocodigo 8 Y
- 197. 157 6.6. Comparación de fuerzas verticales 6.6.1. Comparación con AGIES NR-3:2000, IBC 2009/ASCE-05 y Eurocódigo 8 ENV 1998-1-1:1994 El criterio que utilizan los tres códigos de diseño estructural para asumir las cargas verticales es el mismo porque se basan en el código UBC-97. En tanto para realizar los cálculos de las cargas que actúan en función de la gravedad se consideró el mismo valor para los tres casos, por ejemplo, para la carga viva se utilizaron 250 kg/m2 en donde se puede observar en la Tabla I de este documento.
- 198. 158
- 199. 159 CONCLUSIONES 1. La Norma AGIES es de fácil aplicación. Puede suceder que su aplicación resulte más laboriosa, pero en la misma se analizan las características propias y geométricas de la estructura; parámetros que no se analizan en otros códigos. 2. Cuando se utilizan los códigos IBC-2009/ASCE-05, existe en los mismos una zonificación sísmica de los Estados Unidos de Norteamérica. Para poder aplicar estos códigos en un proyecto en Guatemala, generalmente se utiliza la zona sísmica y parámetros de California, debido a que ésta es la más similar a las condiciones sísmicas de Guatemala. 3. El valor de la fuerza sísmica que se aplica a una estructura se considera como un porcentaje del peso total de la estructura, que para efectos de este trabajo de graduación varió entre el 10% a un 15%. 4. Los valores de los períodos de vibración empíricos, obtenidos por la ecuación recomendada por AGIES, son más conservadores que los obtenidos por las expresiones de los Códigos IBC-2009/ASCE-05 y el Eurocódigo 8. Los valores calculados son más pequeños y por consiguiente el factor de amplificación dinámica es mayor.
- 200. 160 5. El factor de reducción de respuesta sísmica R obtenido por AGIES es más conveniente que el obtenido por IBC-2009/ASCE-05, ya que no depende únicamente del sistema estructural, sino que depende de las características propias de la estructuración y geometría de la estructura. 6. La determinación de la regularidad en planta o en elevación de una estructura por medio de AGIES y Eurocódigo 8 es más objetiva que la utilizada en el IBC-2009/ASCE-05. Con los dos primeros códigos se analizan parámetros numéricos para clasificar la estructura, y no se basa en parámetros asumidos por el calculista al utilizar el IBC-2009. 7. Los mapas de aceleración espectral, son mapas que muestran resultados más exactos que los mapas de aceleración máxima. Éstos son más específicos; debido a que se generan con las condiciones locales de cada sitio. 8. El Eurocódigo 8 utiliza dos espectros de respuesta, uno para zonas de alta sismicidad y el otro para zonas de baja sismicidad. Para adaptar el diseño a las condiciones sísmicas de Guatemala, se optó por utilizar el primero de ambos. 9. El algoritmo del cortante basal es una herramienta que sirve para facilitar el procedimiento del cálculo de la carga sísmica.
- 201. 161 RECOMENDACIONES 1. Tratar de utilizar la Norma AGIES NR-3:2000, al momento de diseñar un edificio en Guatemala, debido a que ésta es de fácil aplicación y toma en cuenta la sismicidad del país. 2. Al realizar un diseño estructural en Guatemala con el código IBC-2009/ASCE-05, utilizar los parámetros sísmicos del estado de California. Estos parámetros son los más similares a los parámetros de Guatemala. 3. Por la región altamente sísmica en la que se encuentra Guatemala, un porcentaje aceptable del cortante basal debe estar dentro de un rango del 10% al 15% del peso total de la estructura. 4. Determinar si es más preciso obtener el período de vibración con base en la geometría de la estructura (la altura y el largo) como se plantea en la Norma AGIES, o si es más preciso obtenerlo con base al sistema estructural y la altura, como se plantea en el IBC-2009 y el Eurocódigo 8. 5. Utilizar el factor de reducción de respuesta sísmica R que se obtiene en AGIES, debido a que no depende únicamente del sistema estructural, sino que toma en cuenta las características propias de la estructuración y geometría de la estructura, debido a que este factor influye directamente en el resultado del cortante basal.
- 202. 162 6. Determinar la regularidad de una planta numéricamente por medio de los índice de calidad q5 (excentricidades en planta) y q6 (isotropía en planta), y no por medio de la subjetividad del calculista. 7. Profundizar más en los estudios sobre sismicidad y geología del país, para incrementar la creación de mapas de aceleraciones espectrales de la República de Guatemala. De esta manera precisar de datos más exactos sobre la condición sísmica del país. 8. Utilizar el espectro de respuesta para la región con sismicidad alta, cuando se utiliza el eurocódigo 8 para calcular el cortante basal actuante en una estructura en Guatemala. 9. Consultar el algoritmo del cortante basal para que el cálculo de la fuerza sísmica sea resuelto de una manera comprensible y simplificada.
- 203. 163 BIBLIOGRAFÍA 1. AMBROSE, James. Análisis y diseño de estructuras. 2° ed. México: Limusa, 1998. 844 p. 2. ASCE STANDARD. Minimum Design Loads for Buildings and Other Structures, American Society of Civil Engineers y Structural Engineering Institute, United States of America. 2005. p. 340-360. 3. Building Code Requirements for Structural Concrete (ACI 318-08). United States of America Standard. ACI Committee. 2008. 400 p. 4. DOWRICK, D. J. Diseño de estructuras resistentes a sismos para ingenieros y arquitectos. México: Limusa, 1984. 410 p. 5. EC8 Part 1. Design of structures for earthquake resistance, covers general rules seismic actions and rules for buildings CEN European Committee for Standardization, ENV 1998–5: 2003. 50 p. 6. International Building Code. United States of America: International Code Council, 2009. 800 p. 7. Normas estructurales recomendadas para la República de Guatemala, AGIES NR-3. Guatemala: Asociación Guatemalteca de Ingenieros Estructurales y Sísmicos, 2000. 350 p.
- 204. 164 8. PAREDES RUIZ, Paola Anaite. “Guía teórica y práctica del curso de diseño e uc u a ”. Trabajo de Graduación de Ing. Civil. Facultad de Ingeniería, Universidad de San Carlos de Guatemala, 1995. 109 p. 9. Uniform Building Code. United States of America: International Code Council. 1997. 1000 p. 10. VELÁSQUEZ JOFRE, Diego. “Características y parámetros principales del cálculo de período de recurrencia de sismos, utilizando el método babi ic a a é ic de e ” yec de i ve igaci interno No. 02-2010 de Ing. Civil. Facultad de Ingeniería, Universidad de San Carlos de Guatemala. 2010. 100 p.
- 205. 165 APÉNDICE a) Protocolo de cálculo de cortante basal mediante AGIES NR-3:2000 Determinar el peso de la estructura Especificar tipo de suelo Calcular el período de vibración de la estructura Calcular las funciones de amplificación dinámica Calcular los espectros de respuesta sísmica de diseño Determinar el sismo básico y sismo frecuente de diseño Realizar el cálculo del cortante basal Determinar las fuerzas que se le inducen a cada nivel b) Protocolo de cálculo de cortante basal mediante IBC-2009/ASCE-5 Calcular el peso total de la estructura Calcular aceleración de respuesta espectral SDS y SD1
- 206. 166 En donde SDS es la aceleración de repuesta espectral de diseño en el período corto, mientras que SD1 es la respuesta espectral para períodos de 1 segundo. Calcular aceleración de respuesta espectral SS y S1 En donde Ss y S1 se refieren a las aceleraciones de respuesta espectral máximas consideradas para períodos cortos tanto como para períodos de 1 seg. Calcular los coeficientes de sitio que depende del tipo de suelo Fa y Fv. Deducir el factor de respuesta sísmica a utilizar Imponerle un factor de importancia a la estructura Calcular el período fundamental Calcular el coeficiente sísmico Cs Calcular el cortante basal Calcular las fuerzas que se le inducen a cada nivel c) Protocolo de cálculo de cortante basal mediante eurocódigo 8 Determinar la fuerza del cortante basal ( )
- 207. 167 V: Cortante basal W: Peso total del edificio S d (T): Espectro de diseño normalizado por la aceleración de la gravedad g T1: período fundamental de vibración del edificio. 0 ≤ T ≤ TB ( ) [ ( )] TB ≤ T ≤ TC ( ) TC ≤ T ≤ TD ( ) [ ] TD ≤ T ( ) [ ] [ ] relación entre la aceleración del suelo de diseño para la aceleración de la gravedad. q: factor de comportamiento para las estructuras q0: valor básico del factor de comportamiento. kD: factor que refleja la clase de ductilidad. kR: factor que refleja la regularidad estructural en la elevación. kW: factor que refleja el modo de fallo que prevalece en los sistemas estructurales.




















































































































![77
Para períodos de vibración (T) menores de 0,15 seg, se multiplican las
ordenadas por un factor de 0,70.
Para períodos de vibración (T) mayores de 0,50 seg, se multiplican las
ordenadas por un factor de 0,50.
Para períodos de vibración (T) entre 0,15 y 0,50 seg, se utilizará
interpolación lineal.
4.3.3. Espectro elástico de respuesta
El espectro elástico de respuesta Se (T) para el período de retorno de
referencia se define por las descritas en la tabla XX.
Tabla XX. Espectro elástico de respuesta
0 ≤ T ≤ TB
[ ]
TB ≤ T ≤ TC
TC ≤ T ≤ TD
[ ]
TD ≤ T [ ] [ ]
Fuente: Normas estructurales de diseño recomendadas para la Unión Europea, Eurocódigo 8,
parte 1-1. p. 19.](https://image.slidesharecdn.com/083312c-160430021757/85/08-3312-c-117-320.jpg)



![81
4.3.5. Espectro de cálculo para análisis lineal
La capacidad de los sistemas estructurales para resistir las fuerzas
sísmicas en el rango no lineal permite generalmente proyectarlos para fuerzas
menores que las que corresponde a una respuesta elástica lineal.
Los valores del factor de comportamiento (q), en el que también influye
que el amortiguamiento viscoso sea diferente del 5%, están dados para los
diversos materiales y sistemas estructurales.
Para el período de retorno de referencia, el espectro de cálculo Sd (T),
normalizado para la aceleración de la gravedad (g), se define mediante a la
tabla XX:
Tabla XXII. Espectro de cálculo para análisis lineal
0 ≤ T ≤ TB
[ ( )]
TB ≤ T ≤ TC
TC ≤ T ≤ TD
[ ]
TD ≤ T [ ] [ ]
Fuente: Normas estructurales de diseño recomendadas para la Unión Europea, Eurocódigo 8,
parte 1-1. p. 21.](https://image.slidesharecdn.com/083312c-160430021757/85/08-3312-c-121-320.jpg)






















































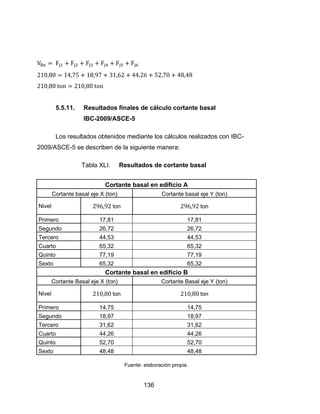



![140
Los factores de suelo, corrección de amortiguamiento, de amplificación de
la aceleración espectral y de los períodos de vibración son obtenidos mediante
la Tabla XX, y el espectro se calcula de la siguiente manera:
( ) [ ] [ ]
Para el espectro elástico de respuesta se reduce en sus ordenadas por un
factor que depende del período de vibración de la estructura como se indica en
el inciso 4.3.2. En este caso por ser el período de vibración mayor a 0.50
segundos, el factor que le corresponde es de 0.50.
( )
En el caso de las cargas sísmicas es similar al procedimiento establecido
en la Norma AGIES NR-3 2000 para el límite de estado de servicio, ya que
solamente es necesario para revisar la acción de carga vertical y no para el
diseño de la estructura.
5.6.4. Cálculo espectro para análisis lineal
En el cálculo del espectro se debe determinar mediante el cociente entre
la aceleración del suelo y de la aceleración de la gravedad para proceder a
determinar el espectro para el análisis lineal:](https://image.slidesharecdn.com/083312c-160430021757/85/08-3312-c-180-320.jpg)
![141
Siendo :
Espectro de respuesta 1 Espectro de respuesta 2
Regiones con alta sismicidad Regiones con baja sismicidad
El espectro se calcula de la siguiente manera, tomando los valores
específicos establecidos en la tabla XXII:
( ) [ ] [ ] ⁄
Para un sistema estructural de marcos rígidos de concreto armado se
utiliza un factor de (q) igual a:
5.6.5. Cálculo de cortante basal
En el cálculo del cortante basal se considera el peso efectivo para la
fuerza sísmica el 100% de la carga muerta + el 25% de la carga viva,
calculándose de la siguiente manera:
( )](https://image.slidesharecdn.com/083312c-160430021757/85/08-3312-c-181-320.jpg)

























![167
V: Cortante basal
W: Peso total del edificio
S d (T): Espectro de diseño normalizado por la aceleración de la
gravedad g
T1: período fundamental de vibración del edificio.
0 ≤ T ≤ TB
( ) [ ( )]
TB ≤ T ≤ TC
( )
TC ≤ T ≤ TD
( ) [ ]
TD ≤ T
( ) [ ] [ ]
relación entre la aceleración del suelo de diseño para la aceleración de la
gravedad.
q: factor de comportamiento para las estructuras
q0: valor básico del factor de comportamiento.
kD: factor que refleja la clase de ductilidad.
kR: factor que refleja la regularidad estructural en la elevación.
kW: factor que refleja el modo de fallo que prevalece en los sistemas
estructurales.](https://image.slidesharecdn.com/083312c-160430021757/85/08-3312-c-207-320.jpg)