1. teoria prob.

DOCENTE:
PROBABILIDADES
MERCEDES AIDA OSORIO MAZA
mosorio@uni.edu.pe
SEMANA
TEORIA
4
2016 - I

 Axiomática de la probabilidad, Teoremas
fundamentales.
 Probabilidad de un suceso.
 Probabilidad condicional. Teorema de la
Multiplicación.
TEMAS A DESARROLLAR

DEFINICIÓN DE PROBABILIDADES
DEFINICIÓN
DE
PROBABILIDADES
Definición Clásica
(Probabilidad Apriori)
Definición de Probabilidad Frecuencial
(Probabilidad Aposteriori)
Definición Axiomática de la Probabilidad
(Kolgomorov)

1.- Definición Clásica (Probabilidad Apriori)
La probabilidad de un evento es la razón entre el
número de casos favorables y el número total de
casos posibles, es decir la probabilidad del evento
“A”, denotado por P(A) es:
 
 
  posiblescasosdeNúmero
favoracasosdeNúmero
n
n
P
A
A 


2.- Definición de Probabilidad Frecuencial
(Probabilidad Aposteriori)
Si un experimento es ejecutado “n” veces bajo las mismas
condiciones y hay n(A) resultados en que ocurrió un hecho
“A”, siendo la frecuencia relativa , entonces la
probabilidad del evento A es:
An
nA
fr
 
n
n
limfrlim
nn
A
AAP



3.- Definición Axiomática de la Probabilidad
Sea E un experimento aleatorio y un espacio muestral
asociado con E si al evento A, le signamos un número Real
tal que satisfaga ciertas propiedades.
Tenemos:
Propiedades o Axiomas:
a)   1P0 A 
b)   1P 

c)
d)
      ntesIndependieeventossonByASiPPP BABA 
A B
       BABABA PPPP  
A B

e)
               CBACBCABACBACBA PPP-PPPPP  
f) Si A’ es un evento complementario
   AA' P1P 
A
A’


g)
   NuloconjuntodeadProbabilid0P 
Nota: Esta definición es más aplicable cuando la probabilidad está
dado como conjunto
h)    BA PPBASi 
A B
C

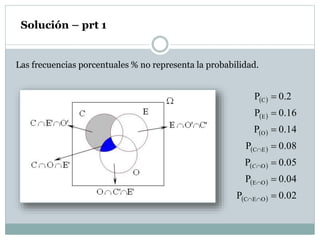
Ejemplo
En una ciudad se publican tres periódicos, Comercio, Extra y Ojo en un
estudio realizado se determinó que el:
 20% lee el Comercio
 16% lee Extra
 14% lee Ojo
 8% lee Comercio y Extra
 5% lee Comercio y Ojo
 4% lee Extra y Ojo
 2% lee los tres periódicos.
Si se selecciona una persona al azar de esta ciudad:
a) Hallar la probabilidad de que no lea el Comercio
b) Hallar la probabilidad de que no lea el Comercio y no lea Extra.
c) Hallar la probabilidad de que lea Comercio y Ojo pero que no lea Extra.
d) ¿Cuál es la probabilidad que lea uno de los periódicos?

Solución – prt 1
Las frecuencias porcentuales % no representa la probabilidad.
 
 
 
 
 
 
  02.0P
04.0P
05.0P
08.0P
14.0P
16.0P
2.0P
OEC
OE
O
EC
O
E
C











C

a) Hallar la probabilidad de que no lea el Comercio
Solución – prt 2
   
ComercioleanoqueadProbabilid80.02.01
P1P CC'


b) Hallar la probabilidad de que no lea el Comercio y no lea Extra.
   
 
         72.008.016.02.01PPP1
P1
ConjuntosdePropiedadPP
ECEC
EC
'ECE'C'







c) Hallar la probabilidad de que lea Comercio y Ojo pero que no lea Extra.
Solución – prt 3
      
   03.002.005.0P
PPP
E'OC
EOCE'OC



 OC
d) ¿Cuál es la probabilidad que lea uno de los periódicos
                     
         
      1.0PPP
02.0304.005.008.0214.016.02.0PPP
P3PPP2PPPPPP
E'C'OO'C'EE'O'C
E'C'OO'C'EE'O'C
OECOEOCECOECE'C'OO'C'EE'O'C







Video de Definición de Probabilidad

Probabilidad Condicional
Sean A y B dos eventos que pertenecen al espacio muestral
,     0P,0P BA 
La probabilidad condicional de A dado B denotado por
se define:
 B
AP
 
 
 
 
 
 A
AB
A
B
B
BA
B
A
P
P
Pó
P
P
P



Axiomas o Propiedades:
1.-
2.-
  1P0
B
A 
   
 
 
1
P
P
P1P
B
B
BB



Nota: Si A y B son mutuamente excluyentes:
     C
B
C
A
C
BA PPP 

Demostración
 
  
 
 
 
 
 
   C
B
C
A
C
CB
C
CA
C
CBA
C
BA
PP
P
P
P
P
P
P
P





     C
B
C
A
C
BA PPP 

Video de Probabilidad Condicional

Teoremas de la Probabilidad
TEOREMAS
DE LA
PROBABILIDAD
Teorema
de la
Multiplicación
Teorema
de
“ Bayes ”
Teorema de la Probabilidad Total

1.- Teorema de la Multiplicación
 Se aplica cuando deseamos hallar la probabilidad conjunta
de dos eventos o más.
 Dados dos eventos A y B de un espacio muestral 
           B
ABBA
A
BABA PPPöPPP  
Prueba de la probabilidad condicional:
 
 
 
     
 
 
 
     A
A
BAB
A
AB
A
B
B
B
ABA
B
BA
B
A
PPP
P
P
P
PPP
P
P
P







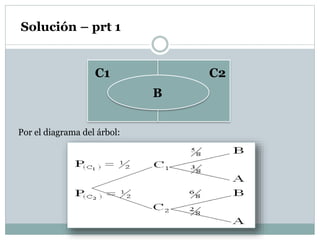
Ejemplo
Una caja contiene cinco fichas blancas y tres azules, otra caja
contiene dos fichas azules y seis blancas. Si se selecciona una
caja al azar y después una ficha de la caja seleccionada.
Nota: Realice el diagrama de árbol de este experimento
a) ¿Cuál es la probabilidad de que la ficha seleccionada sea
blanca y provenga de la caja uno?
b) ¿Cuál es la probabilidad de que la ficha seleccionada sea
azul y provenga de la caja dos?

Solución – prt 1
Por el diagrama del árbol:
B
C1 C2

Solución – prt 2
8
2
C
A8
3
C
A
8
6
C
B8
5
C
B
21
21
PP
PP


























Nota:
Por el Teorema de la Multiplicación
   
  
   
   16
2
2
1
8
2
C
C
ACA
16
5
2
1
8
5
C
C
BCB
2
2
2
1
1
1
PPPb)
PPPa)

















Partición del Espacio Muestral
Sea el espacio muestral , los eventos E1, E2, ...,Ek
forman una partición de dicho espacio si cumplen las
siguientes condiciones:
1)
3)
2)
 k21 E...EE
jiji  EE
iE



1. teoria prob.

Más contenido relacionado

La actualidad más candente (20)

Similar a 1. teoria prob. (20)

Último (20)

1. teoria prob.