56 calculo ii
- 2. 2 dgep-uas
- 3. dgep-uas 3 Autores: Arturo Ylé Martínez José Alfredo Juárez Duarte Faustino Vizcarra Parra Revisión Técnica: Dr. Armando Flórez Arco Cálculo II Cálculo Integral Para Bachillerato Segunda Edición
- 4. 4 dgep-uas
- 5. dgep-uas 5 Cálculo II Cálculo Integral Para Bachillerato Segunda Edición
- 6. 6 dgep-uas Cálculo Integral Tercer grado, segundo semestre Fases especializadas: Físico-Matemáticas y Químico- Biológicas Segunda Edición, Diciembre de 2012. © Arturo Ylé Martínez © José Alfredo Juárez Duarte © Faustino Vizcarra Parra Diseño portada: Eva Margarita Moreno Chávez Diseño de interior: Irán Sepúlveda León Carol Judith Zazueta Rivera Revisión Técnica: Dr. Armando Flórez Arco Servicios Editoriales Once Ríos Río Usumacinta 821 Col. Industrial Bravo. C.P. 80120 Culiacán, Sinaloa, México. Impreso en México Edición con fines académicos, no lucrativos
- 7. dgep-uas 7 Presentación..........................................................................................................................9 Dedicatoria y Agradecimientos............................................................................................ 11 Semblanza...........................................................................................................................13 UNIDAD DE APRENDIZAJE I. DIFERENCIALES, ANTIDERIVADAS E INTEGRAL INDEFINIDA 1.1. Historia y problemas del Cálculo Integral.....................................................................16 1.2. Diferencial de una función............................................................................................18 1.3. Antiderivadas o primitivas de una función....................................................................25 1.4. Integral indefinida.........................................................................................................29 1.5. Aplicaciones de la integral indefinida...........................................................................34 UNIDAD DE APRENDIZAJE II. MÉTODOS Y TÉCNICAS DE INTEGRACIÓN 2.1. Uso de tablas y formularios y propiedades de integración...........................................40 2.2. Métodos de Integración................................................................................................44 2.2.1 Método de sustitución o de cambio de variable..................................................44 2.2.2 Integración por partes.........................................................................................51 2.2.3 Integración por sustitución trigonométrica...........................................................53 2.2.4 Integración por fracciones parciales....................................................................56 2.3. Otras Aplicaciones de la integral indefinida..................................................................62 UNIDAD DE APRENDIZAJE III. CAMBIOS ACUMULADOS E INTEGRAL DEFINIDA 3.1 Cuantificación de cambios acumulados: El problema del área y la distancia..............68 3.2 El área y la Integral definida........................................................................................77 3.3 Teorema fundamental del Cálculo................................................................................85 3.4 Aplicaciones de la integral definida al cálculo de áreas...............................................87 UNIDAD DE APRENDIZAJE IV. APLICACIONES DE LA INTEGRAL 4.1 Introducción................................................................................................................100 4.2 Volumen de sólidos de revolución (método del disco)...............................................100 4.3 Longitud de un segmento de curva............................................................................103 4.4 Otras aplicaciones (basadas en proyectos)..............................................................106 Bibliografía para el estudiante y el profesor.......................................................... 109 ÍNDICE GENERAL:
- 8. 8 dgep-uas
- 9. arturo ylé martínez dgep-uas 9 cálculo integral L a asignatura de Cálculo Integral, forma parte de los estudios de matemáticas del bachillerato de la uas. Actualmente se estudia en el sexto semestre del tercer año del plan 2009. Su estudio es sumamente formativo para el estu- diante, ya que paralelamente al estudio de nuevos conocimientos e ideas en ella, también se reafirman e integran los conocimientos y competencias de toda el área de matemáticas. El Cálculo Integral es, pues, la oportunidad para que el alumno sistematice los estu- dios matemáticos elementales y continúe desarrollando las competencias disciplinares de matemáticas, a la vez que le abre la puerta de entrada para cursos superiores de matemáticas que les serán necesarios en una profesión futura. Considerando que el bachillerato universitario tiene carácter propedéutico, el conte- nido tratado en este texto es de nivel introductorio y elemental, y se desarrolla didáctica- mente de manera intuitiva e informal, enfatizando en aplicaciones sencillas. Así, pues, los autores hemos dejado, deliberadamente, para los niveles de licenciatura la formaliza- ción rigurosa, tan necesaria para la ciencia matemática pero difícil y carente de interés, en la mayoría de los casos, para los estudiantes de la preparatoria. En esta segunda edición, aunque se hicieron algunos agregados y correcciones, la estructura básica del texto se conserva. De donde, en la primera unidad se estudian los diferenciales, la antiderivada y la integral indefinida y el objetivo de la misma es que el estudiante calcule diferenciales, antiderivadas e integrales indefinidas inmediatas, y las aplique en la formulación y resolución de problemas de su vida cotidiana, y de algu- nas áreas de las ingenierías y las ciencias. En esta unidad la integral es tratada, por razones didácticas, a partir del concepto de antiderivada o primitiva de una función. En la segunda unidad de aprendizaje, se estudian los métodos y técnicas de in- tegración básicos. Tales como: el cambio de variable, la integración por partes, la sus- titución trigonométrica y la descomposición en fracciones parciales. El objetivo de la unidad es que los estudiantes demuestren algunas formulas básicas de integración y las apliquen reflexivamente al calculo de integrales indefinidas usando diversos métodos y técnicas de integración. En la tercera unidad de aprendizaje se estudian los cambios acumulados y la in- tegral definida en el marco geométrico del problema del cálculo de áreas. Además, se estudia también el importante Teorema Fundamental del Cálculo como la manera más optima para el cálculo de las integrales definidas y para establecer la relación formal entre el Cálculo Diferencial y el Cálculo Integral. El objetivo de esta unidad es que los PRESENTACIÓN
- 10. unidad Icálculo integral 10 dgep-uas estudiantes calculen numéricamente y mediante el teorema fundamental del cálculo las integrales definidas, y las apliquen principalmente en el cálculo de áreas. Finalmente, en la cuarta y última unidad de aprendizaje, se estudian algunas aplica- ciones de la integral de una función. En particular es obligatorio estudiar aplicaciones respecto al cálculo de volúmenes de sólidos de revolución por el método de discos, así como el cálculo de longitudes de segmentos de curvas. Por otra parte, aquí también se estudiaran otras aplicaciones, en base a proyectos, pero de acuerdo a los intereses específicos de los estudiantes. El objetivo de la unidad es que los estudiantes apliquen el Cálculo Integral en la modelación, formulación y resolución de problemas en diversos contextos, y hagan una evaluación crítica y reflexiva de los resultados. Sugerimos a los profesores, y estudiantes, de Cálculo Integral del bachillerato, que usen este material como lo que es: un material didáctico de apoyo. Ningún texto, por sí solo, resuelve los problemas que conlleva el proceso de enseñanza/aprendizaje del Cál- culo Integral. Por lo cual, el maestro deberá aplicar toda su experiencia y competencias docentes para el uso planificado, crítico y selectivo del texto, mientras que el estudiante deberá desarrollar, con disciplina y con la guía del profesor, su mayor esfuerzo para su comprensión. Finalmente les deseamos respectivamente a los alumnos y profesores mucho éxito en el aprendizaje y enseñanza del Cálculo Integral y esperamos que este libro les ayude en esta empresa académica. Teniendo siempre presente que el aprendizaje significativo se logra cuando la bibliografía se transforma en biografía, y que el mejor camino para ello es la formulación y resolución de problemas matemáticos contextualizados. Estimables lectores, aunque en esta segunda edición se han corregido la mayoria de los errores aparecidos en la primera edición, sin embargo, como toda obra humana el texto sigue siendo suceptible de errores, por lo cual esperamos seguir contando con tu amable y comprometida colaboración para continuar mejorando este texto en ediciones futuras, por lo cual les agradecemos de antemano que nos hagan llegar, a la Academia de Matemáticas de la DGEP-UAS (o la dirección electrónica ylemar@uas.edu.mx, todos los errores que detecten al momento de su lectura, así como sus criticas y sugerencias para mejorarlo conjuntamente con ustedes. Muchas gracias. ATENTAMENTE : LOS AUTORES Culiacán Rosales, Sinaloa, Diciembre de 2012.
- 11. arturo ylé martínez dgep-uas 11 cálculo integral DEDICATORIA Y AGRADECIMIENTOS: D edicamos este libro a todos los estudiantes, maestros y maestras que ha- cen y han hecho, el esfuerzo cotidiano por mejorar la calidad de la educa- ción en general, y del aprendizaje y la enseñanza de las matemáticas en particular, en las aulas del bachillerato. En especial a las maestras Laura Olivia Castellanos Pimentel, Laura Victoria López Peraza, Consuelo Dominguez García y Marina Collazo Bazán y a los maestros Roberto Martínez Huerta, Benjamín Osuna Hernández, Bernardo Félix Cervantes, Ernesto Raul Cota Echave, Francisco Guadalupe Aguilar Camarena, José Luis Díaz Aguilera,Baltazar Perez Cervantes, Gilberto Gil Osuna, Héctor Benjamín Jacobo Cabanillas, Juan Bosco Higuera López y Octavio Avilez. Y, particularmente, a nuestras familias, amigos y amigas, que nos brindan el marco afectivo de apoyo tan necesario para continuar con nuestra ardua tarea docente. Agradecemos también a los directivos de la Dirección General de Escuelas Prepara- torias (DGEP) de la Universidad Autónoma de Sinaloa las facilidades para la elaboración y publicación de esta obra. En particular agradecemos al Dr. Armando Florez Arco por su paciente y experta revisión técnica del texto. Esta edición del libro se ha realizado en los talleres gráficos de Once Ríos Editores, los lectores podrán apreciar la calidad del trabajo que evidencia su profesionalismo, lo que nos produce gran satisfacción, por tal motivo les expresamos nuestro reconocimien- to y felicitación.
- 12. unidad Icálculo integral 12 dgep-uas
- 13. arturo ylé martínez dgep-uas 13 cálculo integral SEMBLANZA Nombre: Arturo Ylé Martínez Estudios realizados: Licenciatura, Especialidad y Maestría en Enseñanza de las Matemáticas, Maestría y Doctorado en Ciencias de la Educación. Puesto y centro de trabajo: Profesor e Investigador de tiempo completo en la Coordinación estatal del área de matemáticas en la Dirección General de Escuelas Preparatorias (DGEP-UAS), y maestro de asignatura en las materias de Cálculo I y II en la Unidad Académica Esc. Preparatoria Emiliano Zapata de la Universidad Au- tónoma de Sinaloa.
- 14. unidad Icálculo integral 14 dgep-uas
- 15. dgep-uas 15 UNIDAD DE APRENDIZAJE I DIFERENCIALES, ANTIDERIVADAS E INTEGRAL INDEFINIDA Competencia de unidad: Calcula diferenciales, antiderivadas e integrales in- definidas inmediatas, y las aplica en la formulación y resolución de problemas de su vida cotidiana, y de algunas áreas de las ingenierías y las ciencias. COMPETENCIAS DISCIPLINARES A DESARROLLAR 1.- Construye e interpreta modelos matemáticos mediante la aplicación de procedimien- tos y operaciones aritméticas, algebraicas, geométricas y variacionales, para la com- prensión y análisis de situaciones reales, hipotéticas o formales. 2.- Formula y resuelve problemas matemáticos, aplicando diferentes enfoques. 3.- Explica e interpreta los resultados obtenidos mediante procedimientos matemáticos y los contrasta con modelos establecidos o situaciones reales. 4.- Argumenta y comunica la solución obtenida de un problema, con métodos numéri- cos, gráficos, analíticos y variacionales, mediante el lenguaje verbal, matemático y el uso de las tecnologías de la información y la comunicación. 5.- Analiza las relaciones entre dos o más variables de un proceso social o natural para determinar o estimar su comportamiento. 8.- Interpreta tablas, gráficas, mapas, diagramas y textos con símbolos matemáticos y científicos. CONTENIDO TEMÁTICO: 1.1 Historia y problemas del Cálculo Integral 1.2. Diferencial de una función: Definición; interpretación geométrica y aplicaciones. 1.3. Antiderivadas o primitivas de una función: Concepto y definición de antideriva- das o primitivas de una función; propiedades de la primitiva de una función; primiti- vas inmediatas; la integral como operación inversa de la derivada. 1.4. Integral indefinida: Concepto, definición, notaciones, interpretaciones y propieda- des de la integral indefinida. 1.5. Aplicaciones de la integral indefinida: Resolución de una ecuación diferencial de variables separables; Resolución de problemas de física, química, biología y econo- mía con condiciones iniciales.
- 16. unidad Icálculo integral 16 dgep-uas Unidad de aprendizaje I Diferenciales, antiderivadas e integral indefinida Actividades de aprendizaje #1: 1) Responde a la siguiente cuestión: ¿Qué es el Cálculo integral? 2) Investiga sobre los antecedentes históricos del Cálculo Integral y repórtaselo a tu profesor(a) en un trabajo escrito bien presentado de 3 a 6 cuartillas en hoja tamaño carta. Posteriormente, socializa y comunica en una exposición de clase los resultados encontrados. 1.1 Historia y problemas del Cálculo Integral Como complemento de lo que has aprendido en el curso de Cálculo I sobre el cál- culo diferencial (y las derivadas), en esta unidad estudiarás las integrales y el cálculo integral. Estos nuevos conocimientos están muy asociados a problemas que han sido muy importantes para el hombre desde la antigüedad, como son: ◆ El cálculo de las longitudes de “segmentos” no rectilíneos. ◆ El cálculo de áreas y de volúmenes de figuras como las siguientes y para las cua- les no se conocen fórmulas. Haciendo un poco de historia, ya desde el siglo V antes de nuestra era, el filósofo y matemático griego Demócrito de Abdera (460a.C.-370a.C.) calculó longitudes, áreas y volúmenes considerándolos formados por un gran número de secciones de grosor infini- tesimal (infinitamente pequeño). Así, por ejemplo, el volumen de un sólido era la suma de los volúmenes de las secciones (o átomos indivisibles) que componían al sólido. y = f (x) x = a x = b
- 17. arturo ylé martínez dgep-uas 17 cálculo integral Tres siglos más tarde, Arquímedes de Siracusa, (287-212 a.C.), notable matemático e inventor griego que escribió importantes obras sobre geometría plana y del espacio, aritmética y mecánica, utilizó un método denominado de agotamiento o exhaución, para encontrar el área de un círculo con la exactitud requerida mediante el uso de polí- gonos inscritos. En el siglo XVII, el matemático italiano Francesco B. Cavalieri (1598-1647), regresa a las ideas de Demócrito y en 1635 publica un tratado en el que describe su método de los indivisibles, y encuentra formas equivalentes a las actuales para calcular algunas integrales, algunas de las cuales las aprenderás a calcular en este curso. De igual modo determinó el área de un seg- mento de parábola utilizando el método antes mencionado, y demostró que era 4/3 del área del triángulo que tiene igual altura que el seg- mento parabólico. (Figura 1.1). Figura 1.1
- 18. unidad Icálculo integral 18 dgep-uas Estimulados por las ideas de Cavalieri, los matemáticos franceses Descartes (1596-1650) y Pierre de Fermat (1601-1665) utilizaron el álgebra para encontrar el área y las tangentes (integración y diferenciación en términos modernos). Posteriormente en el 1670 el matemático alemán Gottfried W. Leibniz (1646-1716) demostró que la derivación y la integración son inversas, lo que se conoce como teo- rema fundamental del cálculo y que también estudiarás en este curso. Es precisamente Leibniz quien por primera vez hizo uso del actual signo de integral. El la denotó por una S alargada que se escribe , y la deriva de la primera letra de la palabra latina Summa que indicaba la suma de los indivisibles de Cavalieri. 1.2 Diferencial de una función Hasta ahora, hemos representado la derivada de y = f (x) por las notaciones Fermat, al igual que el teólogo y matemático inglés Isaac Barrow (1630-1677) tenían la certeza de que ambos cálculos, o sea el cál- culo diferencial y el integral estaban rela- cionados. No obstante, no es hasta el 1660 que el matemático y físico inglés Isaac Newton (1642-1727), calcula por primera vez un área mediante el proceso inverso de lo que conoces como derivación. En el caso de Fermat se destaca el hecho de que consideró el intervalo de área bajo una curva para formar rectángulos circunscritos como los de la fi- gura 1.2. Suma después las áreas de estos rec- tángulos, que considera cada vez más pequeños, y obtiene de este modo el área bajo la curva. ƒ'(x) = f (x) = d dx dy dx Figura 1.2
- 19. arturo ylé martínez dgep-uas 19 cálculo integral En donde el símbolo dx dy , no debe considérese como una fracción ordinaria, dy como numerador y dx como denominador, sino solamente como un símbolo que repre- senta el límite del cociente: Sin embargo, existen muchos problemas, en donde es necesario dar interpretación a dx y dy separadamente. Por ejemplo, hay muchas situaciones, dentro y fuera de las matemáticas, en que necesitamos estimar una diferencia, como en las aproximaciones de valores de funciones, en el cálculo de errores al efectuar mediciones (valor real me- nos valor aproximado) o simplemente al calcular variaciones de la variable dependiente cuando la variable independiente varía “un poco”, etc. Utilizando a la recta tangente como la mejor aproximación lineal a la función en las cercanías del punto de tangencia P (x₀ , f (x₀)), aproximaremos esta diferencia Δy con la diferencia dy sobre la recta tangente, a la que llamaremos el diferencial de la función en el punto. (Ver figura 1.3) Como se observa en la figura 1.3, Δy representa el cambio en la altura de la curva y= f (x) en tanto que dy representa la variación en la variable independiente (y) a lo largo de la recta tangente T cuando x varía en una cantidad Δx = dx. Así, para funciones de una variable y = f (x), se definen respectivamente los incre- mentos de las variables independiente (x) y dependiente (y) como y las diferenciales de las variables como: ƒ'(x) = = lim = lim dx dy Δy Δx ƒ(x+Δx)-ƒ(x) ΔxΔx →0 Δx →0 De la figura se observa que la ecuación de la recta tangente a la curva de la función en P (x₀ , f (x₀)) es: de donde: Mientras que: y - f (x₀) = f ' (x₀) (x - x₀) dy = f '(x₀) (x - x₀) = f '(x₀) Δx = f ' (x₀) dx Δy = f (x₀ + Δx) - f (x₀) Δx = x - x₀ Δy = f (x₀ + Δx) - f (x₀) dx = Δx ; dy = f ' (x₀) . dx f (x0 +∆x) x0 x0 +∆x=x ∆x ∆y T dy f (x0 ) Figura 1.3
- 20. unidad Icálculo integral 20 dgep-uas Ejemplos: El diferencial de Si α es el ángulo que forma la tangente con el eje X, se observa de la figura anterior que: A la expresión dy = f ' (x)· Δx = f '(x) · dx se le denomina diferencial de y = f (x) en el punto P (x, f (x)), y se simboliza también por d f (x). Propiedades de la diferencial P1: La diferencial de una función en un punto depende de dos variables: de la abs- cisa x del punto elegido y del incremento Δx de x. P2: Al ser dy = f ' (x)· Δx = f '(x) · dx, el diferencial de una función en un punto es el incremento (aumento) de la ordenada de la tangente al aumentar en Δx la abscisa x de dicho punto. P3: Cuando Δx→0, como Δx= dx, se tiene que: y = 3x2 - 7x + 2, es: dy = (6x - 7) . dx(a) y = sen(3x2 - 7) es: dy = 6x . cos (3x2 -7) dx(b) y = xe3x , es: dy = (e3x + 3xe3x ) dx(c) d (ln (4x5 + x -8))=(d) 20x4 + 1 4x5 + x - 8 dx Otra manera de plantear y compren- der lo anterior, es la siguiente: Sea una función y = f (x), y dado un punto de abscisa x, se le suma un peque- ño incremento (aumento) Δx y se en- cuentra un punto de abscisa x+Δx. Se traza la tangente a la curva en el punto de abscisa x, y desde x+Δx se levanta una paralela al eje de ordena- das hasta cortar a la curva y a la recta tangente. tan α = f '(x) = dy Δx dy = f '(x)· Δx= f '(x) · dx dy= lim . dx ≈ f (x + ∆x) - f (x) = ∆y f (x+Δx)-f (x) Δx →0 Δx y = f (x) α Recta tangente al punto (x, y) (Δx → 0) dx ∆y dyCurva de f (x) x x + Δx Y X
- 21. arturo ylé martínez dgep-uas 21 cálculo integral O sea, cuando Δx→0 el diferencial dy se puede usar para calcular el incremento de la variable independiente, con la seguridad de que el error cometido será mínimo. Problemas y ejercicios de cálculos aproximados utilizando la diferencial: 1. Un móvil se mueve según la relación s= 5t2 + t, donde s representa el espacio recorrido medido en metros y t el tiempo medido en segundos. Calcular Δs los metros que recorre el móvil en el tiempo comprendido entre 7 segundos y 7 + 1/3 segundos. A) Resolución usando el diferencial ds: Diferenciando la expresión s= 5t2 + t ds= (10t +1) ∙ dt , Por otro lado, Δt = dt = (7 + 1/3) - 7 = 1/3. Sustituyendo en la expresión de ds : ds = (10 x 7 + 1) . - = 23.66 metros1 3 : B) Resolución usando el incremento Δs: Como se observa se ha cometido un error de: _________cm. ¿Por qué? 2. Calcular de manera aproximada el valor de 3.052 . Resolución usando el diferencial dy: Para encontrar un resultado aproximado de 3.052 se considera la función y = x2 , cuyo diferencial es: dy = 2x · dx. Por la proximidad de 3.05 a 3 (5 centésimas) se calculará la diferencial en el punto de abscisa x=3 y se llevará a la expresión del diferencial dy. En este caso: dx = 3.05 – 3 = 0.05 dy = 2(3)(.05) = 0.30 Por tanto, ya que: Δs= 5 7 + - + 7 + - - [5 (7)2 + 7]= 24.22 metros 1 3[ 2 1 3 [ dy ≈ f (x + ∆x) - f (x) = ∆y f (x + ∆x) = f (x) + ∆y ≈ f (x) + dy .·. 3.052 = f (x + ∆x) = f (x) + dy = x2 + dy = 32 + 0.30 = 9.30
- 22. unidad Icálculo integral 22 dgep-uas Si se calcula con exactitud el valor de 3.052 se obtiene: (3 + 0.05)2 =32 + 2 (3) (0.05) + (0.05)2 = 9 + 0.30 + .0025 = 9. 3025 Se observa que se ha cometido un error de 25 diezmilésimas. En este caso podemos considerar que el cálculo aproximado efectuado con el diferen- cial dy es bastante “bueno”, ¿por qué? 3. Calcula el valor aproximado de 124.7 Resolución usando el diferencial dy: Sea la función . Por tanto: 4. La pared lateral de un depósito cilíndrico de radio 60 cm y altura 1m, debe reves- tirse con una capa de concreto de 2 cm de espesor. ¿Cuál es aproximadamente la cantidad de concreto que se requiere? Como: h = 1m = 100 cm, entonces, V (r) =100 cm π r2 . Por lo tanto: dV =200 πr dr. Si sustituimos r = 60 y dr = 2, en dV, obtenemos: dV =200 πr dr = 200 (3.1416)(60)(2) = 75394. 4 cm3 ≈ ∆V Resolución: La cantidad de concreto requerida es la diferencia ∆V entre el volumen del cilindro exte- rior y el cilindro interior como lo podemos observar en la figura de la derecha. Como la fórmula para calcular el volumen del cilindro es V = π r2 h, calcu- laremos ∆V a través del diferencial dV. f (124.7) = f (125 + (–0.3)) = f (x + ∆x) = 124.7 ≈ f (x) + dy de donde: x =125 ; ∆x = dx = −0.3 ; dy = f '(x) ∙ dx = - x dx = = sustituyendo en: f (x + ∆x) = ≈ f (x) + dy = + = 5 + = 4.996 se determina que: ≈ 4.996 3 1 3 -2 dx 124.73 1253 −0.3 ( 1253 3 )2 −0.3 75 124.73 3 f (x) = x3 3 dx ( x23 3 ) ( x3 3 )2
- 23. arturo ylé martínez dgep-uas 23 cálculo integral Lo que representa la cantidad de concreto que se necesita para revestir el depósito ci- líndrico. 5. Una persona tiene un tumor de forma esférica. Calcula el incremento aproxima- do del volumen del tumor cuando el radio aumenta de 3 a 3.1 cm. Resolución: Como el volumen de una esfera se calcula con la fórmula V = — πr3 4 3 , en- tonces: ∆V ≈ dV = V'(r) . dr = 4πr2 dr= 4 (3.1416)(3)2 (0.1) = 11.3 cm3 Actividades de aprendizaje #2: 1. Completa la siguiente tabla considerando la función f (x) = 3x2 : ¿Cómo varia ε a medida que ∆x→ 0 ? ¿Por qué? 2. Calcula el diferencial dy = f '(x) · dx de las siguientes funciones: x ∆x ∆y = f (x + ∆x) - f (x) dy= f ' (x) dx ε = | ∆y - dy | 5 1.0 5 0.5 5 0.3 5 0.1 5 0.01 5 0.001 y = — + x21 x 3 b) y = x 2 + x( (c) y = 0.8 x5 - 3 x + 5a) y = x 4 1+ x( (d) e) f) g) h) i) y = — x - — x + x0 j) 3 33 5 2 7 y = 9x2 - tan x + 4k) y =— 16 - x2 l) 5 4 y = 55x x4 - 2m) f (x) =n) 1 - 2x 5 + 6x y = x + x x y = 3 x + 3 2x - 1 y = 1- x x y = 5 x2 - 1 3x2 + 5x-1 y = 2 x2 - 1 sen 5x3 +3 x
- 24. unidad Icálculo integral 24 dgep-uas 3. De la función f (x) = 3x2 - 3x + 6, determina en el intervalo desde x=5 hasta x=5.8: (a) el incremento y el diferencial de x. (b) el incremento y el diferencial de y = f (x). (c) La diferencia ε = | ∆y - dy |. 4. Un móvil se mueve según la relación s= 6t2 + 2t +1, donde s representa el espacio recorrido medido en metros y t el tiempo medido en segundos. Calcula, usando Δs y ds, los metros que recorre el móvil en el tiempo comprendido entre 5 y 5.09 segundos. Y determina el error cometido al usar ds. 5. Calcula de manera aproximada el valor de 12.083 . Determina la magnitud del error respecto al cálculo directo. 6. Calcula el valor aproximado de 49.15 7. Calcula el incremento aproximado del área de un cuadrado de lado de 4 m, si éste recibe un aumento en sus lados de 10 cm. 8. La pared lateral de un depósito cilíndrico de radio 80 cm y altura 1.5 m, debe revestirse con una capa de concreto de 2.5 cm de espesor. ¿Cuál es aproxima- damente la cantidad de concreto que se requiere? 9. Una persona tiene un tumor de forma esférica. Calcula la variación aproximada del volumen del tumor cuando el radio disminuye de 3 a 2.5 cm. 10. El volumen de un cascaron esférico es el incremento del volumen de una esfera al variar su radio. Calcula el volumen de un cascaron esférico de una esfera cuyo radio interior es de 10 cm y cuyo espesor es de 0.5 cm. 11. Suponiendo que u y v son funciones derivables de x, y considerando que por definición du = u'dx y dv = v' dx, demostrar, en equipo de 3 a 5 integrantes, las siguientes fórmulas de diferenciales, y comunicar los procesos de resolución en una exposición de clase: y = cos 2x-—x3 o) 2 1 3 p) y = −10e4x (cos x2 -3) q) y =20ex (e-2x + x )3 y =r) cos 1- x( ( sen ex + 1( ( s) y=5 csc x2 ·ctg x t) y =2 3x2 - 2x3 + 5 u) 1 - 2x 5 + 6x y = tan v) y= csc x +csc 5x2 4 5 y = ln sen x - 1(x) ( 2 y = + 0.25e4xw) ln x8 8 y = e3x + log x- e3x - log x(y) (( ( z) 9x + ln x x y = 3 d(ku) = k du ; k es una constante d (u ± v) =du ± dv d(u·v) = u · dv + v · du d (cos u) = – sen u · du d(un ) = nun-1 · du d (sen u) = cos u · du d (tan u) = sec2 u · duu v v· du- u· dv v2d =
- 25. arturo ylé martínez dgep-uas 25 cálculo integral 1.3 Antiderivadas o primitivas de una función Del curso anterior de Cálculo Diferencial sabes que dada la función f (x) = x3 , la pri- mera derivada de esa función es f '(x) = 3x2 . Esta operación de calcular la derivada de una función dada se llama derivación. ¿Mediante qué operación se podrá obtener x3 de 3x2 ? ¿Existirá también una opera- ción inversa para la derivación? ¿De qué función resulta la función derivada f '(x) =5x4 ? Como has visto en las referencias históricas, sí existe una operación inversa para la derivación, que en esta unidad vas a aprender, y a la que se denominará integración. Así pues el problema de la integración como operación inversa de la derivación está íntimamente ligado al problema de encontrar una función desconocida F conocida su derivada. A esta nueva función se le denomina antiderivada o primitiva de la función dada. Sea f (x) definida sobre un intervalo I. La función F definida sobre I es una antiderivada o función primitiva de f si F ' (x) = f (x), para cada x ∈ I. Ejemplo: F (x) = x3 es una antiderivada o primitiva de la función f (x) = 3x2 porque F '(x) = (x3 )= 3x2 para todo x ∈(–∞, ∞). Ejemplos resueltos: a) F (x) = — x31 3 es una antiderivada o primitiva de la función f (x) = x2 en (–∞, ∞), puesto que ' F '(x) = — x3 =— x2 = x21 3 3 3 para cada x ∈ ℜ. b) La función 1 3F (x) = - x3 + 5 es también una antiderivada o primitiva de la función f (x) = x2 en (–∞, ∞), puesto que 1 3 ' F '(x) = — x3 + 5 = x2 que para cada x ∈ ℜ. c) La función F (x) = x es una antiderivada o primitiva de la función 1 2 x f (x) = en (0, ∞), puesto que F ' (x) = x =' 1 2 x( ) . En los incisos a) y b) puedes apreciar que la antiderivada o función primitiva de una función dada no es única, pues se ha obtenido para una misma función dada dos funcio-
- 26. unidad Icálculo integral 26 dgep-uas nes primitivas distintas que solo difieren en una constante. De aquí se infiere el siguiente teorema: Demostración del Teorema 1: (F(x) + c)'= F'(x) + (c)'= f (x)+0 = f (x) Sobre el cálculo de primitivas de una función es importante que conozcas que no siempre es fácil determinar una primitiva de una función dada, no obstante si la función f es continua en el intervalo I, se puede afirmar que la antiderivada o primitiva existe aunque no podamos calcularla. Por lo antes planteado el teorema anterior tiene una gran importancia pues significa que cada función continua en un cierto intervalo dado, tiene infinitas antiderivadas o primitivas. De igual modo se cumple que si F (x) y G (x) son dos antiderivadas de una fun- ción f (x) sobre el intervalo I, entonces F (x) - G (x) = c en I, donde c es una constante. Esta propiedad no será demostrada en este curso, pero sí la vamos a utilizar cuando sea necesario. El recíproco de este teorema también es muy útil en el trabajo con primitivas, pues si dos funciones difieren en una constante entonces son antiderivadas de una misma función, ya que sus derivadas son iguales. En este curso nos limitaremos a determinar antiderivadas o primitivas para funciones elementales estudiadas en cursos anteriores. Para ello es necesario que conozcas algu- nas primitivas que se pueden calcular de manera inmediata como las que aparecen en el recuadro siguiente y que, al igual que hiciste con las reglas de derivación, debes lograr memorizarlas mediante la realización de una cantidad suficiente de ejercicios. Teorema 1. Si F(x) es una antiderivada o función primitiva de y= f (x) so- bre I, entonces F (x) + c es también una primitiva de y= f (x), donde c es un número real cualquiera (constante). Teorema 2. En cada intervalo donde están definidas las funciones y = f (x), una antiderivada o primitiva F de la función: a) f (x) = xn es b) f (x) = sen x es F (x) = - cos x c) f (x) = cos x es F (x) = sen x d) f (x) = ex es F (x) = ex F (x) = si : n ≠ -1 F (x) = ln x si : n = -1 y x > 0 n + 1 1 xn + 1
- 27. arturo ylé martínez dgep-uas 27 cálculo integral Demostración del Teorema 2: a) x n+1 = (n + 1)xn+1-1 = xn n+1n + 1 1 1' Si n = − 1, entonces F(x) = ln x pues = — = x -1(ln x)' 1 x b) (- cos x)' = - (cos x)' = - (-sen x) = sen x c) (sen x)'= cos x d) (ex )'= ex Ejemplos resueltos. Determina todas las antiderivadas o primitivas F de: a) f (x) = x-2 b) f (x) = sen x c) f (x) = ex Resolución: a) Por el teorema 2a, una primitiva de x -2 en cualquier intervalo donde esté definida es: Y como todas las primitivas se obtienen sumando una constante, luego las primitivas de x-2 son: F (x) =– - + c1 x . b) Por el teorema 2b una antiderivada es -cos x, y como todas las primitivas se obtienen sumando una constante, entonces: F (x) = - cos x + c c) Por el teorema 2c una antiderivada es ex , y como todas las primitivas se obtienen sumando una constante, entonces: F (x) = ex + c Actividades de Aprendizaje #3: 1. Determina cuáles de las siguientes funciones son antiderivadas o primitivas de la función f (x) = (x +1)2 en ℜ. a) 1 3 F (x) = — (x+1) + 3 b) 1 3 F (x) = — (x+1)3 + 5 c) F (x) = 3 (x+1)3 +5 d) -2 + 1 1 x-2+1 = - x -1 = - —1 x 1 3 F (x) = — x3 + x2 +x + 1
- 28. unidad Icálculo integral 28 dgep-uas 2. Comprueba en cada caso, si F (x) es una primitiva de f (x) en el intervalo dado. a) F (x) = — sen 3x1 3 , f (x) = cos 3x en ℜ b) F (x) = 2x3 - 8 , f (x) = 6x2 - 8 en ℜ c) F (x) = 3 + cos x , f (x) = – sen x en ℜ d) F (x) = 2x + e3x , f (x) = 2 + 3e3x en ℜ e) F (x) = cos 2x + sen x , f (x) = cos x –2 sen 2x + 3x en ℜ f) , en ℜ+ g) F (x) = lnx2 + ln x + 3 , en ℜ+ 3. Determina una primitiva de las siguientes funciones. a) y= x3 b) y= sen x c) y= x-3 d) y= cos x e) y= x3 + x2 x + 1 f) y= ex g) y= 1 x- , x > 0 h) y= cot x sen x 4. Determina todas las primitivas de las siguientes funciones. a) y= cos x b) y= x-7 c) y= ex d) y= sen x e) y= 3 f) y= e2x + 1 ex + 1 g) y= sen 2x 2 cos x h) y= x2 (x+ 1) - x2 5. Dadas las funciones primitivas de la función f (donde: c es una constante), determina dicha función. a) F (x) = 3x2 + 5x + c b) F (x) = ex + cos x + c c) 1 xF (x) = 3x2 - + c d) e) f) F (x) = ex + ln x - 3x6 + c 1 x f (x) = — 3 xf (x) = — x2 4 3 4 3 F (x) = 5x + - x3 + x4 + c 1 x2F (x) = — x 5 2 xF (x) = 4 sen x - 4 x3 + - + c
- 29. arturo ylé martínez dgep-uas 29 cálculo integral 1.4. Integral indefinida Como ya sabes, el problema de la integración como operación inversa de la deriva- ción está íntimamente ligado al problema de encontrar una antiderivada o función primi- tiva de la función dada, o sea encontrar la función conocida su derivada. Este paso de la función derivada a sus primitivas es una operación llamada integra- ción, que es la inversa de la derivación. Esta operación de integración se denota con el símbolo ∫. Entonces si F es una primitiva de f, o sea F'(x) = f (x), F (x) se denota por ∫ f (x) dx y se le llama integral indefinida. Por eso, al cálculo de primitivas se le llama cálculo de integrales o integración. Las partes que componen el símbolo de la integral indefinida son: En general, si F (x) es una de las antiderivadas o primitivas de f (x), podemos escri- bir ∫ f (x) dx = F ( x) + c, teniendo en cuenta que dos primitivas de una misma función se diferencian en una constante que en este caso la hemos llamado c. Utilizando la simbología establecida y los resultados del teorema 2 del epígrafe 3, podemos resumir en la siguiente tabla las reglas o fórmulas para la integración de algu- nas funciones conocidas y que llamaremos integrales inmediatas. Mientras que otras fórmulas que aparecen en la tabla se infieren lógicamente de las fórmulas de derivación, y pueden ser demostradas siguiendo las ideas de la demostración del teorema 2. Integral indefinida ∫f (x) dx El símbolo de integral:∫ dx es el diferencial de x, e indica que x es la variable con respecto a la cual f es derivada, y f (x) se llama funcion subintegral f (x) dx es el integrando La expresión ∫ f (x) dx = F (x) + c se llama integral indefinida de f
- 30. unidad Icálculo integral 30 dgep-uas Ejemplos resueltos de cálculo de integrales indefinidas inmediatas: a) Fórmula 2. b) Fórmula 7. c) Fórmula 8. d) Fórmula 11. e) Fórmula 14. 1. ∫ k dx = k x + c 2. ∫ xn dx = + c (n ≠ -1)xn+1 n+1 3. ∫ x-1 dx =∫ dx = ln |x|+ c1 x 4. ∫sen x dx = – cos x + c 5. ∫cos x dx = sen x + c 6. ∫sec2 x dx = tan x + c 7. ∫csc2 x dx = – cot x + c 8. ∫sec x tan x dx = sec x + c 9. ∫csc x cot x dx = –csc x + c 10. ∫ex dx = ex + c 11. ∫ ax dx = + cax ln a 12. ∫ = arc tan + cdx a2 + x2 1 a x a 13. ∫ = arc sen + cdx a2 - x2 x a 14. ∫ = arc sec + cx a dx x x2 - a2 1 a Tabla: Fórmulas de Integrales Indefinidas Inmediatas ∫ x dx = ∫ x dx = + c = x + c 1 2 3 22 31 2 + 1 x +1 1 2 ∫ = ∫ dx = ∫ csc2 dx = − cot x + c dx sen2 x 1 sen2 x ∫ dx = ∫ dx= ∫ dx = ∫ sec x tan x dx = sec x+ csen x cos2 x sen x cos x cos x 1 cos x sen x cos x ∫ 5x dx = + c5x ln 5 ∫ = arc sec + cx 4 dx x x2 -16 1 4
- 31. arturo ylé martínez dgep-uas 31 cálculo integral Como el proceso de calcular integrales o de integración es inverso del de deriva- ción, muchas de sus propiedades se deducen inmediatamente de las propiedades de las derivadas, como veremos a continuación en el siguiente teorema. Demostración del teorema 3: P1) Por definición: Luego: ∫k f (x) dx = k ∫ f (x) dx P2) Por definición: ∫( f (x) + g (x) ) dx = ( f (x) + g (x)) = f (x) + g (x)[ [' ∫( f (x) dx + ∫g (x) dx = ∫ f (x) dx + ∫ g (x) dx = f (x) + g (x)[ [' [ [' [ [' Luego: ∫ ( f (x) + g (x)) dx = ∫ f (x) + ∫ g (x) dx P3) Sea F (x) una primitiva para f (x), entonces: Teorema 3. Si f (x) y g (x) son funciones continúas, se cumplen en la inte- gral definida las siguientes propiedades: P1) Toda constante k que sea factor de la función subintegral puede ponerse como factor fuera del signo de integración: ∫ k f (x) dx = k ∫ f (x) dx P2) La integral de una suma (o resta) es igual a la suma (o resta) de la integral de cada uno de los sumandos: ∫ (f (x) ± g (x)) dx = ∫ f (x) dx ± ∫ g (x) dx P3) Si F(x) es una primitiva para f (x), y a es una constante, entonces: ∫ f (ax + b) dx = — F (ax + b)1 a ∫k f (x) dx = k f (x)[ [' k∫f (x) dx = k ∫ f (x) dx = k f (x)[ [' [ [' y — F (ax + b) = — F (ax + b)[ ['1 a 1 a [ [' = —(ax + b)' F '(ax + b) Aplicando regla de la cadena 1 a = — a F '(ax + b) = f (ax + b)1 a
- 32. unidad Icálculo integral 32 dgep-uas Las igualdades del teorema 3 son igualdades entre primitivas, es decir, significa que ambos miembros de la igualdad tienen la misma derivada. En otras palabras, la igualdad se interpreta en el sentido de que ambos miembros son primitivas de una misma función, es decir, difieren en una constante. Combinando las propiedades de la integral indefinida del teorema 3 con el uso de la tabla de fórmulas de integrales indefinidas inmediatas vista anteriormente, se pueden calcular integrales indefinidas un poco más complicadas como se muestra en los siguien- tes ejemplos resueltos: P1 del teorema 3. b) P2 del teorema 3. c) d) P2 y P3 del teorema 3. e) P3 del teorema 3. f) g) Actividades de Aprendizaje #4: 1. Calcula las siguientes integrales indefinidas. a) ∫ x6 dx b) ∫ 4x3 dx c) ∫ x-3 dx ; (x ≠ 0 ) d) e) ∫6 sen x dx f) ∫(sen x + cos x) dx g) ∫ 3x-1 dx ;(x > 0) h) ∫ (3x2 - 4x + 7) dx i) ∫ (ex + 6) dx j) ∫ x dx 1 3 a) ∫3x2 dx = 3∫ x2 dx =3 + c = x3 + cx2+1 3 ∫(x2 + x + 1) dx =∫x2 dx+∫x dx +∫dx = —x3 + — x2 + x + c1 3 1 2 ∫(3x-2 + 2 sen x) dx =∫3x-2 dx+∫2 sen x dx = 3∫x-2 dx + 2∫sen x dx = 3 ( —x-1 )+ 2(−cos x) + c =−3 x-1 − 2 cos x + c1 -1 ∫(x2 + e2x ) dx = —x3 +—e2x + c1 3 1 2 ∫10 sen (3x+1)dx = - — cos (3x + 1)+ c10 3 ∫ (2x + 1) dx = ∫(2x + 1) dx = — ∙ — (2x + 1) + c )= — (2x + 1) + c1 2 2 3 1 2 3 2 1 3 3 2 ∫ e2x -- + dx = ∫e2x dx -4∫— dx + 3 ∫ dx = — e2x - 4 ln x + arc tan - + cx 3 1 x9 + x2 3 9 + x2 1 1 2 4 x 1 x∫ (6x2 + x + — ) dx (x > 0)
- 33. arturo ylé martínez dgep-uas 33 cálculo integral k) ∫ (2x + ex ) dx l) ∫ (6x2 + 8x - sen x) dx m) ∫ x (2x + 1) dx n) ∫ (x - 5)2 dx ñ) ∫ x (1- x2 ) dx o) p) ∫ dxx2 + 6x + 5 2 q) r) s) ∫(ex + tan x cos x) dx t) ∫(sen2 x + sen x + cos2 x) dx w) ∫e-2x (e2x - e-2x ) dx 2. Calcula las siguientes integrales indefinidas: a) ∫ (3x - 1)2 dx b) ∫ sen 3x dx c) ∫ ( e5x + sen 6x) dx d) e) ∫ cos (2x + 1) dx f) 3. Escribe en cada caso, dos antiderivadas o primitivas de. a) ∫ -3 dx b) ∫ 4x dx c) d) e) ∫5a2 x3 dx f) ∫ (6x2 + 8x + 3) dx g) ∫ x (x + 3) dx h) ∫ (x + 2) (x + 5) dx i) ∫ (a + bx2 )2 dx j) k) l) ∫(cos 2x + sen 3x) dx m) n) ∫ dxx2 -49 x + 7 ñ) ∫(5e-3x + sen x) dx o) ∫ dx (x > 0)x6 + 3x5 - 6x + 1 x2 ∫ dx (x >- -)3 22x + 3 1 3 ∫ x dx ∫ e-4x + (2x - 1)3 dx[ [ ∫ - x2 dx1 3 ∫- dx1 x3 ∫ x (1-x2 ) dx ∫ (x3 + x-2 + - + x5 ) dx1 5 3 ∫ dt5t2 - 3t t ∫ dx4 sen 2x cos x ∫ dxsen2 x + cos2 x x
- 34. unidad Icálculo integral 34 dgep-uas 4. Sin integrar, comprueba si son válidos los siguientes resultados. a) b) c) d) e) f) g) h) 1.5. Aplicaciones de la integral indefinida En la resolución de muchos problemas de la ingeniería y las ciencias, tales como física, química, biología, economía y por supuesto de matemáticas, se hace necesario determinar una antiderivada o función primitiva particular que cumpla con ciertas condi- ciones iniciales, lo cual es equivalente a calcular un valor particular de la constante de integración c de una familia, o conjunto, de antiderivadas. Ejemplo (1): Determinar una función y = f (x) cuya derivada sea f '(x) = 2x y que f (3) = 6. Resolución: con lo estudiado hasta aquí se sabe que con la integral indefinida podemos determinar dicha función primitiva y = f (x). Ya que: ∫2x dx = 2∫ x dx = + c = x2 + c.2x2 2 Entonces, la antiderivada o función primitiva general (o integral indefinida) de f ' (x) = 2x es : y = f (x) = F(x)= x2 + c. Y en consecuencia: f (3)= F (3)=32 + c = 6 ⇒ c = -3 ∴ y = f (x) = x2 -3 ∫(x3 -sen x) dx = - x4 - cos x + c1 4 ∫ x dx= — x3/2 + c3 2 3 ∫sen ax cos ax dx = + csen 2ax 2a ∫ =- + cdx x3 1 2x2 ∫( x x -2 x )dx = - + c1 2 x5/2 5 4x3/2 3 ∫ = - ln (e2x + 1) + c1 2 e2x dx e2x + 1 ∫ dx =ln (1- cos x) + csen x 1- cos x ∫ dx = - - x + ln (x + 1) + cx2 2 x2 + 2 x + 1
- 35. arturo ylé martínez dgep-uas 35 cálculo integral En la figura 1.4 de abajo se puede observar que para cada valor particular de la constante de integración se obtiene una antiderivada particular, por lo cual se dice que F(x)=x2 +c define una familia de antiderivadas o curvas particulares. Así, podemos afirmar que la parábola con vértice en el origen y = x2 , resulta de la primitiva general F(x)=x2 +c para el caso en que c = 0. En el proceso de resolución anterior se determinó la función primitiva particular y = x2 - 3 a partir de conocer ciertas condiciones iniciales de la misma, tales como: f '(x) =2x y f (3)=6. Ahora bien si aplicamos el concepto de diferencial, entonces este proceso de resolu- ción puede desarrollarse y ser interpretado también de la siguiente manera: Donde: la expresión dy dx = 2x se denomina ecuación diferencial, cuya solución ge- neral es precisamente la función y = x2 + c, tal que, f '(x)=2x. En general, una ecuación diferencial es una ecuación que contiene derivadas o diferenciales, y su solución es una función primitiva cuyas derivadas o diferenciales son F (x) = x2 + -3 2 F (x) = x2 F (x) = x2 -3 - 3 - 6 Figura 1.4 -3 -2 -1 1 2 3 4 5 F (x) = x2 -2π 1 2 3 4 5 6 - 1 - 2 - 4 - 5 y x - 6 - 3 = f '(x)= 2x ⇒ dy = 2x dx Despejando el diferencial dy ⇒ ∫ dy = ∫ 2x dx ⇒ y = x2 + c integrando de donde: y = 6 = 32 + c ⇒ c = -3 ∴ y = x2 -3 dy dx
- 36. unidad Icálculo integral 36 dgep-uas precisamente los que aparecen en dicha ecuación. Y un problema con valor inicial es un problema donde se debe resolver una ecuación diferencial, sujeta a una condición inicial dada, como la del ejemplo (1). Ejemplo (2): Determina la función y = f (x) tal que f ' (x)= —1 x y f (1) = 2. Resolución: Sabemos de la tabla de integrales indefinidas inmediatas que la primitiva general de f ' (x)= —1 x es: F (x) = ln x + c. Para determinar el valor de c, sustituimos para x = 1 en la primitiva general: F (1)= ln (1) + c = 0 + c = 2, luego c = 2, y f (x) = ln x + 2. Ejemplo (3): Se lanza verticalmente hacia arriba una pelota con una velocidad inicial de 85 m/seg desde una plataforma de 15 m de altura. Calcular la altura a la que se en- cuentra la pelota, con relación al nivel del suelo, después de 4 segundos de haber sido lanzada. Resolución: Si h(t) representa la altura de la pelota a los t seg con relación al nivel del suelo, entonces lo que debemos determinar es h(4), para ello debemos recordar que en este caso la aceleración que experimenta la pelota durante su movimiento es la de la gravedad, por tanto, dado que a (t) = v '(t) = - 9.8 m/ seg2 , entonces: v (t) = ∫ v' (t) dt = ∫-9.8 dt = -9.8t + c Pero, cuando t= 0, la velocidad inicial de la pelota es 85 m/seg, de donde: v (0) = -9.8 (0) + c = 85 ⇒ c = 85 Además, como: h'(t) = v(t) = -9.8 t + 85 ⇒ h(t)= ∫ v(t)dt = ∫(-9.8t + 85)dt = -4.9 t2 + 85t + c Pero, cuando t = 0, la altura de la pelota es la de la plataforma, o sea: h (0) = -4.9 (0)2 + 85 (0) + c = 15 ⇒ c = 15 ∴ h(t) = -4.9t2 + 85 t + 15 Por tanto: h(4) = -4.9 (4)2 + 85 (4) + 15 = 276.6 m.
- 37. arturo ylé martínez dgep-uas 37 cálculo integral Ejemplo (4): A través de una investigación se ha determinado que la población P(t) de una colonia de bacterias, t horas después de iniciar la observación, tiene una razón de cambio de P '(t)= 200 e0.1t + 150 e-0.03t . Si la población era de 200,000 bacterias cuando ini- cio la observación, ¿Cuál será la población 10 horas después? Resolución: para determinar la función de población se resuelve la siguiente ecuación diferencial dP(t) dt = P '(t) ⇒ dP(t)= P '(t) dt ⇒ ∫ dP(t)= ∫ P '(t) dt ⇒ P(t)= ∫(200 e0.1t + 150 e-0.03t ) dt = 2000 e0.1t - 5000 e-0.03t + c Ya que para t = 0, se tiene que P (0) = 200, 000, entonces: P(0) = 2000e0.1(0) - 5000e-0.03(0) + c = 200, 000 ⇒ c = 203, 000 Por lo cual, P(t) = 2000e0.1t - 5000 e-0.03t + 203, 000 Y después de 10 horas, la población de bacterias será de: P(10) = 2000e0.1(10) - 5000e-0.03(10) + 203,000 ≈ 204, 732 Actividades de Aprendizaje #5: 1. Determina la primitiva G de g tal que G ( 0 ) = 1. a) g (x) = x4 b) g (x) = cos x c) g (x) = sen x d) g (x) = ex e) f) g (x) = ex + cos x 2. Determina una primitiva F de f bajo las siguientes condiciones. a) x2 - 1 x + 1 f (x) = + 1 ; c = 0 b) c) d) 1 xg (x) = — e2x - 4 ex + 2 f (x) = + 2 ; c = 0 xe5 + e5 e5f (x) = - 1 ; c = 1 2 3f (x) = (x + 3) (x - 3)+ 9 ; F (2) =
- 38. unidad Icálculo integral 38 dgep-uas 3. Determina una función cuya derivada sea y que f (1) = 8. 4. Determina la función y = f (x) cuya tangente tiene una pendiente de 3x2 + 1 para cada valor de x, y cuya gráfica pasa por el punto P (2,6). 5. Un fabricante estima que el costo marginal por producir x unidades de cierto produc- to es C'(x) = 3x2 -24x+48 pesos por unidad. Si el costo de producción de 10 unidades es de $6000.00, ¿cuál es el costo de producción de 40 unidades? 6. Desde un edificio de 40 m de altura se lanza verticalmente hacia arriba una pelota con una velocidad inicial de 90 m/seg. Calcular: (a) la altura a la que se encuentra la pelota, con relación al nivel del suelo, después de 3 y 6 segundos de haber sido lanzada, y (b) el tiempo que tarda la pelota en llegar al suelo. 7. Un automóvil viaja en línea recta a 90 km/h en el instante en que el conductor se ve forzado a aplicar los frenos para evitar un accidente. Si los frenos proporcionan una desaceleración constante de 20 m/s2 , ¿qué distancia recorre el automóvil antes de detenerse por completo? 8. Un minorista recibe un cargamento de 10 toneladas de arroz que se consumirán en un periodo de 5 meses a una tasa constante de 2 toneladas por mes. Si los costos de almacenamiento son 20 centavos por kilogramo al mes, ¿cuánto pagará el minorista en costos de almacenamiento durante los próximos 5 meses? 9. A través de una investigación se ha determinado que la población de P (t) una co- lonia de bacterias, t horas después de iniciar la observación, tiene una razón de cambio de P '(t) = 300 e 0.2t + 250 e -0.04t . Si la población era de 150,000 bacterias cuando inicio la observación, ¿Cuál será la población 15 horas después? 10. Se ha estimado que dentro de t meses la población de una cierta ciudad cambiará a razón de personas por mes. Si la población actual es 10,000, ¿Cuál será la población dentro de 1 año? 3 4 + 5 t2 2 x2f '(x)= 4x3 - +7
- 39. dgep-uas 39 UNIDAD DE APRENDIZAJE II MÉTODOS Y TÉCNICAS DE INTEGRACIÓN Competencia de unidad: Demuestra las fórmulas básicas de integración y calcula reflexivamente integrales indefinidas mediante la aplicación y análisis de fórmulas y diversos métodos y técnicas de integración. COMPETENCIAS DISCIPLINARES A DESARROLLAR 1.- Construye e interpreta modelos matemáticos mediante la aplicación de procedimien- tos y operaciones aritméticas, algebraicas, geométricas y variacionales, para la com- prensión y análisis de situaciones reales, hipotéticas o formales. 2.- Formula y resuelve problemas matemáticos, aplicando diferentes enfoques. 3.- Explica e interpreta los resultados obtenidos mediante procedimientos matemáticos y los contrasta con modelos establecidos o situaciones reales. 4.- Argumenta y comunica la solución obtenida de un problema, con métodos numéri- cos, gráficos, analíticos y variacionales, mediante el lenguaje verbal, matemático y el uso de las tecnologías de la información y la comunicación. 5.- Analiza las relaciones entre dos o más variables de un proceso social o natural para deter- minar o estimar su comportamiento. 8.- Interpreta tablas, gráficas, mapas, diagramas y textos con símbolos matemáticos y científicos. CONTENIDO TEMÁTICO: 2.1. Uso de tablas y formularios de integración 2.2. Métodos de Integración 2.2.1 por cambio de variable 2.2.2 integración por partes 2.2.3 integración por sustitución trigonométrica 2.2.4 integración por fracciones parciales 2.3. Aplicaciones de la integral indefinida
- 40. unidad IIcálculo integral 40 dgep-uas Unidad de aprendizaje II Métodos y técnicas de integración 2.1. Uso de tablas, formularios y propiedades de integración Combinando la tabla de integrales indefinidas inmediatas con los resultados del teo- rema 3 estudiados en la unidad de aprendizaje 1, y considerando que u = f (x), obtene- mos la siguiente tabla de fórmulas y propiedades de las integrales indefinidas. 1. ∫ k dx= k x + c 2. ∫ xn dx= + c (n≠-1)xn+1 n+1 4. ∫ sen x dx = - cos x + c 3. ∫ x-1 dx=∫ dx= ln |x| + c1 x 5. ∫ cos x dx = sen x + c 6. ∫ sec2 x dx = tan x + c 7. ∫ csc2 x dx = -cot x + c 8. ∫ sec x tan x dx = sec x + c 15. ∫ tan u du = ln |sec u|+ c 16. ∫ cot du = ln |sen u|+ c 17. ∫ sec u du = ln |sec u + tan u|+ c 18. ∫ csc u du = ln |csc u - cot u|+ c 9. ∫ csc x cot x dx = - csc x + c 10. ∫ ex dx = ex + c 11. ∫ ax dx = + cax ln a 12. ∫ = arc tan + cdx a2 + x2 1 a x a 13. ∫ = arc sen + cx a dx a2 -x2 14. ∫ = arc sec + cx a dx x x2 - a2 1 a 29. ∫ au du = + cau ln a 30. ∫ = arc tan + cdu a2 + u2 1 a u a 31. ∫ = arc sen + cu a du a2 -u2 35. ∫ = ln | u+ |+ cdu u2 ±a2 u2 ±a2 1 a 32. ∫ = arc sec + cu a du u u2 - a2 19. ∫ du = u + c 20. ∫ un du= + c (n≠-1)un+1 n+1 22. ∫ sen u du = - cos u + c 23. ∫ cos u du = sen u + c 24. ∫ sec2 u du = tan u + c 25. ∫ csc2 u du = -cot u + c 26. ∫ sec u tan u du = sec u + c 27. ∫ csc u cot u du = - csc u + c 28. ∫ eu du = eu + c 21. ∫ u-1 du=∫ du= ln |u| + c1 u 33. ∫ = ln | |+ cdu u2 - a2 1 2a u-a u+a 34. ∫ = ln | |+ cdu a2 - u2 1 2a a+u a-u
- 41. arturo yle martínez dgep-uas 41 cálculo integral P1: ∫ k f (x) dx = k ∫ f (x) dx ; k es una constante P2: ∫ (f (x) ± g (x)) dx = ∫ f (x) dx ± ∫ g (x) dx P3: ∫ f (ax + b) dx = F (ax + b) + c ; siempre que : F ' (x) = f (x)1 a Las tablas, junto con los métodos y técnicas de integración que se estudiarán en el epígrafe siguiente, servirán para calcular integrales inmediatas y no inmediatas. Todas las fórmulas de la tabla anterior pueden ser demostradas a partir de la definición de antiderivada o función primitiva de la función f (x) que se está integrando. O sea: ∫ f (x) dx = F (x) + c es verdadera, si y solo si, (F (x) + c)' = f (x) Por ejemplo: Las fórmulas 6 y 20 son verdaderas o válidas ya que de las fórmulas de derivación se sabe que si u = u(x), entonces (tan u + c)' = (tan u)' + (c)' = sec2 u . u' De donde: ∫ sec2 u ∙ du = ∫ sec2 u . u' (x) dx = ∫ (tan u +c)' dx = tan u + c Fórmula 24 En particular: (tan x + c)' = (tan x)' + (c)' = sec2 x ∙ (x)' + 0 = sec2 x ∙ (1) = sec2 x De donde: ∫ sec2 x dx= tan x + c Fórmula 6 Actividades de aprendizaje # 6: En los siguientes ejemplos del uso de la tabla y fórmulas de integración haz el es- fuerzo individual y colectivo de comprender y explicar cada uno de los pasos del proceso de resolución de cada una de las integrales resueltas. 1 2 a) ∫(3x2 + x ) dx =∫3x2 dx+∫ x dx=3∫x2 dx+∫x dx = 3 + +c =x3 + x +c2 3 x2+1 2 + 1 x 1 2 +1 1 2 +1 3 2 c) ∫ = ∫ dx =∫ sec2 x dx = tan x + cdx cos 2 x 1 cos 2 x d) ∫ dx = ∫ dx =∫ dx =∫csc x cot x dx = -csc x + ccos x sen2 x 1 · cos x sen x · sen x 1 sen x cos x sen x 5x ln 5 e) ∫(5x + 4ex - 1) dx = ∫ 5x dx + ∫ 4ex dx - ∫ dx = + 4ex - x + c b) ∫ dx = ∫ ( x +2) + dx =∫ x dx +∫ 2 dx + ∫ = x2 + 2x + 3 ln|x-1| + c1 2 x2 + x + 1 x - 1 [ 3 x - 1 [ 3 dx x - 1
- 42. unidad IIcálculo integral 42 dgep-uas 3 x2f) ∫ + 2 sen x dx = ∫ 3x-2 dx + ∫ 2 sen x dx = 3 ∫ x-2 dx + 2 ∫ sen x dx 1 -1 = 3 ∙ x-1 + 2 (-cos x) + c = - 3x-1 - 2 cos x + c g) ∫(x2 + e2x )dx = ∫ x2 dx + ∫ e2x dx = x3 + e2x + c1 3 1 2 h) ∫10 sen (3x +1)dx = 10∫sen (3x + 1)dx =- cos (3x + 1) + c10 3 1 2 i) ∫ (2x +1 dx = ∫(2x + 1) dx = . (2x + 1) + c = (2x + 1) + c1 2 2 3 3 2 1 3 3 2 3 9 + x2 j) ∫ e2x - + = ∫ e2x dx - ∫ dx + ∫ dx = e2x - 4 ln x + arc tan + c4 x 4 x 3 9 + x2 1 2 x 3 k) ∫ =10∫ = arc sec + c = 2 arc sec + c10 dx x x2 - 25 dx x x2 - 25 10 5 x 5 x 5 o) ∫ = ∫ =∫ = ∫dx cos x - 1 (cos x + 1) dx (cos x - 1)(cos x + 1) (cos x + 1) dx cos2 x - 1 (cos x + 1) dx sen2 x 1 sen2 x =∫ dx + ∫ dx =∫ csc x ∙ cot x dx + ∫ csc2 x dx 1 · cos x sen x · sen x = - csc x - cot x + c p) ∫(tan x - sec x)2 dx = ∫(tan2 x - 2 tan x · sec x + sec2 x) dx =∫tan2 x dx - 2 ∫ secx tan x dx + ∫sec2 x dx = ∫(sec2 x - 1)dx - 2 sec x + tan x + c =∫sec2 x dx -∫ dx - 2 sec x + tan x + c = 2 tan x - 2 sec x - x+ c x 2 l ) ∫ =- 2∫ = - 2 ∫ = arc sec + c = - arc sec + c- 2 dx x4 - 4x2 dx x2 (x2 - 4) dx |x| (x2 -4) - 2 2 x 2 x 3m) ∫3(9 - x2 ) dx = ∫ =3 ∫ = 3 arc sen + c3dx 9-x2 -1/2 dx 9-x2 n) ∫ dx = 5∫ = arc tan + c5 5 + x2 dx 5 +x2( )2 5 5 5 x
- 43. arturo yle martínez dgep-uas 43 cálculo integral Actividades de aprendizaje # 7: 1. Comprueba, en equipo de 3 a 5 integrantes como máximo, que son válidas las fór- mulas de integración de la tabla anterior, y comunica tus resultados al resto de los equipos. 2. Aplicando la tabla y fórmulas de integración calcula en equipo de 3 a 5 integrantes las siguientes integrales indefinidas inmediatas, y haz la comprobación del resultado mediante derivación: a) ∫(4x3 + x6 – 0.5x-3 ) dx = b) ∫(6 x2 + x + ) dx =3 x 8 c) ∫(x - 5)2 dx = d) ∫(x- 6)(2x + 1) dx = g) ∫x(1- x2 )dx = j) ∫(ex +4x -e0 ) dx = k) ∫(e4x - 3x) dx = l) ∫(9 x3 - 6 sen x) dx =5 m) ∫(sen 5x + cos x) dx = n) ∫(7 e2x -sen (5x - 2))dx = ñ) ∫(e-3x + tan x cos x) dx = o) ∫e-2x (e2x - e-2x ) dx = p) ∫(sen 2x + cos2 x) dx = q) ∫cos (2x + 1) dx = r) ∫(e5x + sen 6 x2 ) dx = s) ∫[e-4x + ctg (2x - 1)]dx = t) ∫(cos x - 1)2 dx = y) ∫(3 tan2 x + 5 ctg2 x) dx = u) ∫ dx = 2x + 3 1 e) ∫ dx = x x6 + 3x5 - 6x + 1 x) ∫ =sen x + 1 dx v) ∫ = x4 - 36 x2 -9 dx w) ∫ dx = x2 + 3 3 i) ∫ dx = x + 2 2x2 - 3x - 2 f) ∫ dx = 2 (x - 3) x2 - 5x + 6 h) ∫ dx =x + 3 x
- 44. unidad IIcálculo integral 44 dgep-uas 2.2. Métodos de integración En la unidad de aprendizaje anterior, a partir del concepto de antiderivada o de función primitiva y de las fórmulas para calcular derivadas de las funciones elementales se calcularon algunas integrales inmediatas, sin embargo, existen otras integrales que requieren de métodos más sofisticados para poder ser calculadas. En este apartado se estudiarán algunos métodos y técnicas elementales para redu- cir a inmediatas aquellas integrales que no lo sean pero que son posible de ser reduci- das, tales como: integración por sustitución o cambio de variable, integración por partes, integración por sustitución trigonométrica e integración por descomposición en fraccio- nes parciales simples. El objetivo de todos los métodos de integración es transformar una integral dada, no inmediata, en otra, o suma de varias, cuyo cálculo resulte inmediato o más sencillo. 2.2.1. Método de sustitución o de cambio de variable. Para ilustrar la aplicación de este sencillo y potente método de integración analice- mos el siguiente par de integrales indefinidas: ¿Qué fórmula del formulario se aplicó? Ahora analicemos si podemos aplicar la misma fórmula usada en la integral ante- rior para esta otra integral parecida: ¿Es correcto este resultado? Como ya sabes para contestar esta pregunta basta derivar el resultado para obser- var si coincide con el integrando: De donde, se concluye que la fórmula 2 del formulario no puede ser aplicada a la segunda integral, sin embargo, esta integral la podemos resolver aplicando la propiedad 3 del formulario: ∫f (ax+ b) dx = F(ax + b) + c ; siempre que F '(x) = f (x)1 a Así: ∫(5x- 2)3 dx = + c1 5 (5x - 2)4 4 ¡Verifica que este resultado es el correcto! 1) ∫5x3 dx = 5∫x3 dx = 5 + c = x4 + c[x3+1 3+1[ 5 4 2) ∫(5x - 2)3 dx = + c = + c (5x - 2)3+1 3+1 (5x - 2)4 4 + c = (5x-2)'+(c)'=(5x-2)3 (5)+0=5 (5x-2)3 ≠ (5x-2)34(5x - 2)4-1 4 (5x - 2)4 4[ '[
- 45. arturo yle martínez dgep-uas 45 cálculo integral La propiedad 3 del formulario puede ser vista como un caso particular del método de cambio de variable o de sustitución que explicamos a continuación. Para ello regresemos de nuevo a la integral: ∫(5x- 2)3 dx Como ya sabemos esta integral no puede ser resuelta con la fórmula 2, sin embargo sí se puede resolver aplicando la fórmula 16 del formulario: ∫un du = + c (n ≠ -1)un+1 n + 1 Para ello, consideremos el siguiente cambio de variable: De donde, sustituyendo estos resultados en la integral, se obtiene que: ∫(5x- 2)3 dx = ∫u3 · du = ∫u3 ∙ du = + c = · + c = (5x - 2)4 + c1 55 u3+1 3+1[ [ 1 5 u4 4 1 20 1 5 Este resultado final, como era de esperarse, coincide con el ya obtenido aplicando la propiedad 3 del formulario. La ventaja del método de cambio de variable sobre la propiedad 3 del formulario se puede apreciar al intentar resolver la siguiente integral: ∫ x x2 +3 dx = ? En este caso la propiedad 3 del formulario no puede aplicarse, sin embargo, con el método de cambio variable resulta relativamente sencillo resolverla tal como se muestra a continuación: Sea el cambio de variable: u(x) = x2 + 3 ⇒ du = 2x . dx ⇒ dx = du 2x De donde: x x2 +3 dx =∫ · = ∫ = ln|u|+ c = |x2 + 3| + cx u du 2x 1 2 du u 1 2 1 2 ∫ Otro ejemplo interesante resuelto mediante el método de cambio de variable es el siguiente: ∫ x x + 3 dx = ? Dado el gran parecido que tiene esta integral con la inmediata anterior, parece natural hacer el siguiente cambio de variable: sea u(x)= x + 3 ⇒ du = dx. De donde: Lo que resulta parece ser una integral mucho más complicada de la que se tiene originalmente. ¿Será que el método no funciona en este caso? u (x) = 5x - 2 ⇒ du= u' (x) . dx = 5 · dx ⇒ dx = du 5 x x + 3 dx = ∫ du∫ x u
- 46. unidad IIcálculo integral 46 dgep-uas El método sí funciona en este caso, pero como sucede frecuentemente con mu- chas integrales, antes de poder aplicarlo se hace necesario modificar antes el integrando mediante algunas manipulaciones algebraicas tal que lo transformen en alguna forma adecuada para la aplicación de algunas de las fórmulas. Así en esta integral un camino a seguir, como preparación para la aplicación del método, es el siguiente: Ahora, haciendo el cambio de variable u=x+3 (⇒du = dx), y sustituyendo en la expre- sión de la derecha, se obtiene que: x x + 3∫ dx = ∫ dx -3 ∫ =∫dx - 3∫ = x-3 ln|u|+c = x-3 ln|x+3|+cdx x + 3 du u Otros ejemplos de este tipo, que requieren manipulación algebraica previa, son los siguientes: 1. ∫ =∫ · =∫ = ?1 cos2 x dx cos2 x · tan x - 5 dx (tan x - 5)1/2 sec2 x dx (tan x - 5)1/2 Haciendo el cambio de variable: u(x)= tan x - 5 ⇒ du = sec2 x dx 2. Para resolver esta integral, es necesario que el binomio que se en- cuentra en el radical, sea transformado primeramente en un trinomio cuadrado perfecto, a saber: Esto indica que tenemos una integral de la forma: ∫ = arc sen + c du a2 - u2 u a Haciendo el cambio de variable: u(x) = x - 2 ⇒ du = dx ; a2 = 4 ⇒ a= 2 dx∫ =? 4x - x2 4x - x2 dx∫ = ∫ =∫ dx 4 -(x - 2)2 dx 4 - 4 + 4x - x2 dx∫ = ∫ =∫ =du a2 - u2 dx 4 - (x - 2)2 u a arc sen + c = arc sen + cx - 2 24x - x2 ∫ =∫ = =∫u-1/2 du = + c = 2 tan x-5 + c dx cos2 x · tan x - 5 u(-1/2) + 1 (-1/2) + 1 sec2 x dx (tan x - 5)1/2 du u1/2 x x + 3∫ dx = ∫ dx =∫ dx =∫ dx - 3∫ dx =∫dx - 3∫x + 3 - 3 x + 3 (x + 3) -3 x + 3 x + 3 x + 3 1 x + 3 dx x + 3
- 47. arturo yle martínez dgep-uas 47 cálculo integral 5. ∫ = ∫ =∫ = ∫ = ?dx x2 + 4x + 5 dx x2 + 4x + 4 + 1 dx (x2 + 4x + 4)+ 1 dx (x + 2)2 + 1 u2 = (x+2)2 ; u= (x+2); du = dx a2 = 1; a = 1 ∫ = ln |u+ u2 +a2 | + c du u2 + a2 ∴ ∫ = ln | (x+2) + (x+2)2 + 1 | + cdx (x + 2)2 + 1 4. ∫ =∫ =∫ =dx x2 - 6x - 16 dx (x2 - 6x + 9) - 16 - 9 dx (x - 3)2 - 25 u2 = (x–3)2 ; u= x-3; du = dx a2 = 25; a = 5 x -3 - 5 x - 3 + 5 ∫ = ln| |+ c = ln | | + cdx (x-3)2 -25 1 2(5) 1 10 x -8 x + 2 –1 x - 4 u2 = (x-4)2 ; u= x-4; du = dx ∫ ∫(x-4)-2 dx = + c = + cdx (x-4)2 3. ∫ =∫ = ⇒ ∫ un du = ; n ≠ -1dx x2 - 8x - 16 dx (x-4)2 un+1 n+1 -1 (x-4)-1 Aplicando la fórmula 35: u a corresponde a la forma: ∫ = arctan + c 6. ∫ =∫ = ∫ =dx x2 + 8x + 25 dx x2 + 8x + 16 + 9 dx (x +4)2 + 9 dx u2 + a2 1 a u2 = (x + 4)2 ; u = x + 4 ; du = dx a2 = 9; a = 3 ∫ = arctan + cdx (x-4)2 + 9 3 x+41 3 7. ∫ dx= ∫ dx = ∫u5 = · + c = + c (2 lnx - 9)5 3x (2 lnx - 9)5 x 1 3 1 3 du 2 1 6 1 6 u6 6 (2 lnx - 9)6 36 u5 =(2 lnx - 9)5 ⇒ u = 2 ln x - 9 ⇒ = ⇑du 2 dx x
- 48. unidad IIcálculo integral 48 dgep-uas 8. ∫sen3 x dx=∫ sen x · sen2 x · dx =∫ sen x (1- cos2 x) dx = ∫(sen x - cos2 x ∙ sen x) dx u2 =cos2 x ⇒ u = cos x ⇒ du = - sen x dx ⇒ - du = sen x dx u3 3 cos3 x 3 ∫ sen x dx -∫cos2 x · sen x dx = ? = -cos x ∫u2 (- du) + c = - cos x + + c = - cos x + + c u = sen 2x ⇒ du = 2cos2x dx ⇒ = cos2xdx ⇑du 2 du 2 9. ∫esen2x cos 2x dx = ∫eu = ∫ eu du = + c = + ceu 2 esen2x 2 10. ∫sen4 x dx=∫ (sen2 x)2 dx =∫ dx = ∫ dx = ? 11. ∫tanx dx =∫ dx = ? ∫tanx dx =∫ dx = ∫ =–∫ = ln |u|+c haciendo u= cos x ⇒ du =–sen x dx ⇒ –du =sen x dx por tanto: u =2x ⇒ du = 2dx ⇒ = dxdu 2 1- cos 2x 2 2 sen x cos x sen x cos x –du u du u 1- 2 cos 2x + cos2 2x 4 = ∫dx - ∫cos 2x dx + ∫cos2 2x dx = - ∫cos u + ∫ cos2 u + c1 4 2 4 1 4 x 4 1 2 du 2 1 4 du 2 1 2 = - ∫cos u du+ ∫cos2 u du + c = - sen 2x + ∫ du + cx 4 1 8 x 4 1 4 1 +cos 2u 2 1 8 1 4 = - sen 2x + ∫(1+ cos 2u)du + c = - sen 2x + ∫du + ∫cos 2u du + cx 4 1 16 x 4 1 4 1 16 1 4 1 16 = - sen 2x + + sen 2u + c = - sen 2x + (2x) + sen 4x + cx 4 u 16 x 4 1 4 1 16 1 4 1 32 1 32 1 4 3x 8 = - sen 2x + sen 4x + c1 32 = ln |cos x|+c
- 49. arturo yle martínez dgep-uas 49 cálculo integral Actividades de Aprendizaje # 8: Calcula en equipó las siguientes integrales indefinidas aplicando el método de sus- titución o de cambio de variable, y haz la comprobación del resultado mediante deri- vación. 1) ∫(9x - 5)4 dx = 2) ∫ 2x + 1 dx = 3) ∫ dx =x x2 + 7 4) ∫ dx =x2 2x3 - 1 5) ∫ dx =x + 5 x - 3 6) ∫ dx =x + 5 1 - x2 7) ∫ = 4x2 - 2x + 1 dx 8) ∫ dx =dx x - 1 9) ∫ =dx sen2 x ctg x - 4 10) ∫ dx =dx x lnx 11) ∫ dx =esen5x sec 5x 12) ∫csc2 w ectg w dw = 13) ∫ dx =ln x2 x 14) ∫ctgx · ln(sen x) dx = 15) ∫ =dx 1 + ex 16) ∫ tan2 x + 1 dx = 17) ∫ dx = 9x x e 18) ∫e2x · tan e2x dx = 19) ∫(1 + ctg2 x)2 csc2 x dx = 20) ∫ 103x + dx =4 e5x 21) ∫x2 · ctg x3 dx = 22) ∫ dx =sen 2x 4 -cos2 x 35) ∫cos 3x · cos 4 x dx = 36) ∫sen 2x · sen x dx = 37) ∫sen5x · cos 2x dx = 38) ∫cos 3x · sen 4x dx = 23) ∫sen5 x dx = 24) ∫sen6 x dx = 25) ∫cos2 3x dx = 26) ∫cos5 x dx = 27) ∫cos4 x dx = 28) ∫cos2 x . sen2 x dx = 29) ∫sen5 x . cos2 x dx = 30) ∫cos3 x . sen6 x dx = 31) ∫tan4 x dx = 32) ∫tan3 x dx = 33) ∫ctg5 x dx = 34) ∫ctg4 x dx =
- 50. unidad IIcálculo integral 50 dgep-uas 39) ∫sec4 x dx = 40) ∫sec3 x dx = 41) ∫csc3 x dx = 42) ∫csc4 x dx = 43) ∫tan4 x · sec4 x dx = 44) ∫tan5 x · sec2 x dx = 45) ∫tan2 x · sec3 x dx = 46) ∫ctg5 x · csc4 x dx = 47) ∫ctg2 x · csc4 x dx = 48) ∫ctg3 x · csc3 x dx = 49) ∫ =dx x + 16 50) ∫ =5x dx x4 - 16 51) ∫ =dx x2 - 9 52) ∫ =dx (x + 4)2 + 16 53) ∫ =dx 9 -x2 54) ∫ = dx 2+5x2 55) ∫ = dx x2 - 4 56) ∫ = dx 9-(x - 3)2 58) ∫ =dx 16 - 9x2 57) ∫ = dx 8x2 - 4 59) ∫ =dx x2 -4x+7 60) ∫ =dx 4x2 - 9 61) ∫ =dx 9x2 - 1 62) ∫ =dx 25x2 + 4 63) ∫ =dx 2 - 4x2 64) ∫ =dx 4x2 - 25 65) ∫ =e2x dx 1 + e2x 66) ∫ =3dx 4 + 7x2 67) ∫ =cos x dx 2 - sen 2 x 68) ∫ (e2x -1) -1/2 dx = 69) ∫ =4xdx 4 - x4 70) ∫ =3dx 9x2 - 25 71) ∫ =x2 dx 100-x6 72) ∫ dx =x+ 6 4-x2
- 51. arturo yle martínez dgep-uas 51 cálculo integral 2.2.2 Integración por partes El método de integración por partes tiene como propósito determinar o calcular la función primitiva del producto de una función por la diferencial de otra función de la misma variable, sea pues: d(uv) = u dv + v du ; integrando ambos lados de la igualdad anterior ∫d (uv) =∫udv + ∫vdu ⇒ uv = ∫ udv + ∫ vdu Despejando la integral: ∫udv, tendremos la fórmula de integración por partes: ∫udv = uv - ∫vdu Para aplicar esta forma de integrar, no existe una regla general para definir quién es u y quién es dv, pero es recomendable que al determinar cuál es la derivada, ésta sea fácilmente integrable. Sin embargo, al momento de integrar son bastante útiles las siguientes recomendaciones generales: 1. Que dx sea siempre una parte de dv. 2. Que dv sea fácilmente integrable 3. Cuando una expresión para integrar es el producto de dos funciones, fre- cuentemente se elige la expresión de apariencia complicada, con tal que pueda integrarse, como parte de dv Ejemplos resueltos: A la integral que nos queda podemos aplicar sucesivamente la misma fórmula, sin embargo ya fue calculada en el ejemplo anterior, por lo cual únicamente retomamos este resultado: 1. ∫xex dx = uv – ∫vdu = xex –∫ex dx = xex − ex + c = ex (x-1) + c u = x ⇒ du = dx dv = ex dx ⇒ v =∫ex dx = ex ∫x2 ex dx = ex x2 – 2∫ex xdx = ex x2 –2ex (x-1) + c 2. ∫x2 ex dx = uv – ∫vdu = ex x2 –∫ex 2xdx = ex x2 − 2∫ex x dx = ? u = x2 ⇒ du = 2xdx dv = ex dx ⇒ v =∫ex dx = ex
- 52. unidad IIcálculo integral 52 dgep-uas Actividades de Aprendizaje # 9: Calcula, en equipo de 4 a 5 integrantes, las siguientes integrales indefinidas apli- cando el método de integración por partes, y realiza la comprobación del resultado mediante derivación. 3. ∫x cos x dx = uv–∫vdu = x sen x –∫senx dx = x sen x– (– cos x) + c = x sen x + cos x + c u = x ⇒ du = dx dv = cos x dx ⇒ v =∫cos x dx = sen x 4. ∫x x – 3 dx = uv –∫vdu = x (x-3)3/2 –∫ (x-3)3/2 dx = ?2 3 2 3 u = x ⇒ du = dx dv = (x-3)1/2 dx ⇒ v =∫(x-3)1/2 dv = = (x-3)3/2(x-3)(1/2)+1 (1/2) + 1 2 3 ∫ (x -3)3/2 dx = ∫(x-3)3/2 dx = · + c = (x-3)5/2 + c2 3 2 3 2 3 (x-3)(3/2)+1 (3/2) + 1 4 15 Resolviendo por cambio de variable la integral: De donde finalmente se obtiene que: ∫x x-3 dx = x(x-3)3/2 - (x-3)5/2 + c2 3 4 15 1) ∫x2 ex dx = 2) ∫x3 ex dx = 3) ∫ln x dx = 4) ∫x ln x dx = 5) ∫x2 ln x dx = 6) ∫x2 e2x dx = 7) ∫ex sen x dx = 8) ∫x3 ln2 x dx = 9) ∫ax x dx = 10) ∫eax x dx = 11) ∫x sen x dx = 12) ∫x2 cos x dx = 13) ∫x2 sen x dx = 14) ∫x sec2 x dx = 15) ∫arc tan 3x dx = 16) ∫ex cos x dx = 17) ∫sec3 x dx = 18) ∫ =sen x dx ex
- 53. arturo yle martínez dgep-uas 53 cálculo integral 2.2.3. Integración por sustitución trigonométrica Este método de integración se aplica cuando en el integrando aparecen expresiones de la formas: a2 - u2 o u2 ± a2. En estos casos la manera más corta o efectiva para calcular la integral es hacer un cambio de variable, de la siguiente manera: 19) ∫arc cos x dx = 20) ∫arc senx dx = 21) ∫(x2 + 3x)cos 2x dx = 22) ∫cos . ln(senx) dx = 23) ∫x3 x2 + 3 dx = 24) ∫x5 x2 - 4 dx = 25) ∫sen x . sen 3x dx = 26) ∫sen 4x . sen 3x dx = CASO FORMATO EN EL INTEGRANDO CAMBIO DE VARIABLE RESULTADO EN EL INTEGRANDO DESPUÉS DEL CAMBIO DE VARIABLE 1 u = a sen z 2 u = a tan z 3 u = a sec z a u a2 - u2 a2 - u2 = a2 - (a sen z)2 = a2 - a2 sen z2 = a2 - (1– sen2 z))2 = a2 cos2 z = acosz a2 + u2 a u a2 + u2 = a2 + (a tan z)2 = a2 + a2 tan2 z = a2 (1+ tan2 z))2 = a2 sec2 z = asecz u2 - a2 u2 - a2 = (a sec z)2 -a2 = a2 sec2 z - a2 = a2 (sec2 z - 1)2 = a2 tan2 z = atanz u a z z z
- 54. unidad IIcálculo integral 54 dgep-uas Caso 1. ∫ = ? cambio; x = u = 2 sen z ⇒ dx = du = 2 cos z dz dx (4 - x2 ) 3 2 ∫ = ∫ = ∫sec2 zdz = + c = ?dz cos2 z23 cos3 z 2 cos z dz 1 22 1 4 tan z 4 Finalmente del triángulo rectángulo se obtiene que: tan z = a2 - u2 u Caso 2. ∫ = ? Esta integral es de la forma: ∫ = ?dx x 4x2 + 9 du u u2 + a2 u2 = 4x2 ; u = 2x; x = ; dx= ; a2 = 9 ; a = 3u 2 du 2 u = a tan z; du = a sec2 zdz ∴ ∫ = ∫ = ∫ =du u u2 + a2 a sec2 dz a tan z a2 tan2 z + a2 a sec2 dz a tan z a2 (tan2 z + 1) ∴ ∫ = ∫ = ∫ = ∫csc zdz = ln (csc z - cot z) + csec zdz tan za tan z . a sec z a sec2 zdz 1 a 1 a dz sen z 1 a 1 a del triángulo rectángulo se tiene que: a2 + u2 u a u ∴ ∫ = ∫ ln - + c = ln - + c du x 4x2 + 9 1 a a2 + u2 u a u 1 3 4x2 + 9 2x 3 2x = ln +c1 3 4x2 + 9 - 3 2x = + cx 4 4 - x2 dx (4 - x2 ) 3 2 ∫De donde: Ejemplos resueltos: ∫ = ∫ = ∫ =dx (22 - x2 )3 2 2 cos z dz (22 - (2 senz)2 ) 3 2 2 cos z dz (22 - 22 sen2 z) 3 2 ∫ = ∫ = ∫ =2 cos z dz (2cos z)3 2 cos z dz ( 22 . cos 2 z)3 2 cos z dz (22 (1-sen2 z)) 3 2 csc z = y cot z =
- 55. arturo yle martínez dgep-uas 55 cálculo integral Actividades de Aprendizaje # 10: Calcula, en equipo de 4 a 5 integrantes, las siguientes integrales indefinidas aplican- do el método de integración por sustitución trigonométrica, y realiza la comprobación del resultado mediante derivación. u2 - a2 duCaso 3. ∫ = ∫ = ?x2 - 9 dx ∴ a2 = 9 ⇒ a = 3 ; cambio: x = u = 3 sec z ⇒ dx = du = 3 sec z . tan z dz ∴ ∫ (3 sec z)2 - 9 . 3 sec z tan z dz = 3∫ 9 (sec2 z - 1) sec z tan z dz = 3∫ 9 tan2 z sec z tan z dz = 9∫secztan2 z dz = 9∫sec z (sec2 z - 1) dz = 9∫sec3 zdz - 9∫sec z dz = 9∫sec3 z dz - 9 ln|sec z + tan z|+ c = ? Resolviendo la primera integral por partes se obtiene que: 9∫sec3 zdz = [sec z . tan z + ln|sec z + tan z | + c9 2 ∴ ∫ x2 - 9 dx = [sec z . tan z + ln|sec z + tan z | - 9 ln|sec z + tan z| + c9 2 = [sec z tan z - ln|sec z + tan z | + c9 2 Finalmente del triángulo rectángulo se obtiene que: tan z = y sec z =x2 - 9 3 De donde: ∫ x2 - 9 dx = x x2 - 9 - ln + x2 - 9 + c9 2 9 x 3 3 1. ∫ dx =x2 9- x2 2. ∫ dx =x2 25 - x2 3. ∫x x2 + 1 dx = 4. ∫ dx =x2 16 + x2 5. ∫ =6 dx x2 - 9 6. ∫ dx =dx 4x2 - 1 7. ∫ =6 dx x 36 - 9x2 8. ∫ dx = x x2 - 16 9. ∫ dx = x 4 + 16 x2 10. ∫ 7 + 49 x2 dx = 11. ∫ =dx x2 - 16 12. ∫ =dx x2 - 5x + 6 x 3
- 56. unidad IIcálculo integral 56 dgep-uas 2.2.4. Integración por fracciones parciales Cuando en una integral el integrando es una fracción en la cual el denominador es factorizable en factores lineales o cuadráticos, o en una combinación de ambos, la forma de cómo estas integrales pueden ser calculadas es recurriendo al método de descom- posición del integrando en una suma de fracciones parciales. Aunque en este tipo de integrales se pueden presentar cuatro casos, en general, el método consiste en lo siguiente: Los requisitos algebraicos básicos para poder aplicar con éxito este método de in- tegración son: primeramente saber factorizar el denominador del integrando, segundo saber resolver el sistema de ecuaciones lineales que resulta de la descomposición del integrando en fracciones parciales en aras de poder determinar los numeradores (que frecuentemente serán constantes) de las fracciones parciales, y tercero saber resolver las integrales inmediatas que resultan al final del proceso de la descomposición y deter- minación de las fracciones parciales. Y finalmente, al expresar los resultados también es necesario conocer y saber aplicar las siguientes propiedades de los logaritmos: Ejemplos resueltos del caso 1. El denominador se factoriza en factores lineales no repetidos. ∫ dx = ∫ dx = ∫ ± ±... ± dx P (x) Q (x) P(x) q1 (x) ∙ q2 (x)...qk (x) p1 (x) q1 (x) p2 (x) qk (x) pk (x) qk (x) p1 (x) q1 (x) p2 (x) q2 (x) pk (x) qk (x) = ∫ dx ± ∫ dx ±... ± ∫ dx logb AB = logb A + logb B logb An = n · logb A logb = logb A - logb BA B dx 4x2 - 9 ∫ = ∫ = ?dx (2x + 3) (2x - 3) Entonces, hágase: Comparando término a término las expresiones resulta que: = + = =1 (2x + 3) (2x - 3) A 2x + 3 B 2x - 3 A (2x -3) + B(2x+3) (2x + 3)(2x - 3) 2 (A + B) x - 3(A-B) (2x + 3)(2x - 3) 2(A + B) x = 0 ⇒ A + B = 0 ⇒ Ec. 1 -3 (A - B) = 1 ⇒ A - B = - ⇒ Ec. 21 3 1.
- 57. arturo yle martínez dgep-uas 57 cálculo integral Sumando miembro a miembro las ecuaciones 1 y 2 del sistema anterior se obtiene: 2A = - ⇒ A = - ⇒ - + B = 0 ⇒ B =1 3 1 6 1 6 1 6 2. ∫ =∫ = ?dx 5x2 - 18x + 9 dx (5x - 3)(x - 3) ⇒ = + =1 (5x- 3)(x - 3) A (5x - 3) B (x - 3) A(x-3)+ B(5x - 3) (5x - 3) (x - 3) Ax -3A + 5Bx - 3B (5x - 3)(x - 3) = = (A+5B)x - 3(A +B) (5x - 3)(x - 3) 1 12 = ln +c2x - 3 2x + 3 Entonces: dx 4x2 - 9 ∫ = ∫ + = ∫ - = ln(2x - 3) - ln(2x + 3) + c (2x + 3) 1 6 - dx (2x - 3) 1 6 dx 1 6 2x - 3 dx 2x + 3 dx 1 12 (A + 5B)x = 0 ⇒ A + 5B = 0 ⇒ Ec. 1 -3(A + B)= 1 = ⇒ A + B =- ⇒ Ec. 21 3 ⇒ A + 5B = 0 A + B = - 1 3 ⇒ 4B = ∴ B = 1 3 1 12 A + 5B = 0 -A- B = 1 3 Sustituyendo B en la Ec. 1 : A + 5 = 0 ⇒ A + = 0 ⇒ A = -1 12 5 12 5 12 x-3 5x - 3∫ = ln + cdx 5x2 - 18x + 9 1 12 ∫ = ∫ -dx 5x2 - 18x + 9 1 12 dx x-3 5dx 5x-3 ∴ 1 (2x + 3) (2x - 3) -1/6 2x + 3 = + 2x - 3 1/6 ∴ 1 12 = [ln (x-3) - ln (5x-3)] + c
- 58. unidad IIcálculo integral 58 dgep-uas 3. ∫ =∫ = ? Descomponiendo el integrado en:(5x - 2)dx x2 - 9x + 8 (5x - 2)dx (x - 8)(x - 1) = + = = Ax-A+ Bx - 8B (x - 8) (x - 1) 5x - 2 (x - 8)(x -1) A x - 8 B x - 1 (A+B)x - (A + 8B) (x - 8) (x - 1) (A+B)x = 5x ⇒ A + B = 5 → Ec. 1 -(A+ 8B) = -2 ⇒ A + 8B = 2 → Ec. 2 Resolviendo el sistema: Comparando los términos de la igualdad ⇒ -7B = 3 ⇒ B= - ⇒ A =7 3 22 3 ∴ ∫ = 22∫ - 7∫ = [22 ln (x-8) - 7 ln (x-1)] + c(5x - 2) dx x2 - 9x + 8 dx x-8 1 3 dx x-1 1 3 (x-8)22 (x-1)7= [ln (x-8)22 – ln (x-1)7 ] + c = ln + c1 3 1 3 A + B = 5 → Ec. 1 -A - 8B = -2 → Ec. 2 (-A -3B + 2C)x = 3x ⇒ -A -3B + 2C = 3 → Ec. 1 Resolviendo el sistema de ecuaciones: 4. ∫ =∫ = ∫ = ?(3x - 4)dx x3 - x2 - 6x (3x - 4)dx x (x2 - x - 6) (3x - 4)dx x (x + 2)(x - 3) = + + =3x - 4 x (x + 2)(x -3) A(x2 -x-6) + B(x2 -3x) + C (x2 +2x) x(x + 2) (x - 3) A x B x + 2 C x - 3 (A +B + C)x2 = 0 ⇒ A + B + C = 0 → Ec. 2 -6A = -4 → Ec. 3 ⇒ B = -1 ⇒ C = 1 3 ∴ A = = ⇒-4 -6 2 3 2 3 - -3B + 2C = 3 2 3 + B + C = 0 = 2 3 B + C = - -3B + 2C =11 3 ∴ ∫ = ∫ -∫ + ∫ = ln x - ln (x +2) + ln (x - 3) + c(3x - 4) dx x3 - x2 - 6x dx x 2 3 dx x+2 1 3 dx x- 3 1 3 2 3
- 59. arturo yle martínez dgep-uas 59 cálculo integral Ejemplo resuelto del caso 2. El denominador se factoriza en factores lineales y algunos son repetidos. Comparando los términos de la igualdad se obtiene que: Ejemplo resuelto del caso 3. El denominador se factoriza en factores cuadráticos y ninguno se repite. Para este caso, por cada factor cuadrático de la forma ax2 + bx + c que resulta de la factorización del denominador, le corresponde en la descomposición del integrando una fracción del tipo Ax + B ax2 + bx + c. Si además, resultan factores lineales, estos se resuelven como en los casos 1 y 2. (A+C)x2 = 0 ⇒ A + C = 0 → Ec. 1 Resolviendo el sistema de ecuaciones: (-2A+B)x = 6x ⇒ -2A + B = 6 → Ec. 2 A + B - C = 3 → Ec. 3 ∫ =∫ =∫ =∫ = ?(6x + 3) dx x3 -x2 -x+1 (6x + 3) dx x2 (x-1) - 1(x -1) (6x + 3) dx (x-1)(x2 -1) (6x + 3) dx (x+1)(x-1)2 = + + = 6x + 3 (x+1)(x-1)2 A (x-1)2 + B (x+1) + C (x + 1)(x-1) (x+1)(x-1)2 A (x+1) B (x-1)2 C x-1 = =A(x2 -2x+1) + Bx + B + Cx2 - C (x+1)(x-1)2 (A +C)x2 + (B - 2A)x + (A + B- C) (x+1)(x-1)2 A + C = 0 -2A + B = 6 A + B - C = 3 ⇒ B = 9/2 A = -3/4 C = 3/4 ∴ ∫ = ∫ + ∫ + ∫ = ln - + c(6x + 3) dx x3 - x2 - x + 1 -3 4 dx x+1 3 4 x -1 x+ 1 dx (x-1)2 9 2 dx x-1 3 4 9 2(x- 1) ∴ ∫ =∫ + +(6x + 3) dx x3 - x2 - x + 1 dx ∫ = ∫ = ?(4x2 + 2x) dx x4 + 3x3 + 4x2 + 3x + 1 2(2x2 + x) dx (x + 1)2 (x2 + x + 1) ∴ = + +A (x + 1)2 (2x2 + x) (x + 1)2 (x2 + x + 1) B (x + 1) Cx + D x2 + x + 1 = A(x2 + x + 1) + B (x + 1)(x2 + x + 1) + (Cx + D)(x + 1)2 (x + 1)2 (x2 + x + 1) x+1 -3/4 (x-1)2 9/2 x-1 3/4
- 60. unidad IIcálculo integral 60 dgep-uas Ejemplo resuelto del caso 4. El denominador se factoriza en factores cuadráticos y algunos se repiten. Para este caso, si resultan factores lineales estos se resuelven como en los casos 1 y 2, y por cada factor cuadrático de la forma (ax2 + bx + c)n que resulta de la factorización del denominador, le corresponde en la descomposición del integrando una suma de n fracciones del tipo: + +... +Ax + B (ax2 +bx +c)n Cx + D (ax2 +bx+c)n-1 Vx + W (ax2 + bx + c) . = (B + C)x3 + (A + 2B + 2C + D)x2 + (A+ 2B + C + 2D)x + (A + B + D) (x + 1)2 (x2 + x + 1) ⇒ (B + C)x3 = 0 ⇒ B + C = 0 → Ec. 1 ⇒ (A + 2B + 2C + D)x2 = 2x2 ⇒ A + 2B + 2C + D = 2 → Ec. 2 ⇒ (A + 2B + C + 2D)x = x ⇒ A + 2B + C + 2D = 1 → Ec. 3 ⇒ A + B + D = 0 → Ec. 4 Resolviendo el sistema de ecuaciones: ⇒ B+ C = 0 A + 2B + 2C + D = 2 A + 2B + C +2D = 1 A + B + D = 0 D = 1 A = 1 B = -2 C = 2 ∴ ∫ = 2∫ + + dx 1 (x + 1)2 -2 (x + 1) 2x + 1 x2 + x + 1 (4x2 + 2x) dx x4 + 3x3 + 4x2 + 3x + 1 = 2∫ -4∫ + 2∫ dxdx (x + 1)2 dx (x + 1) 2x + 1 x2 + x + 1 = - -4 ln|x + 1|+ 2 ln|x2 + x + 1| + c2 (x + 1) Ejemplo: ∫ = ∫ = ?(2x3 + 10x - 3x2 - 12) dx x4 + 8x2 + 16 (2x3 - 3x2 + 10 x - 12) dx (x2 + 4)2 ∴ = + +Ax + B (x2 + 4) (2x3 - 3x2 + 10x - 12) (x2 + 4)2 Cx + D (x2 + 4)2 (Ax + B)(x2 + 4) + (Cx + D) (x2 + 4)2 = Ax3 + Bx2 + (4A + C)x + (4B +D) (x2 + 4)2
- 61. arturo yle martínez dgep-uas 61 cálculo integral Igualando los numeradores de ambas expresiones se concluye que: Actividades de Aprendizaje # 11: Calcula, en equipo de 4 a 5 integrantes, las siguientes integrales indefinidas aplican- do el método de integración por fracciones parciales, y realiza la comprobación del resultado mediante derivación. A=2 ; B = -3 ; 4A + C = 10 ⇒ C = 10 - 4(2) = 2 ; 4B + D = -12 ⇒ D = 0 ∴ ∫ = ∫ + dx = ∫ dx + ∫ dx2x - 3 (x2 + 4) (2x3 + 10x - 3x2 - 12) dx x4 + 8x2 + 16 =∫ -3∫ +∫ dx2x dx x2 + 4 dx x2 + 4 2x (x2 + 4)2 2x + 0 (x2 + 4)2 2x - 3 (x2 + 4) 2x (x2 + 4)2 1 x2 + 4 = ln|x2 + 4|- arc tan - + c3 2 x 2 1. ∫ =dx x2 - x - 12 2. ∫ =xdx 3x2 - 7x + 4 3. ∫ =(3x2 -4x + 3)dx x3 - 6x2 + 12x - 8 4. ∫ = (2x + 1)dx (x2 + 3x - 10) 5. ∫ =(7x + 3) dx 9x4 + 6x2 + 1 6. ∫ = (5x - 2)dx x2 - 8x + 26 7. ∫ dx =(2x3 + 3x2 - 4) x2 - 4x + 3 8. ∫ = (2x2 - 3x + 7)dx x2 - 8x + 26 9. ∫ dx =4x3 + 3x2 - 1 x3 - x2 10. ∫ = (x2 + 4x - 4)dx x3 - 4x 11. ∫ dx =x x3 - x2 + x - 1 12. ∫ dx= 2x3 + 3x2 + 10x + 12 x4 + 8x2 + 16 13. ∫ dx =2x3 - 4x - 8 x4 - x3 + 4x2 - 4x 14. ∫ dx =8x3 + 13x x4 + 4x2 + 4 15. ∫ dx =2x2 - x + 2 x3 + 3x2 + x 16. ∫ dx =4x3 - x2 + 9x + 4.5 x6 + 18x4 + 81x2
- 62. unidad IIcálculo integral 62 dgep-uas 2.3. Otras aplicaciones de la integral indefinida Con los métodos y técnicas de integración estudiados anteriormente el abanico de las aplicaciones de la integral indefinida se amplía considerablemente tal como se mues- tra a continuación en los siguientes problemas. Ejemplo 1: Determinar una función y = f (x) cuya derivada sea f '(x) = 2x+ 1 y que f (4) = 15. Resolución: con lo estudiado en la unidad 1 se sabe que con la integral indefinida podemos determinar dicha función primitiva y = f (x). Y que: De donde, la antiderivada o función primitiva general (o integral indefinida) de f ' (x) = 2x + 1 es: Y en consecuencia: Como ya se estudió en la primera unidad de aprendizaje, este proceso de resolución puede desarrollarse y ser interpretado también de la siguiente manera a partir del con- cepto de diferencial y de ecuación diferencial: Sea la ecuación diferencial: dy dx = f ' (x) = 2x +1 Despejando de la ecuación diferencial el diferencial dy e integrándolo: dy = 2x + 1 dx ⇒ ∫dy = ∫ 2x + 1 dx ⇒ 15 = [2(4) + 1] + c ⇒ c = 6 3 21 3 ∴ y = [2x+1] +6 3 21 3 y = f (4) = F (4) = [2(4) + 1] + c = 15 ⇒ c = 6 ∴ y = f (x) = (2x + 1) + 6 3 2 3 21 3 1 3 F(x) = ∫ (2x + 1) dx = ∫ (2x + 1) dx = ∙ (2x +1) + c = (2x + 1) + c1 2 2 3 3 21 3 3 2 1 2 y = f (x) = F (x) = (2x + 1) + c1 3 3 2 3 21 3 ⇒ y =∫ 2x +1 dx = [2x + 1] + c
- 63. arturo yle martínez dgep-uas 63 cálculo integral Ejemplo 2: Determina la función y = f (x) tal que f ' (x) = x cos x, y f =π 2 3π 2 . Resolución: Para determinar el valor c, sustituimos para x = π / 2 en la primitiva general: Ejemplo 3: Después de t segundos, un cuerpo se mueve con una velocidad v(t)=t e-t/2 metros por segundo. Determine la posición s = s (t) del cuerpo como una función del tiempo, si s = s (0) = 0 Resolución: Si s = s (t) representa la posición del cuerpo en el tiempo de t seg, entonces: Ejemplo 4: La tasa de consumo de petróleo al tiempo t es C'(t) = 16 e0.08t miles de millones de barriles al año. Si el consumo total de petróleo, del tiempo 0 al tiempo t, es C (t). Calcular la cantidad de petróleo consumido en una década. Resolución: F (x) = ∫ x cos x dx = ? Integrando por partes: = uv - ∫vdu = x sen x -∫ sen x dx = x sen x - (- cos x) + c ∴ y = f (x) = F (x) = x senx + cos x + c y = f (π / 2) = F (π / 2) = sen (π / 2) + cos (π / 2) + c = ⇒ c = ππ 2 3π 2 ∴ y = f (x) = F (x) = sen x + cos x + ππ 2 s(t) = ∫v(t)dt = ∫te-t/2 dt = ? Integrando por partes: = -2te-t/2 - 4e-t/2 + c ∴ s (0) = -2(0)(1) - 4(1) + c = 0 ⇒ c = 4 ⇒ s(t) = -2te-t/2 - 4e-t/2 + 4 dC(t) dt = C'(t) ⇒ dC(t) = C'(t)dt ⇒ C(t) = ∫(16e0.08t )dt = e0.08t + c = 200e0.08t + c16 0.08 ⇒ C(0) = 200e0.08(0) + c = 0 ⇒ c = -200 ⇒ C(10) = 200(e0.08(10) -1) ≈ 245 miles de millones de barriles. ∴ C(t) = 200e0.08t - 200 = 200(e0.08t -1)
- 64. unidad IIcálculo integral 64 dgep-uas Ejemplo 5: Si F(x) = ∫f (x)dx entonces, se puede calcular su integral definida corres- pondiente en el intervalo a ≤ x ≤ b de la siguiente manera: A partir de esta consideración calcular el valor de: Resolución: Primeramente calculamos la integral indefinida Resolviendo mediante el cambio de variable: Ejemplo 6: Si y = f (x) es una función continua y f (x) ≥ 0 en el intervalo a ≤ x ≤ b, en- tonces el área A limitada por la curva de y = f (x) , las rectas x = a, x = b y el eje de las X puede ser determinada por la siguiente integral definida: A partir de esta consideración calcular el valor del área bajo la curva f (x) = e-x + x en el intervalo 0 ≤ x ≤ 1. Resolución: Ya que Actividades de Aprendizaje # 12: Resuelve, en equipo de 4 a 5 integrantes, los siguientes problemas aplicando el cál- culo de integrales indefinidas. 1. Determina una función y = f (x) cuya derivada sea f ' (x) = , y que f (5) = 20. 2. Determina la función y = f (x) cuya tangente tiene una pendiente m = para cada valor de x, y cuya gráfica pasa por el punto P (4, 10). ∫ f (x)dx = F (b) - F (a). b a ∫ dx = ? 2 1/4 lnx x ∫ dx = ?lnx x u = lnx ⇒ du = dx x F(x) =∫ dx = ∫lnx =∫u du= u2 + c = (ln x)2 + clnx x dx x 1 2 1 2 ∴ ∫ dx = F(2) - F (1/4) = (ln 2)2 + c - ln + c ≈ 0.721 2 1/4 lnx x 1 2 1 2 1 4 2 ∫ f (x)dx = F (b) - F (a) ; donde: F (x) = ∫f (x) dx b a ∫(e-x + x )dx =-e-x + x3/2 + c ; entonces:2 3 1 0 A =∫ (e-x + x )dx = -e-1 + (1)3/2 + c - e0 + (0)3/2 + c ≈ 32 3 2 3 1 x 4x2 + 9 1 5x2 - 18x + 9
- 65. arturo yle martínez dgep-uas 65 cálculo integral 3. Se lanza verticalmente hacia arriba una pelota con una velocidad inicial de 95 m/seg desde un edificio de 60 m de altura. Calcular: (a) la altura a la que se encuentra la pelota, con relación al nivel del suelo, después de 2 y 7 segundos de haber sido lanzada, y (b) el tiempo que tarda la pelota en llegar al suelo. 4. Se ha determinado que la población P (t) de una colonia de bacterias, t horas después de iniciar la observación, tiene una razón de cambio de P'(t) = 350 e0.18t + 220-0.3t . Si la pobla- ción era de 250,000 bacterias cuando se inició la observación, ¿Cuál será la población 20 horas después? 5. Calcular las siguientes integrales definidas: a) b) 6. Calcular el área debajo de la curva de la función f (x) = sen 2x en el intervalo 0 ≤ x ≤ π / 2. 7. Calcular el área debajo de la curva de la función f (x) = x en el intervalo 0.5 ≤ x ≤ 1. 8. Calcular el área debajo de la curva de la función f (x) = 25-x2 en el intervalo -5 ≤ x ≤ 5. 9. Un biólogo determina que la altura de un cierto tipo de árbol crece a una razón de h'(t) = 0.2t2/3 + t pies/año. Si cuándo se plantó el árbol éste tenía una altura de 2 pies, ¿cuál será su altura en metros dentro de 15 y 30 años? 10. En cierta ciudad el nivel de ozono L(t) a las 7:00 a.m. es de 0.25 ppm. Una predicción del clima anticipa que el nivel de ozono t horas más tarde cambiará a una tasa de: a) ¿Cuál será el nivel de ozono a las 10:00 a.m.? b) ¿en qué tiempo el nivel de ozono será máximo? dx 1 - x2 ∫ =0.5 - 0.5 ∫ cos 3x · esen3x dx =π π /6 L'(t) = 0.24 - 0.03t 36 + 16t - t2 ppm/h
- 67. dgep-uas 67 UNIDAD DE APRENDIZAJE III CAMBIOS ACUMULADOS E INTEGRAL DEFINIDA Competencia de unidad: Calcula numéricamente y mediante el teorema fundamental del cálculo las integrales definidas, y las aplica en el cálculo de áreas. COMPETENCIAS DISCIPLINARES A DESARROLLAR 1. Construye e interpreta modelos matemáticos mediante la aplicación de procedimientos y operaciones aritméticas, algebraicas, geométricas y variacionales, para la comprensión y análisis de situaciones reales, hipotéticas o formales. 2. Formula y resuelve problemas matemáticos, aplicando diferentes enfoques. 3. Explica e interpreta los resultados obtenidos mediante procedimientos matemáticos y los contrasta con modelos establecidos o situaciones reales. 4. Argumenta y comunica la solución obtenida de un problema, con métodos numéricos, grá- ficos, analíticos y variacionales, mediante el lenguaje verbal, matemático y el uso de las tecnologías computacionales, informáticas y de la comunicación. 5. Analiza las relaciones entre dos o más variables de un proceso social o natural para deter- minar o estimar su comportamiento. 6. Cuantifica, representa y contrasta experimental o matemáticamente las magnitudes del es- pacio y las propiedades físicas de los objetos que lo rodean. 8. Interpreta tablas, gráficas, mapas, diagramas y textos con símbolos matemáticos y científi- cos. CONTENIDO TEMÁTICO: 3.1.Cuantificación de cambios acumulados: Cálculo por métodos algebraicos y geométricos de áreas bajo curvas, y de distancias recorridas por cuerpos que se mueven con velocidad variable en un intervalo de tiempo. 3.2. Área e Integral definida: Concepto y definición de integral definida y sus propiedades. Interpre- tación geométrica (como área bajo una curva) y física de la integral definida. 3.3. Teorema fundamental del Cálculo: Cálculo de integrales definidas. 3.4 Aplicaciones de la integral definida: Cálculo mediante la integral definida de áreas bajo y entre- curvas.
- 68. unidad IIIcálculo integral 68 dgep-uas Unidad de aprendizaje III Cambios acumulados e integral definida 3.1 Cuantificación de cambios acumulados: el problema del área y la distancia. Como recordarás, en las referencias históricas de esta unidad se habló del cálculo del área en figuras no elementales, en especial el área bajo la gráfica de una función, y se dijo que había sido un problema de gran importancia desde tiempos remotos. De las soluciones encontradas a dicho problema nos ocuparemos en esta unidad. El problema planteado es calcular el área A comprendida entre la gráfica de una fun- ción f (x) > 0, el eje X y las rectas verticales x = a y x = b. (Ver figura 3.1) Una solución aproximada al cálculo de esta área se puede obtener dividiendo pri- mero el área en rectángulos por debajo o por encima de la gráfica de f (x), después cal- culando el área de cada uno de ellos y finalmente sumando todas las áreas tal como se muestra en las figuras 3.2 (a) y 3.2 (b) de abajo: Figura 3.1 Figura 3.2 (a) A- Figura 3.2 (b) A + A = ? x= a x = b y = f (x) 0 X Y
- 69. arturo yle martínez dgep-uas 69 cálculo integral Obsérvese como la aproximación se puede mejorar aumentando el número de rec- tángulos, y como en la figura 3.2 (a) hay un error por defecto y en la figura 3.2 (b) el error es por exceso. De donde se deduce que: A- < A < A+ Ejemplo 1: Aplicando la idea anterior calcular de manera aproximada el área A com- prendida entre la gráfica de la función y = x, el eje X y las rectas verticales x = 0 y x = 1. Resolución: En las figuras de abajo se puede observar que la figura geométrica que resulta al hacer la representación gráfica de este problema es la del triángulo cuya área puede ser calculada inmediatamente por la fórmula ya conocida: A = = = = = 0.5base x altura 2 1 x 1 2 1 2 8 16 Sin embargo, para ilustrar el poder, generalidad y funcionalidad de la idea de las aproximaciones mediante rectángulos la calcularemos a continuación mediante este nuevo procedimiento. Figura 3.3 Al dividir en cuatro partes iguales a la base del triángulo, se forman los rectángulos, unos por debajo de la recta y los otros por encima de la recta (ver figura 3.3). Si cal- culamos el área aproximada del triángulo en base a los tres rectángulos por debajo de la recta se obtiene que: y = x 1 2 1 4 3 4 1 1 2 1 4 3 4 1 y = x
- 70. unidad IIIcálculo integral 70 dgep-uas Rectángulos y = x Base Área x y (altura) 1 2 3 Sumatoria de las áreas parciales: A- = Σ Ai = A1 + A2 +A3 = + + = 3 i = 1 1 16 1 8 3 16 6 16 1 4 1 2 3 4 1 4 1 2 3 4 1 4 -0 = 1 4 1 2 - =1 4 1 4 3 4 - =1 2 1 4 1 16 1 4 1 4 A1 = x = 1 8 1 4 1 2 A2 = x = 3 16 1 4 3 4 A3 = x = Véase que de esta manera encontrar el área bajo la curva no fue lo más exacto, pero sí una manera aproximada que puede mejorarse aumentando el número de rectán- gulos, ya que se pierden del área real. Obsérvese también que el área faltante está en los cuatro pequeños triángulos que están entre la recta y los rectángulos y cuya suma de áreas no fueron contabilizadas, y que equivalen al faltante como se muestra en los siguientes cálculos: 2 16 4 x = 4 =1 2 1 32 1 4 1 4 2 16 Si ahora calculamos el área del triangulo en base a los cuatro rectángulos que so- brepasan la recta, se obtiene que: 1 4 1 2 3 4 1 4 1 2 3 4 1 4 -0 = 1 4 1 2 - =1 4 1 4 3 4 - =1 2 1 4 1 16 1 4 1 4 A1 = x = 1 8 1 4 1 2 A2 = x = 3 16 1 4 3 4 A3 = x = 4 4 4 4 4 4 - =3 4 1 4 4 16 1 4 4 4 A4 = x = Rectángulos y = x Base Área x y (altura) 1 2 3 4 Sumatoria de las áreas parciales: A+ = Σ Ai = A1 + A2 +A3 + A4 = + + + = 4 1 16 1 8 3 16 10 16 4 16i = 1
- 71. arturo yle martínez dgep-uas 71 cálculo integral Véase que en este caso se ganaron 4/16 con respecto a la primera aproximación y 2/16 con respecto al área real. Obsérvese también que ahora el exceso de área está en los cuatro pequeños triángulos que están sobre la recta y cuya suma de áreas fueron contabilizadas demás, y que equivalen a los 2/16 de exceso. En conclusión el área real se encuentra entre ambas áreas, es decir: A- = < A < A+ =6 16 10 16 En tanto que el área promedio de las dos áreas aproximadas es: A = = = = A — 6 16 10 16+ 2 16 16 2 1 2 Como ya se dijo estos cálculos pueden aproximarse tanto como se desee al área real aumentando el número de rectángulos ya sea por abajo o por arriba de la curva. Así, dividiendo en n partes iguales el área bajo la recta y en el mismo intervalo, entonces el área del triangulo en base a los rectángulos por debajo de la gráfica será: Rectángulo y = x Base Área (base x altura)x y (altura) 1 2 3 4 • • • • • • • • • • • • • • • n -2 n -1 n-2 n 1 n n-2 n n-2 n2 n-1 n 1 n n-1 n n-1 n2 1 n 1 n 1 n 1 n2 2 n 2 n 1 n 2 n2 3 n 3 n 1 n 3 n2 4 n 4 n 1 n 4 n2
- 72. unidad IIIcálculo integral 72 dgep-uas De donde, la suma total de las áreas de los n-1 rectángulos será: A- = = + + + + + ... + +Σ n-1 1 n i n 1 n2 2 n2 3 n2 5 n2 4 n2 n-2 n2 n-1 n2 1 n2= [ 1 + 2 + 3 + 4 + 5 + ... + (n-2) + (n-1)] = (n) =1 n2 n+1 2 n+1 2n Para mejorar la aproximación hasta el máximo aumentamos (imaginariamente) el número de rectángulos hasta el infinito, lo cual implica que: LimA- = Lim = Lim = Lim = =n+1 2n 2n n n n 1 n+ 2 1 1 n+ 1 + 0 2 1 2n→∞ n→∞ n→∞ n→∞ Comparando las áreas obtenidas, por la fórmula del triángulo, el área promedio de los rectángulos y por esta última que la encontramos a través de límite de la sumatoria de las áreas de los rectángulos, encontramos y corroboramos que el área encontrada para los tres casos es la misma. ¿Será una simple coincidencia? A continuación resolveremos un caso más complicado en el cual no se conoce el re- sultado de antemano y donde se aprecia mejor la pertinencia de este método de aproxi- maciones sucesivas infinitas. Ejemplo 2: Calcular con la mejor aproximación posible el área A comprendida entre la gráfica de la función y = x2 , el eje X y las rectas verticales x = 0 y x = 1. (Ver figura 3.4) Resolución: Figura 3.4 1 2 1 4 3 4 1 y = x2 1 2 1 4 3 4 1 y = x2 i = 1 A =
- 73. arturo yle martínez dgep-uas 73 cálculo integral Rectángulo y = x2 Base Área x y (altura) 1 2 3 Sumatoria de las áreas parciales: A- = Σ Ai = A1 + A2 +A3 = + + = 1 4 1 2 3 4 1 4 2 = 1 16 1 2 2 = 1 4 3 4 2 = 9 16 1 4 1 4 1 4 1 64 A1 = 1 16 A2 = 9 64 A3 = 1 64 1 16 9 64 7 32 3 Rectángulo y = x2 Base Área x y (altura) 1 2 3 4 Sumatoria de las áreas parciales: A+ = Σ Ai = A1 + A2 +A3 + A4 = + + + = 1 4 2 4 3 4 1 4 2 = 1 16 2 4 2 = 4 16 3 4 2 = 9 16 1 4 1 4 1 4 1 64 A1 = 4 64 A2 = 9 64 A3 = 4 4 4 4 2 = 1 1 4 1 4 A4 = 1 64 4 64 9 64 1 4 4 15 32 Por tanto: 7 32A- < A < A+= 15 32= Y el área promedio es: A= = A- +A+ 2 2 7 32 15 32+ = 2 22 32 22 64 = = 0.34375 ≈ 1 3 i = 1 i = 1
- 74. unidad IIIcálculo integral 74 dgep-uas Ahora si dividimos en n-partes iguales el intervalo 0 ≤ x ≤ 1 y calculamos el área me- diante la suma de los rectángulos por arriba de la curva cuando el número de ellos crece indefinidamente el resultado es: Rectángulo y = x2 Base Área x y (altura) 1 2 3 • • • • • • • • • • • • • • • n 1 n 1 n2 1 n 1 n3 2 n 3 n n n 4 n2 9 n2 n2 n2 1 n 1 n 1 n n2 n3 32 n3 22 n3 Entonces la suma de las áreas es: 12 n3A+= n2 n3+ 22 n3 + 32 n3 + 42 n3 +...+ = (1 + 22 + 32 + 42 + ... + n2 )1 n3 Pero: S = 1 + 22 + 32 + 42 + ... + n2 = .n(2n + 1)(n+1) 6 12 n3A+= = = n(2n + 1)(n+1) 6 (2n2 + 3n +1) 6n2 2 6 + 3 6n + 1 6n2 2 6= 1 3 2 6 + 3 6n + 1 6n2∴ lim A+ = + 0 + 0 = =An→∞ limn→∞ De donde:
- 75. arturo yle martínez dgep-uas 75 cálculo integral Generalizando y formalizando el procedi- miento anterior para calcular áreas bajo una cur- va, podemos establecer que para determinar el área bajo una curva dividamos el intervalo [a, b] en n subintervalos iguales Δx1 = x1 −a, Δx2 = x2 − x1 ,.., Δxn = b−xn-1 donde cada uno de ellos será la base correspondiente a uno de los rectángulos los cuales podrán estar por arriba o por debajo de la curva, mientras que la altura de dicho rectán- gulo vendrá dada por el valor de la función para algún valor de x dentro de cada subintervalo, o sea y en particular yi = f (xi ). De donde podemos escribir el área aproximada por n rectángulos Sn bajo la curva como la suma de las áreas de todos los rectángulos de la siguiente manera: Sn = f(x1 )Δx1 + f (x2 ) Δx2 + ... + f (xn-1 )Δxn-1 + f (xn )Δxn = Σ f (xi )Δxi n i=1 Esto nos permite visualizar que si consideramos un número infinito de subintervalos en que se divida el intervalo [a,b] entonces,cada Δxi será cada vez más pequeño, Δxi → 0, y tendremos cada vez más rectángulos llenando el área bajo la curva, y en consecuencia el área definida por la suma se aproximará cada vez más al área total buscada hasta llegar a ser igual a ella, es decir: Lo cual nos indica, que el área real puede ser determinada mediante el cálculo del límite de la sumatoria de las áreas de los rectángulos usados en la aproximación. El cálculo del límite anterior también se presenta en el problema de calcular o de- terminar la distancia recorrida por un cuerpo que se mueve a lo largo de una curva, con velocidad variable v = f (t), en el intervalo de tiempo entre t = a y t = b. Supongamos que la función v = f (t) es continua, o sea, que en intervalos pequeños de tiempo la velocidad solo varía ligeramente. Se divide el intervalo [a,b] en n partes de longitudes Δt1 , Δt2 ,Δt3 ,..., Δtn . Para calcular un valor aproximado de la distancia recorri- da en cada intervalo Δti ,(con: i = 1, 2, 3, ..., n) vamos a suponer que la velocidad en este intervalo de tiempo es constante e igual a su verdadero valor en algún punto del mismo intervalo, en particular para ti . Luego, la distancia total recorrida estará expresada aproxi- madamente por la siguiente suma: S = lim Sn = lim ∑ f (ti ) ∆tiΔt → 0 Δt → 0 i = 1 n Sn = f(t1 )Δt1 + f (t2 ) Δt2 + ... + f (tn-1 )Δtn-1 + f (tn )Δtn = Σ f (ti )Δti n i=1 De donde, el valor real de la distancia recorrida en el tiempo b – a, será el límite de tales sumas para subdivisiones cada vez más finas o un número infinito de ellas, o sea cuando Δti → 0, en consecuencia: A = lim Sn = lim ∑ f (xi ) ∆xiΔxi → 0 Δxi → 0 i = 1 n
- 76. unidad IIIcálculo integral 76 dgep-uas Actividades de aprendizaje #13: 1. Completa el siguiente cuadro y menciona que representa geométricamente en cada cálculo :A+ Rectángulos A+ = Interpretación geométrica A+ n = 1 A+ = n = 8 A+ = n = 20 A+ = n = 50 A+ = n = 80 A+ = n = 100 A+ = n = ? A+ = 0.33 2 6 2 6n 1 6n2+ + 2. Aplicando el método de aproximaciones rectangulares sucesivas, y considerando que la suma de los cubos de los primeros n números naturales es igual a , calcular el área A comprendida entre la gráfica de la función y = x3 , el eje OX y las rectas verticales x = 0 y x = 1. (a) Mediante 2 rectángulos (b) Mediante 4 rectángulos (c) Mediante 8 rectángulos (d) Mediante un "número infinito" de rectángulos 3. Investiga cómo puede aplicarse este método de aproximaciones sucesivas pero con triángulos, en lugar de rectángulos, en la determinación de la fórmula para calcular el área de un círculo. 4. En la siguiente tabla se muestra las velocidades promedio que alcanza una persona en una bicicleta en diferentes intervalos de tiempo ∑ j3 =n2 (n+1)2 4j=1 n Horas Velocidad promedio (km / hora) 06: 00 - 07:00 20 07:00 - 08:00 16 08:00 - 09:00 14 09:00 - 10:00 12
- 77. arturo yle martínez dgep-uas 77 cálculo integral (a) Dibujar una gráfica que represente las velocidades promedio en el tiempo. (b) Calcular la distancia total recorrida por la persona entre las 06:00 y las 10:00 horas. 5. Una persona deja caer una pelota desde lo alto de un edificio, y ésta tarda 5 se- gundos en llegar al piso. ¿Qué altura tiene el edificio, si consideramos que la única fuerza que actúa sobre la pelota es la fuerza de gravedad? Nota: resolverlo como un problema de áreas. 6. Calcular la distancia recorrida por un automóvil de carreras que se mueve en el intervalo entre 0 y 1 minutos con velocidad variable según la función v = t2 . 3.2 El área y la Integral Definida. Para comenzar se utilizará un lenguaje y una simbología que posteriormente se precisará mejor. Si f (x) ≥ 0, el área comprendida entre el eje X, la gráfica de la función f (Ver figura 3.5) y las rectas verticales x = a y x = b se denota: y se lee área de f entre a y b. b aS (f (x)) 7 2 7 2 7 2S (3) = [∫3 dx] = [3x + c] = [3(7) + c]-[3(2) + c]= 15 Algunos ejemplos de aplicación de esta nueva notación para el área de figuras ele- mentales conocidas por ti, son las funciones representadas en la Figura 3.6. y y= f (x) x = a x Figura 3.5 x = b b aS (f (x)) f3 (x)= x2 0 1 c) 1 S (x2 )=- 1 0 1 3 S (3) = 15 7 2 3 0 2 7 f1 (x)=3 a) f2 (x)= x + 6 S (- x + 6) = 8 6 2 0 2 6 b) Figura 3.6 Además, usando la integral indefinida también se puede escribir que: 6 2 6 2 6 2S (-x+6) = [∫(-x+6)dx] = [ + 6x + c] = [ + 6(6) + c]-[ + 6(2) + c]= 8-x2 2 -62 2 -22 2
- 78. unidad IIIcálculo integral 78 dgep-uas En los ejemplos a) y b) la función dentro del símbolo para el área es una función lineal cuya gráfica es la recta que limita por arriba a la superficie de la figura sombreada. Por ejemplo, la primera es la recta de ecuación y = 3, y se trata del área de un rectángulo de base cinco (5=7-2) y altura 3. Utilizando la fórmula conocida se tiene que el área de ese rectángulo es 15, y se halla multiplicando la base por la altura del rectángulo (A=5x3=15). La segunda es la recta de ecuación y = -x + 6 , y se trata del área de un triángulo de base cuatro (4=6-2) y altura 4. De igual modo que en el ejemplo anterior, en este caso el área del triángulo (mitad del producto de la longitud de la base por la altura), que en este caso es (4 x 4) ÷ 2 = 8. En el último ejemplo, se trata del área que se forma debajo de la parábola de ecua- ción y=x2 en el intervalo de 0 a 1, y cuyo resultado ya fue determinado (en la página 74) apartir de la suma acumulada de un número infinito de rectángulos. Los resultados de estos tres ejemplos muestran la estrecha relación que existe entre el cálculo de áreas y el cálculo de integrales indefinidas, lo que nos permitirá más ade- lante definir una función de área apartir de la cuál se demostrará formalmente la relación que existe entre el cálculo diferencial y el cálculo integral. Para continuar este análisis introductorio hay que darle sentido a la nueva notación introducida utilizando los conceptos ya conocidos. La relación la establecemos mediante un nuevo concepto al que se denominará integral definida. Definición 1 Sea f (x) una función continua en un intervalo I, se llama Integral definida de f desde a hasta b (a, b ∈ I) y se denota al número donde F es una primitiva cualquiera de f, a y b son límites de integración. Esta definición es correcta pues la expresión F (b) – F (a) no depende de la primitiva, en efecto si G (x) es otra primitiva de f (x), tenemos: ∫ f(x)dx b a ∫ f(x)dx = F(b) - F(a) b a ∫ f(x)dx = G(b) - G(a) b a = [F(b)+c]-[F(a)+c] = F(b) - F(a)
- 79. arturo yle martínez dgep-uas 79 cálculo integral Con respecto a la notación ya conocida para las integrales indefinidas podemos re- tomarla ahora para la integral definida, solamente que en este caso aparecen los límites de integración, tal como se muestra en el esquema de abajo. Integral definida ∫ f(x)dx b a f (x) dx es el integrando ∫ es el símbolo integral • dx: indica que x es la variable con respecto a la cual f es derivada. • f (x): es la función subintegral • a y b son los límites de integración. Con esta definición sobre la integral definida, y retomando lo estudiado en el epígrafe anterior, resulta claro que también podemos escribir la siguiente expresión de igualdad: A = lim Sn = lim ∑ f (xi) ∆xi = ∫ f(x)dxΔxi → 0 Δxi → 0 i = 1 b a n La cual pone en evidencia que detrás del concepto de integral definida está un pro- ceso de cálculo aproximado de área mediante la determinación de un límite al infinito. Veamos ahora cómo se relaciona esta definición de integral definida con los ejem- plos introductorios de cálculo de áreas. Ejemplo 1. El del área del rectángulo. Ya qué: ∫ 3 dx = 3x + c En este caso se tiene, usando la definición y el hecho de que 3x es una primitiva de y = 3, que: Es el mismo resultado que se obtuvo mediante la fórmula conocida para el área de un rectángulo. Ejemplo 2. El del área del triángulo. En este caso se tiene que la primitiva de f (x) = -x + 6 es: ∫ 3dx = 3x + c | = [3(7) + c] - [3(2) + c]= 21 - 6 = 15 7 2 7 2 x2 2 F(x) = ∫(-x + 6)dx = - + 6x + c ∴ ∫ (-x + 6)dx = - + 6x + c = ? b 6 2 (x)2 2a
- 80. unidad IIIcálculo integral 80 dgep-uas = - + 36 + c -(- + 12 + c) = -18 + 36 - 10 = 836 2 4 2 De nuevo se obtiene el mismo resultado que utilizando la fórmula conocida del área del triángulo. Nota: Obsérvese como al calcular una integral definida la constante de integración de su función primitiva correspondiente siempre se elimina, por lo que se puede prescin- dir de ella en los cálculos. Hasta aquí se ha introducido un nuevo concepto, el de Integral Definida y en algu- nos ejemplos introductorios se ha calculado con dichas integrales el área debajo de la gráfica de la función del integrando en el intervalo determinado por los límites de inte- gración. Con ello se ha visto, a modo de introducción, la posibilidad de utilizar dicho concepto en el cálculo de áreas lo que será fundamentado en el epígrafe siguiente y que de ma- nera intuitiva utilizaremos en este epígrafe para ilustrar más claramente. Veamos otros ejemplos de cálculo de integrales definidas. Ejemplo 3. Calcula la integral definida: Resolución: Como , tendremos que ∫ x2 dx 3 1 1 3 F (x) =∫x2 dx = x3 + c A partir de la experiencia con los ejemplos introductorios podemos interpretar que el área debajo de la parábola y = x2 en el intervalo de 1 a 3 es .26 3 La región cuya área estamos postulando es la que aparece sombreada en la figura 3.7. Más adelante fundamentaremos esta afirmación. Figura 3.7 Esto es, se escribe la primitiva y se indican los límites de integración, luego se evalúa la función y se efectúa la diferencia indicada. La notación de la barra con el 6 y el 2 se utiliza para indicar que se debe evaluar la primitiva en 6 y restarle la evaluación en 2, donde 2 y 6 son los límites de integración. Calculando: ∫ (-x + 6)dx = - + 6x + c = - + 6(6) + c - + 6 (2) + c(x2 ) 2 6 6 2 (6)2 2 -(2)2 22 1 3 26 3 ∴ ∫ x2 dx = x3 = [33 - 13 ] =1 3 3 1 3 1
- 81. arturo yle martínez dgep-uas 81 cálculo integral El proceso para calcular integrales definidas se puede sintetizar en la siguiente regla que también se le denomina Regla de Barrow, en honor al teólogo y matemático inglés Isaac Barrow nombrado en las referencias históricas iniciales. Regla de Barrow Pasos para calcular la integral: ∫ f(x)dx a) Se busca una primitiva F(x) de f, Entonces: F(x) = ∫ f(x)dx b) Se calcula F(b) y F(a) y se calcula la diferencia F(b) - F(a) c) Se hace ∫ f(x)dx = F(b) - F(a) b a Las funciones para las que se puede calcular la integral definida desde x=a hasta x=b se llaman integrables en el intervalo [a,b]. De la definición 1 resulta entonces, que las funciones continuas son integrables. Las integrales definidas conservan las propiedades de las integrales indefinidas. Teorema 1 Si f y g son funciones continuas en un intervalo I ; (a, b ∈ I), se cumple: a) Para todo c ∈ ℜ; ∫ cf (x)dx = c ∫ f (x)dx b) ∫ [ f (x) + g(x)] dx = ∫ f (x)dx + ∫ g(x)dx c) ∫ f (cx + d)dx = F(cx + d) ; donde F '(x) = f (x) b a 1 c Estas operaciones resultan inmediatamente a partir de las propiedades de la integral indefinida. b a b a b a b a b a b a b a
- 82. unidad IIIcálculo integral 82 dgep-uas Ejemplo 4. Calcula las siguientes integrales definidas: a) ∫ 2x4 dx 3 0 2 1 b) ∫ + dx1 x 1 x2 c) ∫ cos2x dx π /2 0 d)∫ sen x dx 2π π /2 Resolución: d)∫ sen x dx = - cos x = - [cos 2π - cos (π / 2)]= -(1+ 0) = -12π π /2 2π π /2 En el ejemplo 4d anterior puedes apreciar que el valor de la integral definida también puede ser un número negativo. Eso sucede cuando la función es negativa en un intervalo dado. En este caso no representaría el área geométrica de- terminada por la gráfica sino un “área con signo” como en la figura 3.8. Esta idea se desarrolla en el epígrafe siguiente. Las integrales definidas poseen otras propiedades que dependen del intervalo tal como se muestra en el teo- rema 2. Este teorema no lo vamos a demostrar, pero su demostración es muy sencilla utili- zando de nuevo las propiedades de la derivación. Figura 3.8 c) ∫ cos2x dx = sen2x = (sen π -sen 0) = 01 2 1 2 π /2 0 π /2 0 x5 5 3 0 486 5 ∫ 2x4 dx = 2∫ x4 dx = 2 = 2 - =35 5 05 5a) 3 0 3 0 b) ∫ + dx =∫ dx + ∫ dx = ln x - = ln2 - - ln1- ≈ 1.21 x 1 x2 1 x 1 x2 1 x 2 1 1 2 1 1 2 1 2 1 2 1 Teorema 2. Si y = f (x) es continua en el intervalo (a , b), y además a < c < b, entonces se cumple: 1) ∫ f (x)dx = - ∫ f (x) dx ; Si se intercambian los límites el valor de la integral cambia de signo 2) ∫ f (x)dx = ∫ f (x) dx + ∫ f (x)dx ; La integral se puede calcular por tramos o subintervalos del intervalo principal b a b a b a c a b c
- 83. arturo yle martínez dgep-uas 83 cálculo integral Actividades de aprendizaje #13: 1. En el ejemplo de la figura 3.6c de la parabola (página 77), expresa el resultado usan- do la integral indefinida tal como se hizo en los casos 3.6a y 3.6b. 2. Aplica la integral definida para calcular el siguiente limite: 3. ¿Cumple la integral con las exigencias de la definición? 4. ¿Cuáles de las siguientes igualdades son correctas? Justifica (sin efectuar el cálcu- lo). ∫ dx-1 1 1 x a) ∫ (x - 1)dx = ∫ (1 - x)dx1 2 2 1 5. En equipo de 3 a 5 integrantes calcula las siguientes integrales definidas, y comprue- ba el resultado con un procesador. 8)∫ dx =0 π/4 x cos2 x2 b) ∫ x3 dx = ∫ x2 dx = ∫ (x3 + x2 )dx1 2 1 5 1 5 c) ∫ 6x3 dx = ∫ 6x3 dx = ∫ x3 dx1 2 2 5 1 5 d) ∫ x3 dx + ∫ x2 dx > ∫ (x3 +x2 )dx1 2 1 2 1 2 e) ∫ x2 dx + ∫ x2 dx + ∫ x2 dx = 01 2 2 5 1 5 1)∫ (-x2 +10x - x ) dx =1 2 3)∫ dx =x x2 + 7-2 0 5)∫ dx =x2 - x x +15 7 7)∫ dx =x -17 x2 + x - 123 6 9)∫ (9x - 5)4 dx =1 3 2)∫ (x4 -2x3 + 2)dx =-1 2 4)∫ dx =x2 2x3 -12 3 6)∫ dx =x + 4 2-4 0 10)∫ =dx x - x4 9 Lim + + + + ... + +1 n2 2 n2 3 n2 4 n2 n-2 n2 n-1 n2n → ∞
- 84. unidad IIIcálculo integral 84 dgep-uas 11)∫ dx =0 π/5 esen 5x sec 5x 12)∫ π (5 + x sen x )2 dx = 15)∫ =dx 1 - ex 17)∫ sen3 2x cos 2x dx =0 π/4 18)∫ sen4x dx =0 π 21)∫ cos4 x sen x dx =0 π/2 6. Calcular el área limitada por la recta y = 3x + 5, el eje X y las rectas x = -1 y x =4. 7. Calcular el área limitada por la parábola y = 3x2 + 3, el eje X y las rectas x = -1 y x = 3. 8. Determinar el área de la región R bajo la curva y = x4 -2x3 + 2 en los intervalos: (a) -1 ≤ x ≤ 0 (b) 0 ≤ x ≤ 2 (c) -1 ≤ x ≤ 2 9. Determinar el área de la región R bajo la curva y = 1 + x en los intervalos: a) 0 ≤ x ≤ 2 (b) 2 ≤ x ≤ 4 (c) 0 ≤ x ≤ 4 10. Determinar el área de la región R bajo la curva y = 25 - x2 en el intervalo -3 ≤ x ≤ 5. 13)∫ dx =ln x2 x-2 2 0 1 19)∫ 1 + 4x2 dx =0 4 23)∫ =x1/2 dx 1 + x3/40 1 25)∫ = (4x2 + 2x) dx (x2 + 1)(x2 +2x + 1)0 1 27)∫ x2 lnx dx =0 1 29)∫ ex senx dx =0 1 31)∫ x-2 dx = lim1 ∞ [∫ x-2 dx ]=1 ∞ 0 7 14)∫ dx =x2 - 4 x2 4 16)∫ 4 + 9x2 dx =0 3 4 e5x20)∫ 103x + dx =1 3 22)∫ 25 + x2 dx =0 5 24)∫ =dx (1 + x)3/2 + x + 10 1 26)∫ x lnx dx =-1 4 28)∫ x2 ex dx =0 3 30)∫ x2 cos x dx =0 1 b →∞ 32) ∫ dx = ∞ –∞ ex 1+e2x
- 85. arturo yle martínez dgep-uas 85 cálculo integral 11. Determinar el área de la región R bajo la curva y = sen x en el intervalo 0 ≤ x ≤ π. 3.3 Teorema fundamental del cálculo. En este epígrafe fundamentaremos la relación entre área e integración. Para ello definiremos una función que se le denominará función área debajo de la curva y la denotaremos A(x). Teorema 3 Si f (x) es una función continua en el intervalo [a,b] y definimos la función área A(x) tal que: A(x) = S ( f (x))= ∫ f(x)dx ; con x ∈ [a,b] entonces: a) A'(x)=f (x) para todo x ∈ (a,b) b) ∫ f(x)dx = F(b) - F(a) x a b a x a Una consecuencia de este teorema es que el área de la región comprendida entre la gráfica de la función y el eje X desde a hasta b (a<b) se calcula mediante la integral definida: ∫ f (x)dx , lo que fundamenta las afirmaciones de la introducción y nos permite calcular áreas que antes no podíamos calcular, y de una forma relativamente cómoda. Como te informamos en las referencias históricas de esta unidad, este teorema co- nocido como teorema fundamental del cálculo fue demostrado por el matemático ale- mán Gottfried W. Leibniz (1646-1716) y con él probó que la derivación y la integración son inversas. b a 0 0 Π/2 Π 3Π/2 2Π2Π ϕ Π 3Π/2 ω Π/2 y x y = sen (x) 1 R
- 86. unidad IIIcálculo integral 86 dgep-uas es el área de la región rayada que está comprendido entre el eje X y las verticales x y x+h y es el cociente entre esa área rayada (una especie de trapecio con el lado superior curvo) y su base que es x+h-x = h. Demostración del Teorema 3: Queremos calcular la derivada de la función A(x)=S (f (x)) representada (Fig. 3.9). Para ello usemos la definición de derivada y calculemos el límite: x a como: A(x+h)-A(x)=S (f (x))-S (f (x))=S ( f (x)) x+h a x a x+h x A(x+h) - A(x) h A´(x)= lim = f (x)h→ 0 A(x+h) - A(x) h Figura 3.9 El cociente es entonces la “altura media” que estará comprendida entre f (x) y f (x+h) y será más próxima a f (x) cuanto menor sea h. Por tanto el límite del cociente, cuando h tiende a 0 es f (x): A(x) y = f (x) A (x + h) - A(x) 0 a h x+h b { x ∫ f(x)dx b a lim h→ 0 A(x+h) - A(x) h = ? Ahora bien, como A(x) es una antiderivada o primitiva de f (x) resulta que: A(x)= F (x) + c donde F (x) es otra antiderivada de f (x). Por otro lado para x=a se tiene que: a a A(a)=∫ f (x)dx = F(a) + c = 0 ⇒ c = - F(a) b a ∴ A(b)= F(b) + c = F(b) - F(a)=∫ f (x)dx
- 87. arturo yle martínez dgep-uas 87 cálculo integral Ejemplo 5. Calcula el área de la región limitada por las rectas y = 5x; x = 2 y el eje de la abscisas. Resolución: Como f (x) ≥ 0, para toda x entre 0 y 2 (Ver figura 3.10) se tiene que: 2 0 ∫ 5xdx = 5∫ xdx = 5( x2 ) = 5( · 22 - 0) = 5(2) = 10u21 2 2 0 2 0 1 2 3.4 Aplicaciones de la integral definida al cálculo de áreas. Hasta ahora has visto cómo utilizar la integral definida para calcular el área de una superficie plana limitada por las rectas x = a ; x = b (a < b), el eje de las abscisas y la gráfica de una función f (x)≥ 0 continua para todo x de su dominio. En esos casos el teorema fundamental del cálculo permite calcular dicha área. Si la función es negativa entonces el área se calcula mediante el valor absoluto de la integral o de la función. Como pueden observar, este teorema exige que se conozcan los límites de integra- ción, y no siempre esa condición se cumple, o sea que se nos presentan situaciones en donde no están dados esos límites. Veamos el siguiente ejemplo. Ejemplo 6. Calcula el área de la región comprendida entre la curva y = -x2 + 4 y el eje de las abscisas. Resolución: En este caso no se indican los límites para el cálculo del área. La figu- ra 3.11 ilustra que la gráfica corta al eje “X” en dos puntos y el área comprendida entre la gráfica y el eje “X” está limitada por esos puntos; luego, debemos comenzar por calcular los puntos donde la gráfica corta al eje “X”, es decir, los ceros de f. Ya que sobre el eje X, y = 0, entonces: -x2 + 4 = 0, de donde x = ± 2, luego los límites de integración son -2 y 2. Figura 3.10 y x x = 2 y = 5x 5 0 1 2 3
- 88. unidad IIIcálculo integral 88 dgep-uas En estas condiciones ya podemos apli- car el teorema fundamental del cálculo. El área sería: Figura 3.11 Un análisis que se puede hacer a partir de la función (y =-x2 + 4) dada en el ejemplo anterior es que si reflejamos su gráfica en el eje X, obtenemos la gráfica de la función y = x2 - 4 . En la figura 3.12 aparece rayada su área en el intervalo de -2 a 2. Figura 3.12 Observen que el área rayada corresponde a una integral negativa, pero como el área de una región no varía al reflejarla en una recta, este resultado puede ser utilizado para calcular el área comprendida entre la gráfica de una función continua, positiva o negativa, y el eje “X”; basta utilizar el valor absoluto. (Ver figura 3.12) = - + 8 - -- + (-8)8 3 -8 3 =10 2 3 A = ∫ (-x2 + 4) dx = - + 4x 2 -2 x3 3 2 -2 A = ∫ (-x2 + 4) dx = ∫ (x2 - 4)dx = ∫ | x2 - 4| dx2 -2 2 -2 2 -2
- 89. arturo yle martínez dgep-uas 89 cálculo integral En general se tiene que el área A limitada por la gráfica de una función con- tinua f (x), el eje “X” y las rectas x = a, x = b está dada por: A =∫ f (x) dx b a No obstante esa no es la única situación que te vas a encontrar. Por ejemplo te pue- des encontrar otros casos como el siguiente. La gráfica de la función corta al eje X en un punto (hay un cero de la función) y está limitada por dos rectas que cortan al eje X en los puntos a y b. Observa en la fig 3.13 que en ese caso el resultado de la integral no representa al área buscada pues una parte es positiva y la otra negativa. Figura 3.13 Lo anterior es debido a las compensaciones que se producen de las partes positivas con las negativas como se muestra en la figura 3.13. En los dos casos siguientes la parte de la figura 3.14 representada corta en dos puntos al eje X, o sea, cada una de ellas tiene dos ceros en el intervalo [a,b]. Quedan entonces determinadas regiones que corresponden a resultados positivos y negativos de las integrales respectivas, y de nuevo no representan las áreas buscadas. Figura 3.14 La forma correcta de proceder en estos casos es calcular por separado las inte- grales de los diversos sectores y posteriormente sumar sus valores absolutos. Es decir la solución es calcular el área “a trozos” tomando la integral de la función si el área es positiva y el valor absoluto de la integral de la función si el área es negativa. Luego se suman las áreas obtenidas para obtener el área total. b
- 90. unidad IIIcálculo integral 90 dgep-uas En la figura 3.15 se ilustra que para calcular el área A es necesario descomponer el intervalo de integración en subintervalos, según la función cambie de signo. El área total es, entonces, una suma de áreas: A = ∫ f (x)dx -∫ f (x)dx + ∫ f (x)dx x 1 a x 2 x 1 b x 2 Observa que los límites de integración son las abscisas x=a y x=b, y los puntos de corte de la curva con el eje X, o sea los ceros de la función en ese intervalo. Si no están dados debes calcularlos. Ejemplo 7: Calcular el área de la región comprendida entre la gráfica de y = sen x y el eje “X” en el intervalo [ 0 , 2π]. La gráfica sería como la siguiente (fig. 3.16) : Figura 3.16 Resolución: hay que analizar el signo de y = sen x, sabemos que: Si x ∈[ 0 , π ], sen x ≥ 0 y Si x ∈[ π , 2π ], sen x ≤ 0 Figura 3.15 y 0 a bx1 x2 x y= f (x) y= f (x) y= | f (x) | y= f (x) π
- 91. arturo yle martínez dgep-uas 91 cálculo integral El área debe calcularse de -1 a 2 porque en ese intervalo la función limita un área con el eje “X” (fig. 3.17) pero hay que tener en cuenta que hay un cero intermedio que es x2 = 0. Luego hay que descomponer el intervalo de integración en dos subintervalos. Para encontrar el límite de integración que falta (se conocen 0 y 2π ) se tiene que determinar el cero de la función en ese intervalo pues es donde la función cambia de signo. Este es π pues sen π = 0. Entonces: Ejemplo 8: Calcula el área de la región comprendida entre el gráfico de la función f (x) = x3 - x2 - 2x y el eje “X”. Resolución: Para calcular el área debemos analizar donde la gráfica corta al eje “X”. Como en este caso no tenemos la gráfica debemos calcular donde la función cambia de signo, o sea, los ceros de la misma: x3 - x2 - 2x = 0, o sea x (x - 2)(x+1) = 0 de donde se tiene que x1 = -1 ; x2 = 0 ; x3 = 2 que son también los limites de integración. + + -1 0 2 Figura 3.17 Vemos que f es no negativa en [-1 , 0] y no positiva en [ 0 , 2], (fig. 3.17) Luego el área buscada se calcula mediante la integral: 5 12 = - - = u28 3 37 12 Observa que los ceros encontrados, hay que ordenarlos de menor a mayor para utili- zarlos como límites de integración. En este ejemplo, la gráfica de la función es la siguiente (Figura 3.18): A = ∫sen x dx + ∫ sen x dx = - cos x | + cos x | = - (-1-1) + (1-(-1))=4u2 0 π π 2π 0 π π 2π A = ∫ (x3 - x2 -2x)dx - ∫(x3 -x2 -2x)dx = - - x2 - - - x2 -1 0 0 2 x4 4 x3 3 -1 0 x4 4 x3 3 0 2 = 0 - - - ( - 1)2 - - - 22 -0(- 1)4 4 24 4 23 3 (- 1)3 3
- 92. unidad IIIcálculo integral 92 dgep-uas Por lo general no te van dar la gráfica de la función a la que le debes determinar su área. Si la representas eso te ayudaría a orientar el cálculo que debes hacer. Actividades de aprendizaje #14: 1. En los siguientes ejercicios, traza la gráfica correspondiente y luego, auxiliándote del cálculo integral, determina el área. a) limitada por la recta y = 2x, el eje X y la recta x = 6 b) limitada por la recta x + y = 10, el eje X y las rectas x = 2 y x = 8. c) Comprueba cada resultado de los incisos anteriores, hallando el área por la fór- mula estudiada en geometría. 2. Traza las gráficas de las funciones siguientes y calcula en cada caso el área de la región limitada por el gráfico de la función, el eje X y las rectas x = a y x = b donde a y b son los extremos de los intervalos dados. a) y = x2 [-4,-2] b) y = x + 2 [ -2, 5] c) - x2 + 4 [ -2 , 2] d) y = x [1 , 4] e) y = x2 + 1 [-1, 1] f) y = x3 [-3, 3] Figura 3.18
- 93. arturo yle martínez dgep-uas 93 cálculo integral 3. Demuestra, usando el cálculo integral, que: a) El área de un rectángulo es el producto del largo por el ancho. b) El área de un triángulo rectángulo es el semiproducto de los catetos. c) El área de un trapecio rectángulo es el producto de la semisuma de las bases por la altura. 4. Comprueba que ∫ x dx = 0 y que el área de la región determinada por la función y = x en el intervalo[-1, 1] es igual a 1u2 . Justifica por qué el área no se corresponde con el valor de la integral. 5. Calcula al área de la figura limitada por la parábola y = -- x2 y por las rectas x =1, x = 3 y el eje de las abscisas. 6. Calcula el área limitada por la parábola y = 4x - x2 y el eje de las abscisas. 7. Determina el área bajo cada una de las curvas siguientes en el intervalo indicado. 1 -1 1 2 a) y = x -2 en 2 ≤ x ≤ 5 b) y = x3 en 1 ≤ x ≤ 3 c) y = sen 3x en 0 ≤ x ≤ d) y = ex -1 en -1 ≤ x ≤ 0 e) y = en 2 ≤ x ≤ 4 π 3 3 x 7. La figura 3.19 muestra la curva y = x2 - x3 en el intervalo [0 , 2]. Calcula el área sombreada. Figura 3.19 y 0 1 2 x -4
- 94. unidad IIIcálculo integral 94 dgep-uas 8. Calcula el área de la región limitada por la función f y el eje de las abscisas. a) y = 4x + x2 b) y = x3 - 6x2 + 8x b) y = x3 -7x + 6 d) y = x2 - 7 x + 6 Áreas comprendidas entre dos o más curvas. Otra aplicación importante del cálculo integral es la posibilidad de calcular áreas comprendidas entre dos o más curvas. Sean y = f (x), y = g (x) dos funciones, sus gráficas comprenden una región sobre el intervalo limitado por las abscisas de los puntos de intersección de ambas curvas (fig. 3.20). y f (x) g(x) 0 x1 x2 x Figura 3.20 En la figura 3.20 podemos ver que si ambas funciones son no negativas y g(x) ≤ f (x) para todo x ∈ [x1 , x2 ], el área limitada por ellas puede calcularse: A = ∫ f (x)dx - ∫ g(x)dx = ∫ [f (x) - g(x)] dx x2 x1 x2 x1 x2 x1 En general si f y g son dos funciones continuas, el área entre dos curvas se calcula: A = ∫ | f (x) - g(x)| dx ; donde x1 y x2 son las abscisas de los puntos de inter- sección. Si tenemos más de dos puntos de intersección el área se calcula por partes. x2 x1 Ejemplo 9: Calcula el área limitada por los gráficos de: (a) f (x) = x y g(x)=x2 (b) f (x) = x y g(x) = x3 .
- 95. arturo yle martínez dgep-uas 95 cálculo integral Resolución: (a) En la figura 3.21 se ha representado ambas curvas. Para calcular el área debe- mos determinar los puntos de intersección y para hacerlo planteamos la igualdad x = x2 , equivalente a x2 - x = 0 de donde se tiene que x1 = 0, x2 = 1 Como en el intervalo [ 0, 1] la función x2 - x es no positiva, entonces: x2 2 = - = - = u2x3 3 1 0 1 2 1 3 1 6 (b) También aquí planteamos la igualdad x= x3 que es equivalente a x3 - x = 0. Resol- viendo la ecuación x (x2 -1) = 0 se tiene que: x ( x - 1) (x +1) = 0 ⇒ x1 = 0 ; x2 = 1 ; x3 = -1 Por tanto, los ceros son x = -1, x = 0 y x = 1 estos valores son también los límites de integración. Analicemos el signo de x3 - x. En la figura 3.22, se tiene el comportamiento de los signos de la función en los inter- valos determinados por los ceros. + + -1 0 1 Figura 3.22 Entonces, los intervalos que interesan para la integración son los que están entre los límites. En el intervalo [-1 , 0] es no negativa y en el [ 0 , 1] no positiva. Para calcular el área entre las curvas y = x3 y y = x hay que tener en cuenta el módulo de x3 - x es igual a x3 - x en el intervalo [-1 , 0] pues x3 - x > 0 . De igual modo el módulo de x3 - x es igual a x - x3 en el intervalo [ 0 , 1] pues x3 - x < 0. Entonces el área se calcula mediante la integral: A =∫ |x3 - x|dx + ∫ |x3 -x |dx-1 0 0 1 y x1 = 0 x2 = 1 x Figura 3.21 0 1 -1 0 = ∫ (x3 - x) dx + ∫ ( x - x3 ) dx A = ∫ |x2 - x|dx = ∫ (x - x2 )dx 1 0 1 0 = - + - = - + + - =x4 4 x2 2 -1 0 x4 4 x2 2 0 1 1 4 2 1 2 1 1 4 2 1 y x1 = -1 x2 = 1 x0
- 96. unidad IIIcálculo integral 96 dgep-uas b) -3 -1 0 x y = 1 x y y 0 2 x c) y = x - 1 y y = x2 + 4x - 3 a) 0 x d) y 0 y = sen x y = π x - x2 π x f (x) = 2 cos bx e) y 2 0 xπ π 4 3π 4 x y -1 10 g(x) = x –1 f (x) = x +1 f) Actividades de aprendizaje #15: 1. Calcula el área de las regiones representadas en las figuras de abajo.
- 97. arturo yle martínez dgep-uas 97 cálculo integral Figura 3.23 h(x) = 1- x g) y 0 x g(x) = x +1 q(x) = - x + 4 h) y 0 x f (x) = x +2 2. Calcula el área de las regiones representadas en la figura 3.24. Figura 3.24 a) y = ex y 1 0 1 x SUGERENCIA: (x ln x - x)' = ln x y = lnx y 0 1 e x b)
- 98. unidad IIIcálculo integral 98 dgep-uas 6. El área de la porción del plano limitada por la función f (x) = - (x ≠ 0) y el eje de las abscisas en el intervalo [k , 1] es 26 u2 . ¿Cuál es el valor numérico de k en dicho in- tervalo? 7. Calcula el área limitada por la curva y = x3 - 9x2 + 24x - 18, el eje de las abscisas y dos rectas paralelas al eje de ordenadas y trazadas de manera que pasan por los puntos de extremos locales de la función. 8. Calcula el área comprendida entre la curva y = -x2 - x + 12, el eje de las abscisas y la tangente a la curva en el punto de abscisa x = -1. 3 x4 3. Sean las funciones f (x) = x2 - 6x + 8 y g(x) = – 3x .Determina el área de la región del plano limitada por las funciones f y g. 4. Calcula el área comprendida entre las curvas. a) y = x + 1 , la recta y = x + 1 y el eje "X" b) y = 1 - x , y = ex - e y x = 0 c) y = x , y = 2 - x y y = 0 d) x2 = 4y, x2 = 8y - 4 5. El área bajo la curva comprendida por el gráfico de la función y = x - 3 y el eje “X” en el intervalo 3 ≤ x ≤ b es A = . Determina el valor de b.4 2 3 9. Investiga y contesta las siguientes cuestiones: a) ¿Qué diferencia esencial existe entre el Cálculo Diferencial y el Cálculo Integral? b) ¿Qué afirma y para qué sirve el Teorema Fundamental del Cálculo? c) ¿Cuál es la condición analítica que garantiza que una función sea siempre inte- grable en un intervalo cerrado? d) ¿Conoces algún software con el cual se puedan calcular integrales? Nota: si tu respuesta a esta cuestión es afirmativa describe brevemente dicho soft- ware, en caso contrario, investiga al respecto.
- 99. arturo yle martínez dgep-uas 99 cálculo integral UNIDAD DE APRENDIZAJE IV APLICACIONES DE LA INTEGRAL Competencia de unidad: Aplica en forma crítica y reflexiva el cálculo integral en la modelación, formulación y resolución de problemas en diversos contex- tos, y hace una evaluación de los resultados COMPETENCIAS DISCIPLINARES A DESARROLLAR 1. Construye e interpreta modelos matemáticos mediante la aplicación de procedimien- tos y operaciones aritméticas, algebraicas, geométricas y variacionales, para la com- prensión y análisis de situaciones reales, hipotéticas o formales. 2. Formula y resuelve problemas matemáticos, aplicando diferentes enfoques. 3. Explica e interpreta los resultados obtenidos mediante procedimientos matemáticos y los contrasta con modelos establecidos o situaciones reales. 4. Argumenta y comunica la solución obtenida de un problema, con métodos numéri- cos, gráficos, analíticos y variacionales, mediante el lenguaje verbal, matemático y el uso de las tecnologías computacionales, informáticas y de la comunicación. 5. Analiza las relaciones entre dos o más variables de un proceso social o natural para determinar o estimar su comportamiento. 6. Cuantifica, representa y contrasta experimental o matemáticamente las magnitudes del espacio y las propiedades físicas de los objetos que lo rodean. 8. Interpreta tablas, gráficas, mapas, diagramas y textos con símbolos matemáticos y científicos. CONTENIDO TEMÁTICO: 4.1 Introducción 4.2 Volumen de sólidos de revolución 4.3 Longitud de un segmento de curva 4.4 Otras aplicaciones (en base a proyectos)
- 100. unidad IVcálculo integral 100 dgep-uas UNIDAD DE APRENDIZAJE IV APLICACIONES DE LA INTEGRAL 4.1 Introducción Esta unidad de aprendizaje tiene un carácter integrador de todo el curso, y también de todos los cursos del área de matemáticas, y aunque es de carácter obligatorio al igual que las restantes, aquí se recomienda seleccionar las aplicaciones en función del tiempo disponible para finalizar el curso, y de las capacidades, habilidades e intereses de los alumnos. El concepto y las propiedades de la integral definida y su relación con el área tam- bién pueden ser utilizados en multitud de fenómenos de otra naturaleza no propiamente geométrica como has visto hasta ahora. A continuación verás algunas de estas aplica- ciones. 4.2 Volumen de sólidos de revolución (Método del disco). Si f es una función continua y no negativa en el intervalo cerrado [a, b]. Recibe el nombre de sólido de revolución, el sólido generado al girar alrededor del eje X, la región limitada por la gráfica de la función y = f (x), el eje X y las gráficas de las rectas x=a y x=b. El eje X es un eje de simetría de dicho sólido y una sección recta perpendicular al eje X es un círculo (Ver Figura 4.1). Tal como se ilustra en la figura 4.1 para determinar el volumen de este tipo de sóli- dos, seguiremos un procedimiento similar (llamado método del disco) al utilizado para el área de una región, aproximando el volumen de un sólido de revolución por medio de una suma de volúmenes de sólidos más elementales cuyos volúmenes individuales ya están determinados.
- 101. arturo yle martínez dgep-uas 101 cálculo integral En particular vamos a considerar n discos o cilindros circulares de igual espesor (Δx) como los sólidos elementales, asumiendo que el volumen de un disco circular Vi es, por definición, el producto del área de la base (A= π y2 ) por el espesor. Por tanto, el volumen de un disco o cilindro representativo en base a la función será: Vi = π [f (xi )]2 Δx Luego, el volumen total V del sólido de revolución debe ser aproximadamente igual a la sumatoria de todos los Vi , es decir: V≈ π [f(xi )]2 Δx1 + π [f(xi )]2 Δx2 +...+ π [f(xi )]2 Δxn = ΣVi = Σ π [f(xi )]2 Δxi i=1 i=1 n n Y de manera semejante al problema de área, al considerar el límite de la sumatoria de un número infinito de discos o de cilindros, lo cual es equivalente a decir que n tiende a infinito (n → ∞) o que el espesor de los discos tiende a cero (Δx → 0), se obtendrá el valor exacto del volumen del sólido de revolución, el cual estará determinado por la ex- presión siguiente: Ejemplo 1: Calcula el volumen del sólido de revolución que se genera al girar en torno al eje X, la región limitada por la gráfica de la función f (x) = x y la recta x = 4 . (Ver Figura 4.2) Resolución: V= π ∫ [ f (x)]2 dx = π ∫ x dx = π ∫ x dx = = (42 - 02 ) = 8π u3b a 4 0 2 4 0 πx2 2 4 0 π 2 V= lim Σ π [f(xi )]2 Δx = π . lim Σ [f(xi )]2 Δx = π ∫ [f (x)]2 dxn → ∞ i=1 n Δx → 0 i=1 n b a Figura 4.2
- 102. unidad IVcálculo integral 102 dgep-uas Ejemplo 2: Calcula el volumen de una esfera de radio r. Resolución (ver Figura 4.3): en este caso se puede considerar que la curva que genera a la esfera es la correspondiente a la ecuación de la circunferencia de radio r. O sea: y2 + x2 = r2 . Figura 4.3 Ejemplo 3: Calcula el volumen de un cono de radio R y altura h. Resolución: Primeramente dibujemos un cono en el sistema coordenado tal como se muestra en la figura 4.4. Luego determinamos la ecuación de la función cuya gráfica es una recta que al girar alrededor del eje X genera el sólido de revolución de forma có- nica. A partir de los datos se obtiene que dicha ecuación es: y - y1 = m (x-x1 ) R h ⇒ y - 0 = - (x -h) ∴ y = - x + RR h Por lo tanto, el volumen será: = π - x2 + R2 x = π h - R2 h + R2 h = πR2 h u31 3 h 0 R2 h2 x3 3 R2 h R2 3 Figura 4.5 O -r r y = r2 - x2 ⇒ y = r2 - x2 ∴V = π ∫ r 2 - x2 dx r -r 2 = π r2 x - r -r x3 3 = πr34 3 = π ∫ (r2 -x2 ) dx r -r V= π ∫ [ f (x)]2 dx = π ∫ - x + R dxh h 0 2 R h0 h 0 R2 h2 2R2 h = π∫ x2 - x + R2 dx
- 103. arturo yle martínez dgep-uas 103 cálculo integral 4.3 Longitud de un segmento de curva De manera similar a como el área bajo una curva se puede aproximar por las áreas de los rectángulos bajo (o arriba) de ella, la longitud de una curva puede ser aproximada por pequeños segmentos de recta tal como se muestra en la figura 4.5. Sea una curva cualquiera, definida por una función y = f (x), y supongamos que que- remos aproximar la longitud del arco de curva S desde un punto donde x = a hasta un punto donde x = b. Con este propósito podemos construir una serie de n (n = 6) triángulos rectángulos cuyas hipotenusas concatenadas "cubran" el arco de curva elegido tal como se ve en la figura 4.5. Para facilitar los cálculos podemos hacer que las bases de todos los triángulos sean iguales a Δx, de manera que al aplicar el teorema de Pitágoras existirá para cada triángulo un cateto Δy y una hipotenusa Δs relacionados por las expresiones: Δy Δx = 1 + (Δx) 2 (Δs)2 = (Δx)2 + (Δy)2 ⇒ Δs = (Δx)2 + (Δy)2 = (Δx)2 + (Δy)2 Δx Δx De donde, una aproximación de S estaría dada por la sumatoria de todas las n hipo- tenusas desplegadas. Obteniéndose que: S ≈ ∑ Δyi Δxi 1+ · Δxi 2n i =1 Resulta fácil imaginar que mientras más pequeñas sean estas n hipotenusas (n seg- mentos de recta), mejor será la aproximación buscada. Por lo cual haremos que Δx tienda a cero (Δx→0), lo que equivale a trazar un número infinito de pequeños triángulos rectángulos de hipotenusas infinitamente pequeñas. Figura 4.5 Δy Δx a x1 x2 x3 x4 x5 b x Δs y = f (x)
- 104. unidad IVcálculo integral 104 dgep-uas Pero, cuando Δx→0, Δx es igual a dx, y Δyi / Δxi se transforma en el cociente de dife- renciales dy/dx, que es por definición la derivada de la función ( f '(x)), resulta que como consecuencia de estos cambios, la aproximación de la sumatoria anterior se convierte en un valor exacto para la longitud S del arco de la curva, y da origen a la siguiente integral definida: S = Lim ∑ Δyi Δxi 1+ · Δxi =∫ 1 + (f '(x))2 dx ∞ i =1Δx→0 b a 2 Ejemplo 4: Calcula la longitud S del segmento de la curva y = 4x+2 del punto (-3,-10) al punto (2,10). Resolución: ya que f '(x) = 4, y haciendo a = -3 y b = 2, se obtiene que. S =∫ 1 + (f '(x))2 dxb a =∫ 1 +(4)2 dx = 17 ∫ dx = 17 (2-(-3)) = 5 17 u2 -3 2 -3 Nota: dado que en este caso se trata de una función lineal, comprueba que se obtie- ne el mismo resultado aplicando la conocida fórmula d = (y2 - y1 )2 + (x2 - x1 )2 que se aplica para calcular la distancia entre dos puntos de una recta. Ejemplo 5: Calcula la longitud S del segmento de la curva y = x3/2 de punto (0, y1 ) al punto (4, y2 ). Resolución: ya que f '(x) = x1/2 , y haciendo a= 0 y b= 4, se obtiene que.3 2 S =∫ 1 + (f '(x))2 dx = ∫ 1+ x1/2 dx = ∫ 1+ x dx = ?b a 4 0 3 2 2 4 0 9 4 Esta integral se puede resolver haciendo el siguiente cambio de variable: u = 1+ x ⇒du = dx ⇒ dx = du9 4 9 4 4 9 Por tanto: S =∫ 1 + x dx = ∫ u du = = ∫ u du= u0 4 9 4 0 4 1 2 4 9 4 9 0 4 1 2 8 27 3 2 0 4 3 9 4 = 1+ x = 1+ (4) - 1+ (0) = [10 10-1]≈ 9.078 27 4 0 8 27 9 4 3 9 4 3 8 27
- 105. arturo yle martínez dgep-uas 105 cálculo integral Actividades de aprendizaje #1: 1. Calcula el volumen del sólido de revolución que se genera al girar en torno al eje X, la región limitada por la gráfica de la función f (x) = x + 3 y la recta x = 5. 2. Calcula el volumen del sólido de revolución que se obtiene al girar la gráfica de la función f (x) = x + 2 en torno al eje X en el intervalo [0,4]. 3. Calcula el volumen del sólido de revolución que se obtiene al girar la gráfica de la función f (x) = ex en torno al eje X en el intervalo [0,1]. 4. Calcula el volumen del sólido de revolución que se obtiene al girar la gráfica de la función y = x3 en torno al eje X en el intervalo [0,2]. 5. Calcula el volumen de un cono de radio 5 y altura 20. 6. Calcula el volumen que genera la región limitada por las gráficas de las curvas f (x) = x +2 y f (x) = x2 cuando giran alrededor del eje X. 7. Calcula el volumen del sólido de revolución que se genera al girar alrededor del eje X la región entre las gráficas de las funciones f (x) = x3 y f (x)=x. 9. Calcula la longitud del arco de la curva y = 2 x3 en el intervalo [1, 5]. 10. Calcula la longitud del arco de la gráfica de y = x2 en el intervalo [1, 4]. 11. Calcula la longitud de la curva x2 + y2 = 16 en el intervalo [1, 3]. 12. Calcula la longitud de la curva en el intervalo , . 13. Sea y = f (x) una función continua en el intervalo a ≤ x ≤ b. Entonces el valor pro- medio VP de la función en dicho intervalo está determinado por la integral definida: a) Calcula VP de en el intervalo 0 ≤ x ≤ 6 b) Calcula VP de en el intervalo 50 ≤ x ≤ 70 f (x)= +x4 2 x-2 16 1 2 3 2 8. Cuando en un sólido de revolución el eje de giro es el eje Y, el volumen se de- termina por la expresión . Calcular el volumen que genera la región limitada por x = y y las rectas y = 0 y y =3, si gira alrededor del eje de las Y. V =π ∫ [f (y)]2 dy b a 1 b–a VP = ∫ f (x)dx b a 750x 4x2 +25 f (x) = 100(lnx–2) x f (x) =
- 106. unidad IVcálculo integral 106 dgep-uas 4.4 Otras aplicaciones (basadas en proyectos) El objetivo central de este apartado es que el alumno, conforme a sus intereses, se- leccione un campo disciplinar y al menos tres situaciones problemáticas (o problemas) de dicho campo que requieran para su resolución de los conceptos y procedimientos del cálculo integral. En consecuencia este apartado se trabajará basado en proyectos de investigación grupal. Los problemas seleccionados deberán estar dentro de uno de los siguientes campos disciplinares o de conocimiento: Campo de la matemática: Problemas sobre cálculo de probabilidades Problemas sobre la resolución de ecuaciones diferenciales de variables separables. Problemas contextualizados sobre la determinación del valor promedio de una función. Campo de la física: Problemas sobre el movimiento de un cuerpo. Problemas sobre el cálculo del trabajo producido por una fuerza variable. Problemas sobre la determinación de la presión y fuerza ejercida por un fluido. Problemas sobre la ley de enfriamiento de Newton. Campo de la química, biología y medicina: Problemas sobre velocidades de reacciones químicas. Problemas sobre crecimiento de poblaciones. Problemas sobre la acumulación o concentración de medicamentos Campo de las ingenierías: Problemas sobre cálculo de momentos, centro de masas y centroides de una lámina homogénea. Problemas sobre circuitos eléctricos. Campo de economía y administración: Problemas sobre economía Problemas sobre acumulación de capital y valor presente de flujos de dinero. Problemas sobre costo total de producción.
- 107. arturo yle martínez dgep-uas 107 cálculo integral Justificación, forma, metodología y contenidos del proyecto: Para la ejecución del proyecto, tanto el profesor como los estudiantes deberán tener en consideración que el aprendizaje basado en proyectos está orientado a un saber hacer complejo de donde adquiere su carácter interdisciplinario o multidisciplinario, por lo cual en su desarrollo posiblemente se necesiten múltiples recursos y medios, así como de la promoción y puesta en juego de un conjunto de competencias tanto genéricas como disciplinares que posibilitan una actuación activa, autónoma, creativa y colaborativa del estudiante. De donde, la enseñanza y aprendizaje basada en proyectos se constituye en una estrategia didáctica pertinente para la promoción y evaluación de las competencias disciplinares de matemáticas que conforman el perfil del egresado del nivel medio supe- rior. El proyecto deberá ser realizado de manera colaborativa, donde se integren equipos de 5 a 6 estudiantes, y deberá ser desarrollado y presentado describiendo los siguientes lineamientos de forma, metodología y de contenido: 1. El docente informará a los alumnos de los tiempos y formas del trabajo. 2. Los alumnos informarán al docente sobre los integrantes del equipo y del cam- po disciplinar de donde se seleccionarán los problemas a investigar y resolver durante el proyecto. 3. El equipo deberá justificar brevemente en el reporte escrito las razones por la cual seleccionó el campo disciplinar. 4. En cada problema resuelto se deberá incluir mínimamente el enunciado del problema, los desarrollos matemáticos donde se deducen las fórmulas y ex- presiones matemáticas utilizadas en el proceso de resolución del problema, los cálculos y operaciones matemáticas realizadas, y una evaluación y análisis de la pertinencia de los procedimientos y resultados obtenidos, y finalmente las fuentes de donde obtuvo la información necesaria para resolverlo. 5. El profesor, en el salón de clases, deberá darle asesoría en tiempo y forma a los equipos que lo soliciten previamente, y en caso de que la situación rebase sus posibilidades los orientará para que la busquen con especialistas del campo disciplinar o de conocimiento. 6. El equipo deberá hacer frente al grupo, al menos una vez, un informe y una presentación verbal de los avances y de los resultados parciales obtenidos. Así como, hacer correcciones a su trabajo en caso de que se le señalen errores en el proceso de resolución. 7. El equipo entregará un reporte escrito al maestro, en tiempo y forma, de su in- vestigación final, y con anexos (por ejemplo formularios) al final, en caso de ser necesario. 8. El equipo hará frente al grupo una presentación y defensa de su investigación final. 9. Del cumplimiento de los puntos anteriores se considerarán los criterios e indi- cadores para evaluar el proyecto de investigación realizado por los equipos.
- 108. unidad IVcálculo integral 108 dgep-uas Actividades de aprendizaje #2: 2. Diseña y desarrolla, en equipo de 5 a 6 integrantes, un proyecto sobre aplica- ciones del Cálculo Integral donde resuelvan al menos tres problemas de un campo de conocimiento previamente elegido por el equipo y autorizado por el profesor o profesora de la asignatura. 1. Investiga y contesta las siguientes cuestiones: a) ¿Qué es un modelo matemático? b) ¿Qué diferencia existe entre problema real y el problema matemático mediante el cual se representa?
- 109. arturo yle martínez dgep-uas 109 cálculo integral A) BÁSICA: 1. Oteyza, Elena. (2006). Conocimientos fundamentales de matemáticas: cálculo diferencial e integral. México. Pearson-Educación y UNAM. 2. Fuenlabrada, Samuel. (2008). Cálculo Integral. México. McGrawHill. 3. Cuéllar, C. Juan Antonio. (2007). Matemáticas VI: Cálculo Integral. México. McGrawHill. 4. Larson, R.E. y Hostetler, P.R. y Edwrsds, H.B. (2009). Cálculo Integral: Matemáticas II. México, McGrawHill. 5. GRANVILLE, W. A. (2006). Cálculo Diferencial e Integral. México, Editorial Limusa. 6. Salazar, Guerrero, Ludwing J. y Otros Autores. (2009). Cálculo Integral. México, Grupo Editorial Patria. B) COMPLEMENTARIA: 7. D. Hoffmann, Laurence y Otros autores. (2006). Cálculo Aplicado. México, McGrawHill. 8. Hughes-Hallett y Otros Autores. (2004). Cálculo Aplicado. México, CECSA. 9. Cruse, A. B. y M. Lehman. Lecciones de Cálculo II. Introducción a la integral. Fondo Educativo Interamericano. 1982. 10. Hackett, S. O. y M. Sternstein. (1982). Cálculo por Objetivos. México, Editorial CECSA. 11. Mochon, S. (1994). Quiero entender el Cálculo. México. Grupo Editorial Iberoamérica. BIBLIOGRAFÍA DE CONSULTA PARA EL ESTUDIANTE Y EL PROFESOR
- 110. unidad IVcálculo integral 110 dgep-uas
- 111. arturo yle martínez dgep-uas 111 cálculo integral Cálculo II Cálculo Integral Para Bachillerato Segunda edición Arturo Ylé Martínez José Alfredo Juárez Duarte Faustino Vizcarra Parra Se terminó de imprimir en el mes Diciembre de 2012, en los talleres gráficos de Servicios Editoriales Once Ríos, Rio Usumacinta 821, Col. Industrial Bravo, C.P. 80120 Culiacán, Sinaloa, México. Tel. 7-12-29-50. La edición consta de 6, 500 ejemplares.
- 112. unidad IVcálculo integral 112 dgep-uas





















![arturo ylé martínez
dgep-uas 21
cálculo integral
O sea, cuando Δx→0 el diferencial dy se puede usar para calcular el incremento de
la variable independiente, con la seguridad de que el error cometido será mínimo.
Problemas y ejercicios de cálculos aproximados utilizando la diferencial:
1. Un móvil se mueve según la relación s= 5t2
+ t, donde s representa el espacio
recorrido medido en metros y t el tiempo medido en segundos. Calcular Δs los
metros que recorre el móvil en el tiempo comprendido entre 7 segundos y 7 + 1/3
segundos.
A) Resolución usando el diferencial ds:
Diferenciando la expresión s= 5t2
+ t ds= (10t +1) ∙ dt ,
Por otro lado, Δt = dt = (7 + 1/3) - 7 = 1/3.
Sustituyendo en la expresión de ds : ds = (10 x 7 + 1) . - = 23.66 metros1
3
:
B) Resolución usando el incremento Δs:
Como se observa se ha cometido un error de: _________cm. ¿Por qué?
2. Calcular de manera aproximada el valor de 3.052
.
Resolución usando el diferencial dy: Para encontrar un resultado aproximado de
3.052
se considera la función y = x2
, cuyo diferencial es: dy = 2x · dx. Por la proximidad
de 3.05 a 3 (5 centésimas) se calculará la diferencial en el punto de abscisa x=3 y
se llevará a la expresión del diferencial dy.
En este caso: dx = 3.05 – 3 = 0.05 dy = 2(3)(.05) = 0.30
Por tanto, ya que:
Δs= 5 7 + - + 7 + - - [5 (7)2
+ 7]= 24.22 metros
1
3[
2
1
3 [
dy ≈ f (x + ∆x) - f (x) = ∆y f (x + ∆x) = f (x) + ∆y ≈ f (x) + dy
.·. 3.052
= f (x + ∆x) = f (x) + dy = x2
+ dy = 32
+ 0.30 = 9.30](https://image.slidesharecdn.com/56calculoii-201118004256/85/56-calculo-ii-21-320.jpg)





















![arturo yle martínez
dgep-uas 43
cálculo integral
Actividades de aprendizaje # 7:
1. Comprueba, en equipo de 3 a 5 integrantes como máximo, que son válidas las fór-
mulas de integración de la tabla anterior, y comunica tus resultados al resto de los
equipos.
2. Aplicando la tabla y fórmulas de integración calcula en equipo de 3 a 5 integrantes
las siguientes integrales indefinidas inmediatas, y haz la comprobación del resultado
mediante derivación:
a) ∫(4x3
+ x6
– 0.5x-3
) dx = b) ∫(6 x2
+ x + ) dx =3
x
8
c) ∫(x - 5)2
dx = d) ∫(x- 6)(2x + 1) dx =
g) ∫x(1- x2
)dx =
j) ∫(ex
+4x
-e0
) dx =
k) ∫(e4x
- 3x) dx = l) ∫(9 x3
- 6 sen x) dx =5
m) ∫(sen 5x + cos x) dx = n) ∫(7 e2x
-sen (5x - 2))dx =
ñ) ∫(e-3x
+ tan x cos x) dx = o) ∫e-2x
(e2x
- e-2x
) dx =
p) ∫(sen 2x + cos2
x) dx = q) ∫cos (2x + 1) dx =
r) ∫(e5x
+ sen 6 x2
) dx = s) ∫[e-4x
+ ctg (2x - 1)]dx =
t) ∫(cos x - 1)2
dx =
y) ∫(3 tan2
x + 5 ctg2
x) dx =
u) ∫ dx =
2x + 3
1
e) ∫ dx =
x
x6
+ 3x5
- 6x + 1
x) ∫ =sen x + 1
dx
v) ∫ =
x4
- 36 x2
-9 dx w) ∫ dx =
x2
+ 3
3
i) ∫ dx =
x + 2
2x2
- 3x - 2
f) ∫ dx =
2 (x - 3)
x2
- 5x + 6
h) ∫ dx =x + 3
x](https://image.slidesharecdn.com/56calculoii-201118004256/85/56-calculo-ii-43-320.jpg)













![arturo yle martínez
dgep-uas 57
cálculo integral
Sumando miembro a miembro las ecuaciones 1 y 2 del sistema anterior se obtiene:
2A = - ⇒ A = - ⇒ - + B = 0 ⇒ B =1
3
1
6
1
6
1
6
2. ∫ =∫ = ?dx
5x2
- 18x + 9
dx
(5x - 3)(x - 3)
⇒ = + =1
(5x- 3)(x - 3)
A
(5x - 3)
B
(x - 3)
A(x-3)+ B(5x - 3)
(5x - 3) (x - 3)
Ax -3A + 5Bx - 3B
(5x - 3)(x - 3)
= =
(A+5B)x - 3(A +B)
(5x - 3)(x - 3)
1
12
= ln +c2x - 3
2x + 3
Entonces:
dx
4x2
- 9
∫ = ∫ + = ∫ - = ln(2x - 3) - ln(2x + 3) + c
(2x + 3)
1
6
- dx
(2x - 3)
1
6
dx 1
6 2x - 3
dx
2x + 3
dx 1
12
(A + 5B)x = 0 ⇒ A + 5B = 0 ⇒ Ec. 1
-3(A + B)= 1 = ⇒ A + B =- ⇒ Ec. 21
3
⇒
A + 5B = 0
A + B = - 1
3
⇒ 4B = ∴ B =
1
3
1
12
A + 5B = 0
-A- B = 1
3
Sustituyendo B en la Ec. 1 : A + 5 = 0 ⇒ A + = 0 ⇒ A = -1
12
5
12
5
12
x-3
5x - 3∫ = ln + cdx
5x2
- 18x + 9
1
12
∫ = ∫ -dx
5x2
- 18x + 9
1
12
dx
x-3
5dx
5x-3
∴
1
(2x + 3) (2x - 3)
-1/6
2x + 3
= +
2x - 3
1/6
∴
1
12
= [ln (x-3) - ln (5x-3)] + c](https://image.slidesharecdn.com/56calculoii-201118004256/85/56-calculo-ii-57-320.jpg)
![unidad IIcálculo integral
58 dgep-uas
3. ∫ =∫ = ? Descomponiendo el integrado en:(5x - 2)dx
x2
- 9x + 8
(5x - 2)dx
(x - 8)(x - 1)
= + = =
Ax-A+ Bx - 8B
(x - 8) (x - 1)
5x - 2
(x - 8)(x -1)
A
x - 8
B
x - 1
(A+B)x - (A + 8B)
(x - 8) (x - 1)
(A+B)x = 5x ⇒ A + B = 5 → Ec. 1 -(A+ 8B) = -2 ⇒ A + 8B = 2 → Ec. 2
Resolviendo el sistema:
Comparando los términos de la igualdad
⇒ -7B = 3 ⇒ B= - ⇒ A =7
3
22
3
∴ ∫ = 22∫ - 7∫ = [22 ln (x-8) - 7 ln (x-1)] + c(5x - 2) dx
x2
- 9x + 8
dx
x-8
1
3
dx
x-1
1
3
(x-8)22
(x-1)7= [ln (x-8)22
– ln (x-1)7
] + c = ln + c1
3
1
3
A + B = 5 → Ec. 1
-A - 8B = -2 → Ec. 2
(-A -3B + 2C)x = 3x ⇒ -A -3B + 2C = 3 → Ec. 1
Resolviendo el sistema de ecuaciones:
4. ∫ =∫ = ∫ = ?(3x - 4)dx
x3
- x2
- 6x
(3x - 4)dx
x (x2
- x - 6)
(3x - 4)dx
x (x + 2)(x - 3)
= + + =3x - 4
x (x + 2)(x -3)
A(x2
-x-6) + B(x2
-3x) + C (x2
+2x)
x(x + 2) (x - 3)
A
x
B
x + 2
C
x - 3
(A +B + C)x2
= 0 ⇒ A + B + C = 0 → Ec. 2
-6A = -4 → Ec. 3
⇒ B = -1 ⇒ C = 1
3
∴ A = = ⇒-4
-6
2
3
2
3
- -3B + 2C = 3
2
3
+ B + C = 0
= 2
3
B + C = -
-3B + 2C =11
3
∴ ∫ = ∫ -∫ + ∫ = ln x - ln (x +2) + ln (x - 3) + c(3x - 4) dx
x3
- x2
- 6x
dx
x
2
3
dx
x+2
1
3
dx
x- 3
1
3
2
3](https://image.slidesharecdn.com/56calculoii-201118004256/85/56-calculo-ii-58-320.jpg)



![unidad IIcálculo integral
62 dgep-uas
2.3. Otras aplicaciones de la integral indefinida
Con los métodos y técnicas de integración estudiados anteriormente el abanico de
las aplicaciones de la integral indefinida se amplía considerablemente tal como se mues-
tra a continuación en los siguientes problemas.
Ejemplo 1: Determinar una función y = f (x) cuya derivada sea f '(x) = 2x+ 1 y
que f (4) = 15.
Resolución: con lo estudiado en la unidad 1 se sabe que con la integral indefinida
podemos determinar dicha función primitiva y = f (x). Y que:
De donde, la antiderivada o función primitiva general (o integral indefinida) de
f ' (x) = 2x + 1 es:
Y en consecuencia:
Como ya se estudió en la primera unidad de aprendizaje, este proceso de resolución
puede desarrollarse y ser interpretado también de la siguiente manera a partir del con-
cepto de diferencial y de ecuación diferencial:
Sea la ecuación diferencial:
dy
dx
= f ' (x) = 2x +1
Despejando de la ecuación diferencial el diferencial dy e integrándolo:
dy = 2x + 1 dx ⇒ ∫dy = ∫ 2x + 1 dx
⇒ 15 = [2(4) + 1] + c ⇒ c = 6
3
21
3
∴ y = [2x+1] +6
3
21
3
y = f (4) = F (4) = [2(4) + 1] + c = 15 ⇒ c = 6 ∴ y = f (x) = (2x + 1) + 6
3
2
3
21
3
1
3
F(x) = ∫ (2x + 1) dx = ∫ (2x + 1) dx = ∙ (2x +1) + c = (2x + 1) + c1
2
2
3
3
21
3
3
2
1
2
y = f (x) = F (x) = (2x + 1) + c1
3
3
2
3
21
3
⇒ y =∫ 2x +1 dx = [2x + 1] + c](https://image.slidesharecdn.com/56calculoii-201118004256/85/56-calculo-ii-62-320.jpg)









![unidad IIIcálculo integral
72 dgep-uas
De donde, la suma total de las áreas de los n-1 rectángulos será:
A-
= = + + + + + ... + +Σ
n-1
1
n
i
n
1
n2
2
n2
3
n2
5
n2
4
n2
n-2
n2
n-1
n2
1
n2= [ 1 + 2 + 3 + 4 + 5 + ... + (n-2) + (n-1)]
= (n) =1
n2
n+1
2
n+1
2n
Para mejorar la aproximación hasta el máximo aumentamos (imaginariamente) el
número de rectángulos hasta el infinito, lo cual implica que:
LimA-
= Lim = Lim = Lim = =n+1
2n 2n
n
n
n
1
n+
2
1 1
n+ 1 + 0
2
1
2n→∞ n→∞ n→∞ n→∞
Comparando las áreas obtenidas, por la fórmula del triángulo, el área promedio de
los rectángulos y por esta última que la encontramos a través de límite de la sumatoria de
las áreas de los rectángulos, encontramos y corroboramos que el área encontrada para
los tres casos es la misma. ¿Será una simple coincidencia?
A continuación resolveremos un caso más complicado en el cual no se conoce el re-
sultado de antemano y donde se aprecia mejor la pertinencia de este método de aproxi-
maciones sucesivas infinitas.
Ejemplo 2: Calcular con la mejor aproximación posible el área A comprendida entre
la gráfica de la función y = x2
, el eje X y las rectas verticales x = 0 y x = 1. (Ver figura 3.4)
Resolución:
Figura 3.4
1
2
1
4
3
4
1
y = x2
1
2
1
4
3
4
1
y = x2
i = 1
A =](https://image.slidesharecdn.com/56calculoii-201118004256/85/56-calculo-ii-72-320.jpg)
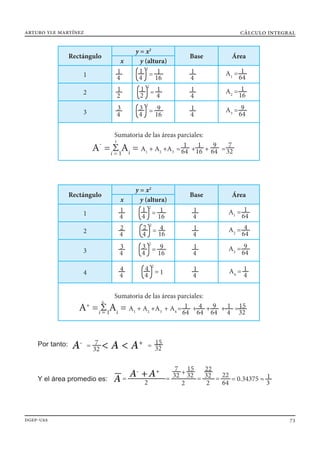

![arturo yle martínez
dgep-uas 75
cálculo integral
Generalizando y formalizando el procedi-
miento anterior para calcular áreas bajo una cur-
va, podemos establecer que para determinar el
área bajo una curva dividamos el intervalo [a, b]
en n subintervalos iguales Δx1
= x1
−a, Δx2
= x2
−
x1
,.., Δxn
= b−xn-1
donde cada uno de ellos será la
base correspondiente a uno de los rectángulos
los cuales podrán estar por arriba o por debajo de
la curva, mientras que la altura de dicho rectán-
gulo vendrá dada por el valor de la función para
algún valor de x dentro de cada subintervalo, o sea y en particular yi
= f (xi
). De donde
podemos escribir el área aproximada por n rectángulos Sn bajo la curva como la suma
de las áreas de todos los rectángulos de la siguiente manera:
Sn = f(x1
)Δx1
+ f (x2
) Δx2
+ ... + f (xn-1
)Δxn-1
+ f (xn
)Δxn
= Σ f (xi
)Δxi
n
i=1
Esto nos permite visualizar que si consideramos un número infinito de subintervalos
en que se divida el intervalo [a,b] entonces,cada Δxi
será cada vez más pequeño, Δxi
→ 0,
y tendremos cada vez más rectángulos llenando el área bajo la curva, y en consecuencia
el área definida por la suma se aproximará cada vez más al área total buscada hasta
llegar a ser igual a ella, es decir:
Lo cual nos indica, que el área real puede ser determinada mediante el cálculo del
límite de la sumatoria de las áreas de los rectángulos usados en la aproximación.
El cálculo del límite anterior también se presenta en el problema de calcular o de-
terminar la distancia recorrida por un cuerpo que se mueve a lo largo de una curva, con
velocidad variable v = f (t), en el intervalo de tiempo entre t = a y t = b.
Supongamos que la función v = f (t) es continua, o sea, que en intervalos pequeños
de tiempo la velocidad solo varía ligeramente. Se divide el intervalo [a,b] en n partes de
longitudes Δt1
, Δt2
,Δt3
,..., Δtn
. Para calcular un valor aproximado de la distancia recorri-
da en cada intervalo Δti
,(con: i = 1, 2, 3, ..., n) vamos a suponer que la velocidad en este
intervalo de tiempo es constante e igual a su verdadero valor en algún punto del mismo
intervalo, en particular para ti
. Luego, la distancia total recorrida estará expresada aproxi-
madamente por la siguiente suma:
S = lim Sn
= lim ∑ f (ti
) ∆tiΔt → 0 Δt → 0 i = 1
n
Sn = f(t1
)Δt1
+ f (t2
) Δt2
+ ... + f (tn-1
)Δtn-1
+ f (tn
)Δtn
= Σ f (ti
)Δti
n
i=1
De donde, el valor real de la distancia recorrida en el tiempo b – a, será el límite de
tales sumas para subdivisiones cada vez más finas o un número infinito de ellas, o sea
cuando Δti
→ 0, en consecuencia:
A = lim Sn = lim ∑ f (xi
) ∆xiΔxi → 0 Δxi → 0 i = 1
n](https://image.slidesharecdn.com/56calculoii-201118004256/85/56-calculo-ii-75-320.jpg)

![arturo yle martínez
dgep-uas 77
cálculo integral
(a) Dibujar una gráfica que represente las velocidades promedio en el tiempo.
(b) Calcular la distancia total recorrida por la persona entre las 06:00 y las 10:00
horas.
5. Una persona deja caer una pelota desde lo alto de un edificio, y ésta tarda 5 se-
gundos en llegar al piso. ¿Qué altura tiene el edificio, si consideramos que la única fuerza
que actúa sobre la pelota es la fuerza de gravedad?
Nota: resolverlo como un problema de áreas.
6. Calcular la distancia recorrida por un automóvil de carreras que se mueve en el
intervalo entre 0 y 1 minutos con velocidad variable según la función v = t2
.
3.2 El área y la Integral Definida.
Para comenzar se utilizará un lenguaje y una simbología que posteriormente se
precisará mejor.
Si f (x) ≥ 0, el área comprendida entre el eje
X, la gráfica de la función f (Ver figura 3.5) y
las rectas verticales x = a y x = b se denota:
y se lee área de f entre a y b.
b
aS (f (x))
7
2
7
2
7
2S (3) = [∫3 dx] = [3x + c] = [3(7) + c]-[3(2) + c]= 15
Algunos ejemplos de aplicación de esta nueva notación para el área de figuras ele-
mentales conocidas por ti, son las funciones representadas en la Figura 3.6.
y
y= f (x)
x = a x
Figura 3.5
x = b
b
aS (f (x))
f3
(x)= x2
0 1
c)
1
S (x2
)=-
1
0
1
3
S (3) = 15
7
2
3
0 2 7
f1
(x)=3
a) f2
(x)= x + 6
S (- x + 6) = 8
6
2
0 2 6
b)
Figura 3.6
Además, usando la integral indefinida también se puede escribir que:
6
2
6
2
6
2S (-x+6) = [∫(-x+6)dx] = [ + 6x + c] = [ + 6(6) + c]-[ + 6(2) + c]= 8-x2
2
-62
2
-22
2](https://image.slidesharecdn.com/56calculoii-201118004256/85/56-calculo-ii-77-320.jpg)
![unidad IIIcálculo integral
78 dgep-uas
En los ejemplos a) y b) la función dentro del símbolo para el área es una función
lineal cuya gráfica es la recta que limita por arriba a la superficie de la figura sombreada.
Por ejemplo, la primera es la recta de ecuación y = 3, y se trata del área de un rectángulo
de base cinco (5=7-2) y altura 3. Utilizando la fórmula conocida se tiene que el área de ese
rectángulo es 15, y se halla multiplicando la base por la altura del rectángulo (A=5x3=15).
La segunda es la recta de ecuación y = -x + 6 , y se trata del área de un triángulo de
base cuatro (4=6-2) y altura 4. De igual modo que en el ejemplo anterior, en este caso el
área del triángulo (mitad del producto de la longitud de la base por la altura), que en este
caso es (4 x 4) ÷ 2 = 8.
En el último ejemplo, se trata del área que se forma debajo de la parábola de ecua-
ción y=x2
en el intervalo de 0 a 1, y cuyo resultado ya fue determinado (en la página 74)
apartir de la suma acumulada de un número infinito de rectángulos.
Los resultados de estos tres ejemplos muestran la estrecha relación que existe entre
el cálculo de áreas y el cálculo de integrales indefinidas, lo que nos permitirá más ade-
lante definir una función de área apartir de la cuál se demostrará formalmente la relación
que existe entre el cálculo diferencial y el cálculo integral.
Para continuar este análisis introductorio hay que darle sentido a la nueva notación
introducida utilizando los conceptos ya conocidos. La relación la establecemos mediante
un nuevo concepto al que se denominará integral definida.
Definición 1
Sea f (x) una función continua en un intervalo I, se llama Integral definida
de f desde a hasta b (a, b ∈ I) y se denota al número
donde F es una primitiva cualquiera de f, a y b son límites de integración.
Esta definición es correcta pues la expresión F (b) – F (a) no depende de la primitiva,
en efecto si G (x) es otra primitiva de f (x), tenemos:
∫ f(x)dx
b
a
∫ f(x)dx = F(b) - F(a)
b
a
∫ f(x)dx = G(b) - G(a)
b
a
= [F(b)+c]-[F(a)+c]
= F(b) - F(a)](https://image.slidesharecdn.com/56calculoii-201118004256/85/56-calculo-ii-78-320.jpg)
![arturo yle martínez
dgep-uas 79
cálculo integral
Con respecto a la notación ya conocida para las integrales indefinidas podemos re-
tomarla ahora para la integral definida, solamente que en este caso aparecen los límites
de integración, tal como se muestra en el esquema de abajo.
Integral definida
∫ f(x)dx
b
a
f (x) dx es el integrando
∫ es el
símbolo integral
• dx: indica que x es la variable con
respecto a la cual f es derivada.
• f (x): es la función subintegral
• a y b son los límites de integración.
Con esta definición sobre la integral definida, y retomando lo estudiado en el epígrafe
anterior, resulta claro que también podemos escribir la siguiente expresión de igualdad:
A = lim Sn
= lim ∑ f (xi) ∆xi = ∫ f(x)dxΔxi → 0 Δxi → 0 i = 1
b
a
n
La cual pone en evidencia que detrás del concepto de integral definida está un pro-
ceso de cálculo aproximado de área mediante la determinación de un límite al infinito.
Veamos ahora cómo se relaciona esta definición de integral definida con los ejem-
plos introductorios de cálculo de áreas.
Ejemplo 1. El del área del rectángulo.
Ya qué: ∫ 3 dx = 3x + c
En este caso se tiene, usando la definición y el hecho de que 3x es una primitiva de
y = 3, que:
Es el mismo resultado que se obtuvo mediante la fórmula conocida para el área de
un rectángulo.
Ejemplo 2. El del área del triángulo.
En este caso se tiene que la primitiva de f (x) = -x + 6 es:
∫ 3dx = 3x + c | = [3(7) + c] - [3(2) + c]= 21 - 6 = 15
7
2
7
2
x2
2
F(x) = ∫(-x + 6)dx = - + 6x + c
∴ ∫ (-x + 6)dx = - + 6x + c = ?
b 6
2
(x)2
2a](https://image.slidesharecdn.com/56calculoii-201118004256/85/56-calculo-ii-79-320.jpg)
![unidad IIIcálculo integral
80 dgep-uas
= - + 36 + c -(- + 12 + c) = -18 + 36 - 10 = 836
2
4
2
De nuevo se obtiene el mismo resultado que utilizando la fórmula conocida del área
del triángulo.
Nota: Obsérvese como al calcular una integral definida la constante de integración
de su función primitiva correspondiente siempre se elimina, por lo que se puede prescin-
dir de ella en los cálculos.
Hasta aquí se ha introducido un nuevo concepto, el de Integral Definida y en algu-
nos ejemplos introductorios se ha calculado con dichas integrales el área debajo de la
gráfica de la función del integrando en el intervalo determinado por los límites de inte-
gración.
Con ello se ha visto, a modo de introducción, la posibilidad de utilizar dicho concepto
en el cálculo de áreas lo que será fundamentado en el epígrafe siguiente y que de ma-
nera intuitiva utilizaremos en este epígrafe para ilustrar más claramente. Veamos otros
ejemplos de cálculo de integrales definidas.
Ejemplo 3. Calcula la integral definida:
Resolución: Como , tendremos que
∫ x2
dx
3
1
1
3
F (x) =∫x2
dx = x3
+ c
A partir de la experiencia con los ejemplos introductorios podemos interpretar que el
área debajo de la parábola y = x2
en el intervalo de 1 a 3 es .26
3
La región cuya área estamos postulando
es la que aparece sombreada en la figura 3.7.
Más adelante fundamentaremos esta
afirmación.
Figura 3.7
Esto es, se escribe la primitiva y se indican los límites de integración, luego se
evalúa la función y se efectúa la diferencia indicada. La notación de la barra con el 6 y
el 2 se utiliza para indicar que se debe evaluar la primitiva en 6 y restarle la evaluación
en 2, donde 2 y 6 son los límites de integración. Calculando:
∫ (-x + 6)dx = - + 6x + c = - + 6(6) + c - + 6 (2) + c(x2
)
2
6 6
2
(6)2
2
-(2)2
22
1
3
26
3
∴ ∫ x2
dx = x3
= [33
- 13
] =1
3
3
1
3
1](https://image.slidesharecdn.com/56calculoii-201118004256/85/56-calculo-ii-80-320.jpg)
![arturo yle martínez
dgep-uas 81
cálculo integral
El proceso para calcular integrales definidas se puede sintetizar en la siguiente regla
que también se le denomina Regla de Barrow, en honor al teólogo y matemático inglés
Isaac Barrow nombrado en las referencias históricas iniciales.
Regla de Barrow
Pasos para calcular la integral: ∫ f(x)dx
a) Se busca una primitiva F(x) de f, Entonces: F(x) = ∫ f(x)dx
b) Se calcula F(b) y F(a) y se calcula la diferencia F(b) - F(a)
c) Se hace ∫ f(x)dx = F(b) - F(a)
b
a
Las funciones para las que se puede calcular la integral definida desde x=a hasta
x=b se llaman integrables en el intervalo [a,b]. De la definición 1 resulta entonces, que
las funciones continuas son integrables.
Las integrales definidas conservan las propiedades de las integrales indefinidas.
Teorema 1
Si f y g son funciones continuas en un intervalo I ; (a, b ∈ I), se
cumple:
a) Para todo c ∈ ℜ; ∫ cf (x)dx = c ∫ f (x)dx
b) ∫ [ f (x) + g(x)] dx = ∫ f (x)dx + ∫ g(x)dx
c) ∫ f (cx + d)dx = F(cx + d) ; donde F '(x) = f (x)
b
a
1
c
Estas operaciones resultan inmediatamente a partir de las propiedades de la integral
indefinida.
b
a
b
a
b
a
b
a
b
a
b
a
b
a](https://image.slidesharecdn.com/56calculoii-201118004256/85/56-calculo-ii-81-320.jpg)
![unidad IIIcálculo integral
82 dgep-uas
Ejemplo 4. Calcula las siguientes integrales definidas:
a) ∫ 2x4
dx
3
0
2
1
b) ∫ + dx1
x
1
x2 c) ∫ cos2x dx
π /2
0
d)∫ sen x dx
2π
π /2
Resolución:
d)∫ sen x dx = - cos x = - [cos 2π - cos (π / 2)]= -(1+ 0) = -12π
π /2
2π
π /2
En el ejemplo 4d anterior puedes apreciar que el valor de la integral definida también
puede ser un número negativo. Eso
sucede cuando la función es negativa
en un intervalo dado. En este caso no
representaría el área geométrica de-
terminada por la gráfica sino un “área
con signo” como en la figura 3.8.
Esta idea se desarrolla en el epígrafe
siguiente.
Las integrales definidas poseen
otras propiedades que dependen del
intervalo tal como se muestra en el teo-
rema 2.
Este teorema no lo vamos a demostrar, pero su demostración es muy sencilla utili-
zando de nuevo las propiedades de la derivación.
Figura 3.8
c) ∫ cos2x dx = sen2x = (sen π -sen 0) = 01
2
1
2
π /2
0
π /2
0
x5
5
3
0
486
5
∫ 2x4
dx = 2∫ x4
dx = 2 = 2 - =35
5
05
5a)
3
0
3
0
b) ∫ + dx =∫ dx + ∫ dx = ln x - = ln2 - - ln1- ≈ 1.21
x
1
x2
1
x
1
x2
1
x
2
1
1
2
1
1
2
1
2
1
2
1
Teorema 2.
Si y = f (x) es continua en el intervalo (a , b), y además a < c < b, entonces se
cumple:
1) ∫ f (x)dx = - ∫ f (x) dx ; Si se intercambian los límites el valor de la
integral cambia de signo
2) ∫ f (x)dx = ∫ f (x) dx + ∫ f (x)dx ; La integral se puede calcular por tramos
o subintervalos del intervalo principal
b
a
b
a
b
a
c
a
b
c](https://image.slidesharecdn.com/56calculoii-201118004256/85/56-calculo-ii-82-320.jpg)

![unidad IIIcálculo integral
84 dgep-uas
11)∫ dx =0
π/5 esen 5x
sec 5x
12)∫ π (5 + x sen x )2
dx =
15)∫ =dx
1 - ex
17)∫ sen3
2x cos 2x dx =0
π/4
18)∫ sen4x dx =0
π
21)∫ cos4
x sen x dx =0
π/2
6. Calcular el área limitada por la recta y = 3x + 5, el eje X y las rectas x = -1 y x =4.
7. Calcular el área limitada por la parábola y = 3x2
+ 3, el eje X y las rectas x = -1 y x = 3.
8. Determinar el área de la región R bajo la curva y = x4
-2x3
+ 2 en los intervalos:
(a) -1 ≤ x ≤ 0 (b) 0 ≤ x ≤ 2 (c) -1 ≤ x ≤ 2
9. Determinar el área de la región R bajo la curva y = 1 + x en los intervalos:
a) 0 ≤ x ≤ 2 (b) 2 ≤ x ≤ 4 (c) 0 ≤ x ≤ 4
10. Determinar el área de la región R bajo la curva y = 25 - x2
en el intervalo -3 ≤ x ≤ 5.
13)∫ dx =ln x2
x-2
2
0
1
19)∫ 1 + 4x2
dx =0
4
23)∫ =x1/2
dx
1 + x3/40
1
25)∫ =
(4x2
+ 2x) dx
(x2
+ 1)(x2
+2x + 1)0
1
27)∫ x2
lnx dx =0
1
29)∫ ex
senx dx =0
1
31)∫ x-2
dx = lim1
∞
[∫ x-2
dx ]=1
∞
0
7
14)∫ dx =x2
- 4
x2
4
16)∫ 4 + 9x2
dx =0
3
4
e5x20)∫ 103x
+ dx =1
3
22)∫ 25 + x2
dx =0
5
24)∫ =dx
(1 + x)3/2
+ x + 10
1
26)∫ x lnx dx =-1
4
28)∫ x2
ex
dx =0
3
30)∫ x2
cos x dx =0
1
b →∞
32) ∫ dx =
∞
–∞
ex
1+e2x](https://image.slidesharecdn.com/56calculoii-201118004256/85/56-calculo-ii-84-320.jpg)
![arturo yle martínez
dgep-uas 85
cálculo integral
11. Determinar el área de la región R bajo la curva y = sen x en el intervalo 0 ≤ x ≤ π.
3.3 Teorema fundamental del cálculo.
En este epígrafe fundamentaremos la relación entre área e integración. Para ello
definiremos una función que se le denominará función área debajo de la curva y la
denotaremos A(x).
Teorema 3
Si f (x) es una función continua en el intervalo [a,b] y definimos la función área A(x)
tal que:
A(x) = S ( f (x))= ∫ f(x)dx ; con x ∈ [a,b] entonces:
a) A'(x)=f (x) para todo x ∈ (a,b)
b) ∫ f(x)dx = F(b) - F(a)
x
a
b
a
x
a
Una consecuencia de este teorema es que el área de la región comprendida entre
la gráfica de la función y el eje X desde a hasta b (a<b) se calcula mediante la integral
definida: ∫ f (x)dx , lo que fundamenta las afirmaciones de la introducción y nos permite
calcular áreas que antes no podíamos calcular, y de una forma relativamente cómoda.
Como te informamos en las referencias históricas de esta unidad, este teorema co-
nocido como teorema fundamental del cálculo fue demostrado por el matemático ale-
mán Gottfried W. Leibniz (1646-1716) y con él probó que la derivación y la integración
son inversas.
b
a
0
0 Π/2 Π 3Π/2 2Π2Π
ϕ
Π
3Π/2
ω
Π/2 y
x
y = sen (x)
1
R](https://image.slidesharecdn.com/56calculoii-201118004256/85/56-calculo-ii-85-320.jpg)



![arturo yle martínez
dgep-uas 89
cálculo integral
En general se tiene que el área A limitada por la gráfica de una función con-
tinua f (x), el eje “X” y las rectas x = a, x = b está dada por:
A =∫ f (x) dx
b
a
No obstante esa no es la única situación que te vas a encontrar. Por ejemplo te pue-
des encontrar otros casos como el siguiente.
La gráfica de la función corta al eje X en un
punto (hay un cero de la función) y está limitada por
dos rectas que cortan al eje X en los puntos a y b.
Observa en la fig 3.13 que en ese caso el resultado
de la integral no representa al área buscada pues
una parte es positiva y la otra negativa.
Figura 3.13
Lo anterior es debido a las compensaciones que se producen de las partes positivas
con las negativas como se muestra en la figura 3.13.
En los dos casos siguientes la parte de la figura 3.14 representada corta en dos
puntos al eje X, o sea, cada una de ellas tiene dos ceros en el intervalo [a,b]. Quedan
entonces determinadas regiones que corresponden a resultados positivos y negativos
de las integrales respectivas, y de nuevo no representan las áreas buscadas.
Figura 3.14
La forma correcta de proceder en estos casos es calcular por separado las inte-
grales de los diversos sectores y posteriormente sumar sus valores absolutos.
Es decir la solución es calcular el área “a trozos” tomando la integral de la función
si el área es positiva y el valor absoluto de la integral de la función si el área es negativa.
Luego se suman las áreas obtenidas para obtener el área total.
b](https://image.slidesharecdn.com/56calculoii-201118004256/85/56-calculo-ii-89-320.jpg)
![unidad IIIcálculo integral
90 dgep-uas
En la figura 3.15 se ilustra que para calcular el área A es necesario descomponer el
intervalo de integración en subintervalos, según la función cambie de signo.
El área total es, entonces, una suma de áreas:
A = ∫ f (x)dx -∫ f (x)dx + ∫ f (x)dx
x
1
a
x
2
x
1
b
x
2
Observa que los límites de integración son las abscisas x=a y x=b, y los puntos de
corte de la curva con el eje X, o sea los ceros de la función en ese intervalo. Si no
están dados debes calcularlos.
Ejemplo 7: Calcular el área de la región comprendida entre la gráfica de y = sen x y
el eje “X” en el intervalo [ 0 , 2π]. La gráfica sería como la siguiente (fig. 3.16) :
Figura 3.16
Resolución: hay que analizar el signo de y = sen x, sabemos que:
Si x ∈[ 0 , π ], sen x ≥ 0 y Si x ∈[ π , 2π ], sen x ≤ 0
Figura 3.15
y
0 a bx1 x2 x
y= f (x)
y= f (x)
y= | f (x) |
y= f (x)
π](https://image.slidesharecdn.com/56calculoii-201118004256/85/56-calculo-ii-90-320.jpg)
![arturo yle martínez
dgep-uas 91
cálculo integral
El área debe calcularse de -1 a 2 porque en ese intervalo la función limita un área con
el eje “X” (fig. 3.17) pero hay que tener en
cuenta que hay un cero intermedio que es
x2
= 0.
Luego hay que descomponer el intervalo de integración en dos subintervalos. Para
encontrar el límite de integración que falta (se conocen 0 y 2π ) se tiene que determinar
el cero de la función en ese intervalo pues es donde la función cambia de signo. Este es
π pues sen π = 0. Entonces:
Ejemplo 8: Calcula el área de la región comprendida entre el gráfico de la función
f (x) = x3
- x2
- 2x y el eje “X”.
Resolución: Para calcular el área debemos analizar donde la gráfica corta al eje “X”.
Como en este caso no tenemos la gráfica debemos calcular donde la función cambia de
signo, o sea, los ceros de la misma:
x3
- x2
- 2x = 0, o sea x (x - 2)(x+1) = 0 de donde se tiene que
x1
= -1 ; x2
= 0 ; x3
= 2 que son también los limites de integración.
+ +
-1 0 2
Figura 3.17
Vemos que f es no negativa en [-1 , 0] y no positiva en [ 0 , 2], (fig. 3.17)
Luego el área buscada se calcula mediante la integral:
5
12
= - - = u28
3
37
12
Observa que los ceros encontrados, hay que ordenarlos de menor a mayor para utili-
zarlos como límites de integración.
En este ejemplo, la gráfica de la función es la siguiente (Figura 3.18):
A = ∫sen x dx + ∫ sen x dx = - cos x | + cos x | = - (-1-1) + (1-(-1))=4u2
0
π
π
2π
0
π
π
2π
A = ∫ (x3
- x2
-2x)dx - ∫(x3
-x2
-2x)dx = - - x2
- - - x2
-1
0
0
2
x4
4
x3
3 -1
0
x4
4
x3
3 0
2
= 0 - - - ( - 1)2
- - - 22
-0(- 1)4
4
24
4
23
3
(- 1)3
3](https://image.slidesharecdn.com/56calculoii-201118004256/85/56-calculo-ii-91-320.jpg)
![unidad IIIcálculo integral
92 dgep-uas
Por lo general no te van dar la gráfica de la función a la que le debes determinar su
área. Si la representas eso te ayudaría a orientar el cálculo que debes hacer.
Actividades de aprendizaje #14:
1. En los siguientes ejercicios, traza la gráfica correspondiente y luego, auxiliándote del
cálculo integral, determina el área.
a) limitada por la recta y = 2x, el eje X y la recta x = 6
b) limitada por la recta x + y = 10, el eje X y las rectas x = 2 y x = 8.
c) Comprueba cada resultado de los incisos anteriores, hallando el área por la fór-
mula estudiada en geometría.
2. Traza las gráficas de las funciones siguientes y calcula en cada caso el área de la
región limitada por el gráfico de la función, el eje X y las rectas x = a y x = b donde a
y b son los extremos de los intervalos dados.
a) y = x2
[-4,-2]
b) y = x + 2 [ -2, 5]
c) - x2
+ 4 [ -2 , 2]
d) y = x [1 , 4]
e) y = x2
+ 1 [-1, 1]
f) y = x3
[-3, 3]
Figura 3.18](https://image.slidesharecdn.com/56calculoii-201118004256/85/56-calculo-ii-92-320.jpg)
![arturo yle martínez
dgep-uas 93
cálculo integral
3. Demuestra, usando el cálculo integral, que:
a) El área de un rectángulo es el producto del largo por el ancho.
b) El área de un triángulo rectángulo es el semiproducto de los catetos.
c) El área de un trapecio rectángulo es el producto de la semisuma de las bases
por la altura.
4. Comprueba que ∫ x dx = 0 y que el área de la región determinada por la función y = x
en el intervalo[-1, 1] es igual a 1u2
. Justifica por qué el área no se corresponde con el
valor de la integral.
5. Calcula al área de la figura limitada por la parábola y = -- x2
y por las rectas
x =1, x = 3 y el eje de las abscisas.
6. Calcula el área limitada por la parábola y = 4x - x2
y el eje de las abscisas.
7. Determina el área bajo cada una de las curvas siguientes en el intervalo indicado.
1
-1
1
2
a) y = x -2 en 2 ≤ x ≤ 5
b) y = x3
en 1 ≤ x ≤ 3
c) y = sen 3x en 0 ≤ x ≤
d) y = ex
-1 en -1 ≤ x ≤ 0
e) y = en 2 ≤ x ≤ 4
π
3
3
x
7. La figura 3.19 muestra la curva y = x2
- x3
en el intervalo [0 , 2].
Calcula el área sombreada.
Figura 3.19
y
0 1 2 x
-4](https://image.slidesharecdn.com/56calculoii-201118004256/85/56-calculo-ii-93-320.jpg)
![unidad IIIcálculo integral
94 dgep-uas
8. Calcula el área de la región limitada por la función f y el eje de las abscisas.
a) y = 4x + x2
b) y = x3
- 6x2
+ 8x
b) y = x3
-7x + 6 d) y = x2
- 7 x + 6
Áreas comprendidas entre dos o más curvas.
Otra aplicación importante del cálculo integral es la posibilidad de calcular áreas
comprendidas entre dos o más curvas.
Sean y = f (x), y = g (x) dos funciones, sus gráficas comprenden una región sobre el
intervalo limitado por las abscisas de los puntos de intersección de ambas curvas (fig.
3.20).
y f (x)
g(x)
0 x1 x2 x
Figura 3.20
En la figura 3.20 podemos ver que si ambas funciones son no negativas y g(x) ≤ f (x)
para todo x ∈ [x1
, x2
], el área limitada por ellas puede calcularse:
A = ∫ f (x)dx - ∫ g(x)dx = ∫ [f (x) - g(x)] dx
x2
x1
x2
x1
x2
x1
En general si f y g son dos funciones continuas, el área entre dos curvas se
calcula: A = ∫ | f (x) - g(x)| dx ; donde x1
y x2
son las abscisas de los puntos de inter-
sección. Si tenemos más de dos puntos de intersección el área se calcula por partes.
x2
x1
Ejemplo 9: Calcula el área limitada por los gráficos de:
(a) f (x) = x y g(x)=x2
(b) f (x) = x y g(x) = x3
.](https://image.slidesharecdn.com/56calculoii-201118004256/85/56-calculo-ii-94-320.jpg)
![arturo yle martínez
dgep-uas 95
cálculo integral
Resolución:
(a) En la figura 3.21 se ha representado ambas curvas. Para calcular el área debe-
mos determinar los puntos de intersección y para hacerlo planteamos la igualdad x = x2
,
equivalente a x2
- x = 0 de donde se tiene que x1
= 0, x2
= 1
Como en el intervalo [ 0, 1] la función
x2
- x es no positiva, entonces:
x2
2
= - = - = u2x3
3
1
0
1
2
1
3
1
6
(b) También aquí planteamos la igualdad x= x3
que es equivalente a x3
- x = 0. Resol-
viendo la ecuación x (x2
-1) = 0 se tiene que: x ( x - 1) (x +1) = 0 ⇒ x1
= 0 ; x2
= 1 ; x3
= -1
Por tanto, los ceros son x = -1, x = 0 y x = 1 estos valores son también los límites de
integración. Analicemos el signo de x3
- x.
En la figura 3.22, se tiene el comportamiento de los signos de la función en los inter-
valos determinados por los ceros.
+ +
-1 0 1 Figura 3.22
Entonces, los intervalos que interesan para la integración son los que están entre los
límites. En el intervalo [-1 , 0] es no negativa y en el [ 0 , 1] no positiva. Para calcular el área
entre las curvas y = x3
y y = x hay que tener en cuenta el módulo de x3
- x es igual a x3
- x en
el intervalo [-1 , 0] pues x3
- x > 0 . De igual modo el módulo de x3
- x es igual a x - x3
en el
intervalo [ 0 , 1] pues x3
- x < 0. Entonces el área se calcula mediante la integral:
A =∫ |x3
- x|dx + ∫ |x3
-x |dx-1
0
0
1
y
x1 = 0 x2 = 1 x
Figura 3.21
0
1
-1
0
= ∫ (x3
- x) dx + ∫ ( x - x3
) dx
A = ∫ |x2
- x|dx = ∫ (x - x2
)dx
1
0
1
0
= - + - = - + + - =x4
4
x2
2 -1
0
x4
4
x2
2 0
1
1
4 2
1
2
1 1
4 2
1
y
x1 = -1
x2 = 1 x0](https://image.slidesharecdn.com/56calculoii-201118004256/85/56-calculo-ii-95-320.jpg)


![unidad IIIcálculo integral
98 dgep-uas
6. El área de la porción del plano limitada por la función f (x) = - (x ≠ 0) y el eje de
las abscisas en el intervalo [k , 1] es 26 u2
. ¿Cuál es el valor numérico de k en dicho in-
tervalo?
7. Calcula el área limitada por la curva y = x3
- 9x2
+ 24x - 18, el eje de las abscisas y
dos rectas paralelas al eje de ordenadas y trazadas de manera que pasan por los puntos
de extremos locales de la función.
8. Calcula el área comprendida entre la curva y = -x2
- x + 12, el eje de las abscisas y
la tangente a la curva en el punto de abscisa x = -1.
3
x4
3. Sean las funciones f (x) = x2
- 6x + 8 y g(x) = – 3x .Determina el área de la región
del plano limitada por las funciones f y g.
4. Calcula el área comprendida entre las curvas.
a) y = x + 1 , la recta y = x + 1 y el eje "X"
b) y = 1 - x , y = ex
- e y x = 0
c) y = x , y = 2 - x y y = 0
d) x2
= 4y, x2
= 8y - 4
5. El área bajo la curva comprendida por el gráfico de la función y = x - 3 y el eje
“X” en el intervalo 3 ≤ x ≤ b es A = . Determina el valor de b.4 2
3
9. Investiga y contesta las siguientes cuestiones:
a) ¿Qué diferencia esencial existe entre el Cálculo Diferencial y el Cálculo
Integral?
b) ¿Qué afirma y para qué sirve el Teorema Fundamental del Cálculo?
c) ¿Cuál es la condición analítica que garantiza que una función sea siempre inte-
grable en un intervalo cerrado?
d) ¿Conoces algún software con el cual se puedan calcular integrales?
Nota: si tu respuesta a esta cuestión es afirmativa describe brevemente dicho soft-
ware, en caso contrario, investiga al respecto.](https://image.slidesharecdn.com/56calculoii-201118004256/85/56-calculo-ii-98-320.jpg)

![unidad IVcálculo integral
100 dgep-uas
UNIDAD DE APRENDIZAJE IV
APLICACIONES DE LA INTEGRAL
4.1 Introducción
Esta unidad de aprendizaje tiene un carácter integrador de todo el curso, y también
de todos los cursos del área de matemáticas, y aunque es de carácter obligatorio al igual
que las restantes, aquí se recomienda seleccionar las aplicaciones en función del tiempo
disponible para finalizar el curso, y de las capacidades, habilidades e intereses de los
alumnos.
El concepto y las propiedades de la integral definida y su relación con el área tam-
bién pueden ser utilizados en multitud de fenómenos de otra naturaleza no propiamente
geométrica como has visto hasta ahora. A continuación verás algunas de estas aplica-
ciones.
4.2 Volumen de sólidos de revolución (Método del disco).
Si f es una función continua y no negativa en el intervalo cerrado [a, b]. Recibe el
nombre de sólido de revolución, el sólido generado al girar alrededor del eje X, la región
limitada por la gráfica de la función y = f (x), el eje X y las gráficas de las rectas x=a y x=b.
El eje X es un eje de simetría de dicho sólido y una sección recta perpendicular al eje X es
un círculo (Ver Figura 4.1).
Tal como se ilustra en la figura 4.1 para determinar el volumen de este tipo de sóli-
dos, seguiremos un procedimiento similar (llamado método del disco) al utilizado para
el área de una región, aproximando el volumen de un sólido de revolución por medio de
una suma de volúmenes de sólidos más elementales cuyos volúmenes individuales ya
están determinados.](https://image.slidesharecdn.com/56calculoii-201118004256/85/56-calculo-ii-100-320.jpg)
![arturo yle martínez
dgep-uas 101
cálculo integral
En particular vamos a considerar n discos o cilindros circulares de igual espesor (Δx)
como los sólidos elementales, asumiendo que el volumen de un disco circular Vi es, por
definición, el producto del área de la base (A= π y2
) por el espesor. Por tanto, el volumen
de un disco o cilindro representativo en base a la función será:
Vi
= π [f (xi
)]2
Δx
Luego, el volumen total V del sólido de revolución debe ser aproximadamente igual
a la sumatoria de todos los Vi
, es decir:
V≈ π [f(xi
)]2
Δx1
+ π [f(xi
)]2
Δx2
+...+ π [f(xi
)]2
Δxn
= ΣVi
= Σ π [f(xi
)]2
Δxi
i=1 i=1
n n
Y de manera semejante al problema de área, al considerar el límite de la sumatoria
de un número infinito de discos o de cilindros, lo cual es equivalente a decir que n tiende
a infinito (n → ∞) o que el espesor de los discos tiende a cero (Δx → 0), se obtendrá el
valor exacto del volumen del sólido de revolución, el cual estará determinado por la ex-
presión siguiente:
Ejemplo 1: Calcula el volumen del sólido de revolución que se genera al girar en
torno al eje X, la región limitada por la gráfica de la función f (x) = x y la recta
x = 4 . (Ver Figura 4.2)
Resolución:
V= π ∫ [ f (x)]2
dx = π ∫ x dx = π ∫ x dx = = (42
- 02
) = 8π u3b
a
4
0
2 4
0
πx2
2
4
0
π
2
V= lim Σ π [f(xi
)]2
Δx = π . lim Σ [f(xi
)]2
Δx = π ∫ [f (x)]2
dxn → ∞ i=1
n
Δx → 0 i=1
n b
a
Figura 4.2](https://image.slidesharecdn.com/56calculoii-201118004256/85/56-calculo-ii-101-320.jpg)
![unidad IVcálculo integral
102 dgep-uas
Ejemplo 2: Calcula el volumen de una esfera de radio r.
Resolución (ver Figura 4.3): en este caso se puede considerar que la curva que
genera a la esfera es la correspondiente a la ecuación de la circunferencia de radio r. O
sea: y2
+ x2
= r2
.
Figura 4.3
Ejemplo 3: Calcula el volumen de un cono de radio R y altura h.
Resolución: Primeramente dibujemos un cono en el sistema coordenado tal como
se muestra en la figura 4.4. Luego determinamos la ecuación de la función cuya gráfica
es una recta que al girar alrededor del eje X genera el sólido de revolución de forma có-
nica. A partir de los datos se obtiene que dicha ecuación es:
y - y1
= m (x-x1
)
R
h
⇒ y - 0 = - (x -h)
∴ y = - x + RR
h
Por lo tanto, el volumen será:
= π - x2
+ R2
x = π h - R2
h + R2
h = πR2
h u31
3
h
0
R2
h2
x3
3
R2
h
R2
3
Figura 4.5
O
-r r
y = r2
- x2
⇒ y = r2
- x2
∴V = π ∫ r 2
- x2
dx
r
-r
2
= π r2
x -
r
-r
x3
3
= πr34
3
= π ∫ (r2
-x2
) dx
r
-r
V= π ∫ [ f (x)]2
dx = π ∫ - x + R dxh h
0
2
R
h0
h
0
R2
h2
2R2
h
= π∫ x2
- x + R2
dx](https://image.slidesharecdn.com/56calculoii-201118004256/85/56-calculo-ii-102-320.jpg)

![unidad IVcálculo integral
104 dgep-uas
Pero, cuando Δx→0, Δx es igual a dx, y Δyi
/ Δxi
se transforma en el cociente de dife-
renciales dy/dx, que es por definición la derivada de la función ( f '(x)), resulta que como
consecuencia de estos cambios, la aproximación de la sumatoria anterior se convierte en
un valor exacto para la longitud S del arco de la curva, y da origen a la siguiente integral
definida:
S = Lim ∑
Δyi
Δxi
1+ · Δxi
=∫ 1 + (f '(x))2
dx
∞
i =1Δx→0
b
a
2
Ejemplo 4: Calcula la longitud S del segmento de la curva y = 4x+2 del punto (-3,-10)
al punto (2,10).
Resolución: ya que f '(x) = 4, y haciendo a = -3 y b = 2, se obtiene que.
S =∫ 1 + (f '(x))2
dxb
a
=∫ 1 +(4)2
dx = 17 ∫ dx = 17 (2-(-3)) = 5 17 u2
-3
2
-3
Nota: dado que en este caso se trata de una función lineal, comprueba que se obtie-
ne el mismo resultado aplicando la conocida fórmula d = (y2
- y1
)2
+ (x2
- x1
)2
que se aplica
para calcular la distancia entre dos puntos de una recta.
Ejemplo 5: Calcula la longitud S del segmento de la curva y = x3/2
de punto (0, y1
) al
punto (4, y2
).
Resolución: ya que f '(x) = x1/2
, y haciendo a= 0 y b= 4, se obtiene que.3
2
S =∫ 1 + (f '(x))2
dx = ∫ 1+ x1/2
dx = ∫ 1+ x dx = ?b
a
4
0
3
2
2
4
0
9
4
Esta integral se puede resolver haciendo el siguiente cambio de variable:
u = 1+ x ⇒du = dx ⇒ dx = du9
4
9
4
4
9
Por tanto:
S =∫ 1 + x dx = ∫ u du = = ∫ u du= u0
4 9
4 0
4
1
2 4
9
4
9 0
4
1
2 8
27
3
2
0
4
3
9
4
= 1+ x = 1+ (4) - 1+ (0) = [10 10-1]≈ 9.078
27
4
0
8
27
9
4
3
9
4
3
8
27](https://image.slidesharecdn.com/56calculoii-201118004256/85/56-calculo-ii-104-320.jpg)
![arturo yle martínez
dgep-uas 105
cálculo integral
Actividades de aprendizaje #1:
1. Calcula el volumen del sólido de revolución que se genera al girar en torno al eje
X, la región limitada por la gráfica de la función f (x) = x + 3 y la recta x = 5.
2. Calcula el volumen del sólido de revolución que se obtiene al girar la gráfica de la
función f (x) = x + 2 en torno al eje X en el intervalo [0,4].
3. Calcula el volumen del sólido de revolución que se obtiene al girar la gráfica de la
función f (x) = ex
en torno al eje X en el intervalo [0,1].
4. Calcula el volumen del sólido de revolución que se obtiene al girar la gráfica de la
función y = x3
en torno al eje X en el intervalo [0,2].
5. Calcula el volumen de un cono de radio 5 y altura 20.
6. Calcula el volumen que genera la región limitada por las gráficas de las curvas
f (x) = x +2 y f (x) = x2
cuando giran alrededor del eje X.
7. Calcula el volumen del sólido de revolución que se genera al girar alrededor del
eje X la región entre las gráficas de las funciones f (x) = x3
y f (x)=x.
9. Calcula la longitud del arco de la curva y = 2 x3
en el intervalo [1, 5].
10. Calcula la longitud del arco de la gráfica de y = x2
en el intervalo [1, 4].
11. Calcula la longitud de la curva x2
+ y2
= 16 en el intervalo [1, 3].
12. Calcula la longitud de la curva en el intervalo , .
13. Sea y = f (x) una función continua en el intervalo a ≤ x ≤ b. Entonces el valor pro-
medio VP de la función en dicho intervalo está determinado por la integral definida:
a) Calcula VP de en el intervalo 0 ≤ x ≤ 6
b) Calcula VP de en el intervalo 50 ≤ x ≤ 70
f (x)= +x4
2
x-2
16
1
2
3
2
8. Cuando en un sólido de revolución el eje de giro es el eje Y, el volumen se de-
termina por la expresión . Calcular el volumen que genera la región
limitada por x = y y las rectas y = 0 y y =3, si gira alrededor del eje de las Y.
V =π ∫ [f (y)]2
dy
b
a
1
b–a
VP = ∫ f (x)dx
b
a
750x
4x2
+25
f (x) =
100(lnx–2)
x
f (x) =](https://image.slidesharecdn.com/56calculoii-201118004256/85/56-calculo-ii-105-320.jpg)







