Ciencias 4

CicloAvanzado-EBACampodeconocimientocienciasGuíaparaelestudianteN°4

Guía para el estudiante N°4 - Ciclo Avanzado - Campo de conocimiento ciencias
© Ministerio de Educación
Programa de Alfabetización y Educación Básica de Adultos
PAEBA - PERÚ
Primera edición
Setiembre 2008
Primera reimpresión
2009
Hecho el Depósito Legal en la Biblioteca Nacional del Perú
Nº 2008-11544
ISBN
Nº 978-9972-246-46-3
Diseño y Diagramación:
Proyectos & Servicios Editoriales - Telf. 564-5900
Impresión:
Tiraje:

3
PresentaciónPresentaciónPresentaciónPresentaciónPresentación 55555
Acerca del Ciclo AvanzadoAcerca del Ciclo AvanzadoAcerca del Ciclo AvanzadoAcerca del Ciclo AvanzadoAcerca del Ciclo Avanzado 77777
■ ¿Qué es el Ciclo Avanzado? 7
■ ¿Cómo se organiza el ciclo avanzado? 7
■ ¿Cómo se organizan los módulos? 8
■ ¿Por qué una guía para ti? 8
■ ¿Cuál es la estructura de la guía? 8
■ ¿Cómo organizar tu tiempo de estudio? 9
■ ¿Cómo utilizar tu guía? 9
■ ¿Cómo iniciar este proceso de aprendizaje? 11
Unidad temática Nº 1: Movimiento y fuerzasUnidad temática Nº 1: Movimiento y fuerzasUnidad temática Nº 1: Movimiento y fuerzasUnidad temática Nº 1: Movimiento y fuerzasUnidad temática Nº 1: Movimiento y fuerzas 1313131313
■ Actividad 1: Los movimientos 15
■ Actividad 2: Las fuerzas 35
■ Actividad 3: Rozamiento, gravedad y trabajo 57
Unidad temática Nº 2: La presión y el calorUnidad temática Nº 2: La presión y el calorUnidad temática Nº 2: La presión y el calorUnidad temática Nº 2: La presión y el calorUnidad temática Nº 2: La presión y el calor 7373737373
■ Actividad 1: La presión 75
■ Actividad 2: Calor o energía térmica 93
■ Actividad 3: Efectos del calor 111
Unidad temática Nº 3: Electricidad, magnetismo y electromagnetismoUnidad temática Nº 3: Electricidad, magnetismo y electromagnetismoUnidad temática Nº 3: Electricidad, magnetismo y electromagnetismoUnidad temática Nº 3: Electricidad, magnetismo y electromagnetismoUnidad temática Nº 3: Electricidad, magnetismo y electromagnetismo 123123123123123
■ Actividad 1: Los imanes y la electricidad estática 125
■ Actividad 2: La electricidad en movimiento 141
■ Actividad 3: Relación entre imanes y corriente eléctrica 159
Unidad temática Nº 4: Fenómenos ondulatoriosUnidad temática Nº 4: Fenómenos ondulatoriosUnidad temática Nº 4: Fenómenos ondulatoriosUnidad temática Nº 4: Fenómenos ondulatoriosUnidad temática Nº 4: Fenómenos ondulatorios 171171171171171
■ Actividad 1: Las ondas 173
■ Actividad 2: El sonido 189
■ Actividad 3: La luz 203
Respuestas de las fichas de trabajoRespuestas de las fichas de trabajoRespuestas de las fichas de trabajoRespuestas de las fichas de trabajoRespuestas de las fichas de trabajo 219219219219219
BibliografíaBibliografíaBibliografíaBibliografíaBibliografía 224224224224224
Índice

5
Esta guía ha sido elaborada para personas como tú,
estudiantes del Ciclo Avanzado de Educación Básica
Alternativa (EBA).
Su propósito es ofrecer diversas actividades para adquirir
nuevos conocimientos y consolidar los que tienes.
Además, plantea situaciones que te motivarán a buscar
información, organizarla y generar procesos de
aprendizaje en forma independiente o con la ayuda de
tu docente, compañeros y compañeras.
Esta guía corresponde al Campo de conocimiento de
ciencias que integra las áreas de Lógico matemática y
Desarrollo humano, equivalentes a las áreas de Matemática
y Ciencia, Ambiente y Salud del DCBN de EBA.
La guía presenta dos partes. En la primera se brinda
información sobre la organización del Ciclo Avanzado y
orientaciones para el uso de la guía. En la segunda se
presentan las unidades temáticas y las actividades que
desarrollarás.
El reto para trabajar las actividades sugeridas exige de
tu parte mucha responsabilidad y compromiso personal.
Se espera de esta experiencia un aprendizaje autónomo,
que resulte significativo para tu desarrollo personal,
académico y laboral.
Presentación

7
¿QuéeselCicloAvanzado?
Es el tramo final de la Educación Básica Alternativa. Está orientado a personas que han
culminado el Ciclo Intermedio o aquellas que al ser evaluadas demuestren conocimientos
suficientes para poder cursarlo con éxito. Se desarrolla en las siguientes formas:
■ PresencialPresencialPresencialPresencialPresencial, que requiere de tu asistencia regular para desarrollar las sesiones de
aprendizaje, en horarios y periodos establecidos.
■ SemipresencialSemipresencialSemipresencialSemipresencialSemipresencial, que requiere tu asistencia obligatoria a algunas clases presenciales y
sesiones de asesoría de acuerdo a tus necesidades. Esta forma de atención te permite
realizar actividades de aprendizaje fuera de clases.
■ A distanciaA distanciaA distanciaA distanciaA distancia, es una forma no presencial donde las actividades de aprendizaje se realizan
a través de materiales educativos y medios de telecomunicación.
En el CEBA se ofertan las dos primeras formas de atención, que te posibilitan compatibilizar
el estudio con tus actividades personales, familiares y laborales.
Como estudiante del Ciclo Avanzado tu reto es culminarlo y adquirir habilidades que te
permitan seguir aprendiendo a lo largo de toda tu vida. Interesa que tengas una formación
integral en los aspectos físico, afectivo y cognitivo que favorezca el afianzamiento de tu
identidad personal y social. También que ejerzas habilidades sociales con el fin de desenvolverte
en diversos ámbitos, organizar tu proyecto de vida y contribuir al desarrollo del país.
¿CómoseorganizaelCicloAvanzado?
Este ciclo se ha organizado en cuatro módulos equivalentes a los cuatro grados de EBA. Cada
uno demanda de tu parte una dedicación de estudio de 420 horas aproximadamente. Este
tiempo podrá prolongarse o reducirse según tu nivel y ritmo de aprendizaje.
Al culminar satisfactoriamente el Ciclo Avanzado, recibirás la certificación que te habilita para
continuar tus estudios en un nivel superior.
AcercadelCicloAvanzado
Módulo 5
(Primer grado)
Ciclo Avanzado
Módulo 6
(Segundo grado)
Módulo 7
(Tercer grado)
Módulo 8
(Cuarto grado)

8
¿Cómoseorganizanlosmódulos?
Cada módulo está organizado en dos campos de conocimiento. Cada campo interrelaciona
áreas curriculares afines para un trabajo global e integral. Así se tiene:
■ Campo de conocimiento de cienciasCampo de conocimiento de cienciasCampo de conocimiento de cienciasCampo de conocimiento de cienciasCampo de conocimiento de ciencias, que articula las áreas de Lógico matemática y
Desarrollo humano. (Equivalentes a Matemática y Ciencia, Ambiente y Salud).
■ Campo de conocimiento de humanidadesCampo de conocimiento de humanidadesCampo de conocimiento de humanidadesCampo de conocimiento de humanidadesCampo de conocimiento de humanidades, que articula las áreas de Comunicación,
Proyección y análisis social. (Equivalentes a Comunicación Integral y Ciencias Sociales).
¿Porquéunaguíaparati?
Generalmente las personas jóvenes y adultas tienen dificultades para compatibilizar el
estudio con el trabajo o con las responsabilidades familiares. Por eso se ha desarrollado
una guía como propuesta de material didáctico para apoyar tu estudio y desarrollar
habilidades que te posibiliten seguir aprendiendo dentro o fuera del CEBA.
¿Cuáleslaestructuradelaguía?
La guía se organiza en cuatro unidades temáticasunidades temáticasunidades temáticasunidades temáticasunidades temáticas. Cada unidad presenta tres
actividadesactividadesactividadesactividadesactividades, que se desarrollan en tres momentos.momentos.momentos.momentos.momentos.
El desarrollo de la guía es lineal, por lo que trabajarás según el orden en que se plantean las
unidades temáticas y actividades.
Al final de cada actividad encontrarás fichas de trabajofichas de trabajofichas de trabajofichas de trabajofichas de trabajo y fichas informativasfichas informativasfichas informativasfichas informativasfichas informativas. Las
primeras presentan situaciones para ejercitar tus capacidades comunicativas y de
razonamiento matemático y científico, y las segundas presentan información
complementaria sobre los temas tratados en las actividades.
Módulo del Ciclo Avanzado
Humanidades Ciencias
Comunicación
Proyección y análisis social
Formación para el desempeño ocupacional
Lógico matemática
Desarrollo humano

9
¿Cómoorganizartutiempodeestudio?
Puedes asistir diariamente a las sesiones de aprendizaje u optar por la forma de atención
semipresencial. Ésta requiere de un compromiso mayor, pues tú serás quien marque los
ritmos y niveles de cómo ir aprendiendo. Pero tendrás en la figura del docente-tutor la
persona que apoye tu proceso educativo y resuelva tus dudas o dificultades.
Ten en cuenta las siguientes sugerencias:
■ Crea un espacio para ti, libre de distracciones (teléfono, televisor, radio, ruidos, etc.) y
comprométete a permanecer allí trabajando por periodos de entre 1 y 2 horas diarias.
■ Diseña un horario mensual de trabajo, y colócalo en un lugar visible de tu casa. Puedes
elaborarlo con la ayuda de tu tutor o compañeros.
¿Cómoutilizartuguía?
■ Lee detenidamente tu guía. Identifica su estructura, contenido y actividades sugeridas
en ella. Este paso es necesario para prever los materiales y recursos que necesitarás para
su desarrollo.
■ Puedes utilizarla en el CEBA, en tu casa o en cualquier espacio que determines. Al interior
de las actividades notarás algunos íconos que te orientarán en su desarrollo.
Responde Investiga
■ Las actividades planteadas pueden ser desarrolladas en forma personal o en pequeños
grupos de trabajo, según las características de las mismas y la forma de atención en la
que estés matriculado.
■ Las fichas de trabajofichas de trabajofichas de trabajofichas de trabajofichas de trabajo son desarrolladas en forma personal y, si lo requieres, podrás
contar con ayuda de tu docente o tutor.

10
Recursosparatuestudio
■ Durante el desarrollo de las actividades realizarás diversas acciones vinculadas con
los temas propuestos: análisis de situaciones, responder a preguntas, experimentos,
resolución de problemas, entrevistas, investigaciones, informes, esquemas, dibujos.
Es necesario registrarlos. Para ello te sugerimos contar con un cuaderno u otro medio.
Este material de registro se llamará carpeta de trabajocarpeta de trabajocarpeta de trabajocarpeta de trabajocarpeta de trabajo.
■ La carpeta de trabajocarpeta de trabajocarpeta de trabajocarpeta de trabajocarpeta de trabajo es una fuente de información de tus avances personales y el
instrumento para que tu docente valore tus progresos y dificultades de aprendizaje.
Siempre debes llevarla a tus sesiones de aprendizaje y a tus reuniones de asesoría.
■ Es necesario que cuentes con un diccionario para reconocer el significado y verificar la
ortografía de algunas palabras. Al final de tu carpeta de trabajo conviene que separes
algunas hojas para que organices un glosarioglosarioglosarioglosarioglosario donde puedas registrar el significado de
las palabras desconocidas.
■ Evalúa tu actuación y desempeño permanentemente, a fin que seas consciente de lo
que has aprendido y puedas determinar aquellos aprendizajes que necesites fortalecer.
No estás solo en el trabajo que inicias, cuentas con una serie de recursos que facilitarán tu
aprendizaje. Depende de ti aprovechar cada uno de ellos.
Bibliotecas
Guía
Diccionario
Páginas web Otras personas
Carpeta de
trabajo
Docente-tutor
Otras fuentes
de información

11
¿Cómo iniciar este proceso de aprendizaje?
Antes de desarrollar las unidades temáticas es necesario que reflexiones sobre tu actuación
como estudiante y te plantees interrogantes, tales como:
Reflexiona en torno a cada una de las preguntas y respóndelas a fin de identificar tus
necesidades y expectativas educativas. Regístralas en tu carpeta de trabajo y tenlas
presentes como memoria de tus metas de estudio. Puedes compartir tus respuestas con
los miembros de tu grupo o tutor.
● ¿Por qué te has matriculado
en este módulo (grado)?
● ¿Qué dificultades has
tenido que superar para
matricularte?
● ¿Qué dificultades crees que
te falta superar?
● ¿Qué aprendizajes esperas
lograr?
Lee atentamente cada una de las unidades temáticas y las actividades para reconocer
los propósitos, capacidades, actitudes y contenidos que desarrollarás y, de esta
manera, seas consciente de lo que aprenderás.

13
● Comprender los conceptos de desplazamiento,
velocidad y aceleración para describir movimientos
que ocurren en el entorno. Representar
gráficamente estas magnitudes físicas.
● Conocer las leyes que permiten explicar las causas
de los movimientos, las cuales se denominan Leyes
de Newton. Identificar las funciones trigonométricas
y su utilidad en la Física.
● Analizar dos fuerzas: rozamiento y gravedad.
Entender los conceptos de trabajo y potencia y
aplicarlos en los diferentes campos de la vida diaria
y la tecnología. Resolver ejercicios sobre trabajo y
potencia.
MOVIMIENTOS Y FUERZASMOVIMIENTOS Y FUERZASMOVIMIENTOS Y FUERZASMOVIMIENTOS Y FUERZASMOVIMIENTOS Y FUERZAS
UNIDAD TEMÁTICA 1UNIDAD TEMÁTICA 1UNIDAD TEMÁTICA 1UNIDAD TEMÁTICA 1UNIDAD TEMÁTICA 1
PropósitoPropósitoPropósitoPropósitoPropósito
Comprender y aplicar conocimientos sobre movimiento, fuerzas y trabajo para tener
una visión más amplia de los procesos naturales y las aplicaciones tecnológicas.
Representar gráficamente las ecuaciones del movimiento en función del tiempo. Conocer
las funciones trigonométricas y resolver ejercicios sobre trabajo y potencia.
ActividadesActividadesActividadesActividadesActividades Propósito de cada actividadPropósito de cada actividadPropósito de cada actividadPropósito de cada actividadPropósito de cada actividad
1.1.1.1.1. Los movimientosLos movimientosLos movimientosLos movimientosLos movimientos
2.2.2.2.2. Las fuerzasLas fuerzasLas fuerzasLas fuerzasLas fuerzas
3.3.3.3.3. Rozamiento, gravedadRozamiento, gravedadRozamiento, gravedadRozamiento, gravedadRozamiento, gravedad
y trabajoy trabajoy trabajoy trabajoy trabajo
Capacidades y actitudesCapacidades y actitudesCapacidades y actitudesCapacidades y actitudesCapacidades y actitudes
Al finalizar esta unidad serás capaz de:Al finalizar esta unidad serás capaz de:Al finalizar esta unidad serás capaz de:Al finalizar esta unidad serás capaz de:Al finalizar esta unidad serás capaz de:
● Establecer relaciones entre las diferentes fuerzas que actúan sobre los cuerpos en
reposo y en movimiento.
● Explicar la relación entre el campo gravitacional y la ley de gravitación universal.
● Comprender que los avances científicos y tecnológicos benefician a las personas y a
la sociedad.
● Explicar ecuaciones físico-matemáticas y operar con ellas.
● Utilizar unidades del Sistema Internacional en la solución de problemas.
● Identificar y representar gráficamente funciones lineales como modelos para el análisis
de diversos fenómenos y situaciones de la realidad.
● Operar con una calculadora para efectuar cálculos y explorar relaciones
numéricas.
● Resolver problemas relacionados con la realidad utilizando funciones
trigonométricas.
Tiempo sugerido:Tiempo sugerido:Tiempo sugerido:Tiempo sugerido:Tiempo sugerido: 51 horas para la unidad
17 horas para cada actividad

15
Los movimientosLos movimientosLos movimientosLos movimientosLos movimientos
AAAAActividadctividadctividadctividadctividad 11111
DescripciónDescripciónDescripciónDescripciónDescripción ContenidosContenidosContenidosContenidosContenidos
MomentosMomentosMomentosMomentosMomentos
1. El movimiento y la velocidad
2. Movimientos rectilíneos
3. Representación gráfica del movimiento
Comprender los conceptos de
desplazamiento, velocidad y aceleración
para describir movimientos que ocurren
en el entorno. Representar gráficamente
estas magnitudes físicas.
● En el primer momento reconocerás
conceptos básicos para el estudio de
los movimientos.
● En el segundo momento estudiarás dos
tipos de movimiento: el movimiento
rectilíneo uniforme (M.R.U.) y el
movimiento rectilíneo uniformemente
variado (M.R.U.V.). Ambos nos sirven
como modelo para explicar los
movimientos reales.
● En el tercer momento recordarás la
representación gráfica de una ecuación
lineal para explicar los diversos tipos
de movimiento.
● ¿Qué estudia la Física? ● Velocidad
● Aceleración
● Punto de referencia
● Caída libre
● Función lineal
● Gráfica
Área de Lógico matemáticaÁrea de Lógico matemáticaÁrea de Lógico matemáticaÁrea de Lógico matemáticaÁrea de Lógico matemática
● Funciones lineales y su representación
gráfica
Área de Desarrollo humanoÁrea de Desarrollo humanoÁrea de Desarrollo humanoÁrea de Desarrollo humanoÁrea de Desarrollo humano
Movimiento de los cuerpos:
● Concepto
● Elementos del movimiento
● La velocidad
Tipos de movimiento:
● Movimiento rectilíneo uniforme (M.R.U.)
● Movimiento rectilíneo uniformemente
variado (M.R.U.V.)
● Caída libre
Ficha informativaFicha informativaFicha informativaFicha informativaFicha informativa Palabras clavePalabras clavePalabras clavePalabras clavePalabras clave
Ficha de trabajoFicha de trabajoFicha de trabajoFicha de trabajoFicha de trabajo
● Uso de la calculadora científica

16 Movimientosyfuerzas
PRIMERMOMENTO:Elmovimientoylavelocidad
● Para Elena, ¿el bus se mueve? ¿Cómo lo sabe?
● Para Elena, ¿Ana y Pedro se mueven? ¿Por qué?
● Para Ana, ¿Pedro se mueve o no se mueve? Fundamenta tu respuesta.
● ¿En qué quedamos? ¿Pedro se mueve o no se mueve?
¿Cuándodecimosqueuncuerposemueve?
Para saber si un cuerpo se mueve debemos tomar puntos de referencia.
Un cuerpo está en movimiento cuando cambia de posicióncambia de posicióncambia de posicióncambia de posicióncambia de posición respecto a otros cuerpos
que se consideran fijos y que se toman como puntos de referenciapuntos de referenciapuntos de referenciapuntos de referenciapuntos de referencia.
Al observar el movimiento de los pasajeros de un bus, diremos que están en reposo si se
toman como referencia los otros pasajeros. Pero, para el observador que está en la calle,
los pasajeros se mueven ya que cambia la distancia entre él y esos pasajeros.
En realidad no hay algo que esté en reposo absoluto. Cuando estamos sentados en una
habitación creemos estar en reposo, pero la Tierra se mueve alrededor del Sol y nosotros
nos movemos con ella.
● Una persona ubicada dentro de un ascensor en subida puede afirmar que está en
movimiento, pero también que está en reposo. Indica las referencias que toma en cada
caso.
Estamos rodeados de cosas que se mueven y creemos que podemos decir con facilidad
cuándo un cuerpo se mueve o no se mueve. Sin embargo, la situación es más compleja.
Observa la imagen y responde las preguntas.
Elena
Ana Pedro

17Movimientosyfuerzas
Elementosdelmovimiento
Para analizar el movimiento de un cuerpo es
necesario reconocer cuáles son sus elementos:
● Móvil:Móvil:Móvil:Móvil:Móvil: es el cuerpo que se mueve.
● Trayectoria:Trayectoria:Trayectoria:Trayectoria:Trayectoria: es el camino que sigue el
móvil.
● Espacio recorrido:Espacio recorrido:Espacio recorrido:Espacio recorrido:Espacio recorrido: es la longitud de la
trayectoria.
● Desplazamiento:Desplazamiento:Desplazamiento:Desplazamiento:Desplazamiento: es la distancia en
línea recta que une el punto de partida
con el de llegada.
● Tiempo:Tiempo:Tiempo:Tiempo:Tiempo: es la duración del movimiento.
● Velocidad:Velocidad:Velocidad:Velocidad:Velocidad: es la relación que existe
entre la distancia recorrida y el tiempo
que tarda en recorrerla.
El movimiento es
uno de los
fenómenos físicos
más comunes de la
naturaleza.
Muchas cosas se
mueven a nuestro alrededor
el agua de los ríos, el aire, las
personas, los animales, los
vehículos de transporte, etc.
Conociendo las trayectorias se puede saber algo de los movimientos. Por ejemplo, si tres
motos dejan las siguientes huellas, ¿cómo ha sido su desplazamiento? Une cada cual con
su trayectoria.
a) Una moto que sólo daba vueltas.
b) Una moto que avanzaba en línea recta por la pista.
c) Una moto que se salió de la pista describiendo una curva.
Desplazamiento

La velocidad
Velocidad de un móvil es el espacio que recorre por unidad de tiempoes el espacio que recorre por unidad de tiempoes el espacio que recorre por unidad de tiempoes el espacio que recorre por unidad de tiempoes el espacio que recorre por unidad de tiempo.
Si un auto va a una velocidad de 80 km/h
quiere decir que recorre 80 kilómetros en una
hora y, cuando se dice que la velocidad de
un corredor es de 10 m/s, significa que
recorre 10 metros en un segundo.
El velocímetro de un auto indica la velocidad
instantánea.instantánea.instantánea.instantánea.instantánea. Por ejemplo, si marca 50 km/h.
Este valor es la velocidad a la que se desplaza
en ese momento.
Sin embargo, lo más probable es que el
automóvil no mantenga esa velocidad
durante una hora, pues en algunos tramos
irá más rápido y en otros más lento. Por eso,
al analizar un movimiento nos interesa
calcular la velocidad promedio o velocidadvelocidadvelocidadvelocidadvelocidad
mediamediamediamediamedia (vvvvvmmmmm).
La velocidad media se calcula dividiendo el espacio recorrido entre el tiempo que
se ha tardado en recorrerlo.
velocidad =
espacio recorrido
tiempo
⇒ v =
e
t
La unidad de velocidad en el Sistema Internacional de unidades es el m/s.
También es muy utilizado el km/h. La equivalencia entre ambas unidades es la
siguiente:
a) 1
km
h
a
m
s
:
1km
1 h
=
1 000 m
3 600 s
= 0,2777 m/s = 0,28 m/s
b) 1 m/s a km/h:
⇒ x =
(1 km/h)(1 m/s)
0,28 m/s
=
1 km/h
0,28
= 3,57
km
h
= 3,6
km
h
Por lo tanto: 1 m/s = 3,6 km/h 1 km/h = 0,28 m/s
En una carrera gana la persona
más rápida o dicho en otra forma, la que demora
menos tiempo en recorrer la misma distancia. Para
expresar la rapidez en que se realiza un movimiento
usamos la magnitud denominada velocidad.
1 km/h ––– 0,28 m/s
x km/h ––– 1 m/s

Ejercicio de aplicación:Ejercicio de aplicación:Ejercicio de aplicación:Ejercicio de aplicación:Ejercicio de aplicación:
Una persona recorre los primeros 20 km en 2 horas y, los siguientes 20 km, en 3 horas.
Calcular cuál es su velocidad media. Después expresar la velocidad en m/s.
a) Fórmula de velocidad media: v = e
t
Datos: Distancia total recorrida = 20 km + 20 km = 40 km
Tiempo total empleado = 2 h + 3 h = 5 h
Reemplazando datos en la fórmula: v =
40 km
5 h = 8
km
h
b) La velocidad expresada en m/s: v = 8
km
h
=
8 000 m
3 600 s = 2,2
m
s
Ejemplos de algunas velocidadesEjemplos de algunas velocidadesEjemplos de algunas velocidadesEjemplos de algunas velocidadesEjemplos de algunas velocidades
La velocidad de la luz es
la mayor reconocida:
300 000 km/s ¡No hay
nada más veloz que la luz!
EjemploEjemploEjemploEjemploEjemplo VelocidadVelocidadVelocidadVelocidadVelocidad
Avión 1 000 km/h
Tren 350 km/h
Bus 150 km/h
Auto de carreras 250 km/h
Caballo 70 km/h
Ciclista profesional 60 km/h
Persona caminando 5 km/h
Sonido (en el aire) 340 m/s – 1 225 km/h
Luz (en el vacío) 300 000 km/s
Investiga datos
curiosos sobre la
velocidad de animales,
vehículos, aviones, viento,
corrientes de agua, etc. y
preséntalos en un afiche.
En tu carpeta de trabajo:En tu carpeta de trabajo:En tu carpeta de trabajo:En tu carpeta de trabajo:En tu carpeta de trabajo:
◆ El atleta norteamericano, Tim Montgomery, batió un record mundial en el año 2002. Él
corrió 100 metros en un tiempo de 9,78 segundos. ¿Cuál fue su velocidad?
◆ Calcula cuánto demoras en correr 100 metros planos. Luego, halla tu velocidad para esta
carrera.
◆ Si la velocidad de una persona que corre es aproximadamente 46 km/h, ¿cuánto equivale
esta velocidad en m/s?
◆ Dibuja el movimiento de un cuerpo e identifica sus elementos.

Tipos de movimiento
Los movimientos se clasifican según su trayectoria
y según su velocidad.
Según su trayectoria, los movimientos pueden ser:
● Rectilíneos:Rectilíneos:Rectilíneos:Rectilíneos:Rectilíneos: la trayectoria del móvil es una
línea recta.
● Curvilíneos:Curvilíneos:Curvilíneos:Curvilíneos:Curvilíneos: la trayectoria es una curva.
Éstos a su vez pueden ser circulares, elípticos
o parabólicos.
Según su velocidad, los movimientos pueden ser:
● Uniformes:Uniformes:Uniformes:Uniformes:Uniformes: el móvil se desplaza a velocidad
constante.
● Variados:Variados:Variados:Variados:Variados: la velocidad del móvil cambia, es
decir, varía.
◆ Indica el tipo de movimiento de los siguiente móviles según la trayectoria.
Al estudiar los movimientos no sólo
aprenderás a describirlos sino también a medir algunas
de sus características; por eso, es necesario que
recuerdes las unidades de medida establecidas en el
Sistema Internacional de unidades.
Las manecillas de un reloj
______________________
Una rueda de la fortuna
______________________
Un avión
______________________
Un trompo
______________________
Una piedra que cae
______________________
¿Cómo es el¿Cómo es el¿Cómo es el¿Cómo es el¿Cómo es el
movimiento de lamovimiento de lamovimiento de lamovimiento de lamovimiento de la
Tierra alrededorTierra alrededorTierra alrededorTierra alrededorTierra alrededor
del Sol?del Sol?del Sol?del Sol?del Sol?
La trayectoria de la
Tierra es una elipse.
Podemos considerar que
la velocidad es constante
porque tarda el mismo
tiempo en recorrer cada
kilómetro.
La velocidad es enorme:
107 300 km/h.
Una pelota
______________________

ElSistemaInternacionaldeunidades
En la guía 3 estudiaste el Sistema Internacional de unidades cuya sigla es SI. El SI
considera siete magnitudes fundamentales con sus respectivas unidades las cuales se
observan en el siguiente cuadro. También se pueden usar múltiplos y submúltiplos de las
unidades fundamentales.
Además de las unidades establecidas, el SI acepta el uso de otras unidades. Por ejemplo,
la unidad de tiempo es el segundo, pero se acepta también la hora y el minuto.
Has reconocido los conceptos básicos para el estudio de los movimientos. En el segundo
momento estudiarás los movimientos rectilíneos que son fáciles de analizar.
Debes tener en cuenta que hay dos tipos de magnitudes: fundamentales y derivadas:
Las magnitudes fundamentalesLas magnitudes fundamentalesLas magnitudes fundamentalesLas magnitudes fundamentalesLas magnitudes fundamentales no guardan relación entre sí. Constituyen la base del
SI, pues no pueden ser definidas a partir de ninguna otra unidad. Ejemplos: longitud,
tiempo, temperatura, masa.
Las magnitudes derivadasLas magnitudes derivadasLas magnitudes derivadasLas magnitudes derivadasLas magnitudes derivadas pueden ser definidas a partir de las unidades fundamentales.
Por ejemplo, la velocidad es el espacio recorrido en una unidad de tiempo. Como la
unidad de longitud es el metro (m) y la del tiempo es el segundo (s), la unidad de
velocidad en el SI es m/s.
◆ ¿Qué son las magnitudes y las unidades de medida? Escribe ejemplos.
◆ ¿Qué es el SI? ¿Cuándo se estableció?
◆ Escribe ejemplos donde utilices las magnitudes fundamentales y las magnitudes derivadas.
◆ ¿Por qué algunas unidades se escriben con letras mayúsculas y otras con minúscula?
Unidades fundamentales del SIUnidades fundamentales del SIUnidades fundamentales del SIUnidades fundamentales del SIUnidades fundamentales del SI
Magnitud físicaMagnitud físicaMagnitud físicaMagnitud físicaMagnitud física UnidadesUnidadesUnidadesUnidadesUnidades Otras unidades aceptadasOtras unidades aceptadasOtras unidades aceptadasOtras unidades aceptadasOtras unidades aceptadas
Longitud metro ( m)
Masa kilogramo (kg) tonelada (t)
Tiempo segundo (s) hora (h) – minutos (min)
Temperatura kelvin (K) grados centígrados (ºC)
Corriente eléctrica amperio (A)
Cantidad de materia mol (mol)
Intensidad luminosa candela (cd)

SEGUNDOMOMENTO:Movimientosrectilíneos
¿En que podría ser útil el estudio de los movimientos para las siguientes
personas: un chofer, un piloto de avión, un ciclista, un astronauta, un
meteorólogo, una persona como tú…?
Movimiento rectilíneo uniforme (M.R.U.)
Un movimiento rectilíneo se caracteriza porque la trayectoria es una rectarectarectarectarecta y la
velocidad se mantiene constanteconstanteconstanteconstanteconstante.
En la imagen se observa que el auto avanza 20 metros cada segundo. Por lo tanto su
velocidad es constante y su valor es de 20 m/s.
En la vida cotidiana es muy difícil que un móvil se desplace con movimiento rectilíneo
uniforme, pues siempre habrá curvas y cambios de velocidad. El M.R.U. es un
modelo que nos permite interpretar los movimientos reales asumiendo que el
móvil se traslada a velocidad constante y en línea recta.
En M.R.U. la distancia recorrida es proporcional a la velocidad y al tiempo. Por
ejemplo, si la velocidad del auto es de 20 m/s, se recorrerán 20 metros en un
segundo, 40 m en dos segundos, 60 m en tres segundos y así sucesivamente.
Para introducirnos en el estudio de los movimientos analizaremos dos tipos de ellos: el
rectilíneo uniforme y el rectilíneo uniformemente variado.
Cuando alguien te lanza una pelota por el aire no tienes
dificultad alguna de atraparla, salvo que te encuentres
distraído. El cerebro, de forma inconsciente, conoce muy
bien las leyes del movimiento y calcula la trayectoria de la
pelota con enorme rapidez, así como la velocidad con la
que ésta viaja. Con estos datos envía órdenes correctas a
tu mano para que la atrape en el lugar y momento preciso.
Lo mismo sucede si cruzamos una pista intuitivamente
calculamos la distancia y la velocidad con la que vienen los
carros para saber si podemos cruzar la pista o no.
t = 0 s
0 m
t = 1 s
20 m
t = 2 s
40 m
t = 3 s
60 m

Recuerda que las
operaciones deben
efectuarse en las
mismas unidades.
El M.R.U. se define mediante la siguiente ecuación matemática: e = v. t
Donde:
e = distancia que recorre el móvil expresada en m, km…
v = velocidad expresada en m/s, km/h….
t = tiempo que tarda el móvil en desplazarse expresado en s, h, min.
Con esta ecuación matemática podemos calcular también la velocidad y el tiempo.
v =
e
t
t =
e
v
● Una persona en bicicleta se desplaza con una velocidad constante de 6 m/s, ¿cuántos
metros recorrerá al cabo de 15 minutos?
Anota los datos: v = 6 m/s t = 15 min
Para reemplazar en la fórmula se debe convertir minutos a segundos.
t = 15 min x
60 s
1 min
= 900 s
Aplica la fórmula: e = v. t
e = 6
m
s
x 900 s = 5 400 m
Respuesta:Respuesta:Respuesta:Respuesta:Respuesta: La persona en bicicleta recorrerá 5 400 m o 5,4 km.
◆ Un automóvil se desplaza a una velocidad constante de 95 km/h ¿Cuántos km recorrerá
al cabo de 5 horas?
◆ Un moderno tren se mueve a una velocidad constante de 350 km/h ¿Cuánto tiempo
empleará en recorrer 2 000 km?
◆ El radar de control de velocidad de la Av. Javier Prado toma dos fotos a un carro. Una, en
el punto A y otra en el punto B. Entre los dos puntos hay 60 metros. El cronómetro indica
que han pasado 2 segundos entre ambas fotos. Calcula cuál es la velocidad del auto.
Luego, exprésala en km/h y di si le pondrán una multa, si se sabe que sólo se puede
transitar por esta avenida a 65 km/h.
◆ Se ha formado un viento fuerte llamado «paracas» en la ciudad de Pisco. Suponiendo
que este viento viaja a velocidad constante de 50 km/h, ¿en qué tiempo llegará a la
ciudad de Ica que se encuentra a 70 km de distancia?

Movimientorectilíneouniformementevariado(M.R.U.V.)
El movimiento rectilíneo uniformemente variado es aquel en que la velocidadvelocidadvelocidadvelocidadvelocidad
varíavaríavaríavaríavaría una cantidad constanteconstanteconstanteconstanteconstante en cada unidad de tiempo.
Por ejemplo, en la figura observas que el auto incrementa su velocidad 5m/s en
cada segundo.
La variación de la velocidad (aumento o disminución) se denomina aceleraciónaceleraciónaceleraciónaceleraciónaceleración.
La aceleración también es una magnitud y se define como la variación de la velocidad
en una unidad de tiempo.
Se expresa con la siguiente ecuación matemática: a =
∆v
t
=
v v
t
f i–
Donde:
a = aceleración ∆v = variación de la velocidad vf = velocidad final
vi = velocidad inicial t = tiempo
● Si una moto parte del reposo (0 m/s) y al cabo de 6 segundos alcanza una velocidad de
30 m/s, ¿cuál es su aceleración?
Anota la ecuación: a =
v v
t
f i–
Sustituye los datos:
a =
30 m/s – 0 m/s
6 s
= 5 m/s2
La aceleración es de 5 m/s2
La unidad de aceleración en el SI es el m/s2
A partir de esta fórmula podemos calcular la velocidad y el espacio de un móvil en
cualquier instante de su recorrido.
vf
= vi
+ at e = vi
t +
1
2
at2
Si vi
= 0 entonces e =
1
2
at2
Aceleración positiva yAceleración positiva yAceleración positiva yAceleración positiva yAceleración positiva y
negativa.negativa.negativa.negativa.negativa. La aceleración
es positiva cuando la
velocidad aumenta y
negativa cuando la
velocidad disminuye. Si es
negativa anteponemos el
signo (–).
t = 0 s
v0 = 0 m/s
t = 1 s
v0 = 5 m/s
t = 2 s
v0 = 10 m/s
t = 3 s
v0 = 15 m/s

Lacaídalibre
La caída libre es un ejemplo de movimiento uniformemente variado. Cuando se
suelta un objeto desde cierta altura, se observa que cae libremente por efecto de la
fuerza de la gravedadfuerza de la gravedadfuerza de la gravedadfuerza de la gravedadfuerza de la gravedad que ejerce la Tierra.
Este objeto cae cada vez más rápido hacia
el suelo. Por ejemplo, una maceta que cae
de un quinto piso tiene más velocidad al
llegar al suelo que cuando pasaba por el
tercer piso.
La velocidad de un cuerpo aumenta 9,8 m/s, es
decir, su aceleración es 9,8 m/s2
(aunque para
efectos prácticos se redondea a 10 m/s2
).
Siguiendo con el ejemplo de la maceta, en
el punto de partida tiene una velocidad de
0 m/s; luego de un segundo habrá
aumentado a 10 m/s; a los dos segundos,
20 m/s; a los tres segundos, 30 m/s; y así
sucesivamente.
La caída libre se debe a la fuerza de gravedad
de la Tierra. Todos los cuerpos caen con una
aceleración constante de 9,8 m/s2
.
Esta
aceleración se llama aceleración de laaceleración de laaceleración de laaceleración de laaceleración de la
gravedadgravedadgravedadgravedadgravedad y se representa con la letra ggggg.
◆ El auto de Juan puede pasar de 0 a 60 km/h en 5 segundos; en cambio, el auto de
Francisca puede pasar de 0 a 80 km/h en 8 segundos. ¿Qué auto tiene mayor aceleración?
¿Por qué?
◆ En cierto tramo de su recorrido, un auto acelera de 100 km/h a 180 km/h en 10 s, ¿cuál
es el valor de la aceleración?
◆ Un camión que viaja a una velocidad de 80 km/h aplica los frenos y se detiene
completamente después de recorrer 60 m ¿Qué tiempo demoró en detenerse?
En resumen un cuerpo se acelera cuando
varía su velocidad. Si la velocidad disminuye se dice
que ha frenado o que tiene una aceleración negativa.
Para calcular la aceleración se divide la variación de
la velocidad entre el tiempo.
V1 = 0
V2 = 10 m/s
V5 = 60 m/s
V3 = 20 m/s

◆ Un libro que cae de un estante tarda 0,4 segundos en llegar al suelo. ¿Cuál es la altura
del estante?
◆ Un ladrillo cae desde el octavo piso (24 m) de un edificio en construcción. ¿Con qué
velocidad se estrella en el piso?
◆ Si una persona cae de un segundo piso, las lesiones que puede sufrir en su cuerpo son
menores que si cae de un quinto piso. Explica cuál es la razón.
● Se deja caer una piedra desde una altura de 10 metros. ¿Cuánto tiempo demorará en
llegar al piso?
Datos:Datos:Datos:Datos:Datos:
vi = 0
t = ¿?
a = g = 10 m/s2
e = h = 10 m
¿Porquécaeprimerounapiedraqueunapluma?
Cuando un cuerpo cae aumenta su velocidad siempre
al mismo ritmo (9,8 m/s2
), independientemente de
cuál sea su peso. Esto significa que, si soltásemos
varios objetos desde una misma altura, todos
deberían llegar al suelo al mismo tiempo.
Sin embargo, si soltamos desde una misma altura
una piedra y una hoja de papel, por experiencia
sabemos que la piedra cae primero. Pero,
deberían llegar al mismo tiempo. ¿Se han
equivocado los científicos? No, lo que ocurre es
que, debido a su forma, en el papel la resistencia
del aire es mayor y por eso retarda su caída. Si la
experiencia se realizara en una cámara al vacío
(un recipiente al que se le ha sacado el aire), los
dos objetos caerían al mismo tiempo.
SoluciónSoluciónSoluciónSoluciónSolución
● Usa la fórmula: e =
1
2
at2
● Despeja t de la fórmula:
t =
2e
a
=
2 10
10
( )
= 2 = 1,41 s
RespuestaRespuestaRespuestaRespuestaRespuesta: La piedra demora en llegar al piso 1,41 s
Cámara
al vacío

Materiales:Materiales:Materiales:Materiales:Materiales:
● Una hoja de papel, una moneda y diversos objetos.
Procedimiento:Procedimiento:Procedimiento:Procedimiento:Procedimiento:
1. Deja caer desde una misma altura una hoja de papel y una moneda. ¿Cuál llega primero?
2. Repite la experiencia, pero ahora arruga la hoja de papel y haz una pelotita con ella.
Explica lo que sucede.
3. Prueba con objetos de diferente peso, pero que tengan una forma igual o parecida.
Galileo Galilei, gran astrónomo y físico italiano (1564-1642), sintió gran interés
por el estudio de los movimientos y en especial por el movimiento de los
planetas.
Sostuvo que la Tierra se movía y que no era el centro del
universo, idea que nos parece evidente en nuestros días pero
en su época fue revolucionaria. Galileo también demostró que
todos los cuerpos caen a la misma velocidad. Para demostrarlo
subió a la torre inclinada de Pisa y
desde allí dejó caer diferentes
objetos de diferente masa pero de
igual forma y tamaño. ¡Todos
llegaron al mismo tiempo al suelo!
La parte de la Física que estudia el movimiento y las
causas que lo producen se llama Mecánica y en su
desarrollo han contribuido Galileo Galilei e Isaac Newton,
entre otros.
● ¿Qué estudia la Física? ¿Cuáles son sus ramas? (Ver Ficha informativa).
● ¿Qué rama de la Física estudia los movimientos y las causas que los producen?
Has aprendido a calcular el espacio, el tiempo, la velocidad y la aceleración de un móvil.
En el tercer momento representarás gráficamente los movimientos aprendidos.
Experimentalacaídalibre

TERCER MOMENTO: Representación gráfica
del movimiento
Elmer trabaja en un taller de cerámica a 10 kilómetros
de su casa. Él suele ir a su trabajo en bicicleta. Su hora
de entrada es 8:10 a.m., por lo que sale todas las mañanas
–de lunes a sábado– a las 7:30 a.m. para no llegar tarde.
En el siguiente plano cartesiano se observa la gráfica
que representa la relación entre la distancia recorrida y
el tiempo que tarda Elmer en recorrer esa distancia.
En el eje x se representa el tiempo cada cinco minutos. Generalmente este eje se representa
con la letra t. Y en el eje y se representa la distancia en kilómetros. Generalmente, este
eje se representa con la letra e.
Para representar gráficamente el movimiento se utiliza el plano cartesiano.
Utilizando la información de la gráfica responde:
◆ ¿Cuántos kilómetros habrá recorrido Elmer a las 7:45?
◆ ¿Cuántos minutos tardó en la primera mitad del recorrido?
◆ ¿Cuántos kilómetros recorrió entre las 7:45 y las 8:00?
◆ Si sabemos que la velocidad es igual a distancia sobre tiempo: v =
e
t
¿Cómo puedes
saber si Elmer ha ido a la misma velocidad en los primeros 20 minutos (de 7:30 a 7:50)?
◆ Si la entrada es a las 8:10, ¿crees que de seguir a la misma velocidad llegará a tiempo?
Determina con cuántos minutos de adelanto o atraso llegará.
10
9
8
7
6
5
4
3
2
1
0
7:30 7:35 7:40 7:45 7:50 7:55 8:00 8:05 8:10 8:15 8:20 8:25
y = e
x = t
(tiempo)

A continuación verás las representaciones gráficas de las magnitudes del movimiento:
● Un objeto se mueve con movimiento rectilíneo uniforme si su trayectoria es en línea recta
y recorre espacios iguales en tiempos iguales.
v = 60 km/h
Movimiento rectilíneo uniforme
En el M.R.U. la velocidad no cambia, se mantiene constante. Al ser la velocidad todo el
tiempo la misma, el objeto que se está moviendo no acelera. En el movimiento rectilíneo
uniforme la aceleración es cero (a = 0).
Ejemplo de cómo se construyen gráficos en el M.R.U.Ejemplo de cómo se construyen gráficos en el M.R.U.Ejemplo de cómo se construyen gráficos en el M.R.U.Ejemplo de cómo se construyen gráficos en el M.R.U.Ejemplo de cómo se construyen gráficos en el M.R.U.
Un móvil inicia su movimiento a una velocidad de 100 km por hora.
v = 100 km/h
x
t0 = 0 t1 = 1 h t2 = 2 h
0 100 km 200 km
Móvil
El móvil después de una hora habrá recorrido 100 km; después de 2 horas, 200 km y así
sucesivamente… Esto se puede escribir en una tabla de datos:
PosiciónPosiciónPosiciónPosiciónPosición TiempoTiempoTiempoTiempoTiempo
(km) (horas)
0 0
100 1
200 2
Luego puedes representar los valores del tiempo y la distancia recorrida por el móvil.
200
100
0
0 1 2 3 t (h)
e (m)
300

Uniendo los puntos obtienes el gráfico de la distancia en función del tiempo:
Gráfico 1
e = f(t)
(Distancia en función del tiempo)
Este gráfico demuestra que el movimiento del móvil es rectilíneo uniforme.
En matemática una función es la relación entre dos variables numéricas, una variable
dependiente y la otra independiente. En el ejemplo anterior sería:
e = f(t)
Utilizamos este concepto en Física para relacionar dos magnitudes, de tal manera que a
cada valor de la magnitud independiente (en nuestro caso el tiempo) le corresponde un
único valor de la magnitud dependiente (el espacio o distancia).
También puedes dibujar los gráficos de velocidad y aceleración en función del tiempo:
Gráfico 2 Gráfico 3
v = f(t) a = f (t)
Velocidad en función del tiempo Aceleración en función del tiempo
En estos 3 gráficos se ven perfectamente las características del M.R.U.:
● El gráfico 1 muestra que la posición aumenta linealmente con el tiempolinealmente con el tiempolinealmente con el tiempolinealmente con el tiempolinealmente con el tiempo. La pendientependientependientependientependiente
de la rectade la rectade la rectade la rectade la recta en el gráfico e = f(t) es la velocidadvelocidadvelocidadvelocidadvelocidad
● El gráfico 2 muestra que la velocidad se mantiene constanteconstanteconstanteconstanteconstante.
● El gráfico 3 muestra que la aceleración es todo el tiempo cerocerocerocerocero.
Pendiente de la recta
200
100
0
0 1 2 3 t (h)
e (m)
300
Cte.
0 1 2 3 t (h)
v
(km/h)
100
0 1 2 3 t (h)
a
a = 0

Observa la ecuación de la recta de la pendiente de m:
Donde: m = pendiente
x = variable independiente (tiempo)
b = lugar donde la recta corta el eje y
Si comparamos la ecuación de la recta y la fórmula de velocidad verás que la pendiente
representa la velocidad.
y = m . x + b
↑ ↑ ↑ ↑
↓ ↓ ↓ ↓
e = v . t + e0
◆ Elabora el gráfico para las siguientes ecuaciones:
a) y =
x − 4
2
b) y = 2x – 1 c) y =
x + 4
2
d) y = 4x – 3
◆ Una persona sale de la posición e0
= 400 km a las 8 h y llega a la posición e = 700 km a
las 11 h (fue en línea recta y con v = constante). Se pide:
a) Calcular con qué velocidad se movió (en km/h y en m/s)
b) Dibujar los gráficos de e = e(t), v = v(t) y a = a(t)
Has aprendido que una ecuación con dos variables relacionadas entre sí puede ser considerada
una función. Además, que las funciones describen fenómenos físicos como el movimiento y
que pueden representarse a través de gráficos que permiten seguir su progreso.
Observa la trayectoria del móvil
Representación de la ecuación
de una recta de pendiente m.
y
b
y = mx + b
x
◆ Representa gráficamente la distancia en función del tiempo, la velocidad en función del
tiempo y la aceleración en función del tiempo.
t0 = 0
0
t1 = 1,5 h v = 80 km/h
120 km
t2 = 3 h
240 km

FICHA INFORMATIVA
¿Qué estudia la Física?
Las Ciencias Naturales son aquellas ciencias que
se encargan de estudiar los fenómenos naturales
físicos, químicos, biológicos, geológicos… Entre
las más conocidas podemos citar la Física, la
Química, la Biología, la Geología, la Astronomía,
etc.
Actualmente nuevos fenómenos descubiertos han
obligado a los científicos a interrelacionar estas
ciencias originándose otras como, la Bioquímica,
la Astrofísica, Biofísica, etc.
La FísicaLa FísicaLa FísicaLa FísicaLa Física es la rama de las Ciencias Naturales que
estudia entre otras cosas: el equilibrio, el
movimiento, el calor, la electricidad, el magnetismo,
las ondas con el propósito de comprenderlos y
aplicarlos en beneficio de la humanidad.
Ramas de la FísicaRamas de la FísicaRamas de la FísicaRamas de la FísicaRamas de la Física
Para un mejor estudio de los fenómenos físicos, la Física se divide en varias ramas.
● MecánicaMecánicaMecánicaMecánicaMecánica: estudia el movimiento.
● AcústicaAcústicaAcústicaAcústicaAcústica: estudia el sonido.
● CalorCalorCalorCalorCalor: estudia los fenómenos térmicos.
● HidrostáticaHidrostáticaHidrostáticaHidrostáticaHidrostática: estudia el comportamiento de los líquidos y gases.
● Electricidad y magnetismoElectricidad y magnetismoElectricidad y magnetismoElectricidad y magnetismoElectricidad y magnetismo: estudia los fenómenos eléctricos y magnéticos y
sus interrelaciones.
● ÓpticaÓpticaÓpticaÓpticaÓptica: estudia la luz.
● Física nuclearFísica nuclearFísica nuclearFísica nuclearFísica nuclear: estudia el átomo.
● Física modernaFísica modernaFísica modernaFísica modernaFísica moderna: estudia el comportamiento de las partículas subatómicas, es
decir, de las partículas que están dentro del núcleo de los átomos.
La mayor parte de la tecnología
está basada en la Física.
La Física procura comprender los fenómenos
de la naturaleza para explicarlos mediante leyes,
principios y teorías. Los conocimientos adquiridos se
aplican en las actividades humanas para mejorar
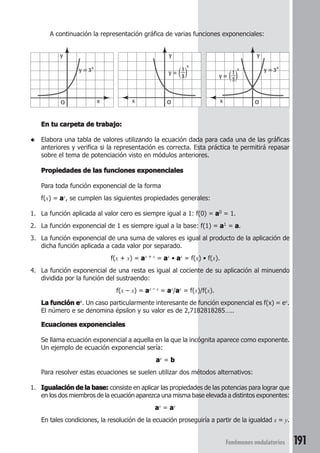
la calidad de vida de las personas.

FICHADETRABAJO
Uso de la calculadora científica
Las calculadoras científicas tienen tres teclas que permiten el cálculo de las funciones
trigonométricas conociendo el ángulo.
Las posiciones de las teclas y su uso es variado,
depende de la marca y el modelo de la calculadora.
Un modelo muy difundido es el siguiente:
Actividad:Actividad:Actividad:Actividad:Actividad:
Calcular el coseno de 60°.
Primero, introduces el valor del ángulo, en este
caso 60. En el visor aparecerá:
Luego, presiona la tecla:
En el visor aparecerá:
Esto quiere decir que cos 60° = 0,5
Utilizando la calculadora científica
podemos resolver fácilmente
problemas relacionados con
funciones trigonométricas.
. +/- 0 + =
– 1 2 3 M+
x 4 5 6 RM
÷ 7 8 9 M
Exp yx
x2
( )
DEG ln log a b →→→→→
hyp sin cos tan F↔↔↔↔↔E CE
Off On/C
πππππ 1/x
√6
√6y √63
↔↔↔↔↔
∑∑∑∑∑x
→→→→→D. MS →→→→→rΘΘΘΘΘ CPLX→→→→→xyex
10x
n!TABarc hyp tan–1sin–1
cos–1
x
sin-1
cos-1
tan-1
sin cos tan
seno coseno tangente
cos-1
cos
La calculadora te dará
resultados en forma decimal.

Comprueba con una calculadora científica el valor de las funciones trigonométricas de
la siguiente tabla.
Puedes resolver diversos problemas haciendo uso de las funciones trigonométricas. Por
ejemplo:
Si quieres saber la altura de un árbol. Lo que puedes hacer es pararte en un lugar
cualquiera y medir la distancia de ese punto al árbol; en este caso, supón que es 8 m.
Después, con un transportador mides el ángulo que hay hasta la punta del árbol;
imagina que aproximadamente mide 30°. Esquemáticamente sería algo así:
Ahora, usando la fórmula de tangente de un ángulo:
tg 30° = Altura del árbol
8 m
Altura del árbol = (8 m) (tg 30°) = (8) (0,577) m = 4,61 m
Altura del árbol = 4,61 m
◆ Calcula las razones trigonométricas del triángulo de lados 7 cm; 7,4 cm y 2,4 cm
para el ángulo de 19°.
ααααα
Sen ααααα
Cos ααααα
Tg ααααα
00000° 3030303030° 4545454545° 6060606060° 9090909090°
0 0,5 0,707 0,866 1
1 0,866 0,707 0,5 0
0 0,577 1 1,732 ∞∞∞∞∞
30°
Altura
8 m

35
Las fuerzasLas fuerzasLas fuerzasLas fuerzasLas fuerzas
1. Las fuerzas y el movimiento
2. Leyes de Newton
3. Funciones trigonométricas para la
suma de fuerzas
Conocer las leyes que permiten explicar
las causas de los movimientos, las cuales
se denominan Leyes de Newton.
Identificar las funciones trigonométricas
y su utilidad en la Física.
● En el primer momento aprenderás a
definir, representar y medir las fuerzas.
● En el segundo momento reconocerás
las tres leyes de Newton, las cuales
nos dan a conocer los efectos de las
fuerzas en el movimiento de los
cuerpos.
● En el tercer momento identificarás las
funciones trigonométricas y su
aplicación para la obtención de una
fuerza resultante.
● Resolución de triángulos rectángulos ● Fuerza
● Inercia
● Gravedad
● Seno
● Coseno
● Tangente
Funciones trigonométricas:
● Seno
● Coseno
● Tangente
Fuerzas:
● Concepto
● Representación y medición
● Composición de varias fuerzas
Leyes de Newton
Ficha de trabajoFicha de trabajoFicha de trabajoFicha de trabajoFicha de trabajo Palabras clavePalabras clavePalabras clavePalabras clavePalabras clave

PRIMERMOMENTO:Lasfuerzasyelmovimiento
No siempre usamos correctamente el concepto de fuerza. Lo empleamos en lugar de
esfuerzo mental, confundimos fuerza con energía, etc.
Para definir lo que es una fuerza, analiza la acción de las fuerzas en un partido de fútbol.
Se necesita de una fuerza para:Se necesita de una fuerza para:Se necesita de una fuerza para:Se necesita de una fuerza para:Se necesita de una fuerza para:
El estudio de las fuerzas ha
permitido al ser humano diseñar desde
una sencilla casa hasta grandes edificios,
puentes y otras estructuras de gran
tamaño y complejidad.
Iniciar el movimiento
de la pelota
Cambiar la dirección
o la velocidad
Detener el movimiento
Sujetar la pelota sin
que caiga al piso
Aplastarla, es decir
deformarla
empujar golpear comprimir sujetar estudiar tener valor
pensar levantar escribir correr morder pedalear
¿Pensaste alguna
vez en cuántas ocasiones haces
fuerza a lo largo del día? Marca
los recuadros en los cuales crees
que ejerces una fuerza.

¿Qué son las fuerzas?
El concepto de fuerza que usan los científicos es el siguiente:
Fuerza es todo aquello que hace que los cuerpos varíen su estado de movimiento
o reposo, cambien de forma o se mantengan en equilibrio.
Observa que en esta definición hay tres efectos:
1) Las fuerzas inician, modifican o detienen un movimiento:Las fuerzas inician, modifican o detienen un movimiento:Las fuerzas inician, modifican o detienen un movimiento:Las fuerzas inician, modifican o detienen un movimiento:Las fuerzas inician, modifican o detienen un movimiento:
● Si el cuerpo estaba en reposo, las fuerzas inician el movimiento. Por ejemplo,
una pelota no se moverá si no ejercemos una fuerza sobre ella; un velero
no se pondrá en movimiento en ausencia de viento.
● Si el cuerpo está en movimiento, las fuerzas cambian su velocidad, lo
detienen o modifican su dirección.
2) Las fuerzas cambian la forma de los objetos:Las fuerzas cambian la forma de los objetos:Las fuerzas cambian la forma de los objetos:Las fuerzas cambian la forma de los objetos:Las fuerzas cambian la forma de los objetos:
Cuando se aplica una fuerza a objetos que no son rígidos, éstos se deforman.
Por ejemplo, piensa lo que sucede cuando aprietas un trozo de plastilina. Hay
deformaciones permanentes y otras temporales.
3) Las fuerzas mantienen en equilibrio un cuerpo:Las fuerzas mantienen en equilibrio un cuerpo:Las fuerzas mantienen en equilibrio un cuerpo:Las fuerzas mantienen en equilibrio un cuerpo:Las fuerzas mantienen en equilibrio un cuerpo:
Por ejemplo, cuando sostenemos una botella en la mano, ésta no se cae
porque ejercemos una fuerza en contra de la fuerza de gravedad.
● Relaciona los efectos de las fuerzas escribiendo la letra que corresponde.
( ) abrir una puerta
( ) encestar una pelota de básquet
a) iniciar un movimiento
( ) sujetar un perro
b) variar un movimiento
( ) sostener un libro en la mano
c) cambiar la forma
( ) acelerar un carro
d) mantener el equilibrio
( ) arrugar una hoja de papel
e) detener un movimiento
( ) hacer un saque de voley
¿Sabías que … las hormigas son animales muy fuertes?
Pueden cargar hasta 20 veces su peso. Si nosotros fuésemos
tan fuertes como ellas, podríamos cargar, sin problemas,
una tonelada y media de peso.

● ¿Qué instrumentos se utilizan para medir las fuerzas?
● ¿Qué quiere decir que la fuerza es una magnitud? ¿Cuál es su unidad?
Mediciónyrepresentacióndefuerzas
La fuerza es una propiedad que se
puede medir. La unidad de fuerza en
el Sistema Internacional de unidades
es el newtonnewtonnewtonnewtonnewton (NNNNN).
Un newton se define como la fuerza
que aplicada a la masa de 1 kg produce
una aceleración de 1 m/s2
.
1 N = 1 kg . m/s2
Para medir las fuerzas se usan
instrumentos llamados dinamómetrosdinamómetrosdinamómetrosdinamómetrosdinamómetros
comúnmente llamados balanza de
resorte.
Un dinamómetro está formado por un resorte y una escala graduada. El resorte se
estira cuando enganchamos un objeto o aplicamos sobre él una fuerza. Una aguja
o indicador marca el valor de la fuerza. La graduación puede estar en N o en kg.
Las fuerzas se representan mediante flechas o vectoresvectoresvectoresvectoresvectores:
● El tamaño de la flechatamaño de la flechatamaño de la flechatamaño de la flechatamaño de la flecha nos indica la intensidad. Cuanto más larga sea una
flecha, mayor será la fuerza.
● La dirección de la flechadirección de la flechadirección de la flechadirección de la flechadirección de la flecha
indica si la fuerza se ejerce
de manera vertical,
horizontal u oblicua.
● La punta de la flechapunta de la flechapunta de la flechapunta de la flechapunta de la flecha
señala el sentido de la
fuerza; es decir, hacia dónde
se dirige. Puede ser hacia
arriba o hacia abajo, a la
izquierda o a la derecha.
Sentido : hacia abajo
Dirección: vertical

Composicióndevariasfuerzas
Normalmente, sobre un cuerpo actúan dos o más fuerzas al mismo tiempo. El
conjunto de fuerzas que actúan en un cuerpo se puede sustituir por una sola fuerza
llamada resultanteresultanteresultanteresultanteresultante. A continuación verás cómo hallar la resultante de varias fuerzas.
● Composición de fuerzas de igual direcciónComposición de fuerzas de igual direcciónComposición de fuerzas de igual direcciónComposición de fuerzas de igual direcciónComposición de fuerzas de igual dirección
Existen dos casos posibles:
1) Si las fuerzas tienen el mismo sentido
(Fig. A), las fuerzas se suman y la
resultante (R) tendrá la misma
dirección y sentido de las fuerzas
aplicadas.
2) Si las fuerzas tienen sentidos
diferentes (Fig. B), las fuerzas se
restan. La resultante tendrá la misma
dirección, pero el sentido será el de la
fuerza de mayor valor.
● Composición de fuerzas enComposición de fuerzas enComposición de fuerzas enComposición de fuerzas enComposición de fuerzas en
diferente direccióndiferente direccióndiferente direccióndiferente direccióndiferente dirección
Para hallar la resultante se utiliza el
método del paralelogramo. Por ejemplo,
sobre un bote (Fig. C) actúa la fuerza de
la corriente del río (fuerza A) y, por otro
lado, actúa la fuerza de la persona que
rema (fuerza B).
Con estas dos fuerzas se dibujan líneas
punteadas paralelas a las fuerzas y se forma
un paralelogramo. La resultante (el camino
que tomará el bote) es la diagonal del
paralelogramo.
◆ Dibuja los esquemas y grafica la fuerza resultante.
◆ Representa gráficamente:
a) Dos fuerzas de igual sentido y diferente intensidad.
b) Dos fuerzas de igual sentido y diferente dirección.
5 N 5 N
10 N 10 N
Figura C
R =
F1 – F2
F1 F2
Figura A
R =
F1 + F2
F2
F1
R
O
fuerza B
fuerzaA
Figura B

● Clavo, tapa de hojalata, cordel, pesas y soporte.
1. Con un clavo, perfora cuatro agujeros equidistantes,
sobre el reborde de una tapa de hojalata.
2. Pasa cordeles por estos orificios y anúdalos en el
extremo libre.
3. Cuelga la tapa en una liga fuerte y ésta a un clavo
grande colocado en un soporte.
4. Haz las graduaciones utilizando pesas.
5. Si no tienes pesas, puedes utilizar volúmenes
conocidos de agua y marca la escala en gramos.
Ten en cuenta que: 10 ml de agua pesan 10 g.
Tiposdefuerzas
Fuerzas de contacto:Fuerzas de contacto:Fuerzas de contacto:Fuerzas de contacto:Fuerzas de contacto: son aquellas en las que existe un contacto físico entre el
cuerpo que produce la fuerza y el cuerpo sobre el que se aplica dicha fuerza. Por
ejemplo, empujar un carro, cargar un objeto con una grúa, patear una pelota.
Fuerzas a distancia:Fuerzas a distancia:Fuerzas a distancia:Fuerzas a distancia:Fuerzas a distancia: son aquellas que se producen entre cuerpos que interactúan
a distancia, es decir, que no están en contacto. Por ejemplo, la fuerza de gravedad
entre la Luna y la Tierra y la fuerza magnética que ejercen los imanes.
◆ Indica de qué tipo son las siguientes fuerzas:
■ La fuerza con que la Tierra atrae a un paracaidista que salta de un avión.
■ La fuerza que ejercemos al presionar un resorte.
■ La fuerza eléctrica entre dos nubes cargadas de electricidad que originan los rayos.
■ La fuerza que ejercemos al cargar un balde con agua.
◆ ¿Cómo podrías demostrar que un imán ejerce una fuerza a distancia?
Experimenta:Construyeun
dinamómetro simple

El estudio de las fuerzas ayuda a emplear y construir
estructuras resistentes. Para comprobarlo realiza dos
actividades:
Actividad 1:Actividad 1:Actividad 1:Actividad 1:Actividad 1:
1. Arma dos columnas de libros y coloca una hoja de
papel entre ellas a manera de puente.
2. Pon monedas, una por una, sobre la hoja de papel y
observa cuántas monedas puede soportar el puente.
3. Ahora haz varios pliegues con la hoja de papel y
colócala como puente. Vuelve a colocar las monedas y
anota el número de monedas que puede soportar.
Actividad 2:Actividad 2:Actividad 2:Actividad 2:Actividad 2:
1. Enrolla una hoja de papel de modo que forme un
tubo y pega una cinta adhesiva para que no se
desenrolle.
2. Ata un trozo de pabilo a una botella que contenga
agua hasta la mitad y levántala con el tubo que hiciste
tal como indica la figura.
3. Con una segunda hoja de papel forma otro tubo,
pero aplástalo para que pierda su forma y quede
como una tira. Ahora levanta la botella como en la
figura 2.
● ¿Cuál de las dos estructuras resultó más fuerte?
● ¿Conoces algunas construcciones (puentes, torres, barandas, etc.) que
tengan estructuras en ángulo como la hoja de papel que hiciste? Menciona
algunas.
● ¿Con cuál tubo pudiste levantar la botella?
● ¿Qué conclusión puedes sacar de esta experiencia?
1
2
3
1
2
3
Experimenta: ¿Qué
formaesmásresistente

SEGUNDOMOMENTO:LeyesdeNewton
● ¿Por qué se sigue moviendo la bicicleta cuando dejas de pedalear?
● ¿Dónde te desplazas más rápido, en una pista asfaltada o sin asfaltar?
¿Por qué?
● ¿Qué pasaría con tu cuerpo si frenaras bruscamente?
Primera Ley de Newton o Ley de la Inercia
Inercia es la propiedad de los cuerpos que hace que éstos tiendan a conservar su
estado de reposo o de movimiento. Newton formuló la ley de la inercia de la
siguiente manera:
Cuando no actúan fuerzas sobre un cuerpo, si está en reposo, seguirá enCuando no actúan fuerzas sobre un cuerpo, si está en reposo, seguirá enCuando no actúan fuerzas sobre un cuerpo, si está en reposo, seguirá enCuando no actúan fuerzas sobre un cuerpo, si está en reposo, seguirá enCuando no actúan fuerzas sobre un cuerpo, si está en reposo, seguirá en
reposo y si está moviéndose seguirá con un movimiento rectilíneoreposo y si está moviéndose seguirá con un movimiento rectilíneoreposo y si está moviéndose seguirá con un movimiento rectilíneoreposo y si está moviéndose seguirá con un movimiento rectilíneoreposo y si está moviéndose seguirá con un movimiento rectilíneo
uniforme.uniforme.uniforme.uniforme.uniforme.
Es obvio que un objeto no se moverá a menos que una fuerza actúe sobre él.
Pero, no es tan obvia la otra parte de la ley que dice: un objeto en movimiento se
moverá siguiendo una misma dirección sin variar su velocidad, a menos que una
fuerza lo frene o lo detenga. Esto quiere decir que si hiciéramos rodar una pelota,
ésta se movería eternamente en línea recta.
En la realidad, observamos que la pelota se detiene y parece que no cumple la ley
de inercia. Lo que ocurre es que sobre la pelota actúa la fuerza de rozamiento del
piso que la detiene. Pero ¿qué sucedería en el espacio donde no hay rozamiento
con el aire o con alguna superficie?... Allí la pelota se movería eternamente.
Para manejar una bicicleta se ponen en juego muchas
fuerzas. Primero, debes ejercer una fuerza; si no la
bicicleta no se mueve. La fuerza es aplicada a los
pedales y se trasmite a las ruedas. Luego, sigues
pedaleando y cuando adquieres cierta velocidad y
dejas de pedalear la bicicleta continúa avanzando.
Durante tu recorrido modificas la velocidad y para
detenerla completamente aplicarás los frenos.
Galileo y otros científicos estudiaron cómo actúan las fuerzas en el movimiento de los
cuerpos, pero fue el físico inglés Isaac Newton (1642 – 1727) quien resumió esta actuación
en tres principios que hoy llamamos Leyes de Newton.

Los efectos de la inercia pueden ser observados cuando se va en un vehículo.
● ¿Exiges a los taxistas y otros chóferes que tengan cinturones de seguridad
en buen estado?
● Haz una encuesta entre tus compañeros y familiares para determinar si
usan o no los cinturones de seguridad. Analiza y comenta los resultados.
Elcinturóndeseguridadesnecesario
Se ha demostrado que si un vehículo va a una
velocidad de 50 km/h y choca frontalmente,
su conductor saldría lanzado por el parabrisas
a la misma velocidad del automóvil.
Los cinturones de seguridad detienen a las
personas y evitan que salgan disparadas por
el parabrisas; gracias a ello se salvan
muchas vidas.
◆ ¿Un objeto puede moverse en ausencia de la fuerza?
◆ Coloca una moneda sobre una hoja de papel y mueve rápidamente la hoja. Dibuja la
experiencia y explícala.
◆ ¿Por qué es peligroso llevar troncos de madera u otros objetos pesados en un camión sin
una baranda de protección?
Cuando el bus arranca bruscamente tu
cuerpo se inclina hacia atrás porque tiende
a mantener el estado de reposo que tenía
hasta el momento de arrancar.
Cuando el bus frena bruscamente, tu cuerpo
se inclina hacia delante porque trata de
seguir en movimiento a pesar de que el
ómnibus se detuvo.

● Una moto de 100 kg va a 108 km/h y frena hasta pararse en 5 segundos. ¿Qué fuerza
ejerció?
Datos: m = 100 kg
v = 108 km/h
t = 5 s
F = ?
Segunda Ley de Newton: Relación fuerza, masa y aceleración
Es más fácil mover una carretilla vacía que
una llena aplicando la misma fuerza. Cuanto
mayor masa tiene un cuerpo, mayor dificultad
tiene para moverse, es decir, para modificar
su velocidad. Por lo tanto, la aceleración que
adquiere un cuerpo no sólo depende de la
fuerza sino de la masa. A mayor masa, menor
aceleración.
Newton en su segunda ley dice:
Todo cuerpo adquiere una aceleración que es directamente proporcionalTodo cuerpo adquiere una aceleración que es directamente proporcionalTodo cuerpo adquiere una aceleración que es directamente proporcionalTodo cuerpo adquiere una aceleración que es directamente proporcionalTodo cuerpo adquiere una aceleración que es directamente proporcional
a la fuerza que actúa sobre él e inversamente proporcional a su masa.a la fuerza que actúa sobre él e inversamente proporcional a su masa.a la fuerza que actúa sobre él e inversamente proporcional a su masa.a la fuerza que actúa sobre él e inversamente proporcional a su masa.a la fuerza que actúa sobre él e inversamente proporcional a su masa.
La ecuación matemática que la define es:
a =
F
m
de donde se deduce que: F = m . a
La fórmula F = m . a es trascendental para la Física pues permite cuantificar las
fuerzas, es decir, medirlas.
Las fórmulas a utilizar son:
F = m . a ................. (1)
a =
v
t
................... (2)
Reemplazando datos en (2): a =
108
5 s
km/h
En la resolución de problemas con magnitudes debemos tener en cuenta siempre que se
deben uniformizar las unidades. En este caso, expresaremos la aceleración en m/s2
; para
ello utilizamos factores de conversión que nos permitirán convertir km a m y h en s.
a =
108
5 s
km/h 1 h
3600 s






1000 m
1 km





 = 6 m/s2
Reemplazando datos en la ecuación (1):
F = (100 kg)(6 m/s2
) = 600
kg.m
s2

Tercera Ley de Newton o Ley de acción y reacción
Supón que vas distraído y te golpeas con un poste. Si te preguntan ¿qué es lo que
pasó?, dirás que golpeaste el poste, que le aplicaste una fuerza. Esa es una buena
respuesta, pero...... ¿por qué te dolió? Ocurre que cuando golpeaste el poste, el
poste también te golpeó.
Veamos otros ejemplos. Cuando un automóvil
choca con un árbol, no sólo el árbol se daña
sino también el automóvil. Aquí el automóvil
ejerce una fuerza sobre el árbol (por eso se
daña) y el árbol también ejerce una fuerza
sobre el automóvil (por eso se daña). Si vas
corriendo y te chocas con otra persona, ésta
será empujada pero tú también te moverás
en sentido contrario.
La forma de actuar de las fuerzas que
intervienen en cuerpos diferentes está descrita
mediante la ley de acción y reacción:
Cuando un cuerpo ejerce una fuerza (fuerza de acción) sobre otro, elCuando un cuerpo ejerce una fuerza (fuerza de acción) sobre otro, elCuando un cuerpo ejerce una fuerza (fuerza de acción) sobre otro, elCuando un cuerpo ejerce una fuerza (fuerza de acción) sobre otro, elCuando un cuerpo ejerce una fuerza (fuerza de acción) sobre otro, el
segundo cuerpo ejerce una fuerza (fuerza de reacción) sobre el primero.segundo cuerpo ejerce una fuerza (fuerza de reacción) sobre el primero.segundo cuerpo ejerce una fuerza (fuerza de reacción) sobre el primero.segundo cuerpo ejerce una fuerza (fuerza de reacción) sobre el primero.segundo cuerpo ejerce una fuerza (fuerza de reacción) sobre el primero.
Ambas fuerzas son iguales, con la misma dirección y sentidos contrarios, pero no
se anulan al estar aplicadas sobre cuerpos distintos.
Como se mencionó anteriormente la unidad de fuerza en el SI es el newton (N) y su
equivalencia es:
1 N = 1 kg.m/s2
Por lo tanto: F = 600
kg.m
s2
= 600 N
◆ Un auto de 8 000 kg de masa arranca con una aceleración de 3 m/s2
. ¿Qué fuerza ha
actuado sobre él?
Gracias a las fuerzas de acción y reacción se pueden mover algunos seres y objetos:
● Un cohete impulsa gases hacia atrás; en consecuencia, los gases empujan al cohete en
sentido contrario y así éste puede avanzar.
● Un calamar expulsa agua hacia atrás; el agua expulsada empuja al calamar hacia adelante
y así puede moverse.
● El remo de un bote empuja al agua hacia atrás y hace que el bote se mueva hacia
adelante.

Los efectos de las fuerzas pueden explicarse mediante las tres leyes de Newton, principios
que nos sirven para explicar diferentes sucesos.
En el tercer momento conocerás las funciones trigonométricas y su utilidad en la resolución
de problemas de Física aplicados a situaciones de la vida diaria.
● Una botella de plástico, sal de frutas, un
sorbete para refresco colocado en un
corcho agujereado, agua.
1. Echa un poco de agua y la sal de frutas
en la botella.
2. Tapa la botella con el corcho que lleva
el sorbete.
3. Pon la botella en una tina con agua.
Observarás que la botella se pone en
movimiento en sentido contrario de la
salida del gas. Este es el fundamento
de la propulsión.
● ¿Por qué se mueve la botella?
● ¿Dónde se ejercen las fuerzas de
acción y reacción?
● ¿Por qué no se anulan las fuerzas?
Investiga cómo
se mueven los aviones
de propulsión a chorro y
los cohetes espaciales.
Experimenta:Construyeun
barquitoapropulsión
1
2
3

TERCER MOMENTO: Funciones trigonométricas
paralasumadefuerzas
● ¿Cuáles son las fuerzas aplicadas sobre el auto?
● ¿Se podría reemplazar estas fuerzas por una sola fuerza resultante para
mover el auto malogrado? Dibuja cómo sería.
Hay dos maneras de calcular la resultante:
1.1.1.1.1. Suma de fuerzas gráficamenteSuma de fuerzas gráficamenteSuma de fuerzas gráficamenteSuma de fuerzas gráficamenteSuma de fuerzas gráficamente
Hallar la suma es encontrar el vector resultante midiendo
cuál es su módulo y cuál es el ángulo que forma con el
eje x. Para sumar gráficamente las fuerzas se utiliza el
método del paralelogramo y el método del polígono.
a) Método del paralelogramo.Método del paralelogramo.Método del paralelogramo.Método del paralelogramo.Método del paralelogramo. Este método se usa cuando se suman dos fuerzas.
Ejemplo. Dos jóvenes jalan una caja aplicando una fuerza F1 y F2 de 3 kgf y 2 kgf
respectivamente. Entre las fuerzas forman un ángulo de 30 grados.
La fuerza se presenta
como un vector.
Hallar la resultante significa calcular cuánto vale la suma de todas las fuerzas que
actúan sobre un cuerpo.
En el primer momento de esta actividad estudiaste que sobre un cuerpo actúan
normalmente dos o más fuerzas al mismo tiempo, y que el conjunto de fuerzas puede
sustituirse por una sola fuerza llamada resultante.
Por ejemplo, habrás visto en alguna ocasión que cuando un auto se malogra en medio de
la pista, el chofer y algunos peatones empujan el carro hacia un costado para no
obstaculizar el tránsito.
F1
F2
30°

Para calcular gráficamente la resultante de las fuerzas, es decir, el módulo y el ángulo
que forma con el eje “x”. Se dibujan las fuerzas en el plano cartesiano
Luego se traza una paralela a cada una de las fuerzas formando un paralelogramo. La
diagonal del paralelogramo formado es la resultante de la suma de estas dos fuerzas.
Midiendo el ángulo con un transportador tendremos αR = 12° y el módulo medido con
una regla es R = 4,7 cm. Pero, como R representa una fuerza: R = 4,7 kgf
b)b)b)b)b) Método del polígono de fuerzas.Método del polígono de fuerzas.Método del polígono de fuerzas.Método del polígono de fuerzas.Método del polígono de fuerzas. Este método se usa cuando se suma más de dos
fuerzas. Este método muchas veces es reemplazado por el método analítico.
Ejemplo. Tres hermanos jalan una soga de tres puntas. Cada uno aplica una fuerza de 2 N.
Para calcular gráficamente la resultante (R) y el ángulo αR que forma con el eje de las “x”
se representan las fuerzas en el plano cartesiano.
F1 = 3 kgf
F 2
= 2 kgf
α = 30°
x
y
F1
F 2
αR ≅ 12°
x
y
R ≅ 4,7 kgf
F1 = 2 N
F3 = 2 N
45°
x
y
45°
F2 = 2 N
2 N
2 N
2 N

Luego, se trasladan las fuerzas y se pone una fuerza a continuación de la otra formando
un polígono. La resultante es la unión del origen de la primera fuerza con la punta de la
última.
Como en el método del paralelogramo, se mide directamente del gráfico el valor de R que
es aproximadamente 3,4 N y el αR que es aproximadamente 58°.
2.2.2.2.2. Suma de fuerzas analíticamenteSuma de fuerzas analíticamenteSuma de fuerzas analíticamenteSuma de fuerzas analíticamenteSuma de fuerzas analíticamente
El método analítico para calcular la suma de fuerzas se basa en el hecho de que la fuerza
es un vector y todo vector se puede descomponer en sus componentes vectoriales que
en este caso es la fuerza proyectada en el eje x y sobre el eje y.
Para entender mejor la suma de fuerzas analíticamente necesitas recordar el teorema de
Pitágoras y conocer algunos conceptos básicos de trigonometría.
F1
F3
x
y
R
F2αR
Como sabes el teorema de Pitágoras permite hallar el valor de la hipotenusa (hip) de un
triángulo rectángulo conociendo el valor del cateto opuesto (op) y el cateto adyacente (ady).
hip2 = ady 2 + op2 ⇒ Teorema de PitágorasTeorema de PitágorasTeorema de PitágorasTeorema de PitágorasTeorema de Pitágoras
Ejemplo:Ejemplo:Ejemplo:Ejemplo:Ejemplo: Si los lados de un triángulo miden 6 y 8 cm, ¿cuánto mide su hipotenusa?
hip2 = (6 cm)2 + (8 cm)2
hip2 = 100 cm2
hip = 10 cm
hip
op
ady
hip
6
8
Recordando el teorema deRecordando el teorema deRecordando el teorema deRecordando el teorema deRecordando el teorema de
Pitágoras:Pitágoras:Pitágoras:Pitágoras:Pitágoras:

Trigonometría es una rama de la matemática que estudia los ángulos y los lados de un
triángulo cualquiera y las relaciones entre ellos.
La trigonometría plana tiene como objetivo resolver triángulos. Como sabes, cada triángulo
está constituido por seis elementos: tres lados y tres ángulos. Resolver un triángulo
significa determinar los elementos desconocidos a partir de algunos datos y ciertas
relaciones entre ellos.
En un triángulo rectángulo encontramos las funciones seno, coseno y tangente, que son
la expresión de las relaciones que existen entre los lados del triángulo y uno de sus
ángulos. Éstas son las denominadas funciones trigonométricasfunciones trigonométricasfunciones trigonométricasfunciones trigonométricasfunciones trigonométricas.
Senα =
cateto opuesto de
hipotenusa
α
Cosα =
cateto adyacente de
hipotenusa
α
Tgα =
cateto opuesto de
cateto adyacente de
α
α
Ejemplo 1:Ejemplo 1:Ejemplo 1:Ejemplo 1:Ejemplo 1:
● Calcula el valor exacto de cada una de las tres funciones trigonométricas en el siguiente
triángulo.
hip
op
ady
■ Primero se debe hallar la longitud del cateto desconocido para lo cual se usa el
teorema de Pitágoras:
a2 = b2 + c2 ⇒ b2 = a2 – c2
b2 = 52 – 32 = 16 ⇒ b = 16 = 4 cm
B
C
A
a = 5 cm
b = ?
c = 3 cm
Reconociendo conceptos básicosReconociendo conceptos básicosReconociendo conceptos básicosReconociendo conceptos básicosReconociendo conceptos básicos
de trigonometríade trigonometríade trigonometríade trigonometríade trigonometría
α

B
C
A
h
86 cm
65°
■ Luego se calcula las razones pedidas:
Senα =
cateto opuesto de
hipotenusa
α
=
4
5
ó 0,8
Cosα =
cateto adyacente de
hipotenusa
α
=
3
5
ó 0,6
Tgα =
cateto opuesto de
cateto adyacente de
α
α
=
4
3
ó 1,3
Ejemplo 2:Ejemplo 2:Ejemplo 2:Ejemplo 2:Ejemplo 2:
● Si los rayos del Sol sobre un mástil forman un ángulo de 65° con la proyección de su
sombra que mide 86 cm sobre el suelo, ¿cuál es la altura (h) del mástil medido en
metros?
Este problema se desarrolla con la función trigonométrica llamada tangente, porque
como sabes la tangente en un triángulo rectángulo relaciona el cateto opuesto con el
cateto adyacente y en este caso el cateto opuesto coincide con la altura (h) cuyo valor se
quiere calcular:
tg 65° =
h
86
⇒ h = 86 tg 65°
Usando una calculadora tenemos que tg 65° = 2,1445069
Reemplazando:
h = 86 (2,1445069)
h = 184,4276 cm = 1,84 m
◆ El cordel de una cometa se encuentra tenso y forma
un ángulo de 48° con la horizontal. Calcula la altura
de la cometa con respecto al suelo, si el cordel mide
87 m y el extremo de la cuerda se sostiene a 1,3 m
del suelo.
◆ Una rampa tiene una inclinación de 45°. Si el desnivel
es de 40 m, ¿cuál es la longitud de la rampa?
◆ Dos lados de un paralelogramo miden 5 m y 8 m,
formando un ángulo de 40°. ¿Cuánto miden las
diagonales?
◆ Una escalera de 6 m de longitud descansa sobre una
pared vertical de tal manera que el pie de la escalera
queda a 1,5 m de la base de la pared. ¿Cuál es el
ángulo que forma la escalera con la pared y hasta
qué altura de la pared llega la escalera?
Elabora una
pequeña
tabla con algunos
valores de las funciones
trigonométricas básicas.
(

Proyecciones de una fuerza
Las proyecciones de la fuerza F, o sea Fx y Fy en los ejes "x" e "y" respectivamente
forman un triángulo rectángulo. Entonces utilizando las funciones trigonométricas puedes
expresar estas fuerzas en función de la fuerza F.
Ahora que has recordado
el teorema de Pitágoras y reconocido
algunas funciones trigonométricas,
verás la resultante de una suma de
fuerzas analíticamente.
Funcionestrigonométricasparaángulosparticulares
Actualmente se puede conocer el valor de una función trigonométrica de cualquier
ángulo recurriendo a una calculadora o ubicando en la computadora una calculadora
de las llamadas científicas. Sin embargo, existen ángulos particulares que forman
parte de algunos triángulos rectángulos que conoces como triángulos notables.
Por ejemplo, son triángulos notables (45°, 45°) y (60°, 30°).
A continuación se presenta una tabla con los valores de las funciones
trigonométricas para algunos de estos ángulos particulares:
Ángulo en gradosÁngulo en gradosÁngulo en gradosÁngulo en gradosÁngulo en grados 00000° 3030303030° 4545454545° 6060606060° 9090909090°
senα 0
1
2
2
2
3
2
1
cosα 1
3
2
2
2
1
2
0
tgα 0
3
3
1 3 no definida
Fx = F . cosα
Fy = F . senα
La proyección de la fuerza
sobre el eje x significa
determinar cuánto mide la
sombra de esa fuerza sobre
ese eje. F
Fy
Fx
Sombra
Sombra de la
fuerza en x (Fx)
F
α
Fx
Fy

De manera similar
se puede hallar la
proyección sobre
el eje y:
Estas últimas expresiones de las proyecciones de una fuerza sobre cada uno de los ejes
del sistema cartesiano son las que se utilizan para resolver una suma de fuerzas
analíticamente.
● Tres hermanos jalan una soga de tres puntas. Cada
uno aplica una fuerza de 2 N. Halla analíticamente
la resultante del siguiente sistema de fuerzas
concurrentes calculando R y αR
.
Para resolver el problema, plantea la sumatoria de las fuerzas en la dirección x y la
sumatoria de las fuerzas en la dirección y:
Rx = ΣFx y Ry = ΣFy
Calcula ahora el valor de Rx y Ry proyectando cada fuerza sobre el eje x y sobre el eje
y. Si miras las fórmulas de trigonometría, te darás cuenta de que la componente de la
fuerza en la dirección x será siempre Fx = F . cosα y la componente en dirección y es
Fy = F . senα (α es el ángulo que la fuerza forma con el eje x).
F
Fy
y
Sombra
Sombra de la
fuerza en y (Fy)
x
FFy
y
Fy = F senα
α
Proyección de una
fuerza en las
direcciones x e y
x
Fx = F cos α
F3 = 2 N
y
x
F2 = 2 N
F1 = 2 N
45° 45°
Para
reconocer cómo se halla la suma
de fuerzas analíticamente, lee el
siguiente ejemplo:
Entonces:
Rx
= ΣFx
= F1 . cosα1 + F2 . cosα2 + F3 . cosα3
⇒Rx
= 2 N . cos 0° + 2 N . cos 45° – 2 N . cos 45°
⇒Rx
= 2 N . (1) + 2 N
2
2








– 2 N
2
2








⇒ Rx
= 2 N ← Resultante en x.
La proyección de F3
sobre x va así: ← y es
negativa.

◆ Hallar las proyecciones en y para una fuerza de 10 N que
forma un ángulo de 30° con el eje de las x.
◆ En la figura x = 6,0 cm y φ = 30°. ¿Cuáles son las longitudes
de y y de r?
Realizando el mismo procedimiento para el eje y:
Ry = ΣFy = F1 . senα1 + F2 . senα2 + F3 . senα3
⇒Ry = 2 N . sen0º + 2 N . sen45º + 2 N . sen45 º
⇒Ry = 2 N .(0) + 2 N
2
2







 + 2 N
2
2







 ⇒ Ry = 4
2
2







 N = 2 2 N
Ry = 2,828 N ← Resultante en y.
● Representando gráficamente la resultante en cada eje:
Rx = 2 N
Ry = 2,828 N
R
αR
Aplicando el teorema de Pitágoras:
R2= (2N)2 + (2,828N)2
R = (2 N) + (2,828 N)2 2
R = 4 N + 7,99 N2 2
R = 11,99 N2 ⇒ R = 3,46 N ← Resultante
● Para hallar el ángulo se utiliza la función tangente: tgαR =
R
R
y
x
Reemplazando: tgαR =
2,828 N
2 N
⇒ tgαR = 1,414
● Para poder calcular αR conociendo tgαR se usa la función arc.tag de la calculadora:
αR = 54,73° ⇒ ángulo que forma R con el eje x.
Has recordado que el teorema de Pitágoras es una ecuación que relaciona los lados de un
triángulo rectángulo. En el triángulo rectángulo se cumplen también determinadas relaciones
denominadas funciones trigonométricas que son de utilidad para hallar la suma de fuerzas
por el método analítico.
x
yr
φ

FICHADETRABAJO
Resolucióndetriángulosrectángulos
1) Se sabe que la diagonal del cuadrado mide 7 cm ¿Cuánto mide su lado?
2) Calcula el perímetro y el área del triangulo isósceles ABC, en el que se sabe que:
AB = BC , AC = 24 cm y h = 5 cm es la altura correspondiente al vértice B.
3) Se sabe que el área del rombo es
d D.
2
, o sea, la mitad del producto de las diagonales.
Obtener el área del rombo de perímetro 40 cm y la diagonal menor d = 12 cm
4) Un triángulo equilátero tiene una altura de 3 cm, ¿cuánto miden sus lados?
5) La hipotenusa de un triángulo rectángulo mide 10 cm y uno de los catetos mide el
triple que el otro. ¿Cuánto miden los catetos y cuál es su área?
6) Determina en cada caso las medidas de las diagonales del rectángulo de base b y
altura h.
a) b = 8cm; h = 6cm b) b = 4cm; h = 8cm
7) Calcula la medida de la diagonal de un cuadrado cuyo lado L mide 0,6.
8) Resuelve el triángulo rectángulo, usando la información dada:
I) b = 5 β = 25°
II) a = 6 β = 45°
III) a = 5 α = 30°
IV) a = 2 b = 8
V) b = 4 c = 6
9) Los lados de un triángulo miden 4 cm, 6 cm y 8 cm, calcula la altura sobre el lado
mayor.
10) Un tramo de carretera forma un ángulo de 15° con la horizontal. Al recorrer 200 m
por la carretera. ¿Cuántos metros se ha ascendido en vertical?
11) Un camino recto con inclinación uniforme lleva desde un hotel a 2 640 metros hasta
un mirador situado a 3 663 metros. Si la longitud del camino es de 4 653 metros,
¿cuál es la pendiente del camino?
A
B
Ca
b
c
α
β

57
Rozamiento, gravedad y trabajoRozamiento, gravedad y trabajoRozamiento, gravedad y trabajoRozamiento, gravedad y trabajoRozamiento, gravedad y trabajo
1. Rozamiento y gravedad
2. Trabajo y potencia
3. Máquinas simples
Analizar dos fuerzas: rozamiento y
gravedad. Entender los conceptos de
trabajo y potencia y aplicarlos en los
diferentes campos de la vida diaria y la
tecnología. Resolver ejercicios sobre
trabajo y potencia.
● En el primer momento se presentan dos
fuerzas que siempre están presentes en
la naturaleza, la fuerza de rozamiento
y la fuerza de gravedad.
● En el segundo momento comprenderás
el significado de trabajo y potencia para
la Física, sus unidades de medida, y
resolverás problemas relacionados con
estas magnitudes.
● En el tercer momento conocerás
algunas máquinas simples que nos
permiten trabajar cómodamente.
● El avión ● Watt
● Joule o julio
● Palanca
● Polea
● Plano inclinado
● Cálculo aritmético
● Funciones trigonométricas
● Fuerzas de rozamiento y gravedad
● Trabajo
● Potencia
● Máquinas simples: palanca, plano
inclinado y polea
● Trabajo, potencia y máquinas simples

PRIMERMOMENTO:Rozamientoygravedad
¿Por qué vamos más rápidamente en una carretera asfaltada que en otra sin asfaltar?
¿Por qué los aviones deben ejercer mucha fuerza para mantenerse en el aire? Como ves,
hay fuerzas que están siempre actuando sobre los cuerpos: el rozamiento y la gravedad.
● ¿Qué sabes acerca de las fuerzas de rozamiento?
● ¿Qué es la fuerza de gravedad? ¿Dónde has podido observarla?
El hielo es una superficie bastante lisa y el
rozamiento en él es menor. Por eso los
patinadores se desplazan con facilidad.
La forma de los automóviles,
aviones, trenes, bicicletas, y aun los
cascos de los ciclistas son cada vez más
aerodinámicos para disminuir el
rozamiento del aire.
Fuerzasderozamiento
Cualquier objeto que rueda o se desplaza sobre una superficie termina deteniéndose.
Esto se debe a la acción de una fuerza que aparece cuando dos superficies se
deslizan, una sobre otra. Esta fuerza se llama fricción o rozamientofricción o rozamientofricción o rozamientofricción o rozamientofricción o rozamiento y se opone
siempre al movimiento.
Las superficies, aunque puedan
parecer muy lisas, presentan
rugosidades que dificultan el
desplazamiento.
Seguramente has podido comprobar
que es más fácil arrastrar un objeto
por una superficie lisa que por una
rugosarugosarugosarugosarugosa. En efecto, cuanto más lisaslisaslisaslisaslisas
son las superficies en contacto, menor
es el rozamiento.
El rozamiento produce calorcalorcalorcalorcalor en los
cuerpos en contacto. Piensa en lo que
sucede cuando te frotas las manos.
Cuando se diseñan máquinas o vehículos,
se debe tener en cuenta el calor que
produce el rozamiento. Es bien conocida la tragedia del Challenger donde murieron 7
astronautas. Cuando el trasbordador ingresó en la atmósfera terrestre se produjo
tanto calor en su superficie, por el rozamiento con el aire, que la nave se incendió.

Rozamiento… ¿necesario o innecesario?
Hay muchas situaciones en las que interesa disminuir las fuerzas de rozamiento. Por
ejemplo, las máquinas deben estar siempre bien engrasadas, pues en caso contrario las
superficies rozarían unas con otras desgastándolas, dificultando el movimiento y
produciendo calor. En nuestras articulaciones tenemos el líquido sinovial que lubrica las
articulaciones evitando que se desgasten.
Sin embargo, el fenómeno del rozamiento es absolutamente necesario en otras
situaciones. Si no hubiese rozamiento, no podríamos caminar, pues nuestros pies
resbalarían en el suelo.
Cuando un auto se mete en el barro disminuye el rozamiento. Sus ruedas giran resbalando,
y para evitarlo, se coloca debajo de ellas una alfombra, maderas u otros objetos que
produzcan rozamiento para que las ruedas empujen el suelo hacia atrás y se impulsen.
● ¿Por qué cuando una carretera está
mojada o con hielo los vehículos
"patinan"?
● ¿Por qué se calientan las llantas de
un vehículo en movimiento?
Investiga qué
son formas
aerodinámicas. Dibuja
objetos que tengan esta
forma y preséntalos en
un afiche.
Investiga
cómo funcionan los
frenos de una bicicleta
o de un auto. Dibújalos
y preséntalos.

Lafuerzade gravedad
Cuando soltamos un objeto desde cualquier altura, éste siempre cae al suelo. Esto
se debe a la fuerza de atracción que ejerce nuestro planeta sobre todos los cuerpos.
Esta fuerza se llama fuerza de gravedadfuerza de gravedadfuerza de gravedadfuerza de gravedadfuerza de gravedad y tiene las siguientes características:
● Es una fuerza universaluniversaluniversaluniversaluniversal, es decir, afecta a todos los cuerpos del Universo.
● Es una fuerza débildébildébildébildébil, sólo se deja notar cuando los cuerpos tienen masa muy
grande. Así, el Sol y los planetas tienen fuerzas de gravedad notorias.
● La intensidad de la fuerza depende de la distancia existente entre los cuerpos;
cuanto más alejados, menor es la fuerza de atracción.
En el siglo XVIII, Isaac Newton estudió esta fuerza y resumió sus investigaciones
en una ley llamada la gravitación universalla gravitación universalla gravitación universalla gravitación universalla gravitación universal, que dice: “Dos cuerpos cualesquiera
se atraen con una fuerza proporcional al producto de sus masasproducto de sus masasproducto de sus masasproducto de sus masasproducto de sus masas e inversamenteinversamenteinversamenteinversamenteinversamente
proporcional al cuadrado de la distanciaproporcional al cuadrado de la distanciaproporcional al cuadrado de la distanciaproporcional al cuadrado de la distanciaproporcional al cuadrado de la distancia que las separa”
Se puede calcular la fuerza de gravedad
mediante la siguiente ecuación
matemática:
F = G
m m
d
1 2
2
Marca verdadero (V) o falso (F):
( ) La fuerza de gravedad sólo se da en cuerpos grandes como los astros del Universo.
( ) La atracción de las estrellas y la Tierra casi no se percibe porque están muy lejos.
( ) La gravedad y la gravitación universal son fuerzas diferentes.
( ) Cuanto mayor es las distancia entre los cuerpos, mayor es la fuerza de gravedad.
Los cuerpos que hay en la Tierra se
atraen mutuamente. Por ejemplo,
una silla y una mesa se atraen, pero
no se acercan porque la fuerza de
gravedad es muy débil.
¿Sabías que en el espacio los
los astronautas no pesan y por eso flotan dentro de las
naves? Esto ocurre porque el peso de los cuerpos está
determinado por la fuerza de gravedad, es decir, la
atracción de la Tierra sobre los cuerpos.
d
F F

◆ ¿Cuánto pesa en la Tierra una persona de 60 kg de masa? ¿Cuánto pesa en la Luna cuya
gravedad es de 1,6 m/s2
?
◆ Elige un tema relacionado con las fuerzas y amplíalo. Luego, haz una breve monografía y
prepara tu exposición.
Una persona tira de una caja mediante una cuerda
moviéndola tal como indica la figura. Dibuja y
explica las fuerzas qué actúan sobre la caja.
Solución:Solución:Solución:Solución:Solución: Sobre la caja actúan: su peso, debido a
la fuerza de gravedad, la fuerza que hace la persona
y la fuerza de rozamiento que actúa en sentido
contrario al movimiento.
¿Es lomismolamasayelpeso?
La masamasamasamasamasa de un cuerpo es la cantidad de materia que tiene. En el Sistema Internacional
la unidad es el kilogramo (kg).
El pesopesopesopesopeso de un cuerpo es la fuerza con que lo atrae la Tierra. Su unidad es el newton (N).
La masa de un cuerpo es siempre la misma, sin importar el lugar donde esté. En
cambio, el peso varía porque depende de la gravedad.
Como el peso es una fuerza se calcula con la ecuación: F = m . a donde a es la
aceleración del planeta llamada también gravedad. En la Tierra ggggg es 10 m/s2 (ver
caída libre). Sustituyendo tenemos:
ω = m × g
Existe otra unidad de peso llamada kilogramo fuerzakilogramo fuerzakilogramo fuerzakilogramo fuerzakilogramo fuerza (kgf) y se define como el peso
de un cuerpo cuya masa es de 1 kg en un lugar donde la gravedad es 10 m/s2
.
Como ésta es la gravedad de la Tierra, se deduce que en nuestro planeta 1 kgf es
igual a 1 kg masa. Por ejemplo, en la Tierra, una persona que pesa 70 kgf tiene
también una masa de 70 kg. Por esta razón, masa y peso en la Tierra son magnitudes
numéricamente iguales.
1 kgf = 1 kg
Has aprendido a reconocer dos fuerzas, el rozamiento y la gravedad. El rozamiento es
necesario muchas veces, pero en otras tratamos de minimizarlo. También has comprendido
la diferencia entre masa y peso. En el segundo momento estudiarás que al ejercer una
fuerza sobre un cuerpo y moverlo se realiza un trabajo.

SEGUNDOMOMENTO:Trabajoypotencia
● Menciona algunas situaciones de tu vida en las que realizas un trabajo.
● Después de leer la definición de trabajo, descarta las situaciones que no
se ajustan a la definición física de trabajo.
¿Qué es el trabajo?
Usamos la palabra trabajo en muchas circunstancias, pero el significado que le
damos no siempre coincide con la definición que emplean los científicos. Observa:
Se realiza trabajo cuando al ejercer una fuerza sobre un cuerpo, éste secuando al ejercer una fuerza sobre un cuerpo, éste secuando al ejercer una fuerza sobre un cuerpo, éste secuando al ejercer una fuerza sobre un cuerpo, éste secuando al ejercer una fuerza sobre un cuerpo, éste se
mueve.mueve.mueve.mueve.mueve.
Hacemos trabajo en muchas situaciones. Por ejemplo:
● Cuando detenemos o aceleramos un movimiento hacemos trabajo. Por ejemplo,
al atrapar una pelota o patearla en otra dirección.
● Las fuerzas de rozamiento realizan un trabajo porque detienen el
movimiento. En este caso el trabajo se considera nulo porque va en contra
del movimiento.
● Cuando levantamos objetos hacemos trabajo porque los movemos en contra
de la gravedad.
Yo he trabajado
tres horas
haciendo mi tarea
de ciencias.
Yo trabajo en
construcción civil y
cargo materiales de un
lado a otro, y a veces
uso una carretilla.
Ana aplica una fuerza y mueve un
armario pequeño, ha realizado un
trabajo.
Juan empuja un armario muy pesado pero éste
no se mueve; ha hecho un esfuerzo, pero no ha
realizado un trabajo.

Todas las máquinas y los mecanismos
que producen movimiento hacen trabajo: un abridor
de latas, un barco, máquinas que cosen, cortan o
trituran, que tiran o golpean, que levantan o lanzan,
giran o doblan, etc.
● Lee la siguiente información:
Para conseguir que una fuerza realice el máximo trabajo es necesario que la dirección de la
fuerza sea paralela a la dirección del movimiento. Por ejemplo, la mejor forma de jalar una
caja con una soga es que la soga esté paralela al piso (mayor desplazamiento, mayor trabajo).
● Un cuerpo realiza un trabajo de 640 J al desplazarse 2 m, ¿qué fuerza actúa sobre dicho
cuerpo?
Datos: W = 640 J
d = 2 m
F = ?
Mayor trabajo:Mayor trabajo:Mayor trabajo:Mayor trabajo:Mayor trabajo: la fuerza
aplicada es paralela al
desplazamiento.
Menor trabajo:Menor trabajo:Menor trabajo:Menor trabajo:Menor trabajo: la fuerza
aplicada no es paralela al
desplazamiento.
No hay trabajo:No hay trabajo:No hay trabajo:No hay trabajo:No hay trabajo: la fuerza
es perpendicular al
desplazamiento.
De la fórmula: W = F × d
Despejamos: F =
W
d
Reemplazando datos:
F =
640 J
2 m
=
640 N m
2 m
×
⇒ F = 320 N
Eltrabajosepuedemedir
El trabajo es una magnitud y se halla con la
siguiente ecuación matemática:
F: fuerza
W = F × d d: distancia recorrida
W: trabajo
La unidad de trabajo en el SI es el joulejoulejoulejoulejoule o juliojuliojuliojuliojulio (JJJJJ). Un joule se define como el
trabajo realizado por la fuerza de 1 newton en un desplazamiento de un metro.
1 joule = 1 N × m
La unidad de trabajo, el
joule o julio, recibe su
nombre del científico
inglés James Joule.

Potencia
¿Cuál es más potente, una máquina que puede envasar 100 botellas de gaseosa
en 15 minutos o la que envasa la misma cantidad en 8 minutos?
En la mayoría de los procesos donde se realiza trabajo, un factor importante es el
tiempo empleado:
● Algunas máquinas realizan el mismo trabajo que otras, pero lo hacen en menos
tiempo. Por ejemplo, un tractor necesita menos tiempo para arar un campo
que un arado tirado por un par de bueyes.
● Algunas máquinas realizan más trabajo que otras en menos tiempo. Una
máquina industrial hace una costura recta en pocos segundos, mientras que
las máquinas domésticas lo hacen en más tiempo.
La relación entre el trabajo realizado y el tiempo empleado se llama potencia.
Potencia es la velocidad a la que se realiza un trabajoPotencia es la velocidad a la que se realiza un trabajoPotencia es la velocidad a la que se realiza un trabajoPotencia es la velocidad a la que se realiza un trabajoPotencia es la velocidad a la que se realiza un trabajo.
Su ecuación matemática es:
En el SI la unidad de medida de potencia es el wattwattwattwattwatt o vvvvvatioatioatioatioatio (WWWWW) que se define así:
1 watt es la potencia desarrollada por 1 joule en un segundo: 1 W = 1 J/s
Como el watt es una unidad muy pequeña, en la práctica se usan otras unidades
como el kilowatt y el caballo de fuerza (HP).
● El kilowatt (kW) equivale a 1 000 W.
● El caballo de fuerza (HP) equivale a 746 W y recibe ese nombre por ser,
aproximadamente, la potencia que desarrolla un caballo de tiro.
● El motor de un ascensor realiza un trabajo de 90 000 J en 14 s, ¿cuál es la potencia en
watt y en caballos de fuerza?
Reemplazando datos en la fórmula: P =
W
t
P =
90 000 J
14 s
= 6 428,57 J/s = 6 428,57 W
Aplicando factor de conversión: P = 6 428,57 W
1 HP
746 W





 = 8,617 HP
P =
W
t
P : potencia
W : trabajo
t: tiempo
Datos: W = 90 000 J
t = 14 s
P = ?
James Watt (1736-1819), ingeniero
natural de Escocia, fue el primer
fabricante de máquinas eficientes. En esa
época eran máquinas a vapor.

Has aprendido los conceptos de trabajo y
potencia y has realizado cálculos matemáticos
para medirlos. En el siguiente momento
analizarás las máquinas simples que nos
permiten hacer trabajos con mayor facilidad.
Eficiencia de las máquinas
Para realizar un trabajo se necesita energía. Por
eso la energía se define como la capacidad de
realizar un trabajo. Parte de la energía que se usa
no se convierte en trabajo útil sino que se degrada
en forma de calor.
Con ayuda de la tecnología se construyen máquinas más eficientes. Las máquinas
eficientes no desperdician mucha energía. No sólo sus motores son mejores sino que
emplean lubricantes especiales para disminuir la fricción. Por otro lado, está también
la preocupación de construir máquinas que, además de ser eficientes, no contaminen
el ambiente.
◆ Un empleado empuja un cajón de frutas a través de 50 m aplicando una fuerza de 30 N
paralela al desplazamiento. Calcula el trabajo efectuado sin considerar el rozamiento.
◆ Calcula la potencia de una grúa que desarrolla una fuerza de 2 280 N para levantar una
caja a 20 m de altura y en 12 segundos.
◆ Indica la diferencia entre:
a) Trabajo y fuerza b) Trabajo y potencia
Elige una máquina
y elabora un tríptico
indicando su evolución y
cómo ha mejorado su
rendimiento.
Evolución del automóvil
ENERGÍA
TRABAJO
CALOR

TERCER MOMENTO: Máquinas simples
Desde la antigüedad, el hombre ha ideado instrumentos que le faciliten su labor. Estos
instrumentos son las máquinas, con las que se pueden ahorrar fuerzas o dar comodidad
a la tarea.
Las máquinas pueden ser simples o compuestas:
● Las máquinas simplesmáquinas simplesmáquinas simplesmáquinas simplesmáquinas simples son la palanca, la polea, el plano inclinado, entre otras.
● Las máquinas complejasmáquinas complejasmáquinas complejasmáquinas complejasmáquinas complejas están constituidas por la combinación de varias máquinas
simples. Ejemplos, la bicicleta, el motor, la grúa, etc.
Es importante determinar el
lugar donde se ubica el punto de apoyo.
Cuanto más cerca esté la resistencia del
punto de apoyo, menor será la fuerza
que tendremos que hacer.
La palanca
Para destapar una botella o levantar objetos pesados puedes utilizar una palanca.
La palanca es una estructura rígida (por
ejemplo, una barra de hierro) con un punto
de apoyo. La barra de hierro no es en sí
misma una máquina, pero si le ponemos
un punto de apoyo se transforma en una
máquina.
Una palanca tiene tres elementos:
● El punto de apoyo A.
● La potencia P que es la fuerza que hacemos.
● La resistencia R que es la fuerza que vencemos.
Experimenta:¿Cómotrabajaunapalanca?
● Una caja de colores, una regla, un plumón.
1. Pon la caja, la regla y el plumón como se
ve en la ilustración. El apoyo es el plumón.
R
A
P

2. Levanta la caja de colores presionando desde el otro extremo de la regla y ubicando el
apoyo en diferentes lugares:
■ Primero, coloca el plumón en el centro de la regla.
■ Después coloca el plumón cerca de tus manos, es decir, cerca del lugar donde
aplicas la fuerza.
■ Por último, pon el plumón cerca de la caja.
● ¿En cuál de todas las posiciones levantaste la caja con menor esfuerzo?
● ¿Qué concluyes con esta observación?
Herramientasqueusamoscomopalancas
Las tijeras.Las tijeras.Las tijeras.Las tijeras.Las tijeras. Son dos palancas de primer grado
que actúan de manera conjunta. Realizan una
fuerte acción de corte cerca del punto de apoyo.
La resistencia la determina el tipo de material que
se corte.
R A P R P A
Palanca de tercerPalanca de tercerPalanca de tercerPalanca de tercerPalanca de tercer
génerogénerogénerogénerogénero
La potencia se aplica
entre el punto de apoyo
y la resistencia. Como la
distancia entre apoyo y
resistencia es corta,
hacemos más fuerza de
la que vencemos, pero el
trabajo es más cómodo.
Palanca de primerPalanca de primerPalanca de primerPalanca de primerPalanca de primer
El punto de apoyo está
entre la potencia y la
resistencia.
Si el apoyo está cerca de
la resistencia, menor
será la fuerza que
tenemos que hacer. Si el
apoyo estuviese al
centro, la potencia sería
igual a la resistencia.
Palanca de segundoPalanca de segundoPalanca de segundoPalanca de segundoPalanca de segundo
La resistencia está entre
el apoyo y la potencia.
Como la distancia entre
el punto de apoyo y la
potencia es grande,
vencemos más fuerza de
la que hacemos.
RA P
Tiposdepalanca
Existen tres tipos de palancas:
P
R
P
A
RP
A
R
A

La caña de pescar.La caña de pescar.La caña de pescar.La caña de pescar.La caña de pescar. Mientras una de las manos actúa como
punto de apoyo, la otra provee la fuerza para mover la
caña. La resistencia es el peso del pez que se puede levantar
a gran altura con un pequeño movimiento de mano.
Destapador.Destapador.Destapador.Destapador.Destapador. Al levantar el mango, se supera
la fuerte resistencia de la tapa.
El funcionamiento de las palancas está basado en la ley de los momentosley de los momentosley de los momentosley de los momentosley de los momentos.
Para comprender la ley de los momentos veamos el ejemplo de un balancín:
El momento de una fuerzamomento de una fuerzamomento de una fuerzamomento de una fuerzamomento de una fuerza se obtiene multiplicando la longitud del brazo por el valor
de la fuerza. En nuestro caso el valor de los momentos será:
■ Momento ejercido en el lado derecho: 40 kgf x 2 m = 80 kgf.m
■ Momento ejercido en el lado izquierdo: 80 kgf x 1 m = 80 kgf.m
Es decir, los dos momentos son iguales. Esa será la condición de equilibrio de la palanca
y ley de equilibrio de los momentos.
Ley de equilibrio de los momentos:Ley de equilibrio de los momentos:Ley de equilibrio de los momentos:Ley de equilibrio de los momentos:Ley de equilibrio de los momentos: Una palanca estará en equilibrio cuando el
momento ejercido por la potencia sea igual al momento ejercido por la resistencia.
Matemáticamente se puede expresar así:
En el lado derecho a 2 m del punto de
apoyo está una persona que pesa 40 kg,
en el lado izquierdo, a 1 m del punto de
apoyo, está una persona que pesa 80 kg.
P × a = R × b
P R
a b
Mediante la ley de equilibrio se puede calcular el valor
de cualquiera de los elementos de una palanca si se
conocen las distancias al punto de apoyo (a o b) y el
valor al menos de una de las fuerzas (P o R).
1 m 2 m

El plano inclinado
El plano inclinado es una superficie inclinadasuperficie inclinadasuperficie inclinadasuperficie inclinadasuperficie inclinada
(rampa) que sirve para subir objetos con menor
esfuerzo, haciéndolos rodar o deslizándolos.
Cuanto más largo y menos inclinado sea el
plano, más fácil resultará el trabajo que se
realiza.
Las rampas facilitan el desplazamiento de las
personas en silla de ruedas y el traslado de
objetos en general.
También las carreteras que suben una montaña
forman un serpentín con planos inclinados.
Investiga ¿Qué tipo de
palanca es una pala y un
subibaja? Dibuja sus
elementos.
● ¿Por qué un alicate es mejor que
una tijera cuando se trata de cortar
un material muy resistente?
● ¿Cómo debes usar un martillo para
sacar un clavo? Dibuja los
elementos de esta palanca.
● ¿Qué opinas de la frase “Dadme
un punto de apoyo y moveré el
mundo”?
HerramientaHerramientaHerramientaHerramientaHerramienta Tipo de palancaTipo de palancaTipo de palancaTipo de palancaTipo de palanca Ventaja mecánicaVentaja mecánicaVentaja mecánicaVentaja mecánicaVentaja mecánica
Tijeras
Destapador
Carretilla
Cortaúñas
Pinza
Perforador de hojas
Engrapador
◆ Completa el cuadro:

● Observa planos inclinados (rampas) que existan en tu comunidad y
determina cuál es su función.
● Describe lugares de tu comunidad en los cuales consideres que debería de
existir rampas y fundamenta por qué.
◆ Analiza el gráfico y responde:
● ¿Cuándo se requiere más fuerza en una rampa? ¿Al aumentar la inclinación o al
disminuirla? ¿En qué caso la distancia recorrida es mayor?
● Al subir una cuesta, ¿por qué nos cansamos más si tomamos el camino corto y la
subimos directamente pero, si hacemos un camino más largo en forma de serpentín,
la subida es más fácil?
La polea
Observa cómo se saca agua de un pozo con
una polea.
Una polea es una rueda que tiene un canal por
donde pasa una cuerda. De un extremo de la
cuerda se coloca la carga y del otro se tira.
Este mecanismo hace más cómodo el trabajo
porque cambia el sentido de la fuerza: es más
fácil levantar un objeto tirando hacia abajo que
hacia arriba. Las poleas se utilizan en los pozos,
las grúas, las persianas, etcétera.
Cuando varias poleas trabajan juntas se ahorra
mucho esfuerzo.
Caso 1 Caso 2
Has reconocido que las máquinas simples como palancas, rampas, poleas y las complejas
como una grúa o una bicicleta han reducido el esfuerzo empleado en la realización de
diversos trabajos. Asimismo la aplicación de sus principios se ha utilizado para crear
diversas herramientas que utilizamos en nuestra vida diaria.

FICHADETRABAJO
Trabajo,potenciaymáquinassimples
1. Calcula el trabajo utilizado para mover un mueble 7 metros empleando una
fuerza de 8 newton.
2. Calcula los metros que recorre un objeto si al aplicar un trabajo de 64 J, se
produce una fuerza de 8 N.
3. Calcula la fuerza ejercida cuando al utilizar 99 J de trabajo, una caja se desplaza
9 metros.
4. Un cuerpo de 2,45 kg de masa se desplaza sin rozamiento por un plano inclinado
de 5 m y 1 m de altura. Determina la distancia recorrida por el cuerpo, que
estaba en reposo, en 1,5 s.
5. Indica el trabajo necesario para deslizar un ropero a 2 m de su posición inicial
mediante una fuerza de 10 N.
6. Una grúa levanta 2 000 kg a 15 m del suelo en 10 s. Expresa la potencia
empleada en:
a) Watt
b) HP
7. ¿Qué potencia deberá poseer un motor para bombear 500 litros de agua por
minuto hasta 45 m de altura?
8. ¿A qué se llama resistencia en una palanca? ¿Y punto de apoyo? ¿Y potencia?
9. En el ejemplo del balancín, ¿qué ocurre si...
a) la persona de 40 kg se mueve hacia adelante?
b) la persona de 40 kg se mueve hacia atrás?
10. Si tuvieras que sentarte en un lado del balancín y, en el otro, dos amigos que
pesan justo el doble que tú, ¿qué harías?
a) Les pedirías que se sentaran más próximos al punto de apoyo y te pondrías
en el extremo alejado.
b) Te sentarías a la misma distancia del centro que ellos.
c) Te sentarías más cerca del punto de apoyo que ellos.

FICHA INFORMATIVA
Elavión
El desarrollo de la aviación ha permitido viajes seguros, el avión es el medio de transporte
con menos accidentes y mucho más rápido que cualquier otro medio. Los hermanos
Wright realizaron en 1903 el primer vuelo a motor en la historia, y desde esa época los
aviones han evolucionado. Sin embargo, hay algo que no ha cambiado: los principios
por los cuales es posible que vuelen los aviones.
ActividadActividadActividadActividadActividad
Para comprender cómo se sostiene un avión en
el aire realiza la siguiente actividad.
Corta una tira de papel cometa de 20 cm de
largo por 3 cm de ancho. Acércala a tus labios
y sopla por encima de ella.
● ¿Se levanta el papel? Explica la razón.
● ¿Cómo relacionas esta experiencia con las
alas de los aviones?
Las alas.Las alas.Las alas.Las alas.Las alas. Los aviones se sostienen porque sus alas tienen
una superficie curva en la parte superior para que la velocidad
del aire sea mayor que la parte inferior. Esto origina un mayor
empuje del aire hacia arriba.
Forma aerodinámica.Forma aerodinámica.Forma aerodinámica.Forma aerodinámica.Forma aerodinámica. Los aviones
terminan en punta para reducir al
mínimo la resistencia del aire.
Propulsión.Propulsión.Propulsión.Propulsión.Propulsión. Los motores turbo succionan
el aire y lo lanzan con gran velocidad hacia
atrás. El aire que sale produce en el avión
un movimiento hacia adelante.
El peso.El peso.El peso.El peso.El peso. Los aviones se fabrican con
materiales livianos, para reducir el
peso todo lo posible.

73
● Reconocer fenómenos relacionados con la presión
de los líquidos y la presión atmosférica para
interpretar fenómenos de la vida cotidiana.
Determinar la relación de proporcionalidad entre
las magnitudes para calcular la presión.
● Diferenciar los conceptos de calor y temperatura
reconociendo y utilizando las diferentes escalas de
temperatura. Identificar las formas de transferencia
del calor y realizar cálculos.
● Comprender los fenómenos físicos de cambio de
estado y dilatación como efectos de la acción del
calor sobre la materia. Aplicar fórmulas para
calcular la cantidad de calor necesaria para lograr
el cambio de estado de diferentes cuerpos.
LA PRESIÓN Y EL CALORLA PRESIÓN Y EL CALORLA PRESIÓN Y EL CALORLA PRESIÓN Y EL CALORLA PRESIÓN Y EL CALOR
Indagar sobre los conocimientos relacionados con la presión y la energía térmica para
explicar fenómenos relacionados con la vida cotidiana y las aplicaciones tecnológicas
derivadas de ellos.
Aplicar estrategias para resolver problemas matemáticos de magnitudes de presión y calor.
1.1.1.1.1. La presiónLa presiónLa presiónLa presiónLa presión
2.2.2.2.2. Calor o energía térmicaCalor o energía térmicaCalor o energía térmicaCalor o energía térmicaCalor o energía térmica
3.3.3.3.3. Efectos del calorEfectos del calorEfectos del calorEfectos del calorEfectos del calor
● Explicar fenómenos naturales observados cotidianamente interesándote por ampliar
tu visión del mundo.
● Conocer el concepto de presión, calor, temperatura y manejar sus unidades de
medida.
● Interpretar en términos científicos diferentes fenómenos relacionados con la presión
y la energía térmica en la vida cotidiana.
● Conocer en qué se basa el funcionamiento de diferentes aparatos que tienen relación
con la presión y el calor.
● Resolver y formular problemas relacionados con tu vida cotidiana haciendo uso de
las operaciones con números reales y sus respectivas propiedades.
● Identificar la relación de proporcionalidad directa e inversa entre magnitudes
relacionadas en una ecuación matemática o fórmula.

75
LLLLLa presióna presióna presióna presióna presión
1. La presión y sus magnitudes
relacionadas
2. Presión de los líquidos
3. Presión atmosférica
Reconocer fenómenos relacionados con
la presión de los líquidos y la presión
atmosférica para interpretar fenómenos
de la vida cotidiana. Determinar la
relación de proporcionalidad entre las
magnitudes para calcular la presión.
● En el primer momento a través de una
experiencia comprenderás la noción de
presión y conocerás sus unidades de
medida. Analizarás la relación de
proporcionalidad entre las magnitudes
presentes en la fórmula para calcular
la presión.
● En el segundo momento analizarás la
presión de los líquidos describiendo dos
principios básicos, el principio de Pascal
y el principio de Arquímedes.
● En el tercer momento a partir de
sencillas experiencias comprenderás la
presión atmosférica y sus efectos.
● Prensa hidráulica
● Hidrostática
● Flotación
● Presión atmosférica
● Presión hidrostática
● Pascal
● Magnitud
● Proporcionalidad
● Magnitudes proporcionales
Presión:
● Concepto
● Unidades de medida
Presión de los líquidos:
● Principio de Pascal (prensa hidráulica)
● Principio de Arquímedes
Presión de gases:
● Presión atmosférica
Fichas de trabajoFichas de trabajoFichas de trabajoFichas de trabajoFichas de trabajo Palabras clavePalabras clavePalabras clavePalabras clavePalabras clave
● Simulando una prensa hidráulica
● Aplicando el principio de Pascal

76 La presión y el calor
PRIMERMOMENTO:Lapresiónysus
magnitudesrelacionadas
● ¿En qué caso pudiste apoyar todo el cuerpo sin deformar el tubo? ¿Por
qué?
1. Coloca un tubo de cartón en el suelo y
apoyándote ligeramente sobre una mesa
párate sobre él en un solo pie.
2. Coloca dos tubos de cartón en el suelo y
párate sobre ellos. Observa lo que
sucede.
3. Luego coloca los tubos formando dos filas
y párate sobre ellos de tal forma que tu
pie abarque todos.
Cuando apoyas tu pie sobre un tubo de cartón, estás aplicando una fuerza (tu peso)
sobre una superficie (el tubo de cartón). Uno o dos tubos no podían soportar tu peso y
por eso se deformaban, pero varios tubos soportaron tu peso sin deformarse. Esto sucede
porque tu peso se distribuye sobre una mayor superficie de tal forma que cada tubo
soporta menos peso.
La acción de una fuerza sobre una superficie se llama presión. Cuanto mayor sea la
superficie, menor será la presión.
De la experiencia
se puede
deducir:
1 2
3
Realiza la siguiente experiencia.
Necesitas 10 tubos de cartón de
papel higiénico.

77La presión y el calor
Relación de proporcionalidad entre magnitudes
La fórmula que acabas de ver P = F/A expresa la relación que existe entre las magnitudes
de presión, fuerza y área.
Concepto de presión y unidades
Como has visto en el experimento anterior, la acción de una fuerza sobre una
superficie se llama presión. Cuanto mayor es la superficie sobre la que actúa la
fuerza, menor será la presión.
La presión es la fuerza ejercida sobre una unidad de áreaLa presión es la fuerza ejercida sobre una unidad de áreaLa presión es la fuerza ejercida sobre una unidad de áreaLa presión es la fuerza ejercida sobre una unidad de áreaLa presión es la fuerza ejercida sobre una unidad de área
Presión =
Fuerza
Área
P =
F
A
La presión es una magnitud. En el Sistema
Internacional de unidades la unidad de presión
es el Pascal (Pa).
Un pascal es la presión que ejerce la fuerza de 1
newton (N) en 1 m2. Por lo tanto, reemplazando
en la fórmula se tiene:
1 Pa = 1 N/m2
En la práctica esta unidad es muy pequeña y se
suele emplear el hectopascal (hPa), es decir,
centenares de pascales.
Existen otras unidades de presión que se usan junto
con el pascal. Estas son la atmósferaatmósferaatmósferaatmósferaatmósfera y el barbarbarbarbar.
La presión también se expresa en kg/cmkg/cmkg/cmkg/cmkg/cm22222
La unidad de presión
lleva el nombre del
científico francés Blas
Pascal.
El pascal se usa con fines
científicos, por ejemplo;
para hacer estudios del
clima. Las otras
unidades se usan en
actividades prácticas;
por ejemplo, para medir
la presión de las llantas.
De la fórmula: P =
F
A
se tiene: P α F y P α
1
A
Relación 1:Relación 1:Relación 1:Relación 1:Relación 1:
La expresión P ααααα F quiere decir que la presión es directamente proporcional a la fuerza
aplicada sobre un área o superficie determinada. Esto significa que la presión obtenida al
aplicar una fuerza sobre una determinada área aumentará si se aumenta la fuerza y
disminuirá, si se reduce la fuerza.
El concepto matemático de
proporcionalidad directa o inversa te
ayudará a analizar las relaciones
existentes entre estas magnitudes.

Comprueba esta situación mediante el siguiente ejercicio:
● Un colchón de una plaza mide 185 × 79 cm, es decir, tiene un área de 14 615 cm2
¿Cuándo se ejercerá mayor presión, si se acuesta una persona de 70 kg o cuando se
acuestan dos personas de 70 kg cada una?
Por una relación de proporcionalidad se puede decir fácilmente que, si el peso aumenta,
la presión sobre el colchón aumenta.
Hagamos los cálculos utilizando la fórmula para obtener la presión.
P =
F
A
................................ (1)
La fuerza F estará determinada por el
peso. Entonces se requiere hallar el peso
del cuerpo que será igual a la fuerza:
ω = 70 kg × 10
m
s2
ω = 700 kg ×
m
s2
ω = 700 N = F
Si la fuerza tiene como unidad el newton,
entonces el área (A) se expresará en m2:
A = 14 615 cm2 ×
1 m
10 000 cm
2
2
= 1,4615 m2
Redondeando: A = 1,5 m2
Reemplazando en la fórmula (1) se tiene:
P1 =
700 N
1,5 m2
= 466,666 Pa
En el caso de las dos personas, la presión será:
ω = 2 70 10kg ×






m
s2
= 1400 kg ×
m
s2
= 1 400 N
El área es la misma, o sea: A = 1,5 m2
Reemplazando en la fórmula (1) se tiene:
P2 =
1 400 N
1,5 m2
= 933,333 Pa
P11111 < P22222
Efectivamente, si la fuerza aumenta la presión también aumenta.
Generalmente se usan indistintamente
los términos peso y masa. Pero debes
recordar que, por ser el peso una
fuerza, se mide en newton (N) y la
masa en kilogramos (kg). Por lo
tanto, cuando te dicen que el peso
es de 70 kg, en realidad te están
dando la masa del cuerpo. Para
calcular el peso se empleará la
fórmula:
ω = m × g
ω = peso del cuerpo
g = aceleración de la gravedad = 10
m
s2
m = masa del cuerpo
Recuerda
que el newton (N) es
la unidad de fuerza:
1 kg ×
m
s2
= 1 N

Relación 2:Relación 2:Relación 2:Relación 2:Relación 2:
La expresión P α
1
A
quiere decir que la presión es inversamente proporcional al área
sobre la cual se aplica la fuerza.
Esto significa que la presión obtenida al aplicar una fuerza sobre una determinada área
aumentará si el área disminuye y disminuirá, si el área aumenta.
Comprueba esta situación mediante el siguiente ejercicio:
● Las personas del ejercicio anterior paradas sobre el colchón aplican una fuerza similar a
su peso sobre un área aproximada de 0,084 m2
. Cuando están echadas su peso presiona
casi toda el área del colchón igual a 1,4615 m2 ¿En qué situación será mayor la presión?
¿Cuándo las personas están paradas o echadas sobre el colchón?
Utilizando la fórmula para calcular la presión:
Del ejercicio anterior tenemos que: ω = 2 70 10kg ×






m
s2
= 1 400 N
Reemplazando en la fórmula (1) para el A = 0,084 m2 , se tiene:
P1 =
1 400 N
0,084 m2
= 16 666,666 Pa
Reemplazando en la fórmula (1) para el A = 1,4615 m2, se tiene:
P2 =
1 400 N
1,4615 m2
= 957,919 Pa
P1 > P2
Efectivamente la presión ejercida por una fuerza sobre un área pequeña es mayor que la
presión ejercida por esa misma fuerza sobre un área mayor.
Quizás has podido experimentar que si te paras
sobre el colchón, éste se hunde en ese lugar. Es decir, en un
área pequeña la presión que ejerce tu peso es mayor. Pero
cuando te acuestas, el colchón se hunde menos porque el
peso de tu cuerpo se distribuye por todo el área.

◆ Para romper un ladrillo de un golpe con la mano, ¿cómo colocan la mano los karatecas?
¿Por qué no golpean con la palma abierta?
◆ Si un fakir se acostara en una cama con dos o tres clavos, éstos lo atravesarían, pero si
se acuesta en una cama con muchos clavos no sufre lesión alguna. ¿Qué explicación das
a este hecho?
◆ ¿Por qué es difícil caminar con zapatos de taco fino en la arena o cualquier superficie
blanda mientras que con zapatos que apoyan toda la planta resulta mejor?
◆ Elabora ejemplos de tu vida cotidiana sobre las relaciones de proporcionalidad entre las
magnitudes.
◆ Una caja con latas de leche mide 60 cm ancho, 80 cm de largo y 40 cm de altura:
a) Determina en cuál de las caras debe apoyarse sobre una mesa de plástico para que
ejerza menor presión.
b) Si la caja pesa 20 kg, ¿qué presión ejerce sobre la mesa en esa posición?
Has definido la presión y sus unidades de medida. Además has analizado la relación
directa e inversa entre las magnitudes presentes en la fórmula para calcular la presión.
En el segundo momento analizarás la presión que ejercen los líquidos.
En nuestras actividades cotidianas a veces nos
interesa repartir la fuerza sobre una superficie grande
para que la presión sea menor. En otras ocasiones nos
interesa concentrar la fuerza en una superficie pequeña
para que la presión sea mayor.
Para no hundirse en la nieve se
usan unas raquetas que tienen
mayor superficie de apoyo que
los zapatos.
Los carniceros tienen
cuchillos afilados que
cortan bien porque la
parte filosa tiene una
superficie muy pequeña.
Un carpintero introduce
clavos con poco esfuerzo: la
punta presenta una superficie
pequeña. ¿Qué pasaría si los
clavos tuviesen punta roma?

SEGUNDOMOMENTO:Presión
de los líquidos
● ¿En qué se utilizan los submarinos? ¿Crees que es útil lo que hacen?
● ¿Has vivenciado la presión de los líquidos en tu cuerpo? Describe tu experiencia.
En las películas de submarinos vemos que siempre se controla la profundidad. Esto se
debe a que el submarino sólo puede descender hasta cierta profundidad: cuanto más
profundo descienda, más agua habrá por encima de él y mayor será la presión que soporta.
Si la presión del agua fuese muy grande aplastaría al submarino.
Los submarinos más modernos están hechos con materiales muy resistentes y pueden
descender hasta 6 000 metros de profundidad.
¿Dequédependelapresióndeloslíquidos?
Los líquidos pesan y ejercen una presión en las
paredes del recipiente que los contiene y sobre
los cuerpos sumergidos en ellos.
La presión que ejerce un fluido se debe al
choque de sus moléculas con las paredes del
recipiente o de cualquier objeto que tengamos
sumergido en él.
La presión depende del peso y de la altura que
alcance el líquido. La altura también puede
considerarse como profundidad.
Por ejemplo, si nos sumergimos en el mar o en
un río notaremos que a mayor profundidad mayor
presión. Notamos ese efecto en los oídos.
La presión que soporta un cuerpo sumergido se denomina Presión hidrostáticaPresión hidrostáticaPresión hidrostáticaPresión hidrostáticaPresión hidrostática.
h1
h2

Fórmula de la presión
en un líquido
La fórmula para calcular la presión hidrostática se deduce de la fórmula de presión
tomando en cuenta el peso y la altura de la columna de líquido que hay encima de
algún objeto.
En la fórmula de presión: P =
F
A
................................. (1)
La fuerza (F) está dada por el peso de la columna de líquido que se halla sobre el cuerpo
sumergido.
F = ω = m × g Pero, como se trata de un líquido la masa (m) se
expresa en función de la densidad del líquido.
d =
m
V
⇒ m = d × V d = densidad del líquido
V = volumen de columna de líquido
Reemplazando la masa de la columna de líquido en función de la densidad se tiene:
F = m × g = d × V × g g = 10 m/s2
Se asume el líquido que se halla sobre el cuerpo sumergido como una columna de
forma cilíndrica cuya altura (h) es lo que conocemos como profundidad; por lo tanto
expresando el volumen de la columna de líquido con la fórmula del volumen de un
cilindro quedará así:
V = volumen
V = A × h A = área de la base de la columna de líquido
h = altura de la columna, que es igual a la
profundidad del objeto sumergido.
Reemplazando se tiene:
F =ω = m × g = d × V × g = d × A × h × g
Reemplazando en la fórmula (1), se tiene:
P =
F
A
=
d A h g
A
× × ×
= P = g × h × d
◆ Calcula a qué presión está sometido un buceador si bucea primero a 3 m y luego a 4 m
de profundidad en una piscina de agua dulce.
Datos: densidad del agua = 1 000 kg/m3 g = 10 m/s2.
◆ Compara los resultados obtenidos y comprueba si es cierto que, a mayor profundidad, la
presión es mayor.

Principio de Pascal
Si presionas una bolsa llena de agua provista
de varios agujeros iguales, observarás que la
presión se trasmite por igual; por eso, el líquido
sale exactamente igual por todos los agujeros.
Este efecto fue estudiado por el físico francés
Blas Pascal (XVII), quien enunció el principio
que hoy lleva su nombre.
Principio de Pascal: Toda presión ejercidaPrincipio de Pascal: Toda presión ejercidaPrincipio de Pascal: Toda presión ejercidaPrincipio de Pascal: Toda presión ejercidaPrincipio de Pascal: Toda presión ejercida
sobre un líquido se trasmite con la mismasobre un líquido se trasmite con la mismasobre un líquido se trasmite con la mismasobre un líquido se trasmite con la mismasobre un líquido se trasmite con la misma
intensidad y rapidez en todos sus puntos.intensidad y rapidez en todos sus puntos.intensidad y rapidez en todos sus puntos.intensidad y rapidez en todos sus puntos.intensidad y rapidez en todos sus puntos.
● Si los agujeros en la bolsa son de diferente tamaño, ¿la presión del líquido
en los agujeros será igual? Compruébalo con una experiencia.
● ¿Por qué puedes regar un jardín con una botella agujereada?
La prensa hidráulica
Una de las aplicaciones del principio de Pascal, es
la prensa hidráulicaprensa hidráulicaprensa hidráulicaprensa hidráulicaprensa hidráulica: un dispositivo donde una
fuerza pequeña se convierte en una fuerza mayor.
Cuando se aplica una fuerza (F1) en el émbolo
más pequeño, aumentamos la presión en el
líquido (aceite generalmente).
La presión ejercida se trasmite hasta el émbolo
más grande multiplicando la fuerza (F2).
El principio de la prensa hidráulica se aplica en
numerosos dispositivos prácticos, como las
gatas para levantar carros, la grúa hidráulica y
los frenos hidráulicos de los automóviles.
Investiga
aplicaciones de los
sistemas hidráulicos en
los frenos y otros
dispositivos. Presenta la
información en un tríptico.Todos los dispositivos
que usa una prensa hidráulica
se llaman sistemas hidráulicos. En la
ficha de trabajo podrás reproducir
el principio de prensa hidráulica.
F1
F2

¿Cómosecalculaelempuje?
La fuerza ascendente que actúa sobre un cuerpo parcial o totalmente sumergido es igual
al peso del líquido desplazado. Este peso depende de la densidad del líquido y del volumen
del cuerpo sumergido. Por ejemplo:
El agua de mar es más densa que el agua dulce, es decir, 1 litro de agua de mar pesa más
que 1 litro de agua dulce.
Un buceador sumergido en agua de mar o en agua dulce desplazará igual cantidad de
agua; sin embargo, puesto que el peso del agua de mar es mayor al del agua dulce, el
empuje (o fuerza ascendente) será mayor en el primer caso que en el segundo. Por tal
razón será más fácil flotar en agua salada que en agua dulce.
Asimismo, un buceador con mayor volumen desplazará mayor cantidad de agua que uno
de menor volumen. Cuando un buceador inmerso en el agua infla su chaleco compensador,
aumenta su volumen sin modificar su peso. Al aumentar su volumen aumenta también el
volumen de agua desplazado, por lo que aumenta su empuje y puede flotar mejor.
Principio de Arquímedes
Cuando un cuerpo se sumerge en el agua desaloja una cierta cantidad de líquido. La
fuerza de empuje corresponde al peso de ese volumen de líquido desalojado. Esto es
lo que se conoce como principio de Arquímedes:
Todo cuerpo sumergido en un fluido experimenta una fuerza de empujeTodo cuerpo sumergido en un fluido experimenta una fuerza de empujeTodo cuerpo sumergido en un fluido experimenta una fuerza de empujeTodo cuerpo sumergido en un fluido experimenta una fuerza de empujeTodo cuerpo sumergido en un fluido experimenta una fuerza de empuje
hacia arriba que es igual al peso del volumen de agua desalojado.hacia arriba que es igual al peso del volumen de agua desalojado.hacia arriba que es igual al peso del volumen de agua desalojado.hacia arriba que es igual al peso del volumen de agua desalojado.hacia arriba que es igual al peso del volumen de agua desalojado.
Si tomas una botella de plástico vacía cerrada con una tapa y tratas de sumergirla
totalmente en un recipiente con agua, comprobarás que hay algo que ofrece resistencia
y que debes ejercer una fuerza para hundirla. Esta fuerza que tiende a evitar que
hundas la botella se llama empujeempujeempujeempujeempuje.
Si sumergimos un cuerpo sólido en el interior de un
líquido, pueden darse las siguientes situaciones:
● El cuerpo se hunde, si su peso es mayor que el empuje.
● El cuerpo queda sumergido sin llegar al fondo, si su
peso es igual al empuje.
● El cuerpo flota, si su peso es menor que el empuje.
● De acuerdo al principio de Arquímedes, ¿qué volumen tendrá un pedazo
de metal si se introduce en un balde con agua y desaloja 30 cm3 de agua?
La presión de los líquidos aumenta con la profundidad. Has reconocido los principios de
Pascal y Arquímedes.

Vivimos inmersos en un océano de aire y el aire pesa ejerciendo una presión llamada
presión atmosférica. Las personas estamos acostumbradas a la presión atmosférica y no
sentimos sus efectos.
TERCER MOMENTO: Presión atmosférica
Experimento1:Labotellaqueseabolla
1. Echa un poco de agua caliente a una botella de plástico vacía.
2. Arroja el agua y tapa la botella. Verás que la botella se abolla porque la presión del aire
exterior la aplasta.
ExplicaciónExplicaciónExplicaciónExplicaciónExplicación.
Al empezar la experiencia, en realidad la botella
no estaba vacía, pues había aire en su interior.
Este aire ejercía una presión en el interior de la
botella igual a la presión del aire exterior.
Al arrojar el agua caliente, has calentado el aire,
el cual se dilata y sale.
Entonces, dentro de la botella se ha producido
un vacío (no hay agua ni aire) y no hay nada
que ejerza presión dentro de la botella por eso
la presión exterior la aplasta.
Otra experiencia que te demostrará la existencia de
la presión atmosférica consiste en tratar de tomar
agua con un sorbete agujereado.
Cuando el sorbete está intacto, el agua sube porque
al succionar sacas todo el aire; en cambio si hay un
agujero, entra aire que presiona el líquido
impidiéndole subir.
Realiza el siguiente
experimento para reconocer las
características de la presión
atmosférica.
Nuestro cuerpo
no se aplasta con la presión atmosférica
porque los líquidos internos de las células
ejercen una presión que equilibra la
presión atmosférica.

◆ Busca una explicación a los siguientes hechos:
● Las cabinas de los aviones se mantienen presurizadas durante el vuelo. ¿En qué
consiste la presurización? ¿Por qué es necesaria?
● ¿Por qué, cuando viajas de la costa a la sierra, al abrir los envases de colonia, champú
o cremas, el contenido se escapa rápidamente y se derrama?
Experimenta:Comprobacióndelapresiónatmosférica
MaterialesMaterialesMaterialesMaterialesMateriales:
● Una vela, un plato, un vaso y agua.
1. Pega una vela pequeña en el centro de un plato hondo.
Echa agua en el plato.
2. Enciende la vela y coloca un vaso invertido como se
señala en la figura.
¿Qué es la presión atmosférica?
La capa de aire que rodea la Tierra recibe
el nombre de atmósferaatmósferaatmósferaatmósferaatmósfera. Está compuesta
por 78% de nitrógeno, 21% de oxígeno y
1% de otros gases.
La atmósfera tiene un grosor de unos 500
km, aunque el 80% del aire se encuentra
en los primeros 15 km. Esto quiere decir
que en las capas más altas casi no hay aire.
El peso de los gasespeso de los gasespeso de los gasespeso de los gasespeso de los gases que componen la
atmósfera ejerce una presión sobre los
cuerpos inmersos en ella. Esta fuerza se
denomina presión atmosférica.
La presión atmosférica varía con la altitudvaría con la altitudvaría con la altitudvaría con la altitudvaría con la altitud: es mayor a nivel del mar y disminuye
con la altura. Esto es así porque el aire es poco denso en las alturas (pesa menos).
Se ha calculado que, a nivel del mar, la presión del aire es de 1 kg/cm2.
● Explica: ¿Qué sucede? ¿Por qué?
h1
h2

◆ ¿Qué habría ocurrido con la columna de mercurio (Hg), si el experimento de Torricelli se
hubiese realizado en la cima de una montaña como el Huascarán?
◆ Cuándo el mercurio queda a una altura de 730 mm en un barómetro, ¿cuánto mide la
presión atmosférica?
◆ ¿Qué quiere decir que la presión atmosférica es de 1 kg/cm2?
◆ Observa el cuadro y calcula cuál es la presión atmosférica aproximada en el lugar
donde vives.
Medicióndelapresiónatmosférica
En 1643, al físico italiano E.Torricelli se le ocurrió
un procedimiento para medir la presión
atmosférica.
● Llenó con mercurio un tubo de 1 m de
largo y de 1 cm2
de diámetro, cerrado por
un extremo.
● Metió el tubo lleno de mercurio, boca
abajo en una cubeta que también
contenía mercurio y observó que el
mercurio del tubo bajaba un poco, pero
se quedaba a cierta altura. A nivel del mar,
en donde se realizó esta experiencia, esa
altura resultó ser 760 mm.
Torricelli dedujo que la presión atmosférica ejerce
una fuerza sobre la superficie del mercurio de la
cubeta que impide el descenso total. Esta fuerza es
igual al peso del mercurio que hay dentro del tubo.
Se demostró así que la presión del aire soporta una
columna de mercurio cuya longitud es de 760 mm.
Podemos decir, entonces, que a nivel del mar la
presión atmosférica es de 760 mm de mercurio. Este
valor se denomina 1 atmósfera (1 atm).
Como 760 mm de mercurio x 1 cm2 de sección pesa
aproximadamente 1 kg, se tiene:
1 atm = 760 mm de Hg (mercurio) =1 kg/cm2
En el SI la unidad de presión es el pascal (Pa).
El instrumento para medir la presión atmosférica se
llama barómetro y su funcionamiento se basa en el
experimento de Torricelli.
Variación de la presiónVariación de la presiónVariación de la presiónVariación de la presiónVariación de la presión
atmosféricaatmosféricaatmosféricaatmosféricaatmosférica
AlturaAlturaAlturaAlturaAltura Presión enPresión enPresión enPresión enPresión en
en metrosen metrosen metrosen metrosen metros mm de Hgmm de Hgmm de Hgmm de Hgmm de Hg
8 000 267
6 000 354
4 000 462
3 000 525
2 000 597
1 500 634
1 000 674
500 716
0 760
1 000 mm
760 mm

Investiga sobre
un instrumento que mide
la presión del aire llamado
manómetro.
El físico italiano E. Torricelli encontró un método para medir la presión. Has
determinado también que la presión total que sufre un cuerpo sumergido en un
líquido expuesto a la atmósfera es la suma de la presión atmosférica más la presión
hidrostática.
Nuestro cuerpo soporta la presión atmosférica.
Algunas veces un cambio de presión muy brusco puede
provocarnos molestias. Por ejemplo cuando viajamos a un
lugar con una altura diferente a donde nos ubicamos se
produce una descompensación entre la presión interna
del oído medio y la existente en el entorno.
Esto puede provocar dolor
a menos que se busque equilibrar
la presión. Para ello debemos
bostezar o mascar chicle.
No se recomienda taparnos la nariz
y “soplar” pues podríamos introducir
mucosidad en el oído interno
y generar infecciones.
La presión de un cuerpo sumergido en un recipiente expuesto a la atmósfera será la
suma de las presiones atmosférica e hidrostática:
Ptotal = Patm + Phidrost = Patm + d × h × g
● ¿Cuál es la presión a 1m y a 10 m de profundidad desde la superficie del mar? Supón que
la densidad del agua de mar es d = 1,03 × 103 kg/m3 y que la presión atmosférica en la
superficie del mar es 1,01 × 105 Pa y que a este nivel de presión la densidad no varía con
la profundidad.
Si se reemplazan estos datos en la fórmula de presión total (Ptotal), se tiene:
Ptotal = 1,01 × 105 Pa + (1,03 × 103 kg/m3)(10 m/s2)(h)
Si reemplazas el dato de las alturas dadas, debes obtener los siguientes resultados:
Si h = 1 m Ptotal = 1,11 × 105 Pa
Si h = 10 m Ptotal = 2,04 × 105 Pa
Efectúa las operaciones y comprueba los resultados obtenidos.

FICHADETRABAJO
Simulando una prensa hidráulica
● Una manguera de aproximadamente 1 cm de diámetro.
● Dos jeringas, de 1 cm y 2 cm de diámetro respectivamente, que serán las jeringas
A y B.
● Alambre delgado para amarrar y asegurar las uniones.
● Un frasco con peso. Puedes llenarlo con piezas de metal o con piedras.
1. Ata la manguera a las jeringas como muestra la ilustración.
2. Llena con agua toda la manguera, incluso la mitad de las jeringas A y B.
3. Pide a un compañero que coloque el frasco con peso sobre la jeringa de diámetro
mayor. Puede sujetarlo, pero no presionarlo.
4. Presiona el émbolo de la jeringa A (la más pequeña) y observa lo que sucede.
Repite la operación, pero esta vez coloca el frasco en la jeringa A.
● ¿Con cuál de las dos jeringas hiciste menor esfuerzo para levantar el mismo peso?
● Explica el funcionamiento de esta prensa hidráulica.
El ser humano fabrica aparatos utilizando principios
muy sencillos. En esta experiencia el fundamento teórico es
el principio de Pascal: los líquidos transmiten íntegramente y
en todas direcciones la presión ejercida en cualquier punto del
mismo. Con una fuerza pequeña y el mecanismo adecuado
podemos conseguir una fuerza mucho mayor.
Jeringa A
Jeringa B

FICHADETRABAJO
Aplicando el principio de Pascal
La prensa hidráulica es un dispositivo mecánico que sirve para multiplicar una fuerza.
Toda la parte hueca se llena con un líquido que puede ser agua o aceite.
Si sobre el pistón chico se aplica
una fuerza F1, sobre el grande
aparece una fuerza F2.
De acuerdo a Pascal, las
presiones en los dos émbolos son
iguales.
P1 = P2
F
S
1
1
=
F
S
2
2
Esta ecuación se suele escribir:
F
F
1
2
=
S
S
1
2
........................... (1)
Relación entre las fuerzas y los diámetros de los émbolosRelación entre las fuerzas y los diámetros de los émbolosRelación entre las fuerzas y los diámetros de los émbolosRelación entre las fuerzas y los diámetros de los émbolosRelación entre las fuerzas y los diámetros de los émbolos
Si d1 y d2 son los diámetros, entonces: S1 =
πd1
2
4
y S2 =
πd2
2
4
Reemplazando en (1):
F
F
1
2
=
π
π
d
d
1
2
2
2
4
4
⇒
F
F
1
2
=
d
d
1
2
2
2
Relación entre las fuerzas y las alturas recorridas por los émbolosRelación entre las fuerzas y las alturas recorridas por los émbolosRelación entre las fuerzas y las alturas recorridas por los émbolosRelación entre las fuerzas y las alturas recorridas por los émbolosRelación entre las fuerzas y las alturas recorridas por los émbolos
El volumen de líquido desplazado por el émbolo menor es igual al volumen
desplazado por el mayor, o sea:
V1 = V2 ⇒ S1h1 = S2h2 ⇒
S
S
1
2
=
h
h
2
1
F1
F2
h1
h2
S1
S2

Comparando esta igualdad con (1).
F
F
1
2
=
h
h
2
1
• Los diámetros de dos pistones de una prensa hidráulica miden 4 cm y 40 cm,
respectivamente. ¿Por cuánto aparece multiplicada en el pistón grande la fuerza
que se aplica en el chico?
Solución:Solución:Solución:Solución:Solución:
Aplica la relación:
F
F
1
2
=
d
d
1
2
2
2
donde: F1 = fuerza aplicada en el pistón chico
F2 = fuerza en el pistón grande
⇒ =
( )
( )
F
F
1
2
2
2
4
40
=
F
F
1
2
=
16
1 600
⇒ F2 =
1 600
16
1
× F
=
1 600
16
1
F
⇒
F2 = 100 F1
Respuesta:Respuesta:Respuesta:Respuesta:Respuesta: La fuerza en el pistón grande se ve multiplicada por 100.
Resuelve los siguientes problemas:Resuelve los siguientes problemas:Resuelve los siguientes problemas:Resuelve los siguientes problemas:Resuelve los siguientes problemas:
1) En un taller de mecánica tienen una gata hidráulica que sirve para levantar los
autos y realizar una mejor revisión en su parte baja. Si este aparato utiliza una
presión de 6 kg/cm2, ¿hasta que peso podrá levantar, si el diámetro del pistón
grande mide 20 cm?
2) El dueño de una fábrica de vinos quiere modernizarla y ha adquirido una máquina
con sistema hidráulico (prensa hidráulica) para prensar las uvas. Las superficies de
los émbolos de la prensa hidráulica son de 8 cm2 y 20 cm2 respectivamente. Si
sobre el primero se aplica una fuerza de 70 N, ¿cuál será la fuerza obtenida por el
otro émbolo?
3) Sobre el émbolo de 12 cm2 de una prensa hidráulica se aplica una fuerza de 40 N,
y en el otro se obtiene una fuerza de 150 N. ¿Cuál es el valor de la superficie de este
émbolo?

93
CCCCCalor o energía térmicaalor o energía térmicaalor o energía térmicaalor o energía térmicaalor o energía térmica
1. Calor y temperatura
2. Propagación del calor
3. Cantidad de calor
Diferenciar los conceptos de calor y
temperatura reconociendo y utilizando las
diferentes escalas de temperatura.
Identificar las formas de transferencia del
calor y realizar cálculos.
● En el primer momento diferenciarás los
conceptos de calor y temperatura
analizando situaciones de la vida
cotidiana. Además identificarás
instrumentos de medida y escalas de
temperatura.
● En el segundo momento reconocerás
tres formas de propagación (transmisión)
del calor, sus efectos en el medio
ambiente y sus aplicaciones tecnológicas.
● En el tercer momento identificarás las
unidades para medir la cantidad de calor
y la forma de calcularla a través de la
capacidad calórica de los materiales.
● Efecto térmico de mares y lagos
● El calor y los seres vivos
● Termómetro
● Puntos fijos
● Energía térmica
● Calor
● Temperatura
● Calor específico
● Capacidad calorífica
● Cálculo aritmético y algebraico
● Razón y proporción de segmentos
Calor y temperatura:
● Diferencia de conceptos
● Instrumentos y unidades de medida
● Formas de transferencia de calor
● Capacidad calórica de los cuerpos
● Ecuación fundamental de la
calorimetría
Fichas informativasFichas informativasFichas informativasFichas informativasFichas informativas Palabras clavePalabras clavePalabras clavePalabras clavePalabras clave
● Calculando la cantidad de calor

● Para “ver” el movimiento de las moléculas de agua realiza la siguiente experiencia:
Llena un recipiente con agua caliente y otro con agua
fría (con la misma cantidad de agua). Cuando el agua
esté quieta echa una gota de colorante o tinta en el
centro de cada recipiente. Observa en qué recipiente
el colorante se difunde más rápidamente. ¿Qué te
demuestra esto?
PRIMERMOMENTO:Calorytemperatura
El calor es una forma de
energía que percibimos fácilmente
a través de nuestros sentidos. Así,
podemos sentir si algo está
caliente o frío.
Diferenciasentrecalorytemperatura
Como sabes, la materia está formada por
partículas (átomos o moléculas) que están
vibrando continuamente.
El calor o energía térmicacalor o energía térmicacalor o energía térmicacalor o energía térmicacalor o energía térmica es una
consecuencia del movimiento de las
partículas que forman la materia. Mientras
mayor sea el movimiento vibratorio de las
partículas de un cuerpo, más caliente se
encontrará éste. Incluso los objetos más
fríos poseen algo de calor porque sus
átomos se están moviendo.
Cuando calentamos algo, estamos incrementando la velocidad de sus moléculas.
La temperaturatemperaturatemperaturatemperaturatemperatura es una medida de la velocidad de las partículas. Así, las moléculas
de agua que están a 100 °C se mueven más rápido que las que están a 10 °C.
Por lo tanto, aunque muchas veces usamos las palabras calor y temperatura como
sinónimos, estos conceptos no son iguales, pero están muy vinculados:
● CalorCalorCalorCalorCalor es una forma de energía llamada energía térmica. Se debe al movimiento
vibratorio de las moléculas del cuerpo.
● TemperaturaTemperaturaTemperaturaTemperaturaTemperatura es una medida de la velocidad con que se mueven las partículas.
Si las moléculas se mueven más rápidamente, la temperatura es mayor. Para
medir la temperatura se usan los termómetros.

Medicióndelatemperatura
La temperatura se mide mediante termómetrostermómetrostermómetrostermómetrostermómetros. Estos instrumentos se basan
en la dilatación que sufren los líquidos al calentarse. Los líquidos utilizados pueden
ser mercurio o alcohol.
Cuando un termómetro se pone en contacto con
un cuerpo cuya temperatura se quiere medir, el
mercurio que hay dentro se dilata al calentarse y
asciende por el tubo. Luego de un tiempo, el
mercurio y el cuerpo llegan a tener la misma
temperatura. La altura que alcanza el mercurio
marca en una escala graduada el valor de la
temperatura.
Escalasdetemperatura
Las escalas de temperatura más usadas son tres y
difieren en los puntos fijos que toman de
referencia.
Escala Celsius o centígradaEscala Celsius o centígradaEscala Celsius o centígradaEscala Celsius o centígradaEscala Celsius o centígrada. Creada por el físico
sueco Andrés Celsius. En esta escala se asigna el
valor 0 °C a la temperatura del hielo y el valor
100 °C a la temperatura de ebullición del agua
(agua hirviendo).
Los valores inferiores a 0 °C se indican mediante
números negativos, por ejemplo –12 °C.
Escala FahrenheitEscala FahrenheitEscala FahrenheitEscala FahrenheitEscala Fahrenheit. En el siglo XVIII, el alemán
David Fahrenheit creó esta escala, que asigna el
valor 32 °F al punto de fusión del hielo y el valor
212 °F al de ebullición del agua.
Escala Kelvin o absolutaEscala Kelvin o absolutaEscala Kelvin o absolutaEscala Kelvin o absolutaEscala Kelvin o absoluta. El británico William Kelvin marcó el 0 K como la
temperatura más baja en que podría encontrarse un cuerpo, y se llama cero
absoluto. El punto más alto de la escala corresponde a la temperatura de ebullición
del agua y es de 373 K.
Investiga sobre
la temperatura normal
de un ser humano y de
algunos animales.
Mercurio
Bulbo
Escala
100
0
–273
212
32
–460
373
273
0
°C °F K

Conversiónentreescalas
Se ha podido establecer una ecuación de conversión (fórmula) entre las escalas, puesto
que las tres utilizan como referencia el punto de fusión y de ebullición del agua. La
relación existente entre las escalas termométricas permite expresar una misma temperatura
en diferentes formas, esto es, con resultados numéricos y con unidades de medida distintas.
La fórmula se deduce utilizando la razón y proporción de segmentos entre las escalas
termométricas de la siguiente manera:
Escala centígradaEscala centígradaEscala centígradaEscala centígradaEscala centígrada Escala FahrenheitEscala FahrenheitEscala FahrenheitEscala FahrenheitEscala Fahrenheit
°C – 0
°F – 32
=
100 – 0
212 – 32
°C – 0
100 – 0
=
°F – 32
212 – 32
Por lo tanto:
°C
100
=
°F – 32
180
Escala centígradaEscala centígradaEscala centígradaEscala centígradaEscala centígrada Escala KelvinEscala KelvinEscala KelvinEscala KelvinEscala Kelvin
°C – 0
K – 273
=
100 – 0
373 – 273
°C – 0
100 – 0
=
K – 273
373 – 273
Por lo tanto:
°C
100
=
K – 273
100
⇒ °C = K – 273
En resumen, la ecuación de conversión entre escalas es:
°C
100
=
°F – 32
180
=
K – 273
100
La escala centígrada se
usa en la mayoría de los países, la
Fahrenheit solo en países de habla inglesa
y la Kelvin es utilizada principalmente
por los científicos.
Los grados K se
escriben sólo con
una letra. El signo
de grado se omite.
100
°C
0
°C
212
°F
32
°F
100
°C
0
°C
373
K
273
K

Ejercicios de aplicación:Ejercicios de aplicación:Ejercicios de aplicación:Ejercicios de aplicación:Ejercicios de aplicación:
● En el noticiero dijeron que la temperatura en Miami (Estados Unidos) era de 95 °F. ¿Cuál
será la equivalencia de esta temperatura en la escala centígrada?
Solución:
1. Convierte de °F a °C utilizando la siguiente ecuación:
°C
100
=
°F – 32
180
2. Resuelve la ecuación despejando °C en el primer miembro:
°C =
100(°F – 32)
180
3. Reemplaza datos:
°C =
100(95 – 32)
180
= 35 °C
La temperatura de 95 °F equivale a 35 °C.
◆ Realiza las conversiones de escala y encierra con un círculo la temperatura mayor:
a) –10 °C o 263 K b) 350 K o 100 °C c) 32 °F o 5 °C
◆ Si una persona tiene 98 °F, ¿está sana o tiene fiebre?
◆ ¿Podría haber algún cuerpo a – 7 K? ¿Por qué?
◆ Completa la siguiente tabla utilizando las ecuaciones de conversión:
CentígradoCentígradoCentígradoCentígradoCentígrado FahrenheitFahrenheitFahrenheitFahrenheitFahrenheit KelvinKelvinKelvinKelvinKelvin
200 °C 40 °F
–5 °C
400 K
◆ Se tiene un termómetro de mercurio al cual se le ha borrado la numeración. ¿Cómo
podrías graduarlo de nuevo?
En el primer momento has analizado dos aspectos de la energía térmica: el calor y
la temperatura. Asimismo, has recordado las escalas de temperatura que más se
usan. En el segundo momento estudiarás las tres formas básicas de propagación
del calor.

SEGUNDOMOMENTO:Propagacióndelcalor
● Menciona otras situaciones en las que hayas observado
estas tres formas de transmisión del calor.
El calor es una forma de energía que está continuamente transfiriéndose (propagándose)
de unos cuerpos a otros. En esta historia se ven las tres formas de propagación del calor:
por conducción, por convección y por radiación. Aunque estos procesos suelen darse
simultáneamente, puede ocurrir que uno de ellos predomine sobre los otros dos.
Convección
Juan fue a la cocina, puso la
tetera en el fuego y calentó
agua para tomar un café…,
Conducción
…lo sirvió en una taza y al
tocarla comprobó que
estaba caliente.
Radiación
Corrió la cortina de la ventana
para que entrara el Sol y sintió
que los tibios rayos calentaban
el ambiente.
Dibujo referido al
texto
● ¿Qué chinche cayó primero? ¿Por qué?
● ¿Cuál crees que fue el mejor conductor del calor?
Experimenta: ¿Quién
conducemejorelcalor?
● Un recipiente resistente al calor, cera de vela, chinches,
agua caliente, cucharas de distintos materiales (metal,
madera, plástico)
1. Derrite cera y pega los chinches en los mangos de las
cucharas. Todos los chinches deben estar a la misma
altura como se indica en la figura.
2. Pon las cucharas dentro del recipiente y agrega agua
muy caliente hasta la mitad.

Calor por conducción
Esta forma de transmisión del calor se da principalmente en los sólidos y se produce
cuando los cuerpos están en contacto directoen contacto directoen contacto directoen contacto directoen contacto directo. Por ejemplo, cuando una cuchara
de metal está en contacto con un líquido caliente, el metal conduce el calor desde
un extremo de la cuchara hasta el otro.
Existen sustancias que son buenas conductoras de calor, como los metales, y
otras que son malas conductoras y se usan como aislantes, como la madera, el
tecknoport, la lana, el plástico, el corcho y el aire.
Observa algunos ejemplos:
● ¿Por qué la base de una sartén es de metal y el mango de plástico?
● Si pones fuentes de comida caliente en una mesa, ¿qué debes usar?
La ropa de lana es mala
conductora y evita que el
calor salga de nuestro
cuerpo.
Las ventanas con doble
vidrio dejan un espacio
de aire que impide que
el calor de la casa salga.
El aire es mal conductor
del calor.
Si hace frío, los pájaros
inflan sus plumas para
atrapar aire entre ellas y
no perder el calor de sus
cuerpos.
Calor por convección
Esta forma de transmisión del calor ocurre
sólo en líquidos y gases. El calor se distribuye
mediante el movimiento de corrientesmovimiento de corrientesmovimiento de corrientesmovimiento de corrientesmovimiento de corrientes
frías y calientesfrías y calientesfrías y calientesfrías y calientesfrías y calientes.
Este movimiento ocurre porque el líquido que
está cerca del calor se calienta primero, se
dilata y pesa menos. Entonces sube, y el de
arriba que está a una temperatura inferior,
desciende.

Es importante comprender y saber utilizar las corrientes de convección. Observa los ejemplos:
Calorporradiación
En la radiación, la transmisión del calor es a través
de ondas electromagnéticas llamadas rayosondas electromagnéticas llamadas rayosondas electromagnéticas llamadas rayosondas electromagnéticas llamadas rayosondas electromagnéticas llamadas rayos
infrarrojosinfrarrojosinfrarrojosinfrarrojosinfrarrojos. Todos los cuerpos calientes emiten
rayos infrarrojos que no son visibles al ojo
humano. Cuando estos rayos llegan a un cuerpo
lo calientan.
Los rayos infrarrojos pueden viajar incluso en el
espacio, ya que no requieren un medio material
para propagarse; de esta forma nos llega el calor
del Sol.
Asimismo, el calor de una fogata o de un foco
encendido se propaga por radiación y podemos
sentirlo sin tocar el foco, basta con acercar la mano.
Los rayos caloríficos pueden atravesar los cuerpos transparentes; por eso, los vidrios
de un carro o de una habitación dejan pasar el calor y éste calienta el interior.
Es mejor que las ventanas de un bus estén
abiertas en la parte alta. Así, el aire caliente
sale con facilidad.
◆ Prende un fósforo y coloca tu mano primero al costado y luego en la parte superior. ¿En
qué caso sientes más calor? Dibuja la experiencia y explícala.
◆ Explica: En una casa de dos pisos, ¿por qué es más caliente el piso superior?
En nuestro planeta las corrientes de
convección distribuyen el calor. El aire
caliente del ecuador asciende y se mueve
hacia los polos. El lugar es ocupado por aire
frío que llega desde los polos.
Frío
Caliente
Frío Caliente

En el segundo momento has reconocido la presencia de formas de propagación del
calor: conducción, convección y radiación en diversas situaciones de la vida diaria. En el
tercer momento identificarás que los materiales o sustancias tienen diferente capacidad
calórica y que cada sustancia tiene un calor específico característico.
● ¿En cuál de los vasos el hielo se derrite primero? ¿Por qué?
● ¿Por qué crees que las personas se visten con ropa oscura en invierno y
clara en verano?
Investiga cómo es un
termo. Presenta un
esquema.
◆ Indica cómo se propaga el calor en cada caso.
■ Tu cuerpo se calienta al sentarte frente a una chimenea.
■ Te quemas la mano al tocar una olla caliente.
■ Se enfría una habitación al abrir una ventana.
■ Tomamos sol echados en la playa.
■ Calientas agua fría echándole agua caliente.
◆ ¿Por qué cuando se estaciona un auto en épocas
de sol se cubren las lunas con cartón?
◆ Cuando cocinamos, movemos los alimentos con un
cucharón. ¿Cuál es el efecto deseado?
Experimenta:Loscuerposylaradiación
No todos los cuerpos se calientan de igual manera cuando reciben las ondas de calor. Los cuerpos
de color negro absorben casi toda la radiación y se calientan más, mientras que los de color
blanco reflejan la radiación y se calientan menos.
Para comprobarlo realiza la siguiente experiencia:
● Elige dos vasos iguales y coloca un cubito de hielo
en cada uno. Cubre uno de ellos con una tela negra
y, el otro, con una tela blanca. (La tela debe ser del
mismo material, por ejemplo, algodón).
● Ubica ambos vasos al sol. Espera 10 minutos y
observa lo que sucede en cada vaso.

El calor tiene la propiedad de pasar de un cuerpo a otro. Así, cuando dos cuerpos
que están a distinta temperatura se ponen en contacto, se produce una transferencia
de calor.
El cuerpo que tiene mayor temperatura
cede calor al que tiene menor temperatura.
Este proceso demora un cierto tiempo hasta
que ambos cuerpos estén a la misma
temperatura, es decir, hasta que alcancen
el equilibrio térmicoequilibrio térmicoequilibrio térmicoequilibrio térmicoequilibrio térmico.
Cuando decimos que un cuerpo está frío o
caliente, no estamos sintiendo su
temperatura sino la transferencia de calor
entre nuestra piel y el objeto. Cuanto mayor
sea la diferencia de temperatura entre la
piel y el objeto, más intensa será la
sensación de frío.
En una habitación cerrada, todos los objetos están a la misma temperaturatodos los objetos están a la misma temperaturatodos los objetos están a la misma temperaturatodos los objetos están a la misma temperaturatodos los objetos están a la misma temperatura
debido al equilibrio térmico. Sin embargo, algunos objetos como los metales nos
parecen más fríos. Esto se debe a que los metales son buenos conductores del
calor. Al tocarlos nuestra piel cede rápidamente su calor al metal de allí que nos
parezca frío. No ocurre lo mismo con otros materiales, como la madera o el plástico,
que son malos conductores.
TERCER MOMENTO: Cantidad de calor
● ¿Has enfriado o entibiado de esa forma un líquido caliente? ¿De qué otra
forma podrías enfriarlo?
● ¿Por qué crees que se enfría el líquido en la taza? ¿Y el agua del tazón se
habrá calentado? ¿Mucho o poco?
No me gusta tomar líquidos muy calientes.
Por eso, generalmente 10 minutos antes de tomar mi
desayuno pongo mi taza de lo que haya preparado
(quinua, café, leche, etc.) dentro de un tazón con agua fría
para que se vaya entibiando.
CALOR

Unidadesdelcalor
La cantidad de calor que trasmite o recibe un cuerpo se
expresa en dos unidades: la caloría y el joule.
● Una caloríaUna caloríaUna caloríaUna caloríaUna caloría es la cantidad de calor que se proporciona
a un gramo de agua para que aumente su temperatura
en 1 °C.
Como la caloría es una unidad muy pequeña con
frecuencia se usa la kilocaloría (kcal). Esta unidad se
utiliza sobre todo para referirnos a las calorías que
aportan los alimentos.
● El jouleEl jouleEl jouleEl jouleEl joule o julio (J) es la unidad de medida de trabajo y energía en el SI. El
calor es una forma de energía; por eso, también emplea esta unidad. El científico
inglés James Joule (1818-1889) demostró que 4,18 J de trabajo eran necesarios
para que un 1 g de agua eleve su temperatura en 1 °C. Por lo tanto:
1 cal = 4,18 J
Si la sumerge en agua demora 3 horas
La cantidad de calor que transfiere un cuerpo depende, entre otras cosas, de su capacidad
calórica.
A temperatura ambiente demora 8 horas
● ¿Cuál es el cuerpo que cede calor en cada uno de los casos? ¿Qué cuerpo
gana calor?
● ¿Por qué crees que, en agua, la carne se descongela más rápidamente
que cuando está al aire libre?
Analiza esta situación:
Elena quiere descongelar 1 kilo de carne y tiene dos ideas: colocarla a la temperatura
ambiente o en agua que también está a temperatura ambiente.

Capacidad calórica
Seguramente has observado que algunos materiales se calientan más rápido que
otros. Observa algunos ejemplos:
Los materiales tienen diferente capacidad calóricadiferente capacidad calóricadiferente capacidad calóricadiferente capacidad calóricadiferente capacidad calórica, es decir, con la misma
cantidad de calor unas sustancias elevan más su temperatura que otras.
● Una sustancia tiene gran capacidad calórica, si al recibir calor no eleva mucho
su temperatura. Por ejemplo, el agua.
● Una sustancia tiene poca capacidad calórica, si
al recibir calor aumenta rápidamente su
temperatura. Por ejemplo, los metales.
Cuando se mide la capacidad calórica por unidad de
masa se obtiene la capacidad calorífica específica o,
simplemente, el calor específico.
El calor específicoEl calor específicoEl calor específicoEl calor específicoEl calor específico es la cantidad de calor que debe
ganar una unidad de masa (1 g) de una sustancia
para subir su temperatura 1 °C.
Así, cuando decimos que el calor específico del
alcohol es de 0,58, quiere decir que se necesitan
0,58 calorías para que un gramo de alcohol suba su
temperatura 1 °C.
El calor específico es característico de cada sustancia.
En la tabla se dan los calores específicos de varias
sustancias comunes. Observa que se requiere diez
veces más calor para que 1 g de agua eleve su
temperatura en 1 °C que para elevar 1 °C la
temperatura de 1 g de hierro.
La arena aumenta más su
temperatura que el agua
de mar, por eso, se siente
más caliente.
Un techo de calamina se
calienta más que uno de
ladrillo.
El metal de un carro que
está bajo el sol se calienta
mucho. Pero el agua de un
balde que también estuvo
bajo el sol no se siente tan
caliente.
Calor específico (Calor específico (Calor específico (Calor específico (Calor específico (CeCeCeCeCe)))))
de varias sustanciasde varias sustanciasde varias sustanciasde varias sustanciasde varias sustancias
comunescomunescomunescomunescomunes
SustanciaSustanciaSustanciaSustanciaSustancia Ce (cal/gCe (cal/gCe (cal/gCe (cal/gCe (cal/g °C)C)C)C)C)
Aluminio 0,2
Cobre 0,09
Hierro 0,1
Acero 0,12
Tierra seca 0,4
Ladrillo 0,2
Madera 0,6
Aceite 0,4
Alcohol 0, 58
Agua 1

Cálculo de la cantidad de calor
La cantidad de calor que cede (transfiere) o recibe un material depende de su masamasamasamasamasa, del
calor específicocalor específicocalor específicocalor específicocalor específico y de la variación de temperaturavariación de temperaturavariación de temperaturavariación de temperaturavariación de temperatura entre los cuerpos puestos en contacto.
Por lo tanto, la fórmula para hallar la cantidad de calor está dada mediante la siguiente
ecuación:
Donde: Q = cantidad de calor
Q = m x Ce x ∆T Ce = calor específico
∆T = variación de la temperatura
En la Ficha de trabajo podrás encontrar más
información sobre el tema y algunos ejemplos de
aplicación.
◆ Analiza la relación de proporcionalidad entre las
magnitudes relacionadas en la fórmula y responde:
a) Si un cuerpo de determinada masa recibe una
cantidad Q de calor, ¿qué pasará con el valor
de la cantidad de calor si la masa aumenta?
Has estudiado que la cantidad de calor que transfiere una sustancia se puede medir
conociendo la masa, el calor específico y el cambio de temperatura que sufre esa sustancia.
Investiga
si los materiales de
construcción de tu casa son
los adecuados para
mantener una temperatura
cómoda en el interior.
Presenta un informe.
Conocer la capacidad
calórica o el calor específico de una
sustancia permite utilizar mejor los
materiales e interpretar lo que
sucede a tu alrededor.
El agua es la sustancia que
tiene el mayor calor
específico; por eso, tarda más
que otras en calentarse y en
enfriarse.
El cobre tiene bajo calor
específico; por eso, se calienta
más rápidamente que otros
metales. Debido a ello, los
peroles y ollas se hacen de
cobre.
La tierra tiene elevado calor
específico; por eso, en los
desiertos africanos se
construyen viviendas frescas
con estos materiales.

FICHADETRABAJO
Calculandolacantidaddecalor
Por ejemplo, si se tiene que el Ce del agua es 1 kcal/kg °C y el Ce del hierro es 0,1 kcal/
kg °C, se puede concluir que se requieren 10 veces más calor para que 1 kg de agua
eleve su temperatura en 1 °C que para elevar 1 °C la temperatura de 1 kg de hierro.
Se puede comprobar numéricamente esta conclusión aplicando la fórmula para calcular
la cantidad de calor.
1. Recuerda la fórmula para calcular la cantidad de calor recibido o entregado por un
cuerpo al calentarse o enfriarse:
Q = m x Ce x ∆T ……………………………… (1)
En esta fórmula:
● Q es el calor que recibirá o entregará un cuerpo o material. Se expresa en cal
(calorías) o en kcal (kilocalorías), depende de las unidades en que se haya
tomado el calor específico (Ce). Además, debes saber que, si Q es (+), el cuerpo
recibió calor (se calentó). Pero, si Q es (–), el cuerpo entregó calor (se enfrió).
● m es la masa del cuerpo. Se expresa en kg o en g
● ∆T es la diferencia de la temperatura final (Tf) menos la temperatura inicial (Ti),
o sea, T = Tf – Ti. Las temperaturas se expresan en °C.
● Ce es el calor específico del cuerpo o material. Sus unidades son:
Ce =
calorías
g °Ci
o Ce =
kcal
kg °Ci
Me parece interesante
identificar si un material cede
o recibe más calor conociendo
su calor específico (Ce).
Cada cuerpo, material o sustancia
tiene su propio calor específico. El calor específico
es una magnitud que expresa la resistencia que
opone un cuerpo a ser calentado o enfriado, es
decir, a cambiar de temperatura.

Reemplazando ∆T = Tf – Ti en la fórmula (1) se tiene:
Q = mCe (Tf – Ti) ................ (2)
2. Calcula qué cantidad de calor hay que entregar a una masa de 3 kg de agua y a una
masa de 3 kg de hierro para calentar estas sustancias de 20 a 100 °C. Luego,
compara los resultados.
● Para el agua, mis datos son:
Ce = 1
kcal
kg °C⋅
; m = 3 kg
Tf = 100 °C ; Ti = 20 °C
Reemplazando los datos en la fórmula (2):
Qagua = (3 kg) 1
kcal
kg °C⋅





 (100 °C – 20 °C)
⇒ Qagua = 240 kcal
● Para el hierro, mis datos son:
Ce = 0,1
kcal
kg °C⋅
; m = 3 kg
Tf = 100 °C ; Ti = 20 °C
Reemplazando los datos en la fórmula (2):
QFe = (3 kg) 0 1,
kcal
kg °Ci





 (100 °C – 20 °C) ⇒ QFe = 24 kcal
Efectivamente, se comprueba que la cantidad de calor que hay que entregar a una
masa de agua para que varíe una determinada temperatura es 10 veces mayor que
el calor que hay que entregar a la misma masa, pero de hierro, para variar la misma
temperatura.
◆ Resuelve:Resuelve:Resuelve:Resuelve:Resuelve:
a) ¿Qué cantidad de calor se requiere para que un kilogramo de hierro eleve su
temperatura de 15 °C a 40 °C?
b) ¿Qué cantidad de calor se requiere para que 400 g de cobre eleven su temperatura
de 15 °C a 40 °C?

El calorímetro
Es un recipiente aislado para evitar pérdidas de calor. Contiene agua cuya masa se ha
medido previamente y un termómetro sumergido que mide su temperatura. Es utilizado
para determinar el calor específico de una sustancia.
Se toma cierta masa de sustancia cuyo calor específico se busca y se calienta a una
temperatura determinada, por ejemplo, 200 °C. Cuando la masa está a esa temperatura,
se echa dentro del recipiente con agua y se agita para que la temperatura sea uniforme.
Se observa el termómetro y éste señala un aumento de temperatura que cada vez se
hace más lento, hasta que llega un momento en que se detiene. En ese momento la
mezcla alcanza el equilibrio térmico.
En una mezcla de sustancias de diferentes temperaturas, “el calor perdido por una o
unas es ganado por otra u otras”.
CALOR GANADO = CALOR PERDIDO
Un calorímetro contiene un litro de agua a 20 °C; se introduce en él 1 kg de limaduras
de hierro, cuya temperatura es de 200 °C. El termómetro indica una temperatura de
equilibrio de 37,8 °C. ¿Cuánto vale el calor específico del hierro?
CALOR PERDIDO POR EL HIERRO = CALOR GANADO POR EL HCALOR PERDIDO POR EL HIERRO = CALOR GANADO POR EL HCALOR PERDIDO POR EL HIERRO = CALOR GANADO POR EL HCALOR PERDIDO POR EL HIERRO = CALOR GANADO POR EL HCALOR PERDIDO POR EL HIERRO = CALOR GANADO POR EL H22222OOOOO
– (mFeCeFe∆TFe) = maguaCeagua∆Tagua
–mFeCeFe(Tfinal Fe – Tinicial Fe) = mH2OCeH2O(Tfinal H2O – Tinicial H2O)
Tfinal Fe = Tfinal H2O = Temperatura de equilibrio = 37,8 °C
1 000 g x CeFe x (200 – 37,8) = 1 000 g x 1
cal
g °Ci
x (37,8 – 20)
De donde se obtiene aproximadamente: CeFe = 0,11
cal
g °Ci
◆ Resuelve:Resuelve:Resuelve:Resuelve:Resuelve:
Se colocan 200 g de hierro a 120 °C en un recipiente que contiene 500 g de agua a 20
°C. Siendo el calor específico del hierro igual a 0,114 cal/g °C y considerando despreciable
el calor absorbido por el recipiente. ¿Cuál es la temperatura de equilibrio térmico?

FICHA INFORMATIVA
Efecto térmico de mares y lagos
Una sorprendente característica del agua es que
posee una capacidad calórica elevada; por eso,
puede absorber una gran cantidad de calor sin
aumentar mucho su temperatura. Asimismo,
cuando se enfría, libera mucho calor al ambiente.
Esta propiedad, unida al hecho de que hay mucha
agua en nuestra planeta (las 3/4 partes son mares
y océanos), hace que la Tierra tenga una
temperatura adecuada para la vida. En efecto,
en el día, los mares y océanos absorben la
radiación solar y, por la noche, al enfriarse, liberan
calor al ambiente. Si esto no fuera así, la Tierra
sería tan caliente como la superficie lunar que
llega a 130 ºC de temperatura en el día, pero en
la noche, baja hasta –170 ºC.
Por esta misma razón, los lugares situados cerca
de mares y lagos tienen mejor clima que los que
están lejos de estas masas de agua. En los
desiertos, en cambio, hace mucho calor en el día,
pero las noches son muy frías.
Otro ejemplo son las ciudades del altiplano. Puno,
que está a orillas al lago Titicaca, tiene mejor
clima que otras ciudades de la región. Así, en
Juliaca, que está casi a la misma altitud de la
ciudad de Puno, las temperaturas son más
extremas.
◆ ¿Por qué los desiertos son muy calientes en
el día y muy fríos en la noche?
◆ ¿A qué se debe que en Puno haga menos frío
que en Juliaca, estando ambas ciudades casi
a la misma altura?
Investiga sobre
otros lugares del Perú
donde se siente el efecto
térmico de mares o lagos.
Presenta la información en
un tríptico.
Mar
Lago
Titicaca

FICHA INFORMATIVA
Elcalorylosseresvivos
El calor y la temperatura son aspectos decisivos para el desarrollo y distribución de los
seres vivos. Se necesita el calor para que se produzcan reacciones químicas dentro de
las células y, en general, todas las funciones vitales.
Las avesavesavesavesaves y los mamíferosmamíferosmamíferosmamíferosmamíferos son animales de
temperatura alta y constante. También se les llama
animales de “sangre caliente”. Ellos tienen la
capacidad de mantener la temperatura interior de su
cuerpo por encima de los 36 °C y, aunque estén en
ambientes fríos, no ceden calor al ambiente. Por eso,
pueden vivir en climas muy fríos o muy calurosos.
Los reptilesreptilesreptilesreptilesreptiles y los anfibiosanfibiosanfibiosanfibiosanfibios tienen temperatura
variable, es decir, cambia según la temperatura
del medio que los rodea. Se les considera
animales de “sangre fría”. En general, estos
animales no pueden vivir en lugares donde las
temperaturas son extremadamente altas o
bajas.
Elcalorylaspersonas
Como mamíferos que somos, las personas
tenemos una temperatura alta y constante
y contamos con mecanismos para
mantenerla estable. Por ejemplo, si la
temperatura del cuerpo sube como
consecuencia del ejercicio, la fiebre o el
ambiente producimos sudor. El sudor enfría
el cuerpo.
En efecto, para evaporarse, el sudor toma el calor del cuerpo; en consecuencia, la
temperatura baja. Como el sudor es principalmente agua y ésta tiene una gran capacidad
calórica, para evaporarse necesita tomar mucho calor.
Por extraño que parezca, el sudor no huele. Las culpables de ese desagradable
olor que acompaña el sudor son las incontables bacterias. La flora bacteriana de
nuestra piel se alimenta de nuestro sudor, y es precisamente en este proceso
cuando el olor surge.

111
EEEEEfectos del calorfectos del calorfectos del calorfectos del calorfectos del calor
1. Cambios de estado
2. Midiendo los efectos del calor
3. Dilatación
Comprender los fenómenos físicos de
cambio de estado y dilatación como efectos
de la acción del calor sobre la materia.
Aplicar fórmulas para calcular la cantidad
de calor necesaria para lograr el cambio
de estado de diferentes cuerpos.
● En el primer momento recordarás los
cambios de estado de la materia y
reconocerás este fenómeno como uno
de los efectos del calor.
● En el segundo momento aprenderás
que la cantidad de calor necesaria para
el cambio de estado y la dilatación de
los cuerpos se puede medir y realizarás
ejercicios prácticos de aplicación.
● En el tercer momento estudiarás la
dilatación, que es otro efecto del calor
sobre los cuerpos, y la forma de utilizar
o prevenir sus efectos.
● Dilatación de los sólidos ● Materia
● Punto de fusión
● Punto de ebullición
● Dilatación
● Calor latente
● Cálculos aritméticos y algebraicos
● Estados de la materia: sólido, líquido
y gaseoso
● Descripción del proceso de cambio de
un estado a otro
● Temperatura de fusión y ebullición
● Fenómeno de dilatación

PRIMERMOMENTO:Cambiosdeestado
Acabo de
comprar mi helado,
pero con el calor
que hace se está
derritiendo.
Sí, es un
hecho conocido
que algunas sustancias
cambian de estado al
calentarse.
Estadosdelamateria
Para comprender los cambios de estado debes recordar los estados de la materia.
¿Cómo ocurren los cambios de estado?¿Cómo ocurren los cambios de estado?¿Cómo ocurren los cambios de estado?¿Cómo ocurren los cambios de estado?¿Cómo ocurren los cambios de estado?
Cuando un sólido se calienta, las moléculas que lo forman empiezan a vibrar con
mayor rapidez hasta que adquieren la suficiente energía para separase unas de
otras; de esta manera, el sólido se convierte en líquido. Luego, al aumentar la
temperatura, las partículas del líquido adquieren más movilidad, se separan y se
transforman en vapor.
En el estado sólidoestado sólidoestado sólidoestado sólidoestado sólido los
átomos o las moléculas
están juntos, lo que les
impide moverse de un
lugar a otro. Por eso, los
sólidos tienen una forma
definida.
En el estado líquidoestado líquidoestado líquidoestado líquidoestado líquido
las moléculas están algo
separadas y pueden
moverse unas sobre
otras. Esto permite a los
líquidos fluir libremente.
En el estado gaseosoestado gaseosoestado gaseosoestado gaseosoestado gaseoso
las moléculas están más
separadas y se mueven
con facilidad en cualquier
dirección. Por esta razón
los gases pueden ocupar
el mayor espacio posible.
CALOR
Sólido Líquido Gaseoso

Los conocimientos sobre los cambios de
estado han conducido a mejorar los procesos
industriales, como la producción de helados, el
trabajo con metales, el transporte de gases y la
fabricación de máquinas como la refrigeradora.
◆ Escribe el cambio de estado que se produce en las siguientes situaciones:
a) Se preparan helados ____________________________________________________
b) Se derrite un helado ___________________________________________________
c) Se evapora el hielo seco ________________________________________________
d) Se derrite oro para moldearlo y hacer joyas_________________________________
e) Se licúa oxígeno para transportarlo en balones______________________________
f) Se tiende la ropa para que se seque_______________________________________
g) Se hierve leche en una cacerola __________________________________________
Solidificación
Cambiosdeestado
Los cambios de estado posibles son:
● FusiónFusiónFusiónFusiónFusión. Es el paso del estado sólido al líquido.
● Evaporación.Evaporación.Evaporación.Evaporación.Evaporación. Es el paso del estado líquido al estado gaseoso. Si la transformación
es rápida y a una temperatura determinada, se llama ebullición; por ejemplo,
cuando hierve el agua.
● Condensación.Condensación.Condensación.Condensación.Condensación. Es el paso del estado gaseoso al líquido. Por ejemplo, el
vapor de agua se condensa en gotitas de agua en el vidrio frío de una ventana.
● Si un gas se hace líquido, el cambio se llama licuaciónlicuaciónlicuaciónlicuaciónlicuación. Así, el gas natural que
sale de los pozos petroleros se licúa para poder ser transportado por los oleoductos.
● La solidificaciónLa solidificaciónLa solidificaciónLa solidificaciónLa solidificación. Es el paso del estado líquido al sólido.
● SublimaciónSublimaciónSublimaciónSublimaciónSublimación. Es el paso del estado sólido a vapor sin pasar por el estado
líquido. Esto ocurre en las bolitas de naftalina.
Sólido
Líquido
Gaseoso
FUSIÓN EVAPORACIÓN
SOLIDIFICACIÓN CONDENSACIÓN

Punto de fusión y ebullición
Si calentamos una barra de hierro y una de aluminio
se funde primero la del aluminio. Esto es así, porque
cada sustancia requiere diferente cantidad de calor
para cambiar de estado.
La temperatura a la que se produce la fusión se llama
punto de fusiónpunto de fusiónpunto de fusiónpunto de fusiónpunto de fusión. Por ejemplo, el punto de fusión
del hielo es 0 °C, el del hierro 1 525 °C y el de
aluminio 660 °C
La temperatura a la cual se produce la ebullición de
una sustancia se llama punto de ebulliciónpunto de ebulliciónpunto de ebulliciónpunto de ebulliciónpunto de ebullición. El
punto de ebullición del agua es de 100 °C , el del
alcohol 78 °C y el del hierro 2 740 °C
Conocer el punto de ebullición o de fusión de los materiales es de gran utilidad.
Por ejemplo:
● El tungstenotungstenotungstenotungstenotungsteno es el elemento que tiene el punto
de fusión más elevado de la naturaleza: 3 422 °C.
Por eso, este metal se emplea en los filamentos
de los focos de luz. Puede calentarse mucho hasta
emitir luz sin fundirse.
● Es necesario conocer los puntos de ebullición para todos los procesos deprocesos deprocesos deprocesos deprocesos de
destilacióndestilacióndestilacióndestilacióndestilación como, en la destilación del petróleo y en el de la caña de azúcar
para obtener alcohol.
● ¿Qué quiere decir que el punto de
fusión del oro es de 1 063 °C?
● ¿Qué hierve primero, el alcohol o el
agua? ¿Por qué?
● ¿Por qué es útil conocer el punto de
fusión de las sustancias?
Fundamenta tu respuesta.
Investiga cómo
funciona una
refrigeradora y presenta
la información en un
afiche.
En el primer momento has recordado los estados de la materia y los cambios de estado
reconociéndolos como consecuencia de la aplicación de una energía como es el calor.
También, que cada sustancia tiene un punto de fusión y ebullición. En el siguiente momento
aprenderás a calcular el calor necesario para un cambio de estado.
Tungsteno

SEGUNDOMOMENTO:Midiendo
los efectos del calor
● Una olla o un vaso metálico, hielo, un mechero.
1. Pon a calentar unos cubos de hielo en una olla pequeña.
2. Espera que se derritan un poco y mientras haya hielo en el recipiente, toca la base de la
olla.
Observarás que la base no se ha calentado sino que permanece helada. Esto se debe a
que, mientras dura el cambio de estado, la temperatura no sube. La energía calorífica
suministrada ha servido para separar las moléculas.
En la actividad 2 aprendiste que, para que un cuerpo aumente o disminuya de temperatura,
tiene que recibir o ceder calor respectivamente. Esta cantidad de calor recibida o cedida
por un cuerpo sin que suceda el cambio de estado se calcula mediante la ecuación
fundamental de la calorimetría (medición del calor):
Q = m x Ce x ∆T
A veces, la sustancia recibe energía (calor) y no incrementa su temperatura. Esto sucede
en los cambios de estado.
La fórmula para calcular la cantidad de calor que necesita una masa dada de una sustancia
para cambiar de estado es:
Q = calor total de transformación
Q = m x L m = masa dada de sustancia a transformar
L = calor latente o calor específico de cambio de estado
El calor latentecalor latentecalor latentecalor latentecalor latente es característico de cada sustancia. Es aquella cantidad de calor necesario
para que se produzca el cambio de estado físico de la unidad de masa de una sustancia.
Según el cambio de estado, se presenta como calor latente de fusión (Lf), de vaporización
(Lv), etc.
Experimenta….

Ejemplo:Ejemplo:Ejemplo:Ejemplo:Ejemplo:
Calor latente de fusión del hielo Lf hielo = 80 kcal/kg significa que, para derretir 1 kilogramo
de hielo, hay que entregar 80 kilocalorías. Este valor es el mismo para el proceso inverso,
pero la interpretación es distinta; es decir: para congelar 1 kilogramo de agua hay que
quitarle 80 kilocalorías.
1) ¿Qué cantidad de calor se necesita para fundir 2 000 gramos de cobre que están a la
temperatura de fusión?
Calor de fusión del cobre: 41 cal/g
Cuando el cobre está a su temperatura de fusión, comienza a ser líquido sin variar dicha
temperatura.
Se sabe que: Q = m x L
Los datos son: m = 2 000 g
L = 41
cal
g
Reemplazando datos: Q = 2 000 g x 41
cal
g
Q = 82 000 cal
2) ¿Qué cantidad de calor es necesaria para transformar en vapor (100 °C) 2 litros de agua
que están a 20 °C?
Si analizas este problema, verás que, para
calcular la cantidad de calor necesaria para
transformar en vapor 2 litros de agua, se
requiere que calcules la cantidad de calor
(Q1
) para elevar la temperatura del agua de
20 a 100 °C. A esta temperatura se calculará
el calor necesario (Q2
) para que se dé la
transformación total de la masa de agua.
Calcular el calor Q1:
Q1 = m Ce ∆T ; en este caso, m = 2 000 gramos porque son 2 litros de agua.
Q1 = 2 000 g x 1
cal
g°C
x (100 °C – 20 °C)
Q1 = 160 000 calorías
20 °C
Q1
Q2
100 °C 100 °C

Una vez que llega el agua a su temperatura de ebullición (100 °C) sin variar esta
temperatura, para pasar al estado gaseoso absorberá una cantidad de calor Q2:
Q2 = m x L en donde: L = 540
cal
g
Q2 = 2 000 g x 540
cal
g
Q2 = 1 080 000 calorías
Finalmente, vemos que la cantidad de calor empleada será:
Q = Q1 + Q2
Q = 160 000 cal + 1 080 000 cal
Q = 1 240 000 calorías
◆ Se desea calentar 50 kg de vapor de agua desde los 100 °C hasta 180 °C. ¿Qué cantidad
de calor deberá suministrarse, sabiendo que el calor específico del vapor de agua es de
0,5 kcal/kg °C?
◆ Calcula la cantidad de calor que hay que entregar a un cubito de hielo de 50 gramos que
está a –30 °C para derretirlo y obtener agua a 0 °C.
◆ ¿Qué cantidad de calor se requiere para que 1 kilogramo de hierro eleve su temperatura
de 15 °C a 40 °C?
Investiga sobre
otros materiales o
sustancias en las que se
aprecie los efectos del
calor y elabora tarjetas
con información.
El calor latente de los cuerpos es una cantidad característica de cada sustancia y nos
permite calcular la cantidad de calor necesario para lograr un cambio de estado. En el
tercer momento estudiarás otro efecto del calor sobre los cuerpos, la dilatación.
El calor al actuar sobre los
cuerpos produce 3 efectos: eleva
su temperatura, los dilata y los
cambia de estado físico

TERCER MOMENTO: Dilatación
A.A.A.A.A. Dilatación de los sólidosDilatación de los sólidosDilatación de los sólidosDilatación de los sólidosDilatación de los sólidos
Apoya una barra metálica (puedes usar un
palillo de tejer) sobre dos ladrillos, uno de los
cuales debe estar apoyado contra la pared.
Coloca sobre el borde del otro ladrillo un vasito
descartable.
Coloca el mechero debajo de la barra metálica
y enciéndelo.
B.B.B.B.B. Dilatación de los líquidosDilatación de los líquidosDilatación de los líquidosDilatación de los líquidosDilatación de los líquidos
Llena una botella con agua colorada y tápala.
Haz un agujero en la tapa para que pueda
pasar una cañita. Introduce la cañita y sella
con plastilina.
Introduce la botella en un tazón con agua bien
caliente y observa el agua dentro del sorbete.
Verás que el agua se dilata, es decir, aumenta
su volumen y sube por el sorbete.
Saca la botella y sumérgela en un tazón con
hielo. Observa y explica lo que sucede.
C.C.C.C.C. Dilatación de los gasesDilatación de los gasesDilatación de los gasesDilatación de los gasesDilatación de los gases
Llena una botella con agua hasta la mitad y
coloca un globo como tapa.
Introduce la botella en un recipiente con agua
y caliéntala como indica la figura.
Todos los cuerpos, ya sean sólidos, líquidos o
gaseosos, aumentan de volumen cuando se los
calienta. Este fenómeno se llama dilatación. Para
comprobarlo realiza las siguientes experiencias.

En los pisos de cemento,
veredas, losetas, etc., se
dejan pequeñas
separaciones que permiten
su dilatación; así, los pisos
no se rompen.
Entre los rieles de las vías
férreas se deja un pequeño
espacio para evitar que el
aumento de temperatura
los deforme.
◆ Explica los siguientes hechos:
a) Cuando la tapa metálica de un frasco está muy ajustada, se sumerge la tapa en agua
caliente. Al hacer esto, se desenrosca con facilidad.
b) ¿Por qué con frecuencia se derrama la leche cuando hierve?
◆ Escribe otros ejemplos de tu experiencia donde hayas observado la dilatación de los
materiales.
Elvidriotemplado
No todos los materiales se dilatan por igual.
Algunos tienen una dilatación notoria y otros
apenas se dilatan. Por ejemplo, el vidrio
templado puede soportar temperaturas altas –
sobre los 800 °C– sin romperse.
● Nombra objetos de tu entorno que son de vidrio templado.
● ¿Qué ventajas tiene el vidrio templado frente al vidrio común?
Efectosdeladilatación
El fenómeno de la dilatación tiene diversas consecuencias en nuestra vida cotidiana.
A veces plantea problemas de difícil solución y, en otros casos es utilizada en
forma provechosa. Por ejemplo:
La formación de grietas en
techo y azoteas es causada,
con frecuencia, por la
dilatación de los materiales
que los forman. Al crecer y
no tener donde expandirse,
revientan.

Dilataciónanormaldelagua
◆ Coloca un trozo de hielo en un vaso con agua y explica por qué flota en lugar de hundirse.
Haz dibujos para que la explicación sea clara.
◆ Debajo de la capa de hielo que hay en los polos hay abundantes peces, focas, crustáceos
y otros seres acuáticos. ¿Por qué no se congela toda el agua?
En el tercer momento has reconocido cómo, por efecto del calor, los cuerpos en cualquiera
de sus tres estados sufren cambios en su volumen y que este efecto recibe el nombre de
dilatación.
Agua
líquida
Hielo
Otro
líquido
Sólido
El agua se dilata al congelarse
porque sus moléculas forman una
estructura que deja espacios
vacíos. Por eso el hielo es menos
denso (más liviano) que el agua
líquida y, en consecuencia, flota.
El hecho que el hielo flote en el
agua en lugar de hundirse tiene
gran importancia en los
ecosistemas acuáticos. El hielo
funciona como un aislante térmico
que impide que se congele el agua
que está debajo de él. Si esto no
sucediese así, los mares y océanos
de las zonas frías se congelarían
desde el fondo hasta la superficie,
y eso acabaría con la vida en esos
lugares.
Todos los cuerpos se dilatan al calentarse y,
al enfriarse, se contraen. Se podría esperar
entonces que el agua líquida, al hacerse hielo,
redujera su volumen. Sin embargo, no es así.
El agua es la única sustancia en la naturaleza
que cuando se hace sólida en lugar de
contraerse se dilata. Esto lo sabemos por
experiencia, pues, si colocamos una botella
con agua o con cualquier otro líquido en el
congelador, cuando se hace hielo; se expande
(dilata) y rompe la botella.

FICHA INFORMATIVA
Dilatacióndelossólidos
La experiencia muestra que los sólidos se dilatan cuando se calientan y se contraen
cuando se enfrían. La dilatación y contracción ocurren en tres dimensiones: largo,
ancho y alto.
A la variación en las dimensiones de un sólido causada por calentamiento o enfriamiento
se le denomina dilatación térmica.
Dilatación linealDilatación linealDilatación linealDilatación linealDilatación lineal
Es aquella en la que predomina la variación en una dimensión de un cuerpo, el largo.
Ejemplo: dilatación en hilos, cabos y barras.
Dilatación superficialDilatación superficialDilatación superficialDilatación superficialDilatación superficial
Es aquella en la que predomina la variación en dos dimensiones de un cuerpo, el largo
y el ancho.
Dilatación volumétricaDilatación volumétricaDilatación volumétricaDilatación volumétricaDilatación volumétrica
Predomina la variación en tres dimensiones de un cuerpo, el largo, el ancho y el alto.
L0
L
∆L
S0
S
V0
∆V
V
∆S

123
● Analizar los fenómenos magnéticos y eléctricos para
explicar situaciones cotidianas.
Conocer la expresión matemática del enunciado
de la ley de Coulomb.
● Conocer cómo se produce y conduce la corriente
eléctrica e identificar las magnitudes relacionadas
con ella, calculando el consumo de energía de los
aparatos eléctricos.
Resolver problemas de matemática recreativa.
● Comprender el fenómeno del electromagnetismo
y sus aplicaciones tecnológicas.
Representar gráficamente un punto del espacio en
un sistema de coordenadas cartesianas en tres
dimensiones (3D).
ELECTRICIDAD, MAGNETISMO Y ELECTROMAGNETISMOELECTRICIDAD, MAGNETISMO Y ELECTROMAGNETISMOELECTRICIDAD, MAGNETISMO Y ELECTROMAGNETISMOELECTRICIDAD, MAGNETISMO Y ELECTROMAGNETISMOELECTRICIDAD, MAGNETISMO Y ELECTROMAGNETISMO
Reconocer la importancia de los conocimientos científicos relacionados con la electricidad y
el magnetismo para explicar situaciones de la vida cotidiana y el funcionamiento de diversos
aparatos eléctricos que se usan habitualmente.
Analizar situaciones de lógica recreativa y estudiar los sistemas de coordenadas cartesianas
bidimensional y tridimensional.
1.1.1.1.1. Los imanes y laLos imanes y laLos imanes y laLos imanes y laLos imanes y la
electricidad estáticaelectricidad estáticaelectricidad estáticaelectricidad estáticaelectricidad estática
2.2.2.2.2. La electricidad enLa electricidad enLa electricidad enLa electricidad enLa electricidad en
movimientomovimientomovimientomovimientomovimiento
3.3.3.3.3. Relación entre imanes yRelación entre imanes yRelación entre imanes yRelación entre imanes yRelación entre imanes y
corriente eléctricacorriente eléctricacorriente eléctricacorriente eléctricacorriente eléctrica
● Observar, investigar y describir los fenómenos eléctricos y electromagnéticos aplicados
a la vida diaria.
● Identificar los elementos de un circuito eléctrico y algunas magnitudes relacionadas
con la corriente eléctrica.
● Asumir una actitud crítica sobre la contaminación por efecto de las pilas y valorar el
ahorro de energía.
● Describir y explicar las propiedades de los imanes y el fundamento de la brújula.
● Realizar experimentos relacionados con la electricidad.
● Representar un punto del espacio en un sistema de coordenadas cartesianas en tres
dimensiones.

125
LLLLLos imanes y la electricidad estáticaos imanes y la electricidad estáticaos imanes y la electricidad estáticaos imanes y la electricidad estáticaos imanes y la electricidad estática
1. El magnetismo
2. Electricidad estática
3. Expresión matemática de la Ley de
Coulomb
Analizar los fenómenos magnéticos y
eléctricos para explicar situaciones
cotidianas.
Conocer la expresión matemática del
enunciado de la ley de Coulomb.
● En el primer momento reconocerás las
propiedades de los imanes y analizarás
el funcionamiento de la brújula.
● En el segundo momento comprenderás
cómo se electrizan los cuerpos y cómo
se producen los rayos.
● En el tercer momento analizarás la
expresión matemática de la Ley de
Coulomb, que permite calcular la
fuerza de atracción o repulsión entre
dos cargas eléctricas.
● Variedad de imanes ● Imán
● Brújula
● Polos magnéticos
● Polos geográficos
● Electricidad estática
● Energía química
● Relación de proporcionalidad entre
diversas magnitudes
Magnetismo:
● Los imanes y sus características
● Campo magnético
● Magnetismo terrestre y brújula
Electricidad estática:
● Electrización de los cuerpos
● Formas de electrización
Ley de Coulomb
● Recordando la notación científica

126 Electricidad,magnetismoyelectromagnetismo
PRIMERMOMENTO:Elmagnetismo
● ¿Qué objetos atrae el imán?
● ¿Qué objetos no atrae el imán?
● Si enfrentas dos imanes, ¿cuándo se atraen y cuándo se rechazan?
Necesitas: pequeños objetos de diferentes materiales (clips, alfileres, monedas, cucharitas
de metal, objetos de plástico, llaves, clavos, limaduras de hierro, etc.) y dos imanes de
barra.
Losimanesyelmagnetismo
La propiedad que tienen los imanes de atraer sólo ciertos materiales no te es
desconocida. En efecto, los imanes tienen la propiedad de atraer objetos de hierrohierrohierrohierrohierro,
níquelníquelníquelníquelníquel y cobaltocobaltocobaltocobaltocobalto. Esta propiedad se llama magnetismomagnetismomagnetismomagnetismomagnetismo.
Experimenta…¿Cómose
comportanlosimanes?
1. Coloca los objetos sobre
una mesa y acerca el
imán a ellos. Agrupa los
objetos según sean
atraídos o no.
2. Acerca el imán a un clip
y, atrae otros clips. ¿Qué
explicación puedes dar
a este hecho?
3. Enfrenta los imanes por
sus polos y observa
cuándo se atraen y
cuando se rechazan.
S N N S
S N S N

127Electricidad,magnetismoyelectromagnetismo
El fenómeno del magnetismo fue conocido hace
miles de años por griegos, romanos y chinos,
pues existe en la naturaleza un mineral llamado
magnetitamagnetitamagnetitamagnetitamagnetita o piedra imán.
La gente de la antigüedad se percató de que la
magnetita tenía la propiedad de atraer objetos
de hierro y, como esta piedra era abundante
en la ciudad de Magnesia (Grecia), el fenómeno
recibió el nombre de magnetismo.
Posteriormente se descubrió que los imanes
podían no sólo atraer al hierro sino también al
níquel y al cobalto.
En la actualidad hay imanes naturalesimanes naturalesimanes naturalesimanes naturalesimanes naturales e
imanes artificialesimanes artificialesimanes artificialesimanes artificialesimanes artificiales. Estos últimos han sido
fabricados a partir de compuestos de hierro,
níquel y cobalto entre otros.
La magnetita tiene la
apariencia de una piedra
negra y químicamente es
un óxido de fierro (Fe3
O4
),
comúnmente llamado
ferrita.
◆ Define: imán – magnetismo
◆ ¿Por qué los adornos de cocina imantados se adhieran a la superficie metálica de la
refrigeradora? ¿Pueden adherirse a una puerta de madera?
◆ Elabora una lista con objetos que poseen imanes y explica qué función cumplen.
Te preguntarás… ¿Por qué ciertos materiales tienen propiedades magnéticas¿Por qué ciertos materiales tienen propiedades magnéticas¿Por qué ciertos materiales tienen propiedades magnéticas¿Por qué ciertos materiales tienen propiedades magnéticas¿Por qué ciertos materiales tienen propiedades magnéticas?
Todos los átomos de la materia están formados por electrones que se mueven
continuamente. El movimiento de los electrones hace que éstos se comporten como
microscópicos imanes.
Característicasdelosimanes
● Atraen objetos de hierro, acero, níquel y cobalto.
● Tienen dos extremos en los que la fuerza magnética es mayor: el polo norte y
el polo sur.
● Los polos iguales se repelen, mientras
que los polos diferentes se atraen.
● Si un imán se rompe, cada trozo vuelve
a ser otro imán. Es imposible que un
imán tenga un solo polo.
S N S N
Atracción

Normalmente, estos pequeños “imanes
atómicos” están orientados al azar en todas
direcciones; sin embargo, en los materiales
magnéticos, los “imanes atómicos” se alinean
en una misma dirección de tal forma que sus
efectos se suman.
Ahora te podrás explicar cómo un clip atraído por
un imán atrae otros clips. El clip está hecho de
hierro y tiene sus “imanes atómicos” en todas
direcciones; al ponerse en contacto con un imán,
éstos se orientan y todo el clip se transforma
también en un imán aunque el efecto sea pasajero.
El plástico, la madera y muchos otros materiales no son atraídos por un imán. La razón es
que no pueden orientar sus electrones cuando se les acerca un imán.
◆ Relaciona las dos columnas. Escribe la letra correspondiente:
( ) Zona donde la fuerza del imán es mayor. a) Electrones
( ) Zona donde el imán ejerce atracción. b) Norte-Sur
( ) Representan el campo magnético. c) Líneas de fuerza
( ) Polos que se atraen. d) Campo magnético
( ) Originan microscópicos campos magnéticos. e) Polos
◆ Consigue un imán en forma circular. Observa su campo magnético y dibújalo.
Elcampomagnético
Si espolvoreas limaduras de hierro sobre un
papel y colocas un imán en forma de barra
debajo de él, observarás que las limaduras de
hierro se concentran en los polos y que,
además, se distribuyen formando líneas que
van de un polo a otro. Esta sencilla experiencia
nos permite visualizar el campo magnético.
El campo magnético de un imán es la zona o espacio en que se manifiestanzona o espacio en que se manifiestanzona o espacio en que se manifiestanzona o espacio en que se manifiestanzona o espacio en que se manifiestan
las fuerzas magnéticaslas fuerzas magnéticaslas fuerzas magnéticaslas fuerzas magnéticaslas fuerzas magnéticas.
El campo magnético se representa mediante
líneas de fuerza imaginarias. Las líneas se
dirigen del polo norte al polo sur del imán.
En la experiencia descrita las líneas de fuerza
coinciden con la distribución que adoptan las
limaduras de hierro.
Normal
Imantado
N S

Has identificado las fuerzas magnéticas que se manifiestan en los imanes. En el segundo
momento analizarás las fuerzas eléctricas.
● Un recipiente con agua, un imán pequeño en forma de
barra, un círculo de tecknoport.
1. Coloca el imán sobre el tecknoport y pon el conjunto en
el agua.
2. Observa el comportamiento del imán. Este girará hasta
que su polo norte apunte hacia el polo Norte geográfico.
El magnetismo terrestre y la brújula
La brújula es un imán en forma de aguja que puede
girar libremente sobre un eje. Desde la antigüedad
los marineros la usaban para orientarse porque
siempre señalaba la dirección Norte-Sur, aunque
nadie sabía porqué sucedía esto.
En el siglo XVII los científicos descubrieron que
la Tierra se comportaba como un inmenso imán
en forma de barra.
En la Tierra se pueden distinguir dos polos
magnéticos que están muy cerca de los polos
geográficos, pero en sentido inverso: el polo sur
magnético se halla cerca del polo Norte geográfico
y el polo norte magnético se halla cercano al polo
Sur geográfico.
La brújula siempre indicará el Norte geográfico porque su polo norte es atraído por el
polo sur magnético de la Tierra. En realidad cualquier imán siempre se colocará en
posición Norte-Sur de la Tierra.
Experimenta….
construye una brújula
Polo
sur
magnético
Polo
norte
magnético
S
N
Polo
Sur
geográfico
Polo
Norte
geográfico
Brújula

SEGUNDOMOMENTO:Electricidad
estática
Seguro que puedes reconocer algunos fenómenos eléctricos por tu
experiencia diaria. De las siguientes situaciones, marca con X los que
creas que se deben a la electricidad.
● El giro de la Luna alrededor de la Tierra. ( )
● El funcionamiento de una licuadora. ( )
● La llama que se desprende de un objeto cuando arde. ( )
● Las chispas que se producen cuando te quitas la ropa en un día seco. ( )
● La explosión de un cohete. ( )
● Los rayos que se producen durante una tormenta. ( )
● Los huracanes que se producen durante las tormentas. ( )
● La atracción que un lapicero frotado ejerce sobre pedacitos de papel. ( )
● La atracción que ejercen los imanes. ( )
La electricidad siempre ha existido, es parte de la naturaleza que nos rodea, el hombre
sólo la ha descubierto.
En el siglo VII a. C. el filósofo griego Tales de MiletoTales de MiletoTales de MiletoTales de MiletoTales de Mileto descubrió que al frotar un trozo
de ámbar (resina) con un paño, éste atraía pequeñas partículas como hojas secas y
plumas. Al fenómeno lo llamo “ámbar” que en griego se escribe “elektrón” y de allí
deriva la palabra electricidad.
A pesar de este primer descubrimiento, ni griegos, ni romanos, ni los personajes de la
Edad Media contribuyeron de manera significativa a la comprensión de la electricidad.
En 1792, Benjamín FranklinBenjamín FranklinBenjamín FranklinBenjamín FranklinBenjamín Franklin demostró que los rayos eran una descarga eléctrica e
inventó el pararrayos. Esto sirvió para renovar el interés por la electricidad.
En 1800, Alejandro VoltaAlejandro VoltaAlejandro VoltaAlejandro VoltaAlejandro Volta descubrió la forma de producir electricidad. Así nació la
primera pila eléctrica. Pocos años después, gracias a los estudios de Oersted y el
ingenio de Faraday se encontró la manera de producir electricidad a gran escala con el
invento de generadores eléctricos.
En 1879, Thomas Alva EdisonThomas Alva EdisonThomas Alva EdisonThomas Alva EdisonThomas Alva Edison, inventó los focos eléctricos, lo cual hizo posible el
alumbrado con energía eléctrica.
Hacia 1890, muchas fábricas de Europa y América usaban motores impulsados por
energía eléctrica y se empezaron a construir los aparatos “electrodomésticos”.

Electrizacióndeloscuerpos
Si frotas una regla o lapicero de plástico, ellos
adquieren la propiedad de atraer cuerpos ligeros como
pedazos de papel. Los cuerpos con esta propiedad se
dice que están electrizados.
Para explicar por qué se electrizan los cuerpos debes
recordar la estructura de la materia.
Como sabes, la materia está formada por átomos que
tienen protones (partículas con carga positiva: +) y
electrones (partículas con carga negativa: –). Es decir,
la materia tiene partículas con carga eléctrica.
Habitualmente los cuerpos no están electrizados porque sus átomos tienen igual número
de protones que de electrones. En este caso decimos que la materia es neutra. Pero si se
frotan dos cuerpos entre sí, algunos electrones pasan de un cuerpo a otro. El cuerpo que
gana electrones se carga negativamente y el que pierde se carga positivamente.
En general, todos los
cuerpos pueden electrizarse ganando o
perdiendo electrones. Haz la prueba
con vidrio, plástico, lana, seda,
cuero o un globo.
Si apoyas una tira de plástico sobre una mesa y
la frotas varias veces con un trapo, al levantarla
con una regla, observarás que las dos partes de
la tira se separan. Esto te demuestra que cargas
de igual signo se rechazan.
Los cuerpos con cargas del mismo signo se repelen y con cargas de distinto signo se
atraen.

◆ Escribe V o F, según sea verdadero o falso. Luego, corrige las expresiones falsas.
( ) En un átomo neutro, el número de protones es igual al número de electrones.
( ) Los cuerpos se electrizan cuando ganan o pierden electrones.
( ) Un cuerpo se carga de electricidad positiva cuando gana protones.
( ) Dos cuerpos con carga positiva se rechazan.
( ) Dos cuerpos cargados con cargas diferentes se atraen.
◆ Frota con tu cabello dos globos inflados. Acércalos uno al otro y explica lo que sucede.
Grafica tu experiencia.
● Un lapicero de plástico, un trocito de papel platina,
hilo nylon (de una media), papel (higiénico, de
servilleta…), cinta adhesiva.
1. Corta un trocito de papel platina, arrúgalo para formar
una bolita y átalo en un extremo del hilo de nylon.
2. Pega con cinta adhesiva el otro extremo al borde de
una mesa de manera que pueda colgar libremente.
3. Frota durante un minuto el lapicero con el papel y
acércalo a la bolita sin tocarla. Observa que, al frotarlo,
el lapicero se ha electrizado y puede atraer a la bolita.
4. Toca con el lapicero la superficie de la bolita. De esta
manera, las cargas pasan del lapicero a la bolita y la
bolita se carga con electricidad del mismo signo que
el lapicero. ¿Qué ocurre?
◆ En tu carpeta de trabajo dibuja y explica cada paso de la experiencia.
La electricidad que aparece al frotar los cuerpos se
llama electricidad estáticaelectricidad estáticaelectricidad estáticaelectricidad estáticaelectricidad estática. Como su nombre lo
indica, es estática (no se mueve) a diferencia de la
corriente eléctrica.
Experimenta…. El péndulo
electrostático

Formasdeelectrización
A través de la experiencia con el péndulo te habrás dado cuenta de que existen
tres formas de electrizar un cuerpo:
a) Por frotamientoPor frotamientoPor frotamientoPor frotamientoPor frotamiento. Uno de los cuerpos que se frotafrotafrotafrotafrota pierde electrones y se
carga positivamente, el otro gana electrones y se carga negativamente.
b) Por contactoPor contactoPor contactoPor contactoPor contacto. Ocurre cuando un cuerpo electrizado tocatocatocatocatoca a uno neutro. Las
cargas del cuerpo electrizado pasan al cuerpo neutro y éste adquiere la carga
del cuerpo que lo tocó.
c) Por inducciónPor inducciónPor inducciónPor inducciónPor inducción. Se produce al acercaracercaracercaracercaracercar un cuerpo electrizado a otro neutro, pero
sin que entren en contacto. En este caso se produce un reacomodo de las cargas
del cuerpo neutro, pues el cuerpo electrizado atrae cargas de distinto signo.
● Los vellos de los brazos se paran cuando pasamos cerca de un televisor
encendido. ¿Qué forma de electrización se ha producido? ¿Por qué se
paran los vellos?
● Cuando tu pelo está seco y te peinas, se esponja y se separa. ¿A qué se
debe? ¿Qué forma de electrización es ésta?
Electricidad atmosférica
Cuando hay tormenta caen rayos, sobre todo
en las partes altas de los cerros. ¿Por qué ocurre
esto?
El aire frota las gotitas de agua que forman las
nubes. Una nube cargada negativamente por
su parte inferior atrae las cargas eléctricas
positivas de la Tierra. Si la diferencia de carga
entre la nube y la Tierra es muy grande se
produce una descarga eléctrica que conocemos
como rayo.
Frotamiento Contacto Inducción

En el segundo momento has reconocido que, al frotar los cuerpos, se puede percibir la
electricidad estática presente en ellos. En el tercer momento realizarás cálculos
matemáticos para medir la fuerza que existe entre dos cuerpos cargados eléctricamente.
En las salientes (cimas de cerros o copas de los árboles) la cantidad de carga es mayor,
y son los puntos donde más fácilmente puede caer un rayo. De allí viene la recomendación
de no colocarse debajo de un árbol cuando hay tormenta.
Un pararrayos es una barra metálica con una o varias puntas. En ellas la acumulación de
cargas inducidas es grande, y por eso atrae al rayo. Los pararrayos están conectados a
tierra por unos cables que llevan el rayo hacia el suelo, y así no se producen daños en los
edificios, árboles o personas.
◆ Elige y subraya la respuesta correcta:
a) Durante las tormentas las nubes se cargan de electricidad porque…
RECIBEN LAS CARGAS DEL SUELO / EL AIRE LAS FROTA
b) En la superficie de la Tierra se acumulan cargas de…
IGUAL SIGNO / DISTINTO SIGNO
c) Las cargas eléctricas se acumulan más en…
LAS PUNTAS / LAS ZONAS PLANAS
d) Los pararrayos…
EVITAN QUE CAIGAN RAYOS /
DIRIGEN LOS RAYOS HACIA EL SUELO DONDE NO CAUSEN DAÑO
◆ Busca información sobre daños provocados por los rayos en el Perú. También, infórmate
sobre las precauciones que debes tener en caso de tormenta.
Cada año caen sobre la tierra
más de 3 000 millones de rayos, que
provocan numerosas muertes. Por eso se
intenta mejorar la eficacia de los
pararrayos.

TERCER MOMENTO: Expresión matemática de la
LeydeCoulomb
Los cuerpos con distinta
carga se atraen y los cuerpos
con igual carga se repelen.
El físico francés Charles Augustin de Coulomb
estableció por experimentación una ley que
tomaría su nombre y fue base para determinar
la fuerza que existe entre dos cargas
eléctricas:
En los imanes pasa algo parecido:
polos opuestos se atraen, polos
iguales se repelen.
En el momento anterior has comprobado cómo los cuerpos cargados eléctricamente se
atraen o se repelen según sea su tipo de carga positiva (+) o negativa (-).
La fuerza con la que dos cargas eléctricas se atraen o repelen es proporcional al
producto de la magnitud de dichas cargas e inversamente proporcional al cuadrado de
la distancia que las separa.
Matemáticamente la Ley de Coulomb se expresa así:
F = K
q q
r
1 2
2
Donde:
● F es la fuerza de atracción (o repulsión) entre las cargas. Se mide en newton (N).
● q1
y q2
son las cargas eléctricas. Se miden en coulomb (C).
● r es la distancia que separa las cargas. Se mide en metros (m)
● K es una constante. Su valor depende del medio en que se encuentran las cargas. En
el vacío es:
K = 9 x 109
Nm
C
2
2
F
F
q1
q2
r

1. Se tienen 2 cargas positivas q1 = 2 C y q2 = 10 C separadas a una distancia de 10 cm en
el vacío. Calcula la fuerza que actúa entre las cargas.
Haciendo un gráfico tenemos: La fórmula de la Ley de Coulomb es:
F = K
q q
r
1 2
2
Los datos a reemplazar en la fórmula son:
K = 9 x 109 N m2/C2
q1 = 2 C
q2 = 10 C
r = 10 cm = 0,1 m
Reemplazando datos:
F = 9 x 109
Nm
C
2
2
(2 C)(10 C)
(0,1) m2 2
=
9 20 10
1 10
9
2
× ×
× –
N m C
C m
2
2 2
2
F = 180 x 1011 N
Este resultado en notación científica se expresa así: (ver Ficha de trabajo)
F = 1,8 x 1013 N
2. Del ejercicio anterior, calcula la fuerza que actúa entre las cargas si se aumenta la distancia
de separación a 20 cm.
Los datos a reemplazar en la fórmula serán los mismos, excepto el valor de la distancia
que cambia a 20 cm.
r = 20 cm = 0,2 m
Reemplazando datos, se tiene:
F = 9 x 109
Nm
C
2
2
(2 C)(10 C)
(0,2) m2 2
=
9 20 10
0 04
9
× ×
,
N m C
C m
2
2 2
2
F =
9 20 10
4 10
9
2
× ×
× –
N m C
C m
2
2 2
2
= 45 x 1011 N = 4,5 x 1012 N
La Ley de Coulomb es
una relación de proporcionalidad entre
diversas magnitudes, como cargas
eléctricas, distancias, fuerzas y una
constante.
10 cm
q1 q2

Según los conceptos de proporcionalidad, podemos llegar a diversas conclusiones y plantear
diversas hipótesis fácilmente comprobables.
Por ejemplo, los ejercicios anteriores nos permiten comprobar que, si la distancia entre
las dos cargas aumenta, la fuerza de repulsión entre ellas disminuye.
Esta conclusión se deduce también del enunciado de la ley que dice que la fuerza es
inversamente proporcional al cuadrado de la distancia que las separa.
3. ¿Qué fuerza es mayor, la que actúa sobre q1 o la que actúa sobre q2?
Esta pregunta permite hacer una aclaración muy importante.
Cuando se tienen 2 cargas separadas a cierta distancia, la fuerza de atracción o de
repulsión que se calcula es tanto la que actúa sobre la carga q1 como la que actúa sobre
la carga q2.
Estas fuerzas son un par acción – reacción. Son opuestas y valen lo mismo. No importa
que una de las cargas sea más grande que la otra.
La ley de Coulomb es importante para interpretar los conceptos de campo eléctrico y
potencial que son necesarios para resolver ciertos problemas de electricidad.
◆ Resuelve los siguientes ejercicios aplicando la fórmula de la Ley de Coulomb:
a) ¿Con qué fuerza se atraerán dos cargas de un coulomb cada una, si están a una distancia
de un km una de la otra?
b) ¿A que distancia, uno del otro, estarán colocados dos cuerpos cargados con un coulomb
cada uno, si se rechazan con la fuerza de un newton?
c) ¿Qué carga tiene una esfera que, a la distancia de 500 m, atrae a otra igual con la fuerza
de 81 N?
En el tercer momento has identificado el enunciado y la expresión matemática de la Ley
de Coulomb, que permite calcular la fuerza de atracción o repulsión que existe entre
cargas eléctricas.
Las fuerzas que
aparecen son
acción - reacción
F F
q1
q2
r

FICHADETRABAJO
Recordando la notación científica
Propósito:Propósito:Propósito:Propósito:Propósito: Reconocer la utilidad del procedimiento matemático denominado “notación
científica” para presentar y operar de manera simplificada números enteros muy grandes
o decimales extremadamente pequeños.
Adicionalmente, 10 elevado a una potencia negativa –n es igual a 1/10n.
10–1 = 1/10 = 0,1
10–3 = 1/1 000 = 0,001
10–9 = 1/1 000 000 000 = 0,000 000 001
Por lo tanto, un número como 156 234 000 000 000 000 000 000 000 000 puede ser
escrito como 1,56234 x 1029, y un número pequeño como 0,0000000000234 puede ser
escrito como 2,34 x 10–11.
Ejemplos:Ejemplos:Ejemplos:Ejemplos:Ejemplos:
34 456 087 = 3,4456087 x 107
0,0004508421 = 4,508421 x 10–4
–5 200 000 000 = –5,2 x 109
–6,1 = –6,1 x 100
La parte potencia de 10 se llama a menudo orden de magnitud del número, y las cifras
decimales son los dígitos significativos del mismo.
Es muy fácil pasar de la notación decimal usual a la científica, y recíprocamente, porque
las potencias de diez tienen las formas siguientes:
Si el exponente n es positivo, entonces 10n es 1 seguido de n ceros:
Por ejemplo 1012 = 1 000 000 000 000 (un billón)
101
= 10 106
= 1 000 000
102
= 100 109
= 1 000 000 000
103
= 1 000 1020
= 100 000 000 000 000 000 000
La notación
científica es un modo
de representar números enteros
mediante potencias de diez.

Si el exponente es negativo, de la forma –n, entonces: 10–n = 0, 000 ... 000 1
(n ceros)
Por ejemplo:Por ejemplo:Por ejemplo:Por ejemplo:Por ejemplo:
10–5 = 0,00001, con cuatro ceros después de la coma decimal y cinco ceros en total.
Esta notación es muy útil para escribir números muy grandes o muy pequeños, como
los que aparecen en la Física: la masa de un protón (aproximadamente 1,67 x 10–27
kilogramos), la distancia a los confines del universo (aproximadamente 4,6 x 1026 metros).
Esta escritura tiene la ventaja de ser más concisa que la usual. Por ejemplo, 1,48 x 1010
resulta más corto que 14 800 000 000.
La notación científica permite hacer cálculos mentales rápidos pero a menudo
aproximados, porque considera por separado los dígitos significativos y el orden de
magnitud (además del signo):
Ejemplos:Ejemplos:Ejemplos:Ejemplos:Ejemplos:
Productos y divisiones:Productos y divisiones:Productos y divisiones:Productos y divisiones:Productos y divisiones:
● 4 x 10–5 multiplicado por 3 x 10–6 = 3 x 4 x 10– 5 – 6
= 12 x 10–11 = 1,2 x 10– 10
● 5 x 10–8 entre por 3 x 105 = (5/3) x 10–8 – 5 = 1,66 x 10–13
Sumas y diferencias:Sumas y diferencias:Sumas y diferencias:Sumas y diferencias:Sumas y diferencias: Para sumar o restar números representados en notación científica
debemos uniformar los exponentes de la base 10.
● 4,1 x 1012 + 8 x 1010 = 4,1 x 1012 + 0,08 x 1012
= 4,18 x 1012
● 1,6 x 10–15 – 8,8 x 10–16 = (16 – 8,8) x 10–16
= 7,2 x 10–16
◆ Resuelve los siguientes ejercicios:Resuelve los siguientes ejercicios:Resuelve los siguientes ejercicios:Resuelve los siguientes ejercicios:Resuelve los siguientes ejercicios:
1. Expresa en notación científica las siguientes cantidades:
a) 857 346 970 586 b) 578 c) 20 000 000 000
2. Los números expresados en notación científica, ¿a qué cantidad aproximada
equivalen?
a) 5,2 x 10–4
b) 3,3 x 105
c) 180 x 1011

FICHA INFORMATIVA
Variedaddeimanes
Hasta hace algunos años sólo habían imanes naturales constituidos por la piedra
magnetita (ferrita). En la actualidad se preparan imanes artificiales producidos por
aleación de diferentes materiales. Por ejemplo:
¿Sabías que¿Sabías que¿Sabías que¿Sabías que¿Sabías que ….Algunos países como China y
Japón han fabricado un tren que en lugar de ruedas tiene
imanes? Este tren se llama MaglevMaglevMaglevMaglevMaglev (levitación magnética). El tren
levita, es decir, flota sobre los rieles aprovechando el principio de
repulsión entre polos iguales. Este tren va muy rápido ya que al
flotar se elimina la fuerza de rozamiento.
Cerámicos.Cerámicos.Cerámicos.Cerámicos.Cerámicos. Son lisos y de color gris oscuro,
de aspecto parecido a la porcelana. Se usan
para pegar en figuras que se adhieren a las
refrigeradoras. Son muy frágiles, pueden
romperse si se caen. Se fabrican con partículas
finas de ferrita (oxido de hierro) y otros
materiales.
Flexibles.Flexibles.Flexibles.Flexibles.Flexibles. Se usan en publicidad, cierres para
refrigeradoras, etc. Tienen gran flexibilidad e
incluso se pueden enrollar. Se fabrican con
aglomeración de finas partículas de ferrita sobre
un plástico.
Imanes de álnico.Imanes de álnico.Imanes de álnico.Imanes de álnico.Imanes de álnico. (El término “álnico”
proviene de tres iniciales que son sus
constituyentes básicos: aluminio, níquel y
cobalto). Tienen la ventaja de ser económicos,
aunque no tienen mucha fuerza. Son plateados
o dorados porque están recubiertos para evitar
la oxidación.
Imanes de “tierras raras”.Imanes de “tierras raras”.Imanes de “tierras raras”.Imanes de “tierras raras”.Imanes de “tierras raras”. Son imanes de
última generación de aspecto dorado o
plateado. Se utilizan en dispositivos mecánicos
y eléctricos como radios y parlantes. Tienen
bastante poder de imantación y están hechos
de neodimio o de samario, elementos conocidos
como “tierras raras”.

141
LLLLLa electricidad en movimientoa electricidad en movimientoa electricidad en movimientoa electricidad en movimientoa electricidad en movimiento
1. Corriente eléctrica
2. Magnitudes relacionadas con la
corriente
3. Matemática recreativa
Conocer cómo se produce y conduce la
corriente eléctrica e identificar las
magnitudes relacionadas con ella,
calculando el consumo de energía de los
aparatos eléctricos.
Resolver problemas de matemática
recreativa.
● En el primer momento estudiarás las
condiciones necesarias para que circule
corriente eléctrica y armarás un
circuito.
● En el segundo momento analizarás
magnitudes relacionadas con la
corriente y la forma de ahorrar energía
eléctrica.
● En el tercer momento desarrollarás tu
pensamiento creativo dando respuesta
a situaciones cuya solución requiere de
razonamiento lógico.
● Elaborando una pila casera ● Voltaje
● Conductores
● Aislantes
● Electrodos
● Resistencia
● Intensidad
● Potencia
● Kilowatt/hora
Matemática recreativa
● Ordenamiento lineal de información
Corriente eléctrica
● Concepto
● Conductores y aislantes
● Circuito eléctrico
● Ley de Ohm
● Las pilas y el medio ambiente

PRIMERMOMENTO:Corrienteeléctrica
● ¿Qué elemento proporciona energía eléctrica?
● ¿Qué elemento utiliza la energía eléctrica?
● ¿Para que sirven los cables?
● ¿Para qué sirven los clips?
¿Qué es la corriente eléctrica?
La corriente eléctrica es el movimiento ordenado y continuo de electronesel movimiento ordenado y continuo de electronesel movimiento ordenado y continuo de electronesel movimiento ordenado y continuo de electronesel movimiento ordenado y continuo de electrones
a través de un cable conductora través de un cable conductora través de un cable conductora través de un cable conductora través de un cable conductor.
La corriente eléctrica no pasa con la misma facilidad en todos los materiales.
Debido a ello, los materiales se clasifican como conductores y malos conductores.
Los conductores,Los conductores,Los conductores,Los conductores,Los conductores, son la mayoría de los metales, el agua y el cuerpo humano
que permiten el paso de la corriente eléctrica.
Uno de los mayores logros de la humanidad ha sido
generar electricidad y utilizarla en forma de corriente
eléctrica. Si armas un circuito eléctrico sencillo, te darás
cuenta de estos dos procesos: generación y utilización.
● Una pila grande, gutapercha, un foquito de linterna (1,5 V), dos clips metálicos, medio
metro de cable de luz simple, un pedazo de cartón.
1. Con la gutapercha, sujeta la pila al cartón.
2. Corta el cable en tres partes: uno de 20 cm y
dos de 15 cm; pela las puntas de cada pedazo.
3. Une un cable, por un lado, a un polo de la
pila; por el otro, a la rosca del foquito. Une el
segundo cable al otro polo de la pila y a uno
de los clips. El tercer cable únelo al otro clip y
a la rosca del foquito. Guíate de la figura.
4. Para fijar los cables a la pila, usa gutapercha; para fijarlos en los clips y en el foquito,
simplemente enróllalos.
5. Junta los clips. Luego, sepáralos. Observa qué sucede en cada caso.

Los malos conductoresLos malos conductoresLos malos conductoresLos malos conductoresLos malos conductores no permiten el paso de la corriente eléctrica. Por ejemplo,
la madera, el plástico, la porcelana, el vidrio y el caucho. Por ello, se les utiliza
como aislantesaislantesaislantesaislantesaislantes.
● Lee la siguiente información:
Se suele comparar la corriente eléctrica con un modelo
hidráulico.
Considera dos recipientes que contienen agua a
diferentes niveles. El agua fluye de un recipiente hacia
el otro hasta que los niveles se igualen. De la misma
manera, los electrones se mueven a través de un
conductor cuando hay una diferencia de potencial
(diferencia de cargas) entre sus extremos.
Si queremos que el flujo del agua se mantenga entre los dos recipientes, es necesaria
una bombauna bombauna bombauna bombauna bomba. En el caso eléctrico, la bomba, es decir, el dispositivo que mantiene la
diferencia de potencial son los generadores eléctricosgeneradores eléctricosgeneradores eléctricosgeneradores eléctricosgeneradores eléctricos.
La diferencia de potencial se llama fuerza electromotrizfuerza electromotrizfuerza electromotrizfuerza electromotrizfuerza electromotriz, también tensión o voltajetensión o voltajetensión o voltajetensión o voltajetensión o voltaje. El
voltaje se mide en voltios (V). Así, una pila da 1,5 V; una batería, 9 V; la red eléctrica, 220 V.
◆ Relaciona las dos columnas escribiendo la letra correspondiente.
a) Flujo de electrones ( ) Plástico del cable eléctrico
b) Fuerza electromotriz ( ) Pila
c) Conductor ( ) Corriente eléctrica
d) Aislante ( ) Cable de cobre
e) Generador de corriente ( ) Voltaje
Circuitoeléctrico
Un circuito eléctrico es el conjunto de dispositivos por los cuales circula la corriente
eléctrica. Los elementos que forman un circuito son:
GeneradoresGeneradoresGeneradoresGeneradoresGeneradores: proporcionan energía eléctrica,
es decir, la energía para que se muevan los
electrones. Ejemplos: pilas y baterías.
ConductoresConductoresConductoresConductoresConductores: son los cables metálicos que
conducen la electricidad.
ReceptoresReceptoresReceptoresReceptoresReceptores: son los aparatos que transforman
la electricidad en otro tipo de energía. Ejemplos:
focos, radio, licuadora, etc.
InterruptorInterruptorInterruptorInterruptorInterruptor: es el elemento que abre o cierra
el circuito.

Pilas y baterías
Las pilas y las baterías son generadores de energía
eléctrica. Ellas convierten energía química en
energía eléctrica.
Las pilas tienen dos electrodos o polos:
● el polo negativopolo negativopolo negativopolo negativopolo negativo es una cubierta metálica
de zinc.
● el polo positivopolo positivopolo positivopolo positivopolo positivo es una barra de carbón.
Ambos electrodos están sumergidos en una pasta
de sustancias químicas. Las reacciones químicas
que se producen entre la pasta y los electrodos
hace que uno de ellos pierda electrones y el otro
los reciba. Se crea así una diferencia de potencial
que pone en movimiento los electrones a través
del cable al que está conectada la pila.
En el primer momento has experimentado cómo se produce una corriente eléctrica y
cómo circula en un circuito eléctrico. En el segundo momento identificarás las magnitudes
eléctricas de uso cotidiano.
◆ Relaciona los elementos de un circuito escribiendo la letra correspondiente.
a) Interruptor ( ) Cables metálicos que unen el generador con los receptores.
b) Generador ( ) Aparato que transforma la energía eléctrica en otro tipo de energía.
c) Receptor ( ) Produce corriente eléctrica.
d) Conductor ( ) Abre y cierra un circuito.
Las pilas y baterías están
hechas con materiales muy tóxicos que
contaminan el ambiente. Por eso debes
usarlas con moderación y sólo cuando
es necesario (ver ficha informativa).
Investiga sobre
los distintos tipos de
pilas. Presenta la
información en un
tríptico.
Polo positivo (+)
Barra de
carbón
Pasta
química
Cápsula
de zinc
Polo negativo (–)

SEGUNDOMOMENTO:Magnitudes
relacionadasconlacorriente
Principales magnitudes
Voltaje.Voltaje.Voltaje.Voltaje.Voltaje. Se le llama también fuerza
electromotriz (fem), diferencia de potencial
o tensión. Es la fuerza que despliega un
generador para llevar las cargas a través del
circuito. La unidad de medida es el voltiovoltiovoltiovoltiovoltio
(V).(V).(V).(V).(V). Por ejemplo, el voltaje de una pila es
1,5 V y el de la red eléctrica, 220 V.
Resistencia (R)Resistencia (R)Resistencia (R)Resistencia (R)Resistencia (R). Es la mayor o menor
oposición que presenta un conductor al paso
de la corriente eléctrica. Por ejemplo, un
cable grueso presenta menor resistencia al
paso de la corriente; por esta razón, se usan
en los cables de alta tensión. La unidad de
medida en el SI es el ohmio (ohmio (ohmio (ohmio (ohmio (Ω).).).).).
Potencia.Potencia.Potencia.Potencia.Potencia. Nos indica la cantidad de energía
que consume un aparato eléctrico. Se mide
en watt o vatio (W).watt o vatio (W).watt o vatio (W).watt o vatio (W).watt o vatio (W). Así, una licuadora
consume 300 W, un foco 100 W, etc.
P = V2
/R
En la vida cotidiana
hablamos frecuentemente de
magnitudes y unidades que se relacionan
con la corriente eléctrica. Por eso es
importante que las conozcas.
La ducha eléctrica
consume: cerca de 600 W.
Mi recibo de luz indica
que he consumido en el mes
150 kilowatts/hora.
Mi primo enchufó su
radio de 110 V a la corriente
de 220 V y lo malogró.

Potenciadelosartefactosyequiposmásutilizadosenelhogar
Estas potencias son referenciales, dependen del tipo o modelo del artefacto. La potencia
de un artefacto generalmente va impresa en la parte posterior del mismo.
Cálculo de consumo de energía eléctrica de algunos artefactos
La energía consumida por nuestros artefactos eléctricos se expresa en kilowattkilowattkilowattkilowattkilowatt horahorahorahorahora
(kWh).
Recuerda que el prefijo kilo significa mil, por lo tanto: 1 kilowatt = 1 000 watts
La energía eléctrica consumida por un artefacto eléctrico se determina multiplicando la
potencia de dicho artefacto (kW) por la cantidad de horas que está encendido:
Potencia del Tiempo que está Energía consumida
artefacto eléctrico x encendido el artefacto = por el artefacto
(kW) (horas) (kWh)
1.1.1.1.1. Si un foco de luz de 100 W (0,1 kW) está encendido cinco horas diarias, ¿cuál será su
consumo de energía en un mes?
Si el foco está encendido cinco horas al día, en un mes de 30 días será:
5 horas/día x 30 días = 150 horas.
Por lo tanto, este foco tiene un consumo de energía mensual de:
0,1 kW x 150 horas = 15 kWh
2.2.2.2.2. Si un televisor de 14”, cuya potencia es de 80 W (0,08 kW) está encendido ocho horas
diarias, ¿cuál será su consumo de energía en un mes?
8 horas/día x 30 días = 240 horas
Por lo tanto, este televisor tiene un consumo de energía mensual de:
0,08 kW x 240 horas = 19,20 kWh

3.3.3.3.3. ¿Cuál será el consumo mensual de una refrigeradora de 250 W (0,25 kW) de potencia?
Considerando que una refrigeradora está enchufada todo el día pero su motor funciona
un promedio de diez horas al día (dependiendo del tipo), entonces en un mes se tendrá:
10 horas/día x 30 días = 300 horas
El consumo de energía mensual será:
0,25 kW x 300 horas = 75 kWh
◆ Tomando como referencia el cuadro siguiente, calcula el consumo de energía eléctrica de
los artefactos de tu vivienda y compáralo con tu recibo de electricidad.
Ten en cuenta:
a) En la columna I anota el tipo de artefacto eléctrico que usas en tu hogar. Por ejemplo:
televisor de 14”, radio, etc.
b) En la columna II anota la potencia de cada uno de los artefactos señalados en la
columna I. Tienes algunas potencias como dato en la página anterior.
c) En la columna III anota la potencia del artefacto en kW. Para ello tendrás que dividir
lo anotado en la columna II entre 1 000, ejemplo:
80/1 000 = 0,08
d) En la columna IV anota la cantidad de artefactos eléctricos del mismo tipo que usas
en tu hogar. Ejemplo: si tienes sólo un televisor de 14”, deberás anotar 1.
e) Anota en la columna V la cantidad de horas al día que está encendido cada uno de
tus artefactos. Si algún artefacto está encendido menos de una hora al día, utiliza las
siguientes equivalencias:
15 minutos = 0,25 (1/4 hora)
30 minutos = 0,50 (1/2 hora)
45 minutos = 0,75 (3/4 hora)
IIIII IIIIIIIIII IIIIIIIIIIIIIII IVIVIVIVIV VVVVV VIVIVIVIVI VIIVIIVIIVIIVII
Artefactos Potencia Potencia Cantidad Horas de Días de Consumo
eléctricos eléctrica kW de consumo consumo mensual
que utilizas W artefactos diario en un mes en kWh
normalmente
Televisor de 14” 80 0,08 1 8 30 19,2
TotalTotalTotalTotalTotal

f) En la columna VI anota la cantidad de días al mes que utilizas tus artefactos. Por
ejemplo, si usas todos los días el televisor de 14” deberás escribir 30.
g) En la columna VII anota el consumo mensual de cada uno de los artefactos. Para ello,
multiplica los valores anotados en las columnas III, IV, V, VI. El resultado de esta
operación será el consumo mensual en kWh de cada uno de los artefactos. Por ejemplo:
1 x 0,08 kW x 8 horas/día x 30 días = 19,2 kWh
h) Finalmente, deberás sumar los consumos mensuales de cada uno de tus artefactos y
anotarlos en el recuadro TOTAL. Este valor representa tu consumo mensual en kWh.
El TOTAL de kWh que has calculado debe coincidir aproximadamente con lo que indica tu
recibo de luz donde dice “consumo a facturar”. Esta cantidad, multiplicada por el valor
unitario de 1 kWh es tu consumo mensual y aparece en el recibo de luz donde dice
“consumo de energía”.
Ahorrodeenergía
El siguiente cuadro te indica la electricidad que consumen los artefactos eléctricos.
Por ejemplo, encender una radio equivale a encender
un foco de 100 W, y una terma equivale a 20 focos.
¡Te recomendamos!¡Te recomendamos!¡Te recomendamos!¡Te recomendamos!¡Te recomendamos!
● Aprovecha la luz natural. Abre las cortinas. Enciende
sólo las luces que sean necesarias.
● Usa focos ahorradores. Sólo consumen el 20% de
energía que un foco normal.
● Junta la mayor cantidad de ropa para planchar y
así evitarás desperdicios de calor en el encendido
y apagado de tu plancha.
● Si los jebes del refrigerador están viejos, cámbialos.
Así evitas que el refrigerador trabaje demás.
El ahorro de energía que puedes lograr beneficiará a tu bolsillo al reducir costos y
contribuirás con la conservación del ecosistema.
DETALLE DE LOS IMPORTES FACTURADOS
Descripción Precio unitario Importe
Cargo fijo 2,19
Mant. y reposición de conexión 0,84
Consumo de energía 0,3086 47,83
Alumbrado público 5,21
Interés compensatorio 0,02
Nota de Débito (Res. N° 423-2007-OS/CD) 1,02
I.G.V. 10,85
Electrificación Rural (Ley N° 28749) 0,0070 1,09
SUBTOTAL DEL MES 69,05
REDONDEO (0,05)
TOTAL IMPORTES FACTURADOS 69,00
ESTEVES SAUL
Und 277 Mza. A Lt 18 Sauces 2A. Surquillo
RECIBO N°. 96327509
PARA CONSULTAS SU
N° DE SUMINISTRO ES:
590297
DATOS DEL SUMINISTRO DETALLE DEL CONSUMO
Medidor: Monofásico CONSUMO DE ENERGÍA ELÉCTRICA
Tarifa: BT5B Lectura actual 1939 (11/02/08)
Conexión: Subterránea Lectura anterior 1784 (10/01/08)
Alimentador: SA-18 Diferencia entre lecturas 155
Potencia contratada 0,80 kW Factor del medidor 1
Consumo a facturar 155 kw/h
20
focos
12
focos
10
focos
3 1/2
focos
2
focos
1 1/2
focos
Terma
2 000 W
Horno
microondas
1 200 W
Plancha
1 000 W
Refrigeradora
350 W
Televisor
21“ a color
200 W
Equipo de
sonido (estéreo)
120 W

Intensidad o corriente eléctrica (I).Intensidad o corriente eléctrica (I).Intensidad o corriente eléctrica (I).Intensidad o corriente eléctrica (I).Intensidad o corriente eléctrica (I). Es el flujo de cargas que circula por un
circuito cerrado depende fundamentalmente de la tensión o voltaje (V) que se
aplique y de la resistencia (R) en ohm que ofrezca al paso de esa corriente la
carga o receptor (consumidor conectado al circuito).
La unidad de medida de la intensidad de la corriente eléctrica (I) es el amperioamperioamperioamperioamperio (AAAAA).
Un amperio (A) es la corriente que produce una tensión de un voltio (1 V) cuando
se aplica a una resistencia de un ohm (1 Ω).
Leyde Ohm
El físico y matemático alemán Georg Simón Ohm estableció la relación constante
que existe entre la intensidad, la fuerza electromotriz y la resistencia, que son los
elementos fundamentales de la corriente eléctrica:
“La intensidad de la corriente en un alambre metálico es directamente proporcional
a la diferencia de potencial que existe en sus extremos e inversamente proporcional
a la resistencia del circuito.”
Matemáticamente la ley de Ohm se expresa así: V = I R
Donde:
VVVVV = Valor de la tensión, diferencia de potencial o voltaje que produce la pila o
generador de corriente eléctrica en voltios (V).
RRRRR = Valor de la resistencia del consumidor o carga conectado al circuito en ohm (Ω).
IIIII =Intensidad de la corriente que recorre el circuito en amperios (A).
Despejando de la fórmula V = IR se tiene.
R = y I =
Otra forma de enunciar la ley de Ohm es:
“El cociente entre la fuerza electromotriz o voltaje y la intensidad de
la corriente es una cantidad constante llamada resistencia”.
A
Resistencia
Ley de Ohm V = IR
Interruptor
Amperímetro
Pila
Otra magnitud que relaciona el voltaje (V), con la
resistencia (R) es la intensidad (I). Estos son tres
componentes presentes en cualquier circuito eléctrico.
Se relacionan entre sí mediante una ley conocida como
la Ley de Ohm la cual estudiarás a continuación.
V
I
V
R

1) La fuerza electromotriz de la corriente eléctrica es de 220 V. Si los focos instalados tienen
110 Ω de resistencia, ¿cuál es el valor de la intensidad?
Datos: V = 220 V R = 110 Ω
Reemplazando en la fórmula: I = V/R
Se tiene: I = 220 V / 110 Ω = 2 A2 A2 A2 A2 A
2) ¿Qué resistencia tendrá un foco, si lo atraviesa una corriente de 220 V con 18 A?
Datos: V = 220 V I = 18 A
Reemplazando en la fórmula: R = V/I
Se tiene: R = 220 V/18 A = 12,212,212,212,212,2 Ω
◆ En un circuito eléctrico se determinaron experimentalmente los siguientes datos del voltaje
e intensidad de corriente:
V 0 1 2 3 4 6 8 10
I 0 1,1879 2,3758 3,5637 4,7516 7,1274 9,5033 11,8791
R = V/I
a) Realiza los cálculos y comprueba que el valor de la resistencia se mantiene constante.
b) Elabora la gráfica de los datos registrados en la tabla y comprueba que la pendiente
de la recta que se obtiene es igual al valor de la resistencia.
En el segundo momento has identificado las magnitudes fundamentales de la corriente
eléctrica y la fórmula mediante la cual se relacionan. También has aprendido cómo
calcular el consumo de energía de los aparatos eléctricos. En el tercer momento te
distraerás con un poco de matemática recreativa.
Investiga sobre el
efecto Joule en todo
circuito eléctrico y
presenta un informe.

TERCER MOMENTO: Matemática recreativa
Antes de dar una respuesta
analiza nuevamente la situación
planteada e intenta dar una
solución lógica a este problema.
Analiza la siguiente situación:
En el segundo piso de un viejo caserón hay 3 habitaciones, cada una tiene un foco.
Los interruptores para encender o apagar los focos están en el primer piso empotrados
en la pared. Se encuentran en posición de “apagado” y no siguen un orden.
¿Cómo puedes saber qué interruptor corresponde a cada foco, si sólo puedes subir y
entrar una sola vez en cada habitación para verificar?
Para solucionar este problema te será útil recordar no sólo que un foco es una fuente de
luz, sino que la energía eléctrica que llega a él se transforma en calor, el cual se percibe
porque el foco se calienta (efecto Joule).
La temperatura del foco depende del tiempo que lleve encendido y puede alcanzar los
70 °C.

Dos estados son sencillos de identificar:
1. Apagado y frío (interruptor en posición “apagado”).
2. Encendido y caliente (interruptor en posición de
“encendido”).
Pero necesitas un tercer estado y lo consigues
cuando apagas un foco que ha estado encendido
(apagado y caliente).
Lo que se haría es lo siguiente:
1. Enciendes un foco, accionando un interruptor que
llamarás A, durante unos 15 minutos, tiempo
suficiente para que se caliente.
2. Luego de los 15 minutos apagas el interruptor A.
De este modo tendrás un foco caliente apagado.caliente apagado.caliente apagado.caliente apagado.caliente apagado.
3. Enciendes luego otro con un interruptor que
llamarás B. Ahora habrá un foco encendidofoco encendidofoco encendidofoco encendidofoco encendido.
4. El interruptor que no hemos pulsado será el C y
corresponde a un foco frío y apagadofoco frío y apagadofoco frío y apagadofoco frío y apagadofoco frío y apagado.
En este momento puedes tocar los focos apagados
para distinguir entre el que está caliente (estuvo
encendido) y el frío. El otro foco es el que está
encendido.
AAAAA : corresponde al foco caliente y apagado.
BBBBB : corresponde al foco encendido.
CCCCC : corresponde al foco frío y apagado.
Como ves, ante
determinada situación, se puede
plantear una solución creativa
reflexionando y empleando un
modo de pensar lógico.
bombillas
Encendido Frío
apagado
Caliente
apagado
Caliente
apagado
Encendido Frío
apagado
A B C

Ahora, verás situaciones lógicas recreativas referidas al ordenamiento lineal de información.
Ejemplo 1Ejemplo 1Ejemplo 1Ejemplo 1Ejemplo 1
Cinco personas rinden un examen. Si se sabe que:
– B obtuvo un punto más que D
– D obtuvo un punto más que C
– E obtuvo dos puntos menos que D
– D obtuvo dos puntos menos que A
Ordena de manera creciente e indica quien obtuvo el mayor puntaje.
Ten presente dos sugerencias importantes para afrontar con éxito estos ejercicios:
1° Toma una orientación.
Por ejemplo, si dibujas una línea, al lado derecho considerarás más puntaje y, hacia el
lado izquierdo menos puntaje.
– +
menos puntaje más puntaje
2° Coloca toda la información en función de esa orientación.
–
D B
+
B obtuvo un punto más que D
–
DC B
+
D obtuvo un punto más que C
–
DC BE
+
E obtuvo dos puntos menos que D
–
ADC BE
+
D obtuvo dos puntos menos que A
–
ADC BE
+
En el diagrama final se puede observar que quien obtuvo mayor puntaje fue A.

Ejemplo 2Ejemplo 2Ejemplo 2Ejemplo 2Ejemplo 2
María está al noreste de Juana. Julio está al sureste de María y al este de Juana. ¿Cuál de
las siguientes afirmaciones es correcta?
A) María está al noreste de Julio. ( )
B) Juana está al este de Julio. ( )
C) Juana está al oeste de Julio. ( )
D) Julio está al suroeste de María. ( )
SoluciónSoluciónSoluciónSoluciónSolución:
Considera las orientaciones cardinales siguientes:
Según el texto enunciado:
María al NE de Juana Julio al SE de María
Julio al E de Juana Conjugando los tres casos, se tiene:
Por lo tanto, la afirmación C es la correcta.
N
S
O E
NO
SE
SO
N
E
N
S
O EJuana
María
N
S
O EMaría
Julio
N
S
O EJuana Julio
María
N
S
O EJuana Julio

1) Seis mujeres están escalando una
montaña.
Carla está más abajo que Juana,
quien se encuentra un lugar más
abajo que María, Fernanda está
más arriba que Carla pero un lugar
más abajo que Paola quien está
más abajo que Rosa, esta última
se encuentra entre Juana y Paola.
¿Quién está en el cuarto lugar del
ascenso?
2) Cuatro autos, uno rojo, uno azul, uno blanco y uno verde, están ubicados en fila horizontal.
El auto blanco y el auto azul no están al lado del rojo, además el azul está entre el verde
y el blanco. ¿Cuál de las afirmaciones es correcta?
a) El auto blanco está más lejos del rojo que del verde. ( )
b) El auto rojo es el que está más a la derecha. ( )
c) A la derecha del auto verde hay dos autos. ( )
3) En un CEBA cinco amigos asisten a un Cineforo, se sientan en una banca uno a continuación
de otro. Zenaida y Pedro se ubican en forma adyacente. Pedro no está al lado de Silvia,
ni de Juan. Zenaida está en un extremo. Si Silvia y Manuel están peleados por el momento,
¿quién se sienta al lado de Silvia?
4) María es mayor que Sofía, Alberto es menor que Sofía, pero mayor que Norma y Norma
es menor que Víctor, ¿cuál de los cinco es el menor de todos?
Ahora te toca a
ti. Utiliza tu habilidad e
ingenio y resuelve los
siguientes ejercicios.
En el tercer momento has puesto en práctica tu habilidad e ingenio para aprender a
resolver situaciones de matemática recreativa en lo referente a problemas de
ordenamiento lineal de información.

FICHADETRABAJO
Elaborando una pila casera
Objetivo:Objetivo:Objetivo:Objetivo:Objetivo: Experimentar la generación de corriente eléctrica mediante la elaboración
de una pila casera.
● Tres limones grandes.
● Seis placas de metal (tres de cobre y tres de zinc) que deben limpiarse con un lija
de fierro antes de iniciar el experimento.
● Cable delgado de cobre, cinta aislante.
● Un foco pequeño llamado ledledledledled (luz emisor diodo). No utilizamos un foco de linterna
porque el voltaje que se consigue con esta experiencia es pequeño.
1. Ablanda con tus manos los limones
y ruédalos sobre una mesa para que
el jugo salga.
2. Con un cuchillo, haz dos cortes a
cada limón separados por 3 cm.
3. Inserta las placas de metal en las
ranuras.
4. Arma el circuito que se ve en el
esquema.
5. Su funcionamiento depende de algunos factores. Para comprobar sus efectos realiza
las siguientes pruebas:
a) Mantén las placas a la misma profundidad y varía la distancia entre ellas. Observa
si hay alguna variación en el circuito.
b) Conserva la misma distancia entre las placas, pero ahora varía la profundidad.
¿Hay algún cambio?
● ¿Qué elemento del circuito se consigue con los limones y los metales?
● ¿Cómo se genera la electricidad?
● ¿Cómo influye la profundidad y la distancia entre las placas?
Led
CobreZinc
3 cm 3 cm 3 cm

FICHA INFORMATIVA
Las pilas y el medio ambiente
En la actualidad hay varios tipos de pilas y baterías.
Las pilasLas pilasLas pilasLas pilasLas pilas producen un voltaje de 1,5 V con lo
que se pueden accionar foquitos de linterna, flash
de cámaras fotográficas, relojes y otros aparatos
eléctricos pequeños.
Las baterías o pilas planasLas baterías o pilas planasLas baterías o pilas planasLas baterías o pilas planasLas baterías o pilas planas que se usan en los
equipos de música son en realidad una asociación
de tres pilas. En conjunto dan 4,5 V.
Las baterías de los carrosLas baterías de los carrosLas baterías de los carrosLas baterías de los carrosLas baterías de los carros están formadas por
seis placas de plomo inmersas en acido sulfúrico.
Producen una corriente de 12 V. En la actualidad
podemos encontrar, además, baterías de otros
materiales, como de níquel y cadmio.
Todas las pilas y baterías están fabricadas con
materiales peligrosos, como plomo, mercurio,plomo, mercurio,plomo, mercurio,plomo, mercurio,plomo, mercurio,
cadmiocadmiocadmiocadmiocadmio y otros que dañan la salud y pueden
dañar mortalmente a los seres vivos.
Si arrojas pilas a la basura llegan a los botaderos
y de allí a los ríos o al mar. Una sola pila de
mercurio contamina miles de litros de agua… ¡Más
del doble que lo que una persona pueda
contaminar durante toda su vida! …¿Te imaginas
la cantidad de peces y otras especies acuáticas
que mueren por efecto de las pilas?
Por si fuera poco, si arrojas las pilas y baterías sin ningún cuidado en el ambiente, éstas
lo contaminan durante 500 años. Por ello, para evitar la destrucción de nuestro planeta,
te sugerimos botarlas en lugares autorizados.
Muchos municipios y supermercados recogen las pilas. Además, tienes derecho a
exigir a tu proveedor de pilas y baterías un sistema de recojo y reciclaje de las
mismas.
• ¿En tu barrio hay sistema de reciclaje de pilas? Si no lo hubiese, ¿cómo podrías
deshacerte de las pilas usadas?
12 V12 V
1,5 V

159
RRRRRelación entre imanes y corriente eléctricaelación entre imanes y corriente eléctricaelación entre imanes y corriente eléctricaelación entre imanes y corriente eléctricaelación entre imanes y corriente eléctrica
1. El electromagnetismo
2. Alternadores y motores
3. Sistema de coordenadas cartesianas,
3D
Comprender el fenómeno del
electromagnetismo y sus aplicaciones
tecnológicas.
Representar gráficamente un punto del
espacio en un sistema de coordenadas
cartesianas en tres dimensiones (3D).
● En el primer momento comprenderás
el fenómeno del electromagnetismo y
reconocerás sus aplicaciones en grúas
y timbres.
● En el segundo momento conocerás los
elementos y principios de dos grandes
inventos electromagnéticos: los
alternadores y los motores eléctricos.
● En el tercer momento estudiarás los
sistemas de coordenadas cartesianas
en dos dimensiones (2D) y tres
dimensiones (3D), representando un
punto del espacio en un sistema de
ejes cartesianos en 3D.
● La electricidad llega a tu casa ● Bobina
● Generador
● Alternador
● Motor eléctrico
● Ejes cartesianos
● Bidimensional
● Tridimensional
● Sistema de coordenadas cartesianas
Electromagnetismo
● Experimento de Oersted
Electroimanes
● Principios y aplicaciones
Producción de corriente eléctrica
● Alternadores
● Motores eléctricos
● Construyendo un motor eléctrico

PRIMERMOMENTO:Elelectromagnetismo
En 1820, el profesor y físico danés Hans Christian Oersted descubrió de manera casual la
relación entre electricidad y magnetismo.
ExperimentodeOersted
Oersted hizo pasar corriente eléctrica por un alambre de cobre debajo del cual había
colocado por descuido una brújula. Observó, sorprendido, que cada vez que conectabaconectabaconectabaconectabaconectaba
la corriente eléctricala corriente eléctricala corriente eléctricala corriente eléctricala corriente eléctrica, la aguja de la brújula se movíase movíase movíase movíase movía.
La conclusión que se puede obtener de este experimento es que la corriente eléctrica es
capaz de producir un campo magnético. Si esto no fuera así, la brújula no se habría
movido.
De esta manera quedó demostrada la relación entre magnetismo y electricidad, lo cual
dio origen al estudio de un fenómeno físico llamado electromagnetismoelectromagnetismoelectromagnetismoelectromagnetismoelectromagnetismo.
Con el experimento de Oersted se abrió el camino para una de las grandes invenciones
del mundo moderno: los electroimanes. Los electroimanes tienen muchísimas
aplicaciones.
Momentosestelaresdelaciencia
Isaac Asimov (1920- 1992) fue un reconocido escritor y científico norteamericano que
produjo libros de divulgación científica donde exponía de manera amena y sencilla
temas científicos. En su libro “Momentos estelares de la Ciencia” publicó una selección
de 30 descubrimientos que revolucionaron al mundo por sus extraordinarias aplicaciones
prácticas… ¡Uno de ellos es el electromagnetismo!

Experimenta...Construyeunelectroimán
● Dos metros de cable eléctrico simple, un clavo grande, una batería y varios clips.
1. Enrolla el cable alrededor del clavo dando 20 vueltas.
2. Conecta los extremos del cable a la batería y ya
tendrás un electroimán.
3. Prueba si funciona levantando clips. Anota cuántos
clips levantaste.
4. Ahora enrolla el cable al clavo dando cuarenta
vueltas. Anota el número de clips que levantas.
Explicación. Al enrollar el hilo de cobre al clavo has
fabricado una bobinauna bobinauna bobinauna bobinauna bobina. Cuando pasa la corriente
eléctrica por una bobina se crea un campo magnético
que imanta el clavo de hierro, por eso éste se
comporta como un imán. Cuando se desconecta, la
imantación desaparece. Cuantas más vueltas tiene
la bobina, el campo magnético creado es más fuerte.
Loselectroimanes
Durante la experiencia anterior has
comprobado que la corriente eléctrica hace
que los objetos de hierro y acero se
comporten como imanes a los cuales se llama
electroimaneselectroimaneselectroimaneselectroimaneselectroimanes.
Los electroimanes se construyen enrrollando
un alambre conductor sobre un trozo de
hierro. El hierro se comporta como un imán
sólo mientras la corriente circula por él.
Los electroimanes de este tipo sirven para
separar o transportar objetos de hierro o
acero.
Para soltar los objetos basta con quitar la
corriente eléctrica. Por ejemplo, se usan en
el proceso de reciclaje para separar los
objetos de hierro y de acero de otros
materiales que forman la basura.

En el primer momento has visto cómo funcionan los electroimanes y sus aplicaciones.
En el segundo momento verás otras aplicaciones de los electroimanes en los generadores
de electricidad y en los motores.
La mayoría de aparatos eléctricos tienen un electroimán que permite su funcionamiento.
Sin electroimanes no podría haber timbres, teléfonos, radios, televisores…….
◆ Completa el esquema:
◆ Busca el significado de: Acero – Aleación - Reciclaje
Eltimbre
El timbre eléctrico es un dispositivo capaz de
producir un sonido cuando se pulsa un interruptor.
Está compuesto por un circuito eléctrico, un
interruptor y un electroimánelectroimánelectroimánelectroimánelectroimán.
1. Al pulsar el interruptor, se cierra el circuito y la
corriente eléctrica que circula activa el electroimán.
2. El electroimán atrae una placa de hierro conectada
a una varilla.
3. La varilla golpea la campana.
4. En ese instante, la varilla se separa del tornillo, el
circuito se abre y se corta la corriente; entonces, el
electroimán deja de funcionar y la varilla vuelve a
su posición inicial. Este proceso se repite mientras
se esté pulsando el interruptor.
La corriente eléctrica origina un
campo magnético; por eso, con
ella se puede imantar un trozo
de hierro.
¿Cómo se descubrió?
Electromagnetismo
¿Qué es
?
¿Enqués
e
aplica?
Interruptor
Placa de
hierroElectroimán
Tornillo
Varilla
Campana

SEGUNDOMOMENTO:Alternadores
ymotores
Producción de corriente eléctrica: alternadores
Una vez encontrada por Oersted la relación entre electricidad y magnetismo, el
siguiente paso lo dio Michael Faraday en el año 1831. Su razonamiento fue el
siguiente: si las corrientes eléctricas generan campos magnéticos, podría darse el
proceso inverso, es decir, crear corrientes eléctricas con imanes. Para comprobarlo,
realizó un montaje similar al siguiente:
● Un alambre de cobre enrollado se conecta a un foco. Tenemos por lo tanto un
circuito que no tiene pilas; es decir, no hay un generador y, por lo tanto, no
circula corriente.
● Si se mueve rápidamente un imán dentro del alambre enrolladoalambre enrolladoalambre enrolladoalambre enrolladoalambre enrollado que llamamos
bobinabobinabobinabobinabobina, se comprueba que el foquito se prende, es decir, se genera una
corriente eléctrica.
● ¿Qué centrales hidroeléctricas conoces? ¿Dónde están ubicadas?
● ¿Qué aparatos de tu hogar tienen motores eléctricos?
● ¿Qué máquinas industriales que conoces tienen motores eléctricos?
En realidad, para que el foco se
encienda, el imán tiene que ser
potente. Si haces la experiencia con
imanes comunes no lograrás el
resultado.
Raúl trabaja en la central
hidroeléctrica de Matucana. Allí hay
grandes generadores eléctricos
llamados también alternadores.
Ellos producen la electricidad que
llega a Lima.
Yo trabajo en
una carpintería, y mi sierra
eléctrica tiene un motor
eléctrico.

¿Cómoesunalternador?
El alternador es un generador de
corriente eléctrica. Consta de un imánun imánun imánun imánun imán
que se mueve dentro de unaque se mueve dentro de unaque se mueve dentro de unaque se mueve dentro de unaque se mueve dentro de una
bobinabobinabobinabobinabobina produciendo electricidad.
Las centrales eléctricas tienen
alternadores muy grandes y para
moverlos se utiliza una gran fuente de
energía como la que tiene una caída de
agua. El agua hace girar las turbinas,las turbinas,las turbinas,las turbinas,las turbinas,
las cuales, a su vez, mueven el imán
del generador produciendo electricidad.
Como ya has aprendido en otros módulos, la energía que mueve las turbinas
puede ser hidráulica, térmica, eólica o nuclear.
◆ Dibuja y explica qué es una bobina.
◆ Explica cómo puede una bobina producir electricidad.
N
S
Represa
Turbina
Generador
La corriente que se consigue con las pilas es
de pequeña intensidad y no sería posible iluminar una
ciudad con ella. Pero, una vez que se conoció cómo
producir corrientes eléctricas con imanes, se empezó a
fabricar generadores electromagnéticos, conocidos también
como alternadores. Con ellos se produce electricidad
a gran escala, la que llega por la red eléctrica.
Las pilas transforman energía
química en energía eléctrica,
mientras que los generadores
e l e c t r o m a g n é t i c o s
transforman energía
mecánica (de movimiento)
en energía eléctrica.

◆ Completa el esquema:
En el segundo momento has conocido el fundamento de un alternador que consiste en
producir electricidad a través de un imán que se mueve dentro de una bobina. Además,
has identificando cómo se produce movimiento a través de un motor eléctrico.
En el tercer momento estudiarás el sistema de coordenadas cartesianas en tres
dimensiones, 3D.
Produccióndemovimiento:motoreseléctricos
El motor eléctrico es un dispositivo que transforma energía eléctrica en movimiento.
El siguiente dispositivo muestra el principio de un motor eléctrico.
● Se tiene dos imanes inmóviles, uno al lado
del otro, y se coloca entre ambos una
bobina, que tampoco se mueve.
● Al circular la corriente eléctrica, la bobina
empieza a girar y si se le conecta un eje
éste puede mover por ejemplo las aspas
de un ventilador o de una licuadora.
Como verás, en el motor eléctrico se produce
un efecto inverso al generador: se transforma
energía eléctrica en mecánica (movimiento).
Continuamente estamos manejando motores eléctricos: la secadora de pelo, la
lavadora, la lustradora, etc. Si tienes alguno de estos aparatos malogrados, puedes
abrirlo y encontrarás siempre un motor que consta de imán y una bobina que se
conecta a la corriente eléctrica. ¡Tú también puedes hacer un motor sencillo! (Ver
ficha de trabajo).
Investiga para
qué sirven los
alternadores que hay
en los carros y haz un
esquema indicando su
funcionamiento.
¿Cuáles son
se utilizan
¿
Cómofuncionan
?
sus elementos?
¿Quéson?
¿Para qué se
Alternadores
N
S
Eje

TERCER MOMENTO: Sistema de coordenadas
cartesianas,3D
Las coordenadas cartesianas
son un sistema de coordenadas formado
por dos ejes en el plano y por tres ejes en
el espacio, mutuamente perpendiculares,
que se cortan en el origen.
Sistema de coordenadas plano (cartesianas 2D = 2 dimensiones)
En el plano, las coordenadas cartesianas o rectangulares xxxxx e yyyyy se denominan
respectivamente abcisa y ordenada. Cuando se escriben valores para estas coordenadas
se indica una distancia del punto (en unidades) y su sentido (+ o –) a lo largo del eje xxxxx
o yyyyy con respecto al sistema de coordenadas o con respecto al punto previo. Por ejemplo:
◆ Señala en el sistema de coordenadas mostrado los cuatro cuadrantes en los que queda
dividido el plano por el sistema de coordenadas cartesianas.
◆ Indica los signos de las coordenadas
cartesianas de un punto según su cuadrante.
CuadranteCuadranteCuadranteCuadranteCuadrante AbcisaAbcisaAbcisaAbcisaAbcisa OrdenadaOrdenadaOrdenadaOrdenadaOrdenada
I
II
III
IV
Coordenadas cartesianas 2D
y
x
6
5
4
3
2
1
–1
–2
–3
–4
–5
–5 –4 –3 –2 –1 1 2 3 4 5 6 7 8 9
y
x
(–4, 2)
(8, 5)
Origen

El espacio real en el que vivimos es de tres
dimensiones (3D) por eso se utiliza un sistema de
coordenadas cartesianas mediante tres ejes
mutuamente perpendiculares. El punto en el que estos
ejes se cortan se llama origen.
Hay ocasiones en que se hace necesario representar un objeto o fenómeno tal y como lo
vemos en la realidad, es decir, en tres dimensiones.
Por ejemplo, el movimiento de una carga eléctrica en un campo magnético.
● Si una carga eléctrica (q) penetra en un campo magnético (B) con una velocidad (v),
se observará que sobre la carga aparece una fuerza (F). Este fenómeno se representa
en tres dimensiones de la siguiente manera:
Sistemadecoordenadasespacial(cartesianas3D=3dimensiones)
Para fijar una figura en el espacio se emplea como sistema de referencia el llamado
sistema de coordenadas espacial. El sistema cartesiano (x, yx, yx, yx, yx, y) puede extenderse hacia
tres dimensiones añadiendo una tercera coordenada zzzzz.
Dibujo de coordenadas cartesianas 3D
–9 –8 –7 –6 –5 –4 –3 –2
–9 –8 –7 –6 –5 –4 –3 –2 –1 1 2 3 4 5 6 7 8 9
2 3 4 5 6 7 8 9
x
–x y
–y
z
–z
6
5
4
3
2
1
–1
–2
–3
–4
–5
–6
Punto de origen del SCU
Ejes x, y, z del sistema de
coordenadas universales
F
B
V
α
q

En el tercer momento has estudiado el sistema de coordenadas cartesianas en 2D y 3D
identificando los elementos de la representación cartesiana. Has visto la forma de
determinar la posición de un punto en el sistema de coordenadas cartesianas 3D.
Investiga
y presenta un informe
sobre otros sistemas de
coordenadas que existen
para representar puntos
en 2D y 3D.
El proceso de introducción de coordenadas cartesianas 3D (x, y, z) es similar al empleado
en las coordenadas 2D (xxxxx, yyyyy). Además de precisar los valores xxxxx e y,y,y,y,y, debe estipular un
valor zzzzz.
En la figura siguiente, la coordenada 3, 2, 5 indica un punto situado a 3 unidades del eje
xxxxx positivo, a 2 unidades del eje yyyyy positivo y a 5 unidades del eje zzzzz positivo. Se pueden
indicar valores de coordenadas absolutas basados en el origen del sistema de coordenadas
o valores de coordenadas relativos basados en el último punto indicado.
◆ Dibuja un sistema de coordenadas cartesianas (x, y, z) y representa los siguientes puntos.
a) P (3,-2,5) b) A (-2, 4,-3) c) B (0, 3,6)
d) G (5,2,-4) e) H (-6,3,-6) f) K (7,4,1)
● ¿En cuántas partes divide el espacio
la intersección de los tres ejes que
forman el sistema cartesiano 3D?
● ¿Cuáles son los signos de cada
coordenada en cada una de estas
partes?
Coordenadas cartesianas 3D
x
–x y
–y
z
–z
(3, 2, 5)
3
5
2

FICHADETRABAJO
Construyendounmotoreléctrico
● 2 m de alambre para bobinas aislado con barniz (se consigue en las ferreterías),
dos imperdibles medianos, dos pequeños imanes de barra, dos pilas grandes en un
portapilas, una tira de hojalata de 2,2 x 10 cm, dos chinches, dos cables de luz de
10 cm cada uno y una base de madera.
1. Haz una bobina enrollando el alambre
alrededor de una tapa de botella o de un
plumón grueso. Antes de empezar a
enrollar deja 5 cm de alambre. Da 10
vueltas y deja otros 5 cm de alambre libre.
Para que la bobina no se desarme, da dos
pasadas con los extremos libres.
Finalmente, quita el barniz de los extremos
con una lija.
2. Dobla la tira de hojalata en forma de U y
sujétala a la madera con los chinches.
3. Fija los imperdibles a los costados de la
tira de hojalata. Conecta uno de los
extremos de los cables a cada imperdible.
4. Mete los extremos libres de la bobina en
los ojos de los imperdibles. Coloca los
imanes en los extremos de la hojalata.
5. Conecta los extremos libres de los cables a
los polos del portapilas para cerrar el
circuito. Si la bobina no gira, empújala
suavemente con la punta del lapicero.
Observa cómo el motor se pone en
funcionamiento.
Como habrás notado, en el motor que has construido se producen las siguientes
transformaciones de energía:
1
2 y 3
4 y 5
➞ ➞ ➞ENERGÍA ENERGÍA ENERGÍA ENERGÍA
QUÍMICA ELÉCTRICA MAGNÉTICA MECÁNICA

FICHA INFORMATIVA
Laelectricidadllegaatucasa
Desde las centrales eléctricas hasta los hogares e industrias la electricidad recorre un
largo camino, durante el cual se va modificando el voltaje. Esto se debe a que en las
centrales eléctricas se producen cientos de miles de voltios, mientras que lo que tú
necesitas es 220 V para hacer funcionar el televisor, la plancha, la radio y cualquier
electrodoméstico de tu casa.
● La electricidad que se produce en una central tiene un voltaje de 20 000 V
aproximadamente. Para transportarla con mayor facilidad “la empaquetan”, es decir,
los transformadores de la central elevan el voltaje a unos 130 000 V. De esta manera
circula por los cables de alta tensión.
● Cerca de la ciudad, y en una gran subestación, otros transformadores la rebajan a
60 000 V para aproximarla a los centros de consumo.
● Al llegar a ellos, la electricidad se reduce en otras subestaciones hasta 10 000 V
para suministro de zonas residenciales e industriales.
● La electricidad de 10 000 V se reduce a 220 V para llegar a las viviendas y pequeñas
industrias. La reducción se hace mediante unos transformadores que se encuentran
en casetas subterráneas o en los postes.
Averigua si en tu localidad hay subestaciones, cables de alta tensión, transformadores
en los postes y otros elementos que distribuyen la electricidad y preséntalos en un
plano. Investiga también los peligros que pueden ocasionar.
Central eléctrica Transformador Subestación
20 000 V
Torre
eléctrica130 000 V
Torres eléctricas
60 000 V
SubestaciónSubestaciónSubestación
10 000 V 10 000 V 10 000 V
Ciudades Hospital Industria

171
● Conocer los elementos de las ondas y describir
cada una de sus clases.
Identificar las funciones seno y coseno como la
representación gráfica de las ondas y reconocer la
función cuadrática.
● Describir las funciones exponenciales y logarítmicas.
Reconocer las principales características de las ondas
sonoras, sus aplicaciones tecnológicas y comprender
los efectos de la contaminación acústica.
● Analizar el comportamiento de la luz en los fenómenos
de reflexión y refracción y sus aplicaciones. Conocer
la proporcionalidad de segmentos para entender
algunos fenómenos ópticos.
FENÓMENOS ONDULATORIOSFENÓMENOS ONDULATORIOSFENÓMENOS ONDULATORIOSFENÓMENOS ONDULATORIOSFENÓMENOS ONDULATORIOS
Indagar sobre los conocimientos científicos relacionados con las ondas electromagnéticas,
sonoras, luminosas y sísmicas para explicar situaciones de la vida cotidiana. Valorar sus
aplicaciones tecnológicas y prevenir efectos nocivos. Describir mediante funciones
matemáticas el comportamiento de estos fenómenos.
1.1.1.1.1. Las ondasLas ondasLas ondasLas ondasLas ondas
2.2.2.2.2. El sonidoEl sonidoEl sonidoEl sonidoEl sonido
3.3.3.3.3. La luzLa luzLa luzLa luzLa luz
● Interpretar situaciones y hechos cotidianos, relacionadas con las propiedades del
sonido y la luz.
● Describir el espectro electromagnético y sus aplicaciones tecnológicas.
● Explicar el funcionamiento de aparatos que usan ondas sonoras, luminosas y
electromagnéticas y que han permitido mejorar la calidad de vida de las personas.
● Interpretar las causas de los sismos como hechos naturales frente a los cuales debemos
estar preparados.
● Identificar y graficar funciones exponenciales y logarítmicas como modelos para el
análisis de diversos fenómenos y situaciones de la realidad.
● Identificar e interpretar la relación de proporcionalidad en el plano, utilizando el
teorema de Thales.

173
Las ondasLas ondasLas ondasLas ondasLas ondas
1. Ondas: elementos y clases
2. Ondas electromagnéticas
3. Función cuadrática
Conocer los elementos de las ondas y
describir cada una de sus clases.
Identificar las funciones seno y coseno
como la representación gráfica de las
ondas y reconocer la función cuadrática.
● En el primer momento a través de
gráficos y observaciones de la vida
cotidiana, comprenderás los elementos
de las ondas y su clasificación.
● En el segundo momento analizarás la
variedad de ondas electromagnéticas
que existen y sus aplicaciones
tecnológicas. Además observarás la
representación gráfica de las ondas
utilizando las funciones periódicas,
seno y coseno.
● En el tercer momento conocerás la
función cuadrática y su representación
gráfica.
● Sismos y terremotos ● Frecuencia
● Amplitud
● Onda mecánica
● Espectro electromagnético
● Función periódica
● Período
● Función cuadrática y su representación
gráfica
● Función seno, coseno y su
representación gráfica
Las ondas
● Concepto y elementos
Clases de ondas
● Mecánicas
● Electromagnéticas
● Aplicando la función cuadrática

174 Fenómenos ondulatorios
PRIMERMOMENTO:Ondas:elementosyclases
● Si se coloca un corcho en una tina con agua, ¿las ondas que se forman al
arrojar la piedra hacen desplazar el corcho o lo hacen subir y bajar sin
desplazarse? Realiza la experiencia y plantea tu respuesta.
¿Qué son las ondas?
Una onda es una vibración que se propagaes una vibración que se propagaes una vibración que se propagaes una vibración que se propagaes una vibración que se propaga. Las ondas transportan energíatransportan energíatransportan energíatransportan energíatransportan energía
pero no materiapero no materiapero no materiapero no materiapero no materia.
Las ondas son capaces de propagar una gran cantidad de energía. Por ejemplo:
● Las olas del mar pueden golpear y voltear
un bote.
● Las ondas sísmicas mueven edificios y
puentes.
● Las ondas sonoras pueden mover y hasta
romper ventanas.
● Las microondas pueden calentar alimentos.
● Las ondas de luz pueden hacer que las
plantas realicen la fotosíntesis.
● En la experiencia que acabas de realizar, el agua estaba tranquila y, al arrojar una piedra,
se ha producido una perturbación que la hace vibrar. Esta vibración se trasmite en forma
de ondas.
● Si hay algún objeto flotando, observarás que, al ser alcanzado por las ondas, no se
desplaza con ellas sino que se eleva y baja en la misma posición. Esto significa que las
ondas no transportan materia –en este caso, agua– sino lo que se transmite es vibración.
¿Has arrojado alguna vez una
piedra en un estanque? Te habrás fijado
que se producen una serie de ondas que se
propagan en círculos desde el punto donde
cae la piedra, alejándose de él.

175Fenómenos ondulatorios
◆ Indica las diferencias que hay entre cada par de ondas.
a) ¿Por qué las lunas de las ventanas vibran cuando pasa un avión?
b) ¿Qué diferencia hay entre frecuencia y amplitud de onda?
Elementosdelasondas
En todas las ondas se pueden distinguir los siguientes elementos: longitud, amplitud
y frecuencia.
Longitud.Longitud.Longitud.Longitud.Longitud. Es la distancia entre dos crestas sucesivas. Por ejemplo, en las olas del
mar sería la distancia entre una ola y otra. Existen ondas que son muy largas y su
distancia se mide en metros. En cambio hay otras muy cortas y se miden en cm,
mm, etc.
Amplitud.Amplitud.Amplitud.Amplitud.Amplitud. Es la máxima altura de la onda. En las olas del mar sería la altura
máxima que alcanzan. Se mide también en metros, cm o mm.
Frecuencia.Frecuencia.Frecuencia.Frecuencia.Frecuencia. Es la rapidez con la que se producen las ondas. En términos científicos
diremos que es el número de ondas que se producen en un segundo. Se mide en
hertzios (Hz). Por ejemplo, las ondas de radio tienen una frecuencia de 106
Hz.
1 Hz = 1 onda/s
Velocidad propagación.Velocidad propagación.Velocidad propagación.Velocidad propagación.Velocidad propagación. Es la velocidad con que se propaga la onda. Se mide
en m/s. Así, la velocidad del sonido en el aire es de 340 m/s y la velocidad de la luz
es 300 000 km/s.
Longitud
Amplitud

Clases de ondas
Las ondas se pueden clasificar en mecánicas y electromagnéticas.
Ondas mecánicasOndas mecánicasOndas mecánicasOndas mecánicasOndas mecánicas. Son aquellas que necesitan un medio materialmedio materialmedio materialmedio materialmedio material para
propagarse. El medio puede ser un líquido, un gas o un sólido. Por ejemplo:
● Las ondas que se producen en un estanque.Las ondas que se producen en un estanque.Las ondas que se producen en un estanque.Las ondas que se producen en un estanque.Las ondas que se producen en un estanque. Estas se propagan a través
del agua, sin la presencia del agua no existiría la onda.
● El sonido.El sonido.El sonido.El sonido.El sonido. El cual se propaga a través, del aire, del agua y de los cuerpos
sólidos.
● Las ondas sísmicas.Las ondas sísmicas.Las ondas sísmicas.Las ondas sísmicas.Las ondas sísmicas. Ellas se propagan a través del suelo.
Ondas electromagnéticasOndas electromagnéticasOndas electromagnéticasOndas electromagnéticasOndas electromagnéticas. Son aquellas que
no necesitan un medio material para
propagarse. Estas ondas se propagan en el
vacíovacíovacíovacíovacío, aunque también pueden desplazarse en
medios materiales. Por ejemplo, la luz del Sol
llega a nosotros por medio de ondas
electromagnéticas que atraviesan el espacio
vacío; sin embargo, la luz también se propaga
en el aire y en el agua.
Son ondas electromagnéticas: la luz visible, las
ondas de radio, los rayos X, entre otras.
En el siglo XIX el físico Inglés
James Maxwell postuló la
existencia de las ondas
electromagnéticas.
Este hecho fue confirmado
años después por los físicos
alemanes Hertz y Roentgen.
En el primer momento has estudiado las características de las ondas y las has clasificado
en mecánicas y electromagnéticas. En el segundo momento analizarás las ondas
electromagnéticas.
En tu carpeta de trabajoEn tu carpeta de trabajoEn tu carpeta de trabajoEn tu carpeta de trabajoEn tu carpeta de trabajo:
◆ Copia y completa el cuadro
Clases de ondasClases de ondasClases de ondasClases de ondasClases de ondas
Ondas mecánicasOndas mecánicasOndas mecánicasOndas mecánicasOndas mecánicas Ondas electromagnéticasOndas electromagnéticasOndas electromagnéticasOndas electromagnéticasOndas electromagnéticas
¿Qué son?
Ejemplos
Las ondas mecánicas pueden
ser fácilmente captadas por nuestros sentidos:
(vemos olas, oímos sonidos, sentimos un temblor).
En cambio, no podemos percibir, las ondas
electromagnéticas con excepción de la luz.

SEGUNDOMOMENTO:Ondaselectromagnéticas
La luz, las microondas, los rayos X y las transmisiones de radio y televisión son
formas de ondas electromagnéticas. Todas ellas son de la misma naturaleza pero
difieren en su frecuencia. Así, las ondas de radio son de menor frecuencia y los
rayos gamma de mayor frecuencia.
Se conoce con el nombre de espectro electromagnéticoespectro electromagnéticoespectro electromagnéticoespectro electromagnéticoespectro electromagnético el conjunto de ondas
electromagnéticas ordenadas según su frecuencia.
Rayos gammaRayos gammaRayos gammaRayos gammaRayos gamma. Son las ondas de más alta frecuencia. Se producen al
desintegrarse los núcleos de los átomos como, por ejemplo, en la explosión
de una bomba atómica. Habrás escuchado que una explosión atómica causa
gran destrucción, esto se debe a que los rayos gamma trasportan gran cantidad
de energía y son capaces de penetrar metales y edificios de concreto;
asimismo, atraviesan cualquier cuerpo vivo (persona, animal o planta) y lo
destruyen.
Rayos XRayos XRayos XRayos XRayos X. Son capaces de penetrar por las partes blandas del cuerpo, pero no los
huesos. Se producen en máquinas de rayos X y se emplean en medicina para
fotografiar huesos y algunos órganos internos. Una exposición rápida no hace
daño, pero si es prolongada puede destruir los órganos.
Rayos ultravioleta (UV)Rayos ultravioleta (UV)Rayos ultravioleta (UV)Rayos ultravioleta (UV)Rayos ultravioleta (UV). No son visibles y sí peligrosos pues pueden producir
cáncer a la piel. Estos rayos constituyen la parte dañina de la radiación solar.
Luz visibleLuz visibleLuz visibleLuz visibleLuz visible. La producen el sol, los focos y las fogatas. Son las únicas ondas
electromagnéticas que impresionan nuestros ojos, es decir, las podemos ver.
Rayos infrarrojosRayos infrarrojosRayos infrarrojosRayos infrarrojosRayos infrarrojos. Nos dan calor. Los emiten todos los cuerpos calientes. El
nombre infrarrojo significa por debajo del rojo.
Microondas.Microondas.Microondas.Microondas.Microondas. Se utilizan en las telecomunicaciones: teléfonos comunes y celulares,
radar, TV y en el horno de microondas.
Ondas de radioOndas de radioOndas de radioOndas de radioOndas de radio. Son las que poseen más baja frecuencia. Reciben este nombre
porque se las emplea en las trasmisiones de radio. Se producen en ciertos
dispositivos eléctricos como las antenas.
Luz visible
Rayos gamma Rayos X Infrarrojo Ondas de radioMicroondas

La energía radiante del sol
Seguramente sabes que cuando los astronautas
viajan al espacio llevan trajes especiales para
protegerse de las radiaciones solares. Es tal el
calor y la cantidad de rayos destructivos que los
astronautas soportan, que sin estos trajes
morirían en el acto.
El Sol produce diferente tipos de radiaciones,
rayos de luz, rayos infrarrojos, rayos ultravioleta
(UV), rayos X y rayos gamma.
Estas radiaciones no llegan totalmente a la Tierra
porque la atmósfera es como un filtro que impide
el paso de alguna de ellas.
● Las nubes, el polvo y los gases del aire
retienen y reflejan parte de la radiación solar.
● La capa de ozono retiene gran parte de la radiación ultravioleta (UV).
Desafortunadamente, por la contaminación atmosférica, la capa de ozono ha
disminuido y los UV entran en mayor cantidad a la Tierra causando daño a las personas,
animales y plantas. Los UV son responsables del cáncer a la piel.
Por ello es necesario controlar las actividades que destruyen la capa de ozono. Además
debes evitar actividades al aire libre cuando la fuerza de los rayos solares es mayor. Lleva
ropa y accesorios que te protejan: sombrero, gorra, lentes de sol con protección de rayos
UV, camisa de manga larga o pantalones largos. Usa protectores solares, etc.
Investiga las
aplicaciones y efectos
de alguna de las ondas
electromagnéticas y
presenta la información
en un tríptico.
● Haz un gráfico circular sobre la
radiación solar que llega a la Tierra.
Datos: 40% son ondas luminosas,
50% rayos infrarrojos y 10% UV.
La exposición al sol
tiene algunos efectos benéficos, pero
tomarlo en exceso puede provocar un
envejecimiento prematuro de la piel y
cambios en su textura.
Capa de ozono
Radiación solar
peligrosa desviada

Para expresar la forma de una onda se usan las funciones periódicas, seno y coseno. Una
función periódica se caracteriza porque en su representación gráfica una forma se repite
cada cierto intervalo de longitud.
Esta gráfica se repite cada intervalo de longitud 2. Este intervalo se conoce como periodo
y se representa con la letra TTTTT. En este caso el periodo es: TTTTT = 2
La importancia de las ondas y de las funciones periódicas ha ido cobrando valor en la
medida en que el ser humano descubre cómo su universo está lleno de ondas y vibraciones,
tanto al mirar a lo lejos, las galaxias, como al explorar lo muy cercano, el interior de los
átomos.
La luz, el sonido, la electricidad, el electromagnetismo, los rayos X son fenómenos ondulatorios
que han sido analizados matemáticamente utilizando las funciones periódicas, seno y coseno.
El ser humano ha aprendido a utilizar el análisis
matemático de los movimientos periódicos
(movimientos que se repiten cada intervalo de
tiempo) de mil formas distintas. La radio, el radar,
el sonar, el microscopio electrónico, los más
modernos instrumentos de exploración del cuerpo
humano como la resonancia magnética, los celulares
son en gran parte consecuencia de este estudio
matemático y físico.
Investiga la
aplicación de la
resonancia magnética
para el diagnóstico de
determinadas
enfermedades y elabora
un informe.
● ¿Qué situaciones de la vida cotidiana
puedes identificar como fenómenos
periódicos, o sea, que se repiten
cada intervalo de tiempo?
y
0 2 4 6 8 10 12 14
x
Existen medidas asociadas a las ondas que necesitas
conocer para describirlas; por ejemplo, cada cuánto
tiempo se repiten (frecuencia), cuán largas son (longitud
de onda) y cuál es su tamaño vertical (amplitud). Para
conocer y predecir su comportamiento, se usa la
representación gráfica de una función matemática.

Has identificado cuáles son y en qué se aplican las ondas electromagnéticas conocidas
hasta hoy. También, que para representar las ondas se utilizan las funciones periódicas,
seno y coseno. En el tercer momento estudiarás las funciones cuadráticas que tienen
otra forma de representación gráfica.
◆ De manera análoga a la representación gráfica de la función
seno, haz una tabla de valores y elabora la gráfica de la
función coseno.
La gráfica que se obtiene es una curva continua en
el plano coordenado, esta se parece a la
representación gráfica de las diversas ondas que
has visto anteriormente.
Función seno
La ecuación matemática que representa la onda más simple es la siguiente:
yyyyy = Sen (xxxxx)
Esta ecuación describe cómo una onda podría ser trazada en un sistema de coordenadas,
donde el eje horizontal (xxxxx) es el valor del ángulo medido en radianes y el eje vertical (yyyyy)
es el valor de la función trigonométrica seno correspondiente a ese ángulo. La gráfica de
la función seno sería:
Tabla de valoresTabla de valoresTabla de valoresTabla de valoresTabla de valores
x (rad) x(grad) y = sen (x)
–π –180° 0
–π/2 –90° –1
0 0 0
π/2 90° 1
π 180° 0
3π/2 270° –1
2π 360° 0
El radián es otra manera de medir los ángulos en la que 2π radianes equivalen a 360º
que definen un círculo completo. Los ángulos más pequeños se definen en fracciones
como las que observas en la tabla de valores.
y
x
(radianes)
–π 2ππ0
–1
1
–π/2 3π/2π/2

TERCER MOMENTO: Función cuadrática
Se llama función cuadrática a una función polinómica de segundo grado de la forma:
y = f(x) = aaaaax2 + bbbbbx + ccccc con aaaaa ≠ 0
Ejemplos de funciones cuadráticas: f(x) = x2 –1 f(x) = – x2
Como ya sabes para elaborar la grafica de estas funciones se da valores a x para ir
obteniendo los valores de y.
Representación gráficaRepresentación gráficaRepresentación gráficaRepresentación gráficaRepresentación gráfica
La gráfica de una función cuadrática es una curva llamada parábola cuyo eje es paralelo
al eje y.
Las funciones matemáticas ayudan a estudiar
diversas situaciones problemáticas en distintas ciencias,
por ejemplo la física. Así la función seno se usa para
describir y representar el comportamiento de las ondas y
la función cuadrática se usa para describir y representar
algunos tipos de movimiento, como el movimiento
rectilíneo uniformemente variado.
Esta parábola se abre hacia arriba si aaaaa > 0,
y se dice que es cóncava hacia arriba.
Por ejemplo: La gráfica que corresponde a
f(x) = 2x2 – 6x + 3 es:
Esta parábola se abre hacia abajo si aaaaa < 0,
y se dice que es cóncava hacia abajo.
Por ejemplo: La gráfica que corresponde a
f(x) = – x2 + 2x + 5 es:

La función cuadrática modela diversas situaciones de nuestro entorno. Por ejemplo, la
variación de la posición en función del tiempo en un M.R.U.V., la trayectoria de proyectiles,
el lanzamiento de una pelota, la curvatura de los zapatos, construcciones o estructuras
de puentes, las curvas de utilidad oferta y demanda de los productos de una empresa, la
forma de algunos celulares o edificios, etc.
◆ Busca en periódicos o revistas imágenes que representan la forma de la función cuadrática
(parábola).
Para apreciar la aplicación de la función cuadrática recuerda lo trabajado en la unidad 1:
El movimiento rectilíneo uniformemente variado (M.R.U.V.), donde la velocidad varía una
cantidad constante en cada unidad de tiempo. Un ejemplo de movimiento rectilíneo
uniformemente variado es el de caída libre.
La ecuación de la posición en función del tiempo para el movimiento uniformemente
variado es: e = e0 + v0t +
1
2
at2
Si analizas verás que cada término de esta ecuación tiene su equivalente con la expresión
de una función cuadrática:
e = e0 + v0 t +
1
2
a t2
↓ ↓ ↓ ↓ ↓ ↓
y = ccccc + bbbbb x + aaaaa x2
La representación grafica de la posición en función del tiempo será una parábola pues se
trata de una función cuadrática:
Gráfico de e = e(t) para el M.R.U.V.
e
t
e0
Parábola

Esta parábola será cóncava hacia arriba o hacia abajo dependiendo del signo de la
aceleración (a).
Si a = (+) será cóncava hacia arriba (∪)
Si a = (–) será cóncava hacia abajo (∩)
Recuerda que la aceleración es positiva cuando la velocidad aumenta y es negativa cuando
la velocidad disminuye.
1) Un móvil sale de la posición 4 m con una velocidad de 1 m/s y una aceleración de 4 m/s2.
a) Escribe la ecuación cuadrática de posición en función del tiempo.
b) Realiza el gráfico e = e(t).
a) Reemplazando valores en la ecuación, e = e0
+ v0
t +
1
2
at2
se obtiene:
e = 4 + (1)t +
1
2
(4)t2
e = 4 + t + 2t2
b) Para representar gráficamente esta ecuación se asigna valores a t y se va calculando
los valores de e. Con estos datos se construye la siguiente tabla.
t(s) 0 1 2 3 4 5
e(m) 4 7 14 25 40 59
La gráfica correspondiente es:
Conclusiones:Conclusiones:Conclusiones:Conclusiones:Conclusiones:
● La parábola se forma cóncava hacia arriba porque a = (+)
● Aunque solo se vea un arco esto es una parábola. Se completaría si se diera valores
negativos para t (–1 s, –2 s, etc.).
1 2 3 4 5
e(m)
t(s)
60
50
40
30
20
10

En el tercer momento has reconocido la aplicación y representación gráfica de una
función cuadrática en diversos objetos de tu entorno y en situaciones donde se presenta
el movimiento rectilíneo uniformemente variado.
2) Una persona está a 20 metros del piso y tira una piedra hacia arriba con una velocidad
inicial de 10 m/s. Escribe la ecuación cuadrática y su representación grafica
correspondiente.
Los movimientos de tiro vertical como es el caso del problema y de caída libre son
ejemplos de M.R.U.V. Las fórmulas que se utilizan son las mismas solo que el espacio (e)
se cambia por altura (h) y la aceleración (a) se representa por la aceleración de la
gravedad (g) que se considera 10 m/s2. Además se debe tomar en cuenta que si se trata
de tiro vertical se está venciendo la fuerza de gravedad entonces ésta es negativa.
La ecuación sería: h = h0 + v0t ± g t2
Para el caso del problema reemplazando valores se tiene:
h = 20 + 10t – 5t2
t (s) 0 1 2 3 4
h (m) 20 25 20 5 –20
La gráfica es:
Conclusiones:
● La parábola es cóncava hacia abajo porque a = g = (–)
● De acuerdo a la gráfica puedes concluir que la altura máxima que alcanza la piedra antes
de comenzar a caer es de 25 m.
◆ Grafica las siguientes funciones:
1) f(x) = x2
– 4x – 5 2) f(x) = –3x2
– 11x + 4 3) f(x) = 4x2
– 12x + 9
◆ Resuelve el siguiente problema:
Una hormiga sale de la posición e0 = 0 y comienza a moverse con una aceleración de
2 m/s2 (v0 = 0). Escribe la ecuación cuadrática y su representación gráfica correspondiente.
1
2
30
20
10
-10
-20
1 2 3 4
h(m)
t(s)

FICHADETRABAJO
Aplicando la función cuadrática
Se desea hacer un corral de forma rectangular con 100 m
de malla, para encerrar algunos pollos. ¿Cuáles deben ser
las dimensiones del corral para cubrir el área máxima?
En primer lugar, dibujaremos la situación que se nos plantea:
Si x representa el ancho, y representa el largo, tendríamos que el perímetro es 2x + 2y.
Como solo contamos con 100 m de malla, entonces este perímetro debe ser igual a
100. Es decir:
2x + 2y = 100
Expresamos y en términos de x, para trabajar con una sola variable:
2x + 2y = 100
2y = 100 – 2x
y =
100 2
2
− x
y = 50 – x
El área de un rectángulo es base por altura, por lo que el área deseada puede expresarse
como: A = xy
Puesto que y expresado en términos de x es (50 ––––– x)
A = x (50 – x)
A = 50x – x2
El área en función del ancho es: A(x) = 50x – x2
x x
y
y
La función cuadrática
nos ayuda a resolver problemas
en los que deseamos obtener el
máximo provecho de una
situación.

Dándole la forma ax2 +bx + c se tiene la función cuadrática A(x) = x2 + 50x + 0, cuyos
resultados se comportan gráficamente como una parábola.
Esto significa que tiene un valor máximo que se obtiene con el vértice, y es precisamente
lo que necesitamos saber.
El xxxxx del vértice se obtiene mediante el eje de simetría.
En este caso: x =
–b
a2
Reemplazando: x =
–
(– )
50
2 1
x = 25
Esto significa que el área máxima se obtiene cuando el largo es 25, y la longitud del
ancho la determinamos por la formula:
y = 50 – x
Reemplazando: y = 50 – 25
y = 25
Por consiguiente, la figura que con un perímetro de 100 m encierra el área máxima es
un cuadrado de 25 m de lado y el área máxima es de 625 m2.
Resuelve el siguiente ejercicio:Resuelve el siguiente ejercicio:Resuelve el siguiente ejercicio:Resuelve el siguiente ejercicio:Resuelve el siguiente ejercicio:
Un granjero dispone de 210 m de malla para delimitar dos corrales adyacentes
rectangulares idénticos, ¿cuáles deben ser las dimensiones para obtener el área máxima?
El dibujo de la situación que se desea calcular es:
x
x
y
y
y
x x

FICHA INFORMATIVA
Sismosyterremotos
La Tierra es un planeta formado por rocas,
pero sólo en el exterior las rocas son
sólidas. La parte exterior sólida se llama
corteza y es muy delgada. Si comparamos
la Tierra con un huevo, la cortezacortezacortezacortezacorteza sería
tan delgada como la cáscara.
El interior de la Tierra es muy caliente y las
rocas están fundidas formando una masa
pastosa (semilíquida) llamada magmamagmamagmamagmamagma.
La corteza, además, está fragmentada en
siete pedazos que llamamos placasplacasplacasplacasplacas.
Estas placas se encuentran flotandoflotandoflotandoflotandoflotando
sobre el magma interior como si
apoyáramos galletas, una junta a otra,
en una gelatina poco cuajada.
Desde hace millones de años, las placas
están en continuo movimientocontinuo movimientocontinuo movimientocontinuo movimientocontinuo movimiento, se
empujan entre sí y se separan. Los
movimientos de las placas son muy lentos
–a razón de 3 cm por año, pero a lo largo
de mucho tiempo producen cambios
como la formación de montañas.
MAGMA
Corteza
50 km
InteriordelaTierra
6300km
Cuando dos placas se acercan y
chocan, se levantan formando
una cordillera.
Si una placa se mete debajo de otra,
la que está arriba se arruga y se
levanta formando una cordillera.
Si una placa se aleja de otra, las
rocas calientes y fundidas de
abajo (magma) suben, se enfrían
y forman más fondo marino.
Placa Placa Placa Placa

¿Por qué se producen los sismos?¿Por qué se producen los sismos?¿Por qué se producen los sismos?¿Por qué se producen los sismos?¿Por qué se producen los sismos?
Las placas que forman la corteza terrestre están
moviéndose continuamente y sus movimientos
son lentos. Pero a veces las placas chocanchocanchocanchocanchocan en
las profundidades o se desplazan bruscamente
produciendo una vibración que se trasmite por
el suelo. Estas son las ondas sísmicas.
El punto donde se produce el choque de las
rocas se llama focofocofocofocofoco del sismo. El punto de la
superficie terrestre que está encima del foco
se llama epicentroepicentroepicentroepicentroepicentro. En este lugar el sismo se
siente con más intensidad.
A veces los sismos son violentos, como los
terremotos, pero en su mayoría son
imperceptibles.
En los lugares del mundo que están situados
donde confluyen dos placasconfluyen dos placasconfluyen dos placasconfluyen dos placasconfluyen dos placas se producen
más sismos. Eso ocurre, por ejemplo, en
nuestro país, concretamente en la costa de Ica;
allí confluyen la placa de Nazca con la placa
Suramericana que está debajo del mar.
¿Cómo se miden los sismos?¿Cómo se miden los sismos?¿Cómo se miden los sismos?¿Cómo se miden los sismos?¿Cómo se miden los sismos?
La intensidad de los sismos se mide mediante aparatos llamados sismógrafos. La escala
más utilizada es la de Richter que va de 1 a 9.
Los sismos de 3,5 grados no se sienten. Sólo son detectados por los sismógrafos.
Los efectos de los sismos son más graves si las viviendas no han sido construidas
siguiendo criterios técnicos básicos (número de columnas, distancias, materiales, etc.).
¿Es tu casa, colegio o
lugar de trabajo un lugar que
puede resistir un sismo fuerte?
¿Qué debes hacer en
caso de sismos?
Propagación
de las ondas
Foco del sismo
Epicentro

189
El sonidoEl sonidoEl sonidoEl sonidoEl sonido
1. Funciones exponencial y logarítmica
2. Características del sonido
3. Reflexión del sonido y contaminación
acústica
Describir las funciones exponenciales y
logarítmicas. Reconocer las principales
características de las ondas sonoras, sus
aplicaciones tecnológicas y comprender
los efectos de la contaminación acústica.
● En el primer momento analizarás el uso
de las funciones exponencial y
logarítmica para entender diversos
fenómenos de la naturaleza.
Distinguirás y resolverás ecuaciones
exponenciales y logarítmicas.
● En el segundo momento a través de
sencillas experiencias comprenderás
cómo se produce y trasmite el sonido
y las cualidades que permiten
reconocerlos.
● En el tercer momento reconocerás la
reflexión del sonido y los efectos de la
contaminación acústica en la salud.
● El ultrasonido en la naturaleza
● El ronquido: la molestia nocturna
● Vibración
● Decibel
● Hercio
● Ultrasonidos
● Sonar
● Ecógrafo
● Logaritmo
● Exponencial
Función logarítmica y exponencial
● Descripción y propiedades
● Ecuaciones exponenciales y logarítmicas
El sonido
● Cualidades
● Reflexión y transmisión
● Aplicaciones de la reflexión
● Contaminación acústica

PRIMERMOMENTO:Funcionesexponencial
ylogarítmica
Funciónexponencial
Se llama función exponencial de base aaaaa aquella cuya forma genérica es:
f(x) = aaaaax siendo aaaaa un número positivo distinto de 1.
La función exponencial puede considerarse como inversa a la función logarítmica
por cuanto se cumple que:
ax = b ⇔ logab = x
1. Para determinar la amplitud (intensidad) de una onda sísmica en la escala de Richter se
debe resolver una ecuación logarítmicalogarítmicalogarítmicalogarítmicalogarítmica en la que se expresa la magnitud MMMMM de un
terremoto en función de la amplitud AAAAA de sus ondas, así:
M = logAAAAA + CCCCC
Donde: CCCCC = 3,3 + 1,66logDDDDD – logTTTTT
CCCCC es una constante que depende del periodo TTTTT de las ondas registradas en el sismógrafo
y de la distancia DDDDD de éste al epicentro.
2. Si se desea calcular la antigüedad de un hueso hallado en un yacimiento arqueológico
mediante el método del carbono 14 se debe resolver una ecuación exponencial:
y = e–0,000121 t
Primero, se mide el porcentaje de carbono 14 que contiene el hueso hallado y este valor
se reemplaza en la ecuación exponencialexponencialexponencialexponencialexponencial. Por ejemplo, si fuera 20% la ecuación a
resolver quedaría así:
0,20 = e–0,000121 t
Existe diversidad de situaciones observables en la
naturaleza y en nuestra vida cotidiana cuyo estudio
implica la aplicación y planteamiento de funciones y
ecuaciones exponenciales y logarítmicas.

A continuación la representación gráfica de varias funciones exponenciales:
◆ Elabora una tabla de valores utilizando la ecuación dada para cada una de las gráficas
anteriores y verifica si la representación es correcta. Esta práctica te permitirá repasar
sobre el tema de potenciación visto en módulos anteriores.
Propiedades de las funciones exponencialesPropiedades de las funciones exponencialesPropiedades de las funciones exponencialesPropiedades de las funciones exponencialesPropiedades de las funciones exponenciales
Para toda función exponencial de la forma
f(x) = aaaaax, se cumplen las siguientes propiedades generales:
1. La función aplicada al valor cero es siempre igual a 1: f(0) = aaaaa0 = 1.
2. La función exponencial de 1 es siempre igual a la base: f(1) = aaaaa1 = aaaaa.
3. La función exponencial de una suma de valores es igual al producto de la aplicación de
dicha función aplicada a cada valor por separado.
f(x + x) = aaaaax + x = aaaaax • aaaaax = f(x) • f(x).
4. La función exponencial de una resta es igual al cociente de su aplicación al minuendo
dividida por la función del sustraendo:
f(x – x) = aaaaax – x = aaaaax/aaaaax = f(x)/f(x).
La función eLa función eLa función eLa función eLa función ex. Un caso particularmente interesante de función exponencial es f(x) = ex.
El número e se denomina épsilon y su valor es de 2,7182818285…..
Ecuaciones exponencialesEcuaciones exponencialesEcuaciones exponencialesEcuaciones exponencialesEcuaciones exponenciales
Se llama ecuación exponencial a aquella en la que la incógnita aparece como exponente.
Un ejemplo de ecuación exponencial sería:
aaaaax = bbbbb
Para resolver estas ecuaciones se suelen utilizar dos métodos alternativos:
1. Igualación de la base:Igualación de la base:Igualación de la base:Igualación de la base:Igualación de la base: consiste en aplicar las propiedades de las potencias para lograr que
en los dos miembros de la ecuación aparezca una misma base elevada a distintos exponentes:
aaaaax = aaaaay
En tales condiciones, la resolución de la ecuación proseguiría a partir de la igualdad x = y.
y
y = 3x
xO
y
x O
y =
x
1
3
y = 3x
y
x O
y =
x
1
3

Función logarítmica
Una función logarítmica es aquella que genéricamente se expresa como: f(x) = logax,
siendo aaaaa la base de esta función, que ha de ser positiva y distinta de 1.
La función logarítmica es inversa a la función exponencial dado que:
logax = b ⇔ ab = x
Resolver la siguiente ecuación exponencial: 42x+1 = (0,5)3x+5
Para solucionar el ejercicio se utiliza el método de igualación de la base:
22(2x + 1) = (1/2)3x + 5
24x + 2 = (1/2)3x + 5
24x + 2 = 2–(3x + 5)
24x + 2 = 2–3x – 5 Como las bases son iguales se igualan exponentes:
4x + 2 = –3x – 5
Resolviendo la ecuación se obtiene: x = –1
◆ Resuelve las siguientes ecuaciones exponenciales:
a) 32 – x2
= 3 b) 2x – 1 + 2x + 22x + 1 = 7 c) ex – 5e–x + 4e–3x = 0
A continuación la representación gráfica de funciones logarítmicas y de sus inversas
(exponenciales):
y y = ax
y = loga
x
xO
y
y = ax
y = log
a x
y
=
x
y
=
x
xO
a > 1 0 < a < 1
2. Cambio de variable:Cambio de variable:Cambio de variable:Cambio de variable:Cambio de variable: consiste en sustituir todas las potencias que figuran en la ecuación
por potencias de una nueva variable, convirtiendo la ecuación original en otra más fácil
de resolver.
22x – 3 . 2x – 4 = 0 ⇔ t2 – 3t – 4 = 0
Luego se deshace el cambio de variable.

Has conocido las funciones exponenciales y logarítmicas. En el siguiente momento
continuarás con el estudio de los fenómenos ondulatorios, específicamente con las
características del sonido.
Investiga sobre
los logaritmos decimales
y neperianos. Presenta 5
ejercicios resueltos.
El logaritmo de un número x es el exponente al cual hay que elevar la base aaaaa para
obtener x.
Esto es, si aaaaa > 0 y aaaaa es diferente de cero, entonces logaaaaax = b (si solo si) aaaaabbbbb ===== x.
Nota:Nota:Nota:Nota:Nota: La notación logloglogloglogaaaaax = bbbbb se lee “el logaritmo de x en base aaaaa es bbbbb”.
Siendo aaaaa la base, x el número y bbbbb el logaritmo.
Ejemplo:
1. log24 = 2 se lee “logaritmo de 4 en base 2 es igual a 2” y su representación en forma
exponencial es: 22 = 4
2. log21 = 0 Entonces 20 = 1
◆ Calcula por la definición de logaritmo el valor de bbbbb:
a) log 1
2
0,25 = b b) log
5
125 = b c) log 0,001 = y
d) ln
1
5
e
= y e) log
3
5 1
81
= y
Logaritmos decimalesLogaritmos decimalesLogaritmos decimalesLogaritmos decimalesLogaritmos decimales
Los logaritmos decimales son los que tienen base
10. Se representan por log(x).
Logaritmos neperianos o logaritmosLogaritmos neperianos o logaritmosLogaritmos neperianos o logaritmosLogaritmos neperianos o logaritmosLogaritmos neperianos o logaritmos
naturalesnaturalesnaturalesnaturalesnaturales
Los logaritmos naturales o logaritmos neperianos
son los que tienen base e. Se representan por ln (x)
o L(x).

SEGUNDOMOMENTO:Característicasdelsonido
Seguramente, alguna vez has visto o tocado una guitarra. Habrás notado que tiene seis
cuerdas y todas son de diferente grosor.
Cuando rasgas la cuerda más delgada se emite
un sonido agudo y cuando rasgas la cuerda más
gruesa se emite un sonido grave.
También habrás observado que en el extremo
de la guitarra hay unas clavijas que sirven para
ajustar las cuerdas y son usadas para afinar el
sonido de cada cuerda. Cuanto más ajustada
está la cuerda, más agudo es el sonido.
El sonido producido por una cuerda resulta muy débil para ser detectado por nuestros
oídos. Para lograr que el sonido se escuche, las guitarras tienen una caja de resonancia.
Esta aumenta la intensidad de las vibraciones que producen las cuerdas.
Las guitarras eléctricas no tienen caja de resonancia pero, en su lugar, tienen un
amplificador eléctrico.
● ¿Qué entiendes por sonidos
graves y sonidos agudos?
● Una tabla de madera, 12 clavitos, hilo nylon (de pescar).
1. Coloca dos hileras de clavos como se ve en el
esquema.
2. Ata entre clavo y clavo un trozo de hilo nylon.
3. Has vibrar las cuerdas: toca la cuerda más larga y
luego la más corta. ¿Cuál produce un tono más
agudo y cuál el más grave?
4. Toca una misma cuerda con diferente intensidad.
¿Cuándo el sonido es fuerte y cuándo débil?
5. Tensa un poco más una de las cuerdas y compara
su sonido con una que esté más suelta. ¿Qué
conclusiones sacas de esta experiencia?
Experimenta...
Cualidadesdel
sonido

◆ El sonido se propaga por ondas ________________________. Se trasmite a través del
___________, ___________y ______________. No se propaga en_______________.
◆ La velocidad del sonido en el aire es _________pero viaja más rápido en ___________.
¿Cómoseproduceytrasmiteelsonido?
Los sonidos se producen cuando los cuerpos vibranvibranvibranvibranvibran.
Por ejemplo, en la guitarra, el sonido se produce
cuando sus cuerdas vibran y, en la voz humana
cuando vibran las cuerdas vocales.
Al vibrar los cuerpos trasmiten la vibración entrasmiten la vibración entrasmiten la vibración entrasmiten la vibración entrasmiten la vibración en
forma de ondasforma de ondasforma de ondasforma de ondasforma de ondas a las partículas de aire, de agua o
de cualquier sólido que está a su alrededor. Finalmente,
si las vibraciones llegan a los oídos se convierten en lo que llamamos sonido.
Recuerda que el sonido son ondas mecánicas, es
decir, para propagarse requieren siempre de un
medio materialmedio materialmedio materialmedio materialmedio material. Por ejemplo, si colocamos un
reloj despertador dentro de una campana de
vidrio, el sonido de la alarma se escucha.
Sin embargo, si mediante una bomba extraemos
el aire de la campana, el sonido no se escucha.
Por esta razón en la Luna, donde no hay aire, no
se escucha ningún sonido.
La velocidad del sonido depende del medio en
que se propaga: es mayor en los sólidos, menor
en los líquidos y mucho menor en el aire. Así,
la velocidad del sonido en las rocas, es de
5 000 m/s, en el agua es de 1 450 m/s y en el
aire es de 340 m/s.
Investiga cómo
se produce el sonido en
un instrumento musical
que sea de tu agrado.
Vacío
Voz

Cualidades del sonido
A pesar de la enorme cantidad de sonidos diferentes que existen, se puede distinguir
con facilidad unos sonidos de otros. Esto se debe a que las ondas sonoras difieren
en cuatro aspectos: la intensidad, la duración, el tono y el timbre.
La intensidad o volumenLa intensidad o volumenLa intensidad o volumenLa intensidad o volumenLa intensidad o volumen. Permite calificar los sonidos en fuertes o débiles. La
intensidad depende de la amplitud de ondas. Por ejemplo, un grito es un sonido
de gran intensidad mientras que un susurro es de poca intensidad. Para medir la
intensidad del sonido se utiliza una unidad llamada decibeldecibeldecibeldecibeldecibel (dBdBdBdBdB).
La duraciónLa duraciónLa duraciónLa duraciónLa duración. Se relaciona con el tipo de vibración del objeto. Así podemos percibir
sonidos largos o cortos.
La frecuencia o tonoLa frecuencia o tonoLa frecuencia o tonoLa frecuencia o tonoLa frecuencia o tono. Es una característica que
permite distinguir entre sonidos graves y agudos.
La frecuencia depende de la rapidez con que se
produzcan las ondas. A los tonos graves
corresponde una frecuencia baja y a los tonos
agudos, las frecuencias altas. La frecuencia se
mide en hercios (Hz). El oído humano puede
detectar ondas comprendidas entre los 20 Hz y
los 20 000 Hz. Las de menor frecuencia se llaman
ultrasonidosultrasonidosultrasonidosultrasonidosultrasonidos y no son percibidas por las
personas, aunque hay animales como los perros
y las ballenas que son capaces de oirlas.
● Un lápiz y dos globos.
1. Pide a un compañero que golpee suavemente la mesa
con la punta de un lápiz.
2. Colócate a 1 metro de distancia de tu compañero y
escucha los sonidos.
3. Ahora, escucha los sonidos apoyando la oreja en la mesa.
¿Percibes alguna diferencia? ¿A qué crees que se deba?
4. Repite la experiencia, pero ahora escucha los sonidos
a través de un globo con aire y con otro lleno de
agua. ¿En qué globo oyes mejor los golpes del lápiz?
¿Por qué?
■ ¿Qué conclusiones puedes sacar de esta actividad?
Experimenta...¿Dóndese
propaga mejor el sonido?
Sonido agudo
Sonido grave

En el segundo momento has visto los elementos que se deben tener en cuenta cuando
se analizan las ondas sonoras. En el tercer momento analizarás la reflexión del sonido
y sus aplicaciones.
El timbre.El timbre.El timbre.El timbre.El timbre. Es una característica que se refiere a la forma de la onda. Debido a
ello, podemos distinguir los sonidos que producen cada voz y cada instrumento.
Dos sonidos producidos por distintos instrumentos, guitarra y violín, por ejemplo,
pueden tener la misma intensidad y el mismo tono, y sin embargo no suenan igual
porque cada material vibra de una forma diferente provocando ondas sonoras
que lo identifican.
◆ Indica cómo es el sonido en cada caso. Escoge las palabras del recuadro.
■ El pito de un policía ________________________
■ El rugido de un león _______________________
■ La sirena de un barco ______________________
■ La corneta del heladero ____________________
■ El canto de un gorrión ______________________
■ El sonido del agua que sale del caño __________
Investiga cómo
funciona un megáfono
y construye uno
usando cartón.
◆ Relaciona las dos columnas escribiendo la letra correspondiente
( ) Permite distinguir tonos graves y agudos. a) intensidad
( ) Distingue la voz de cada persona o instrumento. b) decibel
( ) Se refiere al volumen de los sonidos. c) hercio
( ) Mide el volumen del sonido. d) timbre
( ) Mide la frecuencia. e) ultrasonidos
( ) Son ondas que no escuchan las personas pero f) frecuencia
algunos animales sí.
fuerte y débil débil y grave
fuerte y agudo débil y agudo

Todas estas
situaciones tienen que ver
con la reflexión del sonido:
este es el tema que verás a
continuación.
Reflexióndelsonido
La reflexión es una propiedad del sonido muy conocida. Cuando chocan las ondas
sonoras contra un objeto rebotan y si las condiciones son adecuadas, hasta se
puede producir “eco”. El eco es la repetición nítida del sonido.
La reflexión del sonido suele ser evitada pero
en algunos casos se aprovecha. Por ejemplo:
● En las salas de conferencias o de conciertos
se evita la reflexión porque al reflejarse los
sonidos se superponen y no se escuchan
con nitidez. En estos lugares se suelen
colocar techos, paredes o pisos materiales
porosos o fibrosos, como paneles de
tecknoport, espuma plástica, alfombras y
cortinas.
● Algunas veces en los conciertos se quiere
que los sonidos se reflejen para que puedan
llegar hasta todo el auditorio. En estos
casos se colocan superficies lisas llamadas
reflectantes. Las superficies lisas reflejan
mejor el sonido.
TERCER MOMENTO: Reflexión del sonido y
contaminaciónacústica
Fui a un concierto de
música andina y estuvo
genial. Se escuchaba la
música por todos lados.
Estoy embarazada y
me han tomado una
ecografía para saber cómo
está el bebé.
Cuando mi casa estaba
vacía mi voz se sentía más
fuerte que ahora.

La reflexión del sonido se aprovecha en la
construcción de aparatos como el sonar y el ecógrafo.
El sonarEl sonarEl sonarEl sonarEl sonar es un aparato utilizado en la navegación
para localizar cardúmenes de peces, establecer la
profundidad del mar para buscar submarinos
enemigos o barcos hundidos.
El sonar produce ultrasonidos que, al chocar contra
los objetos sumergidos, se reflejan hasta la
superficie donde son captados por un receptor.
Conociendo la velocidad del sonido en el agua y el
tiempo que emplea en ir y venir, se determina la
distancia a la que se encuentra el objeto.
El ecógrafoEl ecógrafoEl ecógrafoEl ecógrafoEl ecógrafo es el aparato que toma ecografías,
las cuales permiten estudiar los órganos internos
de nuestro cuerpo o ver el estado del bebé de una
mujer embarazada.
Las ecografías se toman con un pequeño instrumento
similar a un micrófono que emite ultrasonidosultrasonidosultrasonidosultrasonidosultrasonidos. Al
llegar a los órganos, los ultrasonidos se reflejan
produciendo diferentes ecos. La computadora
convierte los ecos en un imagen que aparece en la
pantalla de la computadora.
Cuando se habla de contaminación,
inmediatamente pensamos en basura, gases tóxicos en
la atmósfera o sustancias nocivas en mares y ríos.
Pocas veces pensamos que los sonidos fuertes son otra
forma de contaminación.
● ¿Por qué crees que en una habitación vacía los sonidos se sienten más
fuertes que cuando la habitación está con muebles y cortinas?
● ¿Qué lugares conoces en los que la reflexión del sonido es notoria?
● ¿Para qué personas podrían ser útiles el sonar y el ecógrafo?
● ¿Qué clases de ondas son los ultrasonidos? ¿Por qué no podemos
escucharlos?
Sonido
reflejado
Sonido
emitido

En el tercer momento has aprendido cómo se evita y aprovecha la reflexión del sonido
y la forma cómo perjudica tu salud la contaminación acústica.
◆ Indica qué personas están más expuestas a la contaminación acústica.
◆ En tu entorno ¿cuáles son las fuentes de contaminación acústica?
◆ ¿Qué podría suceder a las personas que escuchan música todo el tiempo con audífonos?
◆ Busca el significado de: acústica– audífono.
Contaminación acústica
Los ruidos fuertes y continuos dañan la salud.
En las ciudades hay mucho ruido debido a la
cantidad de carros, radios y equipos de música
a todo volumen, así como máquinas en
funcionamiento y aviones que las sobrevuelan.
Como sabes la intensidad de ruido se expresa
en decibelesdecibelesdecibelesdecibelesdecibeles. El ser humano puede escuchar
sonidos de hasta 70 dB sin problemas. Con
sonidos entre 80 y 110 dB se presentan
molestias y, cuando los sonidos superan los
120 dB, producen dolor en el oído.
La contaminación acústica produce malestares
como dolores de cabeza, insomnio, irritabilidad
y hasta pérdida del oído.
En las ciudades se toman medidas para evitar
que el ruido dañe a las personas.
Por ejemplo:
● Es obligatorio que las motos y carros tengan
en buen estado los tubos de escape.
● La policía multa a los chóferes que tocan
claxon innecesariamente.
● En los trabajos donde hay mucho ruido se
toman medidas de protección como uso
de tapones.
Las leyes establecen que ningún trabajador puede
estar expuesto a ruidos intensos durante una
jornada de ocho horas de trabajo. En ningún caso
se permite sobrepasar el nivel de 115 dB.
Despegue de un
avión
Concierto de rock
Tráfico urbano
Conversación entre
personas
Tic-tac del reloj
Aleteo de una
mariposa
120 dB
100 dB
80 dB
60 dB
40 dB
20 dB20 dB
0 dB

FICHA INFORMATIVA
El ultrasonido en la naturaleza
Para los animales de vida nocturna el empleo del eco es algo habitual. Esta propiedad
recibe el nombre de ecolocalización.
Su principio es muy simple: la onda sonora originada por el animal repercute en los
objetos que se encuentran en el camino y regresa de nuevo. De acuerdo con el tiempo
que se necesite para que la onda sonora regrese, el animal puede determinar la distancia
a la que se encuentra el objeto y, por el carácter del eco, las cualidades del objeto.
De las aves capaces de utilizar la
ecolocalización, las más conocidas son
los guácharos, que viven en las islas
del mar Caribe y en los países
próximos de América Latina. Los
guácharos son aves nocturnas. Pasan
todo el día en la profundidad de las
cuevas. En plena oscuridad atraviesan
rápidamente los sinuosos pasillos
subterráneos, sin tropezar con las
paredes y los salientes.
Un perro privado de la vista puede aprender en un día o dos a no tropezar contra las
paredes y los objetos grandes. El oído tan agudo que posee, distingue fácilmente el
sonido reflejado de las superficies densas que se produjo mediante el ruido de sus
pasos.
El hombre también es capaz de utilizar el eco. Los ciegos de nacimiento, quienes poseen
un oído muy desarrollado, orientándose por el sonido de sus propios pasos o el bastón,
aprenden a no tropezar. En comparación con los delfines o los murciélagos, este en un
método de orientación muy tosco, pero el carácter de los sonidos utilizados por el
hombre no le permite efectuar reacciones más precisas.
A los murciélagos y delfines la ecolocalizacion les sirve no solo para esquivar obstáculos.
Ésta es también necesaria para hallar los alimentos. Por eso necesitan ultrasonidos de
muy altas frecuencias, desde 40 hasta 300 mil ciclos por segundo y una longitud de
onda de 1 a 3 mm.
El ecolocalizador de los murciélagos es tan perfecto que puede distinguir pedacitos
iguales de terciopelo, de papel esmeril (lija) o de madera contrachapada. Cada objeto
refleja de manera distinta las ondas sonoras.
Grandes especialistas en la ecolocalización son las ballenas y las focas de las regiones
polares, quienes durante la mayor parte del año tienen que conseguir peces debajo del
hielo. En las largas noches polares ni siquiera la aurora boreal puede alumbrar el reino
submarino, por ello es natural que haya que recurrir a la ayuda de los oídos.

FICHA INFORMATIVA
Elronquido:lamolestianocturna
¿Quién no conoce a alguien que ronque? En la gran mayoría de los hogares hay personas
que con sus ronquidos impiden el necesario descanso nocturno.
Aunque en principio pueden parecer inofensivos, los ronquidos son fuente de problemas
psíquicos y físicos.
El ronquido puede considerarse como una de las manifestaciones orgánicas más
extendidas. Afecta a alrededor del 25% de las personas adultas. Por lo menos un 65%
de los hombres ronca. En las mujeres el promedio baja hasta el 40%.
Pero ¿qué es un ronquido? Se produce
cuando existe obstrucción del paso del
aire a través de la parte posterior de
la boca y nariz. En ésta coinciden la
lengua con el paladar blando y la úvula
o campanilla. Cuando estas estructuras
chocan las unas con las otras, se
produce una vibración durante la
respiración. Así se genera el ruido típico
del ronquido.
Estos ruidos se producen en la zona de paso entre la boca y la garganta (faringe). En
esta zona se hallan la campanilla y la lengua. Estas estructuras forman una especie de
círculo en el que predominan los músculos.
Como durante el sueño los músculos del organismo se relajan, no es algo difícil que
este círculo se estreche o se cierre. Así, ofrece una cierta dificultad a la entrada del aire
en los pulmones durante la fase de la inspiración. Esta resistencia al paso del aire unida
a las vibraciones de los músculos de esta zona (que suelen actuar como si fueran las
cuerdas de una guitarra) produce el sonido del ronquido. Este se manifiesta de forma
más o menos intensa. Así, los sonidos serán diferentes según el grado de dificultad del
paso del aire, la cantidad de aire, la velocidad, etc.
Un otorrinolaringólogo debe realizar un examen de la nariz, boca, garganta y cuello del
roncador severo. El tratamiento depende del diagnóstico. La cirugía o la utilización de
una máscara nasal para dormir puede ser la solución. Además, existen programas de
remedio para la autoayuda de los roncadores severos.
El ruido de un ronquido puede alcanzar los 80 – 90 decibeles, algo comparable al
sonido que emite un camión a toda velocidad.

203
La luzLa luzLa luzLa luzLa luz
1. Reflexión de la luz
2. Refracción de la luz
3. Proporcionalidad de segmentos
Analizar el comportamiento de la luz en
los fenómenos de reflexión y refracción y
sus aplicaciones. Conocer la
proporcionalidad de segmentos para
entender algunos fenómenos ópticos.
● En el primer momento analizarás cómo
es la luz y cómo se refleja en los
diferentes tipos de espejos.
● En el segundo momento
comprenderás, realizando sencillas
experiencias, la refracción de la luz y
sus aplicaciones tecnológicas.
● En el tercer momento a través de una
situación de tu vida diaria relacionada
con los espejos planos, estudiarás
conceptos básicos del teorema de
Thales en relación a los segmentos
proporcionales.
● Ilusiones ópticas
● Efectos ópticos del cielo
● Reflexión
● Refracción
● Espejo cóncavo
● Espejo convexo
● Lente convergente
● Lente divergente
● Proporcionalidad
● Thales
Segmentos proporcionales
● Teorema de Thales
Ondas luminosas
● Naturaleza de la luz
● Propagación de la luz, reflexión y
refracción
● Espejos y lentes
Aplicaciones
● Cámara fotográfica y microscopio

PRIMERMOMENTO:Reflexióndelaluz
Ondas luminosas
La luz nos permite ver todo lo que nos rodea.
Si no hubiese luz todo sería oscuro.
La luz está formada por ondasondasondasondasondas
electromagnéticas que son captadaselectromagnéticas que son captadaselectromagnéticas que son captadaselectromagnéticas que son captadaselectromagnéticas que son captadas
por nuestros ojospor nuestros ojospor nuestros ojospor nuestros ojospor nuestros ojos.
Si recuerdas el espectro electromagnético, la luz visible es sólo una pequeña parte
de él. La luz se ve blanca, pero en realidad está formada por 7 tipos de ondas
diferentes que son los 7 colores que la forman.
Algunos cuerpos, como los cristales, el agua en un vaso o las gotas de lluvia, pueden
separar la luz blanca en sus siete colores y forman lo que llamamos un arco iris. La
descomposición de la luz en siete colores se conoce como dispersióndispersióndispersióndispersióndispersión de la luz.
Como toda onda electromagnética, la luz no necesita un medio material para
propagarse. Puede propagarse incluso en el vacíopropagarse incluso en el vacíopropagarse incluso en el vacíopropagarse incluso en el vacíopropagarse incluso en el vacío; de esta manera, nos llega
la luz del Sol y de la estrellas.
● ¿Por qué no podemos ver los objetos cuando nos falta luz?
● ¿Qué fuentes de luz conoces?
La luz viaja muy rápidamente.
Se propaga a una velocidad de
300 000 km/s.
Microondas Infrarrojo Luz visible
Rojo
Anaranjado
Amarillo
Verde
Azul
Índigo
Violeta
Ultravioleta Rayos X

◆ Sitúate frente a una pared y, luego, frente a un espejo ¿Por qué ves la pared y el espejo?
¿Por qué te ves reflejado en el espejo pero no en la pared?
◆ Da 5 ejemplos de superficies lisas, de tu entorno, donde se forman imágenes.
Según dejen o no pasar la
luz los cuerpos pueden ser:
opacos, translúcidos y
transparentes.
Reflexióndelaluz
Cuando la luz choca contra un cuerpo opaco,
es decir, que no la deja pasar, los rayos de luzluzluzluzluz
“rebotan”, es decir se reflejan“rebotan”, es decir se reflejan“rebotan”, es decir se reflejan“rebotan”, es decir se reflejan“rebotan”, es decir se reflejan. Este
fenómeno se llama reflexión de la luz y gracias
a él podemos ver los objetos.
La reflexión de la luz puede ser de dos tipos: difusa y regular.
Reflexión difusaReflexión difusaReflexión difusaReflexión difusaReflexión difusa. Los rayos de luz
se reflejan en diferentes direcciones.
Ocurre en superficies rugosas como
una pared, una hoja de papel, una
cortina y la mayoría de objetos que
hay alrededor.
Reflexión regularReflexión regularReflexión regularReflexión regularReflexión regular. Los rayos de luz
se reflejan de manera ordenada y
se forman imágenes de los objetos.
Ocurre en superficies lisas o pulidas,
como en los espejos, los metales
bien bruñidos o un lago tranquilo.
Gracias a la reflexión difusa
puedes leer esta página, porque la
luz se refleja en el papel y de allí
llega a tus ojos.
Reflexión difusa
Superficie
rugosa
Reflexión
regular
Superficie lisa
La naturaleza nos ofrece espejos naturales
en las superficies de agua tranquilas. Desde épocas
remotas, el ser humano, ha construido espejos con
metales bien pulimentados. Mucho más tarde se
construyeron los espejos, hechos de vidrio oscurecido con
una delgada capa de estaño o de plata.

En el primer momento has aprendido que la luz está formada por ondas electromagnéticas
y que, al incidir en un cuerpo opaco como una pared o un espejo, la luz se refleja. En el
segundo momento analizarás otro fenómeno luminoso: la refracción.
Clasesdeespejos
Los espejos reflejan las imágenes de los objetos de acuerdo a la forma de su
superficie.
Espejos planosEspejos planosEspejos planosEspejos planosEspejos planos. Son los que tienen superficies planas. Ellos reflejan la imagen
del objeto sin deformarla. Si escribes una palabra en una hoja de papel y la miras
en un espejo plano, observarás que la imagen es del mismo tamaño que el objeto
y se forma como si estuviese detrás del espejo.
Además, la imagen es simétrica, es decir, la parte derecha de la imagen corresponde
a la parte izquierda del objeto y viceversa.
Espejos con curvaturaEspejos con curvaturaEspejos con curvaturaEspejos con curvaturaEspejos con curvatura. Son aquellos en que la superficie no es plana sino curva.
Estos espejos forman imágenes distorsionadas, como lo puedes observar si te miras
en un metal que puedes doblar ligeramente, como un disco (CD) o una cuchara.
Si curvas el CD hacia adentro tendrás un espejo cóncavo y, si lo curvas hacia
fuera, el espejo es convexo.
Los espejos convexos forman imágenes más pequeñas de los objetos, pero dan
un mayor campo de visión. Por esta razón se usan en los espejos retrovisores de
los carros y en los espejos de control de seguridad en los supermercados.
● Toma una cuchara y mírate por ambos lados. ¿Cuál es la superficie cóncava
y cuál la convexa? ¿Cómo son las imágenes en ambos casos?
● ¿Por qué las ambulancias tienen escrito su letrero así:
AMBULANCIA AMBULANCIA AMBULANCIA AMBULANCIA AMBULANCIA
Espejo plano Espejo cóncavo Espejo convexo

SEGUNDOMOMENTO:Refraccióndelaluz
MaterialesMaterialesMaterialesMaterialesMateriales. Un trozo de alambre fino (puede ser de
cobre), una lupa, una vela, clavo grueso, agua.
Experiencia 1Experiencia 1Experiencia 1Experiencia 1Experiencia 1. Una lupa con una gota de aguaUna lupa con una gota de aguaUna lupa con una gota de aguaUna lupa con una gota de aguaUna lupa con una gota de agua.
Con un alambre de cobre, haz un aro dando vuelta
alrededor de un clavo grueso. Introduce este aro en el
agua y observa a través de él. Obtendrás una pequeña
lupa que tiene aproximadamente un aumento de 4 a 5
veces.
Experiencia 2Experiencia 2Experiencia 2Experiencia 2Experiencia 2. Observa imágenes que forma unaObserva imágenes que forma unaObserva imágenes que forma unaObserva imágenes que forma unaObserva imágenes que forma una
lupalupalupalupalupa
1. Mira a través de una lupa cualquier objeto. Observarás
que se ve el objeto aumentado de tamaño.
2. Ahora, en una habitación, oscurece todas las ventanas
menos una. Coloca la lupa cerca de una pared pero
de cara a la ventana por donde entra luz. Mueve
lentamente la lupa hasta lograr que se formen
imágenes en la pared. Observarás que las imágenes
son invertidas.
ExplicaciónExplicaciónExplicaciónExplicaciónExplicación. El aire, el agua y el vidrio son medios transparentes y, por lo tanto, la luz
puede atravesarlos. Pero estos medios tienen diferente densidad, y por eso al atravesarlos
la luz se desvía. Este fenómeno se llama refracción de la luz.
A causa de la refracción de la luz, las imágenes de los objetos se ven engañosas: más
grandes o más pequeñas e incluso invertidas.
● ¿Por qué se ven las aceitunas u otras frutas contenidas en un frasco cilíndrico
más grandes de lo que en realidad son?
● ¿Para qué sirven las lupas?
Clavo
Alambre delgado
Seguramente te habrá sorprendido que una gota de
agua pueda aumentar el tamaño de los objetos de la
misma forma que lo hace una lupa. Para observar mejor
este fenómeno realiza las siguientes experiencias.
Lent e
Pared o cartón blanco
Ventana
Lupa

Laslentes
Una de las aplicaciones más importantes de la refracción de la luz son las lentes.
Las lentes son cuerpos transparentes (vidrio, plástico) en los cuales por lo menos
una de sus superficies es curva, ya sea cóncava o convexa. Si tocas la superficie
de una lupa con los dedos, notarás que el vidrio no es plano sino curvo.
Las lentes pueden ser convergentes o divergentes.
Las lentes convergentesLas lentes convergentesLas lentes convergentesLas lentes convergentesLas lentes convergentes. Concentran los rayos de luz. Se usan en lupa, cámaras
fotográficas, microscopios, telescopios y anteojos para ver de cerca.
Las lentes divergentesLas lentes divergentesLas lentes divergentesLas lentes divergentesLas lentes divergentes. Separan los rayos de luz. Se usan en los anteojos que
corrigen la miopía y en los faros de autos.
¿Enquéconsistelarefracción?
La refracción de la luz es la desviaciónla desviaciónla desviaciónla desviaciónla desviación que
experimentan los rayos luminosos al pasar
oblicuamente de un medio transparentemedio transparentemedio transparentemedio transparentemedio transparente
a otro de diferente densidad. Los medios
transparentes pueden ser, aire, agua, vidrio,
etc.
Para entender este fenómeno sumerge un
lápiz en un vaso con agua hasta la mitad.
Observarás que el lápiz aparece como
quebrado.
Los rayos de luz viajan en línea recta, pero
al entrar en el agua disminuyen su velocidad,
porque el agua es más densa que el aire. Al
disminuir su velocidad los rayos se desvían
y la imagen se deforma.
◆ Coloca una moneda en un vaso de vidrio y agrega agua hasta la mitad. Pon el vaso a la
altura de tus ojos y mira la moneda desde diferentes ángulos. ¿Qué observas?
◆ Indica las diferencias que hay entre reflexión y refracción.
¿Sabías que a causa de la
refracción los objetos sumergidos en
agua nos parecen más cercanos de lo
que en realidad están? Por eso es difícil
agarrar un pez dentro del agua.
i
r
Rayo
incidente
Rayo
refractado
Aire
Agua

Lee la siguiente información:
Con las lentes se han construido muchos
instrumentos útiles, como microscopios,
telescopios, proyectores de cine, cámaras
fotográficas, fotocopiadoras, etc.
La cámara fotográficaLa cámara fotográficaLa cámara fotográficaLa cámara fotográficaLa cámara fotográfica. Está formada por
una cámara oscura en cuyo frente hay una
lente convergente. En la parte posterior hay
una película fotográfica sensible a la luz.
Los rayos luminosos provenientes de los
objetos pasan a través de la lente, formando
una imagen invertida que queda grabada en
la película fotográfica.
● ¿Por qué podemos quemar un papel con una lupa?
● ¿Por qué es conveniente que los faros de los autos tengan lentes
divergentes?
¿Sabías que… dentro del ojo tenemos el cristalino, el cual es un lente convergente
similar a una lupa que forma las imágenes de los objetos que vemos?
Lente
divergente
Imagen del
objeto
Diafragma
Objeto
Película
Lente convergente
Lente divergente

En el segundo momento has estudiado los efectos de la refracción de la luz en la vida
cotidiana y sus aplicaciones en las lentes. En el tercer momento estudiarás el teorema
de Thales que es un teorema relacionado con la proporcionalidad de segmentos.
El microscopio.El microscopio.El microscopio.El microscopio.El microscopio. Gracias al microscopio podemos ver objetos pequeñísimos como células
y bacterias.
Básicamente los microscopios trabajan con dos lentes llamadas: objetivoobjetivoobjetivoobjetivoobjetivo (que está
cerca del objeto) y ocularocularocularocularocular (por donde se mira). Entre las dos lentes la imagen de los
objetos aumentan de 40 a 1 000 veces.
Los microscopios, por lo general, tienen varias lentes objetivolentes objetivolentes objetivolentes objetivolentes objetivo, cada una con un aumento.
Estas lentes se pueden girar para elegir la que se quiera usar.
El primer microscopio fue inventado por el óptico
holandés Zacharías Janseen en el siglo XVII. Los
microscopios más potentes son electrónicos, ellos permiten
ampliar las imágenes hasta 50 000 veces, lográndose
distinguir los organelos que hay dentro de las células.
Lente
ocular
Lente objetivo
Imagen del
objeto
Ocular
Tornillo
macrométrico
Tornillo
micrométrico
Objetivos
Espejo
Base

TERCERMOMENTO:Proporcionalidaddesegmentos
Por propia experiencia habrás comprobado que en
los espejos planos la imagen se refleja del mismo
tamaño que el objeto y se forma como si
estuviese detrás del espejo.
● ¿Puedes identificar en la figura el objeto, la imagen y el espejo? Identifícalos
mediante las letras.
● Si se trata de un espejo plano, ¿qué puedes decir de los segmentos AB y BA'?
Conociendo las características de los espejos planos, y por el teorema deteorema deteorema deteorema deteorema de ThalesThalesThalesThalesThales, se
podría responder a la siguiente pregunta: ¿Cuál debe ser el tamaño mínimo de un espejo
plano vertical BP y cómo debe estar colocado para que nos veamos de pies a cabeza?
Teorema de ThalesTeorema de ThalesTeorema de ThalesTeorema de ThalesTeorema de Thales
Si dos rectas cualesquiera se
cortan por varias rectas
paralelas, los segmentos
determinados en una de las
rectas son proporcionales a los
segmentos correspondientes
en la otra.
AB
A B’ ’
=
BC
B C’ ’
=
AC
A C’ ’
r s
A
B
C
A‘
B‘
C‘
A B A‘
P
M M‘
Observa la siguiente figura:

1. Halla las medidas de los segmentos a y b.
4
2
=
a
4
⇒ a = 8 cm
4
2
=
6
b
⇒ b = 3 cm
Caso particular del teorema de ThalesCaso particular del teorema de ThalesCaso particular del teorema de ThalesCaso particular del teorema de ThalesCaso particular del teorema de Thales
Si: DE // AC
Entonces:
AB
DB
=
CB
EB
2. En un triángulo ABC, se traza una recta paralela al lado AC que intercepta los lados AB y
BC en los puntos M y N. Si BN = 36 cm y 4(BM) = 3(AM), calculamos la longitud del
segmento CN.
● Del dato 4(BM) = 3(AM) ⇒
BM
AM
=
3
4
● Aplicamos el teorema de Thales:
BM
AM
=
BN
CN
⇒
3
4
=
36
x
⇒ 3x = 144 ⇒ x = 48
La longitud de CN es 48 cm.
◆ Según los datos de la figura, ¿cuánto vale x?
4 cm
2cm
b 6 cm
4
cm
a
A
B
C
D E
A
B
C
x
NM
36
3
12
15
x

Generalización del teorema de ThalesGeneralización del teorema de ThalesGeneralización del teorema de ThalesGeneralización del teorema de ThalesGeneralización del teorema de Thales
L // L1
// L2
// L3
●
AB
AD
=
MN
MP
●
BC
AD
=
NO
MP
●
CD
AD
=
OP
MP
●
AB
CD
=
MN
OP
¿Cuál debe ser el tamaño mínimo de un espejo plano vertical BP y cómo debe¿Cuál debe ser el tamaño mínimo de un espejo plano vertical BP y cómo debe¿Cuál debe ser el tamaño mínimo de un espejo plano vertical BP y cómo debe¿Cuál debe ser el tamaño mínimo de un espejo plano vertical BP y cómo debe¿Cuál debe ser el tamaño mínimo de un espejo plano vertical BP y cómo debe
estar colocado para que nos veamos de pies a cabeza?estar colocado para que nos veamos de pies a cabeza?estar colocado para que nos veamos de pies a cabeza?estar colocado para que nos veamos de pies a cabeza?estar colocado para que nos veamos de pies a cabeza?
Por las características de un espejo plano
podemos decir que AB = BA’. Entonces se
tendría también la siguiente relación:
AA’ = 2AB
Por el teorema de Thales se tiene
AA
AB
’
=
AM
BP
Se sabe que: AA’ = 2AB
Reemplazando:
2AB
AB
=
AM
BP
Entonces: BP =
AM
2
AM es la altura de la persona que se desea reflejar en el espejo.
Conclusión:Conclusión:Conclusión:Conclusión:Conclusión: El espejo plano vertical debe tener la mitad de la altura de la persona que
se desea reflejar. Se debe colocar a la altura de su cabeza.
B
C
A
D
N
M
O
P
L
L1
L2
L3
Ahora que tienes estos alcances
sobre el teorema de Thales puedes
analizar la situación presentada al
comienzo de este momento y dar
respuesta a la pregunta.
A B A‘
P
M M‘

Se coloca un espejo plano en forma de disco de 6 cm de radio sobre una mesa. A 22 cm
arriba del espejo, y sobre su eje, se encuentra una fuente luminosa puntual. Encuentra la
posición de la imagen de la fuente y calcula el diámetro del círculo de luz que se observa
en el techo a 1,5 m de altura.
Identifica los datos
d2 = 150 cm
R1 = 6 cm
d1 = 22cm
R2 = ?
d3 = ?
Resuelve:Resuelve:Resuelve:Resuelve:Resuelve:
d3 = d1
d3 = 22 cm
Por el teorema de Thales:
d
R
1
1
=
d d
R
3 2
2
+
=
( )
( )
22
6
cm
cm
=
( )22 150
2
cm cm+
R ⇒ R2 = 46,9 cm
Respuesta:Respuesta:Respuesta:Respuesta:Respuesta: La imagen de la fuente está a 22 cm por debajo del espejo, y la mancha
luminosa tiene 93,8 cm de diámetro.
◆ Resuelve el siguiente problema: Según el dibujo, halla CB, AP y x
En el tercer momento has podido observar cómo en la resolución de determinados
problemas aplicas diversos conocimientos; en este caso, el teorema de Thales.
d1
d2
d3R1
R2
A
BC
P Q
5 cm
7 cm
x
3 cm

FICHA INFORMATIVA
Ilusionesópticas
Las ilusiones ópticas son imágenes especiales, que
cambian según como las mires o que tienen
alguna trampa que nos lleva a percibir la realidad
erróneamente. Las ilusiones ópticas son el
resultado de la interpretación que hace el cerebro
de las imágenes percibidas por los ojos.
Ciertos diseños confunden tus ojos y tu cerebro,
haciéndote calcular mal el objeto, ángulo, forma,
posición o longitud de un objeto. En los últimos
cien años se han identificado y estudiado más de
200 tipos de ilusiones ópticas, pero todavía no se
ha aclarado definitivamente cuál es su causa.
En la imagen presentada hay una estrella de cinco
puntas. ¿Puedes encontrarla?
Las ilusiones fascinan a los científicos porque
pueden ayudarlos a entender cómo funciona
nuestro sistema visual. Como dijo Pukinje, un
destacado fisiólogo checo del siglo XIX, “Los
engaños de los sentidos son las verdades de
la percepción”.
● Podemos tener distintos tipos de ilusiones ópticas:
¿Qué hay en las intersecciones? ¿Cuántas patas tiene el elefante?

¿Dónde hay un punto negro? ¿Qué imágenes identificas?
¿Las líneas verticales son del mismo tamaño? ¿Qué imágenes identificas?
¿Pato o conejo? Figura imposible

FICHA INFORMATIVA
Efectos ópticos del cielo
¿Por qué el cielo es azul o rojo?¿Por qué el cielo es azul o rojo?¿Por qué el cielo es azul o rojo?¿Por qué el cielo es azul o rojo?¿Por qué el cielo es azul o rojo?
La luz del Sol es blanca; no obstante, es el resultado
de la mezcla de luces de diferentes colores: rojo,
naranja, amarillo, verde, azul, añil y violeta.
Cuando los rayos de Sol llegan a la atmósfera,
chocan con las partículas de aire, vapor de agua
y polvo, y se descomponen en los colores que
los forman. Las ondas azules son las que más
fácilmente se separan y por ello vemos el cielo
azul. Sin embargo, al amanecer y al atardecer,
los rayos inciden sobre la atmósfera de forma
oblicua, y tienen que atravesar más aire. Ello
hace que se lleguen a dispersar los colores
naranjas y rojos y que, en consecuencia, el cielo
adquiera los espectaculares colores propios del
crepúsculo. Además, cuando el número de
partículas suspendidas en el aire es mayor, como
cuando hay mucho polvo o polución, los colores
del cielo tienden a mostrar los tonos rojos y
naranjas.
Nubes blancas y nubes negrasNubes blancas y nubes negrasNubes blancas y nubes negrasNubes blancas y nubes negrasNubes blancas y nubes negras
Las nubes están formadas por millones de
moléculas de agua. Al ser tan grandes consiguen
que, cuando la luz solar choca en ellas, se
descomponga en todos sus colores. Esto se
traduce en el color blanco que las caracteriza.
Pero en ocasiones se oscurecen y muestran tonos
grises e incluso negruzcos. Es entonces cuando
nos preparamos para el chaparrón. Este
fenómeno se explica porque las nubes, además
de dispersar la luz, la reflejan: hacen que rebote
sin descomponerse. Y esta reflexión es mayor
cuanto mayores son las gotas que forman la
nube. Es decir, cuando la nube está bien cargada,
la luz no puede atravesarla porque sus rayos
rebotan en ella. Por eso, cuando las nubes son
oscuras amenaza lluvia.

El arco irisEl arco irisEl arco irisEl arco irisEl arco iris
El arco iris aparece cuando llueve y, a la vez,
los rayos del Sol se abren paso por algún hueco
entre las nubes. Para verlo debemos mirar hacia
la lluvia de espaldas al Sol. Cuando los rayos
solares atraviesan las gotas de lluvia, su color
blanco se descompone en todos los colores que
lo forman: rojo, naranja, amarillo, verde, azul,
añil y violeta. Estos colores se reflejan entonces
en millones de gotas en diferentes ángulos y
forman la banda que conocemos. Cuanto más
cerca está el Sol del horizonte, mayor es el
arco. Si el Sol supera los 42 grados con respecto
al suelo, entonces el arco iris desaparece. Esto
ocurre porque en realidad el arco iris no es un
arco, sino un círculo completo centrado en el
punto frente al Sol. Si no hubiera horizonte,
veríamos el circulo completo, como se puede
ver desde un avión.
El mismo fenómeno que produce el arco iris, a
escala menor, se observa alrededor de los
aspersores de agua o de las cascadas en un
día soleado.
EspejismosEspejismosEspejismosEspejismosEspejismos
Seguro que, en verano, a todos nos ha sorprendido ver que la carretera parece
mojada y, sin embargo, al acercarnos no hay ni rastro de agua. Este fenómeno se
produce cuando la luz solar se refracta al atravesar capas de aire a diferente
temperatura y densidad. Normalmente es necesario que el cielo esté despejado.
El aire distorsiona la proyección de los objetos, y lo puede hacer en dos direcciones:
hacia arriba o hacia abajo. Lo más frecuente es que lo haga hacia abajo, cosa que
sucede en días calurosos, cuando la superficie del suelo y el aire en contacto con
ella se calientan.
En consecuencia, la luz se refracta hacia abajo y se proyecta una imagen sobre la
superficie del suelo. Por eso, en verano, cuando vemos que la carretera está
mojada, lo que en realidad estamos viendo es la proyección del cielo, como si
fuera un espejo.
En cambio, en zonas nevadas o cubiertas de hielo, donde las capas de aire
inferiores están frías y son más densas, los rayos de Sol se desvían hacia arriba
proyectando a más altura los objetos que están en el suelo.
Si nos fijamos, en los fríos días de invierno podemos advertir que las montañas
a lo lejos parecen más altas de lo normal. No es que hayan crecido, sino que el
aire frío proyecta su superficie hacia arriba.

219
Unidad temática 1:
Actividad 1 –Actividad 1 –Actividad 1 –Actividad 1 –Actividad 1 – Los movimientos
Página 19Página 19Página 19Página 19Página 19:
◆ La velocidad del atleta es 10,22 m/s
◆ La velocidad de la persona es 12,77 m/s
◆ El automóvil recorrerá 475 km
◆ El tiempo empleado por el tren es 5,71 s
◆ La velocidad del auto es 108 km/h
◆ El viento llegará en 1,4 h
◆ El auto de Juan tiene mayor aceleración
porque la velocidad varía en menos
tiempo.
◆ El valor de su aceleración es 2,22 m/s2
◆ El camión demoró en detenerse 2,7 s
◆ La altura del estante es 0,8 m
◆ El ladrillo se estrella con una velocidad
de 10,95 m/s
◆ Las gráficas serían:
a)
Respuestas de las fichas de trabajo y ejercicios
b)
c)
d)
◆ a) La velocidad de la persona es 100
km/h o 27,77 m/s
◆ b) Los gráficos son:
–2
4
y
x
–0,5
–1
x
y
2
–4 x
y
0,75
–3
x
y
700 km
400 km
8 h 11 h t
e
27,77
t
v
a
a Si v = cte.
a = 0

220
Actividad 2 –Actividad 2 –Actividad 2 –Actividad 2 –Actividad 2 – Las fuerzas
◆ La fuerza que ha actuado sobre el auto
es 24 000 N
◆ La altura de la cometa con respecto al
suelo es de 65,95 m
◆ La longitud de la rampa es 56,569 m
◆ Las diagonales miden 12,258 m
◆ El ángulo que forma es 75,52° y la altura
5,8092 m
Página 54:Página 54:Página 54:Página 54:Página 54:
◆ Las proyecciones son:
F(x) = 5 3 N y F(y) = 5 N
◆ r = 6,936 cm; y = 3,468 cm
Ficha de trabajoFicha de trabajoFicha de trabajoFicha de trabajoFicha de trabajo: Resolución de
triángulos rectángulos
1) El lado de la diagonal del cuadrado mide
4,949 cm
2) Perímetro = 50 cm; área = 60 cm2
3) El área del rombo es 96 cm2
4) Los lados del triángulo miden 2 3
5) Los catetos miden 3,16 cm y 9,48 cm. Su
área es 15 cm2
6) a) d = 10 cm
b) d = 4 5 cm
7) La medida de la diagonal del cuadrado es
0,8484
8) I) Sen25° =
5
c
⇒ c =
5
sen25°
= 11,848
∴ c = 11,848
Cos25° =
a
c
⇒ a = cCos25° =
11,90(0,906) = 10,781
∴ a = 10,781
De manera análoga se resuelven los
demás ejercicios
II) c = 8,486 III)c = 10
b = 5,999 b = 8,66
IV) c =
8
senα
V) a = 6 cos α
9) La altura es 2,904 cm
10) Se ha ascendido 51,8 m
11) La pendiente es 0,225 m
Actividad 3 –Actividad 3 –Actividad 3 –Actividad 3 –Actividad 3 – Rozamiento, gravedad y
trabajo
◆ El trabajo es 1 500 J
◆ La potencia es 3 800 W
Ficha de trabajo:Ficha de trabajo:Ficha de trabajo:Ficha de trabajo:Ficha de trabajo: Trabajo, potencia y
máquinas simples
1) W = 56 J 2) d = 8 m
3) F = 11 N 4) d = 2,25 m
5) W = 20 J 6) a) P = 30 000 W
7) P = 3 748,5 W
b) P = 40,214 HP
9) En ambos casos se pierde el
equilibrio del balancín.
10) La respuesta es la alternativa a)
Unidad temática 2:
Actividad 1 –Actividad 1 –Actividad 1 –Actividad 1 –Actividad 1 – La presión
◆ A1 = 4 800 cm2;
A2 = 2 400 cm2;
A3 = 3 200 cm2
a) Para ejercer menor presión se apoyara
sobre el área A1.
b) Ejerce una presión de 416,666 Pa

221
◆ P1 = 1 000
kg
m3
(3 m)(9,8
m
s2 ) = 29 400 Pa
◆ P2 = 1 000
kg
m3
(4 m)(9,8
m
s2 ) = 39 200 Pa
A mayor profundidad mayor presión
Ficha de trabajoFicha de trabajoFicha de trabajoFicha de trabajoFicha de trabajo: Aplicando el principio
de Pascal
1) W = 1884,96 kg
2) F2 = 175 N
3) S2 = 45 cm2
Actividad 2 –Actividad 2 –Actividad 2 –Actividad 2 –Actividad 2 – Calor o energía térmica
a) –10 ºC = 263 K
b) 350 K < 100 °C
c) 32 ºF < 5 °C
◆ La persona está sana
◆ –7 K = –280 ºC
No hay organismo vivo descubierto a esta
temperatura
Ficha de trabajoFicha de trabajoFicha de trabajoFicha de trabajoFicha de trabajo: Calculando la cantidad
de calor
a) Q = 2,5 kcal
b) Q = 0,9 kcal
◆ La temperatura de equilibrio térmico es
24,36 ºC
Actividad 3 –Actividad 3 –Actividad 3 –Actividad 3 –Actividad 3 – Efectos del calor
a) Q = 2000 Kcal
b) Q = 2500 cal
c) Q = 2500 cal
Unidadtemática3:
Actividad 1Actividad 1Actividad 1Actividad 1Actividad 1: Los imanes y la electricidad
estática
a) F = 9 x 103
N
b) r = 9,486 x 104
m
c) q = 0,0474 C
Ficha de trabajo:Ficha de trabajo:Ficha de trabajo:Ficha de trabajo:Ficha de trabajo: Recordando la
notación científica
1) a) 8,57346970586 x 1011
b) 5,78 x 102
c) 2 x 1010
2) a) 0,00052
b) 0,000033
c) 18 000 000 000 000
Actividad 2Actividad 2Actividad 2Actividad 2Actividad 2: La electricidad en
movimiento
1) Paola está ubicada en el cuarto lugar del
ascenso.
2) La afirmación correcta es la alternativa a)
3) El que se sienta al lado de Silvia es Juan
(Silvia, Juan, Manuel, Pedro y Zenaida).
4) La menor de todos es Norma.
Unidad temática 4:
Actividad 1 –Actividad 1 –Actividad 1 –Actividad 1 –Actividad 1 – Las ondas
◆ Los gráficos serán los siguientes:
1) f(x) = x2 – 4x – 5

222
2) f(x) = –3x2 – 11x + 4
3) f(x) = 4x2 – 12x + 9
◆ e = e0 + 1 at2
e = t2
ttttt 0 1 2 3 4
eeeee 0 1 4 9 16
Ficha de trabajo:Ficha de trabajo:Ficha de trabajo:Ficha de trabajo:Ficha de trabajo: Aplicando la función
cuadrática
◆ La longitud del rectángulo es 35 m y el
ancho de cada rectángulo es 26,25 m. El
área máxima es de 1 837,5m2
Actividad 2Actividad 2Actividad 2Actividad 2Actividad 2: El sonido
a) x = 1 b) x = 1 c) x1 = 0;
x2 = 0,69
Página 193:Página 193:Página 193:Página 193:Página 193:
a) b = 2 b) b = 6 c) y = –3
d) y = –5 e) y = –
8
5
Actividad 3Actividad 3Actividad 3Actividad 3Actividad 3: La luz
◆ x = 5
◆ CB = 6 AP = 7 x = 5
xxxxx yyyyy
–2 7
–1 0
0 –5
1 –8
2 –9
5 0
xxxxx yyyyy
–4 0
–3 10
–2 14
–1 12
0 4
1 –10
xxxxx yyyyy
–1 2,5
0 9
1 1
1,5 0
2 1
3 9
–1
5
–5
–9
x = –1,8 14
4
–4
0,33
9
1,5
x = 1,5
x
y
0 1 2 3 4
16
9
4
1
__
2

223
Conexiones web
● http://thales.cica.es/rd/Recursos/rd98/Matematicas/02/actipre.html
Presenta problemas relacionados con distancias y tiempos.
● http://www.x.edu.uy/cuadratica.htm#graf
Desarrolla el tema de las funciones cuadráticas.
● http://www.rena.edu.ve/TerceraEtapa/Matematica/TEMA22/Plano Cartesiano.html
Ofrece información y actividades interactivas sobre el plano cartesiano.
● http://eduardoochoa.com/joomla/content/view/371/111/1/2/
Presenta ejercicios de matemática recreativa.
● http://www.educaplus.org/luz/ondas.html
Refiere información sobre la luz como onda. Propiedades de la luz.
● http://www.fisicanet.com.ar/fisica/f2_estatica_fluidos.php
Muestra apuntes y ejercicios de estática de fluidos. Principio de Arquímedes. La
compresibilidad de los gases
● http://www.iestiemposmodernos.com/diverciencia/
Presenta experimentos y prácticas de laboratorio de física y química.
Referencias bibliográficas
ADUNI. Razonamiento matemático. Lumbreras Editores S.R.L. Lima, 2003.
AUCALLANCHI, Félix. Física. RACSO Editores. Perú, 1995.
ANA CAÑAS y otros. Física y Química. Proyecto Ecosfera. Ediciones SM. Madrid, 2003.
DE LA CRUZ SOLÓRZANO, Máximo. Matemática 4to grado de Secundaria. Editorial Brasa
S.A. Perú, 1992.
POZAS MAGARIÑO Antonio. Física y Química 1º Bachillerato. Editorial McGraw-Hill. México,
2002.
EDITORIAL SANTILLANA. Natura.com 2, Editorial Santillana. Perú, 2004.
EDITORIAL SANTILLANA. Natura.com 1, Editorial Santillana. Perú, 2004.
MINISTERIO DE EDUCACIÓN DEL PERÚ. Diseño Curricular Básico Nacional. Educación Básica
Alternativa – Ciclo Avanzado. Lima, 2008.
PROGRAMA DE ALFABETIZACIÓN Y EDUCACIÓN BÁSICA DE ADULTOS – PAEBA-Perú. Diseño
Curricular Diversificado de Educación Básica Alternativa – PEBAJA. Lima, 2006.

Ciencias 4

Más contenido relacionado

La actualidad más candente (20)

Similar a Ciencias 4 (20)

Más de Juan Carlos Huanca Mamani (9)

Último (20)

Ciencias 4