Diagrama de control
- 1. Instituto tecnológico de Mexicali Análisis de datos experimentales 3ra Unidad Diagramas de control Norman Rivera Blancas Wong Luis Alaniz Tolosa Enrique Corona Juarez Oscar Ruben
- 2. Introducción Bueno en esta unidad veremos que tan importante es el control de variables ya que en la industria es imposible crear 2 productos iguales pero gracias a este tipo de herramientas podemos crear limites para minimo mantener el producto dentro de un limite.
- 3. Contenido ¿Qué es una variable? ¿Qué es un atributo? ¿Qué es un diagrama de control? Diagramas de control de variable (X, R, y S) Diagramas de control de atributos Ejemplos
- 4. ¿Qué es una variable? una variable es un símbolo constituyente de un predicado, fórmula, algoritmo o de una proposición. El término «variable» se utiliza aun fuera del ámbito matemático para designar una cantidad susceptible de tomar distintos valores numéricos dentro de un conjunto de números especificados.
- 5. ¿Qué es un atributo? un atributo es una especificación que define una propiedad de un objeto, elemento o archivo. También puede referirse o establecer el valor específico para una instancia determinada de los mismos.
- 6. ¿Qué es un diagrama de control? Los gráficos de control o diagramas de control se utilizan para controlar el desarrollo de los procesos de producción e identificar posibles inestabilidades y circunstancias anómalas.
- 7. A los diagramas de control que se usan para las variables continuas se llaman diagramas de control de variables. Existiendo tres ejemplos: El diagrama X El diagrama R El diagrama S A los diagramas de control que se usan para las variables binarias o discretas se les llama diagramas de control de atributos. El diagrama p es el diagrama mas comúnmente utilizado para variables binarias. El diagrama c se utiliza para las variables discretas.
- 8. Dependiendo del diagrama de control utilizado en los procesos, será esta la característica de calidad con la que se mido una: Variable continua. Variable binaria. Variable discreta.
- 9. los gráficos de control por atributos EN LOS GRÁFICOS DE CONTROL POR ATRIBUTOS, EL CONTROL DEL PROCESO SE REALIZA MEDIANTE ATRIBUTOS DE TIPO DICOTÓMICO. ASÍ, SE PUEDE ANALIZAR SI EL PRODUCTO O SERVICIO POSEE O NO UNA DETERMINADA CARACTERÍSTICA (ATRIBUTO): COLOR, FORMA, DEFECTO, TIPO, ETC. Y EN GENERAL SE ABORDA DICHO ANÁLISIS MEDIANTE PREGUNTAS DEL TIPO: ACEPTABLE/NO ACEPTABLE, SI/NO, FUNCIONA/NO FUNCIONA, ETC.
- 10. Este gráfico trata de mostrarnos la distribución que siguen en el tiempo los estimadoresX (media) y R (rango), identificativos del valor central y la dispersión de los valores de cada muestra extraída. Los valores de estos estimadores variarán de una muestra a otra en el proceso de inspección; por tanto, lo que nos interesará predecir, son los límites entre los que variarán dichos estimadores, supuesto que el proceso está bajo control (esto es, cuando no existen causas especiales que distorsionen el proceso).
- 11. El procedimiento que debe seguirse para su construcción exige contar con una hoja de recogida de datos, en la que se indicará el tamaño de las muestras, la frecuencia con que deben tomarse y el número de muestras necesarias para obtener cierta significación estadística en nuestro estudio
- 12. De cada una de las muestras se van a vigilar dos valores: uno es la media y el otro el rango (diferencia entre el mayor valor y el menor de los datos de la muestra). Puede admitirse que cada uno de estos dos valores sigue una distribución normal a lo largo del proceso de muestreo, es decir:
- 13. Además, la relación que existe entre las desviaciones de estas distribuciones, la desviación estándar de la población (σ), y el rango medio ( ) es:
- 14. donde d2, d3 son coeficientes cuyo valor depende del tamaño de cada muestra.
- 15. INTERPRETACIÓN DEL GRÁFICO (X-R ) Desde el punto de vista del control y mejora del proceso, no basta con saber construir los gráficos de control; es necesario saber interpretarlos, con el fin de averiguar lo que le está sucediendo al proceso en el transcurso del tiempo: causas de variación especiales, sesgos, tendencias, etc.
- 16. Antes de aceptar los gráficos anteriores para el control futuro, es necesario comprobar que el proceso esta bajo control estadístico, lo cual ocurre cuando: - Ninguno de los valores del Rango queda fuera de los limites de control de Rango. - Ninguna de las Medias esta fuera de los limites de control de las Media.
- 17. No haya dos Medias seguidas fuera de los limites de advertencia, (estos se toman con una amplitud de dos veces la desviación típica). - En siete muestras consecutivas no puede haber mas de dos Medias fuera y del mismo lado de los limites de advertencia.
- 18. EJEMPLO DE GRAFICOS X-R. A) A continuación se muestra la representación del gráfico () correspondiente a los datos de 25 muestras de tamaño 5 de los diámetros de determinadas piezas.
- 19. s diámetros de determinadas piezas. x1 x2 x3 x4 x5 001 10.440 10.500 10.450 10.440 10.520 002 10.640 10.530 10.600 10.520 10.510 003 10.550 10.510 10.470 10.450 10.420 004 10.530 10.520 10.560 10.590 10.600 005 10.520 10.430 10.440 10.460 10.500 006 10.450 10.460 10.610 10.480 10.550 007 10.530 10.610 10.480 10.400 10.480 008 10.450 10.500 10.450 10.530 10.470 009 10.520 10.560 10.530 10.580 10.660 010 10.560 10.500 10.400 10.510 10.640 011 10.530 10.480 10.560 10.550 10.580 012 10.560 10.430 10.430 10.420 10.510 013 10.500 10.720 10.480 10.450 10.500 014 10.470 10.530 10.560 10.520 10.470 015 10.530 10.560 10.600 10.690 10.550 016 10.510 10.630 10.620 10.590 10.610 017 10.500 10.510 10.400 10.520 10.520 018 10.540 10.460 10.490 10.450 10.460 019 10.490 10.550 10.510 10.560 10.490 020 10.620 10.500 10.600 10.610 10.620 021 10.540 10.590 10.630 10.580 10.560 022 10.420 10.550 10.480 10.500 10.500 023 10.520 10.600 10.510 10.520 10.500 024 10.570 10.720 10.640 10.730 10.590 025 10.600 10.570 10.600 10.480 10.500 x1 x2 x3 x4 x5 001 10.440 10.500 10.450 10.440 10.520 002 10.640 10.530 10.600 10.520 10.510 003 10.550 10.510 10.470 10.450 10.420 004 10.530 10.520 10.560 10.590 10.600 005 10.520 10.430 10.440 10.460 10.500 006 10.450 10.460 10.610 10.480 10.550 007 10.530 10.610 10.480 10.400 10.480 008 10.450 10.500 10.450 10.530 10.470 009 10.520 10.560 10.530 10.580 10.660 010 10.560 10.500 10.400 10.510 10.640 011 10.530 10.480 10.560 10.550 10.580 012 10.560 10.430 10.430 10.420 10.510 013 10.500 10.720 10.480 10.450 10.500 014 10.470 10.530 10.560 10.520 10.470 015 10.530 10.560 10.600 10.690 10.550 016 10.510 10.630 10.620 10.590 10.610 017 10.500 10.510 10.400 10.520 10.520 018 10.540 10.460 10.490 10.450 10.460 019 10.490 10.550 10.510 10.560 10.490 020 10.620 10.500 10.600 10.610 10.620 021 10.540 10.590 10.630 10.580 10.560 022 10.420 10.550 10.480 10.500 10.500 023 10.520 10.600 10.510 10.520 10.500 024 10.570 10.720 10.640 10.730 10.590 025 10.600 10.570 10.600 10.480 10.500
- 20. Con la tabla inicial de datos los gráficos que se obtienen son los siguientes:
- 21. En el diagrama X se detecta un punto fuera de control correspondiente a la muestra 24, mientras que en el R todos están entre los límites. Enmascarando esta muestra y volviendo a dibujar los gráficos se detecta otro punto fuera de control, esta vez en el gráfico R correspondiente a la muestra 13, la cual volvemos a enmascarar. Para ello seguiremos los siguientes pasos:
- 22. Calcularemos en primer lugar los rangos de cada muestra, Ri , y el rango medio, , con la información contenida en la ficha de control:
- 23. Los limites de control para los rangos vienen dados por las expresiones en función de D3 y D4 es: 𝐿𝐶𝑆 𝑅= 𝐷4* = = 2,115 x 0,126 = 0,266 𝐿𝐶𝐼 𝑅= 𝐷3* = = 2,115 x 0,126 = 0,266 Siendo los valores de D 3 y D 4 los correspondientes a la tabla anterior para un tamaño de muestra, n, igual a 5.
- 24. B) Se comprueba a continuación si el rango de alguna de las muestras cae fuera de los Límites de Control. Si esto ocurre, se interpretará que la(s) muestra(s) correspondiente(s) pertenece(n) a una población distinta o a un momento en el que el proceso estuvo fuera de control. En cualquier caso, dichas muestras no serán consideradas y se procederá a calcular unos nuevos R y LCR con las muestras restantes.
- 25. En el presente caso, sólo el rango de la muestra i=13 está fuera de los límites, pues R13 = 0,27, por lo que debe ser eliminada en la determinación del nuevo rango:
- 26. 𝐿𝐶𝑆 𝑅= 𝐷4* = 2,115 x 0,12 = 0,266 𝐿𝐶𝐼 𝑅= 𝐷3* = 0 x 0,126 = 0,266 c) Una vez fijado se calcula el valor de y LC X, utilizando únicamente las muestras no excluidas4 en el apartado anterior, por medio de las expresiones ya vistas. Asimismo, se tomará R = 0,12.
- 27. 𝐿𝐶𝐼 𝑅= 𝐷3* = 0 x 0,126 = 0,266 𝐿𝐶𝐼 𝑅= 𝐷3* = 0 x 0,126 = 0,266 donde A 2 procede de la tabla anteriormente comentada para n = 5. No obstante algunos autores prefieren considerar todas las muestras.
- 28. Calcule los límites de control 3s superior e inferior del diagrama X– para los datos de humedad de la tabla 10.1. Solución Con la muestra 6 eliminada, el valor de X– es 2.658, y el valor de s– es 0.2354. El tamaño de la muestra es n =5. De la tabla se tiene que A3 1.427. Por tanto, el límite de control superior es 2.658 (1.427)(0.2354) 2.994, y el límite de control inferior es 2.658 – (1.427)(0.2354) 2.322.
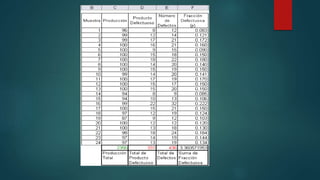
- 29. DIAGRAMA DE CONTROL DE ATRIBUTOS P En la siguiente figura tenemos los datos de 24 muestras de producto producido por turno. En la columna producción tenemos el total de producto fabricado por turno. La columna Producto Defectuoso nos indica el número de artículos defectuosos por turno; la columna Número de Defectos nos indica el número de defectos encontrados en la producción de cada turno, nótese que por cada turno el número de defectos es mayor o igual que el número de defectuosos, ya que un artículo defectuoso puede tener uno o más defectos. Finalmente tenemos la columna de Fracción Defectuosa, la fracción defectuosa de un turno se calcula dividiendo el número de productos defectuosos por la producción de ese turno, es decir, los valores de la columna D divididos por los valores de la columna C.
- 31. Como recordaremos de un post anterior, los límites de control de un gráfico de fracción defectuosa con tamaño de muestra variable vienen dado por la siguiente fórmula:
- 32. Mientras que la fracción defectuosa se p barra, se calcula con la siguiente fórmula: Figura 3 Ahora bien de las ecuaciones de la Figura 2, vemos que para calcular estos límites necesitamos el valor p barra, que es una estimación de la fracción defectuosa y ni, que es el tamaño de muestra de cada turno. Es decir, tendremos límites de control de diferentes tamaños, debido a que los tamaños de muestra son variables. El valor de p barra es entonces: ‘ Entonces tenemos ya el valor de p barra y los valores de ni, los cuales son los artículos producidos en cada turno (tamaño de muestra), cuyos valores se muestran en la columna C de la Figura 1. Ya con esto, calculamos los límites de control con las fórmulas de la Figura 1. Los valores se muestran en las columnas K, L y M de la siguiente figura.
- 34. Por otra parte, en la columna J, de la figura anterior, tenemos la fracción defectuosa de cada muestra o turno, está se calcula para cada turno, dividiendo el número de defectuosos del turno por el total de artículos producidos. Con los valores de las cuatro columnas de la Figura 4, podemos construir el gráfico de control. Reitero que en un post anterior que se encuentra aquí, se muestra como se puede hacer este gráfico de control. Con los datos de la Figura 4, el gráfico de control nos quedaría así: