Mat iii
- 2. SERGIO MUÑOZ VENEGAS LICENCIADO EN MATEMÁTICA CON MENCIÓN EN MATEMÁTICA, DOCTOR EN CIENCIAS EXACTAS, MENCIÓN MATEMÁTICA PONTIFICIA UNIVERSIDAD CATÓLICA DE CHILE. FLORENCIA DARRIGRANDI NAVARRO LICENCIADA EN MATEMÁTICA CON MENCIÓN EN ESTADÍSTICA, MAGISTER EN ESTADÍSTICA, PONTIFICIA UNIVERSIDAD CATÓLICA DE CHILE. Matemática TEXTO DEL ESTUDIANTE 3º Educación Media INICIALES 3º MEDIO-C:Maquetación 1 4/11/10 17:09 Página 1
- 3. El Texto del Estudiante Matemática 3, para Tercer Año de Educación Media, es una obra colectiva, creada y diseñada por el departamento de Investigaciones Educativas de Editorial Santillana, bajo la dirección general de: MANUEL JOSÉ ROJAS LEIVA COORDINACIÓN DE PROYECTO: Eugenia Águila Garay COORDINACIÓN ÁREA MATEMÁTICA: Viviana López Fuster EDICIÓN: Isabel Montes Alcalde AUTORES: Sergio Muñoz Venegas Florencia Darrigrandi Navarro CORRECCIÓN DE ESPECIALISTA: Rodrigo Abarzúa Ortiz CORRECCIÓN DE ESTILO: Isabel Spoerer Varela Gabriela Precht Rojas DOCUMENTACIÓN: Paulina Novoa Venturino La realización gráfica ha sido efectuada bajo la dirección de: VERÓNICA ROJAS LUNA COORDINACIÓN GRÁFICA: Carlota Godoy Bustos COORDINACIÓN GRÁFICA LICITACIÓN: Xenia Venegas Zevallos JEFA DE DISEÑO ÁREA MATEMÁTICA: Mariela Pineda Gálvez DIAGRAMACIÓN: Mariela Pineda Gálvez ILUSTRACIONES: Antonio Ahumada Mora FOTOGRAFÍAS: Archivo Santillana CUBIERTA: La Práctica S.P.A. PRODUCCIÓN: Germán Urrutia Garín Quedan rigurosamente prohibidas, sin la autorización escrita de los titulares del "Copyright", bajo las sanciones establecidas en las leyes, la reproducción total o parcial de esta obra por cualquier medio o procedimiento, comprendidos la reprografía y el tratamiento informático, y la distribución en ejemplares de ella mediante alquiler o préstamo público. © 2010, by Santillana del Pacífico S.A. de Ediciones Dr. Aníbal Ariztía 1444, Providencia, Santiago (Chile) PRINTED IN CHILE Impreso en Chile por WorldColor Chile S.A. ISBN: 978-956-15-1758-5 Inscripción N°: 198.041 Se terminó de imprimir esta 1a edición de 229.200 ejemplares, en el mes de diciembre del año 2010. www.santillana.cl Referencias de los Textos Educación Matemática 2 y 3, Educación Media y del Texto Matemática 2, Educación Media, Mineduc, de los autores: Ángela Baeza Peña, María José García Zattera, Marcia Villena Ramírez, Marcela Guerra Noguera, Patricia Urzúa Figueroa, Rodrigo Hernández Reyes, Mario Zañartu Navarro, Florencia Darrigrandi Navarro, Mauricio Ramos Rivera. Santillana del Pacífico S.A. de Ediciones, Santiago, Chile, 2005 y 2010. INICIALES 3º MEDIO-C:Maquetación 1 23/11/10 16:39 Página 2
- 4. El Texto Matemática 3, para Tercer Año Medio, ha sido creado y diseñado pensando en tus intereses y en que sea un apoyo efectivo en tu proceso de aprendizaje. Este año, en Álgebra, trabajarás con raíces cuadradas y cúbicas, las com- pararás mediante diversos procedimientos y aprenderás a resolver problemas que involucran operatoria con estas raíces. También podrás establecer rela- ciones entre el área y la medida del lado de un cuadrado y entre el volumen y la medida de la arista de un cubo; construirás geométricamente la lon- gitud de las raíces cuadradas de algunos números utilizando el teorema de Pitágoras; trabajarás en la representación y el análisis de los procesos de resolución de inecuaciones lineales y de sistemas de inecuaciones lineales con una incógnita, y podrás analizar sobre la existencia y pertinencia de sus soluciones. Trabajarás con las funciones cuadrática y raíz cuadrada; podrás analizar la función cuadrática f (x) = ax2 + bx + c, respecto de la orientación y aper- tura de las ramas de la parábola, eje de simetría, vértice, intersección de la parábola con ambos ejes del sistema de coordenadas. También resolve- rás ecuaciones de segundo grado con una incógnita por completación de cuadrados, por factorización o por inspección, analizando la existencia y pertinencia de las soluciones obtenidas, y analiza- rás situaciones o fenómenos que pueden ser modelados me- diante funciones cuadráticas. En Geometría, conocerás los Teoremas de Euclides, compararás las diversas maneras de demostrar el Teorema de Pitágoras y aplicarás estos teoremas en construcciones geométricas; trabajarás con razones trigonométricas y con funciones seno, coseno y tangente en el círculo unitario. En Probabilidad, trabajarás con la variable aleatoria en forma teórica y experimental; podrás relacionar la noción de probabi- lidades con la frecuencia relativa y discriminarás entre sucesos dependientes e independientes y resolverás problemas que in- volucran probabilidad condicionada en situaciones sencillas. Todo esto a través de interesantes actividades que te permitirán razonar, reflexionar, analizar y compartir tus conocimientos con tus compañeros y compañeras. Presentación | 3 Presentación INICIALES 3º MEDIO-C:Maquetación 1 4/11/10 17:09 Página 3
- 5. Te damos la bienvenida a este nuevo año escolar y queremos apoyarte en tu crecimiento y desarrollo con este Texto, que te entregará herramientas para enfrentarte de mejor manera en el mundo que te rodea, y te invita a comprender que la Matemática es parte de él. A través de sus cinco Unidades te enfrentarás a diversas situaciones, en las que podrás explorar, aprender, cons- truir y consolidar conceptos relacionados con números, álgebra, geometría, datos y azar. En ellas encontra- rás las siguientes páginas y secciones: Páginas de inicio 4 | Matemática 3º Medio Estructura del Texto • Mediante un esquema, conocerás los contenidos y su vinculación con los principales aprendizajes que se espera que logres con el desarrollo de la Unidad. ¿Cuánto sabes? En esta sección te invitamos a resolver ejercicios y problemas que te ayudarán a evaluar tus conocimientos y a recordar lo que aprendiste en años anteriores, siendo la base para el desarrollo de la Unidad. ¿Qué debes recordar? Podrás activar tus conocimientos previos a través de un resumen que incluye los principales conceptos trabajados en años anteriores y que te servirá como apoyo para los aprendizajes que se espera que logres en la Unidad. Conversemos de... A través de una introduc- ción al tema de la Unidad, conectamos elementos e imágenes de la vida diaria con el contenido que trabajarás.Además, encontrarás preguntas relacionadas con la imagen y con los contenidos de la Unidad que te permitirán exponer tus ideas, dar opiniones y argumentar a partir de tus experiencias. INICIALES 3º MEDIO-C:Maquetación 1 4/11/10 17:09 Página 4
- 6. Páginas de desarrollo Estructura del Texto | 5 Estructura del Texto Actividades Resolverás variadas actividades para ir construyendo los conceptos y reforzando así tu aprendizaje. Analicemos... Por medio de preguntas, trabajarás el razonamiento, explorarás el contenido matemático que aprenderás, pondrás en práctica lo que ya sabes, compartirás tus ideas y extraerás conclusiones. En resumen Encontrarás explicaciones, formalizaciones o definiciones que destacan y precisan lo que vas aprendiendo. Recuerda que... Te recordará un contenido o procedimiento ya aprendido y necesario para lograr tus nuevos aprendizajes. INICIALES 3º MEDIO-C:Maquetación 1 4/11/10 17:09 Página 5
- 7. 6 | Matemática 3º Medio Organizando lo aprendido Podrás organizar y sintetizar lo aprendido utilizando un mapa conceptual.Además, aclararás los conceptos trabajados respondiendo preguntas sobre ellos y sus relaciones. Mi progreso Resolverás actividades que te permitirán evaluar tu progreso en el logro de los aprendizajes. Herramientas tecnológicas Aprenderás a utilizar planillas de cálculo o programas computacionales. Glosario Te presentará nuevos términos matemáticos relacionados con el contenido que se está desarrollando. INICIALES 3º MEDIO-C:Maquetación 1 4/11/10 17:09 Página 6
- 8. Estructura del Texto | 7 Estructura del Texto Páginas de cierre En terreno A partir de una situación desarrollada en un contexto real o laboral, desarrollarás (primero individualmente y luego en equipo) actividades que te permitirán aplicar lo que aprendiste en la Unidad. Cómo resolverlo En estas dos páginas observarás un problema resuelto paso a paso a través de una determinada estrategia y, luego, podrás practicar la estrategia utilizada o aplicar otras que te permitan encontrar la solución. Eso sí, en Matemática siempre hay más de un camino para resolver un problema. INICIALES 3º MEDIO-C:Maquetación 1 4/11/10 17:09 Página 7
- 9. 8 | Matemática 3º Medio SÍntesis de la Unidad Este es un espacio para que construyas tu mapa conceptual de todo lo trabajado en la Unidad a partir de algunos conceptos fundamentales. También responderás preguntas conceptuales para evaluar lo que has aprendido en la Unidad. Evaluación En estas tres páginas podrás autoevaluar los aprendizajes que lograste en la Unidad. Incluye preguntas de verdadero o falso y actividades de desarrollo.Tomando en cuenta que una de las alternativas al egresar de la Educación Media es rendir la PSU, incluimos algunas preguntas tipo de esta prueba. INICIALES 3º MEDIO-C:Maquetación 1 4/11/10 17:09 Página 8
- 10. Índice | 9 ¿Cuánto sabes? 14 Raíces cuadradas 16 Irracionalidad de algunas raíces cuadradas 18 Ubicación de raíces cuadradas en la recta numérica 20 Raíces cúbicas 22 Estimación y comparación de raíces 24 Producto y cociente de raíces 26 Organizando lo aprendido 28 Mi progreso 29 Ampliando el concepto de raíz 30 Cálculo y propiedades de raíces enésimas 32 Relación entre raíces y potencias 36 Expresiones con raíces en el denominador 38 Ecuaciones con radicales 42 Organizando lo aprendido 44 Mi progreso 45 Cómo resolverlo 46 En terreno 48 Síntesis de la Unidad 50 Evaluación 51 ¿Cuánto sabes? 56 Función cuadrática 58 Características de la gráfica de f(x) = x2 60 Forma canónica de funciones cuadráticas 62 Dilatación y contracción de la parábola 64 Desplazamientos de la parábola 66 Simetría y vértice de la parábola 70 La parábola como lugar geométrico 72 Organizando lo aprendido 74 Mi progreso 75 Ecuación de segundo grado 76 Análisis de las raíces de una ecuación cuadrática 80 Ecuaciones reductibles a ecuaciones de segundo grado 82 Análisis general de una función cuadrática 84 Máximos y mínimos 88 Función raíz cuadrada 90 Organizando lo aprendido 96 Mi progreso 97 Cómo resolverlo 98 En terreno 100 Síntesis de la Unidad 102 Evaluación 103 Índice Raíces 12 1 2Función cuadrática y función raíz cuadrada 54 INICIALES 3º MEDIO-C:Maquetación 1 4/11/10 17:09 Página 9
- 11. 10 | Matemática 3º Medio ¿Cuánto sabes? 108 Teorema de Euclides 110 Demostraciones del teorema de Pitágoras 114 Tríos pitagóricos 118 Situaciones que involucran triángulos rectángulos 121 Organizando lo aprendido 124 Mi progreso 125 Razones trigonométricas en el triángulo rectángulo 126 Razones trigonométricas de ángulos especiales 130 Aplicaciones de la trigonometría 132 Propiedades de las razones trigonométricas 134 Identidades trigonométricas 136 Teorema del seno y del coseno 138 Sistemas de medición de ángulos 142 Funciones trigonométricas 144 Reducción al primer cuadrante 148 Funciones trigonométricas inversas 150 Ecuaciones trigonométricas 152 Organizando lo aprendido 154 Mi progreso 155 Cómo resolverlo 156 En terreno 158 Síntesis de la Unidad 160 Evaluación 161 ¿Cuánto sabes? 166 Desigualdades 168 Intervalos de números reales 170 Propiedades de las desigualdades 174 Conjeturas y demostraciones 176 Organizando lo aprendido 178 Mi progreso 179 Inecuaciones con una incógnita 180 Sistemas de inecuaciones con una incógnita 182 Inecuaciones lineales con dos incógnitas 184 Inecuaciones que involucran valor absoluto 188 Organizando lo aprendido 190 Mi progreso 191 Cómo resolverlo 192 En terreno 194 Síntesis de la Unidad 196 Evaluación 197 El triángulo rectángulo y la trigonometría 106 3 Inecuaciones lineales 164 4 INICIALES 3º MEDIO-C:Maquetación 1 4/11/10 17:09 Página 10
- 12. Índice | 11 Índice ¿Cuánto sabes? 202 Espacio y tamaño muestral 204 Sucesos o eventos 206 Principio multiplicativo 210 Permutaciones 212 Combinaciones 214 Organizando lo aprendido 216 Mi progreso 217 Cálculo de probabilidades 218 Sucesos equiprobables 220 Probabilidad del suceso A艛B 222 Frecuencia relativa o probabilidad empírica 224 Ley de los grandes números 226 Probabilidad condicional 228 Probabilidad del suceso A艚B 230 Sucesos independientes 232 Variable aleatoria 234 Organizando lo aprendido 238 Mi progreso 239 Cómo resolverlo 240 En terreno 242 Síntesis de la Unidad 244 Evaluación 245 5Probabilidades 200 Solucionario 256 Taller de evaluación 248 Índice temático 284 Bibliografía 287 INICIALES 3º MEDIO-C:Maquetación 1 4/11/10 17:09 Página 11
- 13. A APRENDERÁS PRENDERÁS A A: : Comprender y aplicar la relación entre potencias y raíces. Conocer y utilizar procedimientos para el cálculo de raíces. Estimar y comparar raíces. Resolver problemas que involucran raíces. Racionalizar expresiones fraccionarias. Conocer y aplicar algunas propiedades de las raíces. Raíces 1 T TRABAJANDO RABAJANDO CON CON: : Ecuaciones con radicales Raíz enésima Potencias Raíz cúbica Raíz cuadrada 12 | Unidad 1 TRABAJANDO CON: APRENDERÁS A: UNIDAD 1 (12-53)C :Maquetación 1 4/11/10 17:10 Página 12
- 14. Raíces | 13 Conversemos de... El columpio es un juego que tiene un movimiento similar al de un péndulo. La principal caracterís- tica del péndulo es que el lapso que le toma completar una ida y una vuelta (su período), si no es un movimiento muy amplio, es proporcional a la raíz cuadrada del radio de giro del columpio. Aproximadamente: , donde L es el radio de giro del columpio y g es la aceleración de gravedad. Las raíces cuadradas y otras raíces son parte de las herramientas matemáticas que nos ayudan a compren- der el mundo que nos rodea. • ¿Qué ocurrirá con el período del péndulo si se alargan las cuerdas o cadenas del columpio?, ¿por qué? • Y si varía la masa o persona sobre el columpio, ¿qué pasa con el período? Averigua. 2 ⋅ ⋅ π L g Latinstock UNIDAD 1 (12-53)C :Maquetación 1 4/11/10 17:10 Página 13
- 15. 14 | Unidad 1 ¿Cuánto sabes? 1. Descompón los siguientes números como producto de factores primos: a. 300 c. 1300 e. 6750 b. 1275 d. 3168 f. 7128 2. Determina si las siguientes expresiones son verdaderas. Explica tu decisión. a. 62 + 82 = 102 c. 4–2 · 24 = 20 e. 53 : 3–3 = 1 b. (33 )2 = 35 d. 33 · 52 = 155 f. 34 : 92 = 1 3. Resuelve cada una de las expresiones siguientes aplicando lo que sabes sobre potencias. a. h. c4a – 2 · c–2a + 5 · c5a + 4 d. 3–3 · 2–2 · 35 · 24 k. f. (3)–2 : 92 m. 4. Resuelve los siguientes problemas.Explica,paso a paso,el procedimiento que utilizaste. a. Si multiplicamos por 3 el lado de un cuadrado, ¿en cuánto au- menta el área del mismo? b. Si disminuimos la arista de un cubo a la mitad, ¿en cuánto varía el volumen de este? b b x y y x 3 4 3 4 2 − − ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ − ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ 4 5 2 3 3 x b c 1 4 5 2 2 ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ + Recuerda lo que aprendiste en años anteriores y resuelve en tu cuaderno. b. i. (x–3 : x5 ) · x8 3 4 5 2 1 2 ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ + ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ − c. (–2)3 + (–2)2 +(–2)0 +(–2)1 j. x x 4 3 2 3 2 ⋅ − ( ) ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ e. 52 : 5–2 l. 1 1 1 2 4 3 a a a ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ ⋅ ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ − − : g. xa + 1 · x–a + 2 · x3a + 4 n. a b c c a b 2 3 4 2 3 2 ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ ⋅ ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ − − UNIDAD 1 (12-53)C :Maquetación 1 4/11/10 17:10 Página 14
- 16. 5. Desarrolla los siguientes productos: a. (x – 3y)2 c. (a – 3b)(a2 + 3ab + 9b2 ) b. (x + 3)(x – 2) d. 6. Factoriza las siguientes expresiones aplicando productos notables. a. c. 27x3 + 8 b. x6 – 4x3 + 4 d. 8x3 – 36x2 y + 54xy2 – 27y3 Verifica en el solucionario si tus respuestas son correctas. ¿Tuviste algún error? Si los tuviste, corrígelos antes de continuar con la Unidad. 4 9 2 2 a b − 1 3 5 2 5 2 1 3 x y y x − ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ + ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ Raíces | 15 Unidad 1 ¿Qué debes recordar? • Algunas propiedades de las potencias son: Multiplicación de potencias División de potencias an · am = an + m an : am = an – m an · bn = (a · b)n an : bn = (a : b)n • Algunas factorizaciones y productos notables son: (a ± b)2 = a2 ± 2ab + b2 (cuadrado de binomio). (a + b)(a – b) = a2 – b2 (suma por diferencia). (x + a)(x + b) = x2 + (a + b) · x + ab (producto de dos binomios con un término común). (a ± b)3 = a3 ± 3a2 b + 3ab2 ± b3 (cubo de binomio). (suma y diferencia de cubos). • Si a y b son números reales positivos, y a < b, se cumple que an < bn para todo n ⺞. • Para todo x IR, x2 0, es decir, el cuadrado de un número real es siempre positivo o cero. • El valor absoluto de todo número real distinto de cero es siempre positivo, es decir, si x pertenece al conjunto de los números reales y x 0, entonces |x| 0. • El valor absoluto de cero es cero, o sea |0| = 0. a b a b a ab b 3 3 2 2 ± = ± ( ) ⋅ + ( ) ∓ UNIDAD 1 (12-53)C :Maquetación 1 4/11/10 17:10 Página 15
- 17. 16 | Unidad 1 Raíces cuadradas Analicemos... Para evaluar el total de baldosas del pasillo de la casa de su abuelo, Ernesto calculó que como tenían 10 cm de lado, en un metro de largo del pasillo tendría 10 baldosas; por lo tanto, en total había 50 · 32 baldosas, es decir, 1600. Para que Ernesto notara que la can- tidad de baldosas de su abuelo era exactamente las que nece- sitaba para la pieza grande, que era cuadrada, debió darse cuenta al medir la longitud de su pieza y obtener 4 metros de largo por 4 metros de ancho, por lo que cabían exactamente 40 · 40 baldosas; o sea, las 1600 del pasillo de la casa de su abuelo. En la situación anterior necesitábamos encontrar un número que al multiplicarlo por sí mismo nos diera 1600, ya que sabíamos que la pieza era cuadrada. Con lo que se obtiene 40. Lo que acabamos de hacer es encontrar la raíz cuadrada de 1600. • ¿Cuál es la cantidad de baldosas que tenía el pasillo del abuelo?, ¿cómo lo resolviste? • ¿Cuánto medía la pieza grande de la casa de Ernesto?, ¿cómo lo supiste? • ¿Era verdad que no faltaría ni sobraría ninguna baldosa para la pieza?, ¿por qué? El pasillo de la casa de los abuelos de Ernesto está embaldosado. Sin embargo, Ernesto lo cambiará y pondrá piso de madera porque aísla mejor el frío. En agradecimiento de su trabajo, su abuelo le regalará las baldosas, que son cuadradas de 10 cm por lado, para que las ponga en la pieza grande de su casa, pero le dijo que antes de trasladarlas debe estar seguro de que le alcancen, o ver si le so- bran, para que solo se lleve las necesarias. Ernesto mide la pieza grande, que es perfectamente cuadrada, y se da cuenta de que las baldosas son justamente las que necesita para la pieza. ¿Cuántas baldosas tiene tu piso? No lo sé, pero el pasillo tiene 5 m de largo y 3,2 m de ancho. UNIDAD 1 (12-53)C :Maquetación 1 4/11/10 17:10 Página 16
- 18. Raíces | 17 Unidad 1 En resumen • Si a es un número positivo o cero (a ≥ 0), la expresión denota al único número (mayor o igual a cero) cuyo cuadrado es a. se lee “raíz cuadrada de a”. • Si a ≥ 0: x = , si a = x2 a a 2 = a a a 1. Encuentra la longitud del lado de un cuadrado, si sabemos que su área es: a. 36 cm2 d. 625 m2 g. 1225 cm2 b. 81 cm2 e. 900 m2 h. 1681 cm2 c. 400 m2 f. 1024 cm2 i. 3600 cm2 2. Calcula el valor de las siguientes expresiones. Explica cómo lo hiciste. a. d. g. b. e. h. c. f. i. 3. Determina si las siguientes afirmaciones son verdadera o falsas. Justifica en cada caso tu decisión. a. Si x 0, entonces . d. Si x 0, entonces IR. b. Si x 0, entonces . e. Si a 0 y b 0, entonces IR. c. Si x 0, entonces . f. Si a 0 y b 0, entonces IR. 4. Piensa, comenta y responde. Justifica tus respuestas. a. ¿Qué ocurre si queremos calcular , si a 0? b. ¿Se cumple que , para todo a, b IR? ab ab –x 1000 000 10 000 − ( ) 3 2 3 5 2 2 · 144 3 2 4 9 · 4 16 + 0 a b a b + = + a – – x x 2 = x x 2 = x x 2 = Actividades Observa que la ecuación x2 = a tiene dos soluciones: y , ya que y , pero para las raíces solo consideramos el valor positivo, , no –a. a a 2 = − ( ) = a a 2 a a 2 = − a a UNIDAD 1 (12-53)C :Maquetación 1 4/11/10 17:10 Página 17
- 19. 18 | Unidad 1 Irracionalidad de algunas raíces cuadradas Observa cómo se determina geométricamente la longitud de la diagonal de un cuadrado. Para encontrar la medida de la diagonal D debemos usar el teorema de Pitágoras; de esta forma, se tiene que D2 = 12 + 12 = 1 + 1 = 2. Entonces, D es lo que ahora conocemos como . Los números, como , fueron descubiertos por los antiguos grie- gos. Una vez que se había demostrado el teorema de Pitágoras, se dieron cuenta de que ese valor, que existía en muchos cuadrados, no era un número racional. Al utilizar una calculadora, es resultado será algo como: = 1,4142135. Esto no significa que: . Al observar el resultado en la calculadora se podría pensar que es un decimal finito pero con muchos decimales; o bien infinito, cuyo período es más largo que la precisión de la calculadora; o infinito, pero no tiene período. Como ya aprendiste en cursos anteriores, estos números forman un conjunto que se llama números irracionales. El número irracional más conocido es π = 3,1415…. Muchas han sido las aproximaciones de π en el transcurso de los años; por ejem- plo, en 1987 se calculó con una precisión de más de cien millones de cifras decimales, sin encontrarse período alguno. La suma de un número racional con un irracional es también un número irracional, por ejemplo, al sumar –5 y (5 + ) obtenemos –5 + 5 + = ; que es un número irracional. Notemos que la suma y el producto de dos números irracionales no siempre es un irracional; por ejemplo, (5 + ) + (3 – ) = 8, cuyo También son irracionales todas las raíces cuadradas de números naturales que no son exactas, es decir, que su resultado no es un número natural. 2 2 2 2 2 2 2 2 2 14 142 135 10 000 000 = 2 Analicemos... • Según los datos de la figura, ¿cuánto mide la diagonal del cuadrado D?, ¿cómo lo supiste? • ¿D es un número racional?, ¿se puede representar como fracción? Teorema de Pitágoras: Si a y b son los catetos y c la hipotenusa de un triángulo rectángulo, entonces: a2 + b2 = c2 Recuerda que... a c b 0 D D 1 2 1 Glosario número irracional: es cualquier número real que no es racional, es decir, no puede ser expresado como una fracción o razón de dos números enteros. resultado es un número racional, al igual que el producto · = 2. 2 2 UNIDAD 1 (12-53)C :Maquetación 1 4/11/10 17:10 Página 18
- 20. Raíces | 19 Unidad 1 En resumen • Un número irracional es el que no puede representarse como fracción. Es un número decimal infinito que no tiene período. Para demostrar que era un número irracional, los griegos razo- naron dando una demostración por reducción al absurdo. Observa. Si existiera un racional igual a , se escribiría como una fracción , con x e y números enteros positivos. Supongamos que simplificamos todos los factores comunes entre x e y, de modo que obtenemos la fracción , que es irreducible. vando al cuadrado, que 2b2 = a2 . Entonces, 2 divide al número en- tero a2 , y como 2 es número primo, 2 divide a a, por lo que a2 es múltiplo de 4, es decir, a2 = 4k, con k algún número entero. Luego, para b se cumple 2b2 = 4k, de donde b2 = 2k, o sea, b2 es múltiplo de 2, el que es primo, por lo que 2 divide a b, pero en- tonces 2 divide a a y a b, aun si no tenían factores comunes, lo cual es una contradicción. Entonces, la suposición de que es un número racional es incorrecta. Por lo tanto, es un número irracional. 2 2 2 2 a b x y 1. Clasifica las siguientes raíces en irracionales o racionales: a. e. i. b. f. j. c. g. k. d. h. l. 2. De manera similar a la demostración anterior, demuestra que y son números irracionales. 2 5 + 400 169 8 7 10 – 360 72 3 5 300 36 1 3 + 200 16 5 3 Actividades Pero de = se obtiene · b = a, de donde se deduce, ele- 2 a b 2 Glosario reducción al absurdo: argumento de demostración,que consiste en supo- ner que la propiedad que se quiere demostrar no es cierta y deducir a partir de esto una contradicción. En- tonces, como tal contradicción se debe a que la suposición era inco- rrecta,la propiedad debe ser cierta. UNIDAD 1 (12-53)C :Maquetación 1 4/11/10 17:10 Página 19
- 21. 20 | Unidad 1 Ubicación de raíces cuadradas en la recta numérica Recuerda que los números racionales son un conjunto que no com- pleta la recta real, ya que quedan “huecos” en la recta que no son ocupados por números racionales, por ejemplo, está en la recta numérica, sin embargo, no es un número racional. 2 Para ubicar en la recta numérica las raíces no exactas como , se puede, utilizando regla y compás, dibujar sobre una recta un trián- gulo rectángulo isósceles cuyos catetos miden 1 unidad, ya que por el teorema de Pitágoras, al trazar un arco de circunferencia con abertura igual a la hipotenusa del triángulo y centrada en el punto 0 de la recta numérica, se obtiene la ubicación de . En general, para localizar de manera geométrica , siendo n cualquier número natural, se puede aplicar el teorema de Pitágo- ras a un triángulo rectángulo de catetos 1 y la raíz cuadrada del número natural anterior, es decir, . Por ejemplo, con el segmento de longitud y un segmento de longitud 1 se construye un nuevo triángulo rectángulo. Se traza un arco de circunferencia centrada en el punto 0, de radio igual a la hipotenusa de este nuevo triángulo. La intersección de este arco con la recta numérica es el punto . Al observar en la recta numérica la ubicación de y , se puede ver que , ya que las raíces cuadradas mantienen el orden, Demostración por reducción al absurdo: Dados a y b números reales positivos con a b, supongamos que no es cierto que . Luego, debe ser cierto que ,entonces será un número positivo o cero, y como el valor de una raíz cuadrada es siempre un número positivo o cero, también lo será. 3 2 a b + a b − a b ≥ a b 2 2 2 3 3 2 n −1 n Analicemos... • ¿Es posible representar todos los números correspondientes a raíces cuadradas no exactas, como ?, ¿cómo? 2 0 0 1 2 1 1 2 2 3 es decir que, si a y b son positivos o cero, y a b, entonces . a b UNIDAD 1 (12-53)C :Maquetación 1 4/11/10 17:10 Página 20
- 22. Unidad 1 En resumen • Algunos números irracionales pueden representarse en la recta numérica; por ejemplo, las raíces cuadradas inexactas de un número natural y expresiones que las contengan. • Si a y b son positivos o cero, y si a b, se cumple que . a b 1. Ubica en una recta numérica las raíces , , y . Explica cómo lo hiciste. 2. Ordena de menor a mayor los siguientes números. a. ; 2; ; 5 b. ; 12; ; ; 15 8 12 100 7 10 18 12 8 5 Actividades Raíces | 21 Recordando que el producto de dos números positivos es siempre positivo, tendremos que será positivo o cero, por diferencia obtenemos , o sea, , de donde se obtiene que b a. Lo cual es una contradicción. Por lo tanto, la suposición era incorrecta, es decir, . a b 0 – ≤ a b 0 2 2 – ≤ ( ) ( ) a b – + ( )( ) a b a b Herramientas tecnológicas En esta actividad aprenderás a ubicar números en la recta numérica usando el programa Regla y Compás, que se encuentra disponible en el sitio web: www.educacionmedia.cl/links/10M2029.html • Una vez instalado el programa, selecciona Mostrar rejilla en el menú Mostrar. • En el menú Aspecto de puntos marca el botón Mostrar valores de objetos, para que indique la posición exacta de cada punto. • Con el botón Círculo marca en el plano cartesiano, primero, el punto (0, 0) y, luego, el punto (1, 1). De esta manera se dibujará el círculo de centro (0, 0) y radio . • Ahora, con el botón Punto marca el punto de intersección entre la circunferencia dibujada y el eje horizontal de la rejilla. Para que efectivamente sea el punto de intersección, ambos deben volverse amarillos. 1. Observa las coordenadas de ese punto, ¿corresponden a ?, ¿cómo lo supiste? 2. Siguiendo el mismo procedimiento, ubica en la recta otras raíces no exactas. 2 2 es decir, , recordando la identidad de suma 0 – ≤ + ( )( ) a b a b UNIDAD 1 (12-53)C :Maquetación 1 4/11/10 17:10 Página 21
- 23. Raíces cúbicas Paula dispone de un pliego de papel de regalo para envolver un joyero para su mamá, que está de cumpleaños; el joyero tiene forma de cubo y su volumen es de 3375 cm3 . En la situación anterior queremos calcular la medida de la altura del joyero; para esto debemos determinar qué número al cubo es igual a 3375, que es igual a 15, ya que 153 = 15 · 15 · 15 = 3375. Entonces, si Paula dispone de un pliego de 7000 cm2 , el papel de regalo le alcanza para cubrir el joyero, ya que la superficie total de este es de 1350 cm2 (15 · 15 · 6 = 1350). El cálculo realizado para encontrar la medida de la arista del cubo corresponde a calcular la raíz cúbica de 3375, y en este caso se es- cribe con el símbolo . Todo número real tiene raíz cúbica, sin la restricción de los signos que tenía la raíz cuadrada, ya que al elevar un número al cubo, este mantiene el signo del número. Por ejemplo: , ya que (–2)3 = –8 − = − 8 2 3 3375 3 22 | Unidad 1 En resumen • Si a es un número real cualquiera, la expresión denota aquel único número cuyo cubo es a, su signo es el mismo que el de a, y se llamará raíz cúbica de a. x = si a3 = x Por lo tanto, . • En general, . a a a a y 3 3 3 3 3 0 0 , ( ) = − ( ) = − = a b a b 3 3 3 + ≠ + a 3 a 3 Analicemos... • ¿Cuánto mide la altura del joyero que quiere envolver Paula?, ¿cómo lo supiste? • ¿Es suficiente el papel que tiene para envolver el regalo de su mamá?, ¿por qué? 70 cm 100 cm UNIDAD 1 (12-53)C :Maquetación 1 4/11/10 17:10 Página 22
- 24. Raíces | 23 Unidad 1 1. Calcula el valor de las siguientes expresiones: a. d. g. b. e. h. c. f. i. 2. Determina cuál es la medida de la arista de un cubo, cuyo volumen es de: a. 8 m3 c. m3 e. 1,331 m3 b. 64 m3 d. 0,125 m3 f. 0,729 m3 3. Resuelve y explica, paso a paso, el procedimiento que utilizaste. a. Determina el área de una cara de un cubo si su volumen es de 64 cm3 . b. El volumen de un cubo es 125 m3 . Se quiere obtener el área de una de sus caras, por lo que se plantea que este cálculo es equivalente a calcular . ¿Es correcta la afirmación anterior?, ¿por qué? c. Si la medida de la arista de un cubo se expresa por , ¿cómo se expresa el área de una de sus caras? 4. Dadas las siguientes expresiones, decide si son verdaderas o falsas. Justifica tu decisión en cada caso. a. d. b. e. c. f. 512 8 512 8 3 3 3 – – + = 1 25 1 5 3 = 27 64 27 64 3 3 3 + = + − = − 1 8 1 8 3 3 – – 1 343 1 343 3 3 = 4 4 2 3 3 2 = ( ) 1 27 125 27 1000 3 3 – 1331 1331 3 3 – + 0 125 3 , 64 125 1 3 3 − 27 27 3 3 − − 1331 3 − + 1 8 1 4 3 1 1 1 3 3 − − + −27 3 V 3 125 3 2 ( ) Actividades UNIDAD 1 (12-53)C :Maquetación 1 4/11/10 17:10 Página 23
- 25. 24 | Unidad 1 Estimación y comparación de raíces Una embotelladora de bebidas lanzará al mercado un nuevo pro- ducto, un envase cilíndrico con una capacidad de 1000 cm3 , para el cual hay dos propuestas. Un envase, como el de la figura, y el segundo con una altura igual al doble de su radio. Si llamamos r1 al radio del primer envase, entonces tendremos que: π · r1 2 · 10 = 1000 , consideremos π 3,14 r1 2 31,85. Solo falta saber el valor de r1 , un número que al cuadrado sea 31,85. Este número será la raíz cuadrada de 31,85. Recordando que el orden de dos o más raíces cuadradas mantiene el de los números, podemos concluir que , porque , remplazando y , obtenemos . Esto origina un método para aproximar raíces. Acercándose más: (5,1)2 = 26,01 y (5,9)2 = 34,81. Por lo tanto, . Tratemos de encontrar un intervalo aún mejor, (5,6)2 = 31,36 y (5,7)2 = 32,49. Luego, . Observa cómo aproximar el valor de a dos decimales. (5,64)2 = 31,8096 y (5,65)2 = 31,9225. Luego, . De continuar así, llegaríamos a tantos decimales correctos para aproximar como necesitemos. 31 85 , 5 64 31 85 5 65 , , , 31 85 , 5 6 31 85 5 7 , , , 5 1 31 85 5 9 , , , 25 31 85 36 , 5 31 85 6 , Analicemos... • ¿Cómo se expresa el volumen de un cilindro? • ¿Cómo puedo obtener una aproximación de las dimensiones de los envases?, ¿cuál de los envases tiene menor radio? r1 2 1000 10 100 = ⋅ = π π 25 5 = 36 6 = 5 31 85 6 , El volumen de un cilindro está dado por: V = πr2 h, donde h es la altura y r el radio. Recuerda que... 10 cm UNIDAD 1 (12-53)C :Maquetación 1 4/11/10 17:10 Página 24
- 26. Raíces | 25 Unidad 1 1. Aproxima con dos decimales el valor de las siguientes raíces: a. c. e. b. d. f. 2. Ordena de menor a mayor las siguientes raíces: a. b. 350 1000 100 3 0 243 3 , 1000 1000 800 3 ; ; 5 21 40 40 3 3 ; ; ; 110 17 Actividades Entonces, una aproximación de será 5,64, ya que es un valor más cercano a la raíz buscada. Si llamamos r2 al radio del segundo envase, tendremos que h = 2r2 , luego, su volumen estará dado por: π · r2 2 · 2r2 = 1000. r2 3 159,24, luego r2 De forma similar a las raíces cuadradas, se puede justificar si a y b son números reales y a b, se cumple que . Usemos este hecho para aproximar . Observa. (5,5)3 = 166,375 y (5,4)3 = 157,464 Podemos notar que r2 se encuentra entre 5,4 y 5,5; sin embargo, r2 es más cercano a 5,4 que a 5,5. Probemos con 5,42. (5,42)3 = 159,220088. Esta estimación es más cercana aún. Entonces, la longitud del radio del cilindro es aproximadamente 5,42 cm, mientras que la altura será aproximadamente 10,84 cm. La aproximación encontrada nos permite comparar raíces cuadradas con raíces cúbicas, en este caso , ya que 5,64 5,42. Por lo tanto, el segundo envase tiene menor radio. 159 24 3 , 159 24 3 , 31 85 , 31 8096 , 31 85 , 159 24 3 , a b 3 3 2 1000 318 47 2 3 r , = ≈ π En resumen • Este método nos permite aproximar el valor de una raíz y comparar dos o más de ellas a pesar de tener diferentes índices. UNIDAD 1 (12-53)C :Maquetación 1 4/11/10 17:10 Página 25
- 27. 26 | Unidad 1 Producto y cociente de raíces Cristián y Macarena quieren calcular, aproximadamente, cuánto es y , respectivamente. Observa cómo lo resuelve cada uno. Cristián: , entonces, . Macarena: , o sea, . 96 6 3 3 12 Para verificar si el procedimiento de Cristián es correcto podemos recordar que “el cuadrado del producto de dos números es igual al producto de los cuadrados de dichos números”. Descomponiendo 12 en dos factores: , y aplicando esto podemos afirmar que , es decir, obtenemos , ya que ambas raíces son positivas. Luego, , ya que . Por lo tanto, . De modo similar, y recordando que “el cociente del cubo de dos números es igual al cubo del cociente de dichos números”, podemos verificar el procedimiento de Macarena. En general, para números no negativos, la raíz de un producto es el producto de las raíces y la raíz de un cociente es el cociente de las raíces. 12 3 46 , ≈ 3 173 , ≈ 4 3 2 3 2 173 3 46 · · , , = ≈ = 4 3 4 3 · · = 12 4 3 · = 4 3 4 3 4 3 2 2 2 · · · ( ) = ( ) ( ) = Analicemos... • ¿Son correctos los procedimientos de Cristián y Macarena?, ¿por qué? • ¿Qué propiedad de las raíces se utiliza en el desarrollo del ejercicio? 12 4 3 4 3 2 3 = ⋅ = ⋅ = 12 3 46 ≈ , 96 6 96 6 16 8 2 8 2 2 2 3 3 3 3 3 3 3 3 = = = ⋅ = ⋅ = 96 6 2 52 3 3 ≈ , (a · b)n = an · bn Recuerda que... y 2 1 26 3 ≈ , 3 1 73 ≈ , a b a b n n n ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ = UNIDAD 1 (12-53)C :Maquetación 1 4/11/10 17:10 Página 26
- 28. Unidad 1 Raíces | 27 1. Reduce las siguientes raíces (con a, b, x e y números positivos): a. c. e. g. b. d. f. h. 2. Considera las aproximaciones , , y calcula: a. b. c. d. 3. Simplifica las siguientes expresiones (con a, b, c y x números positivos) explicando, paso a paso, cómo lo hiciste. a. b. c. 4. Determina si las siguientes afirmaciones son verdaderas o falsas. Justifica tu respuesta. a. b. Si x 0, entonces x x x 6 2 2 3 · = 1331 121 123 123 3 3 3 – = 300 6000 0 5 , 64 4 125 25 49 2 a b 4 12 3 b b ⋅ 2 8 18 ⋅ ⋅ 8 6 4 4 a a b x y x y 2 · a c b c a b c ab c 2 2 4 3 3 3 5 3 2 − − − ⋅ ( ) · 240 6 4 5 2 3 7 a a a a ⋅ ⋅ − 128 32 3 x x 20 5 2 24 ≈ , 3 1 73 ≈ , 2 1 41 ≈ , 108 Actividades En resumen • Si a y b son números reales positivos o cero (a ≥ 0, b ≥ 0), se cumplen las siguientes propiedades: • La raíz cuadrada de un producto es igual al producto de las raíces cuadradas de sus factores. • La raíz cuadrada de un cociente es igual al cociente de las raíces cuadradas de sus términos. • Si a y b son números reales cualesquiera, se cumplen las siguientes propiedades: • La raíz cúbica de un producto es igual al producto de las raíces cúbicas de sus factores. • La raíz cúbica de un cociente es igual al cociente de las raíces cúbicas de sus términos. a b a b 3 3 3 = a b a b = , con b 0 , con b 0 a b a b ⋅ = ⋅ 3 3 3 a b a b ⋅ = ⋅ UNIDAD 1 (12-53)C :Maquetación 1 4/11/10 17:10 Página 27
- 29. 28 | Unidad 1 • En el siguiente mapa conceptual, se muestran algunos de los conceptos presentados hasta ahora en la Unidad. • Utilizando los contenidos aprendidos en la Unidad y, apoyándote en el esquema anterior, responde en tu cuaderno. 1. ¿Crees que faltó un concepto importante en el mapa conceptual?, ¿cuál? Agrégalo. 2. ¿A qué tipo de números no se les puede calcular su raíz cuadrada? 3. ¿La raíz cuadrada de 4 es ± 2?, ¿por qué? 4. ¿La raíz cúbica de un producto es el producto de las raíces de sus factores?, ¿por qué? 5. ¿La raíz cuadrada de una suma es la suma de las raíces de sus sumandos?, ¿por qué? 6. ¿La raíz cúbica de una suma es la suma de las raíces de sus sumandos?, ¿por qué? 7. ¿Toda raíz cuadrada de un número entero positivo es un número entero? 8. ¿La raíz cúbica de 250 es un número entre 5 y 6?, ¿por qué? 9. ¿Qué relación hay entre y x2 – a = 0? Explica. 10. ¿Qué relación hay entre lado y área de un cuadrado de lado a? 11. ¿Qué relación hay entre lado y volumen de un cubo de arista a? 12. ¿Tienes alguna duda sobre los conceptos tratados en las páginas anteriores?, ¿cuál? Compártela con tu curso e intenten aclararla en conjunto. a se aplican a mantienen mantienen RAÍCES CUADRADAS NÚMEROS REALES POSITIVOS O CERO RAÍCES CÚBICAS Organizando lo aprendido se distinguen RAÍCES ORDEN se aplican a TODOS LOS NÚMEROS REALES UNIDAD 1 (12-53)C :Maquetación 1 4/11/10 17:10 Página 28
- 30. Raíces | 29 Unidad 1 1. Determina cuáles de las siguientes desigualdades son verdaderas y cuáles son falsas. Explica en cada caso tu decisión. a. b. c. d. 2. Simplifica las siguientes expresiones: a. c. e. 3. ¿Cuál es el valor de ? 4. Resuelve los siguientes problemas explicando, paso a paso, tu desarrollo. a. Dos triángulos rectángulos comparten la misma hipotenusa. Si las medidas de los catetos de uno de los triángulos son iguales a 11 cm y 3 cm, y la medida de uno de los catetos del segundo triángulo es de 7 cm, halla la medida del cateto restante. b. Encuentra el volumen de un cubo, si el área de una de sus caras es 27 cm2 . 5. Calcula el área pintada de cada figura, sabiendo que cada una no pintada es un cuadrado. a. b. c. 27 3 15 5 144 5 10 3 28 21 7 5 8 3 ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ 5 2 ( ) 3 3 3 3 3 + + + 125 8 1 3 2 30 4 2 3 • Verifica en el solucionario si tus respuestas son correctas. Si tuviste respuestas incorrectas, marca en la tabla el criterio correspondiente y revisa las páginas indicadas. Luego, identifica el error y corrígelas. ¿Cómo voy? Mi progreso A. B. C. D. 2 E. 4 4 3 3 3 4 3 b. d. f. 4 3 24 3 3 5 7 15 7 ⋅ 5 5 ( ) CRITERIO ÍTEMS PÁGINAS DONDE SE TRABAJA Calcular, estimar y comparar raíces. 1 16 a 25 Simplificar expresiones que involucran raíces. 2 y 3 26 y 27 Resolver problemas que involucran raíces. 4 y 5 16 y 17; 22 y 23 3 m2 3 m2 7 m2 x m2 x m2 y m2 4 2 – 4 2 – 4 2 + m2 m2 m2 UNIDAD 1 (12-53)C :Maquetación 1 4/11/10 17:10 Página 29
- 31. 30 | Unidad 1 Ampliando el concepto de raíz En cursos anteriores aprendiste a calcular el promedio o media arit- mética; ahora veremos cómo se puede obtener la media geométrica. Para obtener la media geométrica entre 2 y 18, se calcula: . Geométricamente, este resultado se puede interpretar como la medida del lado del cuadrado que tiene igual área que un rectán- gulo de lados 2 y 18 cm. Para obtener la media geométrica de 6, 16 y 18, se calcula: , es decir, 123 es igual al producto de 6, 16 y 18. Geométricamente, este resultado se puede interpretar como la medida de la arista de un cubo como el de la figura que tiene igual volumen que un prisma de dimensiones 6, 16 y 18 cm. 6 16 18 1728 12 3 3 ⋅ ⋅ = = 2 18 36 6 ⋅ = = La media geométrica depende de la cantidad de números involu- crados. Luego, no siempre se usa la raíz cuadrada o cúbica. La media geométrica de 2, 4, 9 y 18 corresponde a la solución posi- tiva de x4 = 2 · 4 · 9 · 18 = 1296, que corresponde a , lo que se lee como “raíz cuarta de 1296”. De la misma forma, la solución de x5 = a corresponde a y se lee “raíz quinta de a”, y así sucesivamente. En general, la raíz enésima de un número a, que denotamos por , es el número que resuelve la ecuación xn = a. Es decir, se busca el número cuya potencia enésima sea a. Al número n se le llama índice y al número a se le denomina cantidad subradical. a n x a = 5 x = 1296 4 Analicemos... • Si se necesita obtener la media geométrica de 2, 4, 9 y 18, ¿cómo se puede calcular?, ¿corresponde a ?, ¿por qué? • ¿Cómo se relaciona el producto de los cuatro números con su media geométrica? • En el caso de calcular la media geométrica de cinco números, ¿cómo se podría expresar ese número? 2 4 9 18 ⋅ ⋅ ⋅ 18 cm 2 cm 6 cm 12 cm 16 cm 18 cm 6 cm Glosario media geométrica: de n términos x1 , x2 ... xn es la raíz enésima del producto de los n términos. G x x xn n · · ... · = 1 2 UNIDAD 1 (12-53)C :Maquetación 1 4/11/10 17:10 Página 30
- 32. Raíces | 31 Unidad 1 Por ejemplo, para calcular se puede hacer por tanteo: primero, 34 = 3 · 3 · 3 · 3 = 81; luego, revisar 44 = 4 · 4 · 4 · 4 = 256, y también, 54 = 5 · 5 · 5 · 5 = 625. Entonces, por lo anterior, . Al igual que en el caso de las raíces cuadradas y cúbicas, no todas las raíces enésimas son exactas, ni todas son números reales. Por ejemplo, la raíz cuarta de un número negativo no es un número real, porque ningún número real elevado a su cuarta potencia es un número negativo. 625 5 4 = 625 4 1. Calcula el valor de las siguientes expresiones: a. c. e. b. d. f. 2. Determina si las siguientes afirmaciones son verdaderas o falsas. Justifica tus respuestas. a. para cualquier valor de n. d. El número IR. b. , n impar. e. El número IR. c. f. 3. Determina la media geométrica de los siguientes conjuntos de números: a. {4, 6, 9} b. {2, 6, 9, 12} c. {1, 2, 4, 8, 16} d. {2, 4, 6, 9, 18} − = − 128 128 7 7 −5 7 −17 6 64 8 2 6 3 = = − ( ) = − ↔ − = − b a a b n n 0 0 n = 64 81 6 4 + 81 81 4 + 625 32 4 5 + −243 5 1 7 −1 7 Actividades En resumen • Si a es un número real y n un número natural mayor que uno, entonces la expresión denota al número cuya potencia enésima es a. • Si a 0 y n un número natural par, existe y es siempre un número positivo. • Si a 0 y n un número natural par, no es un número real. • Cuando n es un número impar, siempre existe y conserva el signo de a. • Al número n se le llama índice, y al número a se le denomina cantidad subradical. a n a n a n a n a b b a n n = ↔ = Dadas dos afirmaciones A y B, A B se usa para indicar que son equivalentes, es decir, son ambas verdaderas o ambas falsas. A B se lee: A si y solo si B. ↔ ↔ Pon atención UNIDAD 1 (12-53)C :Maquetación 1 4/11/10 17:10 Página 31
- 33. 32 | Unidad 1 Cálculo y propiedades de raíces enésimas Felipe está buscando una estrategia para calcular raíces usando las que ya conoce. Observa. Para comprobar si los cálculos de Felipe están correctos, debemos calcular las potencias que corresponden. En ambos casos vemos que: . 54 = 5 · 5 · 5 · 5 = 625. Luego, ambos resultados son correctos. Pese a lo expuesto, los cálculos anteriores no justifican la estrategia usada por Felipe de separar las raíces de índice mayor, de modo que para comprobar usaremos algunas propiedades de las potencias. Observando los resultados obtenidos, vemos que podemos escribir- los como: . . Por lo tanto, al igual que con raíces cuadradas y cúbicas, las pro- piedades de potencias justifican propiedades de raíces enésimas. Analicemos... • ¿Están correctos los cálculos de Felipe? Comprueba calculando la potencia correspondiente del resultado, en cada caso. • ¿Esta estrategia se puede usar siempre?, ¿sirve para calcular una raíz quinta?, ¿y una raíz octava?, ¿por qué? • Las propiedades de las operaciones de producto y cociente de raíces cuadradas y cúbicas, ¿se extienden a las raíces enésimas?, ¿qué puedes concluir? 1 64 1 64 1 8 1 2 6 3 3 = = = 625 625 25 5 4 = = = 1 2 1 2 1 2 1 8 6 3 2 3 2 ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ = ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ = ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ = ⎛ ⎝ ⋅ ⎜ ⎜ ⎞ ⎠ ⎟ = 2 1 64 5 5 5 25 625 4 2 2 2 2 2 = = ( ) = = ⋅ 1 2 6 ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ En general: Recuerda que... a b a b n n n + ≠ + a b a b n n n − ≠ − 1 2 1 2 1 2 1 2 1 2 1 2 1 64 = ⋅ ⋅ ⋅ ⋅ ⋅ = UNIDAD 1 (12-53)C :Maquetación 1 4/11/10 17:10 Página 32
- 34. Raíces | 33 Unidad 1 Ejemplo 1 Calcular el valor de . Sabemos que para calcular 65 , podemos descomponerlo de la siguiente forma: 65 = (2 · 3)5 = 25 · 35 = 32 · 243 = 7776. Asimismo, podemos calcular la raíz quinta de 7776 a partir del producto anterior, obteniendo: = 2 · 3 = 6. Ejemplo 2 Calcular el valor de la expresiones y . = . Tal como en el producto del ejemplo anterior, podemos descom- poner el cociente de la siguiente forma: = = 0,3. En el caso de la expresión no conocemos el valor exacto de presión. Observa. = 2. Veamos ahora, utilizando lo aprendido, cómo podemos comparar los términos de la siguiente secuencia: . El segundo término de la secuencia es 25, ya que 252 = 625; el tercer término, como vimos anteriormente en el desarrollo del ejercicio de Felipe, es 5, y el cuarto término es . 16 2 3 3 625 25 5 = = 16 3 16 2 3 3 0 0081 4 , 7776 5 7776 32 243 5 5 = ⋅ = ⋅ 32 243 5 5 0 0081 4 , 81 10000 4 81 10000 4 81 10000 4 4 = 3 10 y de ; sin embargo, podemos calcular el valor exacto de la ex- 2 3 16 2 16 2 3 3 3 = = 8 3 625 625 625 625 ; ; ; UNIDAD 1 (12-53)C :Maquetación 1 4/11/10 17:10 Página 33
- 35. 34 | Unidad 1 1. Calcula el valor de las siguientes raíces sin utilizar calculadora: a. c. e. − 0 03125 0 01024 5 , , 64 729 6 1 32 5 Actividades En resumen Si a y b son números reales, n y m números naturales, se cumplen las siguientes propiedades: • Adición y sustracción de raíces: para que dos o más raíces se puedan sumar o restar es nece- sario que sean semejantes; es decir, deben tener el mismo índice e igual cantidad subradical. • Multiplicación de raíces de igual índice (si n es par, a, b 0). • División de raíces de igual índice , con b 0. • Raíz de una raíz . a a a a m n n m m n n m = = = ⋅ ⋅ a b a b n n n ⋅ = ⋅ b a c a b c a n n n ± = ± ( ) a b a b n n n = Podemos encontrar una aproximación para este valor, y tendremos que . Remplazando los valores encontrados, la secuencia es: 625; 25; 5; 2,24. • ¿Cuál sería el siguiente término en la secuencia? • ¿Qué se puede concluir a partir de los resultados? El término siguiente en la secuencia será , que es equiva- lente a ; a partir de los resultados de la secuencia se puede concluir que cada vez el resultado del término es un número más pequeño; por lo tanto, sin necesidad de estimar , su valor será menor a . 5 5 5 4 = 5 4 625 5 2 24 ≈ , b. d. f. − 0 00032 16 807 5 , − 16 384 128 7 0 00243 5 , UNIDAD 1 (12-53)C :Maquetación 1 4/11/10 17:10 Página 34
- 36. Raíces | 35 Unidad 1 2. Resuelve. a. d. c. f. 3. Expresa los siguientes productos y cocientes de raíces de la forma más simple posible (considera que x es un número positivo). a. c. e. 4. Simplifica las siguientes expresiones aplicando las propiedades de las raíces. Indica en cada caso las propiedades utilizadas. a. d. c. f. 5. Para cada una de las secuencias siguientes, calcula los valores numéricos o una aproximación para cada término, y determina cuál es el término que sigue si se mantiene la misma relación. a. d. b. e. c. f. 6. Calcula el valor de cada término en las siguientes secuencias y, luego, compara los resultados. ¿Qué diferencia existe entre los términos de ambas secuencias?, ¿por qué ocurre esta diferencia? a. b. 10 000 10 000 10 000 10 000 ; ; ; − − − − 512 512 512 512 3 3 3 3 3 3 ; ; ; 256 256 256 256 ; ; ; 1 243 1 243 1 243 1 243 ; ; ; 5 9 12 6 3 48 4 − 4 9 729 3 2 2 2 2 2 2 2 2 4 ⋅ ⋅ 3 54 4 4 ⋅ x y xy x y xy 2 5 2 5 2 5 2 5 5 2 11 + − + 25 2 25 5 25 7 25 3 4 3 4 + + − 9 3 9 4 18 15 18 6 6 6 6 − − + x x 6 7 7 ⋅ 64 2 5 5 : 3 4 7 5 5 5 ⋅ ⋅ 7 5 7 2 7 11 7 5 5 5 5 + − + 243 243 243 243 ; ; ; 64 64 64 64 ; ; ; 1 1 1 1 ; ; ; 0 0 0 0 ; ; ; b. d. f. x x 10 11 3 11 256 4 6 6 3 27 4 4 ⋅ b. e. 2 5 1 2 5 3 4 5 4 4 4 − + 12 6 12 4 12 3 12 4 4 4 4 + − + b. e. 36 7 7 3 2 9 49 4 3 4 3 ⋅ ⋅ 3 34 3 7 UNIDAD 1 (12-53)C :Maquetación 1 4/11/10 17:10 Página 35
- 37. 36 | Unidad 1 Relación entre raíces y potencias Jaime debe encontrar el volumen de un cubo cuya arista mide cm, y el área de un cuadrado cuyo lado mide cm. Observa. Cubo: Arista = cm Volumen = cm3 Cuadrado: Lado = cm Área = cm2 Al ver los resultados obtenidos y observar que y y recordando la siguiente propiedad de las potencias (an )m = an · m , Jaime propone las siguientes identidades: Si a 0, entonces Si b IR, entonces A A ( ) = 2 A A ( ) = 2 V V 3 3 ( ) = V V 3 3 ( ) = A V 3 A Analicemos... • ¿Cuál es la relación entre una potencia y raíz, según Jaime? • ¿Te parece correcta la proposición de Jaime?, ¿por qué? En resumen En general, si n y m son números naturales mayores que 1 y a 0, se cumple que: • • a a m n m n = a a n n 1 = a a a a a ( ) ( ) ⋅ 2 2 2 1 2 2 1 2 = = = = b b b b b 3 3 3 3 3 1 3 3 1 3 ( ) ( ) ⋅ = = = = V 3 V cm2 A cm2 Si denotamos (a 0), tendremos que , como por lo tanto n = . En conclusión, la relación propuesta por Jaime es correcta. De la misma forma podemos probar que . a a n ( ) = 2 2 a a 3 1 3 = 1 2 a an = sabemos que , obtendremos que a = a2n , es decir, 2n = 1, a a ( )2 = UNIDAD 1 (12-53)C :Maquetación 1 4/11/10 17:10 Página 36
- 38. Raíces | 37 Unidad 1 Como vimos en el desarrollo anterior, representar las raíces como potencias con exponente fraccionario permite simplificar expre- siones con raíces, usando las propiedades de las potencias. Ejemplo 1 ; con a 0, ya que Ejemplo 2 , ya que 2 5 2 5 2 5 2 5 3 1 2 1 3 1 2 3 3 1 3 2 2 3 6 2 6 ⋅ = ⋅ = ⋅ = ⋅ ⋅ ⋅ = = ⋅ = ⋅ = 2 5 2 5 200 3 6 2 6 3 2 6 6 2 5 2 5 200 3 3 2 6 6 ⋅ = ⋅ = a a a a a a 3 3 1 2 1 3 1 2 1 3 1 2 1 6 6 =( ) = ⎛ ⎝ ⎞ ⎠ = = = ⋅ a a 3 6 = 1. Expresa las siguientes potencias en forma de raíz: a. b. c. d. 2. Escribe las siguientes raíces en forma de potencia y, luego, calcúlalas: a. b. c. d. 3. Utilizando las propiedades anteriores: a. ¿Cómo expresarías como una raíz ? b. ¿Cómo expresarías como una raíz ? 4. Piensa y responde las siguientes preguntas. Explica, paso a paso, cómo lo hiciste. a. ¿Es verdadera la igualdad ? b. ¿Cuál es la medida del lado de un cuadrado de área m2 ? c. ¿Cuál es la medida de la arista de un cubo que tiene por volumen cm3 ? 5. Observa el ejemplo y, luego, resuelve. a. b. c. x x x ⋅ ⋅ 4 3 12 4 5 2 3 3 6 ⋅ ⋅ 2 2 5 ⋅ 5 3 2 5 a a 8 12 2 3 = 3 2 1 3 1 2 ⋅ x 2 3 1 5 ⎛ ⎝ ⎞ ⎠ 512 9 243 5 −0 00001 5 , −343 3 0 00032 1 5 , ( ) 7 10 2 3 ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ −27 5 3 45 1 3 Actividades a a a a a a ⋅ = = = + 2 3 1 2 2 3 7 6 6 Amplificamos ambas fracciones para igualar denominadores UNIDAD 1 (12-53)C :Maquetación 1 4/11/10 17:10 Página 37
- 39. 38 | Unidad 1 Expresiones con raíces en el denominador Marcela debe calcular el lado de un triángulo equilátero. Sabe que su altura mide 6 cm y recuerda que la altura de un triángulo equi- látero la puede calcular utilizando: , donde h es la altura y a el lado del triángulo equilátero. Observa el procedimiento que utiliza para obtener la medida del lado del triángulo. Marcela dice que el lado del triángulo mide cm. 12 3 h a = 3 2 Como observas, la expresión tiene una raíz en el denomi- nador, por lo que es más difícil encontrar un valor aproximado que para ; sin embargo, ambas expresiones son equivalentes, ya que llegamos al mismo resultado. Observa el siguiente procedimiento: Para facilitar cálculos, encontraremos un procedimiento que nos permitirá hallar una expresión equivalente que no posea raíces en el denominador, lo que equivale a racionalizar la expresión. 4 3 6 93 ≈ , 12 3 6 93 ≈ , a 2 a 2 En un triángulo equilátero, ya que, aplicando el teorema de Pitágoras, tenemos: Recuerda que... Analicemos... • ¿Sabes a qué número se aproxima el valor que obtuvo Marcela? Escríbelo con dos cifras decimales y explica cómo lo calculaste. • ¿Cuánto es el valor de si aproximas a dos decimales?, ¿cómo lo hiciste? Compara con el resultado anterior. • ¿Qué aproximación te resultó más fácil de calcular?, ¿por qué? 4 3 Glosario racionalizar: operar para eliminar los radicales del denominador de una fracción, sin cambiar su valor. h A B C a a 6 3 2 = a 12 3 =a a = 12 3 12 3 12 3 3 3 12 3 3 3 = ⋅ = ⋅ ⋅ = ( ) = = 12 3 3 12 3 3 4 3 2 h a = 2 3 h a a 2 2 2 2 +⎛ ⎝ ⎞ ⎠ = h a a 2 2 2 2 = −⎛ ⎝ ⎞ ⎠ h a 2 2 3 4 = h a = 3 2 Multiplicamos por Multiplicamos por 2 Dividimos por UNIDAD 1 (12-53)C :Maquetación 1 4/11/10 17:10 Página 38
- 40. Raíces | 39 Unidad 1 Por lo tanto, la racionalización de es la expresión , que, tal como probamos con los resultados de la aproximación, son expre- siones equivalentes. Ahora observa la figura, ¿cuán mayor es el segmento y que la me- dida del segmento AD? Para encontrar la medida pedida utilizaremos el teorema de Thales, planteando la siguiente proporción: Hemos encontrado la medida del segmento y. La presencia de raíces en el denominador nos dificulta los cálculos para responder a la pregunta inicial. Por ello, racionalizaremos la expresión. Observa el siguiente procedimiento: Si observamos, el procedimiento anterior es bastante extenso; no obstante, la expresión encontrada facilita enormemente los cálculos. Luego al racionalizar se obtiene . Como , entonces, . Por lo tanto, la medida del seg- mento y es aproximadamente mayor que AD en 0,23 cm. 4 2 2 2 + 4 2 1 − ( ) 2 1 41 ≈ , 12 3 4 3 B ED // BC E A D C 4 2 y AC CB AD DE = 2 2 4 2 + = y y ⋅ + ( )= ⋅ 2 2 4 2 y = + 4 2 2 2 4 2 2 2 4 2 2 2 2 2 2 2 + = + ( ) ⋅ − ( ) − ( ) = ( ) − ⋅ ( ) − 4 2 4 2 2 2 2 2 2 2 = ⋅ − − = − − 4 2 8 2 2 4 8 8 2 2 = − ( ) − = − − ( )= − ( ) 8 1 2 2 4 1 2 4 2 1 4 2 1 4 0 41 1 64 − ( )≈ ⋅ ≈ , , Remplazamos las medidas dadas Multiplicamos por 4y Dividimos por ( + 2) Multiplicamos por Suma por diferencia desarrollada Factorizamos y simplificamos 2 UNIDAD 1 (12-53)C :Maquetación 1 4/11/10 17:10 Página 39
- 41. 40 | Unidad 1 Si ahora queremos racionalizar la expresión con raíces cúbicas en el denominador, lo que debemos hacer es amplificar por una ex- presión que nos permita eliminar la raíz cúbica en el denominador; es decir, debemos amplificar por una expresión que le permita obtener en el denominador , ya que, recordando las propiedades de la raíces cúbicas, . Observa. Si queremos ahora racionalizar una expresión como , que tiene un binomio en el denominador, tenemos que amplificar por una expresión que elimine ambas raíces del denominador. Observa el procedimiento que se utilizará, basado en la identidad: Primero, trabajaremos con el denominador de la expresión, para así facilitar cálculos posteriores. En este procedimiento buscare- mos obtener la suma de los cubos de y , es decir, Por lo tanto, En general, para racionalizar una expresión como debemos amplificar de la siguiente forma: 1 4 2 1 4 2 2 2 2 4 2 2 2 4 2 2 2 4 6 3 3 3 3 3 3 3 3 3 3 + = + ⋅ − + − + = − + 2 3 4 3 1 4 2 3 3 + 43 3 7 4 3 4 4 4 3 3 3 3 = ( ) = 7 4 4 4 7 4 4 4 7 4 4 4 7 4 4 7 4 3 2 3 2 3 2 3 3 2 3 2 3 2 3 2 3 3 3 2 ⋅ = ⋅ = ⋅ = = 3 3 4 a b a b a ab b 3 3 2 2 ± = ± ( ) + ( ) ∓ 4 2 4 2 6 3 3 3 3 + = + = 4 2 4 2 4 4 2 2 3 3 3 3 3 3 3 2 3 3 3 2 ( ) +( ) = + ( ) ( ) − ⋅ +( ) ( ) 4 2 4 2 16 8 4 3 3 3 3 3 + = + ( ) − + ( ) 6 4 2 8 2 2 4 3 3 3 3 = + ( ) ⋅ − + ( ) 6 4 2 2 2 2 4 3 3 3 3 = + ( ) − + ( ) a bm n a b b b a b b m n n m n n m n n m n ⋅ = − − − UNIDAD 1 (12-53)C :Maquetación 1 4/11/10 17:10 Página 40
- 42. Raíces | 41 Unidad 1 1. Racionaliza las siguientes expresiones: a. d. g. j. b. e. h. k. c. f. i. l. 2. Determina, racionalizando, si las siguientes expresiones son verdaderas. Justifica tu decisión. a. b. c. d. 3. Determina, racionalizando, el orden de las siguientes expresiones: a. c. e. g. 4 5 3 6 3 5 − − y 3 5 4 13 y 5 2 3 2 2 1 + – y 1 7 3 2 y 3 3 3 = 864 32 3 3 3 = 1 a b a b a b − = + − 1 3 2 1 − 10 25 4 2 8 Actividades En resumen • Racionalizar una fracción es transformarla, sin cambiar su valor, en una expresión que no posea raíces en el denominador. • Al racionalizar expresiones que contienen raíces en el denominador se pueden aproximar y comparar de manera más sencilla. • Para racionalizar una fracción debemos amplificarla por una expresión que nos permita eliminar la raíz o las raíces presentes en el denominador. Así, por ejemplo, observa el procedimiento para racionalizar . 1 2 5 1 2 2 2 2 2 2 2 5 4 5 4 5 4 5 5 5 4 5 ⋅ = = 5 7 4 6 2 − 3 2 2 3 + 5 4 5 2 7 + a a b a a b − + + + 6 4 2 3 3 − 1 1 3 x − 123 5 2 3 − 3 2 3 x 6 2 18 12 3 3 − b. d. f. h. 2 5 1 1 5 2 3 3 − + y 1 2 1 2 1 2 − + y 3 5 4 3 3 3 y 5 12 1 2 y UNIDAD 1 (12-53)C :Maquetación 1 4/11/10 17:10 Página 41
- 43. 42 | Unidad 1 Ecuaciones con radicales Mediante la experimentación y la aplicación de modelos mate- máticos, se ha logrado determinar que la distancia d (medida en metros) a la que cae un objeto, partiendo del reposo en t segun- dos, es aproximada por la fórmula: . Un grupo de estudiantes, un tanto desconfiados, decidió verificar esta fórmula dejando caer una piedra desde un puente (como se muestra en la figura), y tomando el tiempo que la piedra tarda en llegar al río. Para solucionar este problema es necesario resolver una ecuación cuya incógnita forma parte de una cantidad subradical. Para despejar la incógnita (d en este caso) debemos elevar al cuadrado, ya que, recordando la propiedad de la raíces cuadradas ; al hacer esto logramos eliminar la raíz. d = 20 m Ejemplo Resuelve la ecuación . Se consideran primero las restricciones de los valores que puede tomar x. Como la cantidad subradical de una raíz cuadrada debe ser positiva o cero, se tiene que x + 5 0 y x + 2 0; por lo tanto, las soluciones no pueden ser menores que – 2, es decir, la solución debe pertenecer al intervalo x – 2. x x + + + = 5 2 6 x x ( ) = 2 t d = 5 Analicemos... • ¿Cuál es la altura del puente, según la fórmula, si la piedra cayó en dos segundos? Explica, paso a paso, cómo lo resolviste. t d = 5 2 5 = d 2 5 2 2 ( ) ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ = d 4 5 = d La expresión , n indica el índice de la raíz y a señala la cantidad subradical. a n Recuerda que... Remplazamos t por 2 Multiplicamos por 5 Observa la ecuación : la solución no pertenece a los núme- ros reales, pues la expresión debe ser positiva o cero, según la definición de raíz cuadrada. x +1 x + = − 1 3 Pon atención UNIDAD 1 (12-53)C :Maquetación 1 4/11/10 17:10 Página 42
- 44. Siempre debemos comprobar la solución. Observa. Como satisface la igualdad original, la solución encontrada es válida. 12 2 33 x + = x x x + = − + + + 5 36 12 2 2 x x + = − + 5 6 2 Unidad 1 Raíces | 43 En resumen • En una ecuación en la que intervienen raíces cuya incógnita forma parte de una o más cantidades subradicales, las soluciones encontradas algebraicamente deben ser siempre comprobadas, de modo que la ecuación original esté definida para valores reales. 1. Resuelve las siguientes ecuaciones con radicales. Luego, comprueba la solución. a. c. e. g. b. d. f. h. 2. ¿Por qué al resolver una ecuación con radicales existen soluciones que no satisfacen la ecuación? Menciona un ejemplo para responder la pregunta. 3. ¿Existe un número natural, tal que su raíz cuadrada tenga tres unidades más que la raíz cuadrada de su antecesor?, ¿por qué? Actividades x x + + + = 5 2 6 x x + ( ) = − + ( ) 5 6 2 2 2 x + ( ) = ⎛ ⎝ ⎞ ⎠ 2 33 12 2 2 x + = 2 1089 144 x = − = = 1089 144 2 801 144 89 16 89 16 5 89 16 2 89 80 16 89 32 16 + + + = + + + = + = + = = 169 16 121 16 13 4 11 4 24 4 6 x − = 5 5 2 3 1 7 x − = 2 5 1 7 x − = 2 3 4 x = 2 2 3 6 x = 9 1 1 3 x x + − = x x + + = 2 2 x x + + = + 5 3 8 Elevamos al cuadrado Reducimos términos semejantes Elevamos al cuadrado nuevamente UNIDAD 1 (12-53)C :Maquetación 1 4/11/10 17:10 Página 43
- 45. 44 | Unidad 1 • En el siguiente mapa conceptual se muestran algunos de los conceptos presentados hasta ahora en la Unidad. • Utilizando los contenidos aprendidos en la Unidad y, apoyándote en el esquema anterior, responde en tu cuaderno. 1. ¿Crees que faltó un concepto importante en el mapa conceptual?, ¿cuál? Agrégalo. 2. ¿Qué relación hay entre potencias y raíces? Da al menos dos respuestas distintas. 3. ¿De qué modo se comparan expresiones con radicales? Da al menos dos respuestas distintas. 4. ¿Qué significa racionalizar y qué utilidad tiene? 5. ¿Los exponentes fraccionarios se pueden usar en potencias cuya base sea un número negativo? 6. ¿En qué se distinguen las ecuaciones con radicales de otras ecuaciones que conoces? 7. ¿Por qué se deben comprobar las soluciones en las ecuaciones con radicales? Explica. 8. ¿Tienes alguna duda sobre conceptos tratados en las páginas anteriores?, ¿cuál? Compártela con tu curso e intenten aclararla en conjunto. se aplican a se aplican a se pueden simplificar mediante son parte de mantienen ÍNDICE PAR ÍNDICE IMPAR NÚMEROS POSITIVOS O CERO TODO NÚMERO REAL ORDEN ENTRE NÚMEROS Organizando lo aprendido tienen RAÍCES ECUACIONES IRRACIONALES MULTIPLICACIÓN Y DIVISIÓN si aparecen en el denominador debemos RACIONALIZAR UNIDAD 1 (12-53)C :Maquetación 1 4/11/10 17:10 Página 44
- 46. Raíces | 45 Unidad 1 1. Determina si las siguientes igualdades son verdaderas o falsas. Justifica tus decisiones. a. c. e. b. d. f. 2. Racionaliza las siguientes expresiones: a. c. e. g. b. d. f. h. 3. Realiza las siguientes operaciones y simplifica todo lo posible los resultados. a. c. e. g. b. d. f. h. 4. Resuelve las siguientes ecuaciones y comprueba las soluciones encontradas. a. b. c. 5. El valor de es: A. B. C. D. 2 E. Ninguna de las anteriores. 2 7 2 6 2 2 64 18 4 − x x + − − = 8 1 1 2 1 21 x − = 4 3 12 2 x = 3 5 8 6 3 9 + = a a 2 3 10 15 = 3 5 75 6 3 6 ⋅ = 4 3 5 60 3 3 3 ⋅ = 75 25 3 = 2 4 32 3 3 = Mi progreso • Verifica en el solucionario si tus respuestas son correctas. Si tuviste respuestas incorrectas, marca en la tabla el criterio correspondiente y revisa las páginas indicadas. Luego, identifica el error y corrígelas. ¿Cómo voy? 34 12 12 2 3 5 2 3 3 + 8 2 4 19 − 3 6 5 3 + 2 6 4 3 + 10 2 5 a a 7 3 4 5 2 16 7 7 7 ⋅ ⋅ 14 1296 7 6 3 3 7 3 3 243 3 4 4 4 − + 14 256 2 4 6 6 7 7 7 5 6 1 3 1 2 ⋅ ⋅ 3 3 27 a a 2 3 1 3 3 4 1 2 ⎛ ⎝ ⎞ ⎠ ⋅ ⎛ ⎝ ⎞ ⎠ 2 2 2 2 4 3 CRITERIO ÍTEMS PÁGINAS DONDE SE TRABAJA Analizar igualdades que involucran raíces. 1 30 a 35 Racionalizar expresiones con raíces en el denominador. 2 38 a 41 Calcular y simplificar expresiones que involucran raíces. 3 y 5 32 a 37 Resolver ecuaciones irracionales. 4 42 y 43 UNIDAD 1 (12-53)C :Maquetación 1 4/11/10 17:10 Página 45
- 47. Observa, paso a paso, las estrategias utilizadas en la resolución de los siguientes problemas. Ejercicio 1 A un rectángulo cuya altura es a = 1 cm y cuya base mide cm se le quita un cuadrado de lado 1 cm, de modo que resulta otro rec- tángulo. Halla las longitudes de sus lados y prueba que el cociente entre la longitud del lado mayor y el lado menor es el número . Solución Las dimensiones del nuevo rectángulo serán: 1 y (b – 1). Calculemos el cociente entre las longitudes del lado mayor (a’) y del lado menor (b’) del nuevo rectángulo. Racionalizamos Simplificamos Hemos demostrado que el cociente entre las longitudes de los lados del rectángulo es . Ejercicio 2 Considera que la figura representa un cubo de lado a: a. Determina la medida de BG. b. Calcula la altura del triángulo BDG. 1 5 2 + 1 5 2 + b = + 1 5 2 Cómo resolverlo 46 | Unidad 1 Base del rectángulo resultante (b – 1) Rectángulo original 1 cm b = + 1 5 2 1 5 2 1 1 5 2 2 5 1 2 1 + − = + − = − = = b a '; ' a b ' ' = − = − = + ( ) − ( ) + ( ) = + ( ) − = 1 5 1 2 2 5 1 2 5 1 5 1 5 1 2 5 1 5 1 2 2 5 1 4 1 5 2 + ( ) = + A D H G F B E C a a a UNIDAD 1 (12-53)C :Maquetación 1 4/11/10 17:10 Página 46
- 48. Solución a. BG es la diagonal de una cara del cubo, es decir, de un cuadrado de lado a. BG2 = a2 + a2 BG2 = 2a2 BG = BG = Luego, la medida de BG es a . b. El triángulo BDG es equilátero, porque sus lados son las diagonales de las caras del cubo (cuadrados de lado a). Por lo tanto, BD = DG = BG = a Considerando que la altura de un triángulo equilátero de lado l es y que en este caso l = a , se remplaza y se obtiene: Luego, la altura del triángulo BDG mide . h l = 2 3 h a = 6 2 2 2 2 Raíces | 47 Unidad 1 Actividades 1. Aplica el procedimiento aprendido para resolver las siguientes situaciones: a. Considera un cuadrado de lado a, el cual en su parte superior tiene un triángulo isósceles rectángulo de base igual al lado del cuadrado. Calcula el perímetro de la figura formada en términos del lado del cuadrado. b. Considera un paralelepípedo de largo 3a, de ancho 2a y de alto igual al ancho. Determina las medidas de las diagonales de cada una de las caras del paralelepípedo. 2. Busca un procedimiento distinto para resolver los problemas anteriores. Respecto del procedimiento previo, ¿cuál es más simple?, ¿por qué? 3. Resuelve el siguiente problema empleando el método aprendido u otro. Compara el procedimiento que utilizaste con el de algún compañero o compañera. ¿Cuál es más simple?, ¿por qué? Encuentra el área y perímetro de un rectángulo cuyo largo mide lo mismo que la altura de un triángulo equilátero de lado 2a y cuyo ancho es . a 2 2 a a 2 h a a = ⋅ = 2 2 3 6 2 Utilizando el valor obtenido en la parte a Se aplica la propiedad Se aplica el teorema de Pitágoras Se reducen términos semejantes Se aplica la propiedad UNIDAD 1 (12-53)C :Maquetación 1 4/11/10 17:10 Página 47
- 49. 48 | Unidad 1 En terreno En terreno El período del péndulo El péndulo ha servido por siglos como medidor del paso del tiempo. Una de sus características es que, si está adecuadamente construido, el tiempo que le toma cada ir y venir (su período) es casi constante. Eventualmente, el péndulo irá frenando hasta detenerse, pero mientras mejor construido esté, más demorará en frenar. El tiempo que le toma a cada ciclo de ir y venir se puede aproximar por , donde L es el radio de giro y g es la aceleración de gravedad de la Tierra. De este modo, el período del péndulo es proporcional a . Todo esto es válido si su peso en el extremo es realmente mayor que el de la cuerda que lo sostiene y gira con él. Uno de los usos del péndulo y la regularidad de su período es orientar y mantener el ritmo de una composición musical, lo cual es muy útil para cuando los músicos en- sayan. Si hay una batería entre los instrumentos musicales, algunos de sus sonidos reproducen el ritmo que tenía el metrónomo al ensayar. L 2π L g UNIDAD 1 (12-53)C :Maquetación 1 4/11/10 17:10 Página 48
- 50. Actividades 1. Obtén una aproximación del valor con dos cifras decimales, considerando g = 10 y π 3,14. 2. Calcula el período de un péndulo para los siguientes radios de giro: a. L = 1 m b. L = 4 m c. L = 0,4 m d. L = 0,5 m e. L = 0,2 m 3. Determina la longitud L de una cuerda si esperamos un período de: a. 2 segundos. b. 4 segundos. c. 5 segundos. d. 0,5 segundos. Investiguemos... Ahora, trabajen en grupos de tres personas. 1. Comparen las respuestas obtenidas por cada uno y discutan sobre cuáles de las respuestas son correctas si hay diferencias. 2. ¿Qué ocurre si las medidas están en centímetros en vez de en metros?, ¿sigue siendo válida la fórmula? 3. Usando un metro de hilo de coser (o de lana), una goma de borrar y una silla o mesa, pongan nudos al hilo cada 10 cm y construyan un péndulo amarrando la goma al hilo y el hilo al borde de la silla o mesa, de modo que en alguna dirección pueda oscilar sin chocar; no se necesita que el giro sea am- plio, pero sí que sea visible. La idea es que los nudos indiquen la medida L del radio de giro. a. Para las siguientes medidas de L registren el tiempo en segundos que demora el péndulo en completar diez períodos completos. i. L = 0,2 m ii. L = 0,4 m iii. L = 0,5 m iv. L = 0,7 m v. L = 0,9 m b. Para cada tiempo obtenido, dividan por 10 (para obtener el promedio) con el fin de lograr una aproximación del período P asociado a cada valor de L, y registren en una tabla los pares (L, P). c. Para cada una de las medidas de L dadas, calculen el período que debiera dar y comparen con los valores de la tabla. ¿Qué pueden concluir? Evaluemos nuestro trabajo • Comparen los resultados obtenidos. ¿Son similares? Si no es así, ¿qué diferencias hubo?, ¿son errores o pueden explicarse por las diferencias en las circunstancias al medir? • Indaguen respecto de los metrónomos mecánicos (ahora hay electrónicos) que usaban los músicos y su relación con el péndulo, y de qué manera regulaban el ritmo de oscilaciones para distintos ritmos musicales. m s2 2π g Raíces | 49 Unidad 1 UNIDAD 1 (12-53)C :Maquetación 1 4/11/10 17:10 Página 49
- 51. 50 | Unidad 1 Síntesis de la Unidad A continuación, se presentan los conceptos fundamentales trabajados en la Unidad. Construye con ellos un mapa conceptual en tu cuaderno. No olvides agregar las palabras de enlace que indican las relaciones entre los conceptos. A partir de lo trabajado en la Unidad, responde: 1. ¿Crees que faltó un concepto importante en el mapa conceptual?, ¿cuál? Agrégalo. 2. ¿Pertenecen todas las expresiones con raíces al conjunto de los números reales?, ¿por qué? 3. ¿Qué estrategia se puede usar para estimar el valor de una raíz? Explica paso a paso. 4. ¿Es siempre el producto de dos raíces igual a la raíz del producto? Explica. 5. ¿Cuándo es necesario racionalizar una expresión? Da al menos dos ejemplos, explicando, paso a paso, el procedimiento. 6. ¿Cuál es la relación entre potencias y raíces? 7. ¿Cuáles son las ecuaciones irracionales?, ¿cómo se resuelven? 8. ¿Qué relación hay entre área y volumen con las raíces? 9. Al racionalizar una expresión, ¿cambia el valor de esta?, ¿por qué? 10. ¿Qué importancia tienen las propiedades de la potencias para el estudio de las raíces? 11. ¿Tienes alguna duda sobre los conceptos tratados en las páginas anteriores?, ¿cuál? Compártela con tu curso e intenten aclararla en conjunto. RAÍCES CUADRADAS RAÍCES CÚBICAS EXPONENTE FRACCIONARIO ECUACIONES CON RADICALES RAÍCES ENÉSIMAS POTENCIAS RACIONALIZACIÓN UNIDAD 1 (12-53)C :Maquetación 1 4/11/10 17:10 Página 50
- 52. Raíces | 51 Evaluación I. Determina si las siguientes expresiones son verdaderas o falsas. Justifica tu respuesta. 1. Las raíces cúbicas solo se aplican a números positivos. 2. Solo se puede racionalizar si el denominador de una fracción tiene una raíz cuadrada. 3. Ningún número es igual a su propia raíz cúbica. 4. Si x 0, entonces . 5. Todas las raíces cuadradas de un número natural pertenecen al conjunto de los números reales. 6. Para todo n, a y b ⺞ . II. Aplica lo que aprendiste en la Unidad para desarrollar las siguientes actividades: 1. Ordena de mayor a menor las siguientes expresiones: a. b. 2. Simplifica las siguientes expresiones: a. c. e. b. d. f. 3. Racionaliza las siguientes expresiones: a. b. c. d. 4. Resuelve los siguientes problemas: a. La diagonal de un cuadrado es cm. Calcula la mitad de su área. b. Determina el radio de una esfera de 4520 m3 de volumen. 5. Encuentra el valor de x en las siguientes ecuaciones: a. c. b. d. x x − = + + 5 3 1 13 13 8 x x x = x x − = + 2 2 5 5 20 x = 5 2 a a − − 5 5 11 3 2 3 − 3 5 2 − 3 5 3 3 3 3 3 5 4 3 3 7 3 7 5 ⋅ ⋅ 2 5 4 3 2 2 2 2 2 3 11 2 3 11 3 3 + ⋅ − a2 3 − − − − 5 9 33 256 3 3 5 7 , , , 4 16 18 20 3 3 4 3 , , , a b a b n n n + = + x x 2 = − Unidad 1 UNIDAD 1 (12-53)C :Maquetación 1 4/11/10 17:10 Página 51
- 53. 52 | Unidad 1 III. Marca la opción correcta en cada caso. 1. La expresión es igual a: A. –6 B. 0 C. 3 D. 6 E. Ninguna de las anteriores. 2. (DEMRE, 2004). Si la base de un triángulo mide t y su altura mide , ¿cuánto mide el lado de un cuadrado que tiene igual área que el triángulo? A. B. t C. D. E. 3. (DEMRE, 2003). = A. B. C. D. E. 1 2 6 8 6 2 3 4 3 t 2 t2 4 t 4 t 2 27 243 3 5 − ( ) t 2 2 ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ ⋅ 2 2 3 4. Para racionalizar hay que amplificar por: A. 2 B. C. D. E. Ninguna de las anteriores. 5. La racionalización de es: A. B. C. D. E. Ninguna de las anteriores. 6. (DEMRE, 2004). Si , ¿cuál o cuáles de las siguientes expresiones son equivalentes a ? I. 2bc II. III. A. Solo I B. Solo II C. Solo III D. I y II E. I y III a bc 2 a b c 2 2 2 60 2 3 5 = = = a b y c , a b a b 4 4 2 2 3 2 + + a b 4 4 3 + a b − 3 a b + 3 a b a b ab + + + 2 2 3 2 a4 5 a3 5 a 5 1 5 a UNIDAD 1 (12-53)C :Maquetación 1 4/11/10 17:10 Página 52
- 54. Raíces | 53 7. La diagonal de un cuadrado de lado es: A. B. 2d C. D. E. 2d2 8. El producto de es: A. B. C. (xy)xy D. xy E. Ninguna de las anteriores. 9. La racionalización de las expresión es: A. 3 B. C. 9 D. E. 27 10. El número por el cual debe multiplicarse para obtener 4 es: A. B. C. 2 D. 2 E. Ninguna de las anteriores. 11. La expresión es equivalente a: A. –6 B. –2 C. 2 D. 10 E. 10 + 2 12. ¿Cuál es el área total de un cubo cuya arista mide cm? A. 378 cm2 B. 441 cm2 C. 27 cm2 D. 189 cm2 E. 343 cm2 13. Para el número – 10,05, ¿cuál de las siguientes afirmaciones es correcta? A. Es menor que –0,0002. B. Es igual a cero. C. Es positivo y menor que 0,0001. D. Es negativo y mayor que –0,0002. E. Es mayor que 0,0001. 14. El perímetro de un triángulo rectángulo de catetos y es: A. B. 24 C. D. E. No se puede calcular. 4 2 8 2 − ( ) d 2 2 2 d d 2 d 2 24 5 70 14 5 + 8 5 8 5 6 5 101 7 7 63 2 4 2 2 9 9 5 3 9 5 27 27 5 x y x x y y ( ) ⋅ ( ) Unidad 1 Verifica en el solucionario de tu Texto si tus respuestas son correctas. ¿Te equivocaste en alguna?, ¿cuál fue el error? Explícalo y resuelve correctamente el ejercicio. xy xy x y ( ) − xy xy x y ( ) + UNIDAD 1 (12-53)C :Maquetación 1 4/11/10 17:10 Página 53
- 55. Plantear y resolver problemas. Analizar existencia y pertinencia de soluciones. Conocer la parábola como un lugar geométrico. Reconocer la gráfica de una parábola e identificar sus elementos y propiedades. Analizar y conocer el tipo de crecimiento de la función y sus aplicaciones en la modelación de algunos fenómenos. Resolver problemas de máximos y mínimos utilizando parábolas. Describir y analizar una función cuadrática. Función cuadrática y función raíz cuadrada 2 Función raíz cuadrada Máximos y mínimos Ecuación de segundo grado Parábola Función cuadrática 54 | Unidad 2 TRABAJANDO CON: APRENDERÁS A: UNIDAD 2 (54-105)C:Maquetación 1 4/11/10 17:12 Página 54
- 56. Función cuadrática y función raíz cuadrada | 55 Conversemos de... Aunque las leyes que describen el movimiento se estudian con detalle en Física, en esta Unidad analizaremos las expresiones matemáticas que lo representan. Por ejemplo, el salto de las gace- las se podría expresar usando las mismas fórmulas que modelan el lanzamiento de proyectiles y que involucran potencias de segundo grado. La fórmula que describe la altura del salto es: donde g representa la aceleración de gravedad, t el tiempo transcurrido, v0 la velocidad inicial y k una constante que está relacionada con el ángulo del salto. • ¿Conoces el valor de g, o una aproximación para este?, ¿en qué unidades está? • ¿Podrías calcular s, dados los valores de k y t correspondientes?, ¿por qué? • En el caso del salto de la gacela, ¿puede ser v0 = 0?, ¿por qué? • Busca un ejemplo diferente de una ecuación que involucre potencias de segundo grado y que modele algún fenómeno. s v tk gt 0 – = 1 2 2 Latinstock UNIDAD 2 (54-105)C:Maquetación 1 4/11/10 17:12 Página 55
- 57. 56 | Unidad 2 ¿Cuánto sabes? 1. Factoriza las siguientes expresiones: a. x3 – x2 + x – 1 c. 3x2 + 4x + 1 e. x2 – 5x – 6 b. 3x2 – 7x d. a2 – 4 f. y2 + (a + b)y + ab 2. Calcula las siguientes expresiones, considerando que ; y . a. c. e. b. d. f. 3. Encuentra el valor de x en las siguientes igualdades: a. x2 = 144 c. b. d. x(a2 + ab + b2 ) = a3 – b3 4. Determina cuál o cuáles de las siguientes gráficas corresponden a una función. Explica tu decisión. a. c. b. d. x 3 125 = 4 9 + = x 2 2 2 8 − 20 40 60 + + 8 9 125 − + 6 18 24 + + 5 2 23 ≈ , 3 1 73 ≈ , 2 1 41 ≈ , Recuerda lo que aprendiste en años anteriores y resuelve en tu cuaderno. 4 27 2 3 1 − + 1 2 1 3 1 5 + + UNIDAD 2 (54-105)C:Maquetación 1 4/11/10 17:12 Página 56
- 58. 5. Determina cuál o cuáles de los siguientes pares ordenados corresponde a la función f(x) = 3x – 4. Fundamenta tu respuesta. a. (12, 32) c. (–3, 13) b. (0, 4) d. (–2, –10) 6. Determina cuál o cuáles de las siguientes expresiones son positivas para todo x positivo. Explica cómo lo supiste. a. 4 + x c. x2 e. 1 – 3x2 b. 13 – 2x d. 4x2 + 1 f. –8x2 Verifica en el solucionario si tus respuestas son correctas. ¿Tuviste algún error? Si lo tuviste, corrígelo antes de continuar con la Unidad. Función cuadrática y función raíz cuadrada | 57 Unidad 2 ¿Qué debes recordar? • Algunas factorizaciones: • ab + ac = a(b + c) Factor común. • a2 – b2 = (a + b)(a – b) Diferencia de cuadrados. • a2 ± 2ab + b2 = (a ± b)2 Cuadrado de binomio. • x2 + (a + b)x + ab = (x + a)(x + b) Trinomio que es el producto de dos binomios con un término común. • Las raíces enésimas se pueden escribir como una potencia con exponente racional, por ejemplo: • El producto de dos términos es cero si y solo si al menos uno de ellos es cero, es decir: a · b = 0 ⇔a = 0 ∨ b = 0 (el signo ∨ significa “o”). • La raíz de un producto es equivalente al producto de las raíces, es decir: . • El cuadrado de un número real es siempre positivo o cero, es decir, x2 ⱖ 0. • Si dos números son positivos, el orden entre ellos es el mismo orden que entre sus raíces y sus potencias, es decir, si 0 a b y n es un natural, entonces . • Una función y = f(x) es creciente en un intervalo [p, q] cuando para todo par de números a y b del intervalo que cumplan a b, se cumplirá f(a) f(b). • Una función y = f(x) es decreciente en un intervalo [p, q] cuando para todo par de números a y b del intervalo que cumplan a b, se cumplirá f(b) f(a). • Una función es una regla que asocia a cada número x de un conjunto A, llamado dominio, un único valor f(x) de un conjunto B, llamado recorrido. Ejemplo: f(x) = x2 , x 僆 IR. a b y a b n n n n ab a b = ⋅ k k k m n n m m n = ( ) = UNIDAD 2 (54-105)C:Maquetación 1 12/11/10 12:05 Página 57
- 59. 58 | Unidad 2 Función cuadrática Analicemos... Un zoólogo experto en anfibios modeló el salto de una rana me- diante una expresión matemática y obtuvo la siguiente función: h(t) = 2t – t2 , donde t es el tiempo medido en segundos y h la altura en metros. La siguiente tabla muestra la altura de la rana en cinco instantes distintos. • ¿Cuánto demora la rana en volver al suelo?, ¿de qué modo podrías determinarlo? • ¿Cómo determinarías la mayor altura que alcanza la rana? Según la tabla, la rana está en el piso tanto cuando t = 0 y t = 2, ya que la altura a la que está la rana es 0 en ambos instantes (h(t) = 0). El instante t = 0 corresponde al momento de iniciar el salto, y el ins- tante t = 2, a los dos segundos de haber saltado, corresponderá al instante en que, luego del salto, la rana vuelve al piso. Para determinar la mayor altura que alcanza la rana necesitamos conocer bien el comportamiento de la función que nos muestra el salto de la rana. Si vemos los valores de la tabla, la mayor altura mostrada es de un metro cuando ha pasado un segundo. Muchas situaciones son modeladas mediante una función que in- volucra el cuadrado de una variable, como el caso del salto de la rana. Este tipo de funciones son de la forma f(x) = ax2 + bx + c, con a distinto de cero; se denominan funciones cuadráticas y su gráfica correspondiente es una curva llamada parábola, como la de la figura. Observa. t 0 0,5 1 1,5 2 h(t) 0 0,75 1 0,75 0 Rana de coro del Pacífico saltando en una laguna. UNIDAD 2 (54-105)C:Maquetación 1 4/11/10 17:12 Página 58
- 60. Función cuadrática y función raíz cuadrada | 59 Unidad 2 En resumen • Una función cuadrática o de segundo grado tiene la forma: f(x) = ax2 + bx + c, con a, b y c 僆 IR y a 0. • Su dominio es el conjunto de los números reales. • Su gráfico corresponde a una curva llamada parábola. 1. Sea f (x) = x2 – x – 2, calcula los siguientes valores de la función: a. f (0) d. 3 · f (5) – 5 · f (3) g. f(a) – f(b) b. f (1) e. f(a – b) h. 2 · f(c) + 3 · f(c – 1) c. f (–1) + f (5) f. f(a + b) i. f(c – 1) – f(1 – c) 2. Escribe como función la relación que existe entre: a. el lado a de un cuadrado y su área A. b. el radio r de un círculo y su área A. c. la diagonal d de un cuadrado y su área A. 3. Escribe el área de un triángulo equilátero en función de su lado x. ¿Puede ser esta función negativa para algún valor de x? Explica. 4. Una función como f (x) = (x – 3)2 , ¿puede ser negativa para algún valor de x?, ¿por qué? 5. Una función como f (x) = –3x2 , ¿puede ser negativa para algún valor de x?, ¿por qué? Actividades Veremos en esta Unidad que para toda función cuadrática podemos graficar la parábola correspondiente y determinar su comporta- miento a partir del análisis de los coeficientes de la función f(x) = ax2 + bx + c. El dominio de toda función cuadrática es el conjunto de los números reales, ya que para todo x 僆 IR, f(x) = ax2 + bx + c 僆 IR, en cambio, el recorrido no es el mismo en todas las funciones cuadráticas. Para determinar este es necesario tener un mayor conocimiento de las funciones cuadráticas y su respectiva gráfica. UNIDAD 2 (54-105)C:Maquetación 1 4/11/10 17:12 Página 59
- 61. 60 | Unidad 2 Características de la gráfica de f(x) = x2 En cursos anteriores, conocimos la función afín cuya forma es f(x) = mx + n, y la función lineal, ambas gráficas son una línea recta. Ahora, conocemos una nueva: la función cuadrática dada por f(x) = ax2 + bx + c, cuya gráfica es una parábola. Observa la tabla de valores de la función lineal g(x) = x y la función cuadrática f(x) = x2 y sus gráficas respectivas. Podemos darnos cuenta que las gráficas construidas no correspon- den ambas a una recta. Es posible ver que la gráfica de la función f (x) = x2 no es lineal, sino curva. Analicemos... • Si consideramos la función lineal g(x) = x, sabemos que es una recta que pasa por el origen. Si evaluamos x en valores consecu- tivos, los valores de y varían de modo constante. Pero, ¿qué pasa con los valores de y en el caso de f (x) = x2 si x 1?, ¿y si x 1? • ¿Cuánto valen las funciones en x = 1 y x = 0 respectivamente?, ¿por qué? • ¿Cuál es el dominio y recorrido de la función f(x) = x2 ? x –3 –2 –1,5 –1 –0,5 0 0,5 1 1,5 2 3 g(x) = x –3 –2 –1,5 –1 –0,5 0 0,5 1 1,5 2 3 f (x) = x2 9 4 2,25 1 0,25 0 0,25 1 2,25 4 9 • Función afín: f (x) = mx + n • Función lineal: f (x) = mx Donde m es la pendiente de la recta y n el coeficiente de posición. Recuerda que... f(x) = x2 g(x) = x UNIDAD 2 (54-105)C:Maquetación 1 4/11/10 17:12 Página 60
- 62. Función cuadrática y función raíz cuadrada | 61 Unidad 2 En resumen La función cuadrática f(x) = x2 presenta las siguientes características: • Su gráfica es una parábola con vértice en el origen. • El dominio de la función es R, y el recorrido es R0 + . A medida que aumentamos el valor de x (x 1), los valores de y en la función f(x) = x2 crecen cada vez más rápido en comparación a g(x) = x, lo que podemos apreciar tanto en la tabla de valores de ambas funciones como en la gráfica correspondiente a cada una. Notemos que para un mismo valor de x, el valor de y en la función cuadrática es mayor que el de la función lineal; esto se debe a que para x 1, x2 x. Por otro lado, para los valores de x en 0 x 1 se tiene que x2 x, lo que podemos observar claramente, ya que la gráfica de la parábola está bajo la recta; es decir, en este intervalo el valor de la función f(x) = x2 es menor que la función g(x) = x. En x = 1 podemos ver en la tabla que ambas funciones tienen el mismo valor, al igual que en el gráfico; por lo tanto, el punto (1, 1) es un punto de intersección de estas, al igual que el origen (0, 0). El punto (0,0) de la parábola f(x) = x2 corresponde al vértice de la parábola, y en este caso es el punto más bajo de la gráfica, o sea, el menor valor posible. Además, divide la gráfica de la parábola en dos ramas simétricas. Como vimos anteriormente, el dominio de toda función cuadrática es el conjunto de los números reales, y como para todo número real x se tiene x2 ≥ 0, entonces el recorrido de f(x) = x2 es el con- junto de los números reales positivos y el cero, es decir R0 + . 1. Haz una tabla de valores para f(x) = 2x2 con x entre –4 y 4, como en el texto, y compárala con f(x) = x y f(x) = 2x. ¿Qué cambios ocurren? Traza, mediante los puntos de tu tabla, una gráfica de esta función. 2. Determina si es verdadero o falso y justifica. a. La gráfica de la función cuadrática f(x) = x2 es igual a la de una recta que crece hacia la derecha. b. Las gráficas de la función valor absoluto y de la función cuadrática f(x) = x2 no tienen características comunes. Actividades UNIDAD 2 (54-105)C:Maquetación 1 4/11/10 17:12 Página 61
- 63. 62 | Unidad 2 Forma canónica de funciones cuadráticas Anteriormente vimos que la función f(x) = x2 corresponde a una parábola con vértice en el origen; en este caso tenemos que ambos gráficos corresponden a parábolas, pero trasladadas con respecto a f(x) = x2 . Las representaciones gráficas son idénticas, esto se debe a que corresponden a la misma función cuadrática, solo que está escrita de formas diferentes. Observa. g(x) = (x + 2)2 – 1 = x2 + 4x + 4 –1 = x2 + 4x + 3 = f(x) Con lo que probamos que ambas funciones cuadráticas son la misma. Si observamos la función f(x) = x2 + 4x + 3, corresponde a una parábola en su forma general, es decir, de la forma f(x) = ax2 + bx + c, donde a = 1; b = 4 y c = 3. Para poder estudiar mejor el comportamiento de la parábola, aprenderemos a escribir una función cuadrática de la forma en que está g(x) = (x + 2)2 – 1, llamada forma canónica. Observa las siguientes funciones y sus respectivos gráficos: Analicemos... • ¿Son ambas parábolas?, ¿por qué? • ¿Qué diferencias hay en la representación gráfica de las dos funciones cuadráticas?, ¿por qué? f(x) = x2 + 4x + 3 g(x) = (x + 2)2 – 1 Cuadrado de binomio: (a ± b)2 = a2 ± 2ab + b2 Recuerda que... Desarrollando el cuadrado de binomio UNIDAD 2 (54-105)C:Maquetación 1 4/11/10 17:13 Página 62
- 64. Función cuadrática y función raíz cuadrada | 63 Unidad 2 En resumen • Toda función cuadrática de la forma f(x) = ax2 + bx + c se puede escribir en su forma canónica, es decir, de la forma f(x) = a(x – h)2 + k. 1. Dadas las siguientes funciones cuadráticas: f(x) = x2 + 2x – 4 g(x) = 3x2 + 24x + 1 h(x) = (x + 1)2 – 4 n (x) = 3(x + 4)2 – 47 Determina si las siguientes igualdades son verdaderas o falsas. Justifica. a. f(x) = h(x) b. g(x) = h(x) c. g(x) = n(x) 2. Escribe las siguientes funciones cuadráticas en su forma f(x) = a(x – h)2 + k, indicando en cada caso el valor de a, h y k. a. x2 – 6x + 19 c. 2x2 – 4x + 7 e. 3x2 – 24x + 28 b. x2 + 5x – 7 d. –2x2 + 12x – 3 f. –5x2 – 20x – 14 Actividades Toda función cuadrática de la forma f(x) = ax2 + bx + c puede ser escrita en su forma canónica f(x) = a(x – h)2 + k por medio del método de completación de cuadrados. Observa. f(x) = ax2 + bx + c Si llamamos y , tendremos que para todos a, b y c con a distinto de cero, existen h y k tales que f(x) = ax2 + bx + c = a(x – h)2 + k Ejemplo Si queremos escribir la función f(x) = 3x2 + 30x + 71 en su forma canónica, tendremos: f(x) = 3x2 + 30x + 71 = 3(x2 + 10x) + 71 = 3[(x + 5)2 – 25] + 71 = 3(x + 5)2 – 75 + 71 = 3(x + 5)2 – 4 Luego, la función escrita en forma canónica será f(x) = 3(x + 5)2 – 4. k b ac a – – = 4 4 2 h b a – = 2 = a x b a x c 2 + ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ + = a x b a b a c + ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ − ⎡ ⎣ ⎢ ⎢ ⎤ ⎦ ⎥ ⎥ + 2 4 2 2 2 = a x b a b a c a x b a b + ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ − + = + ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ 2 4 2 2 2 2 2 – – 4 4 ac a UNIDAD 2 (54-105)C:Maquetación 1 4/11/10 17:13 Página 63
- 65. Dilatación y contracción de la parábola Observa el gráfico de las funciones cuadráticas f(x) = ax2 para los distintos valores de a. Ambos gráficos corresponden a parábolas con vértice en el origen, es decir, en el punto (0, 0). En el caso del gráfico 1, tenemos que si a 0 y (x, x2 ) es un punto de la gráfica de f(x) = x2 , entonces (x, ax2 ) es un punto de la grá- fica de f(x) = ax2 , luego ambas coordenadas, x2 y ax2 , son positivas o cero, por lo que las dos parábolas se abren hacia arriba. En cambio, si a 0 las coordenadas x2 y ax2 tienen distinto signo, obtenemos que la gráfica de f(x) = ax2 es una parábola que se abre hacia abajo. Podemos darnos cuenta también, a partir de ambos gráficos, que a medida que el valor de a se acerca a 0, la parábola es cada vez más abierta, o sea, se dilata, y mientras a se aleja de 0, la parábola es más cerrada, es decir, se contrae. 64 | Unidad 2 Analicemos... • ¿Cuál es la principal diferencia entre las parábolas de los gráfi- cos 1 y 2? Explica. • En el gráfico 1, ¿qué comparación surge entre la gráfica de g1 (x) = x2 y la de las funciones restantes? • En el gráfico 2, ¿qué comparación surge entre la gráfica de g2 (x) = –x2 y la de las funciones restantes? • ¿Por qué ocurre que para dos valores distintos de x, el valor de la función f(x) = ax2 es el mismo? Explica. f1 (x) = 2x2 g1 (x)= x2 h1 (x) = 0,6x2 t1 (x) = 0,5x2 f2 (x) = –2x2 g2 (x)= –x2 h2 (x) = –0,6x2 t2 (x) = –0,5x Gráfico 1 Gráfico 2 UNIDAD 2 (54-105)C:Maquetación 1 4/11/10 17:13 Página 64
- 66. Observamos que si a 0, la parábola que representa f(x) = –ax2 es una reflexión en torno al eje X de la parábola de f(x) = ax2 , también vemos que los valores de la función se repiten a cada lado del eje Y; esto ocurre porque para cualquier a, x número real se cumple a(–x)2 = ax2 . Función cuadrática y función raíz cuadrada | 65 Unidad 2 En resumen En una función de la forma f(x) = ax2 : • Si a 0, la parábola se abre hacia arriba, mientras que si a 0, se abre hacia abajo. • Si |a| 1, la gráfica de la función f(x) se abre con respecto a la de la función f(x) = x2 (hay dilatación con respecto a f(x) = x2 ). • Si |a| 1, la gráfica de la función se cierra con respecto a la de la función f(x) = x2 (hay contracción con respecto a f(x) = x2 ). • Si a 0, la gráfica de la función f(x) = –ax2 es una reflexión de la función f(x) = ax2 en torno al eje X. 1. Construye un gráfico aproximado para las siguientes funciones cuadráticas, indicando si hay dilatación o contracción con respecto a f(x) = x2 . a. f(x) = 2x2 b. f(x) = –0,1x2 c. f(x) = –2x2 d. f(x) = 0,5x2 2. Una empresa multinacional ha estimado que anualmente sus ingresos en dólares están dados por la función f(x) = 28x2 + 36 000x, mientras que sus gastos (también en la misma moneda) pueden calcularse mediante la función g(x) = 44x2 + 12 000x + 700 000, donde x representa la cantidad de unidades vendidas. a. Determina la función utilidad de la empresa. Explica cómo lo hiciste. b. ¿Cuánto es la utilidad si ha vendido mil unidades? Explica. c. ¿Cuál de estas funciones es una contracción con respecto a f(x) = x2 ? Actividades UNIDAD 2 (54-105)C:Maquetación 1 4/11/10 17:13 Página 65
- 67. 66 | Unidad 2 Desplazamientos de la parábola Vimos qué ocurre al variar el valor de a en la función f(x) = ax2 + bx + c, cómo varía el gráfico de la parábola asociada a la función. Observa ahora las gráficas para las funciones de la forma f(x) = x2 + c, es decir, cuando a = 1 y b = 0. La diferencia en la representaciones gráficas es que la parábola f(x) = x2 + 3 está desplazada tres unidades verticalmente hacia arriba con respecto a g(x) = x2 , y el gráfico de h(x) = x2 – 4 está desplazado cuatro unidades hacia abajo con respecto a g(x) = x2 ; por lo tanto, el gráfico de f(x) = x2 + 10 corresponderá a la parábola g(x) = x2 desplazada en diez unidades verticalmente hacia arriba. La representación gráfica de una función de la forma f(x) = x2 + c corresponde a un desplazamiento de g(x) = x2 verticalmente en |c| unidades, hacia arriba en el caso que c 0, y hacia abajo en el caso que c 0. Analicemos... • ¿En qué se parecen los gráficos de g(x) = x2 y las funciones restantes?, ¿en qué se diferencian? • ¿Hacia dónde se movería la función f(x) = x2 + 10?, ¿y f(x) = x2 + c? El módulo de x se define como: I x I = x para x 0 o I x I = –x para x 0 Recuerda que... f(x) = x2 + 3 g(x) = x2 h(x) = x2 – 4 UNIDAD 2 (54-105)C:Maquetación 1 4/11/10 17:13 Página 66
- 68. Función cuadrática y función raíz cuadrada | 67 Unidad 2 Esto se debe a que los puntos del gráfico de la función cuadrática f(x) = x2 + c son de la forma (x, x2 + c); es decir, solo se modifica la ordenada de los puntos (x, x2 ) de la gráfica de la función f(x) = x2 . Observa ahora el gráfico de las funciones f(x) = x2 ; g(x) = (x – 3)2 y h(x) = (x + 2)2 . ¿Cuál crees que es la parábola correspondiente a g(x) = (x – 3)2 ?, ¿y a h(x) = (x + 2)2 ?, ¿por qué? La representación gráfica de f(x) = x2 la conocemos y tiene vér- tice (0, 0). Podemos observar que la única diferencia entre las parábolas en el gráfico es que g(x) = (x – 3)2 y h(x) = (x + 2)2 corresponden a un des- plazamiento horizontal de la función f(x) = x2 ; la primera en tres unidades a la derecha, y la segunda en dos a la izquierda. Observa que si (p, p2 ) es un punto de la gráfica de f(x) = x2 , en- tonces (p + 3, p2 ) es uno de la gráfica de g(x) = (x – 3)2 , ya que ([p + 3] – 3)2 = p2 . Entonces, la gráfica de g(x) = (x – 3)2 está des- plazada respecto de la gráfica de x2 . El punto (p + 3, p2 ) está tres unidades a la derecha de (p, p2 ), así la gráfica de g(x) = (x – 3)2 , es un desplazamiento de la gráfica de f(x) = x2 en tres unidades a la derecha. UNIDAD 2 (54-105)C:Maquetación 1 4/11/10 17:13 Página 67
- 69. 68 | Unidad 2 Teniendo en cuenta ahora tanto los desplazamientos verticales como horizontales de la representación gráfica de una función cuadrática, realizaremos un gráfico estimado de la función f(x) = (x – 3)2 – 5. Este será una parábola que se abre hacia arriba, obtenida a partir de la gráfica de f(x) = x2 , desplazándola tres unidades a la derecha y cinco hacia abajo. Observa. En resumen • Para cualquier valor de c, positivo o negativo, la función cuadrática f(x) = x2 + c tiene por gráfica una parábola que corresponde a desplazar verticalmente la parábola f(x) = x2 en I c I unidades, hacia arriba si c 0, y hacia abajo si c 0. • Para desplazar una función f(x) horizontalmente en h unidades, debemos considerar la función f (x + h); el sentido del desplazamiento dependerá del signo de h. • Si h 0, f(x) se desplazará h unidades hacia la izquierda. • Si h 0, f(x) se desplazará h unidades hacia la derecha. f(x) = (x – 3)2 – 5 UNIDAD 2 (54-105)C:Maquetación 1 4/11/10 17:13 Página 68
- 70. Unidad 2 Función cuadrática y función raíz cuadrada | 69 Si ahora tenemos la función cuadrática f(x) = –2(x – 4)2 + 1, podemos construir un gráfico estimado a partir de f(x) = –2x2 , desplazando la parábola correspondiente cuatro unidades a la derecha y una hacia arriba. Observa. 1. A partir del gráfico de f(x) = x2 , realiza la representación gráfica aproximada de las siguientes funciones cuadráticas. Indica, paso a paso, cómo lo hiciste en cada caso. a. f(x) = – x2 e. f(x) = x2 – i. f(x) = (x – 1)2 + 3 b. f(x) = –x2 + 12 f. f(x) = –x2 – 10 j. f(x) = –x2 + 12x – 2 c. f(x) = –5 + x2 g. f(x) = x2 – 3 k. f(x) = 2 – 3x – x2 d. f(x) = x2 – 8 h. f(x) = –(x – 2)2 l. f(x) = x2 + x + 1 2. Construye funciones cuadráticas que correspondan al desplazamiento en tres unidades a la derecha de las siguientes funciones: a. g(x) = x2 – 4x + 4 c. g(x) = x2 + 6x + 6 b. g(x) = –x2 + 3x – 5 d. g(x) = 2 – 5x – x2 2 3 2 Actividades f(x) = –2(x – 4)2 + 1 f(x) = –2x2 UNIDAD 2 (54-105)C:Maquetación 1 4/11/10 17:13 Página 69
- 71. Simetría y vértice de la parábola 70 | Unidad 2 Felipe está realizando un experimento que consiste en lanzar una piedra. Él observa que esta describe una trayectoria parabólica, como se observa en la figura. La altura que alcanza la piedra en un determinado momento está dada por la función cuadrática h(t) = –t2 + 10t, donde h(t) es la altura en metros alcanzada por la piedra, y t el tiempo en segundos desde que se lanza la piedra. Al observar el gráfico, podemos darnos cuenta de que existe un punto en el cual la piedra llega a su máxima altura y luego comienza a descender; este punto es el vértice de la parábola. La función correspondiente al lanzamiento de la piedra es h(t) = –t2 + 10t, la cual escrita en su forma canónica es h(t) = –(t – 5)2 + 25, que como vimos anteriormente corresponde a la representación gráfica de una función de la forma f(x) = –x2 , desplazada verticalmente veinticinco unidades hacia arriba y hori- zontalmente cinco hacia la derecha. Esto produce un desplaza- miento de cada punto de la función; por lo tanto, el vértice de la parábola estará veinticinco unidades hacia arriba del origen y cinco a la derecha, es decir, es el punto (5, 25). El vértice de una parábola se puede inferir fácilmente a partir de la función cuadrática en su forma canónica. Observa que en el caso de h(t) = –(t – 5)2 + 25, el vértice es el punto (5, 25). En general, dada una función cuadrática f(x)= a(x – h)2 + k, es decir, escrita en su forma canónica, el vértice de la parábola co- rresponde al punto (h, k), lo que equivale a que en la función f(x) = ax2 + bx + c, el vértice de la parábola sea el punto . Si observamos el gráfico, podemos ver que la piedra está en el aire durante diez segundos, durante cinco segundos sube y luego cae durante los cinco siguientes. En el gráfico se puede apreciar el sen- tido del desplazamiento en las ramas de la parábola. − − − ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ b a b ac a 2 4 4 2 , Analicemos... • ¿Cuál es la altura máxima alcanzada por la piedra?, ¿cómo lo supiste? • ¿Durante cuántos segundos la piedra estuvo en el aire?, ¿durante cuántos subiendo?, ¿y descendiendo? UNIDAD 2 (54-105)C:Maquetación 1 4/11/10 17:13 Página 70
- 72. Función cuadrática y función raíz cuadrada | 71 Unidad 2 Esto se debe a que: • a la izquierda del vértice: si a b, entonces –a2 + 10a –b2 + 10b. Luego, se cumple que f(a) f (b). • a la derecha del vértice: si a b, entonces –a2 + 10a –b2 + 10b. Luego, se cumple que f(a) f (b). Es decir, la rama creciente está a la izquierda del vértice y la rama decreciente está a su derecha. Gráficamente observamos una simetría con respecto a la recta que pasa por el vértice de la parábola. En el caso del lanzamiento de la piedra será la recta t = 5, la cual recibe el nombre de eje de simetría. Observa. 1. Encuentra el eje de simetría y el vértice de las siguientes parábolas: a. f(x) = 2x2 – 3x – 14 b. f(x) = x2 – 7x – 10 c. f(x) = x2 + 5x + 6 2. Encuentra el valor de a tal que la gráfica de la función f(x) = ax2 – 2x + 1 tenga como eje de simetría la recta x = 1. 3. ¿Cuántas parábolas tienen como vértice el punto (0, 0)? ¿Qué particularidad puedes observar en este tipo de funciones cuadráticas con respecto al eje de simetría? 4. ¿Puede una función cuadrática tener como gráfica una parábola que tenga por vértice el punto (1, 2) y pasar por el punto (1, –1)? Explícalo geométricamente. ¿Puedes explicarlo algebraica- mente?, ¿cómo? Actividades En resumen • En toda función cuadrática f(x) = ax2 + bx + c, el eje de simetría está dado por la recta , la cual divide la parábola en dos partes iguales y el vértice es el punto , siendo este la intersección entre la parábola y el eje de simetría. Puedes observar que el vértice es el punto más alto, si la parábola está orientada hacia abajo; y el más bajo, si lo está hacia arriba. − − − ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ b a b ac a 2 4 4 2 , x b a = − 2 t = 5 UNIDAD 2 (54-105)C:Maquetación 1 4/11/10 17:13 Página 71
- 73. 72 | Unidad 2 La parábola como lugar geométrico Hemos estudiado la función cuadrática desde varios puntos y hemos llamado parábola al tipo de curva que se obtiene. Sin em- bargo, esta misma curva se puede obtener a partir del siguiente problema geométrico. Dibujar todos los puntos que se encuentren a igual distancia de un punto fijo F llamado foco y una recta L llamada directriz. Al resolver este problema, aparece una parábola como dibujo. Si ahora utilizamos un sistema de ejes coordenados XY y definimos las coordenadas del vértice V(h, k) y una distancia p desde el vértice al foco F, y desde este a la directriz L, obtenemos la siguiente figura: Así, podemos plantear y desarrollar lo siguiente: (x – h)2 + (y – (k + p))2 = (y – (k – p))2 (x – h)2 = 4yp – 4kp (x – h)2 = 4p(y – k) La parábola no solo es un lugar geométrico, sino que además tiene gran importancia en la tecnología. Por ejemplo, algunos radares y antenas de telecomunicaciones son muestras del aprovechamiento de las características geométricas de las parábolas. Las antenas parabólicas, como la que se muestra en la foto, son utilizadas para recibir señales, por ejemplo, de televisión o de tele- fonía; concentran las señales en un lugar que coincide con el foco de la parábola, el cual se llama “receptor”. x h y k p y k p − ( ) + − + ( ) ( ) − − ( ) 2 2 = Elevamos al cuadrado Ya que la distancia entre un punto (x, y) y F es igual a la distancia entre la recta L y (x, y) Desarrollamos Factorizamos P F M M´ P´ L Y X L h (x, y) p p F k k + p k – p V La distancia entre dos puntos del sistema de coordenadas: A(x1 , y1 ) y B(x2 , y2 ) se denota por d(A, B) y se calcula de la siguiente forma: Si uno de los puntos corresponde al origen del sistema, denotaremos la distancia de un punto A a este por d(A, O), y su ecuación es . d A O x y , ( )= + 1 1 2 2 Recuerda que... d A B x x y y , ( )= − ( ) + − ( ) 1 2 2 1 2 2 UNIDAD 2 (54-105)C:Maquetación 1 4/11/10 17:13 Página 72
- 74. Función cuadrática y función raíz cuadrada | 73 Unidad 2 En resumen • La ecuación (x – h)2 = 4p(y – k) representa la parábola con vértice (h, k) y directriz L: y = k – p y foco F (h, k + p), donde p es la distancia entre el vértice y el foco, y entre el vértice y la directriz. Herramientas tecnológicas Construcción de la parábola con regla y compás Usando el programa computacional Regla y compás, que puedes descargar de la página web www.educacionmedia.cl/mat3/car.exe, construye una parábola siguiendo los pasos que a continuación se indican. 1º Traza una recta L cualquiera y dibuja un punto cualquiera F que no pertenezca a L. Luego, ubica un punto P sobre L. Usa las siguientes herramientas: 2º Traza por P una recta de color rojo que sea perpendicular a L. Usa la herramienta: 3º Une P con F mediante un segmento y ubica el punto medio entre estos puntos. Utiliza las herramientas: 4º Traza, por este punto medio, una perpendicular (de color verde) al segmento PF. Usa la herramienta: 5º Ubica el punto X como intersección de estas dos perpendiculares. 6º Mueve el punto P y observa cómo se mueve el punto X. ¿Funciona? Para comprobar tu cons- trucción, selecciona la herramienta Traza de un punto. Luego, selecciona primero el punto X, después el punto P y, finalmente, mueve el punto P. 7º Varía tu comprobación usando la herramienta Traza automática. Para colocar el nombre a los puntos o cambiar las propiedades de algún objeto usa el botón derecho del mouse. UNIDAD 2 (54-105)C:Maquetación 1 4/11/10 17:13 Página 73
- 75. 74 | Unidad 2 • En el siguiente mapa conceptual se muestran algunos de los conceptos presentados hasta ahora en la Unidad. • Utilizando los contenidos aprendidos en la Unidad, y apoyándote en el esquema anterior, responde en tu cuaderno. 1. ¿Crees que faltó un concepto importante en el mapa conceptual?, ¿cuál? Agrégalo. 2. ¿En qué debes fijarte para determinar si la parábola se abre hacia arriba o hacia abajo en la función f(x) = ax2 + bx + c? 3. ¿En qué debes fijarte para identificar el vértice de una parábola en f(x) = ax2 + bx + c? 4. ¿Qué relación hay entre los coeficientes que aparecen al escribir una función cuadrática en su forma canónica y el vértice? 5. ¿Tienes alguna duda sobre los conceptos tratados en las páginas anteriores?, ¿cuál? Compártela con tu curso e intenten aclararla en conjunto. en su forma canónica se escriben su dominio es f(x) = ax2 + bx + c f(x) = a(x– h)2 + k IR PARÁBOLA Organizando lo aprendido si cada una es se unen en son de la forma su gráfica es una FUNCIÓN CUADRÁTICA a 0 ARRIBA a 0 está formada por dos RAMAS se abre hacia CRECIENTE DECRECIENTE VÉRTICE tiene coordenadas ABAJO se abre hacia − − − ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ b a b ac a 2 4 4 2 , UNIDAD 2 (54-105)C:Maquetación 1 4/11/10 17:13 Página 74
- 76. Función cuadrática y función raíz cuadrada | 75 1. A partir de la representación gráfica de f(x) = x2 , indica si hay dilatación o contracción con respecto a f(x) = x2 y, luego, grafica las funciones reconociendo los desplazamientos de la función inicial. a. f(x) = x2 + 3x – 5 b. g(x) = x2 – 12x + 3 c. h(x) = (x + 3)2 d. p(x) = 4 – 3x – 2x2 2. Determina los intervalos de crecimiento y decrecimiento de las siguientes funciones: a. f(x) = x2 + x + 1 b. g(x) = –3x2 + 2 c. h(x) = x – x2 d. p(x) = –4x2 + x + 1 3. Determina el vértice y el eje de simetría de las siguientes funciones cuadráticas: a. f(x) = (x + 2)2 – 3 b. g(x) = 2 – x2 c. h(x) = 2x2 – 3x + 2 d. p(x) = 5 – x – x2 4. Grafica en tu cuaderno las siguientes funciones: a. f(x) = x2 – 8 b. g(x) = x2 + 3x + 1 c. h(x) = 3 – x2 + 2x d. p(x) = (x + 4)2 – 9 5. La función que está representada por la curva dada es: A. y = x2 + 3 B. y = x2 – 3 C. x = x2 + 3 D. x = x2 – 3 E. y = –x2 – 3 • Verifica en el solucionario si tus respuestas son correctas. Si tuviste respuestas incorrectas, marca en la tabla el criterio correspondiente y revisa las páginas indicadas. Luego, identifica el error y corrígelas. ¿Cómo voy? Mi progreso Unidad 2 CRITERIO ÍTEMS PÁGINAS DONDE SE TRABAJA Reconocer la dilatación, contracción y desplazamientos de la parábola. 1 y 5 64 a 69 Determinar intervalos de crecimiento y decrecimiento. 2 60 y 61, 70 y 71 Determinar vértice y el eje de simetría. 3 70 y 71 Graficar funciones cuadráticas. 4 60 y 61 UNIDAD 2 (54-105)C:Maquetación 1 4/11/10 17:13 Página 75
- 77. 76 | Unidad 2 Ecuación de segundo grado En cinemática, la posición de un objeto lanzado verticalmente hacia arriba está dada por la fórmula y = y0 + v0 t − gt2 , donde v0 es la velocidad inicial con que se lanza el objeto, t el tiempo transcurrido, g la aceleración de gravedad que la aproximamos por 10 e y0 la altura inicial del objeto. Supongamos que se lanza una pelota verticalmente hacia arriba desde la azotea de un edificio de 55 m de altura, con una veloci- dad inicial de 50 , la que luego cae al suelo. m s m s2 1 2 Observa que y0 = 55 y v0 = 50, de modo que la altura de la pelota estará dada por y = 55 + 50t – 5t2 . Cuando la pelota se encuen- tre en el piso su altura será 0, es decir,tenemos que resolver 55 + 50t – 5t2 = 0 . Recordando la identidad (x + a)(x + b) = x2 + (a + b)x + ab, tenemos (sin olvidar que la variable es t): 0 = 5(11 + 10t – t2 ) 0 = 11 + 10t – t2 0 = t2 – 10t – 11 0 = (t + 1)(t – 11) Luego, (t + 1) = 0 o (t – 11) = 0 t = –1 t = 11 Como la pelota no puede llegar al suelo un segundo antes de ser lanzada desde el edificio, la solución encontrada t = –1 la eliminamos; por lo tanto, la pelota demora once segundos en llegar al suelo. Si ahora nos interesa calcular en qué segundo la pelota se encuen- tra a diez metros de altura, debemos entonces resolver la ecuación de segundo grado 10 = 55 + 50t – 5t2 , lo que equivale a resolver la ecuación: 0 = 45 + 50t – 5t2 Analicemos... • ¿Cuál es la ecuación que representa la altura en función del tiempo? • ¿Qué forma tiene el recorrido de la pelota hasta llegar al suelo? • ¿Cuánto tiempo demorará la pelota en llegar al suelo?, ¿por qué? El producto de dos términos es cero si y solo si al menos uno de ellos es cero. a · b = 0 a = 0 ∨ b = 0 ↔ Recuerda que... Glosario cinemática: parte de la Física que estudia el movimiento prescindiendo de las fuerzas que lo producen. Factorizamos por 5 Dividimos por 5 Multiplicamos por –1 Factorizamos UNIDAD 2 (54-105)C:Maquetación 1 4/11/10 17:13 Página 76
- 78. Función cuadrática y función raíz cuadrada | 77 Unidad 2 Encontrar las soluciones por simple inspección o factorizando direc- tamente se dificulta en este caso, por lo que la resolveremos por medio del método de completación de cuadrados. Observa. 0 = 45 + 50t – 5t2 0 = 5t2 – 50t – 45 0 = 5(t2 – 10t) – 45 0 = 5(t – 5)2 – 125 – 45 = (t – 5)2 Luego, las soluciones de la ecuación serán: y ¿Son ambas soluciones válidas en el contexto del problema? En general, para una ecuación de segundo grado o cuadrática cual- quiera, podemos encontrar las soluciones mediante completación de cuadrados. Sean a, b y c números reales con a 0, entonces: ax2 + bx + c = 0. Si llamamos x1 y x2 a las soluciones de la ecuación, estas serán: t = − 5 170 5 t = + 5 170 5 0 5 5 25 45 2 = − ( ) − ⎡ ⎣ ⎢ ⎤ ⎦ ⎥ − t 170 5 t − ( )= ± 5 170 5 a x + b a x +c 2 ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ = 0 a x b a b a c + ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ − + = 2 4 2 2 0 a x b a b ac a + ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ − − = 2 4 2 2 4 0 x b a b a a + ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ = − 2 4 c 4 2 2 2 x b a b a a + ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ = ± − 2 4 c 4 2 2 x b a b a a = − ± − 2 4 c 2 2 x b a b ac a 1 2 = − + − 2 4 2 x b a b ac a 2 2 = − − − 2 4 2 Factorizamos por 5 Factorizamos por a Calculamos la raíz cuadrada Despejamos para encontrar el valor de t Para encontrar las soluciones de la ecuación de segundo grado ax2 + bx + c = 0, utilizamos el método de completación de cuadra- dos, de la misma forma que para es- cribir una función cuadrática en su forma canónica. Pon atención UNIDAD 2 (54-105)C:Maquetación 1 4/11/10 17:13 Página 77
- 79. 78 | Unidad 2 Observa que las soluciones se diferencian entre sí por el término , ya que ambas contienen el término ; sin embargo, restamos. Luego, si , ambas soluciones serán iguales, pues tendremos que y . Observa que si , significa que b2 – 4ac = 0, ya que el denominador de una fracción no puede ser 0, y . Por otro lado, si b2 – 4ac 0, las soluciones serán distintas; sin em- bargo, como el segundo término de las soluciones es una raíz cuadrada, para que las soluciones o raíces de la ecuación sean números reales es necesario que b2 – 4ac sea un número positivo, de lo contrario tendríamos la raíz cuadrada de un número nega- tivo que no existe en el conjunto de los números reales. Como hemos visto, para saber si la ecuación cuadrática tiene o no solución (y si las tiene, saber si son iguales o distintas), basta con saber el valor de b2 – 4ac. Esta expresión es llamada discriminante de la ecuación de segundo grado y se denota por el símbolo Δ. b ac a 2 4 − = 2 0 b ac a 2 4 − = 2 0 − b a 2 b ac a 2 4 − 2 En resumen • Las soluciones de la ecuación ax2 + bx + c = 0 son llamadas también raíces de la ecuación, y en general siempre las podemos determinar por medio de: • Podemos saber la naturaleza de las soluciones por medio del discriminante de la ecuación, que se denota por Δ= b2 – 4ac: • Si Δ 0, la ecuación tiene dos soluciones reales distintas. • Si Δ = 0, la ecuación tiene dos soluciones reales e iguales. • Si Δ 0, la ecuación no tiene soluciones reales. x b a b a 1 0 = − + = − 2 2 x b a b a 2 0 = − − = − 2 2 0 0 = x b a b ac a 1 2 = − + − 2 4 2 x b a b ac a 2 2 = − − − 2 4 2 a una se le suma el segundo término y a la otra se lo b ac a 2 4 − 2 UNIDAD 2 (54-105)C:Maquetación 1 4/11/10 17:13 Página 78
- 80. Función cuadrática y función raíz cuadrada | 79 Unidad 2 1. Resuelve las siguientes ecuaciones indicando el discriminante y la o las soluciones, si existen. a. x2 – 10x + 20 = 0 c. x2 – 4x + 4 = 0 e. 5x2 + 125 = 0 b. 4x2 – 8x + 29 = 3 d. x2 – 6x + 12 = 0 f. 3x2 – 7x = 0 2. Encuentra dos números consecutivos tales que su producto sea 132. Plantea una ecuación que permita resolver este problema. 3. Una embotelladora de bebidas desea crear un envase cilíndrico de 18 centímetros de largo y una superficie de 144 cm2 . ¿Cuál debe ser el radio de dicho cilindro?, ¿cómo lo calculaste? 4. Encuentra todos los valores de k tales que las soluciones de la ecuación cuadrática g(x) = 2x2 + k: a. sean reales distintas. b. sean reales e iguales. c. no sean reales. 5. Encuentra todos los valores de k tales que las soluciones de la ecuación h(x) = 2x2 + 3x – k: a. sean reales distintas. b. sean reales e iguales. c. no sean reales. 6. Si las medidas de un rectángulo de 6 por 8 se aumentan en la misma cantidad cada una, el área del nuevo rectángulo será dos veces el área original. ¿Cuáles serán las dimensiones del nuevo rectángulo? 7. La diagonal de un rectángulo mide 10 cm y su área 48 cm2 . ¿Cuáles son las medidas de los lados del rectángulo? 8. Un deportista caminó 30 km en determinado número de horas. Si hubiese caminado un kilómetro más por hora, habría tardado una hora menos en recorrer la misma distancia. Suponiendo que llevaba la misma rapidez, ¿a cuántos kilómetros por hora recorrió esa distancia? 9. ¿Qué valores puede tomar k en la ecuación 8x2 – (k + 1)x + (k – 7) = 0, para que tenga raíces reales iguales? 10. Expresa el número 192 en dos factores, de modo que estén en la razón 3 : 4. 11. En un círculo, la distancia entre dos cuerdas paralelas congruentes es de 12 cm. Si cada cuerda mide 6 cm más que el radio, calcula la medida del perímetro del círculo. 12. ¿Es posible encontrar dos números consecutivos tales que su producto sea 17? Explica. Actividades UNIDAD 2 (54-105)C:Maquetación 1 4/11/10 17:13 Página 79
- 81. 80 | Unidad 2 Análisis de las raíces de una ecuación cuadrática Observa la siguiente tabla, donde x1 y x2 son raíces de las siguientes ecuaciones cuadráticas: Toda ecuación de la forma ax2 + bx + c = 0 (a 0) es equivalente a la ecuación , luego, se puede factorizar de la forma (x – x1 )(x – x2 ) = 0, donde x1 y x2 son las soluciones de la ecuación (x – x1 )(x – x2 ) = x2 – (x1 + x2 )x + x1 · x2 . Entonces, y , lo que nos permite relacionar raíces de la ecuación de segundo grado con sus coeficientes. Para encontrar una ecuación de segundo grado cuyas soluciones sean x1 = 0 y x2 = –4, usamos la relación encontrada entre las raíces y los coeficientes de la ecuación. Entonces, y , luego, una ecuación de segundo grado con las soluciones dadas será: x2 – (–4)x + 0 = 0 x2 + 4x = 0 c a = x x = = 1 2 0 4 0 ⋅ ⋅ − ( ) − − − b a = x + x = = 1 2 0 4 4 x x = c a 2 2 ⋅ x + x = b a 1 2 − x b a x c a 2 0 + + = Ecuaciones x1 x2 x1 + x2 x1 · x2 – x2 – 5x + 6 = 0 2 3 5 6 5 6 x2 + 4x = 0 0 –4 –4 0 –4 0 x2 – 4x + 4 = 0 2 2 4 4 4 4 b a c a Analicemos... • ¿Existe alguna relación entre la suma de las raíces y los coefi- cientes de las ecuaciones? Explica. • ¿Existe alguna relación entre la multiplicación de las raíces y los coeficientes de las ecuaciones?, ¿cuál? • ¿Podrías obtener una ecuación que tenga como soluciones 0 y –4? Escríbela. ¿Cuántas ecuaciones de segundo grado con estas soluciones se pueden encontrar?, ¿por qué? UNIDAD 2 (54-105)C:Maquetación 1 4/11/10 17:13 Página 80
- 82. Función cuadrática y función raíz cuadrada | 81 Unidad 2 1. Calcula la suma y el producto de las raíces de las siguientes ecuaciones: a. 5x2 + 3x – 10 = 0 b. c. x2 + x + 2 = 0 2. Encuentra una ecuación cuadrática cuyas raíces sean: a. 0 y 3 b. –1 y 1 c. –2 y 2 d. m y m + 1 3. Si en la ecuación cuadrática x2 – 6ax + 11 = 0, una de sus raíces es –1, ¿cuál es el valor de la otra raíz? (si es que la hay). 4. ¿Cuál es el valor de k para que la suma de las raíces de la ecuación cuadrática –3x2 + kx – 10 = 0 sea 13? 5. La suma de las raíces de una ecuación cuadrática es –9 y su producto es 20. Encuentra la ecuación de segundo grado ax2 + bx + c = 0 correspondiente, sabiendo que a = 5. 6. Sean x1 y x2 las raíces de la ecuación 2x2 – 3x – 5 = 0, encuentra el valor de la expresión . 1 1 1 2 x x + x x 2 + 1 4 12 = 0 − Actividades En resumen • Sean x1 y x2 las raíces de la ecuación cuadrática ax2 + bx + c = 0. Entonces: y . x x = c a 1 2 ⋅ x + x = b a 1 2 − Podemos encontrar infinitas ecuaciones que tengan como soluciones 0 y –4; observa los siguientes ejemplos: 2x2 + 8x = 0 –x2 – 4x = 0 3x2 + 12x = 0 A pesar de que estas tres ecuaciones son distintas a x2 + 4x = 0, sus raíces son 0 y –4; esto se debe a que estas ecuaciones se obtienen amplificando x2 + 4x = 0 por algún número. Si tenemos dos o más ecuaciones diferentes, pero que sus soluciones son iguales, se de- nominan ecuaciones equivalentes. UNIDAD 2 (54-105)C:Maquetación 1 4/11/10 17:13 Página 81
- 83. 82 | Unidad 2 Ecuaciones reductibles a ecuaciones de segundo grado Algunas ecuaciones pueden ser reducidas a ecuaciones de segundo grado haciendo algún cambio de variables. Si observas detenidamente la primera ecuación, te podrás dar cuenta de que si remplazamos x2 por y, la ecuación se puede reescribir como y2 – 3y – 4 = 0, transformándose así en una ecuación de se- gundo grado cuyas soluciones son y1 = 4 e y2 = –1. Pero y = x2 , de donde podemos deducir que y ≥ 0, descartando así la solución y = –1. Entonces, la solución será y = 4, es decir, x2 = 4, luego, las soluciones de x4 – 3x2 – 4 = 0 son 2 y –2. En la segunda ecuación utilizaremos la variable auxiliar , tomando en cuenta que . Remplazamos: 7y2 – 9y + 2 = 0 , de donde obtenemos e . Luego, remplazamos para encontrar el valor de x: • Para y1 = 1, , y por lo tanto, x1 = 1. y2 9 5 14 4 14 2 7 = − = = y1 9 5 14 14 14 1 = + = = x = x = x = x 3 4 2 2 3 3 4 3 2 ( ) ⎛ ⎝ ⎞ ⎠ x = 3 4 1 y = 9 9 4 7 2 2 7 = 9 25 14 = 9 5 14 2 ± − ( ) − ⋅ ⋅ ( ) ⋅ ± ± y = x3 4 Analicemos... • ¿Puedes resolver la ecuación x4 – 3x2 – 4 = 0?, ¿cuántas solu- ciones tendrá?, ¿cómo podemos resolverla utilizando lo aprendido de ecuaciones de segundo grado? • ¿Y la ecuación ? 7 9 2 0 3 3 4 x x − + = De este modo, las soluciones de son 1 y . 2 7 3 4 ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ 7 9 2 0 3 3 4 x x − + = Recuerda que... • Para , ,y por lo tanto, . x = 2 4 2 7 3 ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ x = 3 4 2 7 y = 2 2 7 x x n m n m = UNIDAD 2 (54-105)C:Maquetación 1 4/11/10 17:13 Página 82
- 84. Función cuadrática y función raíz cuadrada | 83 Unidad 2 En resumen • Muchas ecuaciones pueden reducirse a una ecuación cuadrática mediante una variable auxiliar y = g(x), de modo que la ecuación que resulta en la nueva variable sea una ecuación cuadrática. Luego, al encontrar los valores solución en la variable y, debemos resolver la ecuación y = g(x) para encontrar los valores de x que resuelven la ecuación original. • Una ecuación de tipo ax4 + bx2 + c = 0 es un caso particular de ecuaciones reductibles a ecuaciones de segundo grado, llamada ecuación bicuadrática, la cual podemos resolver mediante el uso de la variable auxiliar y = x2 . 1. Resuelve las siguientes ecuaciones: a. x4 + 4x2 + 2 = 0 c. x4 + 4x2 – 2 = 0 e. x4 – 5x2 + 6 = 0 g. b. x4 – 16 = 0 d. 3x4 + 9x2 + 12 = 0 f. 3x4 + 7 = 0 h. 9x4 – 24x2 + 16 = 0 2. Resuelve las siguientes ecuaciones utilizando variables auxiliares: a. x4 – 2x2 – 3 = 0 g. m. 32x + 3 = 3x + 1 c. (5 + x2 )(8 – x2 ) = 0 i. o. d. j. p. f. 9x4 – 10x2 + 1 = 0 l. r. 3. Calcula la medida de los lados de un rectángulo sabiendo que su área es 12 cm2 y su diagonal mide 5 cm. La siguiente figura que representa el problema te puede ayudar. a. ¿Qué tipo de ecuación resulta? b. Resuelve un problema similar al anterior, pero en el que el área aumenta a 60 cm2 y la diagonal a 13 cm. 2 1 2 6 0 4 x x − − = x x − = 2 5 2 x x 2 2 9 21 + + = 6 6 10 35 x x + + = 4 12 7 2 5 5 x x + = 5 2 33 x x + = x x 2 2 5 2 1 0 − + = x x x x 2 2 1 1 0 + + + = 2 3 3 1 3 0 4 2 x x − + = Actividades b. h. x4 – 4mx2 – (m2 – n2 ) = 0 n. x x x x 2 2 6 5 6 0 − + − = 2 5 250 3 3 4 x x − = e. x4 – 5x2 + 4 = 0 k. q. x x 4 3 2 3 3 2 0 − + = 5 2 5 2 20 x x + + + = 12 x cm 5 cm x cm UNIDAD 2 (54-105)C:Maquetación 1 4/11/10 17:13 Página 83
- 85. 84 | Unidad 2 Análisis general de una función cuadrática Don José, agricultor de Llanquihue, vende sus gallinas en una feria campesina de la zona. Después de calcular el costo de mantención de cada una y venderlas a un precio p (en miles de pesos), obtiene la utilidad por unidad vendida, que se puede modelar según la siguiente expresión: U(p) = –0,2 (p2 – 20p + 75) El precio de cada gallina está en miles de pesos, por lo tanto para determinar la utilidad correspondiente debemos evaluar la función para p = 7; es decir, si el precio de venta de una gallina es $ 7000, don José obtiene una utilidad de: U(7) = – 0,2 (72 – 20 · 7 + 75) = 3,2 Y como está en miles de pesos son $ 3200. Recordemos que gráficamente una función cua- drática, como es el caso de la función de utilidad dada, es una parábola. Observa. En el gráfico se puede apreciar que la parábola interseca en dos puntos al eje de las abscisas, que en este caso corresponde al precio. Es decir, exis- ten dos valores para los cuales la utilidad es cero. Llamaremos ceros de la función cuadrática f(x) = ax2 + bx + c a los valores de x tales que f(x) = 0, es decir, a los puntos de intersección con el eje X. Una parábola puede cortar en dos pun- tos al eje X, en uno (cuando es tangente) o ninguno, dependiendo de las soluciones que tenga dicha ecuación. Analicemos... • ¿Cuánto será la utilidad si vende una gallina a $ 7000?, ¿cómo lo supiste? • ¿Existe algún precio para el cual la utilidad es cero? Si lo hay, ¿de qué modo podrías determinarlo? • ¿A qué valor debe vender cada gallina para que la utilidad sea positiva?, ¿y negativa? Don José, alimentando a sus gallinas. UNIDAD 2 (54-105)C:Maquetación 1 4/11/10 17:13 Página 84
- 86. Función cuadrática y función raíz cuadrada | 85 Sea f(x) = ax2 + bx + c una función cuadrática cuyo discriminante es Δ = b2 – 4ac, entonces: • Si Δ 0, la gráfica de la función f(x) corta en dos puntos al eje X. • Si Δ = 0, la gráfica de la función f(x) corta en un solo punto al eje X, siendo tangente a este. • Si Δ 0, la gráfica de la función f(x) no corta al eje X. En el caso de U(p) = – 0,2 (p2 – 20 · p + 75), el discriminante es: Δ = (–0,2)2 · (20)2 – 4 · (–0,2)(–0,2)(75) = 4 0, por lo que la parábola que describe la función de utilidad U(p) corta al eje de las abscisas en dos puntos, tal como lo pudimos apreciar en el gráfico. Para determinar cuáles son los precios de venta para que la utili- dad sea igual a cero, debemos encontrar los valores de p tal que U(p) = 0. Observa. –0,2 (p2 – 20p + 75) = 0 –0,2 (p – 5)(p –15) = 0 De donde concluimos que p = 5 o p = 15, que son los ceros o raíces de la función cuadrática. En otras palabras, si vende cada gallina en $ 5000 o $ 15 000 no hay utilidades. Al estudiar esta función de segundo grado se infiere que habrá valores para los cuales la utilidad es positiva y otros para los cuales no hay utilidad. Al observar el gráfico de esta función, se deduce también que si el precio p varía entre 0 y 5, o bien, es mayor que 15, hay utilidades negativas o pierde dinero al vender. Si, por el contrario, el valor de p varía entre 5 y 15, entonces, hay utilidades que alcanzan su máximo en p = 10, y son de $ 5000 por cada gallina. En muchos problemas será necesario resumir la información para tener claro lo que sucede para distintos valores de las variables. En este caso tenemos: Estos gráficos permiten responder más fácilmente preguntas como: ¿en cuánto debe vender cada gallina para no tener pérdidas?, o ¿qué sucede si vende cada gallina a $ 20 000? Unidad 2 5 15 0 U(p) 0 Hay pérdida Hay ganancia Hay pérdida U(p) 0 U(p) 0 – + – UNIDAD 2 (54-105)C:Maquetación 1 4/11/10 17:13 Página 85
- 87. 86 | Unidad 2 En resumen • Dependiendo de los valores de a, b y c en la expresión: f(x) = ax2 + bx + c es posible analizar el signo de la función: f(x) 0 o f(x) 0. • Sea f(x) = ax2 + bx + c una función cualquiera de segundo grado y x1 y x2 sus raíces, entonces, se pueden tener las siguientes situaciones: Caso 1: a 0 Caso 2: a 0 a. Si Δ 0, entonces: • f(x) 0 para x1 x x2 • f(x) 0 para x x1 y x x2 b. Si Δ = 0 hay solo una raíz x1 de f(x), entonces f(x) 0 para todo x x1 c. Si Δ 0, entonces f(x) 0 para todo x 0 para todo x. a. Si Δ 0, entonces: • f(x) 0 para x1 x x2 • f(x) 0 para x x1 y x x2 b. Si Δ = 0 hay solo una raíz x1 de f(x), entonces f(x) 0 para todo x x1 c. Si Δ 0, entonces f(x) 0 para todo x x1 x1 x1 x1 x2 x2 UNIDAD 2 (54-105)C:Maquetación 1 4/11/10 17:13 Página 86
- 88. Función cuadrática y función raíz cuadrada | 87 Unidad 2 1. Grafica las siguientes funciones cuadráticas, calcula cuál es su discriminante e indica claramente dónde corta al eje X, si es que lo corta, según sea el caso. a. f(x) = 2x2 + 3x + 5 c. f(x) = 4x2 – 4x + 1 e. j(x) = 2x2 + 31x b. h(x) = –x2 + 4x – 3 d. g(x) = 2x2 + 5 f. t(x) = x2 + 4x + 4 2. Encuentra todos los valores de k tales que la gráfica de la función f(x) = kx2 + 3x – 4 corte al eje de las abscisas en: a. dos puntos. b. un solo punto. c. no lo corte. 3. Encuentra la ecuación de una parábola cuyas raíces sean (3 + ) y (3 – ). ¿Cuántas parábolas hay con esas condiciones? 4. Encuentra y explica la relación entre las soluciones de una ecuación de segundo grado y el vértice de la parábola asociada. 5. Determina si las siguientes afirmaciones son verdaderas o falsas. Justifica en cada caso tu decisión. Si el vértice de la parábola que grafica a una función cuadrática f(x) = ax2 + bx + c es (p, q) y las raíces de la ecuación de segundo grado asociada son x1 y x2 , entonces: – si p 0 y b 0, la parábola se abre hacia arriba. – si b 0 y x1 + x2 0, la parábola se abre hacia abajo. 6. Determina los valores de k para los cuales la función cuadrática f(x) = kx2 + kx – 4 es siempre positiva. 7. Determina los intervalos en los cuales las siguientes funciones cuadráticas son positivas y aquellos en los cuales es negativa. a. f (x) = 2x2 + 3x – 4 c. f (x) = x2 + 5x + 7 e. f (x) = –6x2 – 4x + 13 b. h(x) = x2 + x – 2 d. h(x) = x2 – 8 f. g(x) = x2 + 3 8. Sea f(x) = 3x2 – x + k, con Δ = 25. a. Determina el valor de k. b. Determina los valores de x para los cuales f(x) 0. c. Determina los valores de x para los cuales f(x) 0. 2 2 Actividades UNIDAD 2 (54-105)C:Maquetación 1 4/11/10 17:13 Página 87
- 89. 88 | Unidad 2 Máximos y mínimos Un grupo de entomólogos estudia los factores que inciden en el crecimiento poblacional de una clase de escarabajos. Inicialmente, tenían una población de 1000 escarabajos. Luego, alteraron los fac- tores de su hábitat y pudieron modelar el crecimiento de esta población mediante la siguiente expresión: P(t) = –t2 + 30t + 1000, en la cual t indica la cantidad de días y P(t) la población existente en ese día. Es claro que al inicio del experimento, t = 0 y P(0) = 1000. Si estudiamos la función cuadrática, podemos deducir que: • Hay dos puntos t1 y t2 para los cuales P(t1 ) = 0 y P(t2 ) = 0. • Tiene un vértice en el punto: ¿Qué información referente al problema nos aporta esto? La función P(t) tiene un valor máximo en 1225 y se alcanza cuando t = 15 días, ya que a 0 (se abre hacia abajo). Esta función tiene su vértice en este punto, luego del cual toma valores menores. La segunda pregunta se reduce a determinar el valor de t tal que P(t) = 0, o sea, debemos resolver la ecuación cuadrática: –t2 + 30t + 1000 = 0 –(t – 50)(t + 20) = 0 t = 50 o t = –20 Como t es el tiempo desde el inicio del experimento t 0; por lo tanto, concluimos que el tiempo buscado es t = 50 días, es decir, cuando deja de existir el último escarabajo. Veamos esta situación en un gráfico. Analicemos... • ¿Al cabo de cuántos días se alcanza la máxima población?, ¿cómo lo supiste? • ¿Cuándo deja de existir el último escarabajo?, ¿por qué? − − ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ = − − − − ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ ⎛ ⎝ b a P b a P 2 2 30 2 30 2 , , ⎜ ⎜ ⎞ ⎠ ⎟ = ( ) ( )= ( ) 15 15 15 1225 , , P punto máximo Escarabajos colorados de la papa. UNIDAD 2 (54-105)C:Maquetación 1 4/11/10 17:13 Página 88
- 90. Función cuadrática y función raíz cuadrada | 89 Unidad 2 1. Grafica las siguientes funciones indicando los puntos de intersección con los ejes (si los hay) y el vértice. Indica si la función tiene un máximo o un mínimo. a. f(x) = 2x2 – 1 d. t(x) = x2 – x g. q(x) = – x2 + 5x – 1 b. g(x) = x2 – x + 1 e. s(x) = x2 + 2x – 3 h. r(x) = x2 + 0,5x c. h(x) = x2 + 1 f. p(x) = x2 – 2x – 3 i. s(x) = x2 – 2x 2. Construye una función cuadrática tal que su máximo sea el punto (1, 0). Luego, otra función cuyo mínimo sea (1, 0). Compara tus respuestas con tus compañeros y compañeras. 3. Calcula el valor de a tal que la gráfica de la función f(x) = ax2 + 2x + 4 tenga su vértice en (1, 5). ¿Existe una función cuadrática de este tipo tal que su vértice sea el (0, 0)? 4. Un malabarista lanza una pelota imprimiéndole una velocidad de 4 . Después de haber sido lanzada, la función que describe su altura (medida en metros) según el tiempo es: h(t) = 1,2 + 4t – 2t2 . a. Calcula la altura máxima que alcanzó la pelota. b. Calcula el tiempo en que se alcanzó la máxima altura. c. ¿Cuánto tiempo permaneció en el aire? Explica. 5. Encuentra la distancia mínima entre la parábola y – 2 = (x – 1)2 y el punto (1, 1). 6. La altura a la que llegan dos proyectiles al ser disparados verticalmente hacia arriba está dada por las funciones f(t) = –0,01t2 + t + 10 y g(t) = + t + 10, respectivamente, donde t es el tiempo medido en segundos. Determina qué proyectil llega más alto y cuánto tiempo demora en hacerlo. 4 3 –t2 81 m s Actividades En resumen Sea la función cuadrática f(x) = ax2 + bx + c, entonces: • si a 0, entonces f tiene un valor máximo para x = . Para calcular este valor máximo hay que obtener . f b a − ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ 2 − b a 2 • si a 0, entonces f tiene un valor mínimo para x = . Para calcular este valor mínimo hay que obtener . f b a − ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ 2 − b a 2 UNIDAD 2 (54-105)C:Maquetación 1 4/11/10 17:13 Página 89
- 91. 90 | Unidad 2 Función raíz cuadrada Para medir la velocidad de un fluido incompresible (como el agua) en un tubo, se utiliza el medidor Venturi que aprovecha el fenó- meno de un fluido que circula por un tubo; cuando este se estrecha en una zona, se ve obligado a incrementar su velocidad en la zona es- trecha. Por razones físicas, eso produce una disminución de la presión del fluido en esta zona. La velocidad que traía el fluido antes de la estrechez se mide por , donde k es una constante que depende del tubo y el tipo de fluido, P1 es la presión del fluido en la zona normal del tubo y p es la presión medida en la estrecha. De este modo, en un tubo de ancho constante se intercala una sec- ción estrecha provista de un medidor de presión, que entrega el valor p, a la vez que se mide la presión normal P1 en la zona normal del tubo, de modo que la velocidad se puede calcular como se indica. v = k P p ⋅ − 1 Con los datos dados, obtenemos . Al completar la tabla, notamos que la velocidad disminuye al au- mentar el valor de la presión en la zona estrecha. v = p 5 8 ⋅ − Analicemos... • Asumiendo k = 5 y P1 = , haz una tabla con los valores de v para los siguientes valores de p: 0,3; 0,5; 1; 3; 4,5; 6; 7. ¿Qué ocurre con la velocidad al aumentar la presión en al zona estrecha?, ¿por qué? • ¿Cuánto es lo máximo a lo que puede aumentar p?, ¿cómo lo supiste? 8 2 N cm p 0,3 0,5 1 3 4,5 6 7 13,87 13,69 13,23 11,18 9,35 7,07 5 v = p 5 8 ⋅ − Glosario fluido incompresible: es cualquier fluidocuyadensidadpermanececons- tante en el tiempo. Un newton (N) es la unidad de fuerza en el Sistema Internacional de Unidades. Es la fuerza necesaria para proporcionar una aceleración de 1 a un objeto de 1 kg de masa. m s2 Recuerda que... v P1 p UNIDAD 2 (54-105)C:Maquetación 1 4/11/10 17:13 Página 90
- 92. Función cuadrática y función raíz cuadrada | 91 Por otra parte, sabemos que no podemos calcular la raíz cuadrada de un número negativo, por lo que obligatoriamente 8 – p 0. Eso significa que 8 p, así que la máxima presión que se puede medir en la zona estrecha es 8. Esto tiene sentido físico, ya que la presión en la zona estrecha no puede ser mayor que la presión en el resto del tubo, que era 8. En ocasiones como la planteada, hay que considerar colectivamente a raíces cuadradas de varios números. Así como, al tratar colectiva- mente los cuadrados de varios números, se definió la función cuadrática, en este caso, definimos la función raíz cuadrada por f(x) = , con la restricción de x 0, es decir, con dominio R0 + . Ob- serva su gráfico. A partir del gráfico podemos ver que la función solo existe para los valores positivos de x, esto se debe a que, como concluimos ante- riormente, su dominio es el conjunto de los números reales posi- tivos y el cero. También se puede apreciar en el gráfico que su recorrido es R0 + , ya que los resultados de las raíces cuadradas nunca son valores negativos. Además, es una función creciente en todo su dominio, ya que si 0 a b, entonces . Sabemos que la raíz cuadrada está relacionada con las potencias de exponente 2; del mismo modo, la función cuadrática está es- trechamente relacionada con la función raíz cuadrada. Anteriormente realizamos un análisis gráfico de la función lineal y la cuadrática; comparemos ahora estas importantes funciones con la función raíz cuadrada. Vimos que a medida que aumentamos el valor de x, los valores de y en g(x) = x2 crecen o decrecen cada vez más rápido en comparación a h(x) = x, ¿pero qué ocurre en el caso de f(x) = ? x a b x Unidad 2 + UNIDAD 2 (54-105)C:Maquetación 1 4/11/10 17:13 Página 91
- 93. 92 | Unidad 2 Podemos ver en el gráfico que la función f(x) = es creciente, ya que si a b, entonces acelerado que la función h(x) = x y que g(x) = x2 , los valores de crecen de manera más lenta, ya que x x2 . Para los valores de 0 x 1 se tiene que x x2 , o sea, para todo x en este intervalo el valor de la función raíz cuadrada es mayor al de la función lineal y cuadrática. En x = 1, las tres fun- ciones valen lo mismo, por lo que el punto (1, 1) es donde se inter- secan las funciones dadas. Si observamos el gráfico, veremos que la función f(x) = la obte- nemos dibujando la gráfica simétrica a la rama de la función cuadrática para x 0 respecto a la recta h(x) = x. A cada punto (x, y) de la gráfica de g(x) = x2 le corresponde en f(x) = el punto que resulta de intercambiar sus coordenadas, es decir, (y, x). De modo similar al visto para analizar los desplazamientos de una función cuadrática, podemos analizar los correspondientes a una función raíz cuadrada. La función que corresponde a desplazar la función f(x) = en 兩a兩unidades horizontalmente (hacia la derecha si a 0 y hacia la izquierda si a 0) y 兩b 兩 unidades verticalmente (hacia arriba si b 0 y hacia abajo si b 0) es f(x) = . x a b – + x x x x x x x g(x) En resumen • La función raíz cuadrada se define por f(x) = , con dominio y recorrido IR+ 0 . • Es una función creciente en todo su dominio. • Cada par ordenado (a, b) de la gráfica de cumple que a 0 y b 0, y el par ordenado (b, a) pertenece a la gráfica de la función f (x) = x2 . x x , pero para x 1 el crecimiento es menos a b UNIDAD 2 (54-105)C:Maquetación 1 4/11/10 17:13 Página 92
- 94. Función cuadrática y función raíz cuadrada | 93 Unidad 2 1. Dada la función f (x) = , ¿entre qué valores varía f(x), si x toma valores: a. entre 0 y 0,2? d. entre 12 y 14? b. entre 0,5 y 0,7? e. entre 50 y 60? c. entre 1 y 3? f. entre 100 y 400? 2. En la expresión matemática T = se relacionan dos magnitudes, donde I es la longitud del péndulo (m) y T es el período (s). Construye una tabla de valores y grafica la función. Luego, analiza la relación que se da entre I y T. a. Si la longitud del péndulo es de 1 m, el tiempo de oscilación es aproximadamente 2 s. Si se duplica la longitud, ¿en cuánto aumentará el período? b. Si la longitud del péndulo es de m, ¿cuánto es T?, ¿y si la longitud es de m? c. Si el tiempo empleado por el péndulo es de s, ¿cuál es la longitud del mismo? d. ¿Qué sucede si alargas la longitud del péndulo? 3. ¿Cuál es la expresión que determina el lado de un cuadrado que tiene por área m2 ?, ¿y m2 ? 4. Determina el dominio, recorrido y gráfica de las siguientes funciones. Explica, paso a paso, cómo lo hiciste. a. f (x) = 3 + e. f (x) = 4 i. b. f. f (x) = 1 – j. f (x) = 3 – c. g. f (x) = 4 – k. f (x) = 2 + 2 d. h. f (x) = – 4 l. f (x) = 2 + 5. Para cada función determina si es creciente o decreciente. Explica cómo lo supiste. a. f (x) = c. f (x) = –2 e. f (x) = b. f (x) = 3 + d. f (x) = f. f (x) = 4 + 3 2 1 x + x − 5 x 5 − x x x + 2 x x f x = ( ) 2 x x x f x = x + ( ) 4 5 − x x f x = x ( ) − 2 f x = + + x ( ) 2 2 x x 2 2 2 2 12 3 3 2 2 I x Actividades UNIDAD 2 (54-105)C:Maquetación 1 4/11/10 17:13 Página 93
- 95. 94 | Unidad 2 Herramientas tecnológicas GeoGebra es un software libre que relaciona aritmética, geometría, álgebra y cálculo. Por una parte, es un sistema de geometría interactiva en el que se pueden construir puntos, vectores, segmentos, rectas, secciones cónicas y funciones, y luego modificarlas dinámicamente. Pero también se pueden ingresar las ecuaciones y coordenadas directamente y, después, obtener las gráficas correspondientes. Esto permite construir y analizar gráficos de diversas funciones. Para utilizar este programa ingresa a www.geogebra.org/cms/es. Pulsa el botón Descarga, y luego haz clic en el botón Applet Start. De este modo podrás trabajar con este software sin tener la necesidad de instalarlo en tu computador. Para abrir el programa, haz doble clic en el icono GeoGebra_3_2_0_0.exe. • Para graficar una función, se debe escribir la que se necesita graficar en la celda Entrada, ubicada en la parte inferior de la ventana. Si quieres que tenga un nombre especial, como v(x) para velocidad, pones v(x) = y a continuación la expresión de la función. • Si la función tiene potencias, los exponentes se escriben usando el símbolo ^. Por ejemplo, para graficar 3x2 + 4 se escribe 3x^2+4 y se presiona Enter. • Para graficar varias funciones simultáneamente, solo agrégalas una después de la otra. Ahora vamos a usar GeoGebra para graficar parábolas, tanto de funciones cuadráticas como de raíces. UNIDAD 2 (54-105)C:Maquetación 1 4/11/10 17:13 Página 94
- 96. Función cuadrática y función raíz cuadrada | 95 Unidad 2 1. Grafica juntas las funciones cuadráticas f (x) = x2 – 3 y g(x) = x2 + 2x – 3 y responde: a. Escribe las funciones cuadráticas del modo adecuado para GeoGebra e ingrésalas en el programa. b. ¿En qué punto se intersecan?, ¿por qué? c. Según la gráfica, ¿cuál es el recorrido de cada función? d. Comprueba tus respuestas mediante las técnicas aprendidas en las secciones anteriores. 2. Grafica juntas las tres funciones cuadráticas f (x) = x2 , g(x) = 2x2 y h(x) = 0,5x2 . En GeoGebra los decimales se ingresan con punto en vez de coma, es decir, 0,5x2 se ingresa como 0.5x^2. a. ¿Qué observas?, ¿puedes explicarlo usando la materia anterior? b. ¿Cuáles son dilataciones y cuáles contracciones de la gráfica de x2 ? c. ¿Dónde está el vértice de cada función? d. Todas crecen a la derecha de su vértice, pero ¿crece h(x) más rápido que f (x)? 3. Grafica en GeoGebra juntas las funciones f (x) = 1 + y g(x) = 1 – . Considera, sin ya que se usa la abreviatura de square root, sqrt, por “raíz cuadrada” en inglés. a. ¿Qué observas al graficar juntas f (x) y g(x)? Explica. b. Toma la inversa de f (x) y la inversa de g(x), y compáralas con h(x). ¿Qué observas? c. En la misma gráfica donde graficaste f (x) y g(x), haz ahora la gráfica de h(x). ¿Es lo que esperabas?, ¿por qué? x x graficar, la función cuadrática h(x) = (x – 1)2 . Para graficar 1 + debes ingresar 1+sqrt(x), x UNIDAD 2 (54-105)C:Maquetación 1 4/11/10 17:13 Página 95
- 97. 96 | Unidad 2 • En el siguiente mapa conceptual se muestran algunos de los conceptos presentados hasta ahora en la Unidad. • Utilizando los contenidos aprendidos en la Unidad, y apoyándote en el esquema anterior, responde en tu cuaderno: 1. ¿Crees que faltó un concepto importante en el mapa conceptual?, ¿cuál? Agrégalo. 2. ¿Qué relación hay entre ecuaciones de segundo grado y funciones cuadráticas? 3. ¿Cuántas soluciones puede tener una ecuación de segundo grado? 4. ¿En qué debes fijarte para saber cuántas soluciones tiene una ecuación de segundo grado? 5. ¿Qué relación hay entre completación de cuadrados y las soluciones de una ecuación de segundo grado de discriminante positivo? 6. ¿Qué relación hay entre el vértice de la gráfica de una función cuadrática y las soluciones que pueda tener? 7. ¿Qué relación hay entre los coeficientes a, b y c en ax2 + bx + c = 0 y sus soluciones? 8. ¿Tienes alguna duda sobre conceptos tratados en las páginas anteriores?, ¿cuál? Compártela con tu curso e intenten aclararla en conjunto. es de la forma mediante permite decidir se relaciona con ECUACIÓN DE SEGUNDO GRADO ax2 + bx + c = 0 DISCRIMINANTE Δ = b2 – 4ac CANTIDAD Y NATURALEZA DE LAS SOLUCIONES FUNCIÓN RAÍZ CUADRADA Organizando lo aprendido su dominio es su recorrido es FUNCIÓN CUADRÁTICA IR0 IR0 es la forma de f (x) = x + + UNIDAD 2 (54-105)C:Maquetación 1 4/11/10 17:13 Página 96
- 98. Función cuadrática y función raíz cuadrada | 97 Unidad 2 1. Determina la cantidad de soluciones de las siguientes ecuaciones mediante el discriminante: a. x2 – 8x + 5 = 0 c. 2x2 + 4x + 3 = 0 b. 3x2 + 6x + 3 = 0 d. 2. Resuelve las siguientes ecuaciones, si tienen solución: a. x2 – 8x + 15 = 0 c. 14x – x2 – 49 = 0 e. x2 – 6x + 14 = 0 b. 2x2 – 6x + 4 = 0 d. 2x2 + 4 x – 18 = 0 f. –3x2 + 6x – 2 = 0 3. Determina en cada caso la función cuadrática f(x) = ax2 + bx + c con los datos dados: a. Sus raíces son 3 y 7 y su vértice es (5, 8). b. Sus raíces son –1 y 4 y la ordenada de su vértice es –6. c. Sus raíces son 0 y 12 y el punto (3, 3) pertenece a su gráfica. d. Una de sus raíces es 9 y el vértice es (2, –4). 4. Resuelve cada ecuación y explica el procedimiento utilizado. a. x4 – 20x2 + 64 = 0 b. 2x4 + 2x2 – 4 = 0 c. 5. ¿Cuál debe ser el valor de k para que la función cuadrática f(x) = 2x2 + kx – 4 tenga como eje de simetría la recta x = –1? A. 2 B. –2 C. –1 D. –4 E. 4 3 x x x x − + − = 1 1 73 24 1 4 3 2 0 2 x x = − + Mi progreso • Verifica en el solucionario si tus respuestas son correctas. Si tuviste respuestas incorrectas, marca en la tabla el criterio correspondiente y revisa las páginas indicadas. Luego, identifica el error y corrígelas. ¿Cómo voy? CRITERIO ÍTEMS PÁGINAS DONDE SE TRABAJA Determinar la cantidad de soluciones de una ecuación de segundo grado a partir de su discriminante. 1 76 a 79 Resolver ecuaciones de segundo grado. 2 y 4 76 a 79 Formular una función cuadrática a partir de sus raíces y un punto de ella. 3 80 a 87 Completar una función cuadrática a partir de su eje de simetría. 5 84 a 87 UNIDAD 2 (54-105)C:Maquetación 1 4/11/10 17:14 Página 97
- 99. Observa, paso a paso, las estrategias utilizadas en la resolución de los siguientes problemas. Ejercicio Determina cuál es la mayor superficie rectangular que se puede cercar con 100 metros de alambre de púas. ¿Cómo relacionarías este proble- ma con el de encontrar máximos y mínimos? Solución La superficie rectangular deberá tener 100 m de perímetro, si nom- bramos por x e y los lados del rectángulo tendremos que: 2x + 2y = 100 x + y = 50 La superficie del rectángulo estará dada por la expresión x · y; sin embargo, para poder resolver el problema debemos dejar la super- ficie en función de una sola variable. Observa la figura. x + y = 50 y = 50 – x Luego, la superficie del rectángulo en función de su largo x está dada por la expresión: s(x) = x(50 – x) s(x) = 50x – x2 s(x) = – x2 + 50x Observa que la función que representa la superficie del rectángulo es una función cuadrática, por lo tanto su gráfica es una parábola. Como en la función cuadrática s(x) = – x2 + 50x, a 0, la parábola se abrirá hacia abajo, por lo que la superficie del rectángulo alcanzará un valor máximo en , luego, para calcular este máximo debemos obtener . x b a = − 2 Cómo resolverlo 98 | Unidad 2 x y x 50 – x s b a − ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ 2 simplificamos despejamos el valor de y UNIDAD 2 (54-105)C:Maquetación 1 4/11/10 17:14 Página 98
- 100. Entonces, el largo del rectángulo para que su superficie sea máxima será: , remplazando el valor de x obtenemos el largo y = 50 – x y = 50 – 25 y = 25 Para responder a la pregunta inicial y encontrar la mayor superficie rectangular que se puede cercar con 100 metros de alambre de púas, calculamos . Por lo tanto, la mayor superficie que se puede cercar es un cuadrado de 25 m de lado, y la superficie total será 625 m2 . s b a − ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ 2 x b a = − = − − = 2 50 2 25 Función cuadrática y función raíz cuadrada | 99 Unidad 2 Actividades 1. Aplica el procedimiento aprendido para resolver las siguientes situaciones: a. ¿Cuáles son las dimensiones del rectángulo de mayor área que se puede inscribir en una circunferencia de radio r?, ¿cómo lo supiste? b. Para la fabricación de canaletas para aguas lluvia se dispone de láminas de 40 cm de ancho. ¿De qué medida se deben hacer los dobleces de modo que se obtenga una canaleta de máxima capacidad? 2. Busca un procedimiento distinto para resolver los problemas anteriores y compáralo con el que te presentamos. ¿Cuál es más simple?, ¿por qué? 3. Resuelve el siguiente problema empleando el método aprendido u otro. Compara el procedimiento que utilizaste con el de algún compañero o compañera. ¿Cuál es más simple?, ¿por qué? • Un granjero dispone de 210 m de malla para delimitar dos corrales adyacentes rectangulares idénticos. ¿Cuáles deben ser las dimensiones para obtener el área máxima? s b a s − ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ = ( ) = − + ⋅ = − + = 2 25 25 50 25 625 1250 625 2 UNIDAD 2 (54-105)C:Maquetación 1 4/11/10 17:14 Página 99
- 101. 100 | Unidad 2 En terreno El agua en movimiento En la naturaleza se pueden observar parábolas al lanzar objetos al aire. Sin em- bargo, donde mejor se distinguen, sin necesitar equipos sofisticados o filmar esce- nas, es en el agua lanzada hacia arriba, pero no totalmente vertical. El efecto tiene que ver con que la velocidad de salida tiene un componente vertical, el que veríamos al mirar en la misma dirección en que sale el chorro de agua, y un com- ponente horizontal, el que vería alguien desde arriba hacia abajo. El movimiento vertical hacia arriba se modela por y(t) = va t – t2 , donde t son los segundos trans- curridos desde que comenzó a subir, y(t) la altura a los t segundos, va la compo- nente vertical de la velocidad, y g es la aceleración de gravedad, que aproximamos ahora por 10 . Por otro lado, el movimiento horizontal viene dado por x(t) = vh t, donde vh es la velocidad horizontal. De este modo, verticalmente el objeto sube, llega a un máximo, y luego baja, a la vez que se mueve horizontalmente con veloci- dad constante. Eso produce el efecto de una parábola. m s2 g 2 UNIDAD 2 (54-105)C:Maquetación 1 4/11/10 17:14 Página 100
- 102. Actividades 1. Supón que va = 30 y vh = 40 . Despeja t en x = vh t y remplaza ese valor de t en y = va t – t2 . Verifica que el resultado es una función cuadrática y analiza su gráfica usando lo aprendido en la Unidad. 2. ¿Qué pasa con la gráfica si vh = –40 ?, ¿qué significado físico tiene? Investiguemos... Ahora, trabajen en grupos de tres personas. 1. Busquen dónde usar una manguera de riego sin estropear nada ni mojarse. 2. Manteniendo un chorro de agua razonable, ni muy débil ni muy fuerte, apunten primero en dirección horizontal y luego vayan apuntando cada vez más hacia la vertical, poco a poco. 3. Registren varias posiciones del vértice que observen, con coordenada x en cm horizontales desde la salida del chorro de agua, y con coordenada y en cm verticales. 4. Registren la tabla de valores. Los pares de valores, ¿pertenecen la gráfica de una parábola?, ¿qué carac- terística notan? 5. ¿Con qué inclinación, aproximadamente, se obtiene el vértice más alto? 6. ¿Con qué inclinación aproximadamente se obtiene el arco más largo (que el agua llegue más lejos). 7. Como la rapidez del agua al salir de la manguera es siempre la misma, ¿cómo explican que la altura haya cambiado?, ¿qué parte de la fórmula de y(t) cambió al ir aumentando la inclinación con que salía? 8. ¿Hay alguna posibilidad de que la parábola resultante tenga por gráfica a una parábola abierta hacia arriba?, ¿qué tendría que cambiar en las fórmulas dadas para x (t) e y(t) para tener vértice como mínimo?, ¿es posible? 9. El vértice ocurre exactamente a la mitad del tiempo que demora el agua en volver a la misma altura desde la que salió. Justifícalo, basándote en el análisis de la gráfica de la parábola obtenida con variables x e y, al eliminar la variable t. Evaluemos nuestro trabajo • Comparen los resultados obtenidos con los de sus compañeros y compañeras. ¿Son similares? Si no es así, ¿qué diferencias hubo?, ¿son errores o pueden explicarse por las diferencias en las circunstan- cias al medir? • Indaguen sobre el lanzamiento de proyectiles, y verifiquen las conclusiones que obtuvieron antes. cm s cm s cm s Función cuadrática y función raíz cuadrada | 101 Unidad 2 3. Intercambiando las velocidades, supón que va = 40 y vh = 30 . ¿Qué pasa con la gráfica?, ¿dónde tiene el máximo? cm s cm s UNIDAD 2 (54-105)C:Maquetación 1 4/11/10 17:14 Página 101
- 103. 102 | Unidad 2 Síntesis de la Unidad A continuación, se presentan los conceptos fundamentales trabajados en la Unidad. Construye con ellos un mapa conceptual en tu cuaderno. No olvides agregar las palabras de enlace que indican las relaciones que hay entre los conceptos. A partir de lo trabajado en la Unidad, responde: 1. ¿Crees que faltó un concepto importante en el mapa conceptual?, ¿cuál? Agrégalo. 2. ¿Las parábolas son funciones crecientes? Explica. 3. ¿Qué estrategia se puede utilizar para resolver una ecuación de segundo grado? Explica paso a paso. 4. ¿Qué relación hay entre las soluciones de una ecuación cuadrática y el gráfico de una parábola? 5. ¿Cuál es el dominio y recorrido de una función cuadrática? Explica. 6. ¿Cuál es el dominio y recorrido de la función raíz cuadrada? 7. ¿Qué relación hay entre el discriminante de una ecuación de segundo grado y las soluciones de esta? 8. ¿Qué relación hay entre los ceros de una función cuadrática y el vértice de la parábola asociada a esta? 9. ¿Tienes alguna duda sobre los conceptos tratados en las páginas anteriores?, ¿cuál? Compártela con tu curso e intenten aclararla en conjunto. PARÁBOLA VÉRTICE DISCRIMINANTE INTERSECCIÓN CON EJE X FUNCIÓN RAÍZ CUADRADA ECUACIÓN DE SEGUNDO GRADO RAÍCES O CEROS DE LA FUNCIÓN MÁXIMOS Y MÍNIMOS FUNCIONES CUADRÁTICAS UNIDAD 2 (54-105)C:Maquetación 1 4/11/10 17:14 Página 102
- 104. Función cuadrática y función raíz cuadrada | 103 Evaluación I. Determina si las expresiones siguientes son verdaderas o falsas. Justifica tu respuesta. 1. El vértice de toda parábola es el mínimo de esta. 2. Toda ecuación cuadrática con discriminante positivo es un múltiplo del producto entre la variable restada con cada raíz. 3. El discriminante es el valor de la primera coordenada del vértice. 4. La cantidad de raíces de una ecuación de segundo grado depende del signo del discriminante. 5. La función raíz tiene por gráfica a una rama de parábola, en sentido horizontal. 6. La abscisa del vértice es igual a la semisuma de las raíces de la ecuación cuadrática. 7. La ecuación de segundo grado tiene por soluciones al máximo y el mínimo de la parábola. 8. Las raíces de la función cuadrática son las raíces cuadradas de los coeficientes a, b y c. II. Aplica lo aprendido en la Unidad para desarrollar las siguientes actividades: 1. Grafica la parábola correspondiente a cada una de las siguientes funciones: a. f (x) = x2 – 8x + 12 f. f (x) = 2x2 – x – 1 b. f (x) = –x2 + 4x + 5 g. f (x) = 2(x – 1)2 + 3 c. f (x) = 2x2 h. f (x) = 2 – 3x – x2 d. f (x) = x2 – 1 i. f (x) = (x – 2)(x – 4) + 1 e. f (x) = x2 + 25 j. f (x) = (x + 1)(x – 3) + 5 2. Determina la función que le corresponde a la parábola de la función f (x) = x2 – 2x – 3, después de trasladar el vértice al punto (2, 3) y orientar su concavidad hacia abajo. 3. Halla los posibles valores que puede tener k para que: a. La ecuación –x2 + x = k tenga sus raíces iguales. b. La ecuación 3x2 + k = 0 no tenga solución en los números reales. c. La ecuación x2 + x = 5k tenga dos raíces reales distintas. d. La ecuación 2x2 – 3x + k = 0 tenga la misma cantidad de raíces reales que la ecuación 2(x2 + 1) – 3x = 4x. 4. Se lanza un proyectil hacia arriba con una velocidad inicial de 40 , desde 20 m de altura sobre el suelo. Cuando han transcurrido t segundos desde el lanzamiento, su altura está dada por la función f (t) = –t2 + 40t + 20. a. Determina la altura máxima que alcanza. b. Determina el tiempo que demora en alcanzar la altura máxima. m s Unidad 2 UNIDAD 2 (54-105)C:Maquetación 1 4/11/10 17:14 Página 103
- 105. 104 | Unidad 2 1. (DEMRE,2004) Si ,entonces el valor de y cuando x = –3 es: A. –8 B. 8 C. 2 D. 1 E. –2 2. (DEMRE, 2003) El largo de una piscina rec- tangular es el doble de su ancho. Se cons- truyó una cerca, rodeándola, separada un metro de sus bordes. Si el área cercada es de 40 m2 , ¿cuál es el largo de la piscina de la figura? A. 3 m B. 6 m C. 12 m D. m E. m 3. Los números –3 y 2 son raíces de: A. x2 – 5x + 6 = 0 B. x2 + x + 6 = 0 C. x2 – x + 6 = 0 D. x2 + 2x + 6 = 0 E. x2 + x – 6 = 0 4. (DEMRE, 2003) El área de un rectángulo es 2x2 + 2x – 24. Si uno de los lados mide (x – 3), el otro mide: A. (x + 8) B. 2(x + 8) C. 2(x – 4) D. 2(x – 3) E. 2(x + 4) 5. Si r1 y r2 son las raíces de la ecuación x2 – 5x – 6 = 0, es igual a: A. B. C. D. E. 6. La suma de las raíces de la ecuación 2x2 – 21x + 12 = 0 es: A. B. C. D. 21 E. 41 1 1 1 2 r r + 80 − + 3 165 2 y x x x = − + + 1 2 1 2 III. Marca la opción correcta en cada caso. 1 m 1 m 1 m 1 m − 5 6 − 4 3 5 6 4 3 5 3 − 21 2 12 2 21 2 UNIDAD 2 (54-105)C:Maquetación 1 4/11/10 17:14 Página 104
- 106. Función cuadrática y función raíz cuadrada | 105 7. La función asociada al gráfico es: A. f (x) = –4x2 + 4x – 3 B. f (x) = 4x2 + 4x – 3 C. f (x) = 4x2 – 4x + 3 D. f (x) = –4x2 – 4x + 3 E. f (x) = 4x2 + 4x + 3 8. La ecuación x2 – 17x + 50 = 0 tiene: I. dos raíces reales e iguales. II. dos raíces reales y distintas. III. no tiene raíces reales. De estas afirmaciones es o son verdaderas: A. Solo I B. Solo II C. Solo III D. I y II E. Ninguna de las anteriores. 9. El lado de un triángulo isósceles mide tres metros más que su base. Su altura mide 12 m. El área es: A. 23 m2 B. 60 m2 C. 65 m2 D. 120m2 E. 130 m2 10. El discriminante de la ecuación cuadrática 3x2 – x + k = 0 es 25, entonces el valor de k es: A. –2 B. C. D. 2 E. 4 11. El vértice de la parábola representada por la función f (x) = 2x2 – 1 es: A. (0, 0) B. (0, 2) C. (0, –1) D. (0, –2) E. (0, 1) 12. Si un sitio rectangular tiene un área de 448 m2 y el largo mide 4 m más que el doble de su ancho, su perímetro es: A. 14 m B. 32 m C. 46 m D. 92 m E. Faltan datos. 13. Al resolver la ecuación se obtiene: A. 30 B. 40 C. 5 D. 25 E. 2 x – 5 5 = Unidad 2 Verifica en el solucionario de tu Texto si tus respuestas son correctas. ¿Te equivocaste en alguna?, ¿cuál fue el error? Explícalo y resuelve correctamente el ejercicio. − 1 5 1 4 UNIDAD 2 (54-105)C:Maquetación 1 4/11/10 17:14 Página 105
- 107. El triángulo rectángulo y la trigonometría 3 106 |Unidad 3 Teorema de Euclides Demostraciones de teorema de Pitágoras Tríos pitagóricos Razones trigonométricas Funciones trigonométricas Sistemas de medición de ángulos Ecuaciones trigonométricas Resolver problemas que involucren propiedades de los triángulos rectángulos. Reconocer la necesidad de la demostración en Matemática. Conocer la historia del teorema de Fermat-Wiles y los tríos pitagóricos. Conjeturar y demostrar propiedades geométricas en triángulos rectángulos semejantes. Reconocer las razones trigonométricas en familias de triángulos rectángulos semejantes. Resolver ecuaciones que involucran razones trigonométricas. TRABAJANDO CON: APRENDERÁS A: UNIDAD 3 (106-163)C :Maquetación 1 4/11/10 17:15 Página 106
- 108. El triángulo rectángulo y la trigonometría| 107 Conversemos de... El sextante es un instrumento que permite determinar el ángulo entre dos objetos. Este instru- mento ha sido, durante varios siglos, de gran importancia en la navegación marítima, ya que conociendo el ángulo de elevación al Sol y la hora del día es posible determinar, mediante cálculos sencillos, la posición exacta en la que se encuentra un navegante en el océano. El nombre sextante proviene de la escala del instrumento, que abarca un ángulo de 60 grados, o sea, un sexto de un círculo completo. • Si utilizamos un sextante y medimos el ángulo al Sol a dos horas del día distintas, ¿obtendremos el mismo resultado en ambos casos?, ¿por qué? • ¿Qué instrumentos de medición de ángulos conoces?, ¿cómo se utilizan? • ¿Qué herramientas matemáticas conoces que relacionen el ángulo de elevación al Sol, con la distancia entre este y un punto de la Tierra? Latinstock UNIDAD 3 (106-163)C :Maquetación 1 4/11/10 17:15 Página 107
- 109. 108 | Unidad 3 ¿Cuánto sabes? 1. Determina, a partir del triángulo rectángulo de la figura, si las siguientes relaciones son verdaderas o falsas. Justifica tu decisión. a. a2 + b2 = c2 b. b2 = c2 + a2 c. a2 = c2 – b2 d. b2 = a2 – c2 2. Encuentra la medida del tercer lado en los siguientes triángulos. Explica cómo lo calculaste. a. b. c. d. 3. Dadas las figuras, calcula las medidas de los lados desconocidos. a. b. c. 4. Fernanda mide 1,5 m; a las 4 de la tarde de un día, su sombra mide 4,05 m; en ese mismo instante, la sombra de un árbol mide 15,12 m. a. Explica cómo se puede calcular la altura del árbol usando semejanza de triángulos. b. Calcula la altura del árbol. 5. En la figura, AC // BD, OA = 8 cm; OC = 6 cm; AB = 12 cm, ¿cuánto mide CD?, ¿cómo lo calculaste? Recuerda lo que aprendiste en años anteriores y resuelve en tu cuaderno. b c a x x x x B O A C D B A C E D y s t 4 cm 17 m 3 cm 13 cm 34 cm 30 cm 40 cm 12 cm 30 cm 10 m 18 m 15 cm 15 cm 5 3 m 12 cm 12 cm 12 cm 8 m ABCD paralelogramo UNIDAD 3 (106-163)C :Maquetación 1 4/11/10 17:16 Página 108
- 110. 6. Encuentra la mayor cantidad posible de parejas de triángulos semejantes e indica, en cada caso, el criterio que fundamenta la semejanza. Verifica en el solucionario de tu Texto si tus respuestas son correctas. ¿Te equivocaste en alguna?, ¿cuál fue el error? Explícalo y resuelve correctamente el ejercicio. El triángulo rectángulo y la trigonometría | 109 Unidad 3 ¿Qué debes recordar? • En un triángulo, la suma de sus ángulos interiores es igual a 180°. • Un triángulo rectángulo es aquel que tiene un ángulo recto. El lado opuesto al ángulo de 90º se llama hipotenusa, y los lados que forman el ángulo recto se llaman catetos. • Teorema de Pitágoras. En todo triángulo ABC, rectángulo en C, se cumple que: c2 = a2 + b2 . • Dos triángulos ABC y A´B´C´ son semejantes si ⬏A = ⬏A’, ⬏B = ⬏B’, ⬏C = ⬏C´, y, además, = = . • Criterios de semejanza: ΔABC ~ ΔA´B´C´ si: • tienen sus lados proporcionales = = = (LLL). • tienen dos pares de ángulos iguales (AA). • tienen dos pares de lados proporcionales y el ángulo comprendido por ellos igual (LAL). CA C´A´ BC B´C´ AB A ´B´ CA C´A ´ BC B´C´ AB A ´B´ Cateto Hipotenusa Cateto B C C A B B´ C´ A ´ A c b a 88º 59º 65º 65º 88º 33º 30º 30º 12 cm 50º 10 cm 8 cm 6 cm 7 cm 10 cm 8 cm 8 cm A B M O N J G H W X V T U S C F E J K P R Q L D UNIDAD 3 (106-163)C :Maquetación 1 4/11/10 17:16 Página 109
- 111. 110 | Unidad 3 Teorema de Euclides Analicemos... El canopy es uno de los deportes de aventura más difundidos en el último tiempo en el sur de nuestro país. Este consiste, básicamente, en lanzarse por un cable, atado, a grandes distancias y diferentes alturas, mediante una polea y un arnés sostenido a ella. Supongamos que tenemos una instalación de este deporte y que se puede representar en la siguiente figura: En la situación anterior, tenemos que para que CD sea lo menor posible, debe ser perpendicular a AB; por lo tanto, la distancia que debe desplazarse la polea corresponderá a la longitud del seg- mento BD. Observa que el triángulo ABC es rectángulo en C, y el triángulo CBD es rectángulo en D; luego, ambos triángulos tienen en común el ángulo correspondiente al vértice B y al ángulo recto, es decir, tienen dos pares de ángulos iguales. Recordando los criterios de semejanza de triángulos tendremos que, por el criterio AA,ΔABC ~ ΔCBD. En consecuencia, sus lados son proporcionales, o sea, el cociente entre los lados correspondientes es constante: = como BC = 9 m y AB = 15 m obtenemos = , de donde podemos determinar la medida del lado del triángulo buscada: BD = = 5,4 m. Por lo tanto, la polea debe desplazarse 5,4 metros para que la dis- tancia a CD sea la menor posible. 81 15 9 15 BD 9 BC AB BD BC • ¿Qué relación existe entre los triángulos BAC y CBD?, ¿por qué? • ¿Cuánto debe desplazarse la polea, suponiendo que esta se en- cuentra en el vértice B del triángulo, para que la distancia entre D y C sea la menor posible?, ¿cómo lo supiste? Si dos triángulos ABC y A`B`C` tienen dos pares de ángulos iguales (AA), entonces se tendrá que ΔABC ~ ΔA`B`C`, es decir, los triángulos son semejantes. Recuerda que... B C D A 9 m 15 m Padre e hijo practicando canopy. UNIDAD 3 (106-163)C :Maquetación 1 4/11/10 17:16 Página 110
- 112. El triángulo rectángulo y la trigonometría | 111 Unidad 3 Este resultado se puede generalizar para todo triángulo rectángulo. Observa. Al trazar la altura h sobre la hipotenusa c de un triángulo rectángulo y considerar los segmentos p y q que la altura deter- mina sobre la hipotenusa, correspondientes a las proyecciones de los catetos a y b respectivamente, se obtiene: ΔABC ~ ΔCBD, pues ⬏ACB = ⬏CDB = 90º ⬏CBA = ⬏DBC. Por criterio AA, los triángulos son semejantes. ΔABC ~ ΔACD, pues ⬏ACB = ⬏ADC = 90º ⬏CAB = ⬏DAC. Por criterio AA, los triángulos son semejantes. Por lo tanto, los tres triángulos son semejantes. Luego, ΔABC ~ ΔCBD ⇒ = ⇒ = ⇒ a2 = p · c ΔCBD ~ ΔACD ⇒ = ⇒ = ⇒ h2 = p · q Hemos obtenido tres relaciones importantes relativas a los triángu- los rectángulos. Estas relaciones son conocidas como el teorema de Euclides. p h h q DB DC CD AD c a a p AB CB BC BD En resumen En todo triángulo rectángulo se cumple que: • el cuadrado de la altura sobre la hipotenusa es igual al producto de las proyecciones de los catetos sobre la hipotenusa. • el cuadrado de un cateto es igual al producto de la hipotenusa por la proyección del cateto so bre la hipotenusa. Es decir, La primera relación en el teorema de Euclides es conocida como el teorema de la altura, y la segunda, como el teorema del cateto. Glosario proyección: dado un segmento AB y una recta L que contiene al punto A,la proyección de AB sobre L es el segmento AC tal que BC es perpen- dicular a L. C A D B B C A L h p q b a c c ΔABC ~ ΔACD ⇒ = ⇒ = ⇒ b2 = q · c c b b q AB AC AC AD h2 = p · q a2 = p · c b2 = q · c C A p q D B h b a UNIDAD 3 (106-163)C :Maquetación 1 4/11/10 17:16 Página 111
- 113. 112 | Unidad 3 1. Dados unos triángulos rectángulos de catetos a y b, donde h es la altura y p y q las proyecciones de los catetos sobre la hipotenusa c, calcula los datos correspondientes para completar la tabla. 2. Los lados de un triángulo rectángulo miden 3 cm, 4 cm y 5 cm. Calcula la altura relativa a la hipotenusa y las dos proyecciones de los catetos. 3. En un rectángulo ABCD se traza desde A la perpendicular a la diagonal BD. Sabiendo que la diagonal queda dividida en dos segmentos que miden 4 y 9 cm, determina la medida de los lados del rectángulo. 4. La diagonal de un rectángulo mide 20 cm y la base es de 16 cm. Calcula la altura y el área del rectángulo. 5. En un triángulo rectángulo de área 30,4 cm2 , el producto de las proyecciones de los catetos sobre la hipotenusa es 9; calcula la altura de la hipotenusa. Haz un boceto del problema. 6. ¿Qué distancia hay entre el origen y la recta que pasa por (0, 5) y (3, 0)? Utiliza la figura para responder. 7. De acuerdo a la figura: a. ¿Hay triángulos semejantes?, ¿cuáles? b. Si AB = 17 cm, BC = 8 cm, AC = 15 cm, ¿cuáles son las longitudes de los segmentos AD, DB y CD? c. Si AB = 14 cm y AC = 7 cm, ¿cuál es la longitud del segmento AD? d. Si AD = 9 cm y DB = 3 cm, ¿cuál es la longitud del segmento CB? e. Si CD = 6 cm y DB = 12 cm, ¿cuál es la longitud del segmento AD? Actividades a b c p q h 8 cm 10 cm 6,4 cm 7,2 cm 2,3 cm 12,2 cm 5,73 cm 5 3 C D B A UNIDAD 3 (106-163)C :Maquetación 1 4/11/10 17:16 Página 112
- 114. El triángulo rectángulo y la trigonometría | 113 Unidad 3 8. El dueño de un terreno rectangular de 100 m de ancho por 250 m de largo desea construir su casa en uno de los vértices del terreno y, además, un puente sobre el río que cruza diagonal- mente el terreno. ¿A qué distancia de su casa estará el puente si desea ubicarlo lo más cercano posible a esta? 9. ¿Cuánto deben medir las vigas de un techo si ambas deben ser iguales y formar un ángulo de 90º y, además, si el ancho del techo es de 4 m?, ¿qué altura tiene el techo? 10. Completa, en tu cuaderno, la siguiente demostración alternativa del teorema de Euclides. En ΔCDA se tiene que b2 = q2 + h2 (1). En ΔCDB se tiene que ______________________ (2). En triángulo ABC se tiene que c2 = a2 + b2 (3). Además, sabemos que p + q = c (4). Sumamos las relaciones (1) y (2) y obtenemos (5). Remplazamos la relación (3) en la (5) y obtenemos (6). Utilizando la relación (4) en la relación (6), ¿qué deduces? Casa Río 4 m C A p q D B h b a c UNIDAD 3 (106-163)C :Maquetación 1 4/11/10 17:16 Página 113
- 115. 114 | Unidad 3 Demostraciones del teorema de Pitágoras Analicemos... Observa la siguiente figura, correspondiente a un triángulo rec- tángulo de catetos a y b, donde h es la altura y p y q, las proyecciones de los catetos sobre la hipotenusa c. Para encontrar las medidas de los catetos del triángulo de la figura, debemos encontrar una relación entre estos y sus proyecciones sobre la hipotenusa, ya que solo conocemos los valores de estas. Recordando el teorema de Euclides, podemos determinar la me- dida de los catetos del triángulo. Observa. a2 = p · c b2 = q · c Luego, sumando ambas ecuaciones obtenemos: a2 + b2 = p · c + q · c = (p + q) · c = c · c = c2 Es decir, a2 + b2 = c2 Como conocemos el valor de p y q, podemos determinar el de c, y de este modo calcular a2 + b2 . Observa que, utilizando el teorema de Euclides, obtuvimos la relación a2 + b2 = c2 , es decir, el teorema de Pitágoras. O sea, demostramos el teorema de Pitágoras utilizando el teorema de Euclides. • ¿Cómo podemos determinar la medida de los catetos del triángulo de la figura, conociendo solo los valores de p y q? • Si utilizamos las relaciones encontradas para determinar la medida de los catetos, ¿cuál es el valor de a2 + b2 ? C A B h p q b a c Factorizando por c Porque p + q = c B C A b c a UNIDAD 3 (106-163)C :Maquetación 1 4/11/10 17:16 Página 114
- 116. El triángulo rectángulo y la trigonometría | 115 Unidad 3 El teorema de Pitágoras es de los que cuentan con un mayor número de demostraciones distintas, utilizando diversos métodos, ya que en Matemática, en general, hay más de una forma correcta de lograr un resultado o una demostración. A continuación, veremos una demostración del teorema de Pitá- goras por medio de una demostración geométrica. Consideremos un cuadrado de lado a + b y un triángulo rectángulo cuyos catetos son a y b y la hipotenusa es c. Copiamos dos veces el cuadrado de lado a + b y, a continuación, copiamos el triángulo rectángulo haciendo coincidir sus lados, como se observa en las siguientes figuras. Luego, calculamos el área de los cuadrados a partir del área de las figuras que forman estos. Observa. (a + b)2 = c2 + 4 (a + b)2 = a2 + b2 + 4 Notemos que la figura 1 está formada por cuatro triángulos rectán- gulos congruentes de área a · b cada uno, y un cuadrado que tiene como lado la hipotenusa del triángulo; entonces, su área es c2 . La figura 2, en cambio, está formada por cuatro triángulos rec- tángulos congruentes de área a · b y dos cuadrados de lados iguales a los catetos del triángulo rectángulo; por lo tanto, el área de un cuadrado será a2 y el del otro será b2 . 1 2 a b · ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ 1 2 a b · ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ 1 2 1 2 En Matemática y otras ciencias, una demostración es un proceso por el cual, mediante una serie de razona- mientos lógicos, se llega a estable- cer la verdad de una proposición o teorema a partir de cierta hipótesis. Generalmente, cuando se hacen afirmaciones que representan mu- chos casos, como el teorema de Pitágoras, es imposible verificar caso a caso, por lo que la argu- mentación lógica es la única forma de justificar la proposición o teo- rema para todos los casos de una sola vez. Pon atención a + b b c c2 b2 a2 c b a a b a Figura 1 Figura 2 UNIDAD 3 (106-163)C :Maquetación 1 4/11/10 17:16 Página 115
- 117. ¿Qué tienen en común el cuadrado de lado c, de la figura 1, con los cuadrados de lados a y b, de la figura 2? El área del cuadrado de la figura 1 es equivalente a la suma de las áreas de los cuadrados de la figura 2, es decir, c2 = a2 + b2 , ya que ambas corresponden al área del cuadrado mayor menos cuatro veces el área del triángulo rectángulo. Esta es solo una de las demostraciones del teorema de Pitágoras, ya que, a través de los años, se han publicado muchas otras. Otra célebre demostración del teorema de Pitágoras es la que con- sidera los cuadrados construidos sobre cada lado de un triángulo rectángulo isósceles. Observa. La suma de las áreas de los cuadra- dos construidos sobre los catetos es a2 + b2 . Si cortamos dichos cuadra- dos por las líneas punteadas, podemos comprobar que estos coinciden, respectivamente, con el área total del cuadrado construido sobre la hipotenusa: c2 . La explicación o demostración formal se basa en que los triángu- los que se forman son todos congruentes. Observa las siguientes igualdades: AD = DB = DC ΔADC 艑 ΔDAM A partir de estas propiedades, se generaliza a los demás triángulos. Por lo tanto, c2 = a2 + b2 . También es posible demostrar el recíproco del teorema de Pitágoras, es decir: “Sea un triángulo ABC de lados a, b, y c, tales que c2 = a2 + b2 , en- tonces el triángulo ABC es rectángulo y su hipotenusa mide c”. Su demostración es de mayor complejidad que la correspondiente al teorema de Pitágoras, para la cual es necesario, por ejemplo, saber trigonometría. 116 | Unidad 3 Por teorema de Euclides Por criterio LAL b2 c2 a2 a b c D C M A B Aplicando el teorema de Euclides a un triángulo isósceles rectángulo, la medida de la altura sobre la hipo- tenusa es la mitad de la medida de la hipotenusa. Pon atención UNIDAD 3 (106-163)C :Maquetación 1 4/11/10 17:16 Página 116
- 118. El triángulo rectángulo y la trigonometría | 117 Unidad 3 1. Considerando el cuadrado ABCD: a. ¿Cuál es la medida de su superficie? b. ¿Cuál es el área de cada uno de los triángulos rectángulos? c. ¿Cuál es la longitud de cada lado del polígono blanco?, ¿qué tipo de polígono es?, ¿cuál es su área? d. Prueba el teorema de Pitágoras comparando los resultados obtenidos en a, b y c. 2. Copia en una hoja cuadriculada la siguiente figura. Si es necesario, amplíala. Luego, recorta por las líneas punteadas y completa el cuadrado construido sobre la hipotenusa con los polígonos A, B, C, D y E obtenidos, para verificar si se cumple el teorema de Pitágoras. 3. Si construyes una semicircunferencia sobre los lados de un triángulo rectángulo, tal como muestra la figura, ¿se verifica el teorema de Pitágoras? Explica. 4. Generalmente, se asocia el teorema de Pitágoras a la relación que hay entre los cuadrados construidos sobre los lados de un triángulo rectángulo. ¿Sucederá lo mismo si sobre los lados de un triángulo rectángulo construyes triángulos equiláteros? 5. Verifica el teorema de Pitágoras construyendo otro tipo de polígono sobre los lados de un trián- gulo rectángulo. ¿Qué condición deben cumplir estos polígonos? Comenta tus respuestas con tus compañeros y compañeras. Actividades D C A A B B C D E b c c c c b c a UNIDAD 3 (106-163)C :Maquetación 1 12/11/10 12:06 Página 117
- 119. 118 | Unidad 3 Tríos pitagóricos En el antiguo Egipto, los constructores hacían nudos igualmente espaciados en una cuerda, de tal forma que esta les sirviera para medir. Se cree que ellos fueron los primeros en darse cuenta de que, uniendo los extremos de la cuerda para formar un triángulo, como se observa en la figura, con las medidas 3, 4 y 5 en sus lados, se formaba un ángulo recto. De esta forma, conseguían poner en forma perpendicular los mástiles en la cubierta de las embarcaciones y también podían restablecer las lindes de las parcelas rectangulares después de las crecidas del río Nilo. Los tríos de números como 3, 4 y 5, que cumplen 52 = 32 + 42 , es decir, el teorema de Pitágoras, forman los lados de un triángulo rectángulo y son llamados tríos pitagóricos. Este hecho corresponde al recíproco del teorema de Pitágoras. No es sencillo encontrar tríos pitagóricos que sean números enteros, aunque existe un método para encontrar estos a partir de tríos pitagóricos conocidos; por ejemplo, si multiplicamos 3, 4 y 5 por un número entero cualquiera, obtendremos un nuevo trío pitagórico. Observa. Sean a, b y c números enteros, tal que a2 + b2 = c2 , y sea k un número entero cualquiera, distinto de cero. Como a, b y c corresponden a un trío pitagórico, tendremos que: a2 + b2 = c2 a2 k2 + b2 k2 = c2 k2 (ak)2 + (bk)2 = (ck)2 Luego, ak, bk y ck corresponden también a un trío pitagórico. Analicemos... • ¿Cómo puedes demostrar que un triángulo de lados 3, 4 y 5 es un triángulo rectángulo? • ¿Puedes dar otro ejemplo de medidas que correspondan a los lados de un triángulo rectángulo?, ¿cómo lo supiste? Multiplicamos por k2 UNIDAD 3 (106-163)C :Maquetación 1 4/11/10 17:16 Página 118
- 120. El triángulo rectángulo y la trigonometría | 119 Unidad 3 Glosario conjetura: juicio o afirmación que se supone cierta, pero no ha sido demostrada. Desde la Antigüedad, algunos personajes han dedicado su tiempo a encontrar regularidades respecto de los números que satisfacen el teorema de Pitágoras. Por ejemplo, además de Pitágoras, Aquitas formuló una expresión para calcular tríos pitagóricos. Observa estas nuevas expresiones. Según la regla que usemos, obtenemos respuestas distintas. Sin embargo, Pierre de Fermat, un abogado francés que creaba matemáticas por afición, conjeturó en 1637 que no hay enteros que cumplan el equivalente a los tríos pitagóricos para potencias mayo- res que 2; es decir, que para todo número entero n mayor que 2 no hay enteros x, y, z, distintos de cero los tres, que cumplan xn + yn = zn . Como era habitual en esa época entre algunos matemáticos por afi- ción, se enviaban afirmaciones como esa entre sí, sin demostrarlas, como un desafío. Fermat escribió, en el margen de una página de un libro, sobre esta conjetura: “He encontrado una demostración realmente maravillosa, pero el margen de esta página es muy estrecho para escribirla aquí”. Nunca se encontró esta demostración, pero su frase obsesionó a muchos matemáticos, tanto profesionales como aficionados. La conjetura de Fermat, cuyo enunciado destaca por su simpleza, llegó, entonces, a convertirse en uno de los problemas “intratables” del siglo XX, y en que generaciones de matemáticos intentaron en vano obtener una demostración general. Pero esta historia todavía no llegaba a su fin. El 25 de junio de 1993, los diarios más importantes del mundo publi- caban un inusual artículo que señalaba la demostración del teo- rema de Fermat. Regla de Pitágoras: a; ; son tríos pitagóricos. Regla de Aquitas: a; –1; +1 son tríos pitagóricos. a2 4 a2 4 a2 + 1 2 a2 – 1 2 UNIDAD 3 (106-163)C :Maquetación 1 4/11/10 17:16 Página 119
- 121. 120 | Unidad 3 Luego de corregir la demostración publicada, en 1995, la conjetura de Fermat pasó a ser un teorema, ya que finalmente se había demostrado; el final feliz estuvo a cargo de Andrew Wiles, un matemático británico al que le tomó siete años de duro trabajo demostrar este teorema, conocido como el último teorema de Fermat. Finalmente, a sus cuarenta años pudo escribir al final de doscientas hojas de trabajo: QED (“qued erat demostrandum”). Lo destacable de la demostración de Wiles es el uso que él hace de una variedad de herramientas matemáticas, hasta ese entonces aparentemente desconectadas. Se necesitó de todo el poder de las matemáticas modernas para llegar a la solución. El teorema de Fermat nos demuestra que la Matemática es una ciencia viva y su demostración es el inicio de nuevas posibilidades para esta. En resumen • Un trío pitagórico es una terna de números a, b y c que satisfacen la igualdad a2 + b2 = c2 , donde geométricamente a y b son los catetos de un triángulo rectángulo y c es su hipotenusa. 1. Verifica si las siguientes medidas corresponden a los lados de un triángulo rectángulo: a. 5 cm; 4 cm; 6 cm e. a cm; (a + 1) cm; (a + 2) cm b. 12 cm; 15 cm; 9 cm f. 1 cm; cm; 2 cm d. 30 cm; 40 cm; 50 cm h. cm; cm; cm 2. Si los catetos de un triángulo rectángulo son 18 cm y 24 cm, ¿cuánto mide la hipotenusa? 3. Si uno de los catetos de un triángulo rectángulo mide 7 cm más que el otro cateto y 1 cm menos que la hipotenusa, ¿cuánto mide el perímetro y el área del triángulo?, ¿cómo lo calculaste? 4. Demuestra que los términos de la regla de Pitágoras y Aquitas forman tríos pitagóricos. a b + 3 b 3 a 3 8 7 Actividades c. 32 cm; 25 cm; 16 cm g. cm; cm; cm 1 5 1 4 1 3 UNIDAD 3 (106-163)C :Maquetación 1 4/11/10 17:16 Página 120
- 122. El triángulo rectángulo y la trigonometría | 121 Unidad 3 Situaciones que involucran triángulos rectángulos Julia quiere medir la altura de cierto árbol que se encuentra en el patio de su casa; para llevar a cabo esto sitúa un espejo en el piso, a 30 metros del árbol, y luego se aleja 3 m, distancia a la cual Julia ve reflejado en el espejo el punto más alto del árbol. De acuerdo a la figura, ΔABC y ΔDBE son rectángulos, el primero en A y el segundo en D. Además, como el rayo de luz que rebota en el espejo se refleja con el mismo ángulo con que llega al es- pejo, tenemos que ⱔABC y ⱔDBE tienen igual medida. Recordando los criterios de semejanza de triángulos, tenemos que, por el criterio AA, ambos triángulos son semejantes. Luego, sus lados son proporcionales; es decir, la razón entre lados correspon- dientes en cada triángulo es la misma para los dos: = h = 1,8 · = 18 La altura del árbol es 18 metros. Ejemplo Determina las medidas de los lados de un triángulo ABC rectán- gulo en C, en que uno de sus catetos tiene una longitud de 2 cm y es semejante a un triángulo rectángulo de medidas 3, 4 y 5 cm, siendo el lado de medida igual a 2 cm, correspondiente al lado de 4 cm del otro triángulo. 30 3 AC AB DE DB Analicemos... • ¿Puedes describir dos triángulos rectángulos en la situación?, ¿cuáles son? • ¿Hay ángulos iguales en ambos triángulos?, ¿por qué? • ¿Qué altura tiene el árbol?, ¿cómo lo supiste? ⱔCAB = ⱔEDB = 90º ⱔCBA = ⱔEBD 1,8m 3m 30m D h E C B A Remplazando las medidas dadas = 1,8 3 h 30 A C C B 2 cm 3 cm 5 cm 4 cm UNIDAD 3 (106-163)C :Maquetación 1 4/11/10 17:16 Página 121
- 123. 122 | Unidad 3 Debemos determinar la medida de la hipotenusa AB y el cateto AC. Como los triángulos son semejantes, sus lados son proporcionales; en consecuencia, obtenemos: = Luego, podemos obtener la medida de la hipotenusa AB utilizando el teorema de Pitágoras o utilizando, nuevamente, semejanza de triángulos; por este último método, tendremos que: = 3 4 AC 2 AB 2 5 4 1. Calcula la altura del edificio según los datos de la figura. 2. Los lados de un triángulo son 8, 10 y 16 cm. Calcula los lados de otro triángulo semejante al anterior, de perímetro 68 cm. 3. ¿Cuánto mide la altura de un árbol que proyecta una sombra de 2,1 cm, si junto a él está Fernando, que mide 1,70 m y proyecta una sombra de 0,8 m a la misma hora? Multiplicamos por 2 AB = 2 · = cm 5 2 5 4 Multiplicamos por 2 AC = 2 · = cm 3 2 3 4 En resumen • La semejanza de triángulos, y más específicamente la semejanza entre triángulos rectángulos, nos entrega un método para calcular distancias o longitudes inaccesibles. Actividades 4 m 5 m 100 m 1,70 m 0,8 m UNIDAD 3 (106-163)C :Maquetación 1 4/11/10 17:16 Página 122
- 124. El triángulo rectángulo y la trigonometría | 123 Unidad 3 4. Calcula la profundidad del pozo de la figura. 5. Thales fue un filósofo y matemático griego que vivió en el siglo VI a. C. El historiador griego Plutarco (siglo I) dijo acerca de él: “Yo te admiro porque, poniendo tu bastón en la extremidad de la sombra de una pirámide, formaste con los rayos del Sol dos triángulos y demostraste que la altura de la pirámide era a la longitud del bastón como la sombra de la pirámide era a la sombra del bastón”. Resuelve, aplicando el método de Thales. Muestra, paso a paso, cómo lo hiciste. a. Un bastón de 50 cm proyecta una sombra de 20 cm. ¿Cuál es la altura de un poste que, a la misma hora, proyecta una sombra de 1,40 m? b. Si un bastón mide 40 cm y su sombra 30 cm, ¿cuánto mide, a la misma hora, la sombra de una persona de 1,70 m de altura? 6. Según la figura, si BE representa la altura de una persona que mide 1,8 m. ¿Cuál es la altura de un edificio. AB = 2,4 m y BC = 12,6 m. 2 m 1,62 m 1 m D C B E A UNIDAD 3 (106-163)C :Maquetación 1 4/11/10 17:16 Página 123
- 125. 124 | Unidad 3 • En el siguiente mapa conceptual se muestran los conceptos tratados en las páginas anteriores. • Utilizando los contenidos aprendidos hasta aquí, y apoyándote en el esquema anterior, responde en tu cuaderno. 1. ¿Crees que faltó un concepto importante en el mapa conceptual?, ¿cuál? Agrégalo. 2. ¿Qué significa que dos triángulos rectángulos sean semejantes? 3. ¿Qué relación existe entre la altura de un triángulo rectángulo y las proyecciones de los catetos sobre la hipotenusa de este? 4. ¿Qué debe cumplir un trío de números para que este sea un trío pitagórico? 5. ¿Puede haber triángulos no rectángulos cuyas medidas formen un trío pitagórico? 6. ¿Puede usarse el teorema de Pitágoras para demostrar el teorema de Euclides? 7. ¿Puede calcularse el área de un triángulo rectángulo conociendo su hipotenusa y la distancia a la hipotenusa desde el vértice opuesto a ella? 8. ¿Son semejantes dos triángulos que tienen un lado y dos ángulos en común? 9. ¿Son semejantes dos triángulos rectángulos que tienen uno de sus ángulos agudos congruentes? 10. ¿Tienes alguna duda sobre los conceptos tratados en las páginas anteriores?, ¿cuál? Compártela con tu curso e intenten aclararla en conjunto. Organizando lo aprendido se aplican TRIÁNGULO RECTÁNGULO TRIÁNGULOS RECTÁNGULOS SEMEJANTES RELACIONES MÉTRICAS algunas son se aplican en la demostración posee TEOREMA DE PITÁGORAS TRÍOS PITAGÓRICOS TEOREMA DE EUCLIDES genera UNIDAD 3 (106-163)C :Maquetación 1 4/11/10 17:16 Página 124
- 126. Mi progreso Unidad 3 1. Determina la medida de los catetos de un triángulo rectángulo, sabiendo que las proyecciones de estos sobre la hipotenusa miden respectivamente: a. 9 cm y 16 cm b. 4 cm y 8 cm c. 3 cm y 9 cm d. 3,6 cm y 6,4 cm 2. En el triángulo ABC rectángulo en C, la altura correspondiente a la hipotenusa mide la mitad de esta. Determina cuáles de las siguientes igualdades son verdaderas y cuáles son falsas. Explica en cada caso tu decisión. a. (p + q)2 = 4pq b. q = c. p = q d. p + q = pq 3. ¿Qué conjunto de números podrían ser las longitudes de los lados de un triángulo rectángulo? I. 9, 40, 41 II. 2, , III. a – b, a + b, 2 A. Solo I B. Solo II C. I y II D. I y III E. I, II y III 4. Resuelve los siguientes problemas explicando, paso a paso, tu desarrollo. a. En un día soleado, un árbol de 7 m de alto proyecta una sombra de 10 m, mientras un hombre de 1,70 m de altura está parado junto al árbol. ¿Cuánto mide la sombra que proyecta el hombre?, ¿qué altura tiene un hombre que en el mismo instante proyecta una sombra de 2 m? b. A cierta hora del día, un árbol que mide 5 m proyecta una sombra de 7 m. A esa misma hora, otro árbol proyecta una sombra que mide 16 m. ¿Cuánto mide su altura? 11 7 p 2 • Verifica en el solucionario del Texto si tus respuestas son correctas. Si tuviste respuestas incorrectas, marca en la tabla el criterio correspondiente y revisa las páginas indicadas. Luego, identifica el error y corrígelas. ¿Cómo voy? El triángulo rectángulo y la trigonometría | 125 CRITERIO ÍTEMS PÁGINAS DONDE SE TRABAJA Aplicar el teorema de Euclides. 1 y 2 110 a 117 Identificar tríos pitagóricos. 3 118 a 120 Resolver problemas que involucran triángulos rectángulos semejantes. 4 121 a 123 B C A p q ab UNIDAD 3 (106-163)C :Maquetación 1 4/11/10 17:16 Página 125
- 127. 126 | Unidad 3 Razones trigonométricas en el triángulo rectángulo El ascensor de un conocido cerro de Valparaíso funciona sobre un riel recto, inclinado en un ángulo α con respecto al plano horizontal. Cuando el ascensor recorre 50 m, llega a una altura de 30 m. Observa la figura que representa esta situación. Analicemos... • ¿Conoces la medida de alguno de los ángulos agudos del trián- gulo rectángulo formado? • ¿A qué altura se encuentra el ascensor cuando ha recorrido 75 m?, ¿y si este ha recorrido 100 m?, ¿cómo lo supiste? • ¿Qué tienen en común los tres triángulos formados? En la figura anterior, podemos observar que los triángulos ABG, ACF y ADE son semejantes, ya que todos ellos tiene un ángulo recto y comparten el ángulo α. Luego, sus lados son respectivamente pro- porcionales; por lo tanto, tendremos que: = = . Es decir, la razón entre la medida del cateto opuesto al ángulo y la medida de la hipotenusa es la misma: = = 0,6. Entonces, la altura a la que se encuentra el ascensor cuando ha recorrido 75 m la podemos encontrar remplazando y despejando CF en la ecuación: = 0,6 CF = 0,6 · 75 = 45. Mientras que cuando este ha recorrido 100 m, la altura a la que se encuentra la podemos encontrar remplazando y despejando DE en la ecuación: = 0,6 DE = 0,6 · 100 = 60. DE 100 CF 75 30 50 cateto opuesto a α hipotenusa DE EA CF FA BG GA Luego, = = = 0,6. DE EA CF FA BG GA Multiplicamos por 75 Multiplicamos por 100 100 m 75 m 50 m 30 m α A G F E D C B Dado un ángulo agudo α en un triángulo rectángulo ABC,podemos nombrar los catetos de acuerdo a su ubicación respecto de dicho ángulo. Recuerda que... α Cateto opuesto a α Cateto adyacente a α Hipotenusa UNIDAD 3 (106-163)C :Maquetación 1 4/11/10 17:16 Página 126
- 128. El triángulo rectángulo y la trigonometría | 127 Como puedes notar, al variar las medidas de los lados en el trián- gulo rectángulo formado por el ascensor obtuvimos que el valor de la razón entre la medida del cateto opuesto al ángulo α y la me- dida de la hipotenusa es la misma. Esto se debe a que el cociente 0,6 se relaciona con el ángulo α y no con las medidas de los lados del triángulo. Si el ángulo de inclinación fuese otro, al recorrer, por ejemplo, 50 metros, el ascensor no estaría a 30 m de altura. A esta razón constante la llamaremos seno de α y la denotaremos por sen(α). Como los triángulos son semejantes, tendremos que la razón entre la medida del cateto adyacente al ángulo α y la medida de la hipotenusa también es constante. = = = = 0,8 A esta razón la llamaremos coseno de α y la denotaremos por cos(α). Por último, también será constante la razón entre la medida del cateto opuesto al ángulo α y la medida del cateto adyacente a este. = = = = 0,75 A esta razón la llamaremos tangente de α y la denotaremos por tan(α). Las razones seno, coseno y tangente son las razones trigonométricas fundamentales; sin embargo, también se definen los valores recípro- cos de ellas como las razones trigonométricas recíprocas. Estas son: Cosecante de α: cosec(α) = = Cotangente de α: cotan(α) = = cateto opuesto a α cateto adyacente a α cateto adyacente a α hipotenusa cateto adyacente a α cateto opuesto a α 1 tan(α) hipotenusa cateto opuesto a α 1 sen(α) DE AD CF AC BG AB AD EA AC FA AB GA Unidad 3 Secante de α: sec(α) = = hipotenusa cateto adyacente a α 1 cos(α) UNIDAD 3 (106-163)C :Maquetación 1 4/11/10 17:16 Página 127
- 129. 128 | Unidad 3 En resumen Los cocientes entre los lados de un triángulo rectángulo dependen del valor de su ángulo agudo α. Dichos cocientes reciben el nombre de razones trigonométricas del ángulo α y son los siguientes: • Razones trigonométricas fundamentales Seno de α: sen(α) = cateto opuesto a α hipotenusa Coseno de α: cos(α) = cateto adyacente a α hipotenusa Tangente de α: tan(α) = cateto opuesto a α cateto adyacente a α Herramientas tecnológicas Uso de la calculadora en trigonometría Las teclas , y , en una calculadora científica, nos permiten hallar el valor aproximado de las razones trigonométricas seno, coseno y tangente de los ángulos. Es muy importante que, antes de calcular dichos valores, tu calculadora esté en el modo DEG, ya que esto nos indica que la calculadora considera los ángulos medidos en grados sexagesimales. El uso de la calculadora depende de la operación que desees realizar. • Si conoces el ángulo y deseas hallar la razón trigonométrica: debes usar la tecla de la razón trigonométrica deseada y luego ingresar el ángulo. Por ejemplo, para aproximar sen 20º: • En otras calculadoras, el orden apropiado es: • Si conoces la razón trigonométrica, ¿cuál es el ángulo asociado? Puedes usar la tecla SHIFT, luego la tecla de la razón trigonométrica involucrada y después la razón conocida. Por ejemplo, aproximemos el valor de α si sabemos que sen(α) = 0,34. • En otras calculadoras, el orden apropiado es: sin tan cos 0,3420201433 sin 2 0 0 · 3 4 = 0,3420201433 sin 2 0 = 19,87687407 19,87687407 SHIFT sin = 0 · 3 4 SHIFT sin = • Razones trigonométricas recíprocas Cosecante de α: cosec(α) = hipotenusa cateto opuesto a α Secante de α: sec(α) = hipotenusa cateto adyacente a α Cotangente de α: cotan(α) = cateto adyacente a α cateto opuesto a α UNIDAD 3 (106-163)C :Maquetación 1 4/11/10 17:16 Página 128
- 130. El triángulo rectángulo y la trigonometría | 129 Unidad 3 Utiliza lo aprendido para desarrollar las siguientes actividades: 1. Calcula las razones trigonométricas seno, coseno y tangente de los dos ángulos agudos de los triángulos rectángulos siguientes: a. b. 2. A partir del valor de la razón trigonométrica dada, completa las restantes en la siguiente tabla: 3. Utiliza tu calculadora para encontrar los valores aproximados de las razones trigonométricas de los siguientes ángulos: a. 19º c. 45º e. 85º b. 25º d. 70º f. 12,5º 4. Determina en cada caso el valor de x. Aproxima el resultado. a. b. β β α α 1 cm 10 cm 6 cm 7 cm sen(α) cos(α) tan(α) sec(α) cosec(α) cotan(α) 0,6 8 15 0,9 1,45 35 12 8 10 61º 56,6º 4 cm 7 cm x x UNIDAD 3 (106-163)C :Maquetación 1 4/11/10 17:16 Página 129
- 131. 130 | Unidad 3 Razones trigonométricas de ángulos especiales Isabel debe encontrar la medida de la hipotenusa c de un trián- gulo rectángulo; sin embargo, para esto solo cuenta con la medida de uno de los catetos y el ángulo opuesto a este. Observa. En la situación anterior debemos encontrar alguna relación entre un cateto del triángulo, el ángulo opuesto a este y la hipotenusa. Recordando las razones trigonométricas, sabemos que el seno de un ángulo es una razón que relaciona estas medidas. Luego, sen(α) = . c = Utilizamos una calculadora para obtener un valor aproximado de c, luego, tenemos que c 艐 11,5 cm Sin embargo, algunos valores de las razones trigonométricas pueden ser calculados directamente, sin usar calculadora. Observa. Ángulos de 30º y 60º Consideremos un triángulo equilátero cuyos lados miden 2 m. Al trazar la altura CD, cuya longitud es m, el triángulo equi- látero queda dividido en dos triángulos rectángulos congruentes. Luego, AD = 1 m, ⬏ACD = 30º y ⬏DAC = 60º y sen(30º) = 1 2 3 10 sen(60º) cateto opuesto a α hipotenusa Analicemos... • ¿Cómo se puede determinar la medida de la hipotenusa con los datos dados? • ¿Existe una forma distinta de calcular la distancia pedida? En este caso, sen(60º) = 10 c sen(60º) = 2 C B A α c 10 cm 60º C D B A 1 m 2 m 60º 30º 3 cos(60º) = 1 2 tan(60º) = 3 cos(30º) = 2 3 tan(30º) = = 1 3 3 3 Despejamos c 3 m UNIDAD 3 (106-163)C :Maquetación 1 4/11/10 17:16 Página 130
- 132. El triángulo rectángulo y la trigonometría | 131 Unidad 3 Ángulo de 45º Consideremos un triángulo rectángulo isósceles de cateto 1 m. Por ser rectángulo e isósceles, cada ángulo agudo mide 45º y por el teorema de Pitágoras la hipotenusa mide . Luego, en el triángulo ABC tenemos que: sen(45º) = = tan(45º) = 1 2 2 1 cos(45º) = = 2 1 En resumen • Algunos valores de las razones trigonométricas pueden ser calculados directamente, sin usar calculadora. En particular, para los ángulos de 30º y 60º estos valores se pueden obtener analizando el triángulo equilátero y para el ángulo de 45º, analizando el triángulo isósceles rectángulo. 1. Completa la tabla con el valor de las razones trigonométricas para los ángulos que aparecen en ella. 2. Sin utilizar calculadora, encuentra el valor de las siguientes expresiones: a. 2 · sen(30º) + 4 · cos(60º) d. sen(60º) + cos2 (45º) – tan(30º) · tan(60º) b. · tan (60º) – 3 · tan(45º) e. (1 – sen2 (45º))2 + 2 · cos(45º) c. sen2 (30º) + cos2 (30º) f. sen(45º) · cos(45º) · tan(30º) Verifica con la calculadora los resultados obtenidos. 3. La longitud del hilo que sujeta un volantín es de 15 m y el ángulo de elevación es de 30º. ¿A qué altura está el volantín?, ¿cómo lo calculaste? 3 Actividades C A B 1 m 1 m 45º 2 2 2 2 α 30º 45º 60º sen(α) cos(α) tan(α) UNIDAD 3 (106-163)C :Maquetación 1 4/11/10 17:16 Página 131
- 133. 132 | Unidad 3 Aplicaciones de la trigonometría Desde la parte superior de una torre vigía de 80 m de altura, un guardabosques localiza una fogata ilegal. El ángulo de depresión que forman la línea de visión hacia el campamento y la horizontal es 10,1º. Observa. En la situación anterior, la distancia a la que se encuentra la fogata corresponderá a la medida del segmento AC. El ángulo de depresión es ⱔABX = 10,1º, el cual es igual a ⱔCAB (ángulos alternos internos entre paralelas); luego, en el triángulo rectángulo ⱔABC se tiene que: tan(10,1º) = Por lo tanto, la fogata se encuentra aproximadamente a 449,1 m de la base de la torre. 80 AC Analicemos... • ¿A qué distancia de la base de la torre se encuentra la fogata?, ¿cómo lo resolviste? • ¿Podemos encontrar una aproximación para la distancia bus- cada, sin utilizar una calculadora? Glosario ángulo de elevación: es aquel for- mado por la visual a un punto y la horizontal cuando el punto se en- cuentra sobre el observador. ángulo de depresión: es aquel for- mado por la visual a un punto y la horizontal cuando el punto se en- cuentra bajo el observador. B C A X 10,1º 10,1º 80 m AC = = 449,1 80 tan(10,1º) En resumen • Las razones trigonométricas proporcionan herramientas matemáticas muy útiles que nos permiten determinar longitudes y ángulos en figuras formadas por triángulos rectángulos, a partir de las medidas de algunos de estos elementos del triángulo rectángulo. • La elección de la razón trigonométrica a usar en la resolución de un problema depende de los datos involucrados; una adecuada elección facilitará esta. Objeto Objeto Observador Observador α β UNIDAD 3 (106-163)C :Maquetación 1 4/11/10 17:16 Página 132
- 134. El triángulo rectángulo y la trigonometría | 133 Unidad 3 1. Determina la altura de un árbol, sabiendo que su sombra mide 8 m cuando el ángulo de elevación al Sol es de 53º. 2. Un avión se encuentra a 2300 m de altura cuando comienza su descenso para aterrizar. ¿Qué distancia debe recorrer el avión antes de tocar la pista, si baja con un ángulo de depresión de 25º? 3. Un edificio tiene una altura de 75 m. ¿Qué medida tiene la sombra que proyecta cuando el Sol tiene un ángulo de elevación de 43º? Haz un dibujo del problema. 4. Manuel, un astrónomo principiante, midió el ángulo que se muestra en la figura para calcular la distancia que hay entre los centros de la Luna y la Tierra. Considerando que el radio de la Tierra es 6380 km, ¿qué resultado obtuvo Manuel? 5. Sobre una montaña está instalada una torre de 25 m, desde donde se observan dos águilas alineadas con la base de la torre. Una es observada con un ángulo de 35º y la otra con un ángulo de 40º. ¿A qué distancia se encuentra un águila de la otra? 6. Los lados de un triángulo isósceles miden 20 cm y cada uno de sus ángulos basales es de 25º. Calcula el valor de la base y el área de este triángulo. Actividades 1º 53º 8 m 25º UNIDAD 3 (106-163)C :Maquetación 1 4/11/10 17:16 Página 133
- 135. 134 | Unidad 3 Propiedades de las razones trigonométricas Felipe y Cristina deben encontrar la medida de uno de los ángulos de un triángulo rectángulo, de tal modo que uno de los catetos de este mida dm y el otro 1 dm. Ambos realizan los cálculos necesarios, pero sus resultados son diferentes. Felipe obtiene que la medida de uno de los ángulos debe ser 30º; en cambio, el resul- tado de Cristina es 60º. 3 En el problema que deben resolver Felipe y Cristina tenemos que, si uno de los catetos mide dm y el otro mide 1 dm, podemos encontrar la medida de la hipotenusa c por medio del teorema de Pitágoras. 2 + 12 = c2 3 + 1 = c2 4 = c2 2 = c Por lo tanto, la hipotenusa de dicho triángulo mide 2 dm. En páginas anteriores, calculamos el valor de las razones trigono- métricas de los ángulos 30º y 60º; obtuvimos que: cos(30º) = sen(60º) = Es decir, ambos resultados son correctos, ya que estos corresponden a las razones trigonométricas de un triángulo con las medidas dadas. Estas igualdades se producen debido a que los ángulos 30º y 60º son ángulos complementarios. En efecto, si consideramos un triángulo ABC, cuyo ángulo BAC es α, entonces, el otro ángulo agudo del triángulo es su complemento, es decir, 90º – α. Luego, cos(α) = y sen(90º – α) = , de donde se concluye que cos(α) = sen(90º – α). Del mismo modo, puedes verificar que sen(α) = cos(90º – α). 3 3 AC AB AC AB 2 3 Analicemos... • ¿Son ambos resultados correctos?, ¿cómo lo supiste? • ¿Qué procedimiento debemos utilizar para llegar a los resultados? • ¿En qué se relacionan los ángulos obtenidos por Felipe y Cristina?, ¿por qué? cos(60º) = sen(30º) = 1 2 B C A α 90º–α Dos ángulos agudos α y β se dicen complementarios si α + β = 90º Recuerda que... UNIDAD 3 (106-163)C :Maquetación 1 4/11/10 17:16 Página 134
- 136. El triángulo rectángulo y la trigonometría | 135 Unidad 3 1. Utiliza el ΔABC para probar las siguientes igualdades: a. tan(α) = c. cosec(α) = 2. ¿Cuál es el valor de la expresión cos(α) · sen(90º – α) + sen(α) · cos(90º – α)? 3. Si sen(20º) = x y cos(20º) = y, calcula en función de x e y: a. cos(70º) c. tan(20º) e. cosec(20º) b. sen(70º) d. sec(20º) f. tan(70º) 4. Calcula el valor de: a. cos(25º) – sen(65º) c. 5. Construye un triángulo en que tan(α) = . A partir de él, calcula el valor de: a. sen(α) c. sec(α) e. cos(90º – α) b. cos(α) d. sen(90º – α) f. sec(90º – α) 2 sen(17º) + 3 cos(73º) sen(17º) 1 sen(α) sen(α) cos(α) 7 2 Actividades En resumen Las razones trigonométricas seno y coseno satisfacen lo siguiente: • cos (α) = sen(90º – α) • sen (α) = cos(90º – α) b. sec(α) = 1 cos(α) B C A α b. cos(243º) · sen(31º) – sen(47º) · cos(59º) d. 3 cos(35º) · 2 sen(55º) cos2 (35º) UNIDAD 3 (106-163)C :Maquetación 1 4/11/10 17:16 Página 135
- 137. 136 | Unidad 3 Identidades trigonométricas Antonia debe calcular el valor de la expresión sen2 (30º) + cos2 (30º), y Diego el valor de sen2 (45º) + cos2 (45º). Observa sus resultados. Antonia Recordando que sen(30º) = y cos(30º) = Diego Recordando que sen(45º) = y cos(45º) = 2 2 2 2 3 2 1 2 Para verificar los resultados de Diego y Antonia, consideremos un triángulo rectángulo ABC, siendo α uno de los ángulos agudos de este. Luego, tenemos que: cos(α)= ⇒AC = AB · cos(α) Por el teorema de Pitágoras: AB2 = AC2 + BC2 AB2 = AB2 · cos2 (α) + AB2 · sen2 (α) AB2 = AB2 (cos2 (α) + sen2 (α)) Al dividir esta última igualdad por AB2 , obtenemos que: cos2 (α) + sen2 (α) = 1. Por lo tanto, los resultados de Antonia y Diego son correctos, ya que para todo ángulo agudo α tendremos que cos2 (α) + sen2 (α) = 1. AC AB Analicemos... • ¿Son correctos los resultados de Diego y Antonia?, ¿cómo lo supiste? • ¿Por qué ambos resultados son iguales?, ¿cuándo ocurre esto? • Si α es un ángulo agudo cualquiera, ¿podemos determinar el valor de cos2 (α) + sen2 (α)? sen2 (30º) + cos2 (30º) = + = + = = 1. 4 4 3 4 1 4 3 2 2 ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ 1 2 2 ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ sen2 (45º) + cos2 (45º) = + = + = = 1. 4 4 2 4 2 4 2 2 2 ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ 2 2 2 ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ sen(α) = ⇒ BC = AB · sen(α) BC AB B α C A • (sen(α))n = senn (α) • (cos(α))n = cosn (α) Pon atención UNIDAD 3 (106-163)C :Maquetación 1 4/11/10 17:16 Página 136
- 138. El triángulo rectángulo y la trigonometría | 137 Unidad 3 Las identidades trigonométricas más conocidas son: cos2 (α) + sen2 (α) = 1 1 + tan2 (α) = sec2 (α) 1 + cotan2 (α) = cosec2 (α) Veamos a continuación las demostraciones de la segunda y tercera identidad a partir de la primera. Observa. • sen2 (α) + cos2 (α) = 1 + = obtenemos la identidad tan2 (α) + 1 = sec2 (α). • sen2 (α) + cos2 (α) = 1 Luego, recordando que = cotan(α) y = cosec(α), obtenemos la identidad 1 + cotan2 (α) = cosec2 (α). 1 sen(α) cos(α) sen(α) 1 cos2 (α) cos2 (α) cos2 (α) sen2 (α) cos2 (α) En resumen Para todo ángulo α, se cumplen las siguientes identidades trigonométricas: • cos2 (α) + sen2 (α) = 1 • 1 + tan2 (α) = sec2 (α) • 1 + cotan2 (α) = cosec2 (α) + = 1 sen2 (α) cos2 (α) sen2 (α) sen2 (α) sen2 (α) Glosario identidad trigonométrica: es una re- lación de igualdad entre expresiones trigonométricas.Estas son útiles para reducir,simplificar o transformar otras expresiones más complejas. Dividimos por cos2 (α) Dividimos por sen2 (α) Luego, recordando que = tan(α) y = sec(α), 1 cos(α) sen(α) cos(α) 1. Simplifica las siguientes expresiones, utilizando las identidades trigonométricas más adecuadas. a. c. : 1 cosec(α) – 1 sen(α) + 1 sen(α) (1 + cos(α)) (1 – cos(α)) sen(α) Actividades b. d. cos2 (α) – sen2 (α) cos4 (α) – sen4 (α) cos(α) – cos3 (α) sen(α) – sen3 (α) UNIDAD 3 (106-163)C :Maquetación 1 4/11/10 17:16 Página 137
- 139. 138 | Unidad 3 Teorema del seno y del coseno Pedro camina 600 metros para llegar desde el colegio a su casa y Fernanda, 800 metros, formando un ángulo de 60º entre ambos caminos, como se muestra en la siguiente figura: En el triángulo ABC, que representa la situación de Pedro y Fer- nanda, solo tenemos la medida del ángulo CAB; por lo tanto, no podemos asegurar que el triángulo ABC es rectángulo. Para calcu- lar las medidas buscadas, podemos utilizar un triángulo rectángulo de la siguiente forma: Si consideramos la altura CD, desde el vértice en que se encuentra la casa de Pedro hacia el lado del triángulo correspondiente al camino desde el colegio a la casa de Fernanda, tendremos que BC será la hipotenusa del triángulo rectángulo CDB. Observa. Para determinar la medida de CB en el triángulo rectángulo CDB, es necesario saber la medida de los catetos de este. La medida del cateto DC la podemos determinar a partir del trián- gulo rectángulo ADC, ya que tenemos la medida de uno de los án- gulos y la medida de la hipotenusa de este. Luego, tendremos que: = sen(60º) DC = 600 sen(60º) DC = 600 · = 300 3 3 2 DC 600 Analicemos... • ¿Es el triángulo ABC un triángulo rectángulo?, ¿por qué? • ¿Qué triángulo rectángulo podemos utilizar para calcular las razones trigonométricas del ángulo CAB? • ¿Cuánto mide la distancia entre las casas de Pedro y Fernanda?, ¿cómo lo supiste? Pedro C Fernanda Colegio 600 m 60º 800 m B A Pedro C Fernanda Colegio 600 m 60º 800 m B A D Multiplicamos por 600 Multiplicamos sen(60º) = UNIDAD 3 (106-163)C :Maquetación 1 4/11/10 17:16 Página 138
- 140. El triángulo rectángulo y la trigonometría | 139 Luego, para determinar la medida del cateto DB, debemos primero calcular la medida de AD. Observa. = cos(60º) AD = 600 cos(60º) AD = 600 · = 300 Luego, la medida del cateto faltante, DB, en el triángulo CDB es: DB = AB – AD DB = 800 m – 300 m DB = 500 m. Conociendo el valor de los catetos CD y DB, podemos determinar mediante el teorema de Pitágoras, la medida de la hipotenusa CB, correspondiente a la distancia entre la casa de Pedro y Fernanda. CB2 = 5002 + CB2 = 250 000 + 270 000 = 520 000 CB = = 200 Pero como CB es una longitud, esta no puede ser negativa; es decir, descartamos la solución negativa de la ecuación CB2 = 520 000. Por lo tanto, la distancia entre la casa de Pedro y Fernanda es 200 metros, que aproximadamente corresponde a 721,11 metros. Este proceso se puede realizar de manera general y corresponde a la generalización del teorema de Pitágoras y es conocido como el teorema del coseno. Observa. En el triángulo de la figura, trazamos la altura h sobre el lado c. Si llamamos p a la proyección del lado b sobre la hipotenusa, del mismo modo que en el problema anterior, tendremos que: sen(α) = ⇒ h = b sen(α) AD 600 13 13 520 000 300 3 2 ( ) h b 1 2 Unidad 3 C b a α β γ A B Multiplicamos por 600 cos(α) = ⇒ p = b cos(α) p b c p h UNIDAD 3 (106-163)C :Maquetación 1 4/11/10 17:16 Página 139
- 141. 140 | Unidad 3 Luego, por el teorema de Pitágoras también tenemos que a2 = h2 + (c – p)2 , donde podemos remplazar los valores encontrados para h y p. Observa. a2 = h2 + (c – p)2 = (b sen(α))2 + (c – b cos(α))2 = b2 sen2 (α) + c2 – 2bc cos(α) + b2 cos2 (α) = b2 (sen2 (α) + cos2 (α)) + c2 – 2bc cos(α) Luego, a2 = b2 + c2 – 2bc cos(α) Este resultado se conoce como teorema del coseno. Tal como el teorema del coseno relaciona la medida de los lados con un ángulo del triángulo correspondiente, existe también el teorema del seno, el cual relaciona la medida de los lados con el seno de los ángulos de un triángulo. Observa. sen(α) = ⇒ h = b sen(α) Luego, b sen(α) = a sen(β), de donde obtenemos que = . Ejemplo 1 Encuentra la distancia entre las casas de Pedro y Fernanda utilizando el teorema del coseno. Utilizando el teorema del coseno tendremos que: CB2 = 6002 + 8002 – 2 · 600 · 800 · cos(60º) = 360 000 + 640 000 – 960 000 · = 360 000 + 640 000 – 480 000 = 520 000 Luego, CB = . b sen(β) 520 000 200 13 721 11 , m m m = ≈ 1 2 a sen(α) h b sen(β) = ⇒ h = a sen(β) p b Pedro C D Fernanda Colegio 600 m 60º 800 m B A Remplazamos recordando la identidad: cos2 (α) + sen2 (α) =1 UNIDAD 3 (106-163)C :Maquetación 1 4/11/10 17:16 Página 140
- 142. El triángulo rectángulo y la trigonometría | 141 Unidad 3 En resumen Teorema del seno En todo triángulo ABC, se tiene que: = = Teorema del coseno En todo triángulo ABC, se tiene que: a2 = b2 + c2 – 2bc cos(α) b2 = a2 + c2 – 2ac cos(β) c2 = a2 + b2 – 2ab cos(γ) c sen(γ) b sen(β) a sen(α) 1. Encuentra la medida de los ángulos interiores y los lados faltantes del triángulo de la figura. Utiliza una calculadora para aproximar los resultados. 2. Considera el triángulo ABC de la figura. Determina la medida del lado faltante en cada uno de los casos. Utiliza una calculadora para aproximar los resultados. a. a = 4 m, b = 2 m y γ = 25º b. b = 6 cm, c = 15 cm y α = 25º 3. Tres pueblos A, B y C están unidos por carreteras rectas y planas. La distancia entre A y B es de 6 km, y entre B y C, 9 km. Si el ángulo formado por ambas carreteras es de 60º, ¿cuál es la distancia entre A y C? 4. Determina si es posible construir un triángulo que posea las siguientes características: a. Dos de sus ángulos miden 60º y 15º, y el lado comprendido entre ellos mide 30 cm. b. Dos de sus ángulos miden 75º y 45º, y el lado comprendido entre ellos mide 8 cm. c. Uno de sus lados mide 9 cm, otro 4 cm, y el ángulo opuesto a este 40º. Actividades C b γ α β A B a c 80º a b c A B C γ α β 50 cm 20º B A C UNIDAD 3 (106-163)C :Maquetación 1 4/11/10 17:16 Página 141
- 143. 142 | Unidad 3 Sistemas de medición de ángulos Para medir ángulos, hasta el momento has usado el conocido sistema sexagesimal, cuya unidad de medida es el grado. Un grado se puede subdividir usando minutos y segundos, de la misma manera que una hora se divide en minutos y segundos, donde un grado equivale a 60 minutos y un minuto a 60 segundos. Simbóli- camente, los minutos se representan por ’ y los segundos por ”. Para poder responder, debemos relacionar los minutos y segundos por separado a su equivalencia en grados. 12’ equivalen a 12 de los 60 minutos, que completarían 1º. 10’’ equivalen a 10 de los 3600 se- gundos que completan 1º. Lo anterior se debe a que 3600 segun- dos equivalen a 60 minutos. Luego, tendremos que: 2º 12’ 10’’ = . En cambio, si queremos expresar 13,5º en grados, minutos y se- gundos, tendremos que 13,5º = 13º + 0,5º. Como sabes que 60’ equivalen a un grado, entonces 0,5º serán 30’; por lo tanto, ten- dremos que: 13,5º = 13º 30’ 0’’. Ahora te presentaremos otro sistema para medir ángulos, pero antes te sugerimos que realices la siguiente actividad: 1. Dibuja con un compás una circunferencia y, luego, marca sobre un hilo de lana el radio de ella. Ver y 2. Coloca el hilo de lana sobre la circunferencia dibujada en el papel y marca sobre ella el radio de la circunferencia. Ver 3. Ahora tienes marcados dos puntos sobre tu circunferencia: únelos con el centro de ella y obtendrás así un ángulo. Ver 4. Con un transportador comprueba que el ángulo obtenido mide aproximadamente 57º. Este ángulo es lo que llamaremos un radián y será una nueva unidad de medida de ángulos. 2 4 3 1 2 12 60 10 3600 2 2 , º º + + ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ ≈ Analicemos... • ¿Cómo podemos expresar 2º 12’ 10’’ en grados, pero con deci- males?, ¿cómo lo supiste? • Si α = 13,5º, ¿cómo podemos expresar el ángulo α en grados, minutos y segundos?, ¿cómo lo averiguaste? 1 2 3 4 UNIDAD 3 (106-163)C :Maquetación 1 4/11/10 17:16 Página 142
- 144. El triángulo rectángulo y la trigonometría | 143 Como la longitud de una circunferencia es 2πr, donde r es su radio, entonces el número de radianes de un ángulo completo es 2π. Si la medida de un ángulo completo es 360º, podemos decir que 360º equivalen a 2π rad (radianes). Ejemplo Expresa en radianes el ángulo 135º. Sean x radianes equivalentes a 135º, como 360º equivalen a 2π rad, formamos la proporción: = ⇒ x = π = 3π 4 135 180 360 2π 135 x Unidad 3 En resumen • Un radián es la medida de un ángulo con vértice en el centro de un círculo de radio r, cuyos lados determinan sobre la circunferencia un arco de longitud igual al radio. • La relación de equivalencia entre grados y radianes es: 360º equivalen a 2π rad. Es decir, si α mide x grados e y radianes, se cumple que = . y 2π x 360 Luego, 135º equivalen a radianes. 3π 4 P A r r α α = x rad si = x AP r 1. Completa la siguiente tabla: 2. Expresa los siguientes ángulos en grados sexagesimales: a. rad c. rad e. rad g. rad 4π 9 2π 5 3π 4 π 15 Actividades Grados 0º 30º 45º 60º 90º 120º 135º 150º Radianes b. rad d. rad f. rad h. rad 7π 10 11π 4 2π 3 π 12 UNIDAD 3 (106-163)C :Maquetación 1 4/11/10 17:16 Página 143
- 145. 144 | Unidad 3 Funciones trigonométricas Consideremos la circunferencia unitaria, de radio 1 con centro en el punto (0, 0), es decir, en el origen de un sistema de coordenadas cartesianas. Observa. Notemos que en la circunferencia unitaria, dado uno de sus ángulos agudos, podemos formar un triángulo rectángulo con hipotenusa correspondiente al radio del círculo. Llamemos P(x, y) al punto que determina el ángulo α sobre la circunferencia, y AOP al triángulo rectángulo formado. La distancia entre el punto M y el centro de la circunferencia, en este caso el punto (0, 0), será: cos , π π 3 3 ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ sen Por lo tanto, el punto M pertenece a la circunferencia unitaria. Luego, la distancia entre el punto N(cos(α), sen(α)) y el centro de la circunferencia será: Analicemos... • ¿Pertenece el punto M a la circunferencia unitaria?, ¿cómo lo supiste? • Si α es un ángulo agudo cualquiera, ¿pertenecen los puntos de la forma N(cos(α), sen(α)) a la circunferencia unitaria?, ¿por qué? • En el triángulo rectángulo de la figura, ¿cuál es el valor de sen(α)?, ¿y cos(α)? cos , π π 3 3 ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ sen Si α es un ángulo con vértice en el origen del sistema de coordenadas y con lado adyacente coincidente con el eje X positivo, entonces α se considera positivo si se mide en el sentido contrario al avance del mi- nutero de un reloj, y se considera negativo si es en el mismo sentido. Pon atención La distancia entre dos puntos del sistema de coordenadas A(x1 , y1 ) y B(x2 , y2 ) se denota por d(A, B) y se calcula de la siguiente forma: . Si uno de los puntos corresponde al origen del sistema, denotaremos la distancia de un punto A a este por d(A, O). Recuerda que... d A B x x y y , ( )= − ( ) + − ( ) 1 2 2 1 2 2 O Y X x P A α y 1 1 –1 –1 α α 0 β 0 β Remplazamos recordando la identidad: cos2 (α) + sen2 (α) = 1 Remplazamos recordando la identidad: cos2 (α) + sen2 (α) = 1 d M O , cos ( )= ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ − ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ + ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ − ⎛ ⎝ π π 3 0 3 0 2 sen ⎜ ⎜ ⎞ ⎠ ⎟ 2 d M O , cos ( )= ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ + ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ 2 3 3 π π sen2 d M O , ( )= = 1 1 d N O , cos ( )= ( )− ( ) + ( )− ( ) α α 0 0 2 2 sen d N O , cos ( )= ( )+ ( ) 2 α α sen2 d N O , ( )= = 1 1 UNIDAD 3 (106-163)C :Maquetación 1 4/11/10 17:16 Página 144
- 146. El triángulo rectángulo y la trigonometría | 145 Unidad 3 Es decir, todos los puntos de la forma (cos(α), sen(α)) pertenecen a la circunferencia unitaria. Luego, en el triángulo AOP de la figura se tiene que: sen(α) = = y y cos(α) = = x. Podemos relacionar, para el punto P, la coordenada x con el coseno y la coordenada y con el seno. Por lo tanto, podemos escribir el punto P(x, y) como (cos(α), sen(α)), es decir, de manera tal que de- pende solo del ángulo α. Para calcular las razones trigonométricas de distintos ángulos siempre hemos considerado ángulos agudos, ya que realizamos los cálculos a partir de un triángulo rectángulo; sin embargo, la circunferencia unitaria nos permite definir las funciones seno y coseno para cualquier valor de α IR. En adelante se hablará de funciones trigonométricas, ya que a par- tir de la medida de un ángulo puedes obtener el valor de la razón en forma independiente del triángulo rectángulo que utilices. Luego, para cada α IR definimos el valor de las funciones trigo- nométricas coseno y seno como la primera y segunda coordenada de los puntos en la circunferencia unitaria, respectivamente. Podemos calcular algunos valores las funciones f(x) = sen(x) y g(x) = cos(x) para los principales ángulos utilizando la circunferen- cia unitaria. Observa la siguiente tabla: x 1 y 1 0 π 2 π 3π 2 2π g(x) = cos(x) 1 0 –1 0 1 f(x) = sen(x) 0 1 0 –1 0 P (1, 0) (0, 1) (–1, 0) (0, –1) (1, 0) El ángulo del centro es un ángulo formado por dos radios del círculo y su medida es igual a la del arco de circunferencia que subtiende el ángulo. Recuerda que... 1 –1 –1 –1 –1 –1 –1 –1 –1 1 Y X Y X Y X Y X Y X 1 –1 –1 1 UNIDAD 3 (106-163)C :Maquetación 1 4/11/10 17:16 Página 145
- 147. 146 | Unidad 3 Notemos que la medida del arco que va del punto (1, 0) al punto (cos(α), sen(α)) será α unidades (si α está en radianes), donde el perímetro de la circunferencia unitaria es 2π, por lo que, cada vez que avanzamos o retrocedemos esa longitud, volvemos al mismo punto. Observa en la tabla que f(0) = f(2π) y g(0) = g(2π). En general, para todo x IR tendremos que: sen(x) = sen(x ± 2π) cos(x) = cos(x ± 2π) Más aún, para todo x IR y k ⺪: sen(x) = sen(x ± 2kπ) cos(x) = cos(x ± 2kπ) Por esta razón es que las funciones seno y coseno se dicen periódi- cas, donde el período de ambas es 2π. En el gráfico de ambas fun- ciones podemos apreciar el período de estas claramente. Observa. Podemos observar que los gráficos de las funciones f(x) = sen(x) y g(x) = cos(x) tienen ciertas características en común: tienen una forma similar y ambas funciones tienen igual período; sin embargo, es importante aclarar que no todas las funciones trigonométricas tienen las mismas características. f(x) = sen(x) g(x) = cos(x) En resumen • Para obtener el valor función f(α) = sen(α) con α IR, utilizamos una circunferencia unitaria, donde sen(α) es igual a la ordenada del punto P(x, y), es decir, es el segmento que determina el punto P sobre el eje Y. • Para obtener el valor función f(α) = cos(α) con α IR, utilizamos una circunferencia unitaria, donde cos(α) es igual a la abscisa del punto P(x, y), es decir, es el segmento que determina el punto P sobre el eje X. UNIDAD 3 (106-163)C :Maquetación 1 4/11/10 17:16 Página 146
- 148. El triángulo rectángulo y la trigonometría | 147 Unidad 3 Herramientas tecnológicas Utilizando el programa GeoGebra, que puedes recordar cómo utilizarlo en la página 94 del Texto, construiremos el gráfico de distintas funciones trigonométricas. • Para cambiar las unidades del eje X a radianes, debes seguir las siguientes indicaciones: 1º En el menú Opciones, selecciona . 2º En la opción Unidad, selecciona π. A continuación, grafica las siguientes funciones trigonométricas: 1. Para cada una de las siguientes funciones trigonométricas, indica el dominio, recorrido y período de la función. a. f(x) = tan(x). b. g(x) = cotan(x), para esto debes introducirla en GeoGebra como y = 1/(tan(x)). c. h(x) = sec(x), debes introducirla en GeoGebra como y = 1/(cos(x)). d. m(x) = cosec(x), debes introducirla en GeoGebra como y = 1/(sin(x)). 2. A partir de las gráficas obtenidas, responde. a. ¿Qué similitudes y diferencias puedes observar entre f(x) = tan(x) y g(x) = cotan(x)? b. ¿Qué similitudes y diferencias puedes observar entre h(x) = sec(x) y m(x) = cosec(x)? 1. Prueba que las funciones trigonométricas del ángulo α no dependen del radio de la circunferencia utilizada para definirlas. Para esto, considera las circunferencias de radio r y r’ y calcula el valor de sen(α) y cos(α) en los triángulos OAP y OBP’. 2. ¿Cómo se definiría la tangente de un ángulo en la circunferencia unitaria? 3. ¿Para qué valores la función tangente es positiva y para cuáles negativa?, ¿por qué? 4. Sin calculadora, determina el signo de las siguientes funciones trigonométricas. Justifica tus respuestas. a. sen(113º) c. cos(–5º) e. cos(99º) b. cos d. cos f. sen(250º) 7 3 π ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ 9 5 π ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ Actividades P AB O P´ α UNIDAD 3 (106-163)C :Maquetación 1 4/11/10 17:16 Página 147
- 149. Miguel debe calcular el valor de sen(α), donde α = ; sin embargo, Para resolverlo, utiliza la circunferencia unitaria. Observa. 5 6 π 148 | Unidad 3 Reducción al primer cuadrante En el problema que debe resolver Miguel, debe calcular sen(α), donde α es un ángulo del segundo cuadrante; por lo tanto, su su- plemento, π – α, será un ángulo del primer cuadrante. Los triángulos de la figura son congruentes, ya que sus tres lados tienen igual medida; los catetos de ambos triángulos miden x e y, y la hipotenusa de estos mide 1, ya que corresponden a radios de la circunferencia; luego, por el criterio LLL, ambos triángulos son congruentes. Recordando que en la circunferencia unitaria tenemos que sen(α) = y y cos(α) = x, es decir, relacionamos el seno de αcon la ordenada del punto y el coseno con la abscisa. Luego, si observa- mos los puntos de la figura podemos observar que el valor de la ordenada es el mismo; en consecuencia, sen(α) = sen(π – α). En el problema de Miguel tendremos entonces que: sen = sen = sen = . Luego, si α es un ángulo del primer cuadrante, entonces su su- plemento, π – α, es un ángulo del segundo cuadrante. Podemos deducir que: sen(π – α) = y = sen(α) cos(π – α) = –x = –cos(α). Nota que para el caso del seno hay dos ángulos: uno en el primer cuadrante y otro en el segundo cuadrante, que tienen igual valor. 1 2 π 6 ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ π π − ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ 5 6 5 6 π ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ Analicemos... • ¿Qué ángulo α tiene igual ordenada que la del punto P?, ¿por qué? • ¿Podemos utilizar el mismo procedimiento para calcular sen(α), siendo α un ángulo del segundo cuadrante?, ¿por qué? • ¿Cuánto es el valor de sen ?, ¿cómo lo supiste? 5 6 π ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ 1 2 π 6 1 2 Y X Y X P(–x, y) P`(x, y) y y x –x α – - α solo conoce las razones trigonométricas para ángulos entre 0 y . π 6 En un sistema de coordenadas, los cuadrantes se numeran desde el eje X positivo. Recuerda que... II III I IV UNIDAD 3 (106-163)C :Maquetación 1 4/11/10 17:16 Página 148
- 150. El triángulo rectángulo y la trigonometría | 149 Ángulos del tercer cuadrante Si α es un ángulo del primer cuadrante, entonces (π + α) es un án- gulo del tercer cuadrante. Según la figura, podemos deducir que: sen(π + α) = –y = –sen(α) cos(π + α) = –x = –cos(α) Ángulos del cuarto cuadrante Sea α un ángulo del primer cuadrante, entonces (2π – α) es un ángulo del cuarto cuadrante. Según la figura, podemos deducir que: sen(2π – α) = –y = –sen(α) cos(2π – α) = x = cos(α) Observa que en el primer y cuarto cuadrante hay dos ángulos que tienen igual coseno. Notemos que para todo valor de α, se cumple que: cos(–α) = cos(α) sen(–α) = –sen(α) Unidad 3 P(–x, –y) P(x, –y) –x –y P`(x, y) P`(x, y) En resumen • Si α es un ángulo agudo, entonces: sen(π – α) = sen(α) cos(π – α) = –cos(α) • Si α es un ángulo agudo, entonces: sen(π + α) = –sen(α) cos(π + α) = –cos(α) • Si α es un ángulo agudo, entonces: sen(2π – α) = –sen(α) cos(2π – α) = cos(α) • Para todo ángulo α, se cumple que: cos(– α) = cos(α) sen(– α) = –sen(α) π+α 2π–α α α –α 1. Calcula el valor exacto de las razones trigonométricas seno, coseno y tangente de los siguientes ángulos: a. rad b. rad c. rad d. rad e. rad f. rad 2. Sin utilizar calculadora, encuentra los ángulos que satisfacen las condiciones siguientes. Recuerda que en algunos casos hay más de una solución, ya que α varía entre 0 y 2π. a. cos(α) = b. sen(α) = c. cos(α) = d. cos(α) = 1 5π 3 11π 6 7π 4 5π 4 4π 3 7π 6 2 2 3 2 3 2 Actividades UNIDAD 3 (106-163)C :Maquetación 1 4/11/10 17:16 Página 149
- 151. 150 | Unidad 3 Funciones trigonométricas inversas Natalia debe decorar el salón comunitario de su junta de vecinos. Para esto dispone de 21 planchas triangulares de madera. Ella quiere formar árboles con todas las planchas sobre una pared blanca sin que queden unas sobre otras, como los de la figura, pero solo tiene las medidas de los lados de cada plancha. En la situación anterior, para que las planchas triangulares no que- den unas sobre otras, debemos fijarnos en las medidas de los án- gulos cuyo vértice es común, ya que la suma de estos no debe exceder los 360º. Natalia solo dispone de las medidas de los lados de los triángulos, pero necesita saber los ángulos de cada figura para hacer el diseño. Recordando el teorema del coseno, si conocemos las medidas de los lados a, b y c de un triángulo, podemos obtener los ángulos despe- jando el valor de cos(α) en este: a2 = b2 + c2 – 2cb cos(α) Luego, 2cb cos(α) = b2 + c2 – a2 cos(α) = Ejemplo 1 Si a = 2, b = 3 y c = 4, obtenemos que cos(α) = 0,875; para poder en- contrar el valor de α, debemos hallar el valor del ángulo que cumpla que el coseno de este es igual a 0,875. Recordando las funciones trigonométricas, tenemos que la función f(x) = cos(x) nos entrega el coseno del ángulo, donde su dominio es el conjunto de los números reales; en este caso queremos calcu- lar el valor de un ángulo para distintos valores del coseno de este. b2 + c2 – a2 2cb Analicemos... • ¿De qué medida depende la cantidad de planchas que debemos utilizar para formar cada árbol?, ¿por qué? • ¿Puede la suma de los ángulos que tocan el centro de cada árbol ser mayor que 360º?, ¿cómo lo supiste? • ¿Cómo podemos obtener la medida de los ángulos de las plan- chas triangulares? Dividimos por 2cb UNIDAD 3 (106-163)C :Maquetación 1 4/11/10 17:16 Página 150
- 152. El triángulo rectángulo y la trigonometría | 151 La razones trigonométricas inversas son las que nos entregan un valor para cada ángulo, a partir de una ecuación de la forma cos(α) = k, si k IR. Luego, la función y = arccos(x), llamada función arcocoseno, con dominio en el intervalo [–1, 1], es la función inversa de y = cos(x), restringida a [0, π]. Por lo tanto, tendremos que para α [0, π], y k [–1, 1], se tiene que arccos(x) = α cos(α) = x. De modo similar, podemos definir las funciones trigonométricas inversas para las funciones seno y tangente. La función y = arcsen(x), llamada función arcoseno, con dominio en el intervalo [–1, 1], es la función inversa de y = sen(x), restringida a [– , ]. La función y = arctan(x), llamada función arcotangente, con dominio en los números reales, es la función inversa de y = tan(x), restringida a ]– , [. π 2 π 2 π 2 π 2 ↔ Unidad 3 En las calculadoras, la función arcoseno, por ejemplo, se obtiene con las teclas , o ,o bien, si existe. arccos INV cos cos SHIFT En resumen • La función trigonométrica inversa de y = cos(x) es y = arccos(x). Su dominio es [–1, 1] y su recorrido [0, π]. • La función trigonométrica inversa de y = sen(x) es y = arcsen(x). Su dominio es [–1, 1] y su recorrido [– , ]. • La función trigonométrica inversa de y = tan(x) es y = arctan(x). Su dominio el conjunto de los números reales y su recorrido ]– , [. π 2 π 2 π 2 π 2 1. Determina el valor de x, en el intervalo [0, π], sabiendo que cos(x) = . 2. Demuestra la igualdad arcsen – arcsen = . 3. Utiliza una calculadora para determinar el valor de y. Expresa los resultados en radianes y en grados. a. y = arccos(0,23) b. y = arcsen(0,9) c. y = arctan(–1) d. y = arctan(1) π 12 1 2 ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ 2 2 ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ 3 2 Actividades Pon atención UNIDAD 3 (106-163)C :Maquetación 1 4/11/10 17:16 Página 151
- 153. 152 | Unidad 3 Ecuaciones trigonométricas Victoria y Mario están buscando un ángulo que cumpla con la ecuación 2 cos(α) = 1. Victoria obtiene que α= , mientras que Mario obtiene que α= . 5π 3 π 3 En la situación presentada, para determinar si alguno o ambos resul- tados son correctos, basta con remplazar los valores obtenidos por Victoria y Mario y verificar si cumplen la ecuación dada. Observa. Victoria: 2 = 2 = 2 · = 1 Luego, ambos resultados son correctos. Esto se debe a que si α es un ángulo en el primer cuadrante, el valor de cos(α) se repite para un ángulo en el cuarto cuadrante (gráfico 1); si α es un ángulo en el segundo cuadrante, el valor de cos(α) se repite para un ángulo en el tercer cuadrante (gráfico 2). La abscisa de los puntos P y Q tiene el mismo valor, luego = . Recordando que cos(–α) = cos(α), también serán soluciones de la ecuación – y – , y que cos(α + 2kπ) = cos(α), las soluciones Ejemplo sen(α) = – Recordando las razones trigonométricas de ángulos especiales, tenemos que sen = , luego, como sen(–α) = –sen(α), ecuación sen(α) = – será α= – . π 4 2 2 2 2 π 4 ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ 2 2 cos 5 3 π ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ cos π 3 ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ 5π 3 π 3 1 2 cos π 3 ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ cos π 3 ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ Analicemos... • ¿Son ambos o alguno de los resultados correctos? • ¿Cuántas soluciones puede tener la ecuación dada? Explica. Mario: 2 = 2 = 2 = 2 · = 1 cos π 3 ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ cos 2 3 π π − ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ cos 5 3 π ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ 1 2 Y Y X X P(x, y) P(–x, y) Q(x, –y) Q(–x, –y) –1 –1 –1 –1 1 1 1 1 de la ecuación serán α = ± + 2kπ, ya que = – + 2π. π 3 5π 3 π 3 tendremos que sen = – , por lo tanto, una solución de 2 2 − ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ π 4 Gráfico 1 Gráfico 2 UNIDAD 3 (106-163)C :Maquetación 1 4/11/10 17:16 Página 152
- 154. El triángulo rectángulo y la trigonometría | 153 Luego, si α es un ángulo en el primer cuadrante, el valor de sen(α) se repite para un ángulo en el segundo cuadrante (gráfico 3); si α es un ángulo en el tercer cuadrante, el valor de sen(α) se repite para un ángulo en el cuarto cuadrante (gráfico 4). Recordando que sen(π – α) = sen(α), encontramos la otra solución: sen = sen . Por lo tanto, las soluciones de la ecuación Por consiguiente, toda ecuación trigonométrica se puede reducir a algunos de los siguientes casos: – sen(α) = x, en este caso sus soluciones están dadas por los va- lores de la forma α1 = 2kπ + arcsen(x) y α2 = 2kπ + π– arcsen(x), k ⺪, – cos(β) = y, en este caso sus soluciones están dadas por los valores de la forma β = 2kπ arccos(y), k ⺪, – tan(γ) = z, en este caso sus soluciones están dadas por los valores de la forma γ = kπ + arctan(z), k ⺪. 5 4 π ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ π π + ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ 4 Unidad 3 serán α1 = – + 2kπ y α2 = + 2kπ,k ⺪. 5π 4 π 4 En resumen • Una ecuación trigonométrica es una relación de igualdad entre expresiones trigonométricas que se verifican para algunos valores angulares. 1. Obtener todos los valores de x, expresados en radianes, que satisfacen cada una de las ecuaciones trigonométricas. a. 2 cos2 (x) + sen2 (x) = 3 d. sen(x)(2 – sen(x)) = cos(2x) b. tan(x) – cotan(x) = cosec(x) e. 2(sen(2x)) = 1 c. 2 cos(x) + 2 = 3 sec(x) f. (tan(x) – 1) (tan(x) + 3) = 2 tan(x) 2. ¿Para qué valores de a, una ecuación de la forma sen(α) = a no tiene solución?, ¿y cos(α) = a? Justifica tu respuesta. 2 Actividades Y X Q(–x, y) P(x, y) –1 –1 1 1 Y X Q(–x, y) P(x, y) –1 –1 1 1 Gráfico 3 Gráfico 4 UNIDAD 3 (106-163)C :Maquetación 1 4/11/10 17:16 Página 153
- 155. 154 | Unidad 3 • En el siguiente mapa conceptual se muestran los conceptos tratados en las páginas anteriores. • Utilizando los contenidos aprendidos hasta aquí, y apoyándote en el esquema anterior, responde en tu cuaderno. 1. ¿Crees que faltó un concepto importante en el mapa conceptual?, ¿cuál? Agrégalo. 2. ¿Se pueden calcular las razones trigonométricas a partir de un triángulo cualquiera? 3. ¿Qué equivalencia hay entre grados y radianes? 4. ¿Qué diferencia hay entre una razón trigonométrica y una función trigonométrica? 5. ¿Cuál es el dominio de la función f(x) = sen(x)?, ¿y de g(x) = cos(x)?, ¿y de h(x) = tan(x)? 6. En un triángulo rectángulo, ¿a qué teorema se reduce el teorema del coseno? 7. ¿Qué es una circunferencia unitaria?, ¿qué utilidad tiene en trigonometría? 8. ¿En qué cuadrantes es positiva la función f(x) = tan(x)? 9. ¿Qué relación hay entre funciones trigonométricas inversas y ecuaciones trigonométricas? 10. ¿Tienes alguna duda sobre los conceptos tratados en las páginas anteriores?, ¿cuál? Compártela con tu curso e intenten aclararla en conjunto. Organizando lo aprendido TRIGONOMETRÍA SISTEMA DE MEDICIÓN DE ÁNGULOS TRIÁNGULO RECTÁNGULO relaciona a partir de él se calculan se extienden a se resuelven existen SEXAGESIMAL su unidad es su unidad es FUNCIONES TRIGONOMÉTRICAS ECUACIONES TRIGONOMÉTRICAS FUNCIONES TRIGONOMÉTRICAS INVERSAS RADIAL GRADO RADIÁN RAZONES TRIGONOMÉTRICAS tienen UNIDAD 3 (106-163)C :Maquetación 1 4/11/10 17:16 Página 154
- 156. El triángulo rectángulo y la trigonometría | 155 Unidad 3 Mi progreso 1. Determina los valores de las siguientes expresiones: a. cos2 c. tan + sen 2. Determina cuáles de las siguientes relaciones son verdaderas y cuáles son falsas. Explica, en cada caso, tu decisión. a. sen2 (α) + cos2 (α) = tan2 (α) d. sen(α) + cos(α) = 1 b. sen2 (α) = 1 – cos2 (α) e. (sen(α) + cos(α))2 = 1 + tan2 (α) c. 1 + tan2 (α) = cosec2 (α) f. cos(α) · tan(α) = sen(α) 3. Las soluciones de la ecuación 2cos(x) = –1 son: A. + 2kπ, k ⺪ D. ± + 2kπ, k ⺪ C. ± + 2kπ, k ⺪ 4. Resuelve el siguiente problema explicando, paso a paso, tu desarrollo. a. En un triángulo rectángulo de lados 6, 8, 10, con ángulo α opuesto al cateto menor, escribe las razones trigonométricas seno, coseno y tangente de α. 2 3 π ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ π 6 ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ π 6 ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ π 3 ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ π 6 ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ π 4 ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ • Verifica en el solucionario del Texto si tus respuestas son correctas. Si tuviste respuestas incorrectas, marca en la tabla el criterio correspondiente y revisa las páginas indicadas. Luego, identifica el error y corrígelas. ¿Cómo voy? CRITERIO ÍTEM PÁGINAS DONDE SE TRABAJA Calcular expresiones que involucran razones trigonométricas. 1 126 a 131 Identificar expresiones correspondientes a identidades trigonométricas. 2 134 a 137 Resolver ecuaciones trigonométricas. 3 142 a 153 Resolver problemas que involucran razones trigonométricas. 4 126 a 133 Unidad 3 b. sen – sec d. sen + cos π 4 ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ π 4 ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ π 6 ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ π 2 ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ B. + 2kπ, k ⺪ E. ± + kπ, k ⺪ 5 6 π ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ 5 6 π ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ UNIDAD 3 (106-163)C :Maquetación 1 4/11/10 17:16 Página 155
- 157. Cómo resolverlo 156 | Unidad 3 Observa, paso a paso, las estrategias utilizadas en la resolución de los siguientes problemas. Ejercicio 1 Determina la pendiente de la recta que pasa por el punto C(1, 2) y forma con el eje X un ángulo de 45º. ¿Cómo se relaciona la trigonometría con la ecuación de una recta dada? Solución La recta cuya pendiente debemos determinar, gráficamente será: Si consideramos el triángulo ABC formado por el punto C, un punto cualquiera pertene- ciente a la recta A, que corres- ponde a la intersección de la recta con el eje de las abscisas y el punto B, que es la proyección del punto C sobre el eje X. Luego, el triángulo ABC es rec- tángulo en B; por lo tanto, podemos calcular las razones trigono- métricas a partir de este, donde tendremos que: tan(45º) = = . Donde tendremos que si las coordenadas de A son (x1 , y1 ) y C son (x2 , y2 ), podemos terminar la medida de los segmentos BC y AB de la siguiente forma: tan(45º) = = . Luego, recordando que la pendiente de una recta que pasa por los puntos (x1 , y1 ) y (x2 , y2 ) está dada por: m = , tendremos que la pendiente de la recta equivale a la tangente del ángulo que forma esta con la horizontal. Luego, como tan(45º) = 1, tendremos que m = 1; es decir, la pendiente de la recta es 1. BC AB y2 – y1 x2 – x1 y2 – y1 x2 – x1 BC AB cateto opuesto cateto adyacente C B A 45º UNIDAD 3 (106-163)C :Maquetación 1 4/11/10 17:16 Página 156
- 158. El triángulo rectángulo y la trigonometría | 157 Unidad 3 Ejercicio 2 Determina el ángulo formado por la intersección de las rectas L1 : y L2 : Solución Llamemos α al ángulo formado por la intersección de ambas rec- tas, β y γ a los otros ángulos interiores del triángulo formado por L1 , L2 y el eje X, y θ al ángulo adyacente a γ. Observa. tan(β) = pendiente de L1 tan(β) = Por lo tanto, β = 30º Luego, tan(θ) = pendiente de L2 = – . Entonces, θ = 120º Por lo tanto, γ = 60º Ahora podemos determinamos el valor de α: α + β + γ = 180º α = 180º – β – γ = 180º – 30º – 60º = 90º Finalmente, el ángulo de intersección entre L1 y L2 mide 90º. 1 3 3 y x = − 8 3 y x = − 3 1 Actividades 1. Aplica el procedimiento aprendido para resolver las siguientes situaciones: a. Halla la ecuación de la recta que pasa por el punto (–2, 1) y cuyo ángulo de inclinación es 30º. b. Determina la medida del ángulo formado por la intersección de las rectas L1 : y L2 : y = x – 3. 2. Busca un procedimiento distinto para resolver los problemas anteriores. Respecto del procedimiento previo, ¿cuál es más simple?, ¿por qué? 3. Resuelve el siguiente problema empleando el método aprendido u otro. Compara el procedimiento que utilizaste con el de algún compañero o compañera. ¿Cuál es más simple?, ¿por qué? La recta R es paralela a la recta x – 2y – 2 = 0. Determina el ángulo de inclinación de la recta. y x = − 3 1 A L2 L1 C B Ya que αABC corresponde al ángulo formado entre L1 y el eje X Ya que tan(30º) = Recordando que en una ecuación de la forma y = mx + n, m corresponde al valor de la pendiente Ya que tan(120º) = – Ya que γ y θ son ángulos suplementarios Ya que α, β y γ son los ángulos interiores de un triángulo α γ θ β UNIDAD 3 (106-163)C :Maquetación 1 4/11/10 17:16 Página 157
- 159. 158 | Unidad 3 En terreno En terreno Mediciones en nuestro entorno La Trigonometría, rama de la Matemática que estudia las relaciones métricas entre las medidas de los ángulos y los lados de un triángulo, ha servido al ser humano como instrumento para resolver problemas tales como determinar distancias inal- canzables, es decir, que no pueden ser medidas por instrumentos como una regla o huincha. Estas las podemos calcular conociendo algunas medidas y el ángulo de elevación o depresión a cierto objeto. Para calcular un ángulo de depresión o elevación a cierto objeto, existen instrumen- tos como el astrolabio, sextante o transportador; luego, utilizando las herramientas que nos entrega la Trigonometría, podemos determinar la altura a la que se en- cuentra el objeto. Si un observador de altura x se encuentra frente a un objeto de altura h y a una distancia d desde la base del objeto, y α es el ángulo de elevación a este desde el observador, podemos determinar la altura del objeto, mediante la expresión: h = d · tan(α) + x De esta forma, es posible medir la altura de árboles, edificaciones, cerros y, en general, objetos de grandes alturas. UNIDAD 3 (106-163)C :Maquetación 1 4/11/10 17:16 Página 158
- 160. Actividades 1. Si un observador de 1,62 m de altura se encuentra a 5 m de la base de un edificio y observa el punto más alto de este con un ángulo de elevación de 30º, ¿cuál es la altura aproximada del edificio? 2. Si en la pregunta anterior el observador se aleja 2 metros de la base del edificio, ¿en cuánto varía el ángulo de elevación? 3. Si el ángulo de elevación con que se observa un objeto es de 45º, ¿cuál será la expresión que determina la altura de este? Investiguemos... Ahora, trabajen en grupos de tres personas. 1. Comparen las respuestas obtenidas por cada uno y discutan cuáles de las respuestas son correctas, si es que existen diferencias. 2. Utilizando un compás, dibuja sobre un pedazo de cartón un cuarto de circunferencia de mínimo 10 cm de radio. 3. Mediante el transportador y la regla, traza líneas como si fueran radios de la circunferencia, de modo que formen ángulo de 5º, 10º, 15º, …, 90º, indicando en la circunferencia los valores de los ángulos. 4. Dobla el hilo por la mitad, y en el extremo que tiene las puntas del hilo amarra una tuerca, o un ob- jeto similar, de manera de formar un péndulo. 5. Usando una tachuela o corchete, une el péndulo formado al centro del cuarto de circunferencia. Luego, pega con una cinta adhesiva una bombilla o el tubo de un lápiz al borde superior de cartón. Hemos construido un astrolabio, el cual utilizaremos para calcular distancias inaccesibles. 6. Desde el patio de tu colegio, mide con tu astrolabio el ángulo de elevación al extremo más alto del borde del techo. Luego, utilizando una huincha, determina la altura a la que estaba el astrolabio y la distancia en el piso desde el lugar de medición hasta el borde del colegio. Utilizando una calculadora, encuentra una aproximación para la altura del colegio. Compara tu resul- tado con el de tus compañeros y compañeras. 7. Utiliza el mismo procedimiento anterior para medir la altura de distintos objetos, como, por ejemplo, la puerta de tu sala, un árbol del patio de tu colegio o la altura de tu sala de clases, y anota tus resultados. Evaluemos nuestro trabajo • Comparen los resultados obtenidos. ¿Son similares? Si no es así, ¿qué diferencia hubo?, ¿a qué crees que se debe? • Averigua o mide las medidas exactas de los objetos con los cuales trabajaste y, luego, compara los valores con tus resultados obtenidos. ¿Son similares? El triángulo rectángulo y la trigonometría | 159 Unidad 3 UNIDAD 3 (106-163)C :Maquetación 1 4/11/10 17:16 Página 159
- 161. 160 | Unidad 3 Síntesis de la Unidad A continuación, se presentan los conceptos fundamentales trabajados en la Unidad. Construye con ellos un mapa conceptual, en tu cuaderno. No olvides agregar las palabras de enlace que indican las relaciones entre los conceptos. A partir de lo trabajado en la Unidad, responde: 1. ¿Cuáles son los elementos de un triángulo rectángulo? 2. ¿Qué relaciones hay entre las funciones seno, coseno y tangente para un mismo ángulo? 3. ¿Qué relación hay entre seno de un ángulo y coseno del ángulo complementario? 4. ¿Qué es un radián? 5. ¿Qué es una identidad trigonométrica? 6. ¿Qué relación tienen las funciones f(x) = arccos(x) y g(x) = cos(x)?, ¿por qué? 7. ¿Qué significa resolver una ecuación trigonométrica? 8. ¿Qué relación hay entre una ecuación trigonométrica y las funciones trigonométricas inversas? 9. ¿Tienes alguna duda sobre los conceptos tratados en las páginas anteriores?, ¿cuál? Compártela con tu curso e intenten aclararla en conjunto. TRIGONOMETRÍA TRIÁNGULO RECTÁNGULO SENO FUNCIONES TRIGONOMÉTRICAS FUNCIONES TRIGONOMÉTRICAS INVERSAS ECUACIONES TRIGONOMÉTRICAS TEOREMA DEL SENO Y DEL COSENO COSENO TANGENTE UNIDAD 3 (106-163)C :Maquetación 1 4/11/10 17:16 Página 160
- 162. El triángulo rectángulo y la trigonometría | 161 Evaluación I. Determina si las expresiones siguientes son verdaderas o falsas. Justifica tu respuesta. 1. En un triángulo rectángulo, el coseno de un ángulo es la medida del cateto adyacente a este. 2. En un triángulo rectángulo, el seno de un ángulo es el cociente entre la medida del cateto opuesto al ángulo y la hipotenusa. 3. En un triángulo rectángulo, la tangente de un ángulo es el cociente entre el coseno y el seno de este. 4. Para todo número real x, se cumple sen(arcsen(x)) = x. 5. Para todo número real x, se cumple arcsen(sen(x)) = x. II. Aplica lo que aprendiste en la Unidad para desarrollar las siguientes actividades: 1. En un triángulo ABC, rectángulo en A, sen(α) = , calcular: a. cos(α) b. tan(α) c. sec(α) d. cotan(β) e. cosec(α) f. sec(β) 2. Resuelve los siguientes problemas: a. Si tan(α) = , y α es un ángulo agudo, calcula el resto de las razones trigonométricas para el ángulo α. b. Si tan(α) = , calcula el valor de . c. Si α es un ángulo agudo y sec(α) = , calcula el valor de . 3. Resuelve las siguientes ecuaciones trigonométricas: a. 3 cos(x) = 1 b. sen(x) = 1 c. 4 cos(x) + 2 = 0 d. 3 tan(x) = 5 3 2 2 sen(α) – 3 cos(α) 4 cosec(α) + 9 cotan(α) 13 5 a sen(α) – b cos(α) a sen(α) + b cos(α) a b 5 4 2 3 Unidad 3 A B β α C UNIDAD 3 (106-163)C :Maquetación 1 4/11/10 17:16 Página 161
- 163. 162 | Unidad 3 1. En el triángulo ABC rectángulo en C, se afirma que: I. a2 + q2 = b2 + p2 II. h2 = p · b III. h2 = De estas afirmaciones, es o son verdaderas: A. Solo I B. Solo II C. Solo III D. I y II E. I y III 2. (DEMRE 2004) ¿Cuál de las siguientes expresiones representa a la tangente de α? A. C. E. Ninguna de las anteriores. 3. Si sen(α) = y α es un ángulo agudo, entonces, de las siguientes afirmaciones son verdaderas: I. cos(α) = III. cosec(α) = A. Solo I B. Solo II C. Solo III D. I y III E. I, II y III 4. El valor de la expresión sen2 (45º) + cos2 (30º) es: A. C. E. Ninguna de las anteriores. 5. ¿Para cuál de los siguientes ángulos se tiene que la tangente de este es un número negativo? A. 181º B. 335º C. 85º D. 0,52º E. 258º 6. ¿Qué altura tiene un árbol si proyecta una sombra de 20 m, cuando el ángulo de elevación del Sol es de 50º? A. 23,8 m B. 15,3 m C. 12,8 m D. 16,8 m E. 1,53 m a2 b2 c2 1 sen(α) sen(α) cos(α) 5 4 2 3 2 + ( ) 2 3 7 7 5 5 7 III. Resuelve los siguientes ejercicios y selecciona la alternativa correcta en cada caso. B C A p q h a b II. sec(α) = 3 6 B. 2 3 4 2 + ( ) D. 5 4 B. cos(α) sen(α) D. 1 cos(α) UNIDAD 3 (106-163)C :Maquetación 1 4/11/10 17:16 Página 162
- 164. El triángulo rectángulo y la trigonometría | 163 7. En la figura, BD = 100 dm. Entonces, AC mide: A. dm B. dm C. dm D. dm E. dm 8. La figura representa los planos de las cerchas del techo de una casa. ¿Cuánto mide la altura del techo? A. 12,25 m B. 5,22 m C. 1,78 m D. 1,53 m E. 1,22 m 9. En la figura, el valor de x es: A. 3 cos(20º) B. 3 tan(20º) C. E. 3 sen(20º) 10. ¿Cuál o cuáles de las siguientes afirmaciones es o son verdaderas? I. sen2 + cos2 = 1 III. sen = sen A. Solo I B. Solo II C. Solo III D. I y II E. II y III 11. ¿Cuál de las siguientes alternativas es falsa? A. sen2 (α) = 1 – cos2 (α) B. cos(15º) = cos(345º) C. –1 tan(α) 1, para a entre 0 y 2π D. sen(40º) = –sen(220º) E. tan(α) = 12. (DEMRE, 2004) ¿Cuál o cuáles de las siguientes expresiones representan el largo de la escalera de la figura? I. metros III. 1,2 · cos(70º) metros A. Solo I B. Solo II C. Solo III D. I y II E. I y III 1,2 sen(20º) sen(α) cos(α) 15 3 3 sen(20º) π 9 ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ 7 18 π ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ 8 9 π ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ π 9 ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ 25 3 50 3 100 3 150 3 Unidad 3 Verifica en el solucionario de tu Texto si tus respuestas son correctas. ¿Te equivocaste en alguna?, ¿cuál fue el error? Explícalo y resuelve correctamente el ejercicio. II. sen = cos 7 18 π ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ π 9 ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ C A D B 30º 60º 20º 30º 8 D. 3 cos(20º) II. metros 1,2 cos(20º) 20º 70º 1,2 m 20º 3 x UNIDAD 3 (106-163)C :Maquetación 1 4/11/10 17:16 Página 163
- 165. Inecuaciones lineales 4 164 |Unidad 4 Desigualdades Intervalos Operaciones entre intervalos Inecuaciones Valor absoluto Gráficos Expresar información diversa a través de desigualdades. Utilizar desigualdades para representar conjuntos numéricos. Conocer y aplicar procedimientos para resolver inecuaciones y sistemas de inecuaciones lineales con una incógnita. Determinar la existencia y pertinencia de las soluciones de una inecuación. Plantear y resolver problemas que involucren inecuaciones y sistemas de inecuaciones lineales con una incógnita. Resolver ecuaciones e inecuaciones que involucren valor absoluto. Graficar la solución de una inecuación o de un sistema de inecuaciones lineales con dos incógnitas. TRABAJANDO CON: APRENDERÁS A: UNIDAD 4 (164-199)C :Maquetación 1 4/11/10 17:18 Página 164
- 166. Inecuaciones lineales | 165 Conversemos de... La Dirección Meteorológica de Chile entrega información y pronóstico de la radiación UV-B, que es la radiación UV más peligrosa que llega a la superficie de la Tierra. El gráfico muestra la variación del índice UV para UV-B en Santiago durante algunos días de diciembre de 2009. La recomendación de la Dirección Metereoló- gica de Chile, cuando el índice alcanza valores iguales o mayores que 11, es: “Evite salir du- rante las horas centrales del día. Busque la sombra. Son imprescindibles camisa, crema de protección solar y sombrero. Use lentes de sol con filtro UV-B y UV-A”. • Investiga sobre los peligros a la piel que trae el exponerse frecuentemente al sol cuando el índice es alto, muy alto o extremadamente alto. • Averigua el rango promedio para el índice UV-B en tu comuna. ¿Necesitas tomar precauciones? 0 12-12 13-12 2 4 6 8 10 12 14 Índice 14-12 15-12 16-12 17-12 18-12 19-12 20-12 21-12 11 11 11 11 12 13 12 10 12 11 Fuente: Dirección Metereológica de Chile, en www.meteochile.cl, consultado en diciembre de 2009. Días Latinstock UNIDAD 4 (164-199)C :Maquetación 1 4/11/10 17:18 Página 165
- 167. 166 | Unidad 4 ¿Cuánto sabes? 1. Expresa la relación de orden contenida en las siguientes afirmaciones, usando los símbolos , , o . Guíate por el ejemplo. El número de estudiantes n es superior a 15 n 15. a. El precio de la entrada p no supera los $ 3000. b. El promedio de edades x es por lo menos 30 años. c. La ganancia que obtuvo g no fue menor de $ 12 000. d. La nota n de Pedro no alcanzó el 6,0. 2. Responde los números obtenidos en cada caso. a. ¿Qué números naturales cumplen con la condición de ser mayores que 3 y menores o iguales que 10? b. ¿Qué números naturales cumplen con la condición de que su doble no sobrepase a 10? c. ¿Qué números naturales cumplen con al menos una de las condiciones dadas en a y en b? d. ¿Qué números naturales cumplen simultáneamente con las condiciones dadas en a y en b? 3. Describe con tus palabras el tipo de número que pertenecen a los siguientes conjuntos numéricos: ⺞, ⺪, ⺡, ⺙, IR. 4. Completa siguiente la tabla, indicando el o los conjuntos a los que pertenece cada número. Recuerda lo que aprendiste en años anteriores y resuelve en tu cuaderno. ⺞ ⺪ ⺡ ⺙ IR 2 –2,43 3 4 π 3 2 + UNIDAD 4 (164-199)C :Maquetación 1 4/11/10 17:18 Página 166
- 168. 5. Determina cuál o cuáles de las siguientes expresiones corresponden a la ecuación de una línea recta; luego, grafícalas. a. y = 3x + 1 c. 2x2 + 5y = 0 e. x – 6 = 4 b. 2y = 6 d. x + y + 3 = 0 f. y = x – 1 + 3x 6. Resuelve las siguientes ecuaciones. Explica, paso a paso, cómo lo hiciste. a. 3x – + 8 = 2x b. = c. 2x – 1 = 2x + 7. Resuelve los siguientes sistemas de ecuaciones. Explica, paso a paso, el procedimiento utilizado. a. x + 2y = 1 b. 6x – 2y = –4 c. 2x + 3y = 12 3x – 2y = 12 3x – y = 1 6x + 9y = 36 Verifica en el solucionario de tu Texto si tus respuestas son correctas. ¿Te equivocaste en alguna?, ¿cuál fue el error? Explícalo y resuelve correctamente el ejercicio. 3 2 x2 x + 3 3x – 2 5 x 5 Inecuaciones lineales | 167 Unidad 4 ¿Qué debes recordar? • Una ecuación es una igualdad que contiene al menos un valor desconocido llamado incógnita. Ejemplo: 2x – 5 = 3. • Resolver una ecuación es encontrar el o los valores de la incógnita que satisfacen la igualdad. Ejemplo: x = 4 es solución de la ecuación 2x – 5 = 3. • Toda expresión que se pueda escribir de la forma ax + by + c = 0 con a, b y c números reales, representa una recta en el plano. Además, si a = 0, la expresión anterior representa una recta horizontal; si b = 0, se trata de una recta vertical. • Un sistema de ecuaciones consiste en varias ecuaciones con varias incógnitas. Ejemplo: x + y = 1 5x – 2y = 11 • Resolver un sistema de ecuaciones es encontrar todos los grupos de valores de las incógnitas, de modo que cada grupo satisface todas las ecuaciones del sistema. Ejemplo: {x = 2, y = 1} es el único grupo que resuelve el sistema x + y = 3 x – y = 1 UNIDAD 4 (164-199)C :Maquetación 1 4/11/10 17:18 Página 167
- 169. 168 | Unidad 4 Desigualdades Analicemos... El índice UV solar mundial (IUV) es un indicador de la intensidad de la radiación ultravioleta (UV) solar en la superficie terrestre. La Or- ganización Mundial de la Salud (OMS) ha presentado el IUV para estandarizar la medición de la radiación ultravioleta en el mundo, a fin de establecer una medida común frente al daño a la piel pro- ducido por la exposición directa a dicha radiación. El IUV se re- dondea a números enteros que miden la intensidad promedio del máximo de radiación recibida en la superficie terrestre, en cuatro horas alrededor del mediodía. La OMS da valores promedio de IUV para distintas zonas del planeta, y se informa, por los medios de co- municación, el rango de valores esperados según su peligrosidad para la piel. Observa. En la situación anterior, el riesgo Moderado corresponde al rango para el IUV entre 3 y 5, ambos incluidos, es decir, cumple dos condi- ciones; que 3 IUV y que IUV 5. Cuando ocurre esto, se puede abreviar de la siguiente manera: 3 IUV 5. Por otra parte, tene- mos que el riesgo es Alto cuando 6 IUV 7. Como los valores del IUV se redondean a números enteros, el rango de valores para riesgo Moderado y Alto es 3 IUV 7. La categoría de exposición es Baja cuando el IUV 2, es decir, para valores menores o iguales a 2. Es considerada Muy Alta para va- lores del IUV de 8 a 10, es decir, para el 8 IUV 10, y Extremada- mente Alta si IUV 11. Lo que hemos realizado es representar el rango de valores para el IUV por medio de desigualdades. Una desigualdad es una expre- sión matemática que sirve para representar que cierta cantidad es mayor o menor que otra. La desigualdad siempre contiene alguno de los signos: , , , . • ¿Qué rango del índice corresponde a las categorías de riesgo Moderado y Alto? • ¿Cómo podemos representar el rango de valores del IUV por medio de desigualdades?, ¿cómo lo supiste? • ¿Es correcto decir que si el IUV 6 y IUV 7, la categoría de exposición es Alta?, ¿podrías expresar lo mismo con la desigual- dad 6 IUV 7?, ¿por qué? Categoría de exposición Rango de valores del IUV Baja hasta 2 Moderada de 3 a 5 Alta de 6 a 7 Muy alta de 8 a 10 Extremadamente alta desde 11 Fuente: Organización Mundial de la Salud, en www.who.int/es/, consultado en diciembre de 2009. UNIDAD 4 (164-199)C :Maquetación 1 4/11/10 17:18 Página 168
- 170. Inecuaciones lineales | 169 Unidad 4 Ejemplo 1 (3 - 1)2 32 – 12 , es una desigualdad numérica que puedes verificar fácilmente calculando el valor de cada lado de la desigualdad, es decir: (3 – 1)2 32 – 12 4 8 Ejemplo 2 En ciertos tramos de las carreteras, la velocidad máxima permitida es de 120 kilómetros por hora. Luego, si representamos por v la velocidad medida en km/h, se tiene: v 120. En resumen • Se denomina desigualdad a toda relación que se establece entre números reales mediante la comparación “menor que” (), “menor o igual que” (),”mayor que” (), o “mayor o igual que” (). • Una desigualdad se cumple si la relación establecida es verdadera. 1. Determina si las siguientes desigualdades son verdaderas o falsas. Justifica. a. 7 b. 1 c. 2. Expresa la siguiente información utilizando desigualdades. a. Para un índice de radiación ultravioleta igual a 10, las personas de piel más sensible (aquellas que se queman con facilidad y nunca se broncean) no deben exponerse al sol sin protección más de 18 minutos. b. Una recomendación general es que se utilice un protector solar con factor de protección 15 o mayor. c. Se considera que la calidad del aire es “regular” si el ICAP es superior a 100 y menor o igual a 200. d. En un examen que mide la cantidad de glucosa en la sangre de una persona adulta, se consideran normales los valores que van de 64 a 110 mg/dL (miligramos por decilitro). 3. Se sabe que la medida de cada lado de un triángulo es menor que la suma de las medidas de los otros dos y mayor que su diferencia. En cierto triángulo, dos de los lados miden 6 cm y 19 cm. Expresa con una desigualdad el rango de posibles valores para la medida del tercer lado. 3 5 · 3 + 5 2 2 · 3 · 5 3 + 5 1,08 – 0,03 0,001 (7 + 2)2 22 Actividades UNIDAD 4 (164-199)C :Maquetación 1 4/11/10 17:18 Página 169
- 171. 170 | Unidad 4 Intervalos de números reales Analicemos... El índice de masa corporal (IMC) es una medida de asociación entre el peso y la talla de un individuo, y corresponde a la razón entre la masa corporal y el cuadrado de la estatura de una persona. Diversos estudios realizados han concluido que el grupo de mejor salud corresponde a un IMC comprendido entre 20 y 25 . kg m2 Para determinar el IMC de una persona, podemos utilizar la siguiente fórmula: IMC = . En la situación anterior, si remplazamos en la fórmula para el cálculo del IMC las medidas de Pedro, obtenemos: 23,03. Luego, el IMC de Pedro es aproximadamente 23,03, el cual cumple que 20 IMC 25; por lo tanto, se puede considerar como una persona saludable. Sabemos que si el IMC de María es tal que 20 IMC 25, se con- sideraría saludable. Como conocemos su estatura, podemos rem- plazarla en la fórmula y, considerando la desigualdad anterior, tendremos que: 20 25 20 25 51,2 masa 64 masa 2,56 masa (estatura)2 65 (1,68)2 masa kg estatura2 m2 • Si Pedro mide 1,68 m y su masa es 65 kg, ¿cuánto es su IMC?, ¿se puede considerar como una persona saludable? • María mide 1,6 m. Para ser considerada saludable, ¿cuáles son los posibles valores para su masa?, ¿por qué? Remplazamos la estatura de María Multiplicamos por 2,56 20 25 masa 1,62 Médico registrando la masa de un paciente. UNIDAD 4 (164-199)C :Maquetación 1 4/11/10 17:18 Página 170
- 172. Inecuaciones lineales | 171 Unidad 4 Lo anterior significa que María debe tener una masa entre 51,2 y 64 kilogramos, incluidos ambos valores, para ser considerada en la categoría saludable. Si quisiéramos hacer una lista de los posibles valores de la masa de María para ser considerada como saludable, no podríamos escribir- los en una secuencia ordenada sin omitir muchos de ellos, ya que estos valores forman un conjunto que tiene infinitos elementos. En casos como estos, podemos representar el conjunto de los posi- bles valores como un intervalo de números reales, utilizando la no- tación [51,2, 64]. Observa que los paréntesis son cerrados en ambos extremos, esto es porque se consideran dentro del intervalo los valo- res 51,2 y 64. En caso de que no los incluyera, se escribiría ]51,2, 64[. Otra forma de representar este intervalo es gráficamente, de la siguiente manera: Observa que en los valores 51,2 y 64 hay un círculo pintado, esto es porque incluye ambos valores. En caso de que no los incluyera, se dibujaría un círculo blanco en cada valor. Ejemplo 1 Considera los intervalos A = ]–1, 10[ y B = [5, +[. Determina A B y A B. A B corresponde al conjunto que contiene todos los números que están entre –1 y 10 o aquellos que son mayores o iguales que 5. Es probable que no te sea difícil observar que A B = ]–1, +[. Representaremos de manera gráfica lo anterior. En la figura que sigue, se ha coloreado con verde la porción de recta que corresponde al conjunto A, y con rojo la que representa a B. Entonces, A B corresponde a todo lo que ha quedado coloreado, ya sea con verde por pertenecer a A, o con rojo por pertenecer a B. 51,2 64 ]–1, 10[ representa a todos los números n que cumplen: –1 n 10. [5, +[ representa a todos los números n que cumplen: 5 n. + y – no son números, estos símbolos se utilizan para representar el concepto de infinito. significa unión. significa intersección. Recuerda que... 5 10 –1 UNIDAD 4 (164-199)C :Maquetación 1 4/11/10 17:18 Página 171
- 173. De la misma figura podemos deducir que A B corresponde a todos los números que están entre –1 y 10, y que además son mayores o iguales que 5. En el gráfico, esto es lo que ha quedado coloreado con verde y rojo simultáneamente, es decir, A B = [5, 10[. Ejemplo 2 Sea C = [1, 5] y D = ]7, +[. Determina C D y C D. Se tiene que C D = , puesto que dichos conjuntos no tienen ele- mentos en común; luego, la unión de ellos solo se puede expresar como C D = [1, 5] ]7, +[. Observa. 172 | Unidad 4 En resumen • Dados dos números reales a y b, con a b, se definen los intervalos que aparecen en la siguiente tabla. Conjunto Notación Representación gráfica Tipo de intervalo {x IR / a x b} [a, b] Intervalo cerrado {x IR / a x b} ]a, b[ Intervalo abierto {x IR / a x b} [a, b[ Intervalo semiabierto {x IR / a x b} ]a, b] {x IR / x a} [a, +[ Intervalos no acotados o infinitos {x IR / x a} ]a, +[ {x IR / x b} ]–, b] {x IR / x b} ]–, b[ b a b a b a b a a a b b 7 1 5 representa al conjunto sin ele- mentos, llamado conjunto vacío. Recuerda que... UNIDAD 4 (164-199)C :Maquetación 1 4/11/10 17:18 Página 172
- 174. Inecuaciones lineales | 173 Unidad 4 1. Considera los siguientes números: 0, π, , y . a. Encuentra un intervalo que contenga a todos estos números. b. Encuentra un intervalo que no contenga a ninguno de ellos. c. Para cada número, encuentra un intervalo que lo contenga, y cuyos extremos sean números enteros consecutivos. d. Explica cómo lo hiciste en cada caso. 2. Expresa como intervalo y representa gráficamente los siguientes conjuntos: a. {x IR / – x} d. {x IR / x –3} c. {x IR / 0 x 0,5} f. {x IR / x } 3. Expresa como intervalo las siguientes representaciones gráficas: a. d. b. e. c. f. 4. Determina las siguientes uniones e intersecciones de intervalos. Expresa tu resultado como intervalo y represéntalo gráficamente. a. [2, 5[ ]3, 18[ d. ]0, +[ b. ]–5, 1] ]1, 7[ e. [0, 1[ (]–3, 1[) [0, 5]) c. ]0, +[ f. (]–, 2[ [12, +[) [0, 20] – , 7 4 5 3 ⎡ ⎣ ⎢ ⎤ ⎦ ⎥ – , 7 4 5 3 ⎡ ⎣ ⎢ ⎤ ⎦ ⎥ 4 5 3 18 2 3 4 Actividades b. {x IR / x 1,33} e. {x IR / –12 x 5,8} 1 5 –5 2 3 –5,2 100 0 3 2 19 3 0 8 UNIDAD 4 (164-199)C :Maquetación 1 4/11/10 17:18 Página 173
- 175. 174 | Unidad 4 Propiedades de las desigualdades En algunos países como Chile, la temperatura se mide en grados Celsius, y en otros como Estados Unidos, se mide en grados Fahren- heit. La expresión F = 1,8 · C + 32 muestra la relación entre grados Celsius (C) y grados Fahrenheit (F). Considera la siguiente información: “Cierto día, la temperatura en Punta Arenas varió entre –1 ºC y 10 ºC”. A partir de la información anterior, podemos expresar la variación de la temperatura en Punta Arenas el día indicado, a través de la desigualdad: –1 C 10. La que, expresada como un intervalo, corresponde a [1, 10]. Para saber cuánto variaron estas temperaturas en grados Fahrenheit, podemos utilizar la expresión F = 1,8 · C + 32, donde C representa la medida en grados Celsius y F en grados Fahrenheit. Observa. –1 C 10 –1,8 1,8C 18 30,2 1,8C + 32 50 30,2 F 50 Lo anterior significa que la temperatura en Punta Arenas ese día varió entre 30,2 ºF y 50 ºF. Observa que al sumar cualquier número real a los términos de una desigualdad, o al multiplicarlos por un número real positivo, la desigualdad se mantiene. Ejemplo 1 –3 –10] –3 · –2 –10 · –2 6 20 Observa que si multiplicamos o dividimos una desigualdad por un número real negativo, la desigualdad se invierte. Analicemos... • ¿Cómo podrías representar esta variación de temperaturas como un intervalo? • ¿Cuál es esta variación de la temperaturas medida en grados Fahrenheit?, ¿cómo lo supiste? Multiplicamos por 1,8 Sumamos 32 Remplazamos en la expresión F = 1,8 · C + 32 Multiplicamos por –2, por lo tanto la desigualdad se invierte Termómetro que muestra la temperatura en grados Celsius y grados Fahrenheit. UNIDAD 4 (164-199)C :Maquetación 1 4/11/10 17:18 Página 174
- 176. Inecuaciones lineales | 175 Unidad 4 En resumen • El sentido de una desigualdad no cambia si se suma o resta un mismo número real en ambos lados de la desigualdad. Es decir, si a b; entonces, a + c b + c y a – c b – c. • El sentido de una desigualdad no cambia si se multiplica o divide por un mismo número real positivo a ambos miembros de la desigualdad. Es decir, si a b y c 0; entonces, ac bc y . a c b c • El sentido de una desigualdad se invierte si se multiplica o divide por un mismo número real negativo a ambos miembros de la desigualdad. Es decir, si a b y c 0; entonces, ac bc y . b c a c 1. Para los valores de a y b dados en la siguiente tabla, se cumple que 0 a b. a. Completa la tabla. b. Compara los valores de y . ¿Qué relación de orden se da entre ellos? c. Completa, en tu cuaderno, la siguiente afirmación: Si 0 a b, entonces, __________________________________. d. Verifica, para otras parejas de valores de a y b, la validez de la propiedad encontrada. 2. Para todos los valores de x en la siguiente tabla, se tiene que 0 x 1. a. Completa, en tu cuaderno, la tabla. b. Compara los valores de x y x2 . ¿Qué relación de orden se da entre ellos?, ¿ocurre lo mismo si x –1 o x 1? c. Completa, en tu cuaderno, la siguiente afirmación: si 0 x 1, entonces, __________________________________. d. Verifica, para otros valores x, la validez de la propiedad encontrada. 1 b 1 a Actividades a b 1 a 1 b 1 2 5 10 1000 10 000 0,1 0,2 0,001 0,01 x 0,95 0,80 0,65 0,20 0,10 0,01 x2 UNIDAD 4 (164-199)C :Maquetación 1 4/11/10 17:18 Página 175
- 177. 176 | Unidad 4 Conjeturas y demostraciones Sea a un número positivo cualquiera. En la siguiente tabla se han asignado distintos valores para a, y se ha calculado la suma de este número con su recíproco. En la situación anterior, si probamos con otros valores positivos de a obtenemos en todos los casos que a + ⱖ 2. No existe ningún valor de a, tal que a + 2. Por lo tanto, podemos enunciar la siguiente conjetura: Para todo a 僆 IR+ , se cumple que a + ⱖ 2. Sin embargo, como existen infinitos números reales, no podemos verificar esta desigualdad para cada uno de los posibles valores de a. En este caso, es necesario demostrar la conjetura, para lo cual se requiere de un argumento que sea válido para todos los valores positivos de a, y que compruebe lo afirmado. Para hacer tal demostración, partiremos de nuestra conjetura y usa- remos las propiedades de las desigualdades con el fin de transfor- marla en otras expresiones. 1 a 1 a 1 a Analicemos... • Todos los resultados obtenidos son mayores o iguales a 2. ¿Qué crees que ocurre si calculamos la misma expresión para otros va- lores positivos de a?, ¿por qué? • ¿Existe algún valor positivo de a, tal que a + 2? • Si a es cualquier número positivo, ¿necesariamente se cumple que a + ⱖ 2? Justifica. 1 a 1 a Multiplicamos por el número positivo a Dividimos por el número positivo a a 1 a a + 1 a 5 0,2 5,2 2,5 0,4 2,9 2 0,5 2,5 1,5 0,6 2,16 1 1 2 0,8 1,25 2,05 0,5 2 2,5 IR+ representa el conjunto de todos los números reales positivos. Recuerda que... a + ⱖ 2 1 a Restamos 2 a Sumamos 2 a a2 + 1 ⱖ 2a Factorizamos Desarrollamos el cuadrado de binomio a2 – 2a + 1 ⱖ 0 (a – 1)2 ⱖ 0 UNIDAD 4 (164-199)C :Maquetación 1 12/11/10 12:08 Página 176
- 178. Inecuaciones lineales | 177 Unidad 4 En el lado derecho, se han indicado las operaciones que permiten transformar la desigualdad inicial. En el lado izquierdo, se mues- tra la operación que permite revertir cada paso. De esta manera, nuestra conjetura ha resultado verdadera en cualquier caso, ya que el cuadrado de todo número es mayor o igual que cero y, por lo tanto, a + 2, para todo a positivo. 1 a En resumen • Conjetura: suposición probable que se forma a partir de las señales observadas. • Demostración: conjunto ordenado de argumentos que permiten obtener una verdad como consecuencia lógica de otra. 1. Lee con atención la demostración de la propiedad a + 2 para todo a positivo. ¿En qué parte del razonamiento fue importante el hecho de que a fuese un número positivo? 2. Si n representa un número natural cualquiera, ¿a qué intervalo pertenecen los posibles valores de la expresión ? Demuestra tu conjetura, utilizando propiedades de las desigualdades. 3. Repite el ejercicio 2 para las expresiones: a. b. 4. Demuestra que (a2 + b2 ) ab para todos los valores reales de a y b. 6. Demuestra que si x 0 e y 0. xy x + y 2 1 2 2n2 – 3 n2 n + 1 2n n + 1 n 1 a Actividades 5. Demuestra que a + b si a 0 y b 0. a2 + b2 a + b 7. Demuestra que + ≥ 1 si a 0 y b 0. a. ¿En qué casos se verifica la igualdad? b. ¿Qué sucede con la desigualdad para a 0 y b 0? 5b 4a a 5b UNIDAD 4 (164-199)C :Maquetación 1 4/11/10 17:18 Página 177
- 179. 178 | Unidad 4 • En el siguiente mapa conceptual se muestran los conceptos tratados en las páginas anteriores. • Utilizando los contenidos aprendidos hasta aquí y, apoyándote en el esquema anterior, responde en tu cuaderno. 1. ¿Crees que faltó un concepto importante en el mapa conceptual?, ¿cuál? Agrégalo. 2. Si a, b IR, y a b, ¿es cierto que a b?, ¿por qué? 3. Si a, b IR, a b y a b, ¿se puede afirmar que a = b?, ¿por qué? 4. ¿Existe algún par de números reales a, b tal que a b y a b? Justifica. 5. ¿En qué caso el sentido de una desigualdad cambia?, ¿por qué ocurre esto? 6. Si a, b y c IR, y b c a, entonces, ¿b – c a – c? 7. Si a, b IR, y b a, entonces, ¿b3 ab2 ? 8. Si a, b y c IR, y b c a, entonces, ¿(a – c) · b (a – c) · c? 9. Si 0 x 1, entonces, ¿1 + x2 (1 + x)2 ? 10. ¿Tienes alguna duda sobre los conceptos tratados en las páginas anteriores?, ¿cuál? Compártela con tu curso e intenten aclararla en conjunto. Organizando lo aprendido DESIGUALDADES INTERVALOS DE NÚMEROS REALES de tipo permiten expresar SEMIABIERTOS INFINITOS ABIERTOS se aplican respecto de CONJETURAS Y DEMOSTRACIONES PROPIEDADES DE LAS DESIGUALDADES UNIDAD 4 (164-199)C :Maquetación 1 4/11/10 17:18 Página 178
- 180. Mi progreso Unidad 4 1. Determina si las siguientes desigualdades son verdaderas o falsas. Justifica tu respuesta. a. 33 4 · 12 d. g. 3 – 3 – c. 3 – 3 3 + f. i. 2. Determina la unión o intersección de los siguientes intervalos. a. [1, 3[ ]2, 7[ c. ]2, 8] [–3, 2] e. [ , ] [2, 5[ b. [1, +[ ]–, 40[ d. ]–1, + [ ]–, 1[ f. [ , [ [ , [ 3. Asumiendo que a y b son números reales, y que a b, justifica las siguientes desigualdades mediante la aplicación de las propiedades de las desigualdades, y lo aprendido sobre conjeturas y demostraciones. a. a + 4 b + 4 c. 2 – b 2 – a e. 0 b – a b. 3a 3b d. 3 + 4a 3 + 4b f. 8 + a – b 8 4. La desigualdad + , se cumple si a y b pertenecen a: A. IR B. ⺪ C. ⺡ D. IR + E. IR – 1 a + b 1 b 1 a 4 5 8 7 7 8 5 4 7 2 1 4 28 22 33 28 5 2 2 5 1 + 22 11 3 + 11 11 5 6 4 5 1 4 1 4 Inecuaciones lineales | 179 • Verifica en el solucionario del Texto si tus respuestas son correctas. Si tuviste respuestas incorrectas, marca en la tabla el criterio correspondiente y revisa las páginas indicadas. Luego, identifica el error y corrígelas. ¿Cómo voy? CRITERIO ÍTEMS PÁGINAS DONDE SE TRABAJA Representar situaciones mediante desigualdades y justificar si son verdaderas o falsas. 1 y 3 168 y 169; 176 y 177 Comprender y utilizar correctamente la notación y operatoria de intervalos. 2 170 a 173 Demostrar desigualdades mediante propiedades. 4 174 a 177 b. (2 + 3)(4 – 2) (2 + 2)(4 – 3) e. (–4)2 (–4)3 h. 1 + 4 7 1 + 4 7 UNIDAD 4 (164-199)C :Maquetación 1 4/11/10 17:18 Página 179
- 181. 180 | Unidad 4 Inecuaciones con una incógnita Un banco ofrece no cobrar gastos de mantención a aquellos clientes que mantengan un saldo superior a $ 100 000 en sus cuentas. Lucas tiene un saldo de $ 100 000; Gabriela tiene un saldo de $ 122 000 y acaba de girar $ 50 000. Analicemos... • Si denotamos por x al saldo total de una persona en su cuenta bancaria, ¿qué desigualdad representa la condición para acceder a la oferta del banco? • ¿Puede Lucas acceder a la oferta del banco?, ¿por qué? • ¿Cuánto dinero debe depositar Gabriela para que el banco no le cobre mantención?, ¿cómo lo supiste? En la situación anterior, la condición necesaria para acceder a la oferta del banco es que el saldo x que tiene una persona en su cuenta debe ser superior a 100 000; es decir, x 100 000. Por otro lado, cuando x = 100 000, como es el caso de Lucas, no se cumple la condición, ya que debe ser superior a este valor. Gabriela, en cambio, tiene $ 122 000 en su cuenta y acaba de girar $ 50 000; por lo tanto, le quedan $ 72 000 en su cuenta bancaria. Como 72 000 100 000, no puede acceder al beneficio ofrecido por el banco. Sin embargo, si denotamos por z el monto que debe de- positar Gabriela para acceder a este, entonces la condición que z de- biera cumplir se puede obtener mediante la siguiente desigualdad: 72 000 + z 100 000 z 100 000 – 72 000 z 28 000 Por consiguiente, el monto que debe depositar Gabriela para acceder a la oferta del banco, y de esta forma no pagar el costo de man- tención, deber ser superior a $ 28 000. Aplicando propiedades de las desigualdades, hemos logrado des- cubrir todos los posibles valores de la variable desconocida. A este tipo de desigualdades las llamaremos inecuaciones, las cuales son de- sigualdades con una o más incógnitas. Para resolver una inecuación, debemos encontrar el conjunto de todos los posibles valores para la incógnita o incógnitas que hacen verdadera la desigualdad. Restamos 72 000 UNIDAD 4 (164-199)C :Maquetación 1 4/11/10 17:18 Página 180
- 182. Inecuaciones lineales | 181 Ejemplo 1 Resuelve la inecuación: 4x – 7 2x – 3 Solución 2x – 7 –3 2x 4 x 2 Luego, todos los valores que satisfacen la inecuación pertenecen al intervalo ]–, 2], el que se puede representar también gráficamente. Algunas inecuaciones se deben resolver considerando el conjunto al cual pertenece la incógnita, analizando las soluciones de estas. Cuando dos inecuaciones tienen el mismo conjunto solución, se dice que estas son equivalentes. En el ejemplo 1, la inecuación 4x – 7 2x – 3 es equivalente a la inecuación x 2. Luego, si x es un número natural, su solución sería el conjunto {1, 2}. Unidad 4 Restamos 2x Sumamos 7 Dividimos por 2 2 En resumen • Una inecuación es una desigualdad que tiene una o más incógnitas. Para resolverla, debemos encontrar todos los valores de las incógnitas que hacen verdadera la desigualdad. • El conjunto solución de la inecuación se puede expresar mediante un intervalo, o bien, representado en la recta real. 1. Determina el conjunto solución de las siguientes inecuaciones y represéntalas gráficamente. a. x – 2(x – 3) 0 c. – 3 + 1 e. 2(x + 3) + 3(x – 1) 2(x + 2) 2. Resuelve las siguientes inecuaciones, considerando la condición dada para x. a. 3x – 2(4x – 7) ≥ 9, x entero positivo. b. 2x + 3 x – 1, x entero negativo. 2x 5 3x 2 Actividades b. (x + 1)2 – 5 ≥ x (x – 2) d. 2x + 3 4x – (x – 10) f. 3 – x – – 5 2x 5 1 3 UNIDAD 4 (164-199)C :Maquetación 1 4/11/10 17:18 Página 181
- 183. 182 | Unidad 4 Sistemas de inecuaciones con una incógnita La acidez del agua en una piscina es considerada normal si el promedio de tres lecturas de pH está entre 7,2 y 7,8, ambos valores incluidos. En la situación anterior, si x, y, z corresponden a las lecturas del pH de una piscina, el valor de corresponderá al promedio entre las tres. Por lo tanto, para que la acidez del agua sea conside- rada normal, se debe cumplir que: 7,2 y 7,8. Si las lecturas del pH de una piscina son 7,1, 7,9 y 7,4, el promedio de ellas es = = 7,5. Luego, la acidez del agua de la piscina es normal, ya que 7,5 7,2 y 7,5 7,8; es decir, cumple con la condición requerida. Si, en cambio, solo tenemos dos lecturas del pH de una piscina, podemos determinar entre qué valores debe estar la tercera lec- tura para que la acidez del agua de la piscina sea considerada nor- mal. Llamemos x al valor de la tercera lectura. El promedio de las tres lecturas de pH es: = , luego, para determinar entre qué valores debe estar x debemos plantear y resolver las siguientes inecuaciones: 7,2 y 7,8 15,3 + x 21,6 y 15,3 + x 23,4 x 6,3 y x 8,1 15,3 + x 3 15,3 + x 3 15,3 + x 3 7,4 + 7,9 + x 3 22,5 3 7,2 + 7,9 + 7,4 3 x + y + z 3 x + y + z 3 x + y + z 3 Analicemos... • Si x, y, z son los valores de tres lecturas del pH en una piscina, ¿cómo representarías la situación anterior, utilizando desigual- dades?, ¿cómo lo supiste? • Si las lecturas de una piscina son 7,2, 7,9 y 7,4, ¿se puede con- siderar normal la acidez del agua? • Si las primeras dos lecturas fueron 7,4 y 7,9, ¿qué valores posibles de la tercera lectura indicarían que el agua tiene acidez normal?, ¿por qué? Multiplicamos por 3 Restamos 15,3 8,1 6,3 UNIDAD 4 (164-199)C :Maquetación 1 4/11/10 17:18 Página 182
- 184. Inecuaciones lineales | 183 Unidad 4 Por lo tanto, el valor de la tercera lectura debe estar entre 6,3 y 8,1, ambos valores incluidos, es decir, en el intervalo [6,3, 8,1]. Observa que en la situación anterior, la respuesta se obtiene al in- tersecar el conjunto solución de ambas inecuaciones. Lo que hemos hecho es resolver cada inecuación para encontrar su conjunto solución, y luego intersecarlas para obtener los valo- res que hacen verdaderas ambas desigualdades a la vez. Dado que la solución final obtenida es un conjunto que está con- tenido en las soluciones de cada inecuación, hemos resuelto un sis- tema de dos inecuaciones con una incógnita. En resumen • Un sistema de inecuaciones con una incógnita es un conjunto de dos o más inecuaciones de una incógnita que deben verificarse a la vez. La solución del sistema está dada por la inter- sección del conjunto solución de cada inecuación. 1. Resuelve los siguientes sistemas de inecuaciones y representa gráficamente su solución. a. 3x + 2 x – 4 c. x + 2 1 e. x – 2 2x g. 2x – 3 x + 1 5 – x – 2 x – 1 –1 x + 3 –8 5 – x 3 b. 2x – 2 x + 5 d. x – 2 2x + 1 f. x + 1 x – 1 h. x + 1 2x + 1 – x + 6 3 x + 3 –2 3x + 1 0 x – 3 4x + 5 2. En un triángulo, las medidas de dos de sus lados son 3 cm y 7 cm. Si la suma de las medidas de dos lados de un triángulo debe ser mayor que el tercer lado y menor que la diferencia entre las me- didas de los lados conocidos, ¿cuáles son las posibles medidas que puede tener el tercer lado, sabiendo que el valor de este es un número entero? 3. Un músico profesional puede gastar entre $ 190 000 y $ 210 000 en un equipo de música y algunos CD. Si el equipo de música cuesta $ 170 000 y los CD $ 8000 cada uno, encuentra la cantidad mínima y máxima de CD que puede comprar. Actividades UNIDAD 4 (164-199)C :Maquetación 1 4/11/10 17:18 Página 183
- 185. 184 | Unidad 4 Inecuaciones lineales con dos incógnitas Para cercar una zona rectangular de una plaza en remodelación, se dispone de 50 metros de malla de alambre. Sin embargo, las dimen- siones de la zona por cercar no están definidas. Si representamos por x e y las dimensiones de la zona a cercar, tendremos la siguiente situación. Observa. En la situación anterior, la zona rectangular que se quiere cercar utilizando una malla, corresponderá al perímetro del rectángulo. Por lo tanto, el que expresado en términos de x e y corresponderá a 2x + 2y. Luego, como la cantidad de malla disponible para cer- car es de 50 metros, el perímetro de la zona rectangular deberá ser igual o inferior a 50 metros. Es decir, 2x + 2y 50 x + y 25 Para representar las dimensiones posibles de la zona a cercar, podemos considerar cada par de dimensiones posibles para x e y, es decir, el ancho y el largo de la zona rectangular respectiva- mente, como un par ordenado (x, y), tal que cumpla la inecuación x + y 25. De este modo, podemos graficar los puntos del plano que satisfagan tal condición, lo cual nos permite representar todas las dimensiones posibles. Analicemos... • ¿Qué relación hay entre el perímetro de la zona por cercar y la cantidad de malla a usar?, ¿por qué? • ¿Cómo podemos expresar la condición que deben cumplir ambas medidas para que alcancen los 50 metros de malla para cercar la zona rectangular?, ¿cómo lo supiste? • ¿De qué forma podemos representar todas las dimensiones posi- bles de la zona cercada?, ¿por qué? x y Dividimos por 2 UNIDAD 4 (164-199)C :Maquetación 1 4/11/10 17:18 Página 184
- 186. Inecuaciones lineales | 185 Unidad 4 Para ello, debemos realizar el siguiente procedimiento: Graficamos la recta x + y = 25. Observa. Consideramos solo los valores en el primer cuadrante, ya que x e y son longitudes, por lo tanto, solo pueden ser valores positivos. La recta la graficamos con una línea continua, pues el signo en la inecuación x + y 25 nos indica que los valores pertenecientes a la recta están incluidos. Nota que la recta x + y = 25 divide al plano en dos regiones. En una de ellas se cumple que x + y 25, y en la otra se cumple que x + y 25. Para saber cuál es la región que a nosotros nos interesa, elegimos cualquier punto del plano que no pertenezca a la recta, y anali- zamos si es o no solución de la inecuación. Escojamos el punto (0, 0) y remplacemos en la inecuación x + y 25: 0 + 0 25, lo cual es verdadero. Luego, la región que nos interesa es aquella que contiene al punto (0, 0) (región pintada). La región pintada nos muestra todas las posibles soluciones del problema. Por ejemplo, si la longitud x del terreno es 15 m, entonces la lon- gitud y del terreno no puede ser más de 10 m. El procedimiento utilizado para resolver el problema anterior nos permite representar también las soluciones de sistemas de inecua- ciones. Como se trata de intersecar las soluciones de cada inecuación, en el plano basta con intersecar las regiones que grafican las solu- ciones de cada inecuación. Si en la inecuación aparecen los sig- nos “” o “”, entonces graficare- mos la recta asociada con una línea punteada. Esto nos indicará que los puntos de la recta no están inclui- dos como posibles soluciones. Si un punto no es solución de la in- ecuación, entonces, la región de- seada será aquella donde no está dicho punto. Pon atención 0 25 X Y 25 0 25 20 15 10 5 X Y 25 20 15 10 5 UNIDAD 4 (164-199)C :Maquetación 1 4/11/10 17:18 Página 185
- 187. 186 | Unidad 4 Ejemplo 1 Determina gráficamente la solución del sistema Grafiquemos con líneas punteadas las rectas x = 3 e y = x + 1. Para la inecuación x 3, probamos con el punto (0, 0): 0 3 es ver- dadero. Luego, pintamos la región que contiene al punto (0, 0). Para la inecuación y x + 1, probamos con el punto (0, 0): 0 0 + 1 es falso. Luego, pintamos la región que no contiene al punto (0, 0). La solución del sistema está dada por todos los puntos que perte- necen a la región pintada. Ejemplo 2 ¿Qué sistema de inecuaciones lineales con dos incógnitas permite describir la región sombreada en el gráfico? Solución Observa que la región sombreada está limitada por las rectas x = 2, y = 0 (el eje X). Además, x + y = 10. A partir de cada una de ellas obtendremos una inecuación. La inecuación que describe la región situada a la derecha de la recta x = 2, es: x 2 La inecuación que describe la región situada sobre la recta y = 0, es: y 0 Para obtener la tercera inecuación, escogemos el punto (3, 1), que sabemos que pertenece a la región sombreada. Luego, rem- plazamos los valores x = 3 e y = 1 en la expresión x + y. x = 3 X x 3 y x + 1 Y 0 y = x + 1 y = x + 1 x = 3 0 Y X (solución) x = 2 2 10 10 x + y = 1 0 X Y La línea continua indica que se incluyen los puntos donde x = 2. La línea continua indica que se incluyen los puntos donde y = 0. UNIDAD 4 (164-199)C :Maquetación 1 4/11/10 17:18 Página 186
- 188. Inecuaciones lineales | 187 Unidad 4 1. Grafica las siguientes inecuaciones de dos incógnitas: a. y x + 2 c. y 6x e. x + y 0 b. y 3x – 1 d. y –2 f. 2x – y 1 2. En el ejemplo de la región rectangular por cercar, ¿puedes cercar el terreno de 12 m por 15 m? Justifica usando la inecuación y el gráfico. 3. Determina una inecuación que represente cada una de las gráficas que se muestran. a. b. 4. Las entradas para asistir a una función del circo cuestan $ 8000 por asiento reservado, y $ 2500 por entrada general. Si el total recaudado debe ser como mínimo $ 150 000 para solventar los gastos, encuentra la inecuación que indique los modos posibles en los que se pueden vender los asientos reservados x y las entradas generales y. Actividades En resumen • Una inecuación lineal de dos incógnitas es una inecuación de la forma Ax + By + C 0 (el signo puede ser , , o ), la cual describe una región del plano limitada por la recta Ax + By + C = 0. Cada punto de la región es una solución de la inecuación. Obtenemos 3 + 1 = 4, que es un valor menor que 10. Por tanto, los puntos de la región satisfacen: x + y 10 Luego, el sistema requerido es: x 2 y 0 x + y 10 La línea discontinua indica que no se incluyen los puntos donde x + y = 10. 0 2 Y X –1 0 2 2 Y X UNIDAD 4 (164-199)C :Maquetación 1 4/11/10 17:18 Página 187
- 189. 188 | Unidad 4 Inecuaciones que involucran valor absoluto Juan y sus amigos se encuentran jugando a la rayuela. Este juego, típico de las zonas campesinas de Chile, consiste en lanzar un tejo metálico sobre un cordel tenso que se encuentra a 5 metros en línea recta del lugar de lanzamiento. Este cordel está justo en la mitad de un cajón de 80 cm de largo, relleno con barro y leve- mente inclinado, como se muestra en la figura. Observa. En la situación anterior, para que el tejo caiga dentro del cajón, el jugador debe lanzarlo a una distancia menor de 40 cm del cordel. Este cordel se encuentra a 5 m del jugador, justo en la mitad del largo del cajón. Observa la imagen que lo representa. Por lo tanto, la distancia a la que debe caer el tejo tendría que estar dentro del intervalo ]4,6, 5,4[. Como x representa la distancia a la cual el jugador lanza el tejo, la distancia a la cual debe lanzarse este para que caiga dentro del cajón tendrá que cumplir que: x – 5 0,4, si x 5 5 – x 0,4, si x 5 Recordando la definición de valor absoluto, podemos representar la situación anterior de la siguiente forma: x – 5 0,4. Notemos que los valores de x que satisfacen la inecuación son x ] 4,6, 5,4 [, que corresponden al intervalo representado en la figura anterior. Analicemos... • Si llamamos x a la distancia a la que el jugador lanza el tejo, ¿dentro de qué intervalo debe estar x para que el tejo caiga den- tro del cajón?, ¿por qué? • ¿Cómo podemos representar la distancia a la que se encuentra el tejo del cordel en términos de x?, ¿qué debe cumplir esta para que el tejo se encuentre dentro del cajón?, ¿cómo lo supiste? 14,4 5,4 5 4,6 40 cm 40 cm El valor absoluto de x se define por: x = {x si x 0 Recuerda que... –x si x 0 cajón UNIDAD 4 (164-199)C :Maquetación 1 4/11/10 17:18 Página 188
- 190. Inecuaciones lineales | 189 Unidad 4 Ejemplo Resuelve la inecuación 2x + 1 3. Solución La inecuación es equivalente a: –3 2x + 1 3 –4 2x 2 –2 x 1 Luego, la solución de esta inecuación es el intervalo ]–2, 1[. 1. Completa en tu cuaderno la siguiente tabla: a. ¿Cómo se interpreta geométricamente x – y ? b. ¿Qué significa x – y d y x – y d? 2. Responde las siguientes preguntas. a. ¿A qué intervalo pertenecen todos los números reales que están a menos de tres unidades del origen? b. ¿A qué intervalo pertenecen todos los números reales que están a más de cinco unidades del origen? c. ¿Cómo se expresa mediante una inecuación el enunciado: “Todos los números reales que están a más de dos unidades de 6”? Actividades –2 En resumen • Si d es un número real positivo, y: • x = d, entonces x = d o x = –d • x d, entonces –d x d • x d, entonces x –d o x d Restamos 1 Dividimos por 2 –d d –d d 1 x y Distancia entre x e y x – y 2 5 –5 –3 –4 2 –d d UNIDAD 4 (164-199)C :Maquetación 1 4/11/10 17:18 Página 189
- 191. 190 | Unidad 4 • En el siguiente mapa conceptual se muestran los conceptos tratados en las páginas anteriores. • Utilizando los contenidos aprendidos hasta aquí y, apoyándote en el esquema anterior, responde en tu cuaderno. 1. ¿Crees que faltó un concepto importante en el mapa conceptual?, ¿cual? Agrégalo. 2. ¿Cuál es la relación entre desigualdad e inecuación?, ¿por qué? 3. ¿Toda inecuación tiene solución?, ¿por qué? 4. ¿Todo sistema de inecuaciones tiene solución? Justifica. 5. ¿Cómo se representan las soluciones de inecuaciones o sistemas de inecuaciones con una sola incógnita? 6. ¿Cómo se representan las soluciones de inecuaciones o sistemas de inecuaciones con dos incógnitas? 7. ¿Cuándo una inecuación con valor absoluto no tiene solución?, ¿cuándo tiene infinitas soluciones? Explica. 8. ¿Tienes alguna duda sobre los conceptos tratados en las páginas anteriores?, ¿cuál? Compártela con tu curso e intenten aclararla en conjunto. Organizando lo aprendido INECUACIONES INECUACIONES LINEALES CON UNA INCÓGNITA SISTEMAS DE INECUACIONES INECUACIONES QUE INVOLUCRAN VALOR ABSOLUTO pueden ser dos o más forman INECUACIONES LINEALES CON DOS INCÓGNITAS UNIDAD 4 (164-199)C :Maquetación 1 4/11/10 17:18 Página 190
- 192. Inecuaciones lineales | 191 Unidad 4 Mi progreso 1. Resuelve las siguientes inecuaciones: a. 3x 2 c. 5x + 2 10 e. 2x – 1 3x + 2 b. 7x 3 d. 3 – 2x 21 f. x + 1 x – 1 2. Resuelve los siguientes sistemas de inecuaciones: a. x + 1 2 b. x + 3 2 c. 2x + 3 1 d. x + 1 0 x – 2 4 x + 7 –1 3 – x 4 x + 2 0 x + 3 0 3. Grafica el conjunto solución para cada una de las siguientes inecuaciones lineales con dos incógnitas, o sistemas de ellas: a. 2x – y 3 b. 2x – 3y 2 x + 4y 1 4. Resuelve las siguientes ecuaciones e inecuaciones con valor absoluto: a. x – 2 = 1 b. x – 4 7 c. x x – 1 d. 0 x – 4 3 5. ¿Cuál de los siguientes números no es solución de la inecuación 5x – 4 12? A. –2 B. 3 C. 0 D. 1,8 E. 4 • Verifica en el solucionario del Texto si tus respuestas son correctas. Si tuviste respuestas incorrectas, marca en la tabla el criterio correspondiente y revisa las páginas indicadas. Luego, identifica el error y corrígelas. ¿Cómo voy? CRITERIO ÍTEMS PÁGINAS DONDE SE TRABAJA Resolver inecuaciones lineales con una incógnita. 1 y 5 180 y 181 Resolver sistemas de inecuaciones lineales con una incógnita. 2 182 y 183 Representar gráficamente en el plano cartesiano el conjunto solución de una inecuación con dos incógnitas, o de un sistema de inecuaciones con dos incógnitas. 3 184 a 187 Resolver ecuaciones e inecuaciones que involucran valor absoluto. 4 188 y 189 Unidad 4 UNIDAD 4 (164-199)C :Maquetación 1 4/11/10 17:18 Página 191
- 193. Cómo resolverlo 192 | Unidad 4 Observa, paso a paso, las estrategias utilizadas en la resolución de los siguientes problemas. Ejercicio 1 En el patio de su casa, la señora Elena tiene un gallinero rectangular de 4 m por 1 m. Ella desea ampliarlo, alargando el largo y el ancho de él en una misma cantidad x. Si la señora Elena no quiere que el área del gallinero exceda los 18 m2 , ¿qué rango de valores puede tomar x? Solución Las dimensiones del gallinero ampliado son: (x + 4) m y (x + 1) m. Entonces, se tiene que: (x + 4)( x + 1) 18 x2 + 5x + 4 18 x2 + 5x – 14 0 (x + 7)(x – 2) 0 La solución de la inecuación (x + 4)(x + 1) 18 es S1 S2 = [–7, 2], pero como x representa una longitud x 0, el rango posible de valo- res para x es el intervalo ]0, 2]. Es decir, el gallinero se puede ampliar sin exceder 18 m2 , siempre y cuando 0 x 2. –7 2 1 m 4 m x m x m Área del gallinero ampliado: (x + 4)(x + 1) El área del gallinero debe ser menor o igual a 18 m2 Restamos 18 Factorizamos el trinomio El producto de dos números es negativo, si uno es positivo y el otro negativo. x + 7 0 y x – 2 0 x –7 y x 2 Gráfico 1 S1 = ∅ x + 7 0 y x – 2 0 x –7 y x 2 Gráfico 2 S2 = [–7, 2] –7 2 UNIDAD 4 (164-199)C :Maquetación 1 4/11/10 17:19 Página 192
- 194. Inecuaciones lineales | 193 Unidad 4 Ejercicio 2 Resuelve la siguiente inecuación: 0 x – 3 0 y x + 5 0 x 3 y x –5 Gráfico 1 S1 = [3, +[ x – 3 0 y x + 5 0 x 3 y x –5 Gráfico 2 S2 = ]–, –5[ Luego, la solución de la inecuación 0 es S1 S2 = ]–, –5[ [3, +[ x – 3 x + 5 x – 3 x + 5 Actividades 1. Aplica el procedimiento aprendido para resolver la siguiente situación: a. En el salón comunitario de la municipalidad se debe cubrir un ventanal de 2 m de alto por 4 m de ancho con una cortina que lo cubra totalmente, pero que sea un poco más larga y ancha que el ventanal. Asumiendo que el excedente de cortina respecto del ventanal es el mismo a lo ancho que a lo alto, y que se dispone de solo 24 m2 de tela para la cortina, determina las posibles dimensiones para esta. 2. Busca un procedimiento distinto para resolver el problema anterior. Respecto del procedimiento previo, ¿cuál es más simple?, ¿por qué? 3. Resuelve las siguientes inecuaciones empleando el método aprendido, u otro. Compara el proce- dimiento que utilizaste con el de algún compañero o compañera. ¿Cuál es más simple?, ¿por qué? a. 1 b. 3 x – 5 x + 7 2x – 3 x – 2 El cociente entre dos números es positivo, si ambos lo son, y es cero si el numerador lo es El cociente entre dos números es positivo, si ambos son negativos y es cero si el numerador lo es –5 3 –5 3 UNIDAD 4 (164-199)C :Maquetación 1 4/11/10 17:19 Página 193
- 195. 194 | Unidad 4 En terreno En terreno La tecnología, una herramienta necesaria En la actualidad, los computadores son una de las principales herramientas de tra- bajo y estudio. Tener conocimientos en computación es prácticamente impres- cindible a la hora de buscar trabajo. Esta importante herramienta trabaja haciendo funcionar conjuntamente el teclado, mouse y pantalla, de modo que el usuario pueda interactuar con los programas. Por ejemplo, en una página web podemos utilizar el mouse para conectarnos sobre palabras enlazadas a otras páginas web, para lo cual lo movemos para que el pun- tero en la pantalla se sitúe sobre el enlace, presionamos uno de los botones del mouse, y el navegador abre la nueva página web. La acción que el computador realiza al presionar uno de los botones del mouse, dependerá de la ubicación en la que se encuentre el puntero de este sobre la pantalla. Para saber qué acción se debe realizar, el computador asume un sistema de coordenadas, de modo que en cada instante el computador dispone de las coor- denadas del mouse respecto de la pantalla, digamos (x, y). Luego, el computador recibe la instrucción, de forma que, según el intervalo donde se encuentra ubicado, el puntero realiza la acción requerida. UNIDAD 4 (164-199)C :Maquetación 1 4/11/10 17:19 Página 194
- 196. Actividades Considera una pantalla rectangular de computador. Asumiremos que esta mide 100 unidades de ancho y 60 de alto. Consideramos un eje de coordenadas, de modo que el origen de este se encuentra en la esquina inferior izquierda, como se muestra en la figura. 1. Asume que la región E tiene vértices de coordenadas (30,30), (50,10), (70,30) y (50,50). Supón que para cada una de las áreas mostradas en la figura se quiere crear una instrucción distinta, de manera que esta se ejecute al presionar el mouse con el puntero ubicado sobre cada una de ellas. 2. Obtén las ecuaciones de cada una de las rectas que separan las diferentes áreas. Investiguemos... Ahora, trabajen en grupos de tres personas. 1. Para cada recta, determina una inecuación lineal tal que la región E esté contenida en el conjunto solución. 2. Determina un sistema de inecuaciones lineales cuya solución sea exactamente la región D. 3. Determina un sistema de inecuaciones lineales cuya solución sea exactamente la región B. 4. Determina un sistema de inecuaciones lineales cuya solución sea exactamente la región E. Evaluemos nuestro trabajo • Comparen los resultados obtenidos. ¿Son similares? Si no es así, ¿qué diferencias hubo?, ¿por qué? Inecuaciones lineales | 195 Unidad 4 10 10 20 30 40 50 60 20 30 40 50 60 70 80 90 100 D A E C B UNIDAD 4 (164-199)C :Maquetación 1 4/11/10 17:19 Página 195
- 197. 196 | Unidad 4 Síntesis de la Unidad A continuación, se presentan los conceptos fundamentales trabajados en la Unidad. Construye con ellos un mapa conceptual, en tu cuaderno. No olvides agregar las palabras de enlace que indican las relaciones entre los conceptos. A partir de lo trabajado en la Unidad, responde: 1. ¿Crees que faltó un concepto importante en el mapa conceptual?, ¿cuál? Agrégalo. 2. ¿Toda inecuación lineal con una incógnita tiene por solución un intervalo de números reales? 3. ¿Se puede representar la solución de una ecuación lineal con dos incógnitas por medio de un intervalo de números reales?, ¿por qué? 4. ¿Puede existir una inecuación que tenga una única solución? Justifica. 5. Si d es un número real positivo, ¿cuál es la solución de una inecuación de la forma x d? 6. Si a es un número real negativo, ¿cuál es la solución de una inecuación de la forma x a? 7. ¿Existen inecuaciones con valor absoluto que tienen una única solución? Explica. 8. ¿Tienes alguna duda sobre los conceptos tratados en las páginas anteriores?, ¿cuál? Compártela con tu curso e intenten aclararla en conjunto. INECUACIONES DESIGUALDADES INECUACIONES LINEALES INECUACIONES CON VALOR ABSOLUTO SISTEMAS DE INECUACIONES INECUACIONES CON UNA INCÓGNITA INECUACIONES CON DOS INCÓGNITAS ECUACIONES CON VALOR ABSOLUTO UNIDAD 4 (164-199)C :Maquetación 1 4/11/10 17:19 Página 196
- 198. Inecuaciones lineales | 197 Evaluación I. Determina si las expresiones siguientes son Verdaderas o Falsas. Justifica tu respuesta. 1. El sentido de una desigualdad se invierte si se suma o resta un mismo número real en ambos lados de la desigualdad. 2. El sentido de una desigualdad se invierte si se multiplica o divide por un mismo número real nega- tivo a ambos miembros de la desigualdad. 3. Intersecar las soluciones de dos inecuaciones equivale a resolver el sistema de inecuaciones que ellas forman. 4. El conjunto solución de la inecuación se puede expresar mediante un intervalo, o bien, represen- tado en la recta real. II. Aplica lo que aprendiste en la Unidad para desarrollar las siguientes actividades: 1. Expresa los siguientes conjuntos como intervalos, o como unión o intersección de estos: a. Los números reales mayores que 3 y menores que 12. b. Los números reales menores que 31. c. Los números reales no menores que 8. d. Los números reales no mayores que 4 pero menores que 7. e. Los números reales negativos mayores que –7. f. Los números reales que están entre 1 y 2, o entre 7 y 9. 2. Resuelve las siguientes inecuaciones: a. 5x 3 c. 13x 4 e. (x – 1)(x – 2) 2 g. x + 10 x + 7 b. 10x 1 d. (x – 1) 2 f. 2 h. 2 3. Grafica la región del plano determinada por la solución de las siguientes inecuaciones y sistemas de inecuaciones con dos incógnitas: a. x + y + 2 0 c. x – y 2 e. 2x – y 1 g. x 1 x + y 3 y 0 y – x 2 b. x – y 2 d. x + y 2 f. x 0 h. x + y 2 y 0 x – y 4 x + y 0 2x + y 1 4. Resuelve las siguientes inecuaciones con valor absoluto: a. x 12 c. x + 3 12 e. x – 5 0 b. x – 2 12 d. x + 3 12 f. x + 6 0 x + 3 x x – 1 x – 2 Unidad 4 UNIDAD 4 (164-199)C :Maquetación 1 4/11/10 17:19 Página 197
- 199. 198 | Unidad 4 1. Para el conjunto de números reales A = {x IR / x },es verdadero que: I. 4 A II. 1,5 A III. A A. Solo I B. Solo II C. I y II D. I y III E. I, II y III 2. ¿Qué condición deben cumplir los números a y b para que ]–, a] [b, +[ = ∅? A. a = b B. a b C. a b D. a + b 0 E. a + b 0 3. Si p es un número real tal que 0 p 1, siempre se cumple que: A. p2 = 2p B. p2 p3 C. p2 p3 D. p2 0 E. p2 p4 4. Si n es un número natural, ¿a qué intervalo pertenecen todos los posibles valores de la expresión ? B. [0, 1[ C. ]0, +[ D. ]–, 0] E. Ninguna de las anteriores. 5. Si a – 5 = 12, entonces a es igual a: A. 17 B. 12 y –12 C. 17 y –7 D. 17 y –17 E. –7 6. La inecuación que representa al siguiente gráfico es: A. x 3 B. x 3 C. x 3 D. x 3 E. x = 3 7. ¿Cuál o cuáles de los siguientes puntos son soluciones de la inecuación 4y – 3x 8? I. (0, 2) II. III. (5, –17,6) IV. A. Solo I B. Solo IV C. I y II D. II y IV E. I y III – , 4 2 5 ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ – , 3 1 2 ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ 18 3 2 n – 1 n π 2 III. Resuelve los siguientes ejercicios y selecciona la alternativa correcta en cada caso. A. [0, – [ 1 2 –3 3 UNIDAD 4 (164-199)C :Maquetación 1 4/11/10 17:19 Página 198
- 200. Inecuaciones lineales | 199 8. ¿Qué expresión describe al gráfico? A. x x + 1 B. y x + 1 C. y x + 1 D. y x + 1 E. y = x + 1 9. El gráfico del conjunto solución de la inecuación x2 + 4x – 21 0 es: A. B. C. D. E. Ninguna de las anteriores. 10. ¿De qué inecuación no es solución el siguiente gráfico? A. –2x 4 B. –4 2x C. –x 2 D. 8 –4x E. –2 x 11. ¿Qué inecuación describe al enunciado:“Todos los números reales que están al menos a tres unidades de –1”? A. x – 1 3 B. x – 3 –1 C. x + 1 3 D. x + 1 3 E. x + 1 3 12. La solución de la inecuación 2x – 3 6 es: A. {x IR /– x } C. {x IR / x } E. Ninguna de las anteriores. 13. En IR la solución de la inecuación (p2 – 2)2 + 3 p4 – 4p2 + p es: A. [7, +[ B. [7, +] C. [–, 7[ D. ]–, 7] E. ]–, 7[ 14. El conjunto solución de la inecuación 0 es igual al conjunto solución de la inecuación: A. x + 3 0 B. x + 3 0 C. 0 D. x + 3 0 E. x + 3 0 2x + 6 5 2 x + 3 9 2 9 2 3 2 Unidad 4 Verifica en el solucionario de tu Texto si tus respuestas son correctas. ¿Te equivocaste en alguna?, ¿cuál fue el error? Explícalo y resuelve correctamente el ejercicio. B. {x IR / x } 9 2 D. {x IR /– x } 9 2 3 2 X Y –7 3 –7 3 –7 3 –7 3 –2 UNIDAD 4 (164-199)C :Maquetación 1 4/11/10 17:19 Página 199
- 201. Probabilidades 5 200 |Unidad 5 Experimentos aleatorios Espacio muestral Sucesos y eventos Probabilidad Ley de los grandes números Variable aleatoria Contar los resultados de un experimento utilizando elementos de combinatoria. Resolver problemas que involucran el cálculo de probabilidad condicionada. Conocer empíricamente la Ley de los grandes números y relacionar la frecuencia relativa con la probabilidad de un suceso. Resolver problemas que involucran suma o producto de probabilidades. Distinguir entre sucesos equiprobables y no equiprobables. Reconocer e interpretar variables aleatorias de acuerdo a los contextos en que se presentan. Calcular e interpretar el valor esperado de una variable aleatoria. TRABAJANDO CON: APRENDERÁS A: UNIDAD 5 (200-247)C :Maquetación 1 4/11/10 17:20 Página 200
- 202. Probabilidades | 201 Conversemos de... Ocasionalmente y cada cierta cantidad de años, que puede ser variable, se conjugan diversos fac- tores que tienen como consecuencia mayores precipitaciones que las habituales, transformando un paisaje árido y desolado, de arenas y piedras, en un verde tapiz. Nacen nuevas hojas de arbus- tos secos, brotan semillas, bulbos y rizomas por años guardados bajo tierra, esperando su cuota de humedad necesaria para volver a la vida. Este fenómeno, de interés tanto para turistas como para científicos, ocurre en el norte de nues- tro país y es conocido como el Desierto Florido; sin embargo, no podemos saber con certeza cuándo sucederá. La floración comienza a fines de julio o en agosto, según cuando hayan sido las precipitaciones, y puede continuar hasta noviembre. • ¿Qué factores crees que influyen en la aparición del Desierto Florido? • Investiga sobre este fenómeno y las características que se deben dar para que este aparezca. Latinstock UNIDAD 5 (200-247)C :Maquetación 1 4/11/10 17:20 Página 201
- 203. 202 | Unidad 5 ¿Cuánto sabes? 1. Clasifica los siguientes experimentos en deterministas o aleatorios. Justifica tus respuestas. a. Lanzar una moneda cuatro veces y contar en cuántos lanzamientos salió cara. b. Poner un globo sobre la superficie del agua y ver si se va al fondo. c. Elegir una ampolleta corriente al azar, conectarla a una lámpara y medir el tiempo que tarda en quemarse. d. Elegir a un estudiante cualquiera de tu colegio y preguntarle el nombre de su profesor favorito. e. Observar un semáforo y registrar qué color se prende después del rojo. 2. En un restaurante ofrecen como menú del día las siguientes opciones: una ensalada, que puede ser lechuga con palta o tomate con cebolla; un plato de fondo, que puede ser cazuela de vacuno o puré con pescado, y papayas al jugo, helado o torta de chocolate de postre. Haz un diagrama de árbol donde se representen todos los posibles almuerzos que puede pedir una persona. 3. Cierto instituto de idiomas tiene inscritos, para el primer semestre de este año, 120 estudiantes distribuidos entre cursos de inglés y de francés. Si algunos de estos estudiantes toman los dos cursos, y hay 68 estudiantes inscritos en inglés y 74 francés: a. ¿cuántos estudiantes están inscritos en cursos de inglés y de francés?, b. ¿cuántos solo están inscritos en cursos de inglés? 4. Al extraer un naipe de una baraja inglesa, determina: a. la probabilidad de que sea una figura (rey, reina, paje), b. la probabilidad de que sea un número par. 5. Se saca, al azar, una carta de un grupo de cartas de una baraja inglesa. Indica la probabilidad de extraer el as de corazón, cuando el grupo de cartas está compuesto por: a. la baraja completa (52 cartas), c. los corazones de la baraja, b. las cartas rojas de la baraja, d. los ases de la baraja. Recuerda lo que aprendiste en años anteriores y resuelve en tu cuaderno. UNIDAD 5 (200-247)C :Maquetación 1 4/11/10 17:20 Página 202
- 204. 6. Supongamos que debes apostar a una de las siguientes situaciones. A: obtener cara al lanzar una moneda. B: obtener un 5 al lanzar un dado. C: obtener el rey de trébol al sacar una carta de una baraja inglesa. ¿Por cuál de las tres situaciones apostarías?, ¿por qué? 7. Se lanza un dado y sale 1.A continuación se lanza otro dado. Indica cuál es la probabilidad de que: a. en el segundo dado salga 5, b. en el segundo dado salga un número primo, c. la suma de los números obtenidos sea mayor que 7, d. la suma de los números obtenidos sea menor que 4. 8. Los siguientes datos corresponden a los resultados de una encuesta aplicada a una muestra de 15 personas sobre el número de inte- grantes que componen el grupo familiar. 2-2-3-3-3-4-4-4-4-4-5-5-5-5-5 Completa la siguiente tabla de frecuencias. Verifica en el solucionario de tu Texto si tus respuestas son correctas. ¿Te equivocaste en alguna?, ¿cuál fue el error? Explícalo y resuelve correctamente el ejercicio. Probabilidades | 203 Unidad 5 ¿Qué debes recordar? • En un experimento, la probabilidad de ocurrencia de un suceso es la razón entre el número de casos favorables al suceso y el número de casos posibles del experimento. • La probabilidad de un suceso puede tomar valores entre 0 y 1, o, expresada en porcentaje, entre 0% y 100%. • La frecuencia absoluta de un suceso es el número de veces que dicho suceso ocurre, cuando se repite un experimento una cierta cantidad de veces. • La frecuencia relativa es la razón entre el número de ocurrencias de un suceso, con respecto al total de repeticiones del experimento. • Los diagramas de árbol son una herramienta útil para analizar los resultados de experimentos sucesivos. Frecuencia absoluta Frecuencia relativa 2 3 4 5 UNIDAD 5 (200-247)C :Maquetación 1 4/11/10 17:20 Página 203
- 205. 204 | Unidad 5 Espacio y tamaño muestral Analicemos... Considera los siguientes experimentos: • Lanzar una pelota en un tanque de agua y ver si flota o se hunde. • Lanzar una moneda dos veces y contar cuántas caras aparecieron. • Lanzar dos dados y sumar los puntos obtenidos. En los experimentos planteados no podemos saber con exactitud cuál será el resultado del experimento; sin embargo, en todos conocemos el conjunto de posibles resultados. En cursos anteriores vimos que este tipo de experimentos se denominan experimentos aleatorios. En cambio, si conocemos de antemano el resultado del experimento, este es un experimento determinista. A pesar de que no podemos saber el resultado exacto de cada ex- perimento, sí podemos determinar el conjunto de todos sus posibles resultados, el cual corresponde al espacio muestral del experimento aleatorio, y lo denotaremos ⍀. La cantidad de elementos que este tiene, es decir, el tamaño del es- pacio muestral, lo denotaremos #⍀. Ejemplo 1 Describe el espacio muestral de los experimentos iniciales, y deter- mina el tamaño de estos. • Lanzar una pelota en un tanque de agua y ver si flota o se hunde. ⍀ = {flota, se hunde} #⍀ = 2 • Lanzar una moneda dos veces y contar cuántas caras aparecieron. ⍀ = {0, 1, 2} #⍀ = 3 • Lanzar dos dados y sumar los puntos obtenidos. ⍀ = {2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12} #⍀ = 11 • ¿Puedes determinar con exactitud el resultado de cada experi- mento antes de realizarlo?, ¿por qué? • ¿Qué tienen en común estos experimentos? • ¿Hay alguna diferencia relevante entre estas situaciones? Un experimento será aleatorio cuan- do el mismo cumpla las siguientes condiciones: • Se puede repetir indefinidamente, pudiéndose obtener resultados distintos en cada repetición. • En cada repetición se obtiene un resultado que pertenece al con- junto de todos los resultados posi- bles del experimento. • Antes de realizar una nueva repetición del experimento, no se puede predecir el resultado que se obtendrá. Recuerda que... La suma de los puntos obtenidos es siete. UNIDAD 5 (200-247)C :Maquetación 1 4/11/10 17:20 Página 204
- 206. Probabilidades | 205 Unidad 5 Ejemplo 2 Considera el experimento de lanzar una moneda hasta que salga la primera cara. Interesa saber el número de lanzamientos necesarios para que esto ocurra. Describe el espacio muestral y determina el tamaño de este. ⍀ = {0, 1, 2, 3, …} En este caso no podemos determinar el tamaño del espacio mues- tral, ya que no hay un número de lanzamientos que nos asegure obtener una cara. En resumen • El conjunto de todos los resultados posibles de un experimento corresponde al espacio muestral de este, el cual denotamos ⍀. • El tamaño del espacio muestral es la cantidad de elementos contenidos en él, denotado #⍀. 1. Describe los espacios muestrales de cada uno de estos experimentos, e indica si son finitos o infinitos. Determina, si es posible, el tamaño de este. a. Lanzar un dado diez veces. Interesa saber cuántos 5 salieron. b. Lanzar un dado hasta que salga por primera vez un 6. Interesa saber cuántos lanzamientos fueron necesarios. c. Extraer aleatoriamente una carta de una baraja de naipe inglés. Interesa registrar su pinta. d. Lanzar una moneda tres veces. Interesa la sucesión de sellos y caras que aparece. e. Tomar al azar una manzana de un árbol. Interesa conocer su peso en gramos. f. Extraer aleatoriamente de una baraja inglesa una carta tras otra, sin reponer la carta extraída del mazo, hasta que salga una carta roja. Interesa saber cuántas cartas fue necesario sacar. 2. Una caja contiene tres bolitas, una roja, una verde y una azul. Considera el experimento que consiste en sacar dos bolitas de la caja, con reposición. a. Describe el espacio muestral del experimento y el tamaño de este. b. Describe el espacio muestral del experimento y el tamaño de este, si la segunda bolita es sacada sin reposición. 3. Considera el experimento aleatorio que consiste en escoger, al azar, a uno de tus compañeros o compañeras y registrar alguna característica (estatura, número de hermanos, notas, etc.). Indica las características que podría interesar observar y describe el espacio muestral adecuado en cada caso. Actividades UNIDAD 5 (200-247)C :Maquetación 1 4/11/10 17:20 Página 205
- 207. 206 | Unidad 5 Sucesos o eventos Analicemos... Manuel y Josefina están realizando un experimento que consiste en lanzar dos dados, como se muestra en la figura. Luego, observan los puntos que aparece en las caras superiores de ambos dados. Supongamos que solo nos interesan las parejas de valores en que: • aparece el mismo número en ambos dados. • los puntos que aparecen suman 12. • sale un 6 en el dado rojo. • el producto de los dados es 55. Una manera sencilla de visualizar el espacio muestral del experi- mento, que realizan Manuel y Josefina, es construir la siguiente tabla: Para saber la cantidad de elementos del espacio muestral podemos calcular: #⍀ = 6 · 6 = 36. Lo que significa que el número de ele- mentos del espacio muestral es 36, los cuales están representados por los pares ordenados de la tabla. De esta manera se pueden identificar fácilmente los elementos que cumplen con las condiciones dadas. • ¿Cuál es el espacio muestral asociado a este experimento?, ¿cómo lo supiste? • ¿Cuál es su tamaño?, ¿por qué? • Para cada una de las situaciones, ¿cuáles son los elementos que cumplen las distintas condiciones? 1 2 3 4 5 6 1 (1, 1) (1, 2) (1, 3) (1, 4) (1, 5) (1, 6) 2 (2, 1) (2, 2) (2, 3) (2, 4) (2, 5) (2, 6) 3 (3, 1) (3, 2) (3, 3) (3, 4) (3, 5) (3, 6) 4 (4, 1) (4, 2) (4, 3) (4, 4) (4, 5) (4, 6) 5 (5, 1) (5, 2) (5, 3) (5, 4) (5, 5) (5, 6) 6 (6, 1) (6, 2) (6, 3) (6, 4) (6, 5) (6, 6) UNIDAD 5 (200-247)C :Maquetación 1 4/11/10 17:20 Página 206
- 208. Probabilidades | 207 Unidad 5 Si llamamos A: aparece el mismo número en ambos dados, entonces: A = {(1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6)} #A = 6. Si llamamos B: los números que aparecen suman 12, entonces: B = {(6, 6)} #B = 1. Si llamamos C: sale un 6 en el dado rojo, entonces: C = {(1, 6), (2, 6), (3, 6), (4, 6), (5, 6), (6, 6)} #C = 6. Si llamamos D: el producto de los dados es 55, entonces: D = ⭋ #D = 0. Cada uno de los conjuntos anteriores corresponde a un suceso o evento asociado al experimento de lanzar un dado verde y un dado rojo. Llamaremos suceso o evento a cualquier subconjunto del espacio muestral. Por lo general, se denotan con mayúsculas. Como, por ejemplo, los sucesos A, B, C y D, de la situación anterior. Diremos que el suceso A ha ocurrido si al realizar una repetición del experimento se observa un elemento que pertenece a este. Si se observa un elemento que no pertenece al suceso A, diremos que este no ha ocurrido; es decir, diremos que el suceso A ha ocurrido si al realizar el experimento observamos en las caras de ambos dados el mismo número. El complemento de un suceso está formado por los resultados de espacio muestral no considerados en él. Por ejemplo, el comple- mento del suceso A estará formado por todas las combinaciones en que los resultados de ambos dados sean diferentes, y lo denotare- mos por Ac . Si un suceso está formado por un solo resultado se llama suceso elemental, como, por ejemplo, el suceso B. Si el suceso es igual al espacio muestral se llama suceso seguro, ya que como el evento está formado por todos los posibles valores, este se observará de todas formas. En cambio, si no hay resultados posibles para cierto suceso, se dice que este es un suceso imposible. UNIDAD 5 (200-247)C :Maquetación 1 4/11/10 17:20 Página 207
- 209. Ejemplo 1 Considera el experimento y los sucesos B y C de la situación inicial. Si se lanza el dado verde y a continuación el dado rojo, obteniendo el siguiente resultado: (6, 6); ¿qué puedes decir del suceso B艚C? En este caso, como (6, 6) cumple tanto la condición del evento B como la de C, diremos que ha ocurrido B艚C. Ahora, si al lanzar los dados se observa (5, 6), diremos que ha ocu- rrido el suceso B艛C, ya que a pesar de que no ocurre el suceso B, sí ocurre C. Ejemplo 2 Manteniendo el experimento de la situación inicial, considera ahora el evento: F: sale un 5 en el dado rojo. F = {(1,5), (2,5), (3,5), (4,5), (5,5), (6,5)} ¿Pueden ocurrir C艚F? Los sucesos C y F no pueden ocurrir simultáneamente, ya que si obtenemos un 5 en el dado rojo, no podemos obtener también un 6. Si dos o más sucesos no tienen posibilidad de ocurrir simultánea- mente, se dice que los sucesos son mutuamente excluyentes. Los siguientes esquemas permiten representar las nociones vistas: 208 | Unidad 5 A Suceso A艚B Suceso A艛B Sucesos mutuamente excluyentes B A B A B Dados dos conjuntos A y B, existen conjuntos llamados unión e inter- sección de A y B, denotados por A艛B y A艚B, respectivamente. Recuerda que... UNIDAD 5 (200-247)C :Maquetación 1 4/11/10 17:20 Página 208
- 210. Probabilidades | 209 Unidad 5 1. Considera el experimento de lanzar cuatro monedas simultáneamente. a. Describe el espacio muestral del experimento. b. Describe el evento “obtener, al menos, dos caras”. c. Describe el evento “no obtener ninguna cara”. d. Describe el evento “obtener, a lo más, dos sellos”. 2. Anita, Bernardo y Cecilia van a la misma escuela; cada día registran el orden en que llegan. Si llega primero Bernardo, luego Anita y finalmente Cecilia, anotan BAC. Determina: a. el espacio muestral de las posibles llegadas, b. el suceso de que Bernardo llegue primero, c. el complemento del suceso descrito en b, d. el suceso de que Anita no llegue en segundo lugar. 3. Todos los días, Sergio controla cuánto tiempo espera el transporte que utiliza para ir al colegio. Para este experimento aleatorio, definimos los siguientes sucesos: A: “El transporte llega junto con Sergio al paradero”. B: “El transporte demora menos de 5 minutos”. C:“El transporte demora más de 10 minutos”. a. Describe el complemento del suceso B. b. Describe el complemento del suceso C. c. A partir de los datos dados anteriormente, describe un suceso seguro y uno imposible. Actividades En resumen • Un suceso A es cualquier subconjunto del espacio muestral. • Si un suceso está formado por un solo resultado, se llama suceso elemental. • Si el suceso es igual al espacio muestral del experimento, se llama suceso seguro. • Si no hay resultados posibles para cierto suceso, se dice que este es un suceso imposible. • El complemento de un suceso A está formado por los resultados del espacio muestral no considerados en A, y se denota por AC . • Si dos o más sucesos no pueden ocurrir simultáneamente, diremos que son sucesos mutuamente excluyentes. UNIDAD 5 (200-247)C :Maquetación 1 4/11/10 17:20 Página 209
- 211. 210 | Unidad 5 Principio multiplicativo Ignacio debe ir de su casa al colegio, pero antes debe pasar por la casa de un amigo. Para ir de su casa a la de su amigo, le sirven tres buses, y para ir de la casa de su amigo al colegio le sirven solo dos. La situación antes descrita se podría representar utilizando un dia- grama de árbol, como se muestra a continuación. Observa. Podemos ver en el diagrama que Ignacio tiene exactamente seis formas de combinar los buses. Notemos que para ir a la casa de su amigo le sirven tres buses, y para ir desde ahí al colegio le sirven dos. En general, se puede decir que si cierto evento A se puede hacer de m maneras y un evento B se puede hacer de n maneras, en- tonces existen m · n formas de realizar A y a continuación realizar B. Esto se conoce como el principio multiplicativo y se puede gene- ralizar a más de dos procedimientos. Por lo tanto, podemos ver también que las posibles combinaciones de buses que tiene Ignacio son 2 · 3 = 6. Analicemos... • ¿Cómo puedes representar gráficamente esta situación? • ¿Cuántas posibles combinaciones de buses tiene Ignacio?, ¿cómo lo supiste? • ¿Qué otra estrategia podrías usar para calcularlo? UNIDAD 5 (200-247)C :Maquetación 1 4/11/10 17:20 Página 210
- 212. Probabilidades | 211 Unidad 5 1. En una cafetería universitaria se ofrece un desayuno por $ 2000 que consiste en elegir una bebida (café, té o leche), un sándwich (jamón o queso) y un pastelillo (manjar, chocolate o frambuesa). ¿Cuántos desayunos diferentes se pueden pedir en esta cafetería?, ¿cómo lo calculaste? 2. Si se lanza cuatro veces una moneda y se observa la sucesión de caras y sellos que aparece, ¿cuántos resultados posibles hay? ¿Cuántos resultados hay si la moneda se lanza cinco veces? Explica, paso a paso, cómo lo resolviste. 3. Si se lanza un dado y una moneda, ¿cuántos resultados diferentes se pueden obtener? Representa los resultados utilizando un diagrama de árbol. Actividades Ejemplo Se dispone de los dígitos 1, 2, 3, 4, 5 y 6. ¿Cuántos números de tres cifras, menores que 400, se pueden formar con ellos, si está permi- tido repetir los dígitos? Imagina que para el número que se quiere formar tienes una caja con tres compartimentos. Como este debe ser menor que 400, el dígito que va en el primer compartimento solo puede ser 1, 2 ó 3. Por consiguiente, hay tres maneras de realizar el procedimiento de tomar un número y ponerlo en ese lugar. Escoger un dígito para el segundo compartimento es un proce- dimiento que se puede realizar de seis maneras, ya que en este caso se pueden repetir los dígitos. Por lo tanto, puede ser 1, 2, 3, 4, 5 ó 6. Para el tercer compartimento hay seis maneras de es- cogerlo, ya que, al igual que para el segundo compartimento, se pueden repetir los dígitos. En este caso, el principio multiplicativo indica que hay 3 · 6 · 6 = 108 números con las condiciones requeridas. En resumen • Si un evento A puede ocurrir de m maneras distintas, y un evento B puede ocurrir de n maneras distintas, entonces existen m · n maneras de que ocurra A, y a continuación B. UNIDAD 5 (200-247)C :Maquetación 1 4/11/10 17:20 Página 211
- 213. 212 | Unidad 5 Permutaciones Gabriela debe ordenar los materiales de la sala de clases antes de irse a su casa. Para terminar, solo le falta ordenar los libros que se muestran en la imagen y ponerlos sobre la repisa. Observa. En la situación presentada, cuando Gabriela escoge un libro para poner en primer lugar, tiene cuatro elecciones posibles. Para el se- gundo lugar van quedando solo tres libros. En el tercer lugar, se puede poner cualquiera de los dos libros restantes y, finalmente, el único libro que falta. Por el principio multiplicativo vemos que es posible ordenar los li- bros en la repisa de 4 · 3 · 2 ·1 = 24 maneras. En general, n objetos diferentes se pueden ordenar de: n · (n – 1) · (n – 2) · … · 1 maneras Cada uno de estos órdenes es llamado una permutación de los n objetos. El producto n · (n – 1) · (n – 2) · … · 1 se usa con frecuencia y se llama el factorial de n o n-factorial y se denota por n!, donde se define 0! = 1. Si ahora Gabriela tuviese siete libros que ordenar, pero solo tiene lugar para cuatro libros, podemos calcular las formas que tiene de seleccionar cuatro libros y ordenarlos en la repisa con un razona- miento similar al del ejemplo anterior. Hay siete opciones para el primer lugar, seis para el segundo, cinco para el tercero, y cuatro para el cuarto. Observa. Usando el principio multiplicativo, tendremos que hay 7 · 6 · 5 · 4 = 840. Por lo tanto, hay 840 formas de seleccionar cuatro de los siete libros y ordenarlos en la repisa. Analicemos... • ¿De cuántas formas puede Gabriela ordenar estos libros en la repisa?, ¿cómo lo calculaste? • Si Gabriela tuviera siete libros, ¿de cuántas formas podría orde- narlos si solo hay espacio para cuatro?, ¿por qué? 7 6 5 4 UNIDAD 5 (200-247)C :Maquetación 1 4/11/10 17:20 Página 212
- 214. Probabilidades | 213 Unidad 5 Este procedimiento se denomina una r-permutación de n objetos diferentes. Es un ordenamiento de r de los n objetos que se tienen, en este caso n = 7 y r = 4. El número de estas permutaciones se denota por nPr y se calcula: nPr = n · (n – 1) · (n – 2) · … · (n – r + 1). Dicho de otro modo, una r-permutación consiste en seleccionar r objetos de un total de n y, a continuación, darle al conjunto de r objetos seleccionados un orden específico. Cada r-permutación será diferente de otra, ya sea por los elementos que la componen o por su orden de colocación. En resumen • Hay n! = n · (n – 1) · (n – 2) · … · 1 maneras diferentes de ordenar n elementos. • Hay nPr = n · (n – 1) · (n – 2) · … · (n – r + 1) maneras de ordenar r elementos, sin repetirlos, seleccionados de un conjunto de n elementos. • Si se pueden repetir los elementos, hay nr maneras de ordenar r elementos seleccionados desde n elementos. 1. La cerradura de una caja fuerte está compuesta de 3 anillos, cada uno marcado con 8 letras diferentes. a. ¿Cuántas posibles combinaciones se pueden hacer? b. Si el dueño de la caja fuerte solo recuerda la letra del anillo del centro, ¿cuántas posibles combinaciones podría intentar?, ¿por qué? 2. La final de 100 metros planos interescolar será disputada por 6 corredores. Si suponemos que no hay empates, ¿cuántos órdenes diferentes hay para que los competidores lleguen a la meta?, ¿cómo lo calculaste? 3. En una fila de 7 asientos se ubicarán 5 personas. ¿De cuántas maneras distintas se pueden sentar? 4. ¿Cuántos números de cuatro cifras distintas, que comiencen con 1 y que sean pares, se pueden formar con los 10 dígitos?, ¿cómo lo supiste? 5. En el alfabeto Morse se utilizan solo dos símbolos: el punto y la raya. Si cada combinación de ellos da origen a una letra, ¿cuántos posibles caracteres distintos se pueden formar si tomas 1, 2, 3 ó 4 de estos símbolos? Actividades UNIDAD 5 (200-247)C :Maquetación 1 4/11/10 17:20 Página 213
- 215. 214 | Unidad 5 Combinaciones La administración de un condominio está compuesta por siete per- sonas, de las cuales se seleccionarán cuatro para formar una comisión que evaluará un proyecto sobre seguridad comunitaria. En la situación anterior, debemos elegir los integrantes para la comisión de un condominio. Para determinar el número de formas que se puede escoger esta no podemos utilizar exactamente el mismo procedimiento que en el ejemplo de los libros visto ante- riormente, ya que, como sabemos, si seleccionamos cuatro de los siete libros podemos al hacer el cálculo 7P4, se obtienen todas las maneras de elegir cuatro objetos de un total de siete y permu- tar los cuatro elegidos, recordemos que esto último se puede hacer de 4! maneras. En cambio, al elegir cuatro personas, y ordenar estas de diferentes formas, el grupo de seleccionadas no cambiará; es decir, sin impor- tar el orden en que estén, serán las mismas personas. Por tanto, si lo que se desea es escoger cuatro objetos, sin considerar sus distintos órdenes o permutaciones, habrá que dividir 7P4 entre 4! Así, hay = = 35 maneras de escoger la comisión. Una combinación de n objetos tomados de r en r es una selección de r objetos de un total de n. El número de estas combinaciones se denota por nCr, y se puede calcular del siguiente modo: nCr = = . Ejemplo 1 Juan Carlos está preparando su maleta para ir por el fin de semana a la playa. Quiere llevar tres de las diez camisas que tiene, dos de sus seis pantalones y cuatro de sus ocho pares de calcetines. ¿De cuán- tas maneras distintas puede hacer la selección de estos objetos? n! r!(n – r)! nPr r! 7 · 6 · 5 · 4 4 · 3 · 2 · 1 7P4 4! Analicemos... • ¿Podemos utilizar el mismo procedimiento que en el problema de ordenar los siete libros en una repisa si solo hay espacio para cuatro, que vimos anteriormente?, ¿por qué? • ¿De cuántas maneras se puede escoger la comisión?, ¿cómo lo supiste? UNIDAD 5 (200-247)C :Maquetación 1 4/11/10 17:20 Página 214
- 216. Probabilidades | 215 Unidad 5 La selección de tres camisas se puede hacer de 10C3 maneras. Los pantalones y calcetines se pueden seleccionar de 6C2 y 8C4 for- mas, respectivamente. Por el principio multiplicativo, la selección de camisas, pantalones y pares de calcetines para llevar a la playa se puede hacer de 10C3 · 6C2 · 8C4 = 120 · 15 · 70 = 126 000 formas en total. En resumen • El número de combinaciones posibles de r elementos seleccionados de n elementos distintos está dado por: nCr = . n! r!(n – r)! 1. Un experimento aleatorio consiste en extraer tres cartas de un mazo de 52, una a continuación de la otra y sin reposición (una vez que se saca la carta, no se regresa al mazo). ¿Cuántos elementos tiene el espacio muestral? a. Si no importa el orden de extracción. b. Sí importa el orden de extracción. 2. Un grupo de cinco amigos se encuentra después de mucho tiempo. Si cada uno se saluda con los demás con un abrazo, ¿cuántos abrazos se dan en total?, ¿cómo lo calculaste? 3. En un grupo de personas hay seis hombres y cuatro mujeres. Se necesita seleccionar de entre ellos a cinco personas. ¿De cuántas maneras se puede hacer la selección? a. Si se deben seleccionar dos hombres y tres mujeres. b. Si debe haber, por lo menos, dos hombres entre los cinco seleccionados. 4. Seis personas van de paseo en dos vehículos que tienen capacidad para dos y cuatro personas, respectivamente. ¿De cuántas maneras se pueden repartir en los vehículos? 5. El número de diagonales que se pueden trazar en un polígono convexo de n lados es , que coincide con nC2 – n. ¿Por qué? Explica. 6. Un experimento aleatorio consiste en extraer cuatro piezas de un juego de dominó (28 piezas distintas). ¿Cuál es el tamaño del espacio muestral?, ¿cómo lo calculaste? n(n – 3) 2 Actividades UNIDAD 5 (200-247)C :Maquetación 1 4/11/10 17:20 Página 215
- 217. 216 | Unidad 5 • En el siguiente mapa conceptual se muestran algunos de los conceptos presentados hasta ahora en la Unidad. • Utilizando los contenidos aprendidos en la Unidad, y apoyándote en el esquema anterior, responde en tu cuaderno. 1. ¿Crees que faltó un concepto importante en el mapa conceptual?, ¿cuál? Agrégalo. 2. Si un evento A puede ocurrir de m maneras distintas, y un evento B puede ocurrir de n maneras distintas, ¿cuántas maneras hay de que ocurra A y a continuación B? 3. ¿Qué es una permutación?, ¿cómo se calcula el valor de esta? 4. ¿Qué diferencia existe entre una combinación y una permutación? Justifica tu respuesta. 5. ¿De cuántas maneras se pueden elegir p elementos de un total de q elementos?, ¿por qué? 6. ¿Cuándo dos o más sucesos son mutuamente excluyentes? 7. Si la cardinalidad del espacio muestral de cierto experimento es #⍀ = r, y la de un suceso A asociado al experimento anterior es #A = s, ¿cuánto es #Ac ? 8. ¿Tienes alguna duda sobre los conceptos tratados en las páginas anteriores?, ¿cuál? Compártela con tu curso e intenten aclararla en conjunto. Organizando lo aprendido EXPERIMENTOS DETERMINÍSTICOS ALEATORIOS conjunto de posibles resultados es se clasifican en TAMAÑO MUESTRAL TÉCNICAS DE CONTEO PRINCIPIO MULTIPLICATIVO PERMUTACIONES COMBINACIONES ESPACIO MUESTRAL EVENTOS O SUCESOS a partir de este se definen determinamos cantidad de elementos mediante su cardinalidad es para determinarlo utilizamos algunas son UNIDAD 5 (200-247)C :Maquetación 1 4/11/10 17:20 Página 216
- 218. Mi progreso Unidad 5 1. Describe un espacio muestral para los siguientes experimentos. Luego, determina, si es posible, el tamaño de cada uno de estos. a. Extraer de una baraja inglesa una carta tras otra, sin reposición, hasta que salga un as. Interesa saber cuántas extracciones fueron necesarias. b. Un dado de seis caras tiene en ellas marcados los números 0, 1, 1, 2, 3 y 3. Tres de estos dados se lanzan sobre una mesa. Interesa la suma de los puntos. c. Se lanzan dos monedas. Interesa saber la distancia a la que quedaron. 2. Para el lanzamiento de dos dados, describe: a. un suceso elemental, c. un suceso seguro, b. dos sucesos mutuamente excluyentes, d. un suceso imposible. 3. Supón que ⍀ = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} es el espacio muestral para un experimento aleatorio. En este es- pacio muestral definimos los sucesos M = {1, 3, 5}, N = {3, 5, 7, 9} y P = {2, 4, 6, 8}. Determina los sucesos: a. M艛N b. M艚N c. (M艚P)c d. (M艛P)艚Nc 4. Considerando solo los dígitos 1, 3, 5, 7 y 9: a. ¿cuántos números distintos de tres cifras se pueden formar?, b. ¿cuántos números distintos de cinco cifras se pueden formar?, c. ¿cuántos de los números de cinco cifras no tienen ninguna cifra repetida?, d. ¿cuántos de los números de cinco cifras, sin cifras repetidas, son menores que 75 000? 5. Si consideramos el experimento de lanzar una moneda y dos dados, ¿cuántos elementos tiene el espacio muestral de este? A. 14 B. 36 C. 24 D. 72 E. 144 • Verifica en el solucionario del Texto si tus respuestas son correctas. Si tuviste respuestas incorrectas, marca en la tabla el criterio correspondiente y revisa las páginas indicadas. Luego, identifica el error y corrígelas. ¿Cómo voy? Probabilidades | 217 CRITERIO ÍTEMS PÁGINAS DONDE SE TRABAJA Describir y determinar el tamaño del espacio muestral de un experimento. 1 y 5 204 y 205 Describir y reconocer tipos de sucesos y relaciones entre estos. 2 y 3 206 a 209 Cálculo de tamaños muestrales utilizando distintas técnicas de conteo. 4 210 a 215 UNIDAD 5 (200-247)C :Maquetación 1 4/11/10 17:20 Página 217
- 219. 218 | Unidad 5 Cálculo de probabilidades Cristóbal, Andrés, Patricia, Carolina y Javiera se han postulado a la directiva de su curso. Los cargos son presidente, secretario y tesorero, por lo que solo se necesitan tres personas, las cuales elegirá al azar el profesor, y ellos deberán organizarse en los diferentes cargos. Analicemos... • ¿Cuántas posibilidades diferentes hay para formar la directiva del curso?, ¿cómo lo supiste? • ¿Cuál es la probabilidad de que la directiva esté formada por Andrés, Patricia y Javiera? En la situación anterior, para seleccionar las tres personas para la di- rectiva, debemos considerar todos los posibles grupos que podemos formar de tres personas. Al ordenar de diferentes formas los inte- grantes del grupo seleccionado, este no cambia; es decir, no importa el orden en que estén, ya que las personas serán las mismas. Recordando los contenidos anteriores, debemos calcular 5C3 para encontrar las combinaciones posibles de tres personas de un total de cinco. Observa. 5C3 = = = = = = 10 A menudo, en nuestra vida diaria tenemos la necesidad de tomar decisiones. La mayoría de las veces lo hacemos en condiciones de incertidumbre. Las probabilidades cuantifican el nivel de certeza con el fin de ayudar a la toma de decisiones. En cursos anteriores aprendiste a calcular probabilidades de suce- sos o eventos de experimentos aleatorios sencillos. Si definimos el suceso A como: A: la directiva del curso está formada por Andrés, Patricia y Javiera; luego, como los casos favorables para el suceso A serán solo en el grupo formado por Andrés, Patricia y Javiera, tendremos entonces que la probabilidad buscada será: P(A) = = 0,1. En general, una probabilidad se expresa como fracción o como deci- mal. También se puede expresar como porcentajes. En la situación anterior la probabilidad buscada corresponde a un 10%. 1 10 20 2 5 · 4 2! 5 · 4 · 3! 3! · 2! 5! 3! · 2! 5! 3! · (5 – 3)! De acuerdo a la regla de Laplace, la probabilidad de ocurrencia de un evento A está dada por: P(A) = . Recuerda que... nº de resultados favorables nº total de resultados UNIDAD 5 (200-247)C :Maquetación 1 4/11/10 17:20 Página 218
- 220. Probabilidades | 219 Unidad 5 Consideremos ahora el experimento de lanzar un dado y observar el número que se obtiene y los sucesos: A: el número obtenido es par. B: el número obtenido es impar. Observa que en el experimento, los elementos pertenecientes al suceso A son A = {2, 4, 6} y a B son B = {1, 3, 5}, por lo que entre ambos completan todo el espacio muestral; por lo tanto, B = Ac . Luego, para todo evento A, A y Ac son eventos mutuamente excluyentes, donde: P(⍀) = P(A艛Ac ) = P(A) + P(Ac ), entonces: P(A) + P(Ac ) = 1, y de aquí obtenemos que P(Ac ) = 1 – P(A). En resumen • La probabilidad de un evento A es tal que 0 ⱕ P(A) ⱕ 1. • La probabilidad de un evento imposible es 0, y la de un evento seguro es 1. • Para todo evento A, P(A) + P(Ac ) = 1, luego P(Ac ) = 1 – P(A). 1. Si en el lanzamiento de un dado definimos los siguientes sucesos: C: el número obtenido es mayor a 6. D: el número obtenido es menor a 7. ¿Cuánto es P(C)?, ¿y P(D)? Explica, paso a paso, cómo lo calculaste. 2. Supón que tienes tres urnas con fichas rojas (R) y verdes (V), como se muestra en la figura. Determina si las siguientes expresiones son verdaderas o falsas. Justifica tus respuestas. a. Es más probable obtener R al extraer una ficha de la urna I que de la II. b. Es más probable obtener R al extraer una ficha de la urna I que de la III. c. Es más probable obtener R al extraer una ficha de la urna II que de la III. 3. Se tiene una bolsa que contiene tarjetas con las letras: A, B, E, I, R, P, S, O. Si se extraen al azar cuatro tarjetas simultáneamente, ¿cuál es la probabilidad de que con estas letras se forme la palabra AIRE?, ¿y RISA? Actividades I II III UNIDAD 5 (200-247)C :Maquetación 1 4/11/10 17:20 Página 219
- 221. 220 | Unidad 5 Sucesos equiprobables Imagina que en cada clase de Historia, el profesor interroga a un alumno o alumna de tu curso acerca de los contenidos vistos en la clase anterior. El procedimiento que utiliza es escribir el número de lista de cada estudiante en una ficha. Todas las fichas son iguales en tamaño, forma y textura. A continuación, introduce las fichas en una caja, mueve esta para revolver las fichas, y luego saca, sin mirar, una de ellas. Analicemos... • ¿Es este un experimento aleatorio?, ¿por qué? • ¿Cuál es el espacio muestral de este experimento?, ¿cómo lo supiste? • ¿Tienen todos los alumnos y alumnas la misma probabilidad de ser seleccionados? En la situación anterior no podemos saber con exactitud cuál será el resultado del experimento, ya que no sabemos cuál será el número que extraerá el profesor, o sea, qué estudiante será selec- cionado. Si conocemos el conjunto de posibles resultados, significa que es un experimento aleatorio. El espacio muestral de este co- rresponde a los números de lista de cada estudiante. El procedimiento utilizado por el profesor de Historia está basado en dos supuestos: nadie sabe quién va a ser interrogado y cual- quiera podría ser el elegido; todos tienen igual oportunidad de ser interrogados; por lo que es un espacio muestral equiprobable. Diremos que un espacio muestral es equiprobable si todos los ele- mentos que lo conforman tienen igual oportunidad de ser elegidos, y, en consecuencia, tienen la misma probabilidad de ocurrencia. Consideremos ahora el experimento de extraer una bolita al azar de una urna como la que se muestra en la figura. Observa. El espacio muestral de este experimento es ⍀ = {rojo, azul}. Si consideramos los eventos: A: extraer una bolita de color azul. B: extraer una bolita de color rojo. UNIDAD 5 (200-247)C :Maquetación 1 4/11/10 17:20 Página 220
- 222. Probabilidades | 221 Unidad 5 Luego, tendremos que las probabilidades asociadas a cada evento serán: P(A) = = . Notemos que en este experimento tenemos un espacio muestral no equiprobable, ya que no todos los elementos que lo conforman tienen igual oportunidad de ser elegidos. Podemos ver que la probabilidad de ocurrencia no es la misma para todos los elemen- tos del espacio muestral. 3 5 número de resultados favorables al evento número total de resultados P(B) = = . 2 5 número de resultados favorables al evento número total de resultados En resumen • Si en un espacio muestral todos los elementos que lo conforman tienen la misma probabilidad, entonces diremos que el espacio muestral es equiprobable. 1. La mamá de Miguel y Carolina los manda a comprar y a lavar los platos. Ocurre que ambos prefieren ir a comprar y detestan el lavado de platos. Para no discutir, deciden repartirse las tareas asignadas lanzando una moneda, donde la obtención de cara podría significar, por ejemplo, que Miguel se en- cargará de las compras y Carolina de los platos. La situación inversa se daría si en el lanzamiento de la moneda sale sello. ¿Es el espacio muestral asociado a este experimento equiprobable?, ¿por qué? 2. Considera el experimento que consiste en esperar que suene el teléfono de tu casa y registrar la hora de la llamada. ¿Es igualmente probable recibir una llamada entre las 2 am y 4 am, que recibirla entre las 6 pm y 8 pm?, ¿por qué? 3. Para sacar un estudiante a la pizarra, un profesor escoge al azar una letra del alfabeto y elige al primer estudiante de la lista, cuyo apellido comienza con esa letra. ¿Tienen todos los estudiantes igual probabilidad de ser elegidos? 4. ¿En cuál de las siguientes ruletas es más probable obtener un número 1? Explica tu decisión. Actividades UNIDAD 5 (200-247)C :Maquetación 1 4/11/10 17:20 Página 221
- 223. 222 | Unidad 5 Probabilidad del suceso A艛B Sergio y María deben calcular la probabilidad de que al extraer al azar una carta de una baraja inglesa obtengan una figura (rey, reina, paje), o un carta cuyo palo o pinta sea trébol. Observa la solución que propone Sergio. La baraja tiene 52 cartas, valor correspondiente al tamaño del espa- cio muestral, en la cual hay 13 tréboles y 12 figuras. Por lo tanto, los casos favorables son 13 + 12 = 25; y la probabilidad buscada es . Sin embargo, María asegura que el resultado correcto es . 22 52 25 52 En la situación que deben resolver María y Sergio, el total de naipes de una baraja inglesa es 52 cartas; por lo tanto, al extraer una carta tendrá 52 resultados posibles. Luego, el tamaño del es- pacio muestral propuesto por Sergio es correcto. Los resultados favorables serán los naipes que sean una figura o cuya pinta sea trébol, que, tal como afirma Sergio, en una baraja hay 12 figuras y 13 naipes cuya pinta es trébol. El error de Sergio es en el cálculo del total de casos favorables: 13 + 12. Al realizar esta suma está contando las figuras de trébol dentro de las 13 cartas de trébol y nuevamente dentro de las 12 figuras. Si restamos del número inicial dado por Sergio aquellas cartas que, por cumplir con ambas condiciones, fueron contadas dos veces, obtenemos la respuesta correcta. Observa. Definamos los eventos: A: la pinta del naipe es trébol. B: es una figura. Analicemos... • ¿Es correcto el tamaño muestral del experimento que propone Sergio?, ¿por qué? • ¿Cuál es el número de resultados favorables en la situación de Sergio y María?, ¿es correcto el resultado de Sergio? • ¿Qué procedimiento crees que utilizó María para llegar al resul- tado propuesto por ella?, ¿por qué? UNIDAD 5 (200-247)C :Maquetación 1 4/11/10 17:20 Página 222
- 224. Probabilidades | 223 Unidad 5 Tendremos así que las probabilidades de cada evento serán: P(A) = , P(B) = , P(A艚B) = , entonces, P(A艛B) = P(A) + P(B) – P(A艚B) = + – = . Es decir, la probabilidad de extraer una carta de una baraja inglesa y que esta sea trébol o figura es de ; por lo tanto, María estaba en lo correcto, ya que el resultado obtenido por Sergio no lo era. Luego, se tiene que: P(A艛B) = P(A) + P(B) – P(A艚B). Notemos que si dos sucesos son mutuamente excluyentes, entonces: P(A艛B) = P(A) + P(B), ya que P(A艚B) = 0. 3 52 12 52 22 52 22 52 3 52 12 52 13 52 13 52 En resumen • Si A y B son sucesos no excluyentes, entonces: P(A艛B) = P(A) + P(B) – P(A艚B). • Si A y B son sucesos mutuamente excluyentes, entonces: P(A艛B) = P(A) + P(B). 1. Una tómbola contiene 90 bolitas numeradas del 1 al 90. Se extrae una bolita al azar. ¿Cuál es la probabilidad de que el número que contiene la bolita sea divisible por 6 o por 10? Explica, paso a paso, cómo lo calculaste. 2. Si se lanzan dos dados, calcula las siguientes probabilidades: a. P(la suma es 4 o la suma es 5). b. P(los números son iguales o la suma es 4). 3. Si P(A) = , P(A艛B) = y P(A艚B) = , ¿cuánto es P(B)? Escribe, paso a paso, el procedi- miento utilizado. 4. Si P(A艛B) = 0,5, P(A) = 0,43 y P(B) = 0,08, ¿son A y B mutuamente excluyentes?, ¿cómo lo supiste? 1 9 12 20 1 5 Actividades UNIDAD 5 (200-247)C :Maquetación 1 4/11/10 17:20 Página 223
- 225. 224 | Unidad 5 Frecuencia relativa o probabilidad empírica Los hermanos Camila y Joaquín se detienen a descansar en una plaza que se encuentra en el camino entre el colegio y su casa. Luego de un rato, deciden jugar a contar el color de los autos. El juego consiste en elegir un color y anotar durante quince minutos el de los autos que pasen. Si el color elegido es el que transita con mayor frecuencia, el jugador gana. El perdedor deberá cargar la mochila del ganador el resto del camino de vuelta a su casa. Camila elige el color blanco y Joaquín el gris. Observa en la tabla los resultados obtenidos. A partir de la tabla en que se registraron los autos según su color, podemos observar en los resultados que Joaquín es quien pierde. La razón de autos verdes que pasaron por la plaza es , que aproximadamente es 0,13. Este resultado corresponde a la frecuencia relativa de los autos de color verde. La probabilidad de un suceso la podemos estimar a través de datos obtenidos en observaciones empíricas o experimentales utilizando la frecuencia relativa. Luego, en la situación de Camila y Joaquín, la probabilidad de que pase un auto verde en los próximos quince minutos es 0,13. Ejemplo 1 Una encuesta realizada a 140 jóvenes residentes de una ciudad, en relación con el tipo de película que prefieren, arrojó los resulta- dos que se muestran en la tabla de la izquierda. Supongamos que la muestra es representativa de la población (consistente en todos los jóvenes de la ciudad) y que se selecciona al azar un joven. Se piden las probabilidades siguientes: 4 30 Analicemos... • ¿Quién gana el juego?, ¿Camila o Joaquín? • ¿Qué razón representa el número de autos de color verde, respecto del total de autos, que pasaron durante el juego? • Con los datos obtenidos por Camila y Joaquín, ¿cómo podemos determinar la probabilidad de que durante los próximos quince minutos pase un auto verde?, ¿por qué? Color Frecuencia Rojo 3 Azul 7 Verde 4 Blanco 9 Gris 7 Total 30 Mujer Hombre Total Acción 18 32 50 Comedia 16 9 25 Drama 16 8 24 Ciencia ficción 8 15 23 Otros 10 8 18 Total 68 72 140 La frecuencia relativa se denota por fi y corresponde a la razón entre el número de veces (ni ) que se observa un evento i y el número total (n) de repecticiones del experimento. fi = ni n Recuerda que... UNIDAD 5 (200-247)C :Maquetación 1 4/11/10 17:20 Página 224
- 226. Probabilidades | 225 Unidad 5 a. P(es mujer) De los 140 jóvenes encuestados, 68 son mujeres. Luego, P(es mujer) = . b. P(prefiere películas de acción) De los 140 entrevistados, 50 prefieren las películas de acción, luego, P(prefiere películas de acción) = . c. P(prefiere las comedias y es hombre) 9 hombres prefieren las comedias, por tanto, P(prefiere las comedias y es hombre) = . 9 140 50 140 68 140 1. En los 200 últimos días laborales, Claudia ha estado enferma 120 días. ¿Cuál es la probabilidad de que esté enferma hoy? 2. Una editorial tiene 75 títulos diferentes de libros, clasificados por materia y costo: Calcula la probabilidad de que un libro elegido al azar: a. sea de ficción y su valor sea $ 10 000, b. tenga un valor de $ 15 000, c. sea de historia. 3. Realiza el siguiente experimento: Lanza un dado 36 veces y cuenta cuántas veces obtuviste 5. Calcula la frecuencia relativa de obtener 5. Compara tus resultados con los obtenidos por tus compañeros y compañeras. ¿Qué observas? 4. ¿Qué piensas que puede pasar con la tabla de frecuencias de Camila, si ella observa nuevamente por media hora los autos que pasan? Actividades En resumen • La probabilidad de un suceso se puede estimar a través de la frecuencia relativa, calculada en base a datos muestrales u obtenida de un número grande de repeticiones de un experimento. Costo Materia $ 10 000 $ 15 000 $ 20 000 Total Ficción 10 8 3 21 Biografía 12 10 9 31 Historia 4 17 2 23 Total 26 35 14 75 UNIDAD 5 (200-247)C :Maquetación 1 4/11/10 17:20 Página 225
- 227. 226 | Unidad 5 Ley de los grandes números Rafael y Francisca deben realizar el experimento de lanzar una moneda una determinada cantidad de veces, y observar el número de caras resultantes. Observa en la tabla los resultados obtenidos. Puedes verificar que cada vez que repites el ejercicio anterior, la tabla será diferente. También variará si se cambia el número de lanzamientos, pero lo importante es destacar la tendencia de la situación estudiada. Podemos observar que, a medida que el número de repeticiones del experimento es mayor, la frecuencia relativa tiende a estabilizarse en torno a 0,5, valor que corresponde a la probabilidad de ocurrencia del suceso. Esta situación la podemos representar también por medio de un gráfico. Observa. Este comportamiento corresponde a la ley de los grandes números, la cual postula que a medida que aumenta el número de repeti- ciones de un experimento aleatorio, la frecuencia relativa de un evento se aproxima cada vez más a su probabilidad clásica. Analicemos... • Si repetimos el experimento de Rafael y Francisca, ¿crees que obtendremos siempre los mismos resultados?, ¿por qué? • ¿Cuál es la probabilidad de obtener cara al lanzar una moneda?, ¿cómo es esta probabilidad con respecto a los resultados obtenidos por Rafael y Francisca?, ¿por qué? N° de lanzamientos N° de caras Frecuencia relativa 5 1 0,20 10 3 0,30 20 12 0,60 30 13 0,43 40 21 0,53 50 27 0,54 0 0 10 0,1 0,2 0,3 0,4 0,5 0,6 0,7 Frecuencia Nº de repeticiones 20 30 40 50 60 UNIDAD 5 (200-247)C :Maquetación 1 4/11/10 17:21 Página 226
- 228. Probabilidades | 227 Unidad 5 1. Lanza un dado 20 veces, registra la frecuencia con que aparece un 6. Repite el experimento realizando 50 lanzamientos. Luego, calcula la frecuencia relativa para el suceso en cada caso. a. Compara los valores obtenidos. ¿Son estos similares?, ¿por qué? b. Calcula la probabilidad del suceso. ¿Son similares las frecuencias relativas a esta probabilidad? ¿en cuál de los dos casos se acerca más a esta?, ¿por qué? c. ¿Qué crees que ocurrirá si repites el experimento 1000 veces?, ¿por qué? Actividades En resumen • La ley de los grandes números dice que al repetir un experimento aleatorio muchas veces, la frecuencia relativa de cada uno de los sucesos tiende a estabilizarse, aproximándose a un número fijo, que es la probabilidad de que el suceso ocurra. Herramientas tecnológicas Utilizaremos una planilla de cálculo, como por ejemplo Excel, para simular el experimento realizado en la actividad anterior. Para esto sigue las siguientes instrucciones: • Ubícate en la celda A1 y escribe: =aleatorio.entre(1,6). La función =aleatorio.entre(1,6) devuelve un número entero aleatorio entre mayor o igual a 1 y menor o igual a 6. • Presiona F9 para cambiar el número aleatorio entregado. Supongamos que cada vez que pre- sionas F9 estás lanzando un dado. De este modo puedes lanzar el dado cuantas veces quieras. • Copia la instrucción dada en 20 casillas, entonces estarás lanzando tu dado 20 veces. Para hacer esto basta con que te ubiques en el vértice inferior derecho de la celda A1 y arrastres con el mouse la cruz que aparece en ese lugar hasta A20. • Copia la instrucción desde A1 hasta C20, puedes interpretarlo como lanzar tu dado 60 veces. • Para hacer un recuento del total de veces en que aparece 6 en la cara superior del dado en la simulación, ingresa en la celda B22 la función =contar.si(A1:C20;”6”). Esta función contará en cuántas celdas aparece un 6 el total de repeticiones del experimento. • En la celda B23 ingresa la fórmula =B22/60, el resultado corresponderá a la frecuencia rela- tiva con que aparece un 6 en la simulación del experimento. • Utilizando el procedimiento aprendido, repite el experimento, simulando 120 lanzamientos. UNIDAD 5 (200-247)C :Maquetación 1 4/11/10 17:21 Página 227
- 229. 228 | Unidad 5 Probabilidad condicional Claudio está jugando a lanzar un dado. Luego, el espacio mues- tral del experimento es ⍀ = {1, 2, 3, 4, 5, 6}. Por otra parte, él sabe que este espacio muestral es equiprobable. Si define el suceso: A: el número obtenido es impar. Donde A = {1, 3, 5}, entonces, se tiene que P(A) = = . Camila se integra al juego y lanza el dado sin que Claudio pueda ver el número obtenido, pero le da una pista: “El número es menor que 4”. 1 2 3 6 Si, en el juego de Claudio y Camila, definimos el evento B: sale un número menor que 4, este corresponderá a B = {1, 2, 3}. De este nuevo conjunto de casos posibles, los favorables para el suceso de interés son solamente 1 y 3, ya que sabemos que el número es menor que 4. Este conjunto corresponde a los elemen- tos del suceso A艚B. Así pues, tenemos dos casos favorables correspondientes a #A艚B, y tres casos posibles que corresponden a #B. Luego, la probabilidad de obtener un número impar sabiendo que el número que se obtuvo es menor que 4 es . Tal como en la situación anterior, hay casos en que la probabilidad de un suceso A se ve afectada por la ocurrencia de otro suceso B. Este tipo de probabilidad se llama probabilidad condicional y se denota por P(A/B) y se lee como “la probabilidad de que ocurra A dado que ha ocurrido B” o “la probabilidad de A dado B”. 2 3 Analicemos... • ¿Piensas que la probabilidad de que salga un número impar cambia en este nuevo escenario?, ¿por qué? • Intuitivamente, ¿crees que la probabilidad ahora, de que salga un número impar es mayor o menor que antes? • ¿Cuál es la probabilidad de que el número que salió sea impar?, ¿cómo lo supiste? UNIDAD 5 (200-247)C :Maquetación 1 4/11/10 17:21 Página 228
- 230. Probabilidades | 229 Ejemplo Una urna contiene dos bolitas negras (N1 y N2 ) y una bolita blanca (B). Se extraen de la urna dos bolitas al azar, sin reposición. ¿Cuál es la probabilidad de que la segunda bolita sea negra, dado que la primera bolita que se sacó es negra? Definimos A como el suceso: “sale bolita negra en la segunda ex- tracción”, y C: ”sale bolita negra en la primera extracción”. Se nos pide calcular P(A/C). Entonces: C = {N1 B, N2 B, N1 N2 , N2 N1 }, donde el orden de las letras indica el orden en que se sacaron las bolitas. Por tanto, #C = 4. A艚C es el suceso en que la primera bolita es negra y la segunda también, es decir: A艚C = {N1 N2 , N2 N1 } y #(A艚C) = 2. Por lo tanto, tenemos que: P(A/C) = = = 1 2 2 4 #A艚C #C Unidad 5 En resumen • Si A y B son sucesos de un espacio muestral equiprobable y #B ⫽ 0, entonces la probabilidad de A dado B está dada por: P(A/B) = . #A艚B #B 1. Para el lanzamiento de un dado, calcula: a. P(número par/es menor que 4). d. P(aparece 1/es primo). b. P(número primo/es par). e. P(es menor que 4/número par). c. P(número impar/es primo). f. P(es primo/número impar). 2. Se lanzan dos dados. Halla la probabilidad de: a. la suma de los números es 10, b. la suma de los números es 10, si se sabe que en uno de ellos salió 6, c. la suma de los números es mayor que 7, si se sabe que “la suma de los números es un número impar”. Actividades UNIDAD 5 (200-247)C :Maquetación 1 4/11/10 17:21 Página 229
- 231. 230 | Unidad 5 Probabilidad del suceso A艚B Cada estudiante de un curso, compuesto por trece hombres y quince mujeres, compró un número de una rifa en la cual se sortearán dos premios. Para sortear la rifa se depositarán los números en una bolsa, y se extraerá al azar uno de ellos para rifar el primer premio; luego, se dejará este número y se sorteará de la misma manera el se- gundo premio. Para representar y comprender situaciones como la anterior, resulta muy útil utilizar un diagrama de árbol. Observa que dos caminos diferentes, como los que están destacados, corresponden siempre a sucesos mutuamente excluyentes (sus probabilidades se suman). Para responder la primera pregunta, definimos los sucesos: H1 = el primer premio lo recibe un hombre. H2 = el segundo premio lo recibe un hombre. Debemos calcular P(H1艚H2), entonces: P(H1艚H2) = P(el primer premio lo reciba un hombre) · P(el segundo premio lo reciba un hombre, dado que el primer premio también lo recibió un hombre). Es decir: P(H1艚H2) = P(H1) · P(H2/H1) = · = . 13 63 12 27 13 28 Analicemos... • ¿Cuál es la probabilidad de que sean hombres los que ganen ambos premios? • ¿Cuál es la probabilidad de que un hombre gane el segundo premio? Primer premio Segundo premio 14 27 15 28 13 28 Mujer 13 27 Hombre 15 27 Mujer 12 27 Hombre Hombre Mujer UNIDAD 5 (200-247)C :Maquetación 1 4/11/10 17:21 Página 230
- 232. Probabilidades | 231 Unidad 5 Veamos ahora cuál es la probabilidad de que un hombre gane el segundo premio. Sea M1: “el primer premio lo recibe una mujer”. Que un hombre gane el segundo premio depende de que ocurra alguno de los sucesos: M1 y H2, o bien H1 y H2. Como estos son mutuamente excluyentes, la probabilidad pedida se puede calcu- lar de la siguiente manera: En resumen • La probabilidad de que ocurran dos sucesos simultáneamente es igual al producto entre la probabilidad de que suceda uno de ellos y la del otro, dado que ocurrió el primero. Es decir: P(A艚B) = P(B) · P(A/B). 1. De un curso de primer año de una carrera universitaria, el 40% de los estudiantes reprobó Geometría y el 10% reprobó tanto Geometría como Álgebra. Si se escoge al azar un estudiante de este curso y resulta ser que ha reprobado Geometría, ¿cuál es la probabilidad de que también haya reprobado Álgebra?, ¿cómo lo calculaste? 2. Dos cartas se extraen sin remplazo de una baraja inglesa. Encuentra la probabilidad de: a. que ambas cartas no sean figuras, b. que la segunda carta sea una figura. Explica, paso a paso, cómo lo hiciste. 3. Tres cartas se extraen sin remplazo de una baraja inglesa. Encuentra la probabilidad de: a. que las tres sean cartas negras, b. que al menos una de ellas sea roja, c. que exactamente una de ellas sea roja. Explica, paso a paso, el procedimiento utilizado. Actividades P(hombre gane el segundo sorteo) = P(M1艚H2) + P(H1艚H2) = P(M1) · P(H2/M1) + P(H1) · P(H2/H1) = · + · 12 27 13 28 13 27 15 28 = 0,46 351 756 UNIDAD 5 (200-247)C :Maquetación 1 4/11/10 17:21 Página 231
- 233. 232 | Unidad 5 Sucesos independientes Daniel está realizando un experimento que consiste en extraer dos cartas de una baraja sin remplazo, y luego calcular ciertas proba- bilidades, para lo cual define los siguientes eventos: A: la primera carta es una reina. B: la segunda carta es una reina. Analicemos... • ¿Cuál es el valor de P(A), P(B/A) y P(A艚B)?, ¿cómo lo supiste? • Si Daniel repite el experimento, pero con remplazo, ¿cuál será el valor de las probabilidades anteriores? • ¿Existen diferencias en ambos resultados?, ¿por qué? En el experimento anterior, Daniel extrae las cartas en primer lugar, sin remplazo. Luego, sabemos que para extraer la primera carta te- nemos un espacio muestral con #⍀ = 52 y que además es equipro- bable. Por otra parte, solo hay cuatro reinas en un mazo, luego P(A) = . Si ya hemos extraído una reina, el tamaño del espacio muestral se redujo de 52 a 51 y para B solo quedan tres opciones, por lo tanto, P(B/A) = . Luego, como P(A艚B) = P(B) · P(A/B), tendremos que P(A艚B) = · = . Para el caso de la extracción con remplazo, P(A), al igual que en el caso anterior, es , pero ahora para B hay cuatro opciones y #⍀ Si la primera carta extraída se remplaza cuando extraemos la se- gunda, es como empezar todo de nuevo, es decir: P(B) = P(A) = . Observemos que P(B/A) = P(B) = . Intuitivamente, lo que ocurre es que, cuando la extracción es con remplazo, la ocurrencia de A no afecta la de B, es decir, A y B son sucesos independientes. Entonces: P(A艚B) = P(A) · P(B/A) = P(A) · P(B) = · = . 16 2704 4 52 4 52 4 52 4 52 4 52 12 2652 3 51 4 52 3 51 4 52 se mantiene en 52, luego P(B/A) = . 4 52 UNIDAD 5 (200-247)C :Maquetación 1 4/11/10 17:21 Página 232
- 234. Probabilidades | 233 Unidad 5 En resumen • Si dos sucesos A y B son independientes, entonces: • P(A/B) = P(A). • P(A艚B) = P(A) · P(B). 1. Determina si los siguientes pares de sucesos son dependientes o independientes. Justifica. a. De una baraja de naipe inglés, extraer un as y “sacar una carta roja”. b. De una baraja de naipe inglés, extraer “corazón” y “sacar una carta roja”. c. En el lanzamiento de dos dados, “obtener siete puntos” y “obtener dos números iguales”. d. En el lanzamiento de un dado, sacar “número primo” y “sacar número menor que 3”. 2. Inventa dos sucesos que sean independientes, explica por qué lo son y compártelos con tus compañeros y compañeras. 3. Para el lanzamiento de un dado con su espacio muestral equiprobable ⍀ = {1, 2, 3, 4, 5, 6} se definen los sucesos A = {1, 2} (sale un número menor que 3), B = {1, 3, 5} (sale un número impar). ¿Los sucesos A y B son independientes?, ¿por qué? 4. Un barco de guerra, al lanzar misiles, acierta su objetivo en doce de cada quince lanzamientos. Si el barco lanza dos misiles, ¿cuál es la probabilidad de que falle en ambos lanzamientos? Explica, paso a paso, cómo lo resolviste. 5. Se lanza una moneda y un dado. ¿Cuál es la probabilidad de obtener “sello” y “tres”?, ¿cómo lo calculaste? 6. En un hospital se cuenta con un registro de los pacientes que tienen diabetes, organizado por sexo y tipo de diabetes. Hay 50 varones registrados, de los cuales 35 tienen diabetes tipo I, y 15 diabetes tipo II. Hay también 25 mujeres con diabetes tipo I, y 20 mujeres con diabetes tipo II. Si se selecciona una de las fichas de este registro al azar, encuentra la probabilidad de sacar: a. una correspondiente a una mujer, b. una correspondiente a diabetes tipo II, c. una correspondiente a hombre con diabetes tipo I. ¿Son independientes los sucesos “es hombre” y “tiene diabetes tipo I”? Actividades UNIDAD 5 (200-247)C :Maquetación 1 4/11/10 17:21 Página 233
- 235. 234 | Unidad 5 Variable aleatoria Claudia se encuentra realizando el experimento de lanzar dos dados y luego anotar la suma de los valores obtenidos en estos. Quiere saber qué valor es más probable observar, para lo cual cons- truye una tabla que muestra los posibles valores y combinaciones para ambos dados. Observa. Podemos observar en los datos de la tabla que los posibles valores que puede obtener Claudia al realizar el experimento son: 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12. Para que la suma de los dados sea 2 solo puede ocurrir que al lanzar dos dados se observe el par (1, 1), luego: P(2) = P((1, 1)) = . De la misma forma, para que la suma de los dados sea 3, se tienen que dar los sucesos (1, 2) y (2, 1), que son excluyentes, luego: P(3) = P((1, 2)) + P((2, 1)) = + = . De igual forma podemos obtener las probabilidades asociadas a cada valor posible, que podemos resumir en la siguiente tabla: 2 36 1 36 1 36 1 36 Analicemos... • ¿Cuáles son los posibles resultados que puede obtener Claudia? • ¿Cuál es la probabilidad de que la suma de los valores obtenidos en los dados sea 2?, ¿y 3?, ¿cómo lo supiste? • ¿Cuánto es la suma de las probabilidades de todos los posibles valores en el experimento de Claudia?, ¿por qué? 1 2 3 4 5 6 1 (1, 1) (1, 2) (1, 3) (1, 4) (1, 5) (1, 6) 2 (2, 1) (2, 2) (2, 3) (2, 4) (2, 5) (2, 6) 3 (3, 1) (3, 2) (3, 3) (3, 4) (3, 5) (3, 6) 4 (4, 1) (4, 2) (4, 3) (4, 4) (4, 5) (4, 6) 5 (5, 1) (5, 2) (5, 3) (5, 4) (5, 5) (5, 6) 6 (6, 1) (6, 2) (6, 3) (6, 4) (6, 5) (6, 6) x 2 3 4 5 6 7 8 9 10 11 12 P(X = x) 1 36 2 36 3 36 4 36 5 36 6 36 5 36 4 36 3 36 2 36 1 36 Generalmente, se utilizan letras ma- yúsculas como X, Y,... para designar variables aleatorias, y las respectivas minúsculas x, y,... para designar valores particulares de las mismas. Pon atención UNIDAD 5 (200-247)C :Maquetación 1 12/11/10 15:14 Página 234
- 236. Probabilidades | 235 Lo que acabamos de construir es una variable aleatoria. Obtenemos una variable aleatoria si a cada suceso elemental de un experi- mento aleatorio le asociamos un único valor numérico. Escribiremos P(X = x) para representar la probabilidad de que la variable aleatoria X tome el valor x. En el experimento de Claudia podemos definir la variable aleatoria: X = suma de las caras en el lanzamiento de dos dados. Luego: P(X = 2) = . Si calculamos las probabilidades para cada uno de los valores posi- bles de la variable aleatoria, obtendremos que el resultado es 1, puesto que es la suma de las probabilidades de sucesos mutua- mente excluyentes que, en conjunto, forman todo el espacio muestral. Observa: P(X = 2) + P(X = 3) + P(X = 4) + P(X = 5) + P(X = 6) + P(X = 7) + P(X = 8) + P(X = 9) + P(X = 10) + P(X = 11) + P(X = 12) = + + + + + + + + + + = = 1 En general, si una variable aleatoria puede tomar n valores llama- dos x1 , x2 , x3 , …, xn , se tiene que: P(X = x1 ) + P(X = x2 ) + P(X = x3 ) +… + P(X = xn ) = 1 Una variable aleatoria que puede asumir una cantidad finita de valores, o una sucesión infinita de valores como 0, 1, 2, …, se llama variable aleatoria discreta. Si, en cambio, el conjunto de posibles valores de una variable aleatoria corresponde a un intervalo de números reales, decimos que es una variable aleatoria continua. Ejemplo 1 Sea Z la variable aleatoria que cuenta el número de lanzamientos de un dado hasta que salga el primer 6. ¿A que tipo de variable aleatoria corresponde Z? Los valores posibles de Z son 1, 2, 3, 4,… Luego, esta corresponde a una variable aleatoria discreta. 36 36 1 36 2 36 3 36 4 36 5 36 6 36 5 36 4 36 3 36 2 36 1 36 1 36 Unidad 5 Glosario sucesión: conjunto ordenado de ele- mentos que responden a una regla de formación. UNIDAD 5 (200-247)C :Maquetación 1 4/11/10 17:21 Página 235
- 237. 236 | Unidad 5 Ejemplo 2 Si se escoge al azar una manzana de un árbol y se mide su peso en gramos, los valores posibles de esta variable aleatoria están en el rango ]0, + ⬁[. Aunque en la práctica tal vez nos interesen los pesos de las manzanas aproximados a números enteros, sabemos que en un rango de 100 a 101 gramos es posible, al menos en teoría, en- contrar infinitos pesos distintos. Muchas veces será de utilidad visualizar la correspondencia de un valor de la variable aleatoria con su probabilidad a través de un grá- fico. Generalmente, usaremos un diagrama de barras, colocando en el eje horizontal los posibles valores de la variable aleatoria, y en el eje vertical las probabilidades de que estos ocurran. Ejemplo 3 Un jugador, que suele encestar el 70% de sus tiros, tiene que realizar un lanzamiento. Si el jugador acierta el primer tiro, puede repetir el lanzamiento. Por lo tanto, es posible que consiga 0 puntos (fallando el primer lanzamiento), 1 punto (acertando el primero y fallando el segundo) o 2 puntos (acertando ambos lanzamientos). Sea X la variable aleatoria que representa el puntaje obtenido: a. Calcula P(X = 0), P(X = 1), P(X = 2). b. Dibuja un gráfico de barras para la distribución de probabili- dades de la variable X. Solución a. Usaremos una A para “acierto” y una F para “fallo” y supon- dremos que lo que ocurra en el primer lanzamiento no tiene ningún efecto sobre el segundo lanzamiento. Entonces: P(A艚A)=0,7 · 0,7 = 0,49 P(A艚F) =0,7 · 0,3 = 0,21 P(F) = 0,3 = 0,30 Por lo tanto: P(X = 0) = 0,30 ; P(X = 1) = 0,21 ; P(X = 2) = 0,49. Probabilidad de acertar ambos lanzamientos Probabilidad de acertar un lanzamiento y fallar otro Jugadores de básquetbol. UNIDAD 5 (200-247)C :Maquetación 1 4/11/10 17:21 Página 236
- 238. Probabilidades | 237 Unidad 5 b. En resumen • Obtenemos una variable aleatoria si a cada suceso elemental de un experimento aleatorio le asociamos un único valor numérico. • Si una variable aleatoria puede tomar n valores llamados x1 , x2 , x3 , …, xn , se tiene que: P(X = x1 ) + P(X = x2 ) + P(X = x3 ) +… + P(X = xn ) = 1. • Existen variables aleatorias discretas o continuas, según como sea su conjunto de posibles valores. 1. Clasifica las siguientes variables aleatorias como discretas o continuas. a. El número de hijos que tiene una persona. b. El volumen de jugo que puede extraerse de un limón sacado al azar de un árbol. c. La estatura de una persona escogida aleatoriamente dentro de un grupo. d. El número de televisores que hay dentro de un hogar chileno escogido al azar. 2. Sea la variable aleatoria Z el producto de los números obtenidos en el lanzamiento de dos dados. a. ¿Es Z discreta o continua? b. Indica los posibles valores de Z. c. Calcula P(Z = z) para todos los valores posibles de z. d. Verifica que se cumple la propiedad P(Z = z1 ) + … + P(Z = zn ) = 1. e. Calcula P(Z 5), P(Z 8) y P(5 ⱕ Z ⱕ 10). 3. Una profesora tiene una caja con ocho calculadoras, tres de las cuales ya no funcionan. Un alumno escoge aleatoriamente dos de estas calculadoras. Sea Y la variable aleatoria cuyos valores son las posibles calculadoras defectuosas escogidas por el alumno. Determina los posibles valores de Y y calcula sus probabilidades. Actividades 0,1 0 0 1 2 Puntos Probabilidad 0,2 0,3 0,4 0,5 0,6 UNIDAD 5 (200-247)C :Maquetación 1 4/11/10 17:21 Página 237
- 239. 238 | Unidad 5 • En el siguiente mapa se muestran algunos conceptos presentados hasta ahora en la Unidad. • Utilizando los contenidos aprendidos hasta aquí, y apoyándote en el esquema anterior, responde en tu cuaderno. 1. ¿Crees que faltó un concepto importante en el mapa conceptual?, ¿cuál? Agrégalo. 2. ¿Cuándo es 0 la probabilidad de ocurrencia de un suceso? 3. ¿Qué quiere decir que la probabilidad sea igual a 1? 4. ¿Qué significa que un espacio muestral sea equiprobable? 5. ¿Cómo es la probabilidad de A艚B si A y B son sucesos no excluyentes?, ¿y si A y B son sucesos excluyentes. 6. Si P(A) = 0,7, ¿cuál es el valor de P(Ac )? 7. Explica con tus propias palabras la ley de los grandes números. 8. ¿Cómo se calcula P(A/B)? ¿Qué pasa si A y B son eventos independientes?, ¿cómo se interpreta? 9. ¿Cómo se calcula P(A艛B)?, ¿qué pasa si A y B son independientes? 10. ¿Tienes alguna duda sobre los conceptos tratados en las páginas anteriores?, ¿cuál? Compártela con tu curso e intenten aclararla en conjunto. Organizando lo aprendido PROBABILIDADES se calculan a partir de PROBABILIDAD CONDICIONAL EXPERMIENTO ALEATORIO ESPACIO MUESTRAL VARIABLE ALEATORIA UNIÓN DE SUCESOS COMPLEMENTO DE UN SUCESO INTERSECCIÓN DE SUCESOS SUCESOS en algunos casos de del cual se definen los posibles resultados forman se asocian a PROBABILIDADES UNIDAD 5 (200-247)C :Maquetación 1 4/11/10 17:21 Página 238
- 240. Probabilidades | 239 Unidad 5 Mi progreso 1. Se realizan 2000 lanzamientos de tres monedas. ¿Cuántas veces, aproximadamente, se esperaría que ocurra el suceso A: sale exactamente una cara? A. 100 B. 500 C. 1000 D. 1500 E. 2000 2. Se preguntó a 50 jóvenes si estaban de acuerdo con remplazar el servicio militar obligatorio por un sistema voluntario. Las respuestas fueron las siguientes: Si se escoge al azar uno de estos jóvenes, a. ¿cuál es la probabilidad de que esté de acuerdo con el cambio?, b. ¿cuál es la probabilidad de que sea una mujer que no está de acuerdo?, c. ¿cuál es la probabilidad de que el encuestado sea un hombre? 3. Ana y Juan están tratando de resolver un problema. La probabilidad de que Ana resuelva el problema es de un 75% y la probabilidad de que lo resuelva Juan es de un 65%. Determina: a. la probabilidad de que ambos resuelvan el problema, b. la probabilidad de que ninguno de ellos resuelva el problema, c. la probabilidad de que al menos uno de ellos resuelva el problema, d. la probabilidad de que Juan haya resuelto el problema, dado que el problema fue resuelto por Ana. 4. Una variable aleatoria X toma valores 2, 4, 5, 7, 8 y 9, con probabilidades 0,15; 0,12; 0,21; 0,25; 0,16 y 0,11, respectivamente. a. Verifica que se cumple la propiedad P(X = x1 ) + … + P(X = xn ) = 1. b. Calcula P(X 5). c. Calcula P(X = 6) y P(X = 9). • Verifica en el solucionario del Texto si tus respuestas son correctas. Si tuviste respuestas incorrectas, marca en la tabla el criterio correspondiente y revisa las páginas indicadas. Luego, identifica el error y corrígelas. ¿Cómo voy? CRITERIO ÍTEMS PÁGINAS DONDE SE TRABAJA Comprender y utilizar la ley de los grandes números. 1 226 y 227 Relacionar la frecuencia relativa con la probabilidad de ocurrencia de un suceso. 2 224 y 225 Calcular probabilidades de diferentes sucesos y reconocer variables aleatorias. 3 y 4 218 a 223 y 228 a 237 Unidad 5 De acuerdo En desacuerdo Hombres 18 12 Mujeres 16 4 UNIDAD 5 (200-247)C :Maquetación 1 4/11/10 17:21 Página 239
- 241. Cómo resolverlo 240 | Unidad 5 Observa, paso a paso, las estrategias utilizadas en la resolución de los siguientes problemas. Ejercicio 1 Silvia está realizando el siguiente experimento: lanza una moneda dos veces y luego cuenta el número de caras que obtiene. La tabla muestra los resultados obtenidos por Silvia luego de diez repeticiones del experimento. Observa. a. ¿Cuál es el número promedio de caras que obtuvo Silvia? b. Imaginemos ahora que se realiza un número muy grande de lan- zamientos. Sabemos que, en tal caso, las frecuencias relativas con que aparecen los distintos sucesos tienden a estabilizarse en torno a un valor, que es, precisamente, la probabilidad del suceso. ¿Cuál será el promedio que espera observar Silvia? Solución a. Hubo tres lanzamientos en los que Silvia obtuvo 0 caras, seis lanza- mientos en que obtuvo una cara y un lanzamiento en el que obtuvo dos caras. Luego, tendremos que el promedio obtenido por Silvia es: = 0,8. Por lo tanto, en estos diez lanzamientos, Silvia obtuvo en promedio 0,8 caras por lanzamiento. Reescribiendo la expresión anterior obtenemos: 0 · + 1 · + 2 · = 0,8. La expresión anterior nos muestra que el promedio se puede calcu- lar utilizando la frecuencia relativa o probabilidad de casa suceso. b. Si imaginamos ahora que Silvia realiza un número muy grande de lanzamientos, tendremos que, en tal caso, las frecuencias relativas con que aparecen los distintos sucesos tienden a estabilizarse en torno a un valor, que es, precisamente, la probabilidad del suceso. Luego, podemos calcular el promedio que espera ver Silvia, utili- zando las probabilidades de ocurrencia de cada posible suceso. El espacio muestral correspondiente al experimento de Silvia es: E = {cc, cs, sc, ss}. 1 10 6 10 3 10 0 · 3 + 1 · 6 + 2 · 1 10 X Frecuencia 0 3 1 6 2 1 UNIDAD 5 (200-247)C :Maquetación 1 4/11/10 17:21 Página 240
- 242. Probabilidades | 241 Unidad 5 Definamos la variable aleatoria: X = número de caras en ambos lanzamientos. Por lo tanto: P(X = 0) = , P(X = 1) = , P(X = 2) = , luego: 0 · P(X = 0) + 1 · (X = 1) + 2 · P(X = 2) = 0 · + 1 · + 2 · = 1 Es decir, si realizamos un gran número de repeticiones del experimento, obtendremos, en promedio, 1 cara. Este valor es conocido como el valor esperado o esperanza matemática, y se denota por E(X). Por lo tanto: E(X) = 1. 1 4 1 2 1 4 1 2 1 4 1 4 Actividades 1. Aplica el procedimiento aprendido para resolver la siguiente situación: Jaime está participando en un juego en el que se lanzan dos monedas; se ganan 50 puntos cada vez que salen dos caras y se pierden 30 puntos en cualquier otra situación. Sea X la variable aleatoria cuyos posibles valores son los puntos que gana o pierde Jaime en un lanzamiento: a. calcula P(X = 50) y P(X = –30). b. calcula E(X). ¿Qué interpretación se puede dar al valor E(X)? c. en doscientas repeticiones, ¿cuántos puntos, en promedio, se esperaría ganar o perder? 2. Busca un procedimiento distinto para resolver el problema anterior. Respecto del procedimiento previo, ¿cuál es más simple?, ¿por qué? 3. Resuelve el siguiente problema empleando el método aprendido u otro. Compara el procedimiento que utilizaste con el de algún compañero o compañera. ¿Cuál es más simple?, ¿por qué? X representa los puntos obtenidos al tirar un dado cargado, además: • P(X = 1) = – 2k • P(X = 3) = P(X = 4) = • P(X = 6) = + 2k Determina el valor de k, de modo que el valor esperado sea igual a 4. 1 6 1 6 • P(X = 2) = – k • P(X = 5) = + k 1 6 1 6 1 6 UNIDAD 5 (200-247)C :Maquetación 1 4/11/10 17:21 Página 241
- 243. 242 | Unidad 5 En terreno En terreno Siniestros de tránsito y consecuencias Una de las principales causas de muerte en Chile son los accidentes de tránsito, alcanzando cifras alarmantes. La causa de mayor frecuencia de estos accidentes es la generada por imprudencias del conductor, donde en su mayoría se deben a conducir sin mantener una distancia razonable ni prudente. Otra importante causa de accidentes de tránsito son los producidos por la ingesta de alcohol. Durante el año 2008 hubo 4946 siniestros asociados a la presencia de alcohol, en los cuales murieron 378 personas y hubo 3897 lesionados. El total de accidentes causados por presencia de alcohol corresponde a un 8,66% del total gene- ral; sin embargo, el total de fallecidos por esta causa fue de un 21,21% del total. Está demostrado que el alcohol deteriora marcadamente la función psicomotora y la capacidad para conducir con seguridad. Quizás uno de los efectos más importantes es que el alcohol dilata el tiempo de reacción; es decir, aumenta el tiempo que tarda la persona, después de percibir plenamente las sensaciones y/o recibir infor- mación, en decidir qué debe hacer y cuándo actuar. La siguiente tabla muestra las causas de siniestros de tránsito y consecuencias du- rante el año 2008. Causas de siniestros de tránsito y consecuencias (año 2008) Causa de siniestro Siniestros Fallecidos Lesionados Imprudencia del peatón 3896 398 3897 Presencia de alcohol 4946 378 6145 Imprudencia del conductor 25 116 362 19 297 Pérdida de control 4706 287 6311 Velocidad imprudente 1703 116 2063 Desobediencia a señalización 7110 92 8417 Otras causas 2904 62 2482 Drogas y/o fatiga del conductor 488 57 818 Causas no determinadas 934 10 1384 Fallas mecánicas 4407 8 3645 Imprudencia del pasajero 420 7 384 Deficiencias viales 457 5 443 Fuente: www.carabinerosdechile.cl www.conaset.cl UNIDAD 5 (200-247)C :Maquetación 1 4/11/10 17:21 Página 242
- 244. Actividades Considera los datos de la tabla anterior y responde. 1. ¿Cuál es la probabilidad de que un siniestro producido durante el año 2008 haya sido causado por la presencia de alcohol? 2. Si seleccionamos al azar un accidentado durante el año 2008: a. ¿cuál es la probabilidad de que este haya fallecido, dado que sufrió un accidente causado por la presencia de alcohol?, b. ¿cuál es la probabilidad de que este haya sufrido un accidente causado por la presencia de alcohol, dado que este falleció? Investiguemos... Ahora, trabajen en grupos de tres personas. 1. Comparen las respuestas obtenidas por cada uno y discutan sobre cuáles de las respuestas son correc- tas si hay diferencias. 2. Busca información en el sitio web www.carabinerosdechile.cl sobre el número de accidentes produci- dos en tu comuna o ciudad durante el año anterior, el total de tu región y el total a nivel nacional del total de fallecidos y lesionados. 3. Calcula, utilizando la información encontrada, las siguientes probabilidades: a. P(accidentado en tu región haya sufrido lesiones). b. P(accidentado en tu ciudad o comuna haya fallecido). c. P(accidente de tu región haya pertenecido a tu comuna). Evaluemos nuestro trabajo • Comparen los resultados obtenidos. ¿Son similares? Si no es así, ¿qué diferencia hubo?, ¿a qué crees que se debe? • Indaguen respecto a las causas de accidentes de tránsito en Chile, y qué podemos hacer para prevenir estos. Probabilidades | 243 Unidad 5 UNIDAD 5 (200-247)C :Maquetación 1 4/11/10 17:21 Página 243
- 245. 244 | Unidad 5 Síntesis de la Unidad A continuación, se presentan los conceptos fundamentales trabajados en la Unidad. Construye con ellos un mapa conceptual, en tu cuaderno. No olvides agregar las palabras de enlace que indican las relaciones entre los conceptos. A partir de lo trabajado en la Unidad, responde. 1. ¿Qué es un experimento aleatorio? 2. ¿Qué es el espacio muestral de un experimento aleatorio? 3. ¿Cuál es la diferencia entre una permutación y una combinación? 4. ¿Entre qué rangos de valores puede estar una probabilidad?, ¿por qué? Ejemplifica utilizando la regla de Laplace. 5. ¿Cuándo el espacio muestral de un experimento es equiprobable?, ¿por qué? Nombra un ejem- plo de un espacio muestral equiprobable y un ejemplo de un espacio muestral no equiprobable. 6. Si P(A/B) = P(A), ¿qué relación hay entre los sucesos A y B?, ¿por qué? 7. ¿Cómo se relaciona la P(A) y la de P(Ac ) para un evento A cualquiera? 8. ¿Qué relación existe entre la frecuencia relativa de una variable aleatoria con su probabilidad de ocurrencia? 9. Si P(A艚B) = P(A) · P(B), ¿qué relación hay entre los sucesos A y B?, ¿por qué? 10. ¿Tienes alguna duda sobre los conceptos tratados en las páginas anteriores?, ¿cuál? Compártela con tu curso e intenten aclararla en conjunto. PROBABILIDADES SUCESOS EQUIPROBABLES PROBABILIDAD CONDICIONAL SUCESOS INDEPENDIENTES ESPACIO MUESTRAL VARIABLE ALEATORIA UNIDAD 5 (200-247)C :Maquetación 1 4/11/10 17:21 Página 244
- 246. Probabilidades | 245 Evaluación I. Determina si las expresiones siguientes son verdaderas o falsas. Justifica tu respuesta. 1. En todo experimento aleatorio el espacio muestral es un conjunto finito de elementos. 2. Si P(A y B) = P(A) · P(B), entonces A y B son eventos independientes. 3. P(A) + P(Ac ) = 1. 4. Si A y B son eventos excluyentes, entonces P(A艚B) = 0. 5. Si A y B no son eventos excluyentes, entonces P(A艛B) = P(A) + P(B) – P(A艚B). II. Aplica lo que aprendiste en la Unidad para desarrollar las siguientes actividades: 1. Responde las siguientes preguntas. Indica, paso a paso, el procedimiento utilizado. a. ¿De cuántas maneras pueden distribuirse diez personas en diez asientos dispuestos en fila si cuatro de ellas deben estar siempre juntas? b. ¿De cuántas formas pueden sentarse en una fila cuatro niñas y cinco niños, si deben colocarse alternadamente? 2. Para formar una comisión se debe escoger uno de los tres ingenieros civiles A, B y C, uno de los dos economistas M y N, y uno de los dos abogados S y T. La elección será hecha al azar y se anotará el resultado con siglas del tipo ANT, BMS, etc. Determina: a. el espacio muestral de este experimento aleatorio, b. la probabilidad del suceso de que sea elegido el abogado S, c. el complemento del suceso descrito en b, d. dos sucesos del experimento, distintos de los anteriores, que sean mutuamente excluyentes. 3. Un inspector medioambiental visitará tres fábricas de plásticos para vigilar el nivel de emisiones contaminantes en el proceso de producción. Si el nivel es aceptable, anotará en su planilla A; si no lo es, anotará I. La sucesión AAI indica, por ejemplo, que las dos primeras fábricas tenían un nivel aceptable y la última no. a. Dibuja un diagrama de árbol que muestre los resultados posibles y describe el espacio muestral. b. Determina la probabilidad del suceso A: hay exactamente dos fábricas con nivel aceptable. c. Determina la probabilidad del suceso B: hay al menos una fábrica con nivel aceptable. 4. De una bolsa que hay 7 pelotas blancas, 5 azules y 6 verdes se sacan 4 pelotas. a. Considera la variable Z como la cantidad de pelotas blancas y calcula P(Z = z) para todos los posibles valores de z. b. Considera la variable Y como la cantidad de pelotas verdes y calcula P(Y = y) para todos los posibles valores de y. c. Considera la variable X como la cantidad de pelotas azules y calcula P(X = x) para todos los posibles valores de x. Unidad 5 UNIDAD 5 (200-247)C :Maquetación 1 4/11/10 17:21 Página 245
- 247. 246 | Unidad 5 1. ¿De cuántas formas se puede dividir un grupo de nueve personas en dos grupos de cinco y cuatro personas? A. 45 B. 126 C. 252 D. 5760 E. 15 876 2. Cierto dado de seis caras tiene marcados en ellas los números 0, 1, 1, 2, 2, 2. Dos de estos dados se lanzan simultáneamente sobre una mesa.¿Cuál es la probabilidad de que la suma de los puntos sea 3? A. C. E. 3. ¿Cuál es la probabilidad de obtener a lo menos un 5 al tirar simultáneamente dos dados? A. C. E. 4. Una prueba tiene 10 preguntas de verdadero y falso. Si Felipe contesta todas las preguntas al azar, ¿cuál es la probabilidad de que responda todas correctamente? A. 0,5 B. 0,1 C. 0,05 D. 0,0019531 E. 0,0009765 5. De una baraja inglesa se extraen dos cartas, una a continuación de la otra y sin reposición. Sea M el suceso “ambas cartas son figuras” y N el suceso “la primera carta es corazón y la se- gunda carta es trébol”, ¿cuántos elementos tiene el suceso M艛N? A. 226 B. 235 C. 292 D. 301 E. 808 6. Considera todos los números de cuatro cifras formados solamente con los dígitos 1 y 2. Si se escoge al azar uno de estos números, ¿cuál es la probabilidad de que sea un múltiplo de 6? A. C. E. 7 8 3 8 1 16 1 2 1 6 11 36 1 2 1 6 1 3 III. Resuelve los siguientes ejercicios y selecciona la alternativa correcta en cada caso. B. 1 4 D. 1 18 B. 5 36 D. 1 5 B. 3 16 D. 1 2 UNIDAD 5 (200-247)C :Maquetación 1 4/11/10 17:21 Página 246
- 248. Probabilidades | 247 7. Loreto arrojó un dado no cargado cuatro veces y en todos los tiros obtuvo 6. ¿Cuál es la proba- bilidad de que en el próximo tiro obtenga un 6? A. C. E. 8. Si se escoge al azar una carta de una baraja inglesa, ¿cuál es la probabilidad de que sea menor que 3 y roja? A. C. E. 9. Se extrae aleatoriamente una carta de una baraja inglesa. Los sucesos “sacar carta menor que 3” y “sacar carta roja” son: A. equiprobables. B. independientes. C. dependientes. D. mutuamente excluyentes. E. elementales. 10. De una baraja de naipe inglés se sacan sucesi- vamente dos cartas sin reposición. ¿Cuál es la probabilidad de que ambas sean reinas? A. C. E. 11. Las cifras que forman un número son 1, 2, 3, 4 y 5. ¿Cuántos números de cinco cifras, menores que 54 000, pueden formarse, sin que se repitan las cifras? A. 18 B. 96 C. 114 D. 120 E. Otro valor. 12. Si se extraen dos cartas de una baraja inglesa sin reposición, ¿cuál es la probabilidad de que la segunda carta sea una figura, dado que la primera carta extraída fue un as? A. C. E. 12 52 11 51 4 51 7 52 1 221 3 676 4 52 26 52 34 52 7 8 1 6 4 ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ 1 2 Unidad 5 Verifica en el solucionario de tu Texto si tus respuestas son correctas. ¿Te equivocaste en alguna?, ¿cuál fue el error? Explícalo y resuelve correctamente el ejercicio. B. 30 52 D. 8 52 B. 30 221 D. 1 169 B. 4 52 D. 12 51 B. 1 6 5 ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ D. 1 6 UNIDAD 5 (200-247)C :Maquetación 1 4/11/10 17:21 Página 247
- 249. Taller de evaluación 1. La expresión es igual a: A. 10 B. 14 C. 12 D. 28 E. Ninguna de las anteriores. 2. El resultado de es: A. B. C. D. 78 E. Ninguna de las anteriores. 3. La expresión es equivalente a: A. B. C. D. E. Ninguna de las anteriores. 4. La medida de la diagonal de un cuadrado es . ¿Cuál es el área? A. B. C. 5 D. 10 E. Ninguna de las anteriores. 5. El valor de es: A. B. C. 18mq D. E. 6. Al racionalizar la fracción se obtiene: A. B. C. D. E. Ninguna de las anteriores. 7. La suma de es: B. 2 C. E. 3 2 5 2 0 125 4 0 25 3 , , + 7 5 − 5 7 − 5 7 + 1 2 1 7 5 + 18 2 m q 2 2 m q 18 2 mq 18 2 2 m q 2 72 5 18 3 98 2 2 m q m q m q − + 2 5 5 10 29 7 8 12 2 12 8 4 2 2 2 3 26 3 15 3 10 3 2 75 4 48 + 121 64 81 3 4 + − Marca la opción correcta en cada caso. 248 | Matemática 3º Medio Taller de evaluación Raíces 1 A. 1 2 D. –3 2 PAGS 248-255:Maquetación 1 4/11/10 17:35 Página 248
- 250. 8. La(s) solución(es) de la ecuación es(son): A. 1 B. 4 C. 5 D. 12 E. No tiene solución real. 9. La expresión es equivalente a: A. m + n B. n – m C. m – n D. m – n2 E. (n – m)2 10. La expresión es igual a: A. 13 B. C. 40 D. 100 E. Ninguna de las anteriores. 1. La(s) solución(es) de la ecuación (x + 4)2 + (x – 3)2 = (x – 5)2 es(son): A. 0 y 8 B. 12 C. 0 y –12 D. 0 y –8 E. 0 y 12 13 4 10 + 5 8 2 + ( ) 4 2 9 2 2 2 ( ) ( ) m n mn m n + − − − 3 15 + = + x x Taller de evaluación | 249 Función cuadrática y función raíz cuadrada 2 2. Al resolver la ecuación = el valor de x es: I. III. A. Solo I B. Solo II C. Solo III D. I y II E. II y III 3. Si las raíces de la ecuación x2 + ax + b = 0 son –2 y 4, entonces el valor de b es: A. –8 B. –2 C. 2 D. 6 E. 8 4. Para que el producto de las raíces de la ecuación 4x2 + 3m – 5x = –6 sea 48, el valor de m debe ser: A. 3 B. 16 C. 62 D. 64 E. 128 4 7 3 2 29 6 x2 + 5 x II. 10 3 PAGS 248-255:Maquetación 1 4/11/10 17:35 Página 249
- 251. 250 | Matemática 3º Medio Taller de evaluación 5. En la funcion f(x) = 4x2 – 4x – 3, las coordenadas de su vértice son: A. B. (2, –4) C. D. (2, 4) E. 6. Una de las ecuaciones cuyas raíces son (2 + ) y (2 – ) es: A. x2 – 4x + 6 = 0 B. x2 – 6x + 4 = 0 C. x2 + 4x + 2 = 0 D. x2 – 4x + 2 = 0 E. Ninguna de las anteriores. 7. Si x1 y x2 son raíces de la ecuación x2 – 5x – 2 = 0, entonces, el valor de (x1 + 1)(x2 + 1) es: A. –7 B. –6 C. 4 D. 5 E. 8 8. El área de un terreno de forma rectangular es 133 m2 . Calcula su perímetro si el largo es el doble del ancho, aumentado en 5 m. A. 26 m B. 52 m C. 64 m D. 66,5 m E. Falta información. 9. Dadas las funciones f(x) = x2 – 5x + 3, g(x) = x2 + 5x + 3, r(x) = x2 + 3, se afirma que: A. Todas tienen su vértice en el origen (0,0). B. Todas abren hacia arriba y la ecuación del eje de simetría es x = 0. C. Todas tienen igual eje de simetría. D. Todas abren hacia arriba e intersecan al eje Y en el mismo punto. E. Todas las afirmaciones anteriores son falsas. 10. El punto mínimo de la función f(x) = 3x2 – 7x + 1 es: A. (–37, 7) B. C. (7, –37) D. E. (6, 12) 1. Si sen(α) = , entonces, el valor de tan(α) es: B. D. E. Ninguna de las anteriores. 2 10 3 2 10 7 3 7 − ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ 7 6 37 12 , 7 6 37 12 , − ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ 2 2 − ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ 1 2 4 , 1 2 4 ,− ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ − − ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ 1 2 4 , El triángulo rectángulo y la trigonometría 3 A. 3 7 C. 3 10 20 PAGS 248-255:Maquetación 1 4/11/10 17:36 Página 250
- 252. Taller de evaluación | 251 2. Sabiendo que sen(α) = , entonces, el valor de cos(α) + tan(α) – sen(α) es: A. 0,95 B. 1,45 C. 1,55 D. 1,95 E. Ninguna de las anteriores. 3. El valor de la expresión cos(270º) · (sen(90º) + cos(180º)) – sen(270º) es: A. –1 B. 0 C. 1 D. 2 E. Ninguna de las anteriores. 4. ¿A qué cuadrantes pertenecen los ángulos cuya cotangente es positiva? A. I y IV B. I y II C. I y III D. II y III E. Ninguna de las anteriores. 5. En el triángulo ABC de la figura DE//AB y = , se puede afirmar que: I. CD = CE II. = 1 3 CE EB 1 3 CD DA 3 5 De estas afirmaciones, es o son verdaderas: A. Solo I B. Solo II C. Solo III D. I y II E. II y III 6. Si un edificio proyecta una sombra de 25 m y tiene una altura de 70 m, ¿cuánto mide el ángulo de elevación al Sol? A. 19,6º B. 20,9º C. 69º D. 70,3º E. Ninguna de las anteriores. 7. Cuando el ángulo de elvación al Sol es de 60º sobre el horizonte, un árbol de 15 m de alto proyecta una sombra que mide: A. 9 m B. m C. m D. m 8. En el triangulo ABC, rectángulo en C, el valor de p2 + q2 + 2pq es: A. 100 B. 196 C. 100 + 2pq D. 196 + 2pq E. Ninguna de las anteriores. 15 3 2 5 3 15 3 III. = 1 4 DE AB C D A B A C B p q 6 8 E E. m 15 2 PAGS 248-255:Maquetación 1 4/11/10 17:36 Página 251
- 253. 252 | Matemática 3º Medio Taller de evaluación 9. Si los catetos de un triángulo rectángulo miden 5 cm y 12 cm, entonces, la altura correspondiente a la hipotenusa mide: A. cm C. cm D. 30 cm E. Ninguna de las anteriores. 10. En la cima de un cerro se ha levantado una an- tena de telefonía celular. Desde un punto ubicado en el valle se miden los ángulos de elevación del extremo superior y la base de la antena. ¿Cuál es la altura del cerro si estos ángulos son 57º y 42º, respectivamente, y además la antena mide 80 m de alto? A. 100 m B. 112,6 m C. 154 m D. 168,3 m E. Ninguna de las anteriores. 1. El conjunto A = {x 僆 IR/ –2 ⱕ x 6} es equiva- lente al intervalo: A. [–2, 6] B. ]–2, 6[ C. [–2, 6[ D. ]–2, 6] E. Ninguna de las anteriores. 2. Si a ⱖ b + c, entonces, se cumple que: A. a – c ⱖ b B. a – b ⱕ c C. a + c ⱕ b D. b – a ⱖ –c E. a + b c 3. La inecuación 2x + 3y ⱕ 12 se cumple para el par ordenado: A. (6, 1) B. (–1, 6) C. (2, 2) D. (0, 9) E. 4. El par (–1, 7) satisface la desigualdad: A. 3x – 7y 8 B. 2x + y ⱖ 9 C. + – 3 D. x + y ⱕ x E. –x + y ≥ y 5. El siguiente gráfico es la solución de la inecuación: A. 兩x – 3兩 ⱖ 10 B. 兩3x兩 ⱕ 10 C. 兩x – 3兩 ⱕ 10 D. 兩x + 10兩 ⱕ 3 E. Ninguna de las anteriores. 1 y 1 x 7 2 7 3 , ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ 60 13 17 13 B. cm 7 5 Inecuaciones lineales 4 –7 13 PAGS 248-255:Maquetación 1 4/11/10 17:36 Página 252
- 254. Taller de evaluación | 253 6. El conjunto solución de la inecuación x2 – 3x ⱕ 18 es: A. {x 僆 IR / x ⱕ –3 y x ⱖ 6} B. {x 僆 IR / x 6} C. {x 僆 IR / x ⱖ –3} D. {x 僆 IR / –3 x 6} E. {x 僆 IR / –3 ⱕ x ⱕ 6} 7. El siguiente gráfico es solución de: A. 2x 4 B. 3x + 2 ⱖ – 4 C. 5 – x ⱖ 3 D. 7 + 2x 3 E. Ninguna de las anteriores. 8. La solución de la inecuación 3 – 4x ⱖ 2x – 15 es: A. x ⱖ 3 B. x ⱕ 3 C. [–⬁, 9] D. 3 E. Ninguna de las anteriores. 9. La solución del sistema de inecuaciones 4x + 5 ⱖ x – 1 , es: 6 – x – 3 A. [–2, 9[ B. ]9, +⬁[ C. ]–⬁, –2]艛]9, +⬁[ D. [–2, 3[ E. Ninguna de las anteriores. 10. En el gráfico, se representa el intervalo: A. ]–⬁, 4[ B. ]–⬁, 4] C. [4, +⬁[ D. ]4, +⬁[ E. Ninguna de las anteriores. 1. En el experimento de lanzar dos monedas al aire y ver la cantidad de caras (C) y sellos (S) que aparecen en el espacio muestral es: A. {C, S} B. {(C, C), (C, S), (S, S)} C. {(C, C), (C, S), (S, C), (S, S)} D. {1, 2, 3} E. Ninguna de las anteriores. 2. El resultado de 8C5 + 3C2 es equivalente o igual a: A. 11C7 B. 13C5 C. 24C10 D. 59 E. 342 –2 4 Probabilidades 5 PAGS 248-255:Maquetación 1 4/11/10 17:36 Página 253
- 255. 254 | Matemática 3º Medio Taller de evaluación 3. ¿De cuántas maneras se pueden combinar 2 pares de zapatos, 4 de pantalones y 5 camisas? A. 8 B. 11 C. 20 D. 40 E. Ninguna de las anteriores. 4. De 18 vestidos que hay en una tienda se eligen 6. El número de maneras distintas de elegirlo es: A. 18 564 B. 9282 C. 4541 D. 5184 E. 72 5. Calcula la probabilidad de que al extraer una tarjeta al azar de una bolsa que tiene 9 tarjetas numeradas de 1 a 9, esta sea par. A. C. E. Ninguna de las anteriores. 6. Una compañía telefónica establece para sus lla- madas de larga distancia un código de 3 dígitos. Si el primer dígito no puede ser 0 ó 1 y el segundo dígito debe ser 0 ó 1, los códigos que podrían formarse son: A. 160 B. 320 C. 500 D. 720 E. 1000 7. La expresión equivale a: A. x2 + 10x + 25 B. x2 + 12x + 36 C. x + 5 D. x + 6 E. x2 + 11x + 30 8. Si P(A艛B) = ;P(A) = ; P(A艚B) = . ¿Cuánto es la P(B)? A. C. E. 8 7 3 7 1 7 1 7 2 7 5 7 (x + 6)! (x + 4)! 1 2 2 9 B. 3 9 B. 2 7 D. 4 7 D. 4 9 PAGS 248-255:Maquetación 1 4/11/10 17:36 Página 254
- 256. Taller de evaluación | 255 9. Un examen tiene 10 preguntas que deben responderse con Verdadero o Falso. Si Felipe responde todas las preguntas al azar, ¿cuál es la probabilidad de que responda todas correctamente? A. B. 0,5 C. 0,0019531 D. 0,05 E. 0,0009765 10. El 15% de los habitantes de una ciudad pre- fiere las bebidas bajas en calorías. Si se eligen al azar dos personas de esa ciudad, ¿cuál es la probabilidad que ambos prefieran las bebidas bajas en calorías? A. C. E. No se puede determinar. 11. Según el censo 2002, la siguiente es una dis- tribución de jefes de hogar según grupo étnico en Chile. Fuente: Instituto Nacional de Estadísticas (www.ine.cl) Si se escoge una de estas personas al azar y resulta ser de la etnia quechua, ¿cuál es la pro- babilidad de que sea una mujer jefe de hogar? A. C. E. Ninguna de las anteriores. 570 54 395 570 186 867 15 100 7 330 1 10 B. 9 400 B. 1760 186 867 D. 570 1760 D. 14 99 Hombre Mujer Total Mapuche 117 650 46 895 164 545 Aymara 9137 4686 13 823 Atacameño 4495 2244 6739 Quechua 1190 570 1760 Total 132 472 54 395 186 867 PAGS 248-255:Maquetación 1 4/11/10 17:36 Página 255
- 257. Páginas 14 y 15 1. a. 2 2 · 3 · 5 2 d. 2 5 · 3 2 · 11 b. 3 · 5 2 · 17 e. 2 · 3 3 · 5 3 c. 2 2 · 5 2 · 13 f. 2 3 · 3 4 ·11 2. a. Verdadero d. Falso b. Falso e. Falso c. Verdadero f. Verdadero 3. a. f. k. b. g. x 3a + 7 l. a 9 c. –5 h. c 7a + 7 m. b 14x – 14y d. 36 i. 1 n. e. 625 j. 64x 30 4. a. Aumenta a 9 veces el área del cuadrado original. b. Disminuye a la octava parte del volumen del cubo original. 5. a. x 2 – 6xy + 9y 2 c. a 3 – 27b 3 b. x 2 + x – 6 d. – y 2 6. a. c. (3x + 2)(9x 2 – 6x + 4) b. (x 3 – 2) 2 d. (2x – 3y) 3 Página 17 1. a. 6 cm d. 25 m g. 35 cm b. 9 cm e. 30 m h. 41 cm c. 20 m f. 32 cm i. 60 cm 2. a. 0 d. 6 g. 6 b. 3 e. 12 h. 15 c. 3 f. 100 i. 1000 3. a. Verdadero d. Verdadero b. Verdadero e. Verdadero c. Falso f. Falso 4. a. Si a 0, la expresión no está definida en el conjunto de los números reales, por lo que no podremos calcular su valor. b. No se cumple para todo a, b IR. Página 19 1. a. Racional g. Irracional b. Racional h. Racional c. Irracional i. Irracional d. Racional j. Irracional e. Irracional k. Irracional f. Irracional l. Irracional 2. Indicación: Si existiera un número racional igual a , se escribiría como una fracción , con x e y números enteros positivos. Luego, suponga que se simplifican todos los factores de modo de obtener una fracción irreducible. Entonces, demuestre por reducción al absurdo que esto no puede ocurrir, por lo tanto, es un número irracional. Para demostrar que es un número irracional siga las mismas indicaciones. Página 21 1. 2. a. b. Página 23 1. a. –3 d. 3 g. 0 b. 11 e. 6 h. – c. 0,5 f. 0 i. 4,7 1 5 8 12 100 12 15 ; ; ; ; 2 7 10 5 ; ; ; 5 3 x y 3 256 | Matemática 3º Medio Solucionario Raíces 1 91 –– 12 1 729 –64x 6 b 9 125c 3 b 5 ac 2 x 2 9 25 4 401 16 2 3 4 5 8 12 18 (2 –– a – 3 –– b )(2 –– a + 3 –– b ) a SOLUCIONARIO 3º (256-283):Maquetación 1 4/11/10 17:25 Página 256
- 258. 2. a. 2 m c. m e. 1,1 m b. 4 m d. 0,5 m f. 0,9 m 3. a. 16 cm 2 b. Sí c. 4. a. Verdadero d. Verdadero b. Verdadero e. Falso c. Falso f. Falso Página 25 1. a. 4,12 d. 31,62 b. 10,49 e. 4,64 c. 18,71 f. 0,62 2. a. b. Página 27 1. a. e. b. f. c. g. d. 4 h. 2. a. 4,48 b. 17,3 c. 77,504 d. 0,709 aproximadamente. 3. a. 2x b. c. 4. a. Falso b. Falso Página 29 1. a. Verdadero c. Verdadero b. Falso d. Verdadero 2. a. 5 d. b. e. c. 5 –– 16 f. 2 3. E 4. a. 9 cm b. cm 3 5. a. m 2 b. m 2 c. m 2 Página 31 1. a. –1 c. –3 e. 6 b. 1 d. 7 f. 5 2. a. Verdadero d. Falso b. Verdadero e. Verdadero c. Verdadero f. Verdadero 3. a. 6 b. 6 c. 4 d. 6 Páginas 34 y 35 1. a. c. e. – b. d. –2 f. – 2. a. d. b. e. c. f. 3. a. d. 2 b. 3 e. x c. 2 f. Solucionario Solucionario | 257 Solucionario 1 3 1 2 3 10 2 3 5 4 1 35 V V 3 2 2 3 ( ) = 5 21 40 40 3 3 ; ; ; 1000 800 1000 3 ; ; 6 3 12 2 5 10 3 a a c a b c b 5 5 9 7a b 4 3 2 b a 2 2 2 a b 25 5 2 21 3 − 15 7 5 6 12 4 11 18 2 3 6 3 − 84 5 x7 11 6 25 5 5 3 − 9 4 5 4 16 2 5 2 5 xy x y − 2 xy x − 2 14 2 4 + − 5 21 2 3 81 3 c b 5 – 2 SOLUCIONARIO 3º (256-283):Maquetación 1 4/11/10 17:25 Página 257
- 259. 258 | Matemática 3º Medio Solucionario 4. a. d. b. e. 1 c. 6 f. 5. a. 0; 0; 0; 0. El término que sigue es: b. 1; 1; 1; 1. El término que sigue es: c. 64; 8; 2,83; 1,68. El término que sigue es: d. 256; 16; 4; 2. El término que sigue es: e. –512; –8; –2; –1.26. El término que sigue es: f. 10 000; 100; 10; 3,16. El término que sigue es: 6. a. 243; 15,59; 3,95; 1,99 b. 0,0041; 0,064; 0,252; 0,501 Existen diferencias entre las secuencias, ya que los términos de la segunda secuencia son los inversos multiplicativos de los términos de la primera secuencia. Página 37 1. a. c. b. d. 2. a. (–343) = –7 c. b. 243 = 3 d. 512 = 2 3. a. b. 4. a. Sí b. m c. cm 5. a. b. c. Página 41 1. a. g. b. h. c. i. d. j. e. k. f. l. 2. a. Falso c. Verdadero b. Verdadero d. Verdadero 3. a. e. b. f. c. g. d. h. Página 43 1. a. x = 30 d. x = g. x = 0 b. x = e. x = h. x = –5 c. x = f. x = 0 2. Porque surgen de elevar al cuadrado. Ejemplo: tiene una solución que no satisface la ecuación: x = 9. 3. No Página 45 1. a. Verdadero d. Verdadero b. Falso e. Verdadero c. Falso f. Falso x x – 2 2 = + 729 16 1 7 3 2 5 12 1 2 3 5 4 13 3 5 4 3 3 3 5 2 3 2 2 1 – + 1 2 1 2 1 2 – + 4 5 3 6 3 5 – – 2 5 1 1 5 2 3 3 – + 1 5 162 8 45 3 − 275 3 x2 15 2 2 35 7 2 6 2 + ( ) 3 3 4 − 5 2 5 7 26 − ( ) 2 2 a a b a b b + ( ) − − 2 5 3 3 x x x x x 2 3 3 1 1 + + − 25 5 2 4 3 3 + + 3 2 2 2 4 3 3 + + ( ) 2 3 12 6 2 18 3 3 + + ( ) 72 6 2 10 5 9 49 100 3 0 00032 5 , 2 8 8 15 864 6 3 8 4 − 3 3 0 1 64 256 −512 3 3 3 3 10 000 445 4 53 20 16 3 1 – 3 1 – 9 1 – 5 (– 1 ) = – 1 –– 10 10000 27 10 600 6 x x5 4 6 SOLUCIONARIO 3º (256-283):Maquetación 1 4/11/10 17:25 Página 258
- 260. Solucionario | 259 2. a. e. c. g. 3. a. 30 e. b. 12 f. c. g. d. 14 h. 4. a. 36 b. c. 17 5. C Página 47 1. a. b. 3. Área: Perímetro: Página 49 1. 1,99 2. a. 1,99 s d. 1,41 s b. 3,98 s e. 0,89 s c. 1,26 s 3. a. 1,01 m c. 6,31 m b. 4,04 m d. 0,06 m Página 51 I. 1. Falso 4. Falso 2. Falso 5. Verdadero 3. Falso 6. Falso II. 1. a. b. 2. a. c. 1 e. b. d. 9 f. b. d. 4. a. 12,5 cm 2 b. m 5. a. x = 10 b. x = 2 c. No tiene solución en los números reales. d. No tiene solución en los números reales. Página 52 III. 1. B 6. A 11. C 2. E 7. B 12. A 3. B 8. D 13. D 4. D 9. D 14. D 5. A 10. D Páginas 56 y 57 1. a. (x 2 + 1)(x – 1) d. (a + 2)(a – 2) b. x(3x – 7) e. (x – 6)(x + 1) c. (3x + 1)(x + 1) f. (y + a)(y + b) 2. a. 11,5479 d. –4,23 b. 10,97 e. 0,2311 c. 18,4644 f. 1,723 3. a. x = ±12 c. x = 1 953 125 b. x = 49 d. x = a – b 4. b, c y d 5. a y d 6. a, c y d 2 2 13 13 a a a ; y 3390 3 π a – 5 3 5 2 + ( ) 343 60 215 16 2 60 a 3 20 16 18 4 3 3 4 3 ; ; ; − − − − 5 33 9 256 3 5 3 7 ; ; ; 2 3 2 a a + a a 3 a 3 2 + ( ) 445 4 2 217 24 a2 3 3 3 8 7 49 3 − 3 4 5 16 5 5 4 3 2 9 29 3 3 − + ( ) 3 3 2 10 6 + ( ) 17 3 3 Solucionario s m 3. a. c. − + + ( ) 11 9 2 3 4 5 3 3 3 25 5 3 d. h. a6 7 − + ( ) 8 2 4 19 3 b. f. 6 12 3 3 + 6 4 3 Función cuadrática y función raíz cuadrada 2 SOLUCIONARIO 3º (256-283):Maquetación 1 4/11/10 17:25 Página 259
- 261. 260 | Matemática 3º Medio Solucionario Página 59 1. a. –2 b. –2 c. 18 d. 34 e. a 2 – 2ab + b 2 – a + b – 2 f. a 2 + 2ab + b 2 – a – b – 2 g. a 2 – a – b 2 + b h. 5c 2 – 11c – 4 i. 2 – 2c 2. a. A(a) = a 2 b. A(r) = π · r 2 c. A(d) = · d 2 3. A(x) = . No. 4. No 5. Sí Página 61 1. 2. a. Falso b. Falso Página 63 1. a. Falso b. Falso c. Verdadero 2. a. (x – 3) 2 + 10; a = 1, h = 3, k = 10 b. ; a = 1, h = – , k = – c. 2(x – 1) 2 + 5; a = 2, h = 1, k = 5 d. –2(x – 3) 2 + 15; a = –2, h = 3, k = 15 e. 3(x – 4) 2 – 20; a = 3, h = 4, k = – 20 f. –5(x + 2) 2 + 6; a = –5, h = –2, k = 6 Página 65 1. a. contracción b. dilatación c. contracción d. dilatación 1 2 x + ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ 5 2 2 53 4 5 2 x2 3 4 X –4 –3 –2 –1 0 1 2 3 4 f(x) = 2x 2 32 18 8 2 0 2 8 18 32 f(x) = x –4 –3 –2 –1 0 1 2 3 4 f(x) = 2x –8 –6 –4 –2 0 2 4 6 8 SOLUCIONARIO 3º (256-283):Maquetación 1 4/11/10 17:25 Página 260
- 262. Solucionario | 261 2. a. h(x) = –16x 2 + 24 000x – 700 000 b. 7 300 000 c. Ambas. Página 69 4. a. g. b. h. c. i. d. j. e. k. f. l. 2. a. g(x) = x 2 – 10x + 25 b. g(x) = – x 2 + 9x – 23 c. g(x) = x 2 – 3 d. g(x) = – x 2 + x + 8 Página 71 1. a. c. 2. a = 1 3. Infinitas. Todas tienen como eje de simetría la recta x = 0. 4. No Página 75 1. a. No hay dilatación ni contracción con respecto a f(x) = x 2 . b. No hay dilatación ni contracción con respecto a f(x) = x 2 . x V = ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ – ; – , – 5 2 5 2 1 4 x V = ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ ; , – 3 4 3 4 121 8 Solucionario b. x V = ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ ; , – 7 2 7 2 9 4 SOLUCIONARIO 3º (256-283):Maquetación 1 4/11/10 17:25 Página 261
- 263. 262 | Matemática 3º Medio Solucionario c. No hay dilatación ni contracción con respecto a f(x) = x 2 . d. Hay contracción con respecto a f(x) = x 2 . 2. 3. a. V(–2, –3); x = –2 c. V ; x = 4. a. b. c. d. 5. B Página 79 1. a. Δ = 20 x 1 = x 2 = b. Δ = –352 No tiene solución real. c. Δ = 0 x 1 = x 2 = 2 d. Δ = –12 No tiene solución real. e. Δ = –2500 No tiene solución real. f. Δ = 49 x 1 = 0 x 2 = 7 3 5 5 − 5 5 + 3 4 3 4 7 8 , ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ Decrecimiento Crecimiento a. ]–⬁, –0,5[ ]–0,5, +⬁[ b. ]0, +⬁[ ]–⬁, 0[ c. ]0,5, +⬁[ ]–⬁, 0,5[ d. ]0,125, +⬁[ ]–⬁, 0,125[ b. V(0, 2); x = 0 d. V ; x = – , 1 2 21 4 ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ –1 2 SOLUCIONARIO 3º (256-283):Maquetación 1 4/11/10 17:25 Página 262
- 264. Solucionario | 263 2. a. x(x + 1) = 132 b. x 1 = 11 y x 2 = 12 o x 1 = –11 y x 2 = –12 3. r = 1,19 cm 4. a. k 0 b. k = 0 c. k 0 5. a. k – c. k – 6. y 7. 8 cm y 6 cm 8. 5 9. k = 15 10.12 y 16 11.20π cm 12.No Página 81 1. a. x 1 + x 2 = – x 1 · x 2 = –2 b. x 1 + x 2 = – x 1 · x 2 = –12 c. x 1 + x 2 = – 1 x 1 · x 2 = 2 2. a. x 2 – 3x = 0 b. x 2 – 1 = 0 c. x 2 – 4 = 0 d. x 2 – 2xm – x + m + m 2 = 0 3. x = –11 4. k = 39 5. 5x 2 + 45x + 100 = 0 6. – Página 83 1. a. No tiene raíces reales. b. x 1 = 2 x 2 = –2 c. x 1 = x 2 = d. No tiene raíces reales. e. x 1 = x 2 = – x 3 = x 4 = – f. No tiene raíces reales. g. x 1 = x 3 = h. x 1 = 2. a. x 1 = x 2 = – 3 3 2 3 3 9 73 2 − 9 73 2 + 2 2 3 3 − − + 2 6 − + 2 6 3 5 1 4 3 5 km h 97 1 − ( ) 97 1 + ( ) 9 8 9 8 Solucionario b. k = – 9 8 x 2 = − + 9 73 2 x 4 = − − 9 73 2 x 2 = – 2 3 3 SOLUCIONARIO 3º (256-283):Maquetación 1 4/11/10 17:25 Página 263
- 265. 264 | Matemática 3º Medio Solucionario b. x = c. x 1 = x 2 = – d. No tiene soluciones reales. e. x 1 = 2 x 2 = –2 x 3 = 1 x 4 = –1 f. x 1 = –1 x 2 = 1 x 3 = g. x 1 = x 2 = – x 4 = – x 2 = x 4 = j. x 1 = k. x = m. x = –1,413 n. No tiene soluciones reales. o. x 1 = 4 x 2 = –4 p. No tiene soluciones reales. q. x 1 = – x 2 = x 3 = –1 x 4 = 1 r. x = 3. a. Una ecuación bicuadrática. Los lados del rectángulo son 3 y 4 cm. b. Los lados del rectángulo son 12 y 5 cm. Página 87 1. a. Δ = –31 No corta el eje X. b. Δ = 4 Corta al eje X en (3, 0) y (1, 0) 1 193 8 4 + ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ 2 2 2 2 14 5 1 32 − + 2 5 2 2 m m n – – – 2 5 2 2 m m n − 2 2 2 2 1 3 2 2 2 2 25 2 25 2 3 x 4 = – 1 3 x 3 = 2 2 h. x 1 = 2 5 2 2 m m n – – x 3 = 2 5 2 2 m m n + – i. 167 2 166 25 − x 2 = – 16 807 32 l. 71 181 12 − SOLUCIONARIO 3º (256-283):Maquetación 1 4/11/10 17:25 Página 264
- 266. Solucionario | 265 c. Δ = 0 Corta al eje X en (0,5 , 0) d. Δ = –40 No corta el eje X e. Δ = 961 Corta al eje X en (0, 0) y f. Δ = 0 Corta al eje X en (–2, 0) b. k = – 3. Infinitas. f(x) = k(x 2 – 6x + 7), k IR – {0} 4. Vértice: 5. – Falso – Verdadero 6. No existe 7. 8. a. k = –2 b. – x 1 2 3 x x f x x 1 2 1 2 2 2 , + + ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ 9 16 – , 31 2 0 ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ Solucionario 2. a. k – 9 16 c. k = – 9 16 Positiva Negativa a. −∞ − − ⎤ ⎦ ⎥ ⎥ ⎤ ⎦ ⎥ ⎥ ∪ − + ∞ ⎡ ⎣ ⎢ ⎢ ⎡ ⎣ ⎢ ⎢ , , 3 41 4 3 41 4 − − − + ⎤ ⎦ ⎥ ⎡ ⎣ ⎢ 3 41 4 3 41 4 , b. ]– ⬁, –2][1, +⬁[ ]–2, 1[ c. x IR – d. −∞ − ⎤ ⎦ ⎤ ⎦ ⎡ ⎣ ⎡ ⎣ , , 2 2 2 2 + − ⎤ ⎦ ⎡ ⎣ 2 2 2 2 , e. − − − + ⎡ ⎣ ⎢ ⎢ ⎤ ⎦ ⎥ ⎥ 2 82 6 2 82 6 , −∞ − − ⎤ ⎦ ⎥ ⎥ ⎡ ⎣ ⎢ ⎢ ∪ − + ∞ ⎤ ⎦ ⎥ ⎥ ⎡ ⎣ ⎢ ⎢ , , 2 82 6 2 82 6 + f. x IR – c. x – y x 1 2 3 SOLUCIONARIO 3º (256-283):Maquetación 1 4/11/10 17:25 Página 265
- 267. 266 | Matemática 3º Medio Solucionario Página 89 1. a. Vértice: (0, –1): es un mínimo. Intersección eje X: y . b. Vértice = : es un mínimo. No interseca al eje X. c. Vértice: (0, 1) : es un mínimo. No interseca al eje X. d. Vértice = : es un mínimo. Intersección eje X: (0, 0) y (1, 0). e. Vértice = (–1, –4): es un mínimo. Intersección eje X: (–3, 0) y (1, 0). f. Vértice = (1, –4): es un mínimo. Intersección eje X: (3, 0) y (–1, 0). g. Vértice = : es un máximo. h. Vértice = : es un mínimo. – , – 1 4 1 16 ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ 5 2 21 4 , ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ 1 2 1 4 ,– ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ 1 2 3 4 , ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ 2 2 0 , ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ − ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ 2 2 0 , Intersección eje X: y 5 21 2 0 − ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ , 5 21 2 0 + ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ , Intersección eje X: (0, 0) y . – , 1 2 0 ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ SOLUCIONARIO 3º (256-283):Maquetación 1 4/11/10 17:25 Página 266
- 268. Solucionario | 267 i. Vértice = (1, –1): es un mínimo. Intersección eje X: (0, 0) y (2, 0). 2. Todas las funciones de la forma: f(x) = k(x – 1) 2 son correctas, k IR – {0}. Si k 0, entonces (1,0) es mínimo. Si k 0, entonces (1,0) es máximo. 3. a = –1. No 4. a. 3,2 metros. b. 1 segundo. c. 2 segundos. 5. 1 unidad. 6. El proyectil que llega más alto es el que su altura está dada por la función g(t), y demora 54 segundos en alcanzar esta altura. Página 93 1. a. Entre 0 y 0,45. b. Entre 0,71 y 0,84. c. Entre 1 y 1,73. d. Entre 3,46 y 3,74. e. Entre 7,07 y 7,75. f. Entre 10 y 20. 2. a. s b. T = s; T = s c. I = 3 m d. El periodo será mayor. 3. m; m 4. a. Dom: [0, +⬁[ Rec: [3, +⬁[ b. Dom: [2, +⬁[ Rec: [0, +⬁[ c. Dom: [–4, +⬁[ Rec: [0, +⬁[ d. Dom: [0, +⬁[ Rec: [0, +⬁[ 8 8 8 4 2 27 4 2 2 4 2 2 1 0 83 − ( )≈ , Solucionario SOLUCIONARIO 3º (256-283):Maquetación 1 4/11/10 17:25 Página 267
- 269. 268 | Matemática 3º Medio Solucionario e. Dom: [0, +⬁[ Rec: [0, +⬁[ f. Dom: [0, +⬁[ Rec: ]–⬁, 1] g. Dom: [0, +⬁[ Rec: ]–⬁, 4] h. Dom: [0, +⬁[ Rec: [–4,+⬁[ i. Dom: [–2, +⬁[ Rec: [2, +⬁[ j. Dom: ]–⬁, 5] Rec: ]–⬁, 3] k. Dom: [0, +⬁[ Rec: [2, +⬁[ l. Dom: [0, +⬁[ Rec: [2, +⬁[ SOLUCIONARIO 3º (256-283):Maquetación 1 4/11/10 17:25 Página 268
- 270. Solucionario | 269 Solucionario 5. a. Creciente d. Creciente b. Creciente e. Decreciente c. Decreciente f. Creciente Página 95 1. b. (0, –3) c. Rec f (x) = [–3, +⬁[ Rec g(x) = [–4, +⬁[ 2. b. g(x) es una contracción de f (x), y h(x) es una dilatación de f (x). c. (0, 0) d. No, f (x) crece más rápido que h(x). 3. a. Forman una parábola. b. La unión de la inversa de f (x) y de g(x) es igual a h(x). c. Sí. Página 97 1. a. Dos soluciones. b. Una solución. c. No tiene solución en los reales. d. Dos soluciones. 2. a. x 1 = 3 x 2 = 5 b. x 1 = 2 x 2 = 1 c. x 1 = x 2 = 7 d. x 1 = x 2 = e. No tiene solución en los reales. f. x 1 = 3. a. f(x) = –2x 2 + 20x – 42 b. f(x) = 24x 2 – 72x – 96 c. f(x) = – x 2 + x d. f(x)= 4x 2 – 16x– 180 4. a. x 1 = 4 x 2 = –4 x 3 = 2 x 4 = –2 5. E Página 103 I. 1. Falso 5. Verdadero 2. Verdadero 6. Verdadero 3. Falso 7. Falso 4. Verdadero 8. Falso II. 1. a. f. b. g. c. h. d. i. e. j. −3 3 4 3 1 9 3 3 3 − 3 b. x 1 = 1 x 2 = –1 c. x 1 = –0,6 x 2 = 1,6 x 2 = 3 3 3 + SOLUCIONARIO 3º (256-283):Maquetación 1 4/11/10 17:25 Página 269
- 271. 270 | Matemática 3º Medio Solucionario 2. –x 2 + 4x – 1 3. a. k = b. k 0 c. k – 4. a. 420 metros b. 20 segundos Pagina 104 1. A 8. B 2. B 9. B 3. E 10. A 4. E 11. C 5. A 12. D 6. C 13. A 7. D Páginas 108 y 109 1. a. Verdadero c. Verdadero b. Falso d. Falso 2. a. 5 cm c. 16 cm b. 5 cm d. 50 cm 3. a. x = 15 m b. x = 9 cm c. x = 4 m 4. a. b. 5,6 m 5. CD –– – = 9 cm 6. ΔABC; ΔKJL (criterio AA). ΔDEF; ΔUST (criterio AA). Páginas 112 y 113 2. p = 3,2 cm q = 1,8 cm h = 2,4 cm 3. y cm 4. Altura = 12 cm Área = 192 cm 2 5. 3 cm 6. 2,57 cm 7. a. Si, elΔABC, ΔCBD y ΔACD b. AD = 13,24 cm DB = 3,76 cm CD = 7,06 cm c. AD = 3,5 cm d. CB = 6 cm e. AD = 3 cm 8. Estará a 92,8 m de la casa. 9. Vigas = m Altura techo = 2 m Página 117 1. a. c 2 b. c. Es un cuadrado de lado b; su área es b 2 . c 2 – 2 2 52 117 1 20 1 4 d. k 9 8 El triángulo rectángulo y la trigonometría 3 1,5 m x 4,05 m 15,12 m a b c p q h 8 cm 6 cm 10 cm 6,4 cm 3,6 cm 4,8 cm 4,7 cm 8,3 cm 9,5 cm 7,2 cm 2,3 cm 4,1 cm 8,36 cm 8,88 cm 12,2 cm 6,47 cm 5,73 cm 6,1 cm SOLUCIONARIO 3º (256-283):Maquetación 1 4/11/10 17:25 Página 270
- 272. Solucionario | 271 Solucionario d. El área del cuadrado ABCD es igual a la suma de las áreas de los 4 triángulos y del cuadrado blanco. Al igualar ambas áreas se obtiene el teorema de Pitágoras. 3. Sí. 4. Sí. 5. Deben ser polígonos semejantes. Página 120 1. a. No e. No b. Sí f. No c. No g. No d. Sí h. Sí 2. 30 cm 3. P = 30 cm A = 30 cm 2 4. Regla de Pitágoras Regla de Aquitas Páginas 122 y 123 1. 130 m 2. 16,20 y 32 cm 3. 4,46 m 4. 3,24 m 5. a. 3,5 m b. 1,275 m 6. 11,25 m Página 125 1. a. 15 y 20 cm c. 6 y 6 cm b. y cm d. 6 y 8 cm 2. a. Verdadero b. Falso c. Verdadero d. Falso 3. E 4. a. 2,4 m; 1,4 m b. 11,4 m Página 129 1. a. sen(α) = 0,8 cos(α) = 0,6 tan(α) = 1,3 sen(β) = 0,6 cos(β) = 0,8 tan(β) = 0,75 b. sen(α) = 0,14 cos(α) = 0,99 tan(α) = 0,14 sen(β) = 0,99 cos(β) = 0,14 tan(β) = 7 3 4 6 4 3 a a a 2 2 2 2 2 1 2 1 2 + ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ = + + ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ = + + – a a a 2 4 2 2 1 4 = + + a a 4 2 2 1 4 = + ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ a2 2 1 2 a a a 2 2 2 2 2 4 1 4 1 – + ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ = + ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ = + + – a a a 2 4 2 4 2 1 = + + a a 4 2 4 2 1 = + ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ a2 4 1 – SOLUCIONARIO 3º (256-283):Maquetación 1 4/11/10 17:25 Página 271
- 273. 272 | Matemática 3º Medio Solucionario 2. 3. a. sen(19º) = 0,33 d. sen(70º) = 0,94 cos(19º) = 0,95 cos(70º) = 0,34 tan(19º) = 0,34 tan(70º) = 2,75 b. sen(25º) = 0,42 e. sen(85º) = 0,99 cos(25º) = 0,91 cos(85º) = 0,09 tan(25º) = 0,47 tan(85º) = 11,43 c. sen(45º) = 0,71 f. sen(12,5º) = 0,22 cos(45º) = 0,71 cos(12,5º) = 0,98 tan(45º) = 1 tan(12,5º) = 0,22 4. a. x = 3,5 cm b. x = 5,84 cm Página 131 1. 2. a. 3 d. b. 0 e. c. 1 f. 3. 7,5 m Página 133 1. x = 10,62 m 2. 5442 m aproximadamente 3. 80,43 m 4. 365 510 km 5. 5,91 m 6. base = 36,25 cm área = 153,1 cm 2 Página 135 2. cos 2 α + sen 2 α 3. a. x d. c. f. 4. a. 0 c. 5 b. –0,61 d. 6 5. a. d. c. f. Página 137 1. a. sen(α) c. cotan 2 (α) b. tan(α) d. 1 53 7 2 53 53 53 2 7 53 53 x y y x 1 y 3 6 1 4 2 4 + 3 1 2 − b. y e. 1 x b. e. 7 53 53 2 53 53 sen(α) cos(α) tan(α) sec(α) cosec(α) cotan(α) 0,6 0,8 0,75 1,25 1,6 1,3 8 17 15 17 8 15 17 15 17 8 15 8 0,44 0,9 0,48 1,1 2,29 2,06 0,72 0,69 1,05 1,45 1,38 0,95 12 37 35 37 12 35 37 35 37 12 35 12 8 10 6 10 8 6 10 6 10 8 6 8 α 30º 45º 60º sen(α) 1 2 2 2 3 2 cos(α) 3 2 2 2 1 2 tan(α) 3 3 1 3 SOLUCIONARIO 3º (256-283):Maquetación 1 4/11/10 17:25 Página 272
- 274. Solucionario | 273 Página 141 1. AC = 17,36 cm AB = 50 cm ⱔACB = 80º 2. a. c = 2,35 m b. a = 9,89 cm 3. km 4. a. Sí b. Sí c. No Página 143 1. 2. a. 12º e. 72º b. 15º f. 495º c. 135º g. 80º d. 120º h. 126º Página 147 1. ΔOAP ΔOBP´, por criterio AA de semejanza de triángulos, ya que comparten el ángulo α y tienen un ángulo recto. Por lo tanto, sus lados son proporcionales = = = k. se tiene = , donde cada razón representa el seno de α. 2. tan(α) = = 3. Positiva en el I y III; negativa en el II y IV, dado que seno y coseno tienen igual signo en el I y III cuadrante y distinto en el II y IV cuadrante. 4. a. Positivo d. Positivo b. Positivo e. Negativo c. Positivo f. Negativo Página 149 1. a. sen = – tan = b. sen = – tan = c. sen = – tan = 1 d. sen = – tan = –1 e. sen = – tan = – cos = y x sen(α) cos(α) OB P`O OA P`O PO P`O PA PB OA OB 7 4 π ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ 7 4 π ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ 11 6 π ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ 11 6 π ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ 5 3 π ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ 1 2 3 3 1 2 2 2 5 4 π ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ 2 2 5 4 π ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ 3 4 3 π ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ 3 2 4 3 π ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ 3 3 7 6 π ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ 1 2 7 6 π ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ 3 7 Solucionario Considerando la igualdad = PO P`O OA OB Grados 0º 30º 45º 60º 90º 120º 135º 150º Radianes 0 π 6 π 4 π 3 π 2 2π 3 3π 4 5π 6 cos = – 2 2 5 4 π ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ cos = 7 4 π ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ 2 2 cos = 11 6 π ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ 3 2 f. sen = – 3 2 5 3 π ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ cos = – 3 2 7 6 π ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ cos = –1 2 4 3 π ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ tan = – 3 5 3 π ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ SOLUCIONARIO 3º (256-283):Maquetación 1 4/11/10 17:25 Página 273
- 275. 274 | Matemática 3º Medio Solucionario Página 151 1. rad 2. Basta notar que arcsen , arcsen y luego restamos. 3. a. 76,7º; 0,43π rad c. –45º; –0,25π rad b. 64,16º; 0,36π rad d. 45º: 0,25π rad Página 153 1. a. x 1 = rad; x 2 = rad b. x 1 = rad; x 2 = rad d. x 1 = rad f. x 1 = rad; x 2 = rad 2. Para a mayor que 1 o menor que –1. Página 155 1. a. 0,5 b. c. d. 2. a. Falso b. Verdadero c. Falso d. Falso e. Falso f. Verdadero 3. D 4. a. sen(α) = cos (α) = tan (α) = Página 157 1. a. b. 3. 26,6º Páginas 161 a 163 I. 1. Falso 4. Verdadero 2. Verdadero 5. Verdadero 3. Falso II. 1. a. b. c. d. e. f. 2. a. sen(α) = cos(α) = cotan(α) = sec(α) = cosec(α) = b. c. 3. a. 70,53º b. 45º c. 150º d. 59,04º III. 1. E 4. D 7. C 10. E 2. A 5. B 8. C 11. C 3. C 6. A 9. E 12. A Página 166 1. a. p 艋 3000 b. x ≥ 30 c. g 艌 12 000 d. n 6,0 2. a. 4, 5, 6, 7, 8, 9, 10 b. 1, 2, 3, 4, 5 c. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 d. 4, 5 3 2 3 3 − 5 3 2 5 3 6 5 3 π π + ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ k π π 3 + ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ k 2 2 π π + ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ k 5 3 2 π π + ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ k 3 2 π π + ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ k 3 4 2 π π + ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ k π 6 b. α 1 = y α 2 = d. α 1 = 0 y α 2 = 2π 2π 3 π 3 2 2 4 ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ = π 1 2 6 ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ = π y x = + + 3 3 2 3 3 1 π 12 2. a. α 1 = y α 2 = c. α 1 = y α 2 = 7π 4 π 4 11π 6 π 6 x 3 = rad; x 4 = rad 7 4 2 π π + ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ k 5 4 2 π π + ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ k c. x 1 = rad; x 2 = rad 7 4 2 π π + ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ k 4 2 π π + ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ k e. x 1 = rad; x 2 = rad 5 12 2 π π + ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ k π π 12 + ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ k Inecuaciones lineales 4 3 5 4 5 3 4 2 5 5 3 5 5 2 5 5 3 2 3 2 5 41 41 4 5 41 5 4 41 41 41 4 a 2 – b 2 108 1261 4 2 π π + ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ k SOLUCIONARIO 3º (256-283):Maquetación 1 4/11/10 17:25 Página 274
- 276. Solucionario | 275 Solucionario 18 18 2 4. 5. a. b. c. La ecuación no d. corresponde a una recta. e. f. 6. a. x = – 10 c. No tiene solución b. x = 2, x = 3 –– 2 7. a. x = 13 –– 4 ; y = – 9 –– 8 b. No tiene solución c. Tiene infinitas soluciones Página 169 1. a. Verdadero b. Falso c. Verdadero 2. a. Si IUV = 10, entonces, t 艋 18, donde t es el tiempo de exposición al sol. b. FP ≥ 15 c. Si 100 ICAP 艋200, entonces, la calidad del aire es regular. d. 64 艋G 艋110 3. 13 a 25 Página 173 1. a. [0, ] b. ]–⬁, 0[ ] , +⬁[ c. 0: [–1, 1], π: [3,4], : [1,2] : [0,1] : [4,5] 2. a. b. c. ]0, 0,5] d. ]–⬁, –3] e. [–12, 5,8] f. 3. a. [3, +⬁[ b. c. ]–⬁, 100[ d. e. [0, 8[ f. ]–5,2, +⬁[ 4. a. [2, 18[ b. ø c. d. e. [0, 1[ f. [0, 20] 18 3 4 − +∞ ⎡ ⎣ ⎢ ⎡ ⎣ ⎢ 7 4 , 4 5 ,+∞ ⎤ ⎦ ⎥ ⎡ ⎣ ⎢ 1 5 133 , , ⎤ ⎦ ⎥ ⎤ ⎦ ⎥ − +∞ ⎤ ⎦ ⎡ ⎣ 3, ⺞ ⺪ ⺡ ⺙ IR 2 ✘ ✘ ✘ ✘ –2,43 ✘ ✘ 3 –– 4 ✘ ✘ π ✘ ✘ ✘ ✘ 3 2 + − 3 –7 –– 4 1 –– 5 4 –– 5 1,33 0 0,5 –12 5,8 –3 2 18 0 5 –– 3 0 5 3 , ⎤ ⎦ ⎥ ⎤ ⎦ ⎥ − ⎤ ⎦ ⎥ ⎤ ⎦ ⎥ 5 2 0 , 3 2 19 3 , ⎡ ⎣ ⎢ ⎤ ⎦ ⎥ 0 1 0 20 SOLUCIONARIO 3º (256-283):Maquetación 1 4/11/10 17:25 Página 275
- 277. Solucionario 276 | Matemática 3º Medio Página 175 1. a. b. 1 –– a 1 –– b c. 1 –– a 1 –– b 0 2. a. b. x 2 x. Si x 艋 –1 o x ≥ 1, entonces x 艋 x 2 . c. x 2 x Página 177 1. a. Al multiplicar por a. 2. ]1, 2] 3. a. b. [–1, 2[ 4. Como (a – b) 2 ≥0, a 2 – 2ab + b 2 ≥0 a 2 + b 2 ≥2ab / ⫼ 2 1 –– 2 (a 2 + b 2 ) ≥ab 5. Si a 0 y b 0 entonces, ab 0 / · 2 2ab 0 / + (a 2 + b 2 ) a 2 + 2ab + b 2 a 2 + b 2 (a + b) 2 a 2 + b 2 (a + b)(a + b) a 2 + b 2 / : (a + b) a + b a 2 + b 2 a + b 6. Como x + y ≥ x + y ≥ 2 7. (2a – 5b) 2 ≥0 4a 2 – 20ab + 25b 2 ≥0 / + 20ab 4a 2 + 25b 2 ≥20ab / : 20ab 25b 2 + 4a 2 ≥ 1 20ab a + 5b ≥ 1 5b 4a b. La desigualdad será también verdadera. Página 179 1. a. Verdadero d. Falso g. Verdadero b. Verdadero e. Falso h. Verdadero c. Verdadero f. Verdadero i. Verdadero 2. a. [1, 7[ b. [1, 40[ c. ø d. IR e. f. 3. a. a b / + 4 a + 4 b + 4, b. a b / · 3, como 3 0 3a 3b c. a b / · (– 1) –a –b / + 2 2 – a 2 – b d. a b / · 4 4a 4b / + 3 3 + 4a 3 + 4b e. a b / – a 0 b – a f. a b / – b a – b 0 / + 8 8 + a – b 8 1 4 5 , ⎡ ⎣ ⎢ ⎡ ⎣ ⎢ ( ) x y − ≥ 2 0 1 2 1 , ⎤ ⎦ ⎥ ⎤ ⎦ ⎥ a b 1 –– a 1 –– b 1 2 1 0,5 5 10 0,2 0,1 1000 10 000 0,001 0,0001 0,1 0,2 10 5 0,001 0,01 1000 100 x 0,95 0,80 0,65 0,20 0,10 0,01 x 2 0,9025 0,64 0,4225 0,04 0,01 0,0001 2 xy xy 7 8 8 7 , ⎡ ⎣ ⎢ ⎡ ⎣ ⎢ x – + y ≥0 2 xy SOLUCIONARIO 3º (256-283):Maquetación 1 4/11/10 17:25 Página 276
- 278. Solucionario | 277 Solucionario 4. Como a 0 y b 0 a 2 + ab + b 2 艌 0 / + ab a 2 + 2ab + b 2 艌 ab (a + b) 2 ≥ab / : (a + b)(ab) a + b ≥ 1 ab a + b 1 + 1 ≥ 1 a b a + b Luego, la alternativa correcta es D. Página 181 1. a. ]–⬁, 6[ b. [1, 3] c. d. [–7, +⬁[ e. f. 2. a. x = 1 b. {x ⺪ – / x –4} Página 183 1. a. [–3, 7] b. ø c. ]0, +⬁[ d. ]–5, –3[ e. ]–11, –1] f. g. ø h. 2. Puede medir 5 cm, 6 cm, 7 cm, 8 cm o 9 cm. 3. La cantidad mínima de CD que puede comprar es 3, y la máxima es 5. Página 187 1. a. b. c. d. e. f. 2. No 3. a. x + y ≥ 2 b. 2y – x ≥ – 2 4. 16x + 5y ≥ 300 6 1 3 – 40 –– 11 1 –– 3 –7 115 –––– 21 − +∞ ⎤ ⎦ ⎥ ⎡ ⎣ ⎢ 40 11 , 1 3 ,+∞ ⎤ ⎦ ⎥ ⎡ ⎣ ⎢ 115 21 ,+∞ ⎡ ⎣ ⎢ ⎡ ⎣ ⎢ − +∞ ⎤ ⎦ ⎥ ⎡ ⎣ ⎢ 1 3 , −∞ − ⎤ ⎦ ⎥ ⎤ ⎦ ⎥ , 8 3 –3 7 –5 –3 –11 –1 0 –1 3 –8 3 SOLUCIONARIO 3º (256-283):Maquetación 1 4/11/10 17:25 Página 277
- 279. 278 | Matemática 3º Medio Solucionario Página 189 1. a. La distancia entre x e y. b. La primera desigualdad significa que la distancia entre x e y es menor que d, la segunda significa que esta distancia es mayor que d. 2. a. ]–3, 3[ b. ]–⬁, –5[]5, +⬁[ c. |x – 6| 2 Página 191 1. a. x 2 –– 3 b. x 3 –– 7 c. x 艋 8 –– 5 d. x 艋 –9 e. x –3 f. No tiene solución. 2. a. ]–⬁, 1[ b. ]–1, +⬁[ c. ]–⬁, –1[ d. ]–⬁, –3] 3. a. b. 4. a. x 1 = 3; x 2 = 1 b. [–3, 11] c. No tiene solución. d. [–7, –4 [] 4, 7] 5. E Página 193 1. a. La cortina puede ser de: • 4 m de alto por 6 m de ancho. • 3 m de alto por 5 m de ancho. 3. a. ]–⬁, 1][2, +⬁[ b. ]–⬁, –13[]–7, +⬁[ Página 197 I. 1. Falso 3. Verdadero 2. Verdadero 4. Verdadero II. 1. a. ]3, 12[ b. ]–⬁, 31[ c. [8, +⬁[ d. ]–⬁, 4[ e. ]–7, 0[ f. ]1, 2[]7, 9[ 2. a. x 3 –– 5 b. x 艋 c. x 艋 d. x 3 e. 0 x y x 3 f. ]2, 3[ g. IR h. 0 x 艋 3 3. a. b. c. d. e. f. x y Distancia entre x e y | x – y | 2 5 3 3 –5 –3 2 2 –4 2 6 6 1 10 4 13 SOLUCIONARIO 3º (256-283):Maquetación 1 4/11/10 17:25 Página 278
- 280. Solucionario | 279 Solucionario g. h. 4. a. ]–12, 12[ b. ]–10, 14[ c. ]–15, 9[ d. ]–⬁, –15][9, +⬁[ e. IR – {5} f. ø Páginas 198 y 199 III. 1. A 5. C 9. D 12. D 2. B 6. D 10. C 13. A 3. C 7. E 11. C 14. D 4. B 8. B Páginas 202 y 203 1. a. Aleatorio b. Determinista c. Aleatorio d. Aleatorio e. Determinista 2. 3. a. 22 estudiantes b. 46 estudiantes 4. a. 12 ––– 52 b. 20 ––– 52 5. a. 1 –– 52 b. 1 –– 26 c. 1 –– 13 d. 1 –– 4 6. A 7. a. 1 –– 6 b. 1 –– 2 c. 0 d. 1 –– 3 8. Página 205 1. a. Ω = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9 ,10} Finito #Ω = 11 b. Ω = {1, 2, 3, 4, ….} Infinito c. Ω = {♠, ♣, ♦, ♥} Finito #Ω = 4 Probabilidades 5 Cazuela de vacuno Papayas al jugo Torta de chocolate Helado Papayas al jugo Torta de chocolate Helado Puré con pescado Tomate cebolla Cazuela de vacuno Papayas al jugo Torta de chocolate Helado Papayas al jugo Torta de chocolate Helado Puré con pescado Frecuencia absoluta Frecuencia relativa 2 2 2 –– 15 3 3 3 –– 15 4 5 5 15 5 5 5 –– 15 Lechuga palta SOLUCIONARIO 3º (256-283):Maquetación 1 4/11/10 17:25 Página 279
- 281. 280 | Matemática 3º Medio Solucionario d. Ω = {ccc, ccs, csc, scc, scs, ssc, css, sss} Finito #Ω = 8 e. Ω = {x IR x 0} Infinito f. Ω = {1, 2, 3, 4, 5, …, 27} Finito #Ω = 27 2. a. Ω = {RR, RV, RA, VV, VA, VR, AA, AR, AV} #Ω = 9 b. Ω = {RV, RA, VA, VR, AR, AV} #Ω = 6 Página 209 1. a. Ω = {cccc, cccs, ccss, csss, ssss, cssc, cscs, sssc, scss, sscs, ccsc, cscc, sccc, sscc, sccs, scsc} b. A = {cccc, cccs, ccss, cssc, cscs, ccsc, cscc, sccc, sscc, sccs, scsc} c. B = {ssss} d. C = {cccc, cccs, ccss, cssc, cscs, ccsc, cscc, sccc, sscc, sccs, scsc} 2. a. Ω = {ABC, ACB, BCA, BAC, CAB, CBA} b. A = {BAC, BCA} c. Ac = {ABC, ACB, CAB, CBA} d. B = {ABC, ACB, BCA, CBA} 3. a. “El transporte demora 5 minutos o más en pasar.” b. “El transporte demora 10 minutos o menos en pasar. Llega junto con Sergio.” c. Suceso seguro: la micro demora más de 10 minutos o menos de 10 minutos. Suceso imposible: la micro no pasa. Página 211 1. 18 2. 16 y 32, respectivamente. 3. 12 Página 213 1. a. 512 b. 64 2. 720 3. 2520 4. 280 5. 30 Página 215 1. a. 22 100 b.132 600 2. 10 3. a. 60 b. 246 4. 15 5. El número de diagonales en un polígono convexo serán todas las uniones entre los n vértices de este, o sea, nC2, menos las que correspondan a la unión de dos vértices consecutivos, es decir, los n lados de esta. 6. #Ω = 20 475 Página 217 1. a. Ω = {1, 2, 3, …49} #Ω = 49 b. Ω = {0, 1, 2, …9} #Ω = 10 c. Ω = infinito Cara 1 2 3 4 5 6 Sello 1 2 3 4 5 6 SOLUCIONARIO 3º (256-283):Maquetación 1 4/11/10 17:25 Página 280
- 282. Solucionario | 281 Solucionario 1 3 2 11 2. a. A = Se obtiene un 2. b. B = Se obtiene un número par. C = Se obtiene un número impar. c. D = Se obtiene un número menor que 10. d. E = Se obtiene un múltiplo de 10. 3. a. M∪N = {1, 3, 5, 7, 9} b. M∩N = {3, 5} c. (M∩P) C = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} d. (M∪P)∩NC = {1, 2, 4, 6, 8} 4. a. 125 b. 3125 c. 120 d. 84 5. D Página 219 1. P(C ) = 0 P(D) = 1 2. a. Falso b. Falso c. Verdadero 3. P(AIRE) = 1 –– 70 P(RISA) = 1 –– 70 Página 221 1. Sí 3. No 2. No 4. En la primera ruleta. Página 223 1. 7 –– 30 2. a. 7 –– 36 b. 3. P(B) = 23 –– 45 4. No Página 225 1. 3 –– 5 2. a. 10 –– 75 b. 35 –– 75 c. 23 –– 75 4. Las frecuencias relativas debieran ser similares. Página 227 1. a. Sí, son similares. b. Son similares. En el caso de los 50 lanzamientos, la frecuencia relativa se acerca más a la probabilidad. c. La frecuencia relativa se acercará más a la probabilidad. Página 229 1. a. 1 –– 3 b. 1 –– 3 c. 2 –– 3 d. 0 e. 1 –– 3 f. 1 2. a. 1 –– 12 b. c. Página 231 1. 1 –– 4 2. a. 10 –– 17 b. 3. a. 2 –– 17 b. 15 –– 17 c. 13 ––– 102 Página 233 1. a. Independiente b. Dependiente c. Dependiente d. Independiente 3. Sí 4. 1 –– 25 5. 1 –– 12 6. a. 45 –– 95 b. 35 –– 95 c. 35 –– 95 No son independientes los sucesos “es hombre” y “tiene diabetes tipo I”. Página 237 1. a. Discreta b. Continua c. Continua d. Discreta 2. a. Discreta b. {1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 16, 18, 20, 24, 25, 30, 36} 2 9 3 13 SOLUCIONARIO 3º (256-283):Maquetación 1 4/11/10 17:25 Página 281
- 283. 282 | Matemática 3º Medio Solucionario c. P(Z = 1) = 1 –– 36 ; P(Z = 2) = 2 –– 36 ; P(Z = 3) = 2 –– 36 ; P(Z = 4) = 3 –– 36 ; P(Z = 5) = 2 –– 36 ; P(Z = 6) = 4 –– 36 ; P(Z = 8) = 2 –– 36 ; P(Z = 9) = 1 –– 36 ; P(Z = 10) = 2 –– 36 ; P(Z = 12) = 4 –– 36 ; P(Z = 15) = 2 –– 36 ; P(Z = 16) = 1 –– 36 ; P(Z = 18) = 2 –– 36 ; P(Z = 20) = 2 –– 36 ; P(Z = 24) = 2 –– 36 ; P(Z = 25) = 1 –– 36 ; P(Z = 30) = 2 –– 36 ; P(Z = 36) = 1 –– 36 e. P(Z 5) = 8 –– 36 ; P(Z 8) = 20 –– 36 ; P(5 艋 Z 艋 10) = 11 –– 36 3. Y = 0, 1, 2 La dos funcionan: P(Y = 0) = 5 –– 14 Una funciona: P(Y = 1) = 15 –– 28 La dos no funcionan: P(Y = 2) = 3 –– 28 Página 239 1. B 2. a. 34 –– 50 b. 4 –– 50 c. 30 –– 50 3. a. 39 –– 80 b. 7 –– 80 c. 73 –– 80 d. 13 –– 20 4. b. P(X 5) = 0,52 c. P(X = 6) = 0 P(X = 9) = 0,11 Página 241 1. a. P(x = 50) = 0,25; P(x = –30) = 0,75 b. E(x) = –10 c. –2000 3. k = Página 243 1. 0,087 2. a. 0,076 b. 0,212 Página 245 I. 1. Falso 2. Verdadero 3. Verdadero 4. Verdadero 5. Verdadero II. 1. a. 120 960 b. 2880 2. a. Ω = {AMS, AMT, ANS, ANT, BMS, BMT, BNS, BNT, CMS, CMT, CNS, CNT} b. 1 –– 2 c. 1 –– 2 d. A = El economista elegido es M. B = El economista elegido es N. 3. a. A I AA AI IA II AAA AAI AIA AII IAA IAI IIA III Ω = {AAA, AAI, AIA, AII, IAA, IAI, IIA, III} b. 3 –– 8 c. 7 –– 8 4. a. P(Z = 0) = 330 –––– 3060 ; P(Z = 1) = 1155 –––– 3060 ; P(Z = 2) = 1155 –––– 3060 ; P(Z = 3) = 385 –––– 3060 ; P(Z = 4) = 35 –––– 3060 b. P(Y = 0) = 495 –––– 3060 ; P(Y = 1) = 1320 –––– 3060 ; P(Y = 2) = 990 –––– 3060 ; P(Y = 3) = 240 –––– 3060 ; P(Y = 4) = 15 –––– 3060 c. P(X = 0) = 715 –––– 3060 ; P(X = 1) = 1430 –––– 3060 ; P(X = 2) = 780 –––– 3060 ; P(X = 3) = 130 –––– 3060 ; P(X = 4) = 5 –––– 3060 Páginas 247 y 248 1. E 4. E 7. D 10. C 2. A 5. C 8. E 11. C 3. A 6. B 9. B 12. D 1 26 SOLUCIONARIO 3º (256-283):Maquetación 1 4/11/10 17:25 Página 282
- 284. Solucionario | 283 Solucionario Páginas 248 a 255 Taller de evaluación 1. C 2. C 3. A 4. C 5. E 6. E 7. C 8. A 9. B 10. B 1. C 2. D 3. A 4. C 5. C 6. D 7. C 8. B 9. D 10. B 1. C 2. A 3. C 4. C 5. B 6. D 7. C 8. A 9. C 10. B 1. C 2. A 3. C 4. E 5. C 6. E 7. B 8. B 9. A 10. D 1. C 2. D 3. D 4. A 5. D 6. A 7. E 8. D 9. E 10. B 11. D Raíces 1 Inecuaciones lineales 4 Función cuadrática y función raíz cuadrada 2 El triángulo rectángulo y trigonometría 3 Probabilidades 5 SOLUCIONARIO 3º (256-283):Maquetación 1 4/11/10 17:25 Página 283
- 285. A Afín, función, 60 Ángulo - de elevación, 132 - de depresión, 132 - del centro, 145 - negativo, 144 - positivo, 144 - sistemas de medición de, 142, 143 B Bicuadráticas, ecuaciones, Binomio, - cuadrado de, 15, 62 - cubo de, 15 C Cantidad subradical, 31 Combinaciones, 214, 215 Conjetura, 119, 176, 177 Contracción de la parábola, 64 Coseno, 127 - función coseno, 145, 146 D Demostración, 115, 176, 177 - del teorema de Pitágoras, 114, 115, 116 - por reducción al absurdo, 19, 20 Desigualdades, 168 - propiedades de las, 174, 175 Dilatación de la parábola, 64 Directriz, 72 Discriminante de una ecuación cuadrática, Distancia - entre dos puntos, 72, 144 Dominio, - de la función raíz cuadrada, 91, 92 - de la función cuadrática, 61 E Ecuación, 167 - bicuadrática, 83 - con radicales, 42 - de segundo grado, 76, 77, 78 - lineal, 167 - reductibles a ecuaciones de segundo grado, 82, 83 - sistemas de, 167 - trigonométrica, 152, 153 Ecuación de segundo grado, 76, 77, 78 - análisis de las raíces de una, 80, 81 - discriminante de una, 78 - ecuaciones reductibles a, 82, 83 - soluciones o raíces de una, 77, 78, 81 Espacio muestral, 204, 205 Euclides, teorema de, 110, 111 Eventos, 206 - complemento de un, 207, 209 - elemental, 207, 209 - equiprobables, 220, 221 - imposible, 207, 209 - independientes, 232, 233 - mutuamente excluyentes, 208, 209 - seguro, 207, 209 Experimento, - aleatorio, 204 - determinista, 204 F Factorizaciones, 15, 57 - cuadrado de binomio, 15 - cubo de binomio,15 - factor común, 57 - producto de binomios con término común, 15 - suma por diferencia, 15 - suma y diferencia de cubos, 15 Foco, 72, 73 Frecuencia - absoluta, 203 - relativa, 203, 224, 225 Función, 57 - afín, 60 - creciente, 57 - decreciente, 57 - dominio de una, 57 - lineal, 60 284 | Matemática 3º Medio Índice temático I?NDICE TEM (284-287):Maquetación 1 4/11/10 17:26 Página 284
- 286. - raíz cuadrada, 90, 91, 92 - recorrido de una, 57 - trigonométrica, 144, 145, 146, 147 - trigonométrica inversa, 150, 151 Función cuadrática, 58, 59, 60, 61 - análisis general de una, 84, 85, 86 - dominio de, 58, 59 - forma canónica de, 62, 63 - gráfico de una, 58 - máximo de una, 88, 89 - mínimo de una, 88, 89 Función trigonométrica, 144, 145, 146, 147 - dominio de, 145, 146 - gráfico de, 146 - período de, 146 - recorrido de, 145, 146 G Gráfica - de la función coseno, 146 - de la función raíz cuadrada, 91, 92 - de la función seno, 146 - de una función cuadrática, 58, 60, 61 - de una función lineal, 60, 61 I Identidades trigonométricas, 136, 137 Inecuaciones lineales - con dos incógnitas, 184, 185, 186, 187 - con una incógnita, 180, 181 - con valor absoluto, 188, 189 - sistemas de, 182, 183 Inecuaciones no lineales, 192, 193 Intervalos de números reales, 170, 171, 172 - abierto, 172 - cerrado, 172 - intersección de, 171, 172 - no acotados o infinitos, 172 - semiabierto, 172 - unión de, 171, 172 Irracional, - número, 18 - raíz, 18 L Ley de los grandes números, 226, 227 M Media geométrica, 30 Medición de ángulos, - sistemas de, 142, 143 Módulo, 66 N Número irracional, 18, 19, 21 Números reales, 27 - intervalos de, 170, 171, 172 P Parábola - como lugar geométrico, 72, 73 - contracción de la, 64, 65 - desplazamientos de la, 66, 67, 68, 69 - dilatación de la, 64, 65 - simetría de la, 70, 71 - vértice de la, 70, 71 Permutaciones, 212, 213 Potencias, 15 - división de, 15 - multiplicación de, 15 - relación con raíces, 36, 37 - propiedades, 57 Principio multiplicativo, 210, 211 Probabilidad, 203, 218, 219, 222, 223, 230, 231 - condicional, 228, 229 - empírica, 224, 225 R Radián, 142, 143 Razones trigonométricas, 126 - de ángulos especiales, 130, 131 - propiedades de, 134, 135 Raíces - aproximación de, 24, 25 - cantidad subradical, 42 - comparación de, 24, 25 Índice temático Índice temático | 285 Índice temático I?NDICE TEM (284-287):Maquetación 1 4/11/10 17:26 Página 285
- 287. 286 | Matemática 3º Medio Índice temático - cuadradas, 16, 17 - cúbicas, 22, 23 - ecuaciones con, 42, 43 - enésimas, 30, 31, 57 - índice de, 42 - producto y cociente de, 26, 27, 57 - propiedades de, 32, 33, 34 - racionalización, 38, 39, 40, 41 - relación con potencias, 36, 37 Raíces cuadradas, - cociente de, 26, 27 - irracionalidad de algunas, 18 - no exactas, 20 - producto de, 26, 27 - ubicación en la recta numérica, 20 Raíces cúbicas, 22, 23 - cociente de, 26, 27 - producto de, 26, 27 Raíces enésimas, 30, 31 - cálculo de, 32, 33, 34 - propiedades de, 32, 33, 34 Recta, 167, 185, 186 - horizontal, 167 - vertical, 167 Regla - de Aquitas, 119 - de Laplace, 218 - de Pitágoras, 119 S Semejanza, - criterios de, 109, 110 - en el triángulo rectángulo, 111 Sistema, - de ecuaciones, 167 - de inecuaciones, 182, 183 Sucesos, 206 - complemento de un, 207, 209 - elemental, 207, 209 - equiprobables, 220, 221 - imposible, 207, 209 - independientes, 232, 233 - mutuamente excluyentes, 208, 209 - seguro, 207, 209 Sucesión, 235 T Tamaño muestral, 204, 205 Teorema - del coseno, 138, 139, 140, 141 - del seno, 138, 139, 140, 141 - de Euclides, 110, 111, 114 Teorema de Pitágoras, 18, 109 - demostraciones del, 114, 115, 116 - recíproco del, 116 - tríos pitagóricos, 118, 119, 120 Triángulos, 109 - semejanza de, 109, 110 Triángulos rectángulos, 109 - semejanza de, 121, 122 Trigonometría - aplicaciones de la, 132 - ecuaciones trigonométricas, 152, 153 - identidades trigonométricas, 136, 137 - propiedades de las razones, 134, 135, 148, 149 - razones trigonométricas, 126, 127, 128, 129, 130, 131 V Valor absoluto, 15 - inecuaciones que involucran valor absoluto, 188, 189 Variable aleatoria, 234, 235, 236, 237 - valor esperado de una, 240, 241 Volumen cilindro, 24 I?NDICE TEM (284-287):Maquetación 1 4/11/10 17:26 Página 286
- 288. Bibliografía | 287 Documentos oficiales • Mineduc. Objetivos Fundamentales y Contenidos Mínimos Obligatorios de la Educación Media. Ministerio de Educación de Chile, 2001. • Ministerio de Educación. Matemática. Programa de Estudio. Tercer Año Medio. Formación General Educación Media. Ministerio de Educación de Chile, Unidad de Currículum y Evaluación. Libros • Centeno, Julia. Números decimales. Síntesis, Madrid,1995. • Corbalán, Fernando. La matemática aplicada a la vida cotidiana. Graó, Barcelona, 1995. • Enzensberger, Hans Magnus. El diablo de los números. Ediciones Siruela, España, 1998. • Ernst, Bruno. El espejo mágico de M.C.Escher. Taschen, 1994. • Gardner, Martin. ¡Ajá! Paradojas. Paradojas que hacen pensar. Labor S.A., Barcelona, 1989. • Gardner, Martin. Carnaval matemático. Alianza Editorial, Madrid, 1980. • Guedj, Denis. El imperio de las cifras y los números. Ediciones B, S.A., Barcelona,1998. • Guedj, Denis. El teorema del loro. Anagrama, 2000. • Jouette, André. El secreto de los números. Ediciones Robinbook, S.L., Barcelona, 2000. • Julius, Edward. Matemáticas rápidas. Norma, Bogotá, 2002. • Perelman, Yakov. Matemáticas recreativas. Ediciones Martínez Roca S.A., Barcelona, 1987. • Perero, Mariano. Historia e historias de matemáticas. Grupo Editorial Iberoamericano, México,1994. • Stewart, Ian. Ingeniosos encuentros entre juegos y matemáticas. Gedisa, Barcelona, 1990. • Tahan, Malba. El hombre que calculaba. Publitecsa, Barcelona, 1985. Recursos tecnológicos • Software geométrico GeoGebra. En este sitio encontrará un programa geométrico libre, para descargar, que le permitirá enseñar y trabajar con sus alumnos y alumnas. http://www.geogebra.org Buscador recomendado • Sitio educativo con diversos recursos, planificaciones e información de todas las áreas. Incluye buscador. http://www.educarchile.cl/home/escritorio_docente Sitios webs • Ministerio de Educación de Chile http://www.mineduc.cl • Centro Comenius. Software educativos, en especial de matemáticas, recursos y muchas cosas más. Patrocinado por la USACH. http://www.comenius.usach.cl • REDUC. Red Latinoamericana de información y documentación en educación. Contiene base de datos sobre investigaciones, textos completos, recortes de prensa. http://www.reduc.cl • Sociedad de Matemática de Chile http://www.sochiem.cl • Recursos matemáticos Redemat http://www.recursosmatematicos.com/redemat.html • Instituto Nacional de Estadísticas. http://www.ine.cl • Ministerio de salud. http://www.redsalud.gov.cl • Dirección metereológica de Chile http://www.meteochile.cl • El paraíso de las Matemáticas http://www.matematicas.net • Sector Matemática http://www.sectormatematica.cl • Demostraciones del teorema de Pitágoras (en inglés): http://www.ies.co.jp/math/java/geo/pythagoras.html Bibliografía I?NDICE TEM (284-287):Maquetación 1 4/11/10 17:26 Página 287
- 289. I?NDICE TEM (284-287):Maquetación 1 4/11/10 17:26 Página 288

























































![5. Determina cuál o cuáles de los siguientes pares ordenados
corresponde a la función f(x) = 3x – 4. Fundamenta tu respuesta.
a. (12, 32) c. (–3, 13)
b. (0, 4) d. (–2, –10)
6. Determina cuál o cuáles de las siguientes expresiones son positivas
para todo x positivo. Explica cómo lo supiste.
a. 4 + x c. x2
e. 1 – 3x2
b. 13 – 2x d. 4x2
+ 1 f. –8x2
Verifica en el solucionario si tus respuestas son correctas. ¿Tuviste
algún error? Si lo tuviste, corrígelo antes de continuar con la Unidad.
Función cuadrática y función raíz cuadrada | 57
Unidad
2
¿Qué debes recordar?
• Algunas factorizaciones:
• ab + ac = a(b + c) Factor común.
• a2
– b2
= (a + b)(a – b) Diferencia de cuadrados.
• a2
± 2ab + b2
= (a ± b)2
Cuadrado de binomio.
• x2
+ (a + b)x + ab = (x + a)(x + b) Trinomio que es el producto de dos binomios
con un término común.
• Las raíces enésimas se pueden escribir como una potencia con exponente racional, por ejemplo:
• El producto de dos términos es cero si y solo si al menos uno de ellos es cero, es decir:
a · b = 0 ⇔a = 0 ∨ b = 0 (el signo ∨ significa “o”).
• La raíz de un producto es equivalente al producto de las raíces, es decir: .
• El cuadrado de un número real es siempre positivo o cero, es decir, x2
ⱖ 0.
• Si dos números son positivos, el orden entre ellos es el mismo orden que entre sus raíces y
sus potencias, es decir, si 0 a b y n es un natural, entonces .
• Una función y = f(x) es creciente en un intervalo [p, q] cuando para todo par de números
a y b del intervalo que cumplan a b, se cumplirá f(a) f(b).
• Una función y = f(x) es decreciente en un intervalo [p, q] cuando para todo par de números
a y b del intervalo que cumplan a b, se cumplirá f(b) f(a).
• Una función es una regla que asocia a cada número x de un conjunto A, llamado dominio,
un único valor f(x) de un conjunto B, llamado recorrido. Ejemplo: f(x) = x2
, x 僆 IR.
a b y a b
n n n n
ab a b
= ⋅
k k k
m
n n
m
m
n
= ( ) =
UNIDAD 2 (54-105)C:Maquetación 1 12/11/10 12:05 Página 57](https://image.slidesharecdn.com/matiii-210328014130/85/Mat-iii-58-320.jpg)





![Función cuadrática y función raíz cuadrada | 63
Unidad
2
En resumen
• Toda función cuadrática de la forma f(x) = ax2
+ bx + c se puede escribir en su forma
canónica, es decir, de la forma f(x) = a(x – h)2
+ k.
1. Dadas las siguientes funciones cuadráticas:
f(x) = x2
+ 2x – 4 g(x) = 3x2
+ 24x + 1 h(x) = (x + 1)2
– 4 n (x) = 3(x + 4)2
– 47
Determina si las siguientes igualdades son verdaderas o falsas. Justifica.
a. f(x) = h(x) b. g(x) = h(x) c. g(x) = n(x)
2. Escribe las siguientes funciones cuadráticas en su forma f(x) = a(x – h)2
+ k, indicando en cada caso
el valor de a, h y k.
a. x2
– 6x + 19 c. 2x2
– 4x + 7 e. 3x2
– 24x + 28
b. x2
+ 5x – 7 d. –2x2
+ 12x – 3 f. –5x2
– 20x – 14
Actividades
Toda función cuadrática de la forma f(x) = ax2
+ bx + c puede ser
escrita en su forma canónica f(x) = a(x – h)2
+ k por medio del
método de completación de cuadrados. Observa.
f(x) = ax2
+ bx + c
Si llamamos y , tendremos que para todos a,
b y c con a distinto de cero, existen h y k tales que
f(x) = ax2
+ bx + c = a(x – h)2
+ k
Ejemplo
Si queremos escribir la función f(x) = 3x2
+ 30x + 71 en su forma
canónica, tendremos:
f(x) = 3x2
+ 30x + 71 = 3(x2
+ 10x) + 71
= 3[(x + 5)2
– 25] + 71 = 3(x + 5)2
– 75 + 71
= 3(x + 5)2
– 4
Luego, la función escrita en forma canónica será f(x) = 3(x + 5)2
– 4.
k
b ac
a
–
–
=
4
4
2
h
b
a
–
=
2
= a x
b
a
x c
2
+
⎛
⎝
⎜
⎞
⎠
⎟ + = a x
b
a
b
a
c
+
⎛
⎝
⎜
⎞
⎠
⎟ −
⎡
⎣
⎢
⎢
⎤
⎦
⎥
⎥
+
2 4
2 2
2
= a x
b
a
b
a
c a x
b
a
b
+
⎛
⎝
⎜
⎞
⎠
⎟ − + = +
⎛
⎝
⎜
⎞
⎠
⎟
2 4 2
2 2 2 2
–
– 4
4
ac
a
UNIDAD 2 (54-105)C:Maquetación 1 4/11/10 17:13 Página 63](https://image.slidesharecdn.com/matiii-210328014130/85/Mat-iii-64-320.jpg)



![Función cuadrática y función raíz cuadrada | 67
Unidad
2
Esto se debe a que los puntos del gráfico de la función cuadrática
f(x) = x2
+ c son de la forma (x, x2
+ c); es decir, solo se modifica la
ordenada de los puntos (x, x2
) de la gráfica de la función f(x) = x2
.
Observa ahora el gráfico de las funciones f(x) = x2
; g(x) = (x – 3)2
y h(x) = (x + 2)2
.
¿Cuál crees que es la parábola correspondiente a g(x) = (x – 3)2
?,
¿y a h(x) = (x + 2)2
?, ¿por qué?
La representación gráfica de f(x) = x2
la conocemos y tiene vér-
tice (0, 0).
Podemos observar que la única diferencia entre las parábolas en el
gráfico es que g(x) = (x – 3)2
y h(x) = (x + 2)2
corresponden a un des-
plazamiento horizontal de la función f(x) = x2
; la primera en tres
unidades a la derecha, y la segunda en dos a la izquierda.
Observa que si (p, p2
) es un punto de la gráfica de f(x) = x2
, en-
tonces (p + 3, p2
) es uno de la gráfica de g(x) = (x – 3)2
, ya que
([p + 3] – 3)2
= p2
. Entonces, la gráfica de g(x) = (x – 3)2
está des-
plazada respecto de la gráfica de x2
. El punto (p + 3, p2
) está tres
unidades a la derecha de (p, p2
), así la gráfica de g(x) = (x – 3)2
, es
un desplazamiento de la gráfica de f(x) = x2
en tres unidades a
la derecha.
UNIDAD 2 (54-105)C:Maquetación 1 4/11/10 17:13 Página 67](https://image.slidesharecdn.com/matiii-210328014130/85/Mat-iii-68-320.jpg)
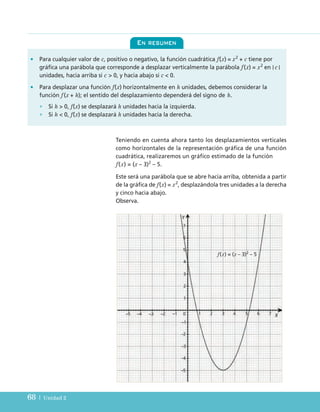


















































































![El triángulo rectángulo y la trigonometría | 151
La razones trigonométricas inversas son las que nos entregan un
valor para cada ángulo, a partir de una ecuación de la forma
cos(α) = k, si k IR.
Luego, la función y = arccos(x), llamada función arcocoseno, con
dominio en el intervalo [–1, 1], es la función inversa de
y = cos(x), restringida a [0, π].
Por lo tanto, tendremos que para α [0, π], y k [–1, 1], se tiene
que arccos(x) = α cos(α) = x.
De modo similar, podemos definir las funciones trigonométricas
inversas para las funciones seno y tangente.
La función y = arcsen(x), llamada función arcoseno, con dominio
en el intervalo [–1, 1], es la función inversa de y = sen(x),
restringida a [– , ].
La función y = arctan(x), llamada función arcotangente, con dominio
en los números reales, es la función inversa de y = tan(x),
restringida a ]– , [.
π
2
π
2
π
2
π
2
↔
Unidad
3
En las calculadoras, la función
arcoseno, por ejemplo, se obtiene
con las teclas , o
,o bien,
si existe.
arccos
INV cos
cos
SHIFT
En resumen
• La función trigonométrica inversa de y = cos(x) es y = arccos(x). Su dominio es [–1, 1]
y su recorrido [0, π].
• La función trigonométrica inversa de y = sen(x) es y = arcsen(x). Su dominio es [–1, 1]
y su recorrido [– , ].
• La función trigonométrica inversa de y = tan(x) es y = arctan(x). Su dominio el conjunto
de los números reales y su recorrido ]– , [.
π
2
π
2
π
2
π
2
1. Determina el valor de x, en el intervalo [0, π], sabiendo que cos(x) = .
2. Demuestra la igualdad arcsen – arcsen = .
3. Utiliza una calculadora para determinar el valor de y. Expresa los resultados en radianes y en grados.
a. y = arccos(0,23) b. y = arcsen(0,9) c. y = arctan(–1) d. y = arctan(1)
π
12
1
2
⎛
⎝
⎜
⎞
⎠
⎟
2
2
⎛
⎝
⎜
⎞
⎠
⎟
3
2
Actividades
Pon atención
UNIDAD 3 (106-163)C :Maquetación 1 4/11/10 17:16 Página 151](https://image.slidesharecdn.com/matiii-210328014130/85/Mat-iii-152-320.jpg)



















![Inecuaciones lineales | 171
Unidad
4
Lo anterior significa que María debe tener una masa entre 51,2
y 64 kilogramos, incluidos ambos valores, para ser considerada en
la categoría saludable.
Si quisiéramos hacer una lista de los posibles valores de la masa de
María para ser considerada como saludable, no podríamos escribir-
los en una secuencia ordenada sin omitir muchos de ellos, ya que
estos valores forman un conjunto que tiene infinitos elementos.
En casos como estos, podemos representar el conjunto de los posi-
bles valores como un intervalo de números reales, utilizando la no-
tación [51,2, 64]. Observa que los paréntesis son cerrados en ambos
extremos, esto es porque se consideran dentro del intervalo los valo-
res 51,2 y 64. En caso de que no los incluyera, se escribiría ]51,2, 64[.
Otra forma de representar este intervalo es gráficamente, de la
siguiente manera:
Observa que en los valores 51,2 y 64 hay un círculo pintado, esto
es porque incluye ambos valores. En caso de que no los incluyera,
se dibujaría un círculo blanco en cada valor.
Ejemplo 1
Considera los intervalos A = ]–1, 10[ y B = [5, +[. Determina A B
y A B.
A B corresponde al conjunto que contiene todos los números
que están entre –1 y 10 o aquellos que son mayores o iguales que 5.
Es probable que no te sea difícil observar que A B = ]–1, +[.
Representaremos de manera gráfica lo anterior.
En la figura que sigue, se ha coloreado con verde la porción de recta
que corresponde al conjunto A, y con rojo la que representa a B.
Entonces, A B corresponde a todo lo que ha quedado coloreado,
ya sea con verde por pertenecer a A, o con rojo por pertenecer a B.
51,2 64
]–1, 10[ representa a todos los
números n que cumplen:
–1 n 10.
[5, +[ representa a todos los
números n que cumplen: 5 n.
+ y – no son números,
estos símbolos se utilizan para
representar el concepto de infinito.
significa unión.
significa intersección.
Recuerda que...
5 10
–1
UNIDAD 4 (164-199)C :Maquetación 1 4/11/10 17:18 Página 171](https://image.slidesharecdn.com/matiii-210328014130/85/Mat-iii-172-320.jpg)
![De la misma figura podemos deducir que A B corresponde a todos
los números que están entre –1 y 10, y que además son mayores o
iguales que 5. En el gráfico, esto es lo que ha quedado coloreado
con verde y rojo simultáneamente, es decir, A B = [5, 10[.
Ejemplo 2
Sea C = [1, 5] y D = ]7, +[. Determina C D y C D.
Se tiene que C D = , puesto que dichos conjuntos no tienen ele-
mentos en común; luego, la unión de ellos solo se puede expresar
como C D = [1, 5] ]7, +[. Observa.
172 | Unidad 4
En resumen
• Dados dos números reales a y b, con a b, se definen los intervalos que aparecen en la
siguiente tabla.
Conjunto Notación Representación gráfica Tipo de intervalo
{x IR / a x b} [a, b] Intervalo cerrado
{x IR / a x b} ]a, b[ Intervalo abierto
{x IR / a x b} [a, b[
Intervalo semiabierto
{x IR / a x b} ]a, b]
{x IR / x a} [a, +[
Intervalos no
acotados o infinitos
{x IR / x a} ]a, +[
{x IR / x b} ]–, b]
{x IR / x b} ]–, b[
b
a
b
a
b
a
b
a
a
a
b
b
7
1 5
representa al conjunto sin ele-
mentos, llamado conjunto vacío.
Recuerda que...
UNIDAD 4 (164-199)C :Maquetación 1 4/11/10 17:18 Página 172](https://image.slidesharecdn.com/matiii-210328014130/85/Mat-iii-173-320.jpg)
![Inecuaciones lineales | 173
Unidad
4
1. Considera los siguientes números: 0, π, , y .
a. Encuentra un intervalo que contenga a todos estos números.
b. Encuentra un intervalo que no contenga a ninguno de ellos.
c. Para cada número, encuentra un intervalo que lo contenga, y cuyos extremos sean números
enteros consecutivos.
d. Explica cómo lo hiciste en cada caso.
2. Expresa como intervalo y representa gráficamente los siguientes conjuntos:
a. {x IR / – x} d. {x IR / x –3}
c. {x IR / 0 x 0,5} f. {x IR / x }
3. Expresa como intervalo las siguientes representaciones gráficas:
a. d.
b. e.
c. f.
4. Determina las siguientes uniones e intersecciones de intervalos. Expresa tu resultado como
intervalo y represéntalo gráficamente.
a. [2, 5[ ]3, 18[ d. ]0, +[
b. ]–5, 1] ]1, 7[ e. [0, 1[ (]–3, 1[) [0, 5])
c. ]0, +[ f. (]–, 2[ [12, +[) [0, 20]
– ,
7
4
5
3
⎡
⎣
⎢
⎤
⎦
⎥
– ,
7
4
5
3
⎡
⎣
⎢
⎤
⎦
⎥
4
5
3
18
2
3
4
Actividades
b. {x IR / x 1,33} e. {x IR / –12 x 5,8}
1
5
–5
2
3
–5,2
100
0
3
2
19
3
0 8
UNIDAD 4 (164-199)C :Maquetación 1 4/11/10 17:18 Página 173](https://image.slidesharecdn.com/matiii-210328014130/85/Mat-iii-174-320.jpg)
![174 | Unidad 4
Propiedades de las desigualdades
En algunos países como Chile, la temperatura se mide en grados
Celsius, y en otros como Estados Unidos, se mide en grados Fahren-
heit. La expresión F = 1,8 · C + 32 muestra la relación entre grados
Celsius (C) y grados Fahrenheit (F).
Considera la siguiente información:
“Cierto día, la temperatura en Punta Arenas varió entre –1 ºC y
10 ºC”.
A partir de la información anterior, podemos expresar la variación
de la temperatura en Punta Arenas el día indicado, a través de la
desigualdad: –1 C 10. La que, expresada como un intervalo,
corresponde a [1, 10].
Para saber cuánto variaron estas temperaturas en grados Fahrenheit,
podemos utilizar la expresión F = 1,8 · C + 32, donde C representa la
medida en grados Celsius y F en grados Fahrenheit. Observa.
–1 C 10
–1,8 1,8C 18
30,2 1,8C + 32 50
30,2 F 50
Lo anterior significa que la temperatura en Punta Arenas ese día
varió entre 30,2 ºF y 50 ºF.
Observa que al sumar cualquier número real a los términos de una
desigualdad, o al multiplicarlos por un número real positivo, la
desigualdad se mantiene.
Ejemplo 1
–3 –10]
–3 · –2 –10 · –2
6 20
Observa que si multiplicamos o dividimos una desigualdad por un
número real negativo, la desigualdad se invierte.
Analicemos...
• ¿Cómo podrías representar esta variación de temperaturas como
un intervalo?
• ¿Cuál es esta variación de la temperaturas medida en grados
Fahrenheit?, ¿cómo lo supiste?
Multiplicamos por 1,8
Sumamos 32
Remplazamos en la expresión
F = 1,8 · C + 32
Multiplicamos por –2, por lo
tanto la desigualdad se
invierte
Termómetro que muestra la
temperatura en grados Celsius
y grados Fahrenheit.
UNIDAD 4 (164-199)C :Maquetación 1 4/11/10 17:18 Página 174](https://image.slidesharecdn.com/matiii-210328014130/85/Mat-iii-175-320.jpg)




![Mi progreso
Unidad
4
1. Determina si las siguientes desigualdades son verdaderas o falsas. Justifica tu respuesta.
a. 33 4 · 12 d. g. 3 – 3 –
c. 3 – 3 3 + f. i.
2. Determina la unión o intersección de los siguientes intervalos.
a. [1, 3[ ]2, 7[ c. ]2, 8] [–3, 2] e. [ ,
] [2, 5[
b. [1, +[ ]–, 40[ d. ]–1, + [ ]–, 1[ f. [ ,
[ [ ,
[
3. Asumiendo que a y b son números reales, y que a b, justifica las siguientes desigualdades mediante la
aplicación de las propiedades de las desigualdades, y lo aprendido sobre conjeturas y demostraciones.
a. a + 4 b + 4 c. 2 – b 2 – a e. 0 b – a
b. 3a 3b d. 3 + 4a 3 + 4b f. 8 + a – b 8
4. La desigualdad + , se cumple si a y b pertenecen a:
A. IR B. ⺪ C. ⺡ D. IR
+
E. IR
–
1
a + b
1
b
1
a
4
5
8
7
7
8
5
4
7
2
1
4
28
22
33
28
5
2
2
5
1 + 22
11
3 + 11
11
5
6
4
5
1
4
1
4
Inecuaciones lineales | 179
• Verifica en el solucionario del Texto si tus respuestas son correctas. Si tuviste respuestas incorrectas,
marca en la tabla el criterio correspondiente y revisa las páginas indicadas. Luego, identifica el error
y corrígelas.
¿Cómo voy?
CRITERIO ÍTEMS PÁGINAS DONDE SE TRABAJA
Representar situaciones mediante desigualdades
y justificar si son verdaderas o falsas.
1 y 3 168 y 169; 176 y 177
Comprender y utilizar correctamente la notación
y operatoria de intervalos.
2 170 a 173
Demostrar desigualdades mediante propiedades. 4 174 a 177
b. (2 + 3)(4 – 2) (2 + 2)(4 – 3) e. (–4)2
(–4)3
h. 1 +
4
7
1 + 4
7
UNIDAD 4 (164-199)C :Maquetación 1 4/11/10 17:18 Página 179](https://image.slidesharecdn.com/matiii-210328014130/85/Mat-iii-180-320.jpg)

![Inecuaciones lineales | 181
Ejemplo 1
Resuelve la inecuación: 4x – 7 2x – 3
Solución
2x – 7 –3
2x 4
x 2
Luego, todos los valores que satisfacen la inecuación pertenecen al
intervalo ]–, 2], el que se puede representar también gráficamente.
Algunas inecuaciones se deben resolver considerando el conjunto
al cual pertenece la incógnita, analizando las soluciones de estas.
Cuando dos inecuaciones tienen el mismo conjunto solución, se
dice que estas son equivalentes.
En el ejemplo 1, la inecuación 4x – 7 2x – 3 es equivalente a la
inecuación x 2. Luego, si x es un número natural, su solución sería
el conjunto {1, 2}.
Unidad
4
Restamos 2x
Sumamos 7
Dividimos por 2
2
En resumen
• Una inecuación es una desigualdad que tiene una o más incógnitas. Para resolverla, debemos
encontrar todos los valores de las incógnitas que hacen verdadera la desigualdad.
• El conjunto solución de la inecuación se puede expresar mediante un intervalo, o bien,
representado en la recta real.
1. Determina el conjunto solución de las siguientes inecuaciones y represéntalas gráficamente.
a. x – 2(x – 3) 0 c. – 3 + 1 e. 2(x + 3) + 3(x – 1) 2(x + 2)
2. Resuelve las siguientes inecuaciones, considerando la condición dada para x.
a. 3x – 2(4x – 7) ≥ 9, x entero positivo.
b. 2x + 3 x – 1, x entero negativo.
2x
5
3x
2
Actividades
b. (x + 1)2 – 5 ≥ x (x – 2) d. 2x + 3 4x – (x – 10) f. 3 – x – – 5
2x
5
1
3
UNIDAD 4 (164-199)C :Maquetación 1 4/11/10 17:18 Página 181](https://image.slidesharecdn.com/matiii-210328014130/85/Mat-iii-182-320.jpg)

![Inecuaciones lineales | 183
Unidad
4
Por lo tanto, el valor de la tercera lectura debe estar entre 6,3 y 8,1,
ambos valores incluidos, es decir, en el intervalo [6,3, 8,1].
Observa que en la situación anterior, la respuesta se obtiene al in-
tersecar el conjunto solución de ambas inecuaciones.
Lo que hemos hecho es resolver cada inecuación para encontrar
su conjunto solución, y luego intersecarlas para obtener los valo-
res que hacen verdaderas ambas desigualdades a la vez.
Dado que la solución final obtenida es un conjunto que está con-
tenido en las soluciones de cada inecuación, hemos resuelto un sis-
tema de dos inecuaciones con una incógnita.
En resumen
• Un sistema de inecuaciones con una incógnita es un conjunto de dos o más inecuaciones de
una incógnita que deben verificarse a la vez. La solución del sistema está dada por la inter-
sección del conjunto solución de cada inecuación.
1. Resuelve los siguientes sistemas de inecuaciones y representa gráficamente su solución.
a. 3x + 2 x – 4 c. x + 2 1 e. x – 2 2x g. 2x – 3 x + 1
5 – x – 2 x – 1 –1 x + 3 –8 5 – x 3
b. 2x – 2 x + 5 d. x – 2 2x + 1 f. x + 1 x – 1 h. x + 1 2x + 1
– x + 6 3 x + 3 –2 3x + 1 0 x – 3 4x + 5
2. En un triángulo, las medidas de dos de sus lados son 3 cm y 7 cm. Si la suma de las medidas de dos
lados de un triángulo debe ser mayor que el tercer lado y menor que la diferencia entre las me-
didas de los lados conocidos, ¿cuáles son las posibles medidas que puede tener el tercer lado,
sabiendo que el valor de este es un número entero?
3. Un músico profesional puede gastar entre $ 190 000 y $ 210 000 en un equipo de música y algunos
CD. Si el equipo de música cuesta $ 170 000 y los CD $ 8000 cada uno, encuentra la cantidad mínima
y máxima de CD que puede comprar.
Actividades
UNIDAD 4 (164-199)C :Maquetación 1 4/11/10 17:18 Página 183](https://image.slidesharecdn.com/matiii-210328014130/85/Mat-iii-184-320.jpg)




![188 | Unidad 4
Inecuaciones que involucran valor absoluto
Juan y sus amigos se encuentran jugando a la rayuela. Este juego,
típico de las zonas campesinas de Chile, consiste en lanzar un tejo
metálico sobre un cordel tenso que se encuentra a 5 metros en
línea recta del lugar de lanzamiento. Este cordel está justo en la
mitad de un cajón de 80 cm de largo, relleno con barro y leve-
mente inclinado, como se muestra en la figura. Observa.
En la situación anterior, para que el tejo caiga dentro del cajón, el
jugador debe lanzarlo a una distancia menor de 40 cm del cordel.
Este cordel se encuentra a 5 m del jugador, justo en la mitad del
largo del cajón. Observa la imagen que lo representa.
Por lo tanto, la distancia a la que debe caer el tejo tendría que
estar dentro del intervalo ]4,6, 5,4[.
Como x representa la distancia a la cual el jugador lanza el tejo, la
distancia a la cual debe lanzarse este para que caiga dentro del
cajón tendrá que cumplir que:
x – 5 0,4, si x 5
5 – x 0,4, si x 5
Recordando la definición de valor absoluto, podemos representar
la situación anterior de la siguiente forma: x – 5 0,4.
Notemos que los valores de x que satisfacen la inecuación son
x ] 4,6, 5,4 [, que corresponden al intervalo representado en la
figura anterior.
Analicemos...
• Si llamamos x a la distancia a la que el jugador lanza el tejo,
¿dentro de qué intervalo debe estar x para que el tejo caiga den-
tro del cajón?, ¿por qué?
• ¿Cómo podemos representar la distancia a la que se encuentra
el tejo del cordel en términos de x?, ¿qué debe cumplir esta para
que el tejo se encuentre dentro del cajón?, ¿cómo lo supiste?
14,4
5,4
5
4,6
40 cm 40 cm
El valor absoluto de x se define por:
x = {x si x 0
Recuerda que...
–x si x 0
cajón
UNIDAD 4 (164-199)C :Maquetación 1 4/11/10 17:18 Página 188](https://image.slidesharecdn.com/matiii-210328014130/85/Mat-iii-189-320.jpg)
![Inecuaciones lineales | 189
Unidad
4
Ejemplo
Resuelve la inecuación 2x + 1 3.
Solución
La inecuación es equivalente a:
–3 2x + 1 3
–4 2x 2
–2 x 1
Luego, la solución de esta inecuación es el intervalo ]–2, 1[.
1. Completa en tu cuaderno la siguiente tabla:
a. ¿Cómo se interpreta geométricamente x – y ?
b. ¿Qué significa x – y d y x – y d?
2. Responde las siguientes preguntas.
a. ¿A qué intervalo pertenecen todos los números reales que están a menos de tres unidades
del origen?
b. ¿A qué intervalo pertenecen todos los números reales que están a más de cinco unidades
del origen?
c. ¿Cómo se expresa mediante una inecuación el enunciado: “Todos los números reales que
están a más de dos unidades de 6”?
Actividades
–2
En resumen
• Si d es un número real positivo, y:
• x = d, entonces x = d o x = –d
• x d, entonces –d x d
• x d, entonces x –d o x d
Restamos 1
Dividimos por 2
–d d
–d d
1
x y
Distancia entre
x e y
x – y
2 5
–5 –3
–4 2
–d d
UNIDAD 4 (164-199)C :Maquetación 1 4/11/10 17:18 Página 189](https://image.slidesharecdn.com/matiii-210328014130/85/Mat-iii-190-320.jpg)


![Cómo resolverlo
192 | Unidad 4
Observa, paso a paso, las estrategias utilizadas en la resolución de
los siguientes problemas.
Ejercicio 1
En el patio de su casa, la señora Elena tiene un gallinero rectangular
de 4 m por 1 m. Ella desea ampliarlo, alargando el largo y el ancho
de él en una misma cantidad x. Si la señora Elena no quiere que el
área del gallinero exceda los 18 m2
, ¿qué rango de valores puede
tomar x?
Solución
Las dimensiones del gallinero
ampliado son: (x + 4) m y (x + 1) m.
Entonces, se tiene que:
(x + 4)( x + 1) 18
x2
+ 5x + 4 18
x2
+ 5x – 14 0
(x + 7)(x – 2) 0
La solución de la inecuación (x + 4)(x + 1) 18 es S1
S2
= [–7, 2],
pero como x representa una longitud x 0, el rango posible de valo-
res para x es el intervalo ]0, 2]. Es decir, el gallinero se puede ampliar
sin exceder 18 m2
, siempre y cuando 0 x 2.
–7 2
1 m
4 m x m
x m
Área del gallinero ampliado: (x + 4)(x + 1)
El área del gallinero debe ser menor o igual
a 18 m2
Restamos 18
Factorizamos el trinomio
El producto de dos números
es negativo, si uno es
positivo y el otro negativo.
x + 7 0 y x – 2 0
x –7 y x 2
Gráfico 1
S1
= ∅
x + 7 0 y x – 2 0
x –7 y x 2
Gráfico 2
S2
= [–7, 2]
–7 2
UNIDAD 4 (164-199)C :Maquetación 1 4/11/10 17:19 Página 192](https://image.slidesharecdn.com/matiii-210328014130/85/Mat-iii-193-320.jpg)
![Inecuaciones lineales | 193
Unidad
4
Ejercicio 2
Resuelve la siguiente inecuación: 0
x – 3 0 y x + 5 0
x 3 y x –5
Gráfico 1
S1
= [3, +[
x – 3 0 y x + 5 0
x 3 y x –5
Gráfico 2
S2
= ]–, –5[
Luego, la solución de la inecuación 0 es
S1
S2
= ]–, –5[ [3, +[
x – 3
x + 5
x – 3
x + 5
Actividades
1. Aplica el procedimiento aprendido para resolver la siguiente situación:
a. En el salón comunitario de la municipalidad se debe cubrir un ventanal de 2 m de alto por 4 m
de ancho con una cortina que lo cubra totalmente, pero que sea un poco más larga y ancha
que el ventanal. Asumiendo que el excedente de cortina respecto del ventanal es el mismo a
lo ancho que a lo alto, y que se dispone de solo 24 m2
de tela para la cortina, determina las
posibles dimensiones para esta.
2. Busca un procedimiento distinto para resolver el problema anterior. Respecto del procedimiento
previo, ¿cuál es más simple?, ¿por qué?
3. Resuelve las siguientes inecuaciones empleando el método aprendido, u otro. Compara el proce-
dimiento que utilizaste con el de algún compañero o compañera. ¿Cuál es más simple?, ¿por qué?
a. 1 b. 3
x – 5
x + 7
2x – 3
x – 2
El cociente entre dos números es
positivo, si ambos lo son, y es cero si
el numerador lo es
El cociente entre dos números es positivo,
si ambos son negativos y es cero si el
numerador lo es
–5 3
–5 3
UNIDAD 4 (164-199)C :Maquetación 1 4/11/10 17:19 Página 193](https://image.slidesharecdn.com/matiii-210328014130/85/Mat-iii-194-320.jpg)




![198 | Unidad 4
1. Para el conjunto de números reales
A =
{x IR / x
},es verdadero que:
I. 4 A
II. 1,5 A
III. A
A. Solo I
B. Solo II
C. I y II
D. I y III
E. I, II y III
2. ¿Qué condición deben cumplir los números
a y b para que ]–, a] [b, +[ = ∅?
A. a = b
B. a b
C. a b
D. a + b 0
E. a + b 0
3. Si p es un número real tal que 0 p 1,
siempre se cumple que:
A. p2
= 2p
B. p2
p3
C. p2
p3
D. p2
0
E. p2
p4
4. Si n es un número natural, ¿a qué intervalo
pertenecen todos los posibles valores de
la expresión ?
B. [0, 1[
C. ]0, +[
D. ]–, 0]
E. Ninguna de las anteriores.
5. Si a – 5 = 12, entonces a es igual a:
A. 17
B. 12 y –12
C. 17 y –7
D. 17 y –17
E. –7
6. La inecuación que representa al siguiente
gráfico es:
A. x 3
B. x 3
C. x 3
D. x 3
E. x = 3
7. ¿Cuál o cuáles de los siguientes puntos son
soluciones de la inecuación 4y – 3x 8?
I. (0, 2)
II.
III. (5, –17,6)
IV.
A. Solo I
B. Solo IV
C. I y II
D. II y IV
E. I y III
– ,
4
2
5
⎛
⎝
⎜
⎞
⎠
⎟
– ,
3
1
2
⎛
⎝
⎜
⎞
⎠
⎟
18
3 2
n – 1
n
π
2
III. Resuelve los siguientes ejercicios y selecciona la alternativa correcta en cada caso.
A. [0, – [
1
2
–3 3
UNIDAD 4 (164-199)C :Maquetación 1 4/11/10 17:19 Página 198](https://image.slidesharecdn.com/matiii-210328014130/85/Mat-iii-199-320.jpg)
![Inecuaciones lineales | 199
8. ¿Qué expresión describe al gráfico?
A. x x + 1
B. y x + 1
C. y x + 1
D. y x + 1
E. y = x + 1
9. El gráfico del conjunto solución de la inecuación
x2
+ 4x – 21 0 es:
A.
B.
C.
D.
E. Ninguna de las anteriores.
10. ¿De qué inecuación no es solución el
siguiente gráfico?
A. –2x 4
B. –4 2x
C. –x 2
D. 8 –4x
E. –2 x
11. ¿Qué inecuación describe al enunciado:“Todos
los números reales que están al menos a tres
unidades de –1”?
A. x – 1 3
B. x – 3 –1
C. x + 1 3
D. x + 1 3
E. x + 1 3
12. La solución de la inecuación 2x – 3 6 es:
A. {x IR /– x }
C. {x IR / x }
E. Ninguna de las anteriores.
13. En IR la solución de la inecuación
(p2
– 2)2
+ 3 p4
– 4p2
+ p es:
A. [7, +[
B. [7, +]
C. [–, 7[
D. ]–, 7]
E. ]–, 7[
14. El conjunto solución de la inecuación 0
es igual al conjunto solución de la inecuación:
A. x + 3 0
B. x + 3 0
C. 0
D. x + 3 0
E. x + 3 0
2x + 6
5
2
x + 3
9
2
9
2
3
2
Unidad
4
Verifica en el solucionario de tu Texto si tus respuestas son correctas. ¿Te equivocaste en alguna?,
¿cuál fue el error? Explícalo y resuelve correctamente el ejercicio.
B. {x IR / x }
9
2
D. {x IR /– x }
9
2
3
2
X
Y
–7 3
–7 3
–7 3
–7 3
–2
UNIDAD 4 (164-199)C :Maquetación 1 4/11/10 17:19 Página 199](https://image.slidesharecdn.com/matiii-210328014130/85/Mat-iii-200-320.jpg)




































![236 | Unidad 5
Ejemplo 2
Si se escoge al azar una manzana de un árbol y se mide su peso en
gramos, los valores posibles de esta variable aleatoria están en el
rango ]0, + ⬁[. Aunque en la práctica tal vez nos interesen los pesos
de las manzanas aproximados a números enteros, sabemos que en
un rango de 100 a 101 gramos es posible, al menos en teoría, en-
contrar infinitos pesos distintos.
Muchas veces será de utilidad visualizar la correspondencia de un
valor de la variable aleatoria con su probabilidad a través de un grá-
fico. Generalmente, usaremos un diagrama de barras, colocando en
el eje horizontal los posibles valores de la variable aleatoria, y en el
eje vertical las probabilidades de que estos ocurran.
Ejemplo 3
Un jugador, que suele encestar el 70% de sus tiros, tiene que realizar
un lanzamiento. Si el jugador acierta el primer tiro, puede repetir el
lanzamiento. Por lo tanto, es posible que consiga 0 puntos (fallando
el primer lanzamiento), 1 punto (acertando el primero y fallando el
segundo) o 2 puntos (acertando ambos lanzamientos). Sea X la
variable aleatoria que representa el puntaje obtenido:
a. Calcula P(X = 0), P(X = 1), P(X = 2).
b. Dibuja un gráfico de barras para la distribución de probabili-
dades de la variable X.
Solución
a. Usaremos una A para “acierto” y una F para “fallo” y supon-
dremos que lo que ocurra en el primer lanzamiento no tiene
ningún efecto sobre el segundo lanzamiento. Entonces:
P(A艚A)=0,7 · 0,7 = 0,49
P(A艚F) =0,7 · 0,3 = 0,21
P(F) = 0,3 = 0,30
Por lo tanto: P(X = 0) = 0,30 ; P(X = 1) = 0,21 ; P(X = 2) = 0,49.
Probabilidad de acertar ambos
lanzamientos
Probabilidad de acertar un
lanzamiento y fallar otro
Jugadores de básquetbol.
UNIDAD 5 (200-247)C :Maquetación 1 4/11/10 17:21 Página 236](https://image.slidesharecdn.com/matiii-210328014130/85/Mat-iii-237-320.jpg)





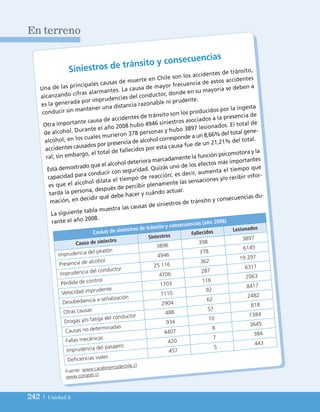









![252 | Matemática 3º Medio
Taller de evaluación
9. Si los catetos de un triángulo rectángulo miden
5 cm y 12 cm, entonces, la altura correspondiente
a la hipotenusa mide:
A. cm
C. cm
D. 30 cm
E. Ninguna de las anteriores.
10. En la cima de un cerro se ha levantado una an-
tena de telefonía celular. Desde un punto ubicado
en el valle se miden los ángulos de elevación del
extremo superior y la base de la antena. ¿Cuál
es la altura del cerro si estos ángulos son 57º y
42º, respectivamente, y además la antena mide
80 m de alto?
A. 100 m
B. 112,6 m
C. 154 m
D. 168,3 m
E. Ninguna de las anteriores.
1. El conjunto A = {x 僆 IR/ –2 ⱕ x 6} es equiva-
lente al intervalo:
A. [–2, 6]
B. ]–2, 6[
C. [–2, 6[
D. ]–2, 6]
E. Ninguna de las anteriores.
2. Si a ⱖ b + c, entonces, se cumple que:
A. a – c ⱖ b
B. a – b ⱕ c
C. a + c ⱕ b
D. b – a ⱖ –c
E. a + b c
3. La inecuación 2x + 3y ⱕ 12 se cumple para el
par ordenado:
A. (6, 1)
B. (–1, 6)
C. (2, 2)
D. (0, 9)
E.
4. El par (–1, 7) satisface la desigualdad:
A. 3x – 7y 8
B. 2x + y ⱖ 9
C. + – 3
D. x + y ⱕ x
E. –x + y ≥ y
5. El siguiente gráfico es la solución de la inecuación:
A. 兩x – 3兩 ⱖ 10
B. 兩3x兩 ⱕ 10
C. 兩x – 3兩 ⱕ 10
D. 兩x + 10兩 ⱕ 3
E. Ninguna de las anteriores.
1
y
1
x
7
2
7
3
,
⎛
⎝
⎜
⎞
⎠
⎟
60
13
17
13
B. cm
7
5
Inecuaciones lineales
4
–7 13
PAGS 248-255:Maquetación 1 4/11/10 17:36 Página 252](https://image.slidesharecdn.com/matiii-210328014130/85/Mat-iii-253-320.jpg)
![Taller de evaluación | 253
6. El conjunto solución de la inecuación
x2
– 3x ⱕ 18 es:
A. {x 僆 IR / x ⱕ –3 y x ⱖ 6}
B. {x 僆 IR / x 6}
C. {x 僆 IR / x ⱖ –3}
D. {x 僆 IR / –3 x 6}
E. {x 僆 IR / –3 ⱕ x ⱕ 6}
7. El siguiente gráfico es solución de:
A. 2x 4
B. 3x + 2 ⱖ – 4
C. 5 – x ⱖ 3
D. 7 + 2x 3
E. Ninguna de las anteriores.
8. La solución de la inecuación 3 – 4x ⱖ 2x – 15 es:
A. x ⱖ 3
B. x ⱕ 3
C. [–⬁, 9]
D. 3
E. Ninguna de las anteriores.
9. La solución del sistema de inecuaciones
4x + 5 ⱖ x – 1 , es:
6 – x – 3
A. [–2, 9[
B. ]9, +⬁[
C. ]–⬁, –2]艛]9, +⬁[
D. [–2, 3[
E. Ninguna de las anteriores.
10. En el gráfico, se representa el intervalo:
A. ]–⬁, 4[
B. ]–⬁, 4]
C. [4, +⬁[
D. ]4, +⬁[
E. Ninguna de las anteriores.
1. En el experimento de lanzar dos monedas al aire
y ver la cantidad de caras (C) y sellos (S) que
aparecen en el espacio muestral es:
A. {C, S}
B. {(C, C), (C, S), (S, S)}
C. {(C, C), (C, S), (S, C), (S, S)}
D. {1, 2, 3}
E. Ninguna de las anteriores.
2. El resultado de 8C5 + 3C2 es equivalente o igual a:
A. 11C7
B. 13C5
C. 24C10
D. 59
E. 342
–2
4
Probabilidades
5
PAGS 248-255:Maquetación 1 4/11/10 17:36 Página 253](https://image.slidesharecdn.com/matiii-210328014130/85/Mat-iii-254-320.jpg)








![262 | Matemática 3º Medio
Solucionario
c.
No hay dilatación ni contracción con respecto a
f(x) = x
2
.
d.
Hay contracción con respecto a f(x) = x
2
.
2.
3. a. V(–2, –3); x = –2 c. V ; x =
4. a.
b.
c.
d.
5. B
Página 79
1. a. Δ = 20
x
1
=
x
2
=
b. Δ = –352
No tiene solución real.
c. Δ = 0
x
1
= x
2
= 2
d. Δ = –12
No tiene solución real.
e. Δ = –2500
No tiene solución real.
f. Δ = 49
x
1
= 0
x
2
= 7
3
5 5
−
5 5
+
3
4
3
4
7
8
,
⎛
⎝
⎜
⎞
⎠
⎟
Decrecimiento Crecimiento
a. ]–⬁, –0,5[ ]–0,5, +⬁[
b. ]0, +⬁[ ]–⬁, 0[
c. ]0,5, +⬁[ ]–⬁, 0,5[
d. ]0,125, +⬁[ ]–⬁, 0,125[
b. V(0, 2); x = 0 d. V ; x =
– ,
1
2
21
4
⎛
⎝
⎜
⎞
⎠
⎟
–1
2
SOLUCIONARIO 3º (256-283):Maquetación 1 4/11/10 17:25 Página 262](https://image.slidesharecdn.com/matiii-210328014130/85/Mat-iii-263-320.jpg)


![Solucionario | 265
c.
Δ = 0
Corta al eje X en (0,5 , 0)
d.
Δ = –40
No corta el eje X
e.
Δ = 961
Corta al eje X en (0, 0) y
f.
Δ = 0
Corta al eje X en (–2, 0)
b. k = –
3. Infinitas. f(x) = k(x
2
– 6x + 7), k IR – {0}
4. Vértice:
5. – Falso
– Verdadero
6. No existe
7.
8. a. k = –2
b. – x 1
2
3
x x
f
x x
1 2 1 2
2 2
,
+ +
⎛
⎝
⎜
⎞
⎠
⎟
⎛
⎝
⎜
⎞
⎠
⎟
9
16
– ,
31
2
0
⎛
⎝
⎜
⎞
⎠
⎟
Solucionario
2. a. k – 9
16
c. k = – 9
16
Positiva Negativa
a. −∞
− −
⎤
⎦
⎥
⎥
⎤
⎦
⎥
⎥
∪
− +
∞
⎡
⎣
⎢
⎢
⎡
⎣
⎢
⎢
, ,
3 41
4
3 41
4
− − − +
⎤
⎦
⎥
⎡
⎣
⎢
3 41
4
3 41
4
,
b. ]– ⬁, –2][1, +⬁[ ]–2, 1[
c. x IR –
d. −∞ −
⎤
⎦
⎤
⎦
⎡
⎣
⎡
⎣
, ,
2 2 2 2 + −
⎤
⎦
⎡
⎣
2 2 2 2
,
e.
− − − +
⎡
⎣
⎢
⎢
⎤
⎦
⎥
⎥
2 82
6
2 82
6
, −∞
− −
⎤
⎦
⎥
⎥
⎡
⎣
⎢
⎢
∪
− +
∞
⎤
⎦
⎥
⎥
⎡
⎣
⎢
⎢
, ,
2 82
6
2 82
6
+
f. x IR –
c. x – y x 1
2
3
SOLUCIONARIO 3º (256-283):Maquetación 1 4/11/10 17:25 Página 265](https://image.slidesharecdn.com/matiii-210328014130/85/Mat-iii-266-320.jpg)


![268 | Matemática 3º Medio
Solucionario
e.
Dom: [0, +⬁[
Rec: [0, +⬁[
f.
Dom: [0, +⬁[
Rec: ]–⬁, 1]
g.
Dom: [0, +⬁[
Rec: ]–⬁, 4]
h.
Dom: [0, +⬁[
Rec: [–4,+⬁[
i.
Dom: [–2, +⬁[
Rec: [2, +⬁[
j.
Dom: ]–⬁, 5]
Rec: ]–⬁, 3]
k.
Dom: [0, +⬁[
Rec: [2, +⬁[
l.
Dom: [0, +⬁[
Rec: [2, +⬁[
SOLUCIONARIO 3º (256-283):Maquetación 1 4/11/10 17:25 Página 268](https://image.slidesharecdn.com/matiii-210328014130/85/Mat-iii-269-320.jpg)






![Solucionario | 275
Solucionario
18
18
2
4.
5. a. b.
c. La ecuación no d.
corresponde a
una recta.
e. f.
6. a. x = – 10 c. No tiene solución
b. x = 2, x = 3
––
2
7. a. x = 13
––
4
; y = – 9
––
8
b. No tiene solución
c. Tiene infinitas soluciones
Página 169
1. a. Verdadero b. Falso c. Verdadero
2. a. Si IUV = 10, entonces, t 艋 18, donde t es el
tiempo de exposición al sol.
b. FP ≥ 15
c. Si 100 ICAP 艋200, entonces, la calidad del
aire es regular.
d. 64 艋G 艋110
3. 13 a 25
Página 173
1. a. [0, ]
b. ]–⬁, 0[ ] , +⬁[
c. 0: [–1, 1], π: [3,4], : [1,2]
: [0,1]
: [4,5]
2. a.
b.
c. ]0, 0,5]
d. ]–⬁, –3]
e. [–12, 5,8]
f.
3. a. [3, +⬁[ b. c. ]–⬁, 100[
d. e. [0, 8[ f. ]–5,2, +⬁[
4. a. [2, 18[
b. ø
c.
d.
e. [0, 1[
f. [0, 20]
18
3
4
− +∞
⎡
⎣
⎢
⎡
⎣
⎢
7
4
,
4
5
,+∞
⎤
⎦
⎥
⎡
⎣
⎢
1
5
133
, ,
⎤
⎦
⎥
⎤
⎦
⎥
− +∞
⎤
⎦
⎡
⎣
3,
⺞ ⺪ ⺡ ⺙ IR
2 ✘ ✘ ✘ ✘
–2,43 ✘ ✘
3
––
4
✘ ✘
π ✘ ✘
✘ ✘
3 2
+
− 3
–7
––
4
1
––
5
4
––
5
1,33
0 0,5
–12 5,8
–3
2 18
0 5
––
3
0
5
3
,
⎤
⎦
⎥
⎤
⎦
⎥
−
⎤
⎦
⎥
⎤
⎦
⎥
5
2
0
,
3
2
19
3
,
⎡
⎣
⎢
⎤
⎦
⎥
0 1
0 20
SOLUCIONARIO 3º (256-283):Maquetación 1 4/11/10 17:25 Página 275](https://image.slidesharecdn.com/matiii-210328014130/85/Mat-iii-276-320.jpg)
![Solucionario
276 | Matemática 3º Medio
Página 175
1. a.
b. 1
––
a
1
––
b
c. 1
––
a
1
––
b
0
2. a.
b. x
2
x. Si x 艋 –1 o x ≥ 1, entonces x 艋 x
2
.
c. x
2
x
Página 177
1. a. Al multiplicar por a.
2. ]1, 2]
3. a. b. [–1, 2[
4. Como (a – b)
2
≥0,
a
2
– 2ab + b
2
≥0
a
2
+ b
2
≥2ab / ⫼ 2
1
––
2
(a
2
+ b
2
) ≥ab
5. Si a 0 y b 0
entonces, ab 0 / · 2
2ab 0 / + (a
2
+ b
2
)
a
2
+ 2ab + b
2
a
2
+ b
2
(a + b)
2
a
2
+ b
2
(a + b)(a + b) a
2
+ b
2
/ : (a + b)
a + b
a
2
+ b
2
a + b
6. Como
x + y ≥
x + y
≥
2
7. (2a – 5b)
2
≥0
4a
2
– 20ab + 25b
2
≥0 / + 20ab
4a
2
+ 25b
2
≥20ab / : 20ab
25b
2
+ 4a
2
≥ 1
20ab
a
+
5b
≥ 1
5b 4a
b. La desigualdad será también verdadera.
Página 179
1. a. Verdadero d. Falso g. Verdadero
b. Verdadero e. Falso h. Verdadero
c. Verdadero f. Verdadero i. Verdadero
2. a. [1, 7[ b. [1, 40[ c. ø
d. IR e. f.
3. a. a b / + 4
a + 4 b + 4,
b. a b / · 3, como 3 0
3a 3b
c. a b / · (– 1)
–a –b / + 2
2 – a 2 – b
d. a b / · 4
4a 4b / + 3
3 + 4a 3 + 4b
e. a b / – a
0 b – a
f. a b / – b
a – b 0 / + 8
8 + a – b 8
1
4
5
,
⎡
⎣
⎢
⎡
⎣
⎢
( )
x y
− ≥
2
0
1
2
1
,
⎤
⎦
⎥
⎤
⎦
⎥
a b 1
––
a
1
––
b
1 2 1 0,5
5 10 0,2 0,1
1000 10 000 0,001 0,0001
0,1 0,2 10 5
0,001 0,01 1000 100
x 0,95 0,80 0,65 0,20 0,10 0,01
x
2 0,9025 0,64 0,4225 0,04 0,01 0,0001
2 xy
xy
7
8
8
7
,
⎡
⎣
⎢
⎡
⎣
⎢
x – + y ≥0
2 xy
SOLUCIONARIO 3º (256-283):Maquetación 1 4/11/10 17:25 Página 276](https://image.slidesharecdn.com/matiii-210328014130/85/Mat-iii-277-320.jpg)
![Solucionario | 277
Solucionario
4. Como a 0 y b 0
a
2
+ ab + b
2
艌 0 / + ab
a
2
+ 2ab + b
2
艌 ab
(a + b)
2
≥ab / : (a + b)(ab)
a + b
≥
1
ab a + b
1
+
1
≥
1
a b a + b
Luego, la alternativa correcta es D.
Página 181
1. a. ]–⬁, 6[
b. [1, 3]
c.
d. [–7, +⬁[
e.
f.
2. a. x = 1 b. {x ⺪
–
/ x –4}
Página 183
1. a. [–3, 7]
b. ø
c. ]0, +⬁[
d. ]–5, –3[
e. ]–11, –1]
f.
g. ø
h.
2. Puede medir 5 cm, 6 cm, 7 cm, 8 cm o 9 cm.
3. La cantidad mínima de CD que puede comprar
es 3, y la máxima es 5.
Página 187
1. a. b.
c. d.
e. f.
2. No
3. a. x + y ≥ 2 b. 2y – x ≥ – 2
4. 16x + 5y ≥ 300
6
1 3
– 40
––
11
1
––
3
–7
115
––––
21
−
+∞
⎤
⎦
⎥
⎡
⎣
⎢
40
11
,
1
3
,+∞
⎤
⎦
⎥
⎡
⎣
⎢
115
21
,+∞
⎡
⎣
⎢
⎡
⎣
⎢
− +∞
⎤
⎦
⎥
⎡
⎣
⎢
1
3
,
−∞ −
⎤
⎦
⎥
⎤
⎦
⎥
,
8
3
–3 7
–5 –3
–11 –1
0
–1
3
–8
3
SOLUCIONARIO 3º (256-283):Maquetación 1 4/11/10 17:25 Página 277](https://image.slidesharecdn.com/matiii-210328014130/85/Mat-iii-278-320.jpg)
![278 | Matemática 3º Medio
Solucionario
Página 189
1.
a. La distancia entre x e y.
b. La primera desigualdad significa que la distancia
entre x e y es menor que d, la segunda significa
que esta distancia es mayor que d.
2. a. ]–3, 3[
b. ]–⬁, –5[]5, +⬁[
c. |x – 6| 2
Página 191
1. a. x 2
––
3
b. x 3
––
7
c. x 艋 8
––
5
d. x 艋 –9
e. x –3
f. No tiene solución.
2. a. ]–⬁, 1[
b. ]–1, +⬁[
c. ]–⬁, –1[
d. ]–⬁, –3]
3. a. b.
4. a. x
1
= 3; x
2
= 1
b. [–3, 11]
c. No tiene solución.
d. [–7, –4 [] 4, 7]
5. E
Página 193
1. a. La cortina puede ser de:
• 4 m de alto por 6 m de ancho.
• 3 m de alto por 5 m de ancho.
3. a. ]–⬁, 1][2, +⬁[
b. ]–⬁, –13[]–7, +⬁[
Página 197
I. 1. Falso 3. Verdadero
2. Verdadero 4. Verdadero
II. 1. a. ]3, 12[ b. ]–⬁, 31[
c. [8, +⬁[ d. ]–⬁, 4[
e. ]–7, 0[ f. ]1, 2[]7, 9[
2. a. x 3
––
5
b. x 艋
c. x 艋 d. x 3
e. 0 x y x 3 f. ]2, 3[
g. IR h. 0 x 艋 3
3. a. b.
c. d.
e. f.
x y Distancia entre x e y | x – y |
2 5 3 3
–5 –3 2 2
–4 2 6 6
1
10
4
13
SOLUCIONARIO 3º (256-283):Maquetación 1 4/11/10 17:25 Página 278](https://image.slidesharecdn.com/matiii-210328014130/85/Mat-iii-279-320.jpg)
![Solucionario | 279
Solucionario
g. h.
4. a. ]–12, 12[ b. ]–10, 14[
c. ]–15, 9[ d. ]–⬁, –15][9, +⬁[
e. IR – {5} f. ø
Páginas 198 y 199
III. 1. A 5. C 9. D 12. D
2. B 6. D 10. C 13. A
3. C 7. E 11. C 14. D
4. B 8. B
Páginas 202 y 203
1. a. Aleatorio b. Determinista
c. Aleatorio d. Aleatorio
e. Determinista
2.
3. a. 22 estudiantes b. 46 estudiantes
4. a. 12
–––
52
b. 20
–––
52
5. a. 1
––
52
b. 1
––
26
c. 1
––
13
d. 1
––
4
6. A
7. a. 1
––
6
b. 1
––
2
c. 0 d. 1
––
3
8.
Página 205
1. a. Ω = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9 ,10}
Finito
#Ω = 11
b. Ω = {1, 2, 3, 4, ….}
Infinito
c. Ω = {♠, ♣, ♦, ♥}
Finito
#Ω = 4
Probabilidades
5
Cazuela
de vacuno
Papayas al jugo
Torta de chocolate
Helado
Papayas al jugo
Torta de chocolate
Helado
Puré con
pescado
Tomate
cebolla
Cazuela
de vacuno
Papayas al jugo
Torta de chocolate
Helado
Papayas al jugo
Torta de chocolate
Helado
Puré con
pescado
Frecuencia absoluta Frecuencia relativa
2 2 2
––
15
3 3 3
––
15
4 5
5
15
5 5 5
––
15
Lechuga
palta
SOLUCIONARIO 3º (256-283):Maquetación 1 4/11/10 17:25 Página 279](https://image.slidesharecdn.com/matiii-210328014130/85/Mat-iii-280-320.jpg)









