Mezcladores.pdf

Electrónica de Comunicaciones
CONTENIDO RESUMIDO:
1- Introducción
2- Osciladores
3- Mezcladores.
4- Lazos enganchados en fase (PLL).
5- Amplificadores de pequeña señal para RF.
6- Filtros pasa-banda basados en resonadores piezoeléctricos.
7- Amplificadores de potencia para RF.
8- Demoduladores de amplitud (AM, DSB, SSB y ASK).
9- Demoduladores de ángulo (FM, FSK y PM).
10- Moduladores de amplitud (AM, DSB, SSB y ASK).
11- Moduladores de ángulo (PM, FM, FSK y PSK).
12- Tipos y estructuras de receptores de RF.
13- Tipos y estructuras de transmisores de RF.
14- Transceptores para radiocomunicaciones
ATE-UO EC mez 00

3- Mezcladores
Idea fundamental:
Obtener una señal cuya frecuencia sea la suma o la diferencia de
la frecuencia de otras dos
Mezclador
Señal de
frecuencia f2
Señal de
frecuencia f1
ƒ Señal de frecuencias (f1+ f2) y ⏐f1 - f2⏐
ƒ O señal de frecuencia (f1 + f2)
ƒ O señal de frecuencia ⏐f1 - f2⏐
Mucho más difícil
ATE-UO EC mez 01

ATE-UO EC mez 02
Mezclador que genera (f1+ f2) y ⏐f1 - f2⏐
Mezclador
ve2 de
frecuencia f2
ve1 de
frecuencia f1
vs de frecuencias
(f1+ f2) y ⏐f1 - f2⏐
ve2
ve1
vs
f1 = 3 MHz
f2 = 5 MHz
f2- f1 = 2 MHz
f1+f2 = 8 MHz
f1 f2 (f1+ f2)
(f2- f1)

¿Cómo generar una señal con frecuencias (f1+ f2) y ⏐f1 - f2⏐
partiendo de dos de frecuencias f1 y de f2?
Un poco de trigonometría:
cos(A+B) = cosA·cosB - senA·senB
cos(A-B) = cosA·cosB + senA·senB
Luego:
cosA·cosB = 0,5[cos(A+B) + cos(A-B)] (1)
senA·senB = 0,5[cos(A-B) - cos(A+B)] (2)
sen(A+B) = senA·cosB + senB·cosA
sen(A-B) = senA·cosB - senB·cosA
Luego:
senA·cosB = 0,5[sen(A+B) + sen(A-B)] (3)
senB·cosA = 0,5[sen(A+B) - sen(A-B)] (4)
cos(2A) = cos2A – sen2A y 1 = cos2A + sen2A
Luego:
cos2A = 0,5[1 + cos(2A)] (5)
sen2A = 0,5[1 - cos(2A)] (6) ATE-UO EC mez 03

Particularizamos al caso de señales (usando la expresión (1)):
cosω1t·cosω2t = 0,5·cos(ω1+ω2)t + 0,5·cos(ω1-ω2)t
Componente de
frecuencia f1+f2
Componente de
frecuencia ⏐f1 - f2⏐
ƒ Basta con multiplicar las señales para obtener la señal deseada
ƒ Lo mismo pasa con (2-4), pero con determinados desfases
¿Qué pasa si las señales que se mezclan no están en fase?
cosω1t·cos(ω2t+φ) = 0,5·cos[(ω1+ω2)t+φ] + 0,5·cos[(ω1-ω2)t–φ]
Componente de
frecuencia ⏐f1 - f2⏐
Componente de
frecuencia f1+f2
ƒ El desfase φ sólo provoca desfases,
no nuevas componentes
ATE-UO EC mez 04

¿Cómo multiplicar dos señales (I)?
ATE-UO EC mez 05
ƒ Usando un multiplicador analógico clásico ⇒ no adecuado para alta
frecuencia.
ƒ Usando dispositivos de respuesta cuadrática:
vs = V0 + k·(V1cosω1t + V2cosω2t)2 =
V0 + k·(V1
2 cos2ω1t + V2
2 cos2ω2t + 2V1cosω1t·V2cosω2t); usamos (1) y (5):
vs = V0 + 0,5k·V1
2 + 0,5k·V2
2 + 0,5k·V1
2cos(2ω1t) + 0,5k·V2
2cos(2ω2t) +
k·V1V2cos(ω1+ω2)t + k·V1V2cos(ω1-ω2)t
Componente
de continua
Componente de
frecuencia 2f1
Componente de
frecuencia 2f2
Componente de
frecuencia f1+f2
Componente de
frecuencia ⏐f1-f2⏐
Señal de
frecuencia f2
Señal de
frecuencia f1
+ k·x2
ƒ Nos sobran las componentes de
continua y de frecuencias 2f1 y 2f2

¿Cómo multiplicar dos señales (II)?
ƒ Usando dispositivos de respuesta proporcional + cuadrática:
vs = V0 + kA·(V1cosω1t + V2cosω2t) + kB·(V1cosω1t + V2cosω2t)2 =
V0 + kA·(V1cosω1t + V2cosω2t) + kB·(V1
2 cos2ω1t + V2
2 cos2ω2t +
2V1cosω1t·V2cosω2t); usamos (1) y (5):
vs = V0 + 0,5kB·V1
2 + 0,5kB·V2
2 + kA·V1cosω1t + kA·V2cosω2t +
0,5kB·V1
2cos(2ω1t) + 0,5kB·V2
2cos(2ω2t) + kB·V1V2cos(ω1+ω2)t +
kB·V1V2cos(ω1-ω2)t
ATE-UO EC mez 06
Componente
de continua
Componente
de frecuencia f1
Componente de
frecuencia 2f2
Componente de
frecuencia f1+f2
Componente de
Señal de
frecuencia f2
Señal de
frecuencia f1
+ kA·x + kB·x2
continua y de frecuencias f1, f2 2f1 y 2f2
Componente de
frecuencia 2f1
Componente
de frecuencia f2

¿Cómo multiplicar dos señales (III)?
ƒ Usando dispositivos de respuesta no lineal (en general):
vs = V0 + kA·(V1cosω1t + V2cosω2t) + kB·(V1cosω1t + V2cosω2t)2 +
kC·(V1cosω1t + V2cosω2t)3 + … nos fijamos en el último término:
(V1cosω1t + V2cosω2t)3 = V1
3 cos3ω1t + V2
3 cos3ω2t + 3V1
2cos2ω1t·V2cosω2t
+ 3V1cosω1t·V2
2cos2ω2t; analizamos cada término:
• cos3ω1t = cosω1t·0,5[1+ cos(2ω1t)] = 0,75cosω1t + 0,25cos(3ω1t)
• cos3ω2t = 0,75cosω2t + 0,25cos(3ω2t)
• cos2ω1t·cosω2t = 0,5[1+ cos(2ω1t)]·cosω2t = 0,5·cosω2t +
0,5cos(2ω1t)·cosω2t = 0,5·cosω2t + 0,25cos(2ω1+ω2)t + 0,25cos(2ω1-ω2)t
• cosω1t·cos2ω2t = 0,5·cosω1t + 0,25cos(2ω2+ω1)t + 0,25cos(2ω2-ω1)t
Finalmente habrá componentes:
Deseadas: (f1+f2), ⏐f1-f2⏐
Indeseadas: f1, f2, 2f1, 2f2, 3f1, 3f2,
4f1, 4f2 …, (2f1+f2), ⏐2f1-f2⏐, (2f2+f1),
⏐2f2-f1⏐, (3f1+f2), ⏐3f1-f2⏐, (3f2+f1),
⏐3f2-f1⏐, (2f1+2f2), ⏐2f1-2f2⏐... ATE-UO EC mez 07
Señal de
frecuencia f2
Señal de
frecuencia f1
+ kA·x + kB·x2 + kC·x3 + …

Ejemplos (I)
Dispositivo cuadrático con:
V0 = 0 V1 = V2 k = 0,5
ve1
f1
f1
ve2
f2
f2
0 2f1 2f2
(f1+ f2)
(f2- f1)
( dispositivo cuadrático)
vs
ƒ Es más difícil filtrar el caso
real (cuadrático) para aislar
una única frecuencia
vs (ideal)
(f1+ f2)
(f2- f1)
ATE-UO EC mez 08

Ejemplos (II)
ATE-UO EC mez 09
Dispositivo proporcional + cuadrático con:
V0 = 0 V1 = V2 kA = 0,25 kB = 0,5
ve1
f1
f1
ve2
f2
f2
0 2f1 2f2
ƒ Más difícil de filtrar para
aislar una única frecuencia
vs (ideal)
(f1+f2)
(f2-f1)
(f1+ f2)
(f2- f1)
( dispositivo proporcional +
cuadrático)
vs

ATE-UO EC mez 10
¿Por qué es importante que el mezclador genere el mínimo
número posible de componentes en la mezcla?
ƒ Para facilitar el filtrado.
ƒ Más importante aún: para facilitar el filtrado cuando las señales
de entrada no son señales senoidales puras.
ve2 de
frecuencia f2
ve1 de frecuencias
f1A y f1B
Mezclador
vs
Mezclador ideal. Componentes de
frecuencias:
(f1A+f2), (f1B+f2), ⏐f1A-f2⏐ y ⏐f1B-f2⏐
Mezclador cuadrático. Componentes
de frecuencias:
0, (f1A+f2), (f1B+f2), ⏐f1A-f2⏐, ⏐f1B-f2⏐,
2f1A, 2f1B y 2f2
Mezclador proporcional + cuadrático.
Componentes de frecuencias:
0, (f1A+f2), (f1B+f2), ⏐f1A-f2⏐, ⏐f1B-f2⏐,
f1A, f1B, f2, 2f1A, 2f1B y 2f2
ƒ Aún más difícil de filtrar para
aislar una única frecuencia

Objetivos de la realización física de los
mezcladores con dispositivos electrónicos
ƒ Comportamiento adecuado a las frecuencias de trabajo.
ƒ Uso de dispositivos con comportamiento lo más parecido a
cuadrático, sin términos apreciables en x, x3, x4, etc.
ƒ Cancelación de componentes indeseadas por simetrías en los
circuitos.
• Pasivos (diodos)
• Activos (transistores)
• Simples
• Equilibrados
• Doblemente equilibrados
Tipos de
mezcladores
• Simples
• Equilibrados
• Doblemente equilibrados
ATE-UO EC mez 11

Mezcladores con diodos. Ideas generales (I)
2
1
0
-2
-1
20
10
0 30
-20 -10
-30
iD [µA]
vD [mV]
Modelo proporcional
+ cuadrático
Modelo exponencial
iD = IS·(eVD/VT -1)
iD
vD
+
-
IS = 1 µA
VT = 26 mV
iD = kA·vD + kB·vD
2
ƒ Casi coinciden en este margen de
tensiones (± 30 mV)
kA = 4,467·10-5
kB = 7,984·10-4
ATE-UO EC mez 12

Mezcladores con diodos. Ideas generales (II)
Comportamiento con niveles mayores de tensión
iD [µA] 2
1
0
-2
-1
40
20
0 60
-40 -20
-60
vD [mV]
Modelo exponencial
ƒ Comportamiento
muy distinto en este
margen.
ƒ El equivalente tendría un comportamiento más
complejo iD = kA·vD + kB·vD
2 + kC·vD
3 + kD·vD
4 + kE·vD
5 + ...
ƒ Es muy importante que los niveles
de las señales sean los correctos.
ƒ Se generarían
componentes de
otras frecuencias. ATE-UO EC mez 13
Modelo proporcional
+ cuadrático

Teoría del mezclador con un diodo
+
v1 = V1cosω1t
v2 = V2cosω2t
vs
Idea general
ƒ Ecuaciones:
vs + vD = v1 + v2
vs = R·iD
iD ≈ kA·vD + kB·vD
2
vs ≈ R[0,5kBV1
2 + 0,5kBV2
2 + kAV1cosω1t + kAV2cosω2t + 0,5kBV1
2cos(2ω1t)
+ 0,5kBV2
2cos(2ω2t) + kBV1V2cos(ω1+ω2)t + kBV1V2cos(ω1-ω2)t]
vs << vD, v1, v2
vD ≈ v1 + v2
+
+
-
vs
R
v1
v2
+
+ -
vD
Realización práctica sin
terminal común en las fuentes
iD
ATE-UO EC mez 14

Mezclador con un diodo. Realización práctica
+
+
-
vs
R
v1
v2
+
ATE-UO EC mez 15
+
-
vs
R
+
v1
v2
+
+ -
vD
Realización práctica con terminal
común en las fuentes y la carga
+
-
vs
R
+
v1 v2 +
+ -
vD
R1 R1
Realización práctica sin
transformador y con terminal
común en las fuentes y la carga

Teoría del mezclador equilibrado
con dos diodos
+ +
-
vs
R
v1
v2
+
+ -
vD
iD
v2
+
R
+
v1 +
-
vs1
+ -
vD1
iD1
+
-
vs2
+
v1
iD2
+ -
vD2
R
+
-
vs
ƒ vs1 ≈ R[0,5kBV1
2 + 0,5kBV2
2cos(2ω1t)
+ 0,5kBV2
ƒ vs2 ≈ R[0,5kBV1
2 + 0,5kBV2
2 - kAV1cosω1t + kAV2cosω2t + 0,5kBV1
2cos(2ω1t)
+ 0,5kBV2
2cos(2ω2t) - kBV1V2cos(ω1+ω2)t - kBV1V2cos(ω1-ω2)t]
ƒ vs = vs1 - vs2 = 2R[kAV1cosω1t + kBV1V2cos(ω1+ω2)t + kBV1V2cos(ω1-ω2)t]
ƒ Sólo nos sobra la componente de frecuencia f1 ATE-UO EC mez 16

Mezclador equilibrado con dos
diodos. Realización práctica.
ATE-UO EC mez 17
v2
+
R
+
v1 +
-
vs1
+ -
vD1
iD1
+
-
vs2
+
v1
iD2
+ -
vD2
R
+
-
vs
vs = R·(iD1 - iD2) = vs1 - vs2
Lo mismo que en el caso anterior
+ -
vD1
+ -
vD2
+
-
vs
R
v2
+
+
v1
iD1
iD2
iD1 - iD2
1:1:1 1:1:1

Teoría del mezclador doblemente equilibrado con cuatro diodos (I)
Ecuaciones:
iD = f(vD) ≈ kA·vD + kB·vD
2
iD1 ≈ f(v1 + v2)
iD2 ≈ f(-v1 + v2)
iD3 ≈ f(v1 - v2)
iD4 ≈ f(-v1 - v2)
vs = v13 - v24 = i13R - i24R =
R[iD1 - iD3 - (iD2 - iD4)] =
R[iD1 - iD3 - iD2 + iD4] =
R
+
v1
+ -
vD1
iD1
+
v1
iD2
vD2
R
+ -
v2
+
+
-
v13
+
-
v24
+
-
vs
i13
i24
vD3
-
+
iD3
vD4
- +
iD4
Por tanto:
vs ≈ R[f(v1 + v2) - f(v1 - v2) - f(-v1 + v2) + f(-v1 - v2)]
ATE-UO EC mez 18

Teoría del mezclador doblemente equilibrado con cuatro diodos (II)
ƒ f(v1 + v2) ≈ 0,5kBV1
2 + 0,5kBV2
2cos(2ω1t) +
0,5kBV2
ƒ -f(-v1 + v2) ≈ -0,5kBV1
2 - 0,5kBV2
2 + kAV1cosω1t - kAV2cosω2t - 0,5kBV1
2cos(2ω1t)
- 0,5kBV2
ƒ -f(v1 - v2) ≈ -0,5kBV1
2 - 0,5kBV2
2 - kAV1cosω1t + kAV2cosω2t - 0,5kBV1
2cos(2ω1t)
- 0,5kBV2
ƒ f(-v1 - v2) ≈ 0,5kBV1
2 + 0,5kBV2
2 - kAV1cosω1t - kAV2cosω2t + 0,5kBV1
2cos(2ω1t) +
0,5kBV2
ƒ Σf(v) ≈ 4[kBV1V2cos(ω1+ω2)t + kBV1V2cos(ω1-ω2)t]
vs ≈ 4RkB[V1V2cos(ω1+ω2)t + V1V2cos(ω1-ω2)t]
Finalmente sólo habrá componentes
de (f1+f2) y de ⏐f1-f2⏐ ATE-UO EC mez 19

Teoría del mezclador doblemente equilibrado con cuatro diodos (III)
Ecuaciones:
iD = f(vD) ≈ kA·vD + kB·vD
2
iD1 ≈ f(v1 - v2)
iD2 ≈ f(-v1 + v2)
iD3 ≈ f(v1 + v2)
iD4 ≈ f(-v1 - v2)
i13 = iD1 - iD3
I24 = iD2 - iD4
vs = -(i13 + i24)R =
R[-iD1 + iD3 - iD2 + iD4] =
Por tanto:
R
+
v1
+ -
vD1
iD1
+
v1
iD2
vD2
+ -
v2
+
-
+ vs
i13
i24
vD3
-
+
iD3
vD4
- +
iD4
v2
+
Otra forma de realizar el conexionado
Es la misma ecuación que en el caso anterior, por lo
que sólo habrá componentes de (f1+f2) y de ⏐f1-f2⏐ ATE-UO EC mez 20

Mezclador doblemente equilibrado
con cuatro diodos. Realización
práctica (I)
R
+
v1
+
v1
R
v2
+
+
-
vs
Como antes:
vs ≈ 4RkBV1V2cos(ω1+ω2)t +
4RkBV1V2cos(ω1-ω2)t
ATE-UO EC mez 21
+
-
vs
R
v2
+
+
v1
1:1:1 1:1:1

Mezclador doblemente equilibrado con
cuatro diodos. Realización práctica (II)
Otra forma de
dibujar el circuito
+
-
vs
R
v2
+
+
v1
1:1:1
1:1:1
Anillo de diodos
(normalmente diodos Schottky)
ATE-UO EC mez 22

Mezclador doblemente equilibrado con
cuatro diodos. Realización práctica (III)
ATE-UO EC mez 23
Otra forma de realizar el
conexionado del circuito
+
-
vs
R
v2
+
+
v1
1:1:1
1:1:1
R
+
v1
+
v1
v2
+
-
+
vs
v2
+
R
+
v1
+
v1
v2
+
-
+
vs
v2
+

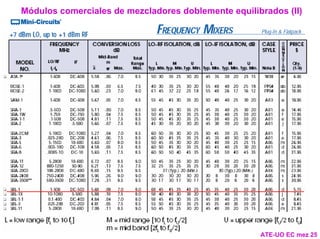
Módulos comerciales de mezcladores doblemente equilibrados (I)
Circuito interno del módulo
Mezclador
Oscilador Local
(terminal L)
Señal de RF
(terminal R)
Salida de IF
(terminal I)
ATE-UO EC mez 24

Módulos comerciales de mezcladores doblemente equilibrados (II)
ATE-UO EC mez 25

Carga de salida de un mezclador con diodos (I)
Mezclador
ve2 de
frecuencia f2
ve1 de
frecuencia f1
vs de frecuencias
(f1+ f2) y ⏐f1 - f2⏐
Frecuencia
⏐f1 - f2⏐
Lo normal es conectar
un filtro a la salida
Ze filtro
+
+
-
vs
R
v1
v2
+
+ -
vD
En todos los casos se
ha supuesto que la
carga era resistiva
ƒ La Ze filtro no va a ser resistiva, sino que va a depender de
la frecuencia
ƒ Hay que buscar un tipo de filtro con Ze filtro independiente
de la frecuencia. Se puede usar un diplexor
ATE-UO EC mez 26

Carga de salida de un mezclador con diodos (II)
R
L
C
R
L
C
Ecuaciones:
ƒ Ze1 = Ls + R/(RCs + 1) =
(RLCs2 + Ls + R)/(RCs + 1)
ƒ Ze2 = 1/Cs + RLs/(Ls + R) =
(RLCs2 + Ls + R)/[(Ls + R)Cs]
Ze,
Ye
Ze1,
Ye1
Ze2,
Ye2
ƒ Ye1 = (RCs + 1)/(RLCs2 + Ls + R)
ƒ Ye2 = (Ls + R)Cs/(RLCs2 + Ls + R)
ƒ Ye = (LCs2 + 2RCs + 1)/(RLCs2 + Ls + R)
ƒ Ze = R·(LCs2 + Ls/R + 1)/(LCs2 + 2RCs + 1)
Por tanto, para que Ze = R hace falta:
Diplexor
L/C = 2R2
ATE-UO EC mez 27

Carga de salida de un mezclador con diodos (III)
ƒ vs1/ve = 1/(LCs2 + Ls/R + 1)
ƒ vs2/ve = LCs2 /(LCs2 + Ls/R + 1)
Sustituimos R = (L/2C)1/2:
ƒ vs1/ve = 1/(LCs2 + (2LC)1/2s + 1)
ƒ vs2/ve = LCs2 /(LCs2 + (2LC)1/2s + 1)
Calculamos las funciones de
transferencia
ATE-UO EC mez 28
R
L
C
R
L
C
+
-
vs2
+
-
vs1
+
-
ve
0,1fC fC 10fC
-40
-30
-20
-10
0
10
[dB]
⏐vs2/ve⏐
⏐vs1/ve⏐

Carga de salida de un mezclador con diodos (IV)
ƒ ⏐vs1(jω) /ve(jω)⏐= ⏐1/(1 - LCω2 + j·(2LC)1/2ω⏐
ƒ ⏐vs2(jω) /ve(jω)⏐= ⏐-LCω2/(1 - LCω2 + j·(2LC)1/2ω⏐
ƒ Llamamos ωC a la ω tal que ⏐vs1(jω)/ve(jωC)⏐= ⏐vs2(jω)/ve(jωC)⏐
Entonces: ωC = 1/(LC)1/2, fC = ωC/2π y ⏐vs1/ve(jωC)⏐ = -3dB
0,1fC fC 10fC
-40
-30
-20
-10
0
10
[dB]
⏐vs2/ve⏐
⏐vs1/ve⏐
Conocidas las frecuencias fsum = f1 + f2 y fdif = ⏐f1 - f2⏐, fC debe colocarse
centrado entre ellas en el diagrama de Bode (que es logarítmico):
fC = (fsum·fdif)1/2
R
L
C
R
L
C
+
-
vs2
+
-
vs1
+
-
ve
R
L
C
R
L
C
R
L
C
R
L
C
+
-
vs2
+
-
+
-
vs2
+
-
vs1
+
-
+
-
vs1
+
-
ve
+
-
+
-
ve
Resumen:
fC = (fsum·fdif)1/2
fC = 1/[2π(LC)1/2]
L/C = 2R2 fC
fdif fsum
ATE-UO EC mez 29

Teoría del mezclador con un transistor bipolar
ƒ Ecuaciones:
vBE = v1 + v2
vs = R·iC
iC ≈ ISC + kA·vBE + kB·vBE
2
vs ≈ R[ISC + 0,5kBV1
2 + 0,5kBV2
2 + kAV1cosω1t + kAV2cosω2t +
0,5kBV1
2cos(2ω1t) + 0,5kBV2
2cos(2ω2t) + kBV1V2cos(ω1+ω2)t +
kBV1V2cos(ω1-ω2)t] ƒ Nos sobran las componentes de
ATE-UO EC mez 30
+
v1 = V1cosω1t
v2 = V2cosω2t
vs
Idea general
Realización
práctica sin
terminal común
en las fuentes
R
+
-
vs
+
-
vBE
+
v1
v2
+
+ VCC
iC
IC (VEB=0) = -ISC

Mezclador con un transistor bipolar. Realizaciones prácticas (I)
RB
iB
Polarización, pero
manteniendo la
operación no lineal
ATE-UO EC mez 31
R
+
-
vs
+
-
vBE
+
v1
v2
+
+ VCC
iC
+
v1
v2
+
vBE
R
+
-
vs
+
-
+ VCC
iC
Realización práctica con
transformador

Mezclador con un transistor bipolar. Realizaciones prácticas (II)
RB
iB
Polarización, pero
manteniendo la
R
+
-
vs
+
-
vBE
+
v1
v2
+
+ VCC
iC
vBE
R
+
-
vs
+
-
+
v1
v2
+
+ VCC
iC
Realización práctica sin transformador.
Ahora vBE = v1 - v2, pero las componentes
finales son las mismas
ATE-UO EC mez 32

Mezclador con un transistor bipolar. Realizaciones prácticas (III)
RB
iB
Polarización, pero
manteniendo la
Realización práctica sin transformador.
Ahora vBE = (v1 + v2)/2 , pero las
componentes finales son las mismas
vBE
R
+
-
vs
+
-
+ VCC
iC
+
v1 v2 +
R1 R1
R
+
-
vs
+
-
vBE
+
v1
v2
+
+ VCC
iC
ATE-UO EC mez 33

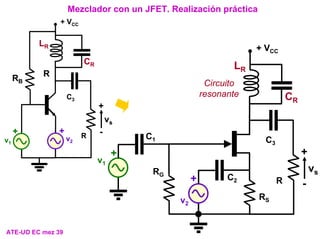
Mezclador con un transistor bipolar. Realizaciones prácticas (IV)
ATE-UO EC mez 34
Filtrado de la frecuencia deseada
RB
+
v1
v2
+
+ VCC
RC
+ VCC
RB
+
v1
v2
+ R
+
-
vs
LR
CR
CB
Circuito
resonante

Mezclador con varios transistores bipolares
ƒ Se puede conseguir cancelación de componentes
indeseadas por simetrías
ƒ Montajes equilibrados y doblemente equilibrados
ATE-UO EC mez 35
ƒ Sólo nos sobra la
componente de frecuencia f1.
Se cancelan las de f2 2f1 y 2f2
Ejemplo de mezclador
equilibrado
vBE1
+
vBE2
+
Q1
VCC
R
iC1
1:1:1
iC2
+
-
-
Q2
+
vS
+
-
v1
v2
1:1:1

Teoría general del mezclador con un transistor de
efecto de campo (JFET, MOSFET o MESFET) (I)
Diapositiva de la asignatura “Dispositivos Electrónicos”
VDS [V]
ID [mA]
4
2
8
4 12
0
VGS = -2V
VGS = -1,5V
VGS = -1V
VGS = -0,5V
VGS = 0V
VGS = -VPO
Cálculo de las corrientes en la zona de fuente
de corriente (canal contraído)
ATE-UO Trans 94
ID0PO
Partimos de conocer el valor de la corriente de drenador
cuando VGS = 0 y el canal está contraído, ID0PO.
También se conoce la
tensión de contracción
del canal, VPO
Ecuación ya conocida:
VDSPO = VPO + VGS
Muy importante
Ecuación no demostrada:
IDPO ≈ ID0PO·(1 + VGS/VPO)2
IDPO
VDS [V]
ID [mA]
4
2
8
4 12
0
VGS = -2V
VGS = -1,5V
VGS = -1V
VGS = -0,5V
VGS = 0V
VGS = -VPO
VDS [V]
ID [mA]
4
2
8
4 12
0
VGS = -2V
VGS = -1,5V
VGS = -1V
VGS = -0,5V
VGS = 0V
VDS [V]
ID [mA]
4
2
8
4 12
0 VDS [V]
ID [mA]
4
2
8
4 12
0
ID [mA]
4
2
4
2
8
4 12
0
VGS = -2V
VGS = -1,5V
VGS = -1V
VGS = -0,5V
VGS = 0V
VGS = -VPO
VGS = -VPO
ATE-UO Trans 94
ATE-UO Trans 94
ID0PO
ID0PO
del canal, VPO
del canal, VPO
del canal, VPO
VDSPO = VPO + VGS
VDSPO = VPO + VGS
Muy importante
IDPO
IDPO
IDPO
ATE-UO EC mez 36

efecto de campo (JFET, MOSFET o MESFET) (II)
Otra diapositiva de la asignatura “Dispositivos Electrónicos”
Circuito
equivalente ideal
B
C
E
-IE IC
IB
α·(-IE)
β·IB
Circuitos equivalentes para un transistor NPN
ATE-UO Trans 73
IE = -IF + IR·αR
IC = -IR + IF·αF
IF = ISE·(eVBE/VT-1)
IR = ISC·(eVBC/VT-1)
B
C
E
IE IC
IB
VBE
- + + -
VBC
IF
IR
αR·IR αF·IF
Modelo de
Ebers-Moll
Circuito
equivalente ideal
B
C
E
-IE IC
IB
α·(-IE)
β·IB
Circuito
equivalente ideal
B
C
E
-IE IC
IB
α·(-IE)
β·IB
ATE-UO Trans 73
ATE-UO Trans 73
IE = -IF + IR·αR
IC = -IR + IF·αF
B
C
E
IE IC
IB
VBE
- + + -
VBC
IF
IR
αR·IR αF·IF
Modelo de
Ebers-Moll
IE = -IF + IR·αR
IC = -IR + IF·αF
B
C
E
IE IC
IB
VBE
- + + -
VBC
IF
IR
αR·IR αF·IF
IE = -IF + IR·αR
IC = -IR + IF·αF
B
C
E
IE IC
IB
VBE
- + + -
VBC
IF
IR
αR·IR αF·IF
B
C
E
IE IC
IB
IE
IE IC
IC
IB
IB
VBE
- +
VBE
- +
- + + -
VBC
+ -
+ -
VBC
IF
IR
αR·IR αF·IF
αR·IR αF·IF
Modelo de
Ebers-Moll
ATE-UO EC mez 37

efecto de campo (JFET, MOSFET o MESFET) (III)
ƒ Ecuaciones del transistor bipolar:
iC = ISC - αFISE + αFISEeVBE/VT ≈ ISC + kA·vBE + kB·vBE
2 + kC·vBE
3 + kD·vBE
4 + …
ƒ Ecuaciones del transistor de efecto de campo:
IDPO ≈ ID0PO·(1 + VGS/VPO)2 = ID0PO + 2ID0PO VGS/VPO + ID0PO·(VGS/VPO)2
Sólo hemos considerado
estos términos, pero hay más
Prácticamente sólo hay estos términos
ƒ Un transistor de efecto de campo tiene una respuesta
“más cuadrática” ⇒ Sirve mejor para hacer mezcladores
ATE-UO EC mez 38

Mezclador con un JFET. Realización práctica
C1
+
v1
+
v2
C2
RG
RS
+ VCC
LR
CR
Circuito
resonante
R
C3
+
-
vs
RB
R
+
-
vs
+
v1
v2
+
+ VCC
LR
CR
R
C3
RB
R
+
-
vs
+
-
+
-
-
vs
+
v1
+
v1
v2
+
+ VCC
LR
CR
R
C3
ATE-UO EC mez 39

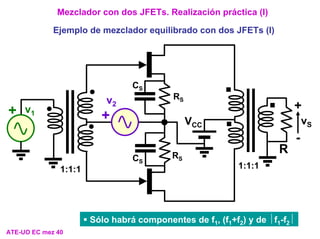
Mezclador con dos JFETs. Realización práctica (I)
Ejemplo de mezclador equilibrado con dos JFETs (I)
vS
+
+
VCC
R
1:1:1
+
-
v1
v2
1:1:1
RS
CS
RS
CS
ƒ Sólo habrá componentes de f1, (f1+f2) y de ⏐f1-f2⏐
ATE-UO EC mez 40

Mezclador con dos JFETs. Realización práctica (II)
Ejemplo de mezclador equilibrado con dos JFETs (II)
vS
+
+
VCC R
1:1:1
+
-
v1
v2
1:1:1
RS
CS
ƒ Sólo habrá componentes de f1, (f1+f2) y de ⏐f1-f2⏐
ATE-UO EC mez 41

Ejemplos de esquemas reales de mezcladores
equilibrados con JFETs (obtenidos del ARRL Handbook 2001) (I)
ATE-UO EC mez 42

Ejemplos de esquemas reales de mezcladores
equilibrados con JFETs (obtenidos del ARRL Handbook 2001) (II)
ATE-UO EC mez 43

Mezclador con un MOSFET de doble puerta
+
-
vs
C1
+
v1
+
v2
C2
RG1
RS
+ VCC
LR
CR
Circuito
resonante
R
C3
G1
D
S
G2
CS
RG2
G1
D
S
G2
Acumulación
G1
D
S
G2
Deplexión
ATE-UO EC mez 44

MOSFET de doble puerta comercial (I)
ATE-UO EC mez 45

MOSFET de doble puerta comercial (II)
ATE-UO EC mez 46

MOSFET de doble puerta comercial (III)
BF961
ATE-UO EC mez 47
VG2S = 4 V

MOSFET de doble puerta comercial (IV)
ATE-UO EC mez 48
BF998

MOSFET de doble puerta comercial (V)
BF998
Comportamiento frente a la tensión en cada una de las puertas
ATE-UO EC mez 49

Teoría básica de una etapa diferencial (I)
ƒ Ecuaciones:
iC1 ≈ Ise vBE1/VT iC2 ≈ ISevBE2/VT
iO = iC1/α + iC2/α
vd = vB1 - vB2 = vBE1 - vBE2
+ VCC
R
iC1
+
-
vs
Q1
vBE1
+
-
vBE2
+
-
iC2
+
-
R
+ -
- VCC
Q2
vB1
vB2
iO
+
-
vd
Por tanto:
iC1 ≈ αiO/(1+ e-vd/VT)
iC2 ≈ αiO/(1+ evd/VT)
ATE-UO EC mez 50

Teoría básica de una etapa diferencial (II)
+ VCC
R
iC1
vs
Q1
iC2
R
+ -
- VCC
Q2
iO
+
-
vd
iC1/(αiO) ≈ 1/(1 + e-vd/VT)
iC2/(αiO) ≈ 1/(1 + evd/VT)
-4 -3 -2 -1 0 1 2 3
0
0,5
1
1,5
4
vd/VT
iC2/(αiO) iC1/(αiO)
Se observa que ambas funciones son
muy lineales alrededor de vd/VT = 0
iC1/(αiO) ≈ 0,5 + 0,25vd/VT
iC2/(αiO) ≈ 0,5 - 0,25vd/VT
Expresión válida para -1 < vd/VT < 1
ATE-UO EC mez 51

Teoría básica de una etapa diferencial (III)
+ VCC
R
iC1
vs
Q1
iC2
R
+ -
- VCC
Q2
iO
+
-
vd
iC1 ≈ αiO0,5 + 0,25αiOvd/VT
iC2 ≈ αiO0,5 - 0,25αiOvd/VT
vs = R·(iC2 - iC1) ≈ -0,5RαiOvd/VT
Luego: vs = -0,5RαiOvd/VT
Es decir, la tensión de salida es
producto de la tensión de entrada
y del valor de la fuente de
corriente
iO
- VCC
- VCC
iO
ATE-UO EC mez 52

La etapa diferencial como mezclador (I)
ATE-UO EC mez 53
Hacemos:
vd = v1 = V1cosω1t
iO = IOdc + gOV2cosω2t
Por tanto:
vs = -(0,5RαIOdc/VT)·(V1cosω1t) -
(0,5RαgO/VT)·(V1cosω1t)·(V2cosω2t)
vs = -(0,5RαIOdc/VT)·V1cosω1t -
(0,25RαgO/VT)·V1V2cos(ω1 + ω2)t -
(0,25RαgO/VT)·V1V2cos(ω1 - ω2)t
Es decir:
Componente de
frecuencia f1
Componente de
frecuencia f1+f2
Componente de
+ VCC
R
iC1
vs
Q1
iC2
R
+ -
- VCC
Q2
iO
+
v1
+
v2
0,6 V
Q3

La etapa diferencial como
mezclador (II)
2:1:1
+ VCC
Q1 Q2
+
v1
+
v2
1:1:1
+ VCC
R1
Q3
R2
R3
R4
R5
C1
C2
C3
vS
+
-
ATE-UO EC mez 54

Ejemplo de esquema real de mezclador con etapa
diferencial (obtenidos de una nota de aplicación de Intersil)
ATE-UO EC mez 55
Circuito integrado CA3028
Condensadores para cancelar la
reactancia magnetizante del
transformador

Q2
- VCC
IO
+
v2
Q1
+ VCC
R
iC11
Q11
R
vs
+ - Q12
iC12
iC1
iC2
i1 i2
+
v1
Teoría básica de la célula
de Gilbert (I)
iC21
Q21 Q22
iC22
ATE-UO EC mez 56

ATE-UO EC mez 57
Ecuaciones:
vs = (i2 - i1)R = (iC12 + iC22 - iC11 - iC21)R
iC11 ≈ αiC10,5 + 0,25αiC1v1/VT
iC12 ≈ αiC10,5 - 0,25αiC1v1/VT
iC21 ≈ αiC20,5 - 0,25αiC2v1/VT
iC22 ≈ αiC20,5 + 0,25αiC2v1/VT
iC1 ≈ αIO0,5 + 0,25αIOv2/VT
iC2 ≈ αIO0,5 - 0,25αIOv2/VT
Q2
Teoría básica de la
célula de Gilbert (II)
- VCC
IO
+
v2
Q1
+ VCC
R
iC11
Q11
R
vs
+ - Q12
iC12
iC1
iC2
i1 i2
+
v1
iC21
Q21
Q22
iC22
Q2
- VCC
IO
+
v2
Q1
+ VCC
R
iC11
Q11
R
vs
+ -
vs
+ - Q12
iC12
iC1
iC2
i1
i1 i2
i2
+
v1 +
v1
iC21
Q21
Q22
iC22
Por tanto:
iC12 - iC11 ≈ -0,5αiC1v1/VT =
-0,25α2IOv1/VT - 0,125α2IOv1v2/VT
2
iC22 - iC21 ≈ 0,5αiC2v1/VT =
0,25α2IOv1/VT - 0,125α2IOv1v2/VT
2
vs = - 0,25α2RIOv1v2/VT
2

La célula de Gilbert como mezclador (I)
vs = - 0,25α2RIOv1v2/VT
2
Hacemos:
v1 = V1cosω1t
v2 = V2cosω2t
Por tanto:
vs = -(0,25α2RIO/VT
2)·(V1cosω1t)·(V2cosω2t)
vs = -(0,125α2RIO/VT
2)·V1V2cos(ω1 + ω2)t
-(0,125α2RIO/VT
2)·V1V2cos(ω1 - ω2)t
Es decir:
Componente de
frecuencia f1+f2
Componente de
ATE-UO EC mez 58

La célula de Gilbert como mezclador (II)
+ VCC
1:1:1
vS
+
-
+ Vp1
2:1:1
+
v1
+
v2
2:1:1
+ Vp2
Para que la etapa esté
correctamente polarizada:
VCC > Vp1 > Vp2
ATE-UO EC mez 59

La célula de Gilbert como mezclador (III)
+ VCC
1:1:1
vS
+
-
+ Vp1
+ Vp2
1:1
+
v1
1:1
+
v2
VCC > Vp1 > Vp2
ATE-UO EC mez 60

Ejemplo de mezclador con célula de Gilbert:
el SA602A (NE602) (I)
ATE-UO EC mez 61

Ejemplo de mezclador con célula de Gilbert: el SA602A (II)
ATE-UO EC mez 62

Ejemplo de mezclador con célula de Gilbert: el SA602A (III)
ATE-UO EC mez 63

Ejemplo de mezclador con célula de Gilbert: el SA602A (IV)
Circuito de entrada de bajo nivel (RF)
ATE-UO EC mez 64

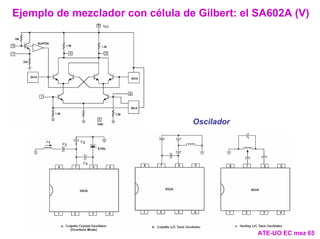
Ejemplo de mezclador con célula de Gilbert: el SA602A (V)
Oscilador
ATE-UO EC mez 65

Circuito de salida de bajo nivel (IF)
ATE-UO EC mez 66
Ejemplo de mezclador con célula
de Gilbert: el SA602A (VI)

ATE-UO EC mez 67
Ejemplo de esquema real de mezclador con célula
de Gilbert (obtenidos de una nota de aplicación de Philips)

Parámetros característicos de un mezclador
Ligados al uso de un mezclador en un receptor superheterodino
Mezclador
Entrada del
oscilador local
(LO)
Frecuencia f2
Entrada de
radiofrecuencia
(RF)
Frecuencia f1
Salida de frecuencia intermedia (IF)
Frecuencia (f2 - f1)
ƒ Perdidas de conversión:
L[dB] = -10log(PIF/PRF)
ƒ Aislamiento RF-IF :
IRF-IF[dB] = 10log(PRF/PRF-IF)
(siendo PRF-IF la potencia de RF
en la salida de IF)
ƒ Aislamiento OL-IF:
IOL-IF[dB] = 10log(POL/POL-IF)
ƒAislamiento OL-RF:
IOL-RF[dB] = 10log(POL/POL-RF)
ATE-UO EC mez 68

Ejemplo de uso de los parámetros de un mezclador
ƒ Perdidas de conversión:
L[dB] = 5,6 dB
ƒ Aislamiento OL-IF:
IOL-IF[dB] = 45 dB
-50 dBm
15 MHz
7 dBm
6 MHz
9 MHz
Componente de 9 MHz: -50 dBm - 5,6 dB = -55,6 dBm
Componente de 6 MHz: 7 dBm - 45 dB = -38 dBm
ATE-UO EC mez 69

Mezcladores.pdf

Más contenido relacionado

La actualidad más candente (20)

Similar a Mezcladores.pdf (20)

Más de Manuel Mazariegos (10)

Último (20)

Mezcladores.pdf