Numeros 3
- 1. NÚMEROS Ms. Ana María Teresa Lucca Facultad de Ingeniería Departamento de Matemática matematicaconhistoria.jimdo.com
- 3. Segunda mitad del Siglo XIX Acepto los conjuntos infinitos.
- 4. Afirmaciones verdaderas suenan como falsas Afirmaciones falsas suenan como verdaderas Aplicadas al infinito…
- 5. Tratamiento riguroso del infinito
- 6. Zenón de Elea (490 a.C. – 435 a.C.)
- 7. Toda la realidad es manifestación de un solo ser. Zenón pensaba… eterno – inmutable El cambio es imposible.
- 8. • Usan algún aspecto del infinito para llegar a una conclusión que contradice nuestra visión de la realidad. Paradojas de Zenón
- 9. • Pretende demostrar la no existencia del movimiento. Dicotomía
- 10. Puesto que toma un instante pasar cada uno de estos puntos, y puesto que hay un número infinito de puntos, correr la carrera debe llevar un tiempo infinitamente largo. La única conclusión posible es que… el movimiento es imposible. Conclusión de Zenón
- 11. • ¿Qué quiere decir un número infinito? • ¿Cómo podemos distinguir los conjuntos infinitos de los grandes pero finitos?
- 12. • Libro IXEuclides de Alejandría (325 a.C. – 265 a.C.) Elementos Existen infinitos números primos.
- 13. • Un número primo es un número que es divisible solamente por sí mismo y por 1. • Cada número compuesto es divisible por al menos otro número además de sí mismo y 1. • Nadie ha encontrado jamás una fórmula que permita listar todos los números primos. Hechos importantes
- 14. • Euclides comienza suponiendo que el conjunto de todos los números primos contiene sólo un número finito de números primos. Hay infinitos números primos.
- 15. • No nos dice prácticamente nada sobre los conjuntos infinitos. • Todo lo que se necesita saber acerca de los conjuntos infinitos es que no son finitos. • Es un buen ejemplo de lo que los griegos entendían acerca de los conjuntos infinitos. Para remarcar…
- 16. • El matemático asume algo que es falso y a continuación muestra que la suposición conduce necesariamente a una conclusión falsa. • Si la lógica entre el supuesto y la conclusión no tiene errores, entonces la única explicación es que el supuesto hecho al principio de la prueba es falso. • Debido a que la hipótesis es falsa se puede concluir con seguridad que lo contrario de la suposición debe ser verdadero. Demostración por contradicción
- 17. ¿Cómo se las arreglaron para hacer matemática sin la idea de conjunto infinito? Matemática griega
- 18. Siempre hay tantos números como necesitamos.
- 19. conjuntos infinitos procesos infinitos
- 20. Proceso infinito • Es un procedimiento que consiste en una serie de pasos. • Podemos repetir el proceso tantas veces como queramos. • No hay un límite teórico, aparte de la finitud de la vida, para repetir el procedimiento cualquier número de veces.
- 21. • Método de agotamiento o exhaución Eudoxo de Cnido (408 a.C. – 355 a.C.) Ejemplo
- 22. • los matemáticos islámicos • los matemáticos europeos hasta principios del siglo XIX Esta preferencia griega se extendió a…
- 24. Galileo Galilei (1563 – 1642)
- 25. • Sus observaciones astronómicas de la Luna, Venus y Júpiter • Desacreditar la idea de su tiempo: La Tierra como centro del universo. Lo recordamos por…
- 26. Diálogos acerca de dos nuevas ciencias Naturaleza de los conjuntos infinitos
- 28. Salvati quiere demostrar a sus amigos que hay tantos cuadrados perfectos como números naturales. Objetivo de la conversación…
- 29. Salvati quiere demostrar a sus amigos que hay tantos cuadrados perfectos como números naturales. Objetivo de la conversación… Números cuya raíz cuadrada es un número natural.
- 30. Todos los cuadrados perfectos son ellos mismos números naturales, pero… muchos números naturales no son cuadrados perfectos. Notemos que…
- 31. El conjunto de todos los cuadrados perfectos es un subconjunto propio del conjunto de los números naturales. Matemáticamente…
- 32. Si eliminamos el conjunto de números que no son cuadrados perfectos del conjunto de los números naturales, el conjunto de los números restantes es del mismo tamaño que el conjunto original. A veces todo el conjunto no es mayor que una parte. Pero Galileo dice…
- 33. • Galileo hace una lista numerada… Demostración Lugar 1 2 3 4 … Cuadrado perfecto 1 4 9 16 … En la 𝒏-ésima posición estará 𝒏 𝟐.
- 34. Podemos emparejar un subconjunto con el conjunto padre de tal manera que cada elemento en el conjunto padre esté en pareja con un único elemento en el subconjunto y ningún miembro de ninguno de los conjuntos sobre. Para conjuntos infinitos Números naturales Cuadrados perfectos
- 35. Dado cualquier conjunto infinito, podemos siempre eliminar cualquier colección finita de elementos sin cambiar el tamaño del conjunto original.
- 36. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, … 11, 12, 13, 14, 15, … En la 𝒏-ésima posición estará 𝒏 + 𝟏𝟎.
- 37. A veces es posible eliminar un número infinito de elementos de un conjunto infinito sin cambiar el tamaño del conjunto.
- 38. La propiedad “el todo puede ser igual a la parte” es cierta sólo para conjuntos infinitos.
- 39. reconoce la importancia de establecer una correspondencia uno a uno entre un conjunto cuyas propiedades más o menos están entendidas y un conjunto con cuyas propiedades estamos menos familiarizados. Además Galileo…
- 40. Si un subconjunto propio de un conjunto infinito es del mismo tamaño que el conjunto del que se extrae, entonces las ideas de "mayor que", "igual" y "menor que" no tienen lugar en una discusión de lo infinito. Galileo concluye…
- 41. Bernhard Bolzano (1781 – 1848)
- 42. Como Galileo A diferencia de Galileo estaba fascinado por el hecho de que un conjunto se puede poner en correspondencia uno a uno con subconjuntos propios de sí mismo. estaba interesado en lo que llamamos el conjunto de los números reales. Bolzano…
- 43. 𝟎 𝟏 𝟐 𝟏, 𝟐 Aunque el segmento que contiene las coordenadas 𝒚 es dos veces mayor que el segmento que contiene las coordenadas 𝒙, hay tantos puntos en el segmento más corto como hay en el más largo.
- 44. Existe una correspondencia uno a uno entre el conjunto de puntos en el intervalo de puntos finales 0 y 1 y el intervalo con extremos 0 y 𝑛, en el que tomamos a 𝑛 como cualquier número natural mayor que 0. En general…
- 45. 𝑦 = 𝑥 − 1/2 / 𝑥 − 𝑥2 Aquí tenemos una correspondencia uno a uno entre el conjunto de los números reales entre 0 y 1 (exclusivo) y todo el eje 𝒚.
- 46. Debemos a Bolzano Una colección de objetos cuya definición no depende del orden en el que aparecen sus elementos.
- 47. Cantor La lógica del infinito
- 48. “En matemática el arte de hacer preguntas es más valioso que la resolución de problemas” Georg Cantor (1845-1918)
- 50. • Identificar ese aspecto que cada conjunto infinito comparte, y ese que distingue todos los conjuntos infinitos de todos los finitos. 1° objetivo de Cantor
- 51. "El todo es mayor que la parte" Decisión audaz Euclides
- 52. • lo que sirve para distinguir todos los conjuntos infinitos de todos los finitos es "Hay partes que son iguales a la totalidad" Es que…
- 53. Los conjuntos infinitos son aquellos conjuntos que tienen subconjuntos propios que son del mismo tamaño que el conjunto padre. Cantor define…
- 54. Un conjunto es infinito siempre que pueda ser puesto en correspondencia uno a uno con un subconjunto propio de sí mismo. Más formalmente…
- 55. Dos conjuntos, infinitos o no, tienen el mismo tamaño siempre que sus elementos se puedan poner en correspondencia uno a uno. Además…
- 56. El conjunto de los números racionales tiene el mismo tamaño que el conjunto de los números naturales. Cantor descubrió que… cardinalidad
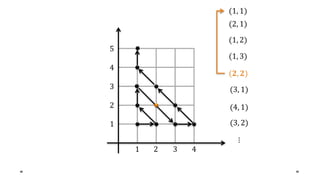
- 57. 𝒂 𝒃 ⇝ (𝒂, 𝒃) mínima expresión enteros positivos
- 58. 1 2 3 4 4 3 2 1 5 (1, 1) (2, 1) (1, 2) (1, 3) (𝟐, 𝟐) (3, 1) (4, 1) (3, 2) ⋮
- 59. El conjunto de los números racionales tiene el mismo tamaño que el conjunto de los números naturales. Cantor descubrió que… cardinalidad
- 60. Galileo estaba equivocado "mayor" y "menor" no son aplicables a conjuntos infinitos
- 61. El conjunto de los números reales es un conjunto más grande que el conjunto de los números naturales. Cantor demuestra que…
- 62. Los números transfinitos son números que representan el tamaño de los conjuntos infinitos. Números transfinitos
- 63. • Los números naturales, el conjunto de los cuadrados perfectos, el conjunto de los números racionales y el conjunto de los números algebraicos son todos ejemplos del número transfinito que Cantor llama ℵ0 (aleph cero). ℵ0
- 64. Un conjunto potencia de un conjunto 𝑆 es el conjunto de todos los subconjuntos de 𝑆. Conjunto potencia
- 65. 𝑺 = 𝒂, 𝒃 𝒂 𝒃 { 𝒂, 𝒃 , 𝒂 , 𝒃 , ∅ } Conjunto potencia
- 66. El conjunto potencia de cualquier conjunto no vacío es más grande que el propio conjunto.
- 67. • El conjunto de todos los números reales y el conjunto potencia de los números racionales son todos ejemplos del número transfinito que Cantor llama ℵ 𝟏 (aleph 1). ℵ 𝟏
- 68. Simplemente tomando el conjunto potencia de un conjunto que es un ejemplo de ℵ1, Cantor es capaz de obtener un ejemplo de ℵ2, y así sucesivamente. Pequeña fábrica!!!
- 69. ℵ 𝟎, ℵ 𝟏, ℵ 𝟐, ℵ 𝟑, … Extensión del sistema numérico
- 70. • ¿Hay otros números transfinitos además de estos? • ¿Existe un número transfinito que sea estrictamente mayor que ℵ0 y estrictamente menor que ℵ1? Cuestiones pendientes!!! Hipótesis del continuo
- 71. Expresar toda la matemática en el lenguaje de conjuntos. Nueva esperanza…
- 73. • enumeramos los elementos del mismo. • indicamos una condición que nos permita comprobar si un objeto dado es un miembro del conjunto o no. Para definir un conjunto…
- 74. • La definición de un conjunto a través de una simple condición de membresía puede dar lugar a contradicciones lógicas.
- 75. • Sea 𝑈 el conjunto formado por todos los conjuntos que no son miembros de sí mismos. ¿Es 𝑈 un miembro de sí mismo? 𝑼 no es un miembro de sí mismo 𝑼 es un miembro de sí mismo
- 76. • Sea 𝑈 el conjunto formado por todos los conjuntos que no son miembros de sí mismos. ¿Es 𝑈 un miembro de sí mismo? 𝑼 es un miembro de sí mismo 𝑼 no es un miembro de sí mismo
- 77. Un enfoque para ubicar la teoría de conjuntos en una base matemática firme era expresar las ideas básicas de la teoría como un conjunto de axiomas escogidos de tal manera de descartar la existencia de conjuntos muy grandes.
- 79. • Conjunto de siete axiomas, de los que era posible deducir todos los principales resultados de la teoría de conjuntos de Cantor. Solución de Zermelo
- 80. Establece que dada cualquier colección de conjuntos disjuntos no vacíos, es posible crear un nuevo conjunto que comparte exactamente un elemento en común con cada uno de los conjuntos en la colección original. Axioma de elección
- 81. adoptar el axioma de elección y aceptar una nueva clase de matemática, una matemática que consistía de ideas y soluciones que eran ocasionalmente no constructivas abandonar nuevas y útiles ideas matemáticas porque esas ideas estaban basadas en procedimientos no constructivos Opciones…
- 82. Legado de Cantor
- 83. David Hilbert (1862-1943) Fundamentos de la matemática
- 84. • Dar un conjunto de 21 axiomas que proporcionan una base completa y lógica para la geometría euclidiana, la más antigua de todas las geometrías. Éxito de Hilbert
- 85. Hilbert quería hacer por todo el campo de la matemática lo que había hecho por la geometría euclidiana. Objetivo mayor
- 86. • mirar dentro de la matemática para descubrir la forma en que trabaja. Objetivo de Hilbert
- 87. Si los teoremas son consecuencias directas y lógicas de los axiomas. Único interés…
- 88. • completo si, dada una afirmación en el sistema matemático descrito por los axiomas, la afirmación puede ser siempre demostrada como verdadera o falsa. • consistente siempre que toda afirmación que es una consecuencia de los axiomas es verdadera o falsa, pero no verdadera y falsa. Un conjunto de axiomas es…
- 89. • Comenzando a partir de primeros principios, esperaba derivar la matemática de una secuencia de pasos lógicos cuidadosamente ordenados. Objetivo de Russell Henry North Whitehead
- 91. Descubrió que ciertas cosas no son posibles. ARITMÉTICA Dentro de cualquier sistema matemático existen afirmaciones que no pueden ser ya sea probadas o refutadas Teoremas de Incompletitud de Gödel
- 92. El resultado de Gödel garantiza la existencia de afirmaciones que son para siempre imposibles de demostrar.
- 93. Alan Turing (1912-1954) Modelo teórico de ordenador
- 94. • Memoria ilimitada • Ningún límite en la cantidad de tiempo que podía dedicar a un cómputo particular • Completamente fiable: sin errores – sin roturas Máquina de Turing
- 95. • Para Turing una computadora es un dispositivo que calcula… pero entonces ¿cuáles son sus límites? problema de la parada
- 96. A B calcular la respuesta a algún problema problema dado a A información acerca de A ¿A resuelve el problema, o entra en un ciclo sin fin? Turing descubre que la máquina B no puede determinar si se detendrá o no la máquina A.
- 97. La búsqueda de un marco conceptual que permita al usuario distinguir lo matemáticamente verdadero de lo matemáticamente falso, sin dejar ninguna ambigüedad, ha llegado a un callejón sin salida.