Redes Neuronales

Aprendizaje supervisado
Función de coste
Descenso por gradiente
Regla delta
Algoritmo LMS o
Algoritmo de Widrow y Hoff.
Factor de aprendizaje

Función de coste
Sistema
x1
xi
xn
.
.
.
.
y1
yj
ym
.
.
.
.
Entrenamiento secuencial:
Una fila adapta el parámetro
Entrenamiento por lotes:
Todos los datos utilizados para entrenar
Época

Adaptación del parámetro
Neurona
Diferencial de la función de coste
con respecto a la neurona
Diferencial de la neurona
con respecto al parámetro
Número
de capas
Número de
capas previas

Formas de alterar el parámetro
- 'trainlm' (Levenberg-Marquard)
- 'traingdx' (Gradiente descendente con momento y f.a.
adaptativo)
- 'traingdm' (Gradiente descendente con momento)
- 'traingda' (Gradiente descendente con f.a. adaptativo)
- 'trainbfg' (BFGS Quasi-Newton)
- 'trainrp' (Resilient Backpropagation)
- 'trainoss' (Secante de un paso)
- 'trainscg' (Conjugado escalado)
- 'traingd' (Gradiente descendente)

Factor de aprendizaje
Se define en el intervalo: ]0, 1]
•Elevado: El algoritmo oscila y se convierte en inestable
•Bajo: Tarda en obtener el modelo
Si el error se incrementa por encima de un determinado porciento
(5%):
•No se actualizan los parámetros
•El factor de aprendizaje se reduce en un factor 0.95 (5%)
Si el error se reduce más de un determinado porciento (5%):
•Se actualizan los parámetros
•El factor de aprendizaje se incrementa en un factor 1.05 (5%)
En cualquier otro caso:
•Se actualizan los parámetros
•Se mantiene el valor del factor de aprendizaje
Dinámico o momento
∆e
0.95(∆e)
1.05(∆e)

Red lineal (I)
Núcleo estimador

Red lineal (III)
Pasos para el aprendizaje supervisado
[Paso 1] Definir la estructura del modelo y las condiciones iniciales
[Paso 2] Obtener los datos de entrada-salida ( x1, x2, . . .,xn; y )
[Paso 3] Aplicar el núcleo estimador
[Paso 4] Adaptar los parámetros
[Paso 5] Determinar la condición de finalización en la obtención del modelo,
si este no se cumple, repetir a partir del [Paso 2]
[Paso 6] Aplicar el criterio para validación del modelo.
Si los resultados no son los deseados, repetir a partir del [Paso 1]

Solución de ecuaciones lineales

Matlab
WEB
Aplicaciones Modelos Redes Neuronales

Filtro lineal con RN
Se desea representar el siguiente filtro:
y = 0.5*x1-0.3*x2
En este ejemplo los parámetros son: w1= 0.5 y w2= -0.3.
Se desea determinar la salida equivalente al vector de entradas:
>>x =
[1 3
2 4
3 5
4 6]

Filtro lineal con RN (II)
Solución:
% Se define la matriz de entradas x[n,K]=x[2,4]
>> x=x'
x =
1 2 3 4
3 4 5 6
% Se define el filtro lineal (versión antigua)
>>interx1=[1 4] % Intervalo [min, max] de x1
>>interx2=[3 6] % Intervalo [min, max] de x2
>>numsal=1 % Número de salidas
>>net=newlin([interx1; interx2], numsal);
% Nueva versión (adquiere información de matrices)
>>net=newlin(x, y); % net=newlin(x, 1);

Filtro lineal con RN (III)
% Se definen los parámetros del filtro
>>net.IW{1,1}=[0.5 -0.3]
>>net.b{1}=0; % La ganancia es cero
% Se verifican los parámetros del filtro
>> net.IW{1,1}
ans =
0.5000 -0.3000
>> net.b{1}
ans =
0

Filtro lineal con RN (IV)
% Se obtiene la salida de la red
>>y=sim(net,x)
y =
-0.4000 -0.2000 0 0.2000
% Se comprueba
>> x'*net.IW{1,1}'
ans =
-0.4000
-0.2000
0
0.2000

Filtros sin ganancia
Planos pasan
por el origen

Limitaciones de filtros sin ganancia
Cuando las entradas son cero,
los parámetros no se adaptan
1
Determinada clasificación:
Líneas que no pasen por el origen
Función AND

Filtro con ganancia
Adaptar nuevo parámetro
Solución lineal

Ejemplo
% Se obtienen datos de entrada-salida
>>load dryer2
>>t=[0:.08:80-.08]';
>>a=.1; b=.1; c=.1; d=.1; e=.1; f=.1;

Ejemplo (II)
Tools  Parameter Estimation…

Ejemplo (III)
Método de entrenamiento y parámetros estimados

Neurona
Neurona: Función no lineal, derivable, cuyo argumento
es un filtro lineal con ganancia.

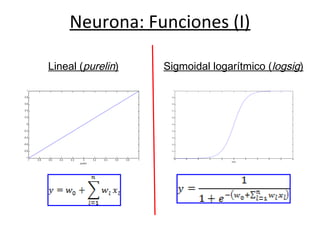
Neurona: Funciones (I)
-1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1
-1
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1
purelin
Lineal (purelin)
-10 -8 -6 -4 -2 0 2 4 6 8 10
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
logsig
Sigmoidal logarítmico (logsig)

Neurona: Funciones (II)
Tangente sigmoidal
hiperbólica (tansig)
Limitador fuerte (hardlim)
-10 -8 -6 -4 -2 0 2 4 6 8 10
-1
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1
tansig
-10 -8 -6 -4 -2 0 2 4 6 8 10
-1
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1
hardlim
Perceptrón

Neurona en Matlab
Representación de variables
nntool

Capa de Neuronas
Función de coste
Gradiente

Ejemplo
En WEB: Aplicaciones  Modelos  Capa de neuronas
% Se crean las matrices para la red
>> x=xudx(:,1:5)';
>> y=xudx(:,6:7)';
% Se determinan los intervalos de entrada
>> interv=minmax(x);
% Se define el número de salidas
>> numsal=2;
% Se define la función de activación
>> funact={'logsig'};

Ejemplo (II)
% Se define la red, entrenamiento: gradiente
net=newff(interv, numsal, funact, 'traingd');
% Se verifican los parámetros de entrenamiento
>> net.trainParam
epochs: 100
goal: 0
lr: 0.0100
max_fail: 5
min_grad: 1.0000e-010
show: 25
time: Inf

Ejemplo (III)
% Se alteran algunos parámetros
>>net.trainParam.epochs = 20000;   % Épocas
>>net.trainParam.goal = 0.001;       % Error deseado
>>net.trainParam.lr = 0.1;             % fa inicial
% Se entrena la red, alterando parámetros
% de entrenamiento según resultados
>> net = train(net,x,y);
% Se visualizan resultados basado en:
>> ynet=sim(net,x)';
>> y=y';
% Para determinar el error
>> error=y1-ynet

Ejemplo (IV)
% Identificación de parámetros
>> net.IW{1,1}
7.7054 -1.0928 1.3820 -0.2252 1.2570
7.9476 4.7789 -0.6219 1.0261 -0.7004
>> net.b{1}
-4.4500
-3.4097

Ejemplo (V)
% Creo matriz con unos incluidos (considerar ganancias)
[m,n]=size(x);
unos=ones(1,n);
xx=[unos ;x];
% Se une ganancia y pesos
pesos_tot=[net.b{1} net.IW{1,1}];
% Se obtiene salida filtro lineal
filtros=pesos_tot*xx;
% Se aplica función de activación
sal=logsig(filtros);
Modelo resultante

Red Neuronal Multicapas
Se desea obtener el modelo de un sistema con 4 variables de entrada
y 3 variables de salida.
Posible configuración:
Capa 1: Tres neuronas
Capa 2: Dos neuronas
Capa 3: Tres neuronas (definidas por el número de salidas del sistema)
Representación: 4 – 3 – 2 – 3
donde:
n : Número de variables de entrada
Sc : Número de neuronas de la capa c
C : Número de capas

Ecuaciones generales
Capa 1
Capas
intermedias
Para el ejemplo, representación: 4 – 3 – 2 – 3

Capas 2 y 3
Para el ejemplo, representación: 4 – 3 – 2 – 3

Aplicación del gradiente
El diferencial de la función de coste
con respecto a los parámetros
Secuencial:
Por lotes: El diferencial de la función que
representa a la capa de salida con
respecto a los parámetros

Aplicación del gradiente (Capa 3, C)
Capa(3)
Parámetro: Corresponde a la capa 3, segunda variable de
entrada (segunda neurona de la capa 2),
primera neurona
Variable de salida Variable de entrada

Aplicación del gradiente
(otras capas)
Capa 1
Capa 2
Secuencial

Pasos para crear una red
perceptrón multicapas
1.- Se definen el número de variables de entrada (n)
y variables de salida ( ) del sistema que se pretende modelar.
2.- Se definen el número de capas (C).
3.- Se definen el número de neuronas de cada capa
, para (excepto la de salida, que ha sido
definida en el paso 1).
4.- Se definen las funciones de activación para cada capa
(la única condición, en teoría, para definir estas funciones,
es que sean derivables).

Ejemplo
Planta con 6 variables de entrada y dos de salida
20 30 40 50 60 70 80 90 100
-5
-4
-3
-2
-1
0
1
2
3
10 20 30 40 50 60 70 80 90 100
-5
-4
-3
-2
-1
0
1
2
3

Ejemplo (II)
% Se configuran datos de entrada-salida
>> entradas=entradas(10:1001,:)';
>> salidas=salidas(10:1001,:)';
Representación: 6 – 5 – 4 – 2
% Número de capas
>> num_capas=[5 4];
% Funciones de activación
>> funcact={'tansig' 'logsig' 'purelin'};
% Se define la red
>> net=newff(entradas,salidas, num_capas, funcact,
'trainlm', 'learngdm', 'mse');
>> view(net)

Ejemplo (III)
% Se entrena la red
>> train(net, entradas, salidas)
% Tamaño de matrices de parámetros
>> size(net.IW{1}) % Capa 1
5 6
>> size(net.LW{2,1}) % Capa 2
4 5
% Modelo resultante
% Salida Capa 1
filtro1=net.IW{1}*entradas(:,1)+net.b{1};
capa1=tansig(filtro1)
% Salida Capa 2
filtro2=net.LW{2,1}*capa1+net.b{2};
capa2=logsig(filtro2)
% Salida Capa 3
filtro3=net.LW{3,2}*capa2+net.b{3};
capa3=purelin(filtro3)

Red de base radial
S1
: Número de entradas
a1
[S1
x1]: Variables de entrada
S2
: Número de variables de salida
IW21 [S2
xS1
]: Parámetros de la segunda capa
b2
[S2
x1]: Ganancias de la segunda capa
a2
[S2
x1]: Variables de salida de la red

Red de base radial(II)
R: Número de entradas
x [Rx1]: Vector de variables de entrada
S1
: Número de variables de salida de la capa 1
IW11 [S1
xR]: Parámetros
b1
[S1
x1]: Ganancias
d [S1
x1]: Distancias

Red de base radial (Programa)
% Capa I
% Vector de variables de entrada (R=5)
x=[1, 2, 3, 4, 5]';
[R,S]=size(x);
% Número de variables de salida de la primera capa
S1=3;
% Vector de parámetros debe ser de tamaño [S1xR]
IW11=rand([S1,R]);
% Ganancias de la primera capa [S1x1]
b1=rand([S1,1]);
% Se obtiene la norma euclídea
for i=1:S1
d(i,1)=sqrt(sum((x-IW11(i,:)').^2));
end
% Se aplica la función de base radial
a1=exp(-(b1.*d).^2);

Red de base radial (Programa II)
% Capa II
%Número de variables de salida de la segunda capa
S2=2;
% Vector de parámetros debe ser de tamaño [S2,S1]
LW21=rand([S2,S1]);
% Ganancias de la segunda capa [S2x1]
b2=rand([S2,1]);
% Se obtiene la salida
y=LW21*a1+b2;

Función no lineal equivalente
i=1…R : Subíndice que representa a las R variables de entrada
j=1… S1
: Subíndice que representa a las S1
salidas de la primera capa
k=1.. S2
: Subíndice que representa las S2
salidas de la segunda capa
Salida de la primera capa
Salida de la segunda capa
Función equivalente

Adaptación de parámetros
Primera capa
Segunda capa
Gradiente descendente
ó

Programa en Matlab
%Se crean las matrices de entrada-salida para la red
>> entrada=xudx(:,1:8)';
>> salida=xudx(:,9)';
% Se entrena la red, error medio cuadrático deseado: 0.1
>> net = newrb(entrada,salida,0.1);
% Número de parámetros de la primera capa
>> size(net.IW{1})
ans =
1062 8
>> size(net.b{1})
ans =
1062 1
% Número de parámetros de la segunda capa
>> size(net.LW{2,1})
ans =
1 1062
>> size(net.b{2})
ans =
1 1

Resultado de aplicar
la entrada a la red
Clasificación de sexo de conchas (datos Avalon)

Ejemplo
sim('planta3');
% Datos de entrada-salida
entradas=entradas(10:1001,:)';
salidas=salidas(10:1001,:)';
% Procede a adaptación
net = newrb(entradas,salidas)
% Comprobación del resultado
salidas_net=net(entradas);
plot(salidas'); hold on; plot(salidas_net')';

Ejemplo (II)
>> view(net)
% Comprobación de parámetros
>> size(net.IW{1})
992 6
>> size(net.b{1})
992 1
2 992
>> size(net.b{2})
2 1

Tipos de redes
-
+
Salida conocida
y(t+1)
ε(t+1)
Sistema III
∆
∆
Salida del
modelo
Sistema
II
Sistema
I
∆
∆
∆
∆
F
Entradas
conocidas
Red
estática
Red
dinámica hacia
adelante
Red
dinámica recurrente
)1( +ty


Redes estáticas vs recurrentes

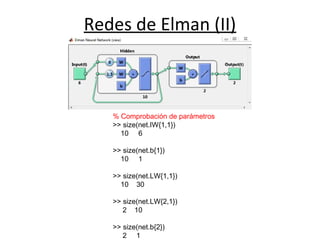
Redes de Elman
sim('planta_2');
% Datos de entrada-salida
entradas=entradas(10:1001,:)';
salidas=salidas(10:1001,:)';
% Red de Elman
net = elmannet(1:3,10)
% Procede a adaptación
net = train(net,entradas,salidas);
view(net)
% Comprobción del resultado
salidas_net=net(entradas);
plot(salidas'); hold on; plot(salidas_net','r')';

Redes de Elman (II)
% Comprobación de parámetros
>> size(net.IW{1,1})
10 6
>> size(net.b{1})
10 1
10 30
2 10
>> size(net.b{2})
2 1

Redes estáticas vs dinámicas
Red dinámica

Redes Neuronales

Más contenido relacionado

La actualidad más candente (20)

Similar a Redes Neuronales (20)

Más de Omar Sanchez (20)

Último (20)

Redes Neuronales