Tsf1
- 4. COLEGIO DE BACHILLERES DEL ESTADO DE SONORA Director General Mtro. Víctor Mario Gamiño Casillas Director Académico Mtro. Martín Antonio Yépiz Robles Director de Administración y Finanzas Ing. David Suilo Orozco Director de Planeación Mtro. Víctor Manuel Flores Valenzuela Director de Vinculación e Imagen Institucional Lic. José Luis Argüelles Molina temas selectos de física 1 Módulo de Aprendizaje. Copyright © 2016 por Colegio de Bachilleres del Estado de Sonora Todos los derechos reservados. Primera edición 2016. Impreso en México. DIRECCIÓN ACADÉMICA Departamento de Innovación y Desarrollo de la Práctica Docente. Blvd. Agustín de Vildósola, Sector Sur. Hermosillo, Sonora, México. C.P. 83280 COMISIÓN ELABORADORA Elaboración: José Carlos Enríquez Rangel Julia Isabel Ramos de los Ríos Corrección de estilo: Ana Martha Bogue Villegas Diseño y edición: Jesús Ramón Franco Hernández Diseño de portada: Yolanda Yajaira Carrasco Mendoza Fotografía de portada: Héctor Guillermo Corrales López Coordinación técnica: Rubisela Morales Gispert Supervisión académica: Vanesa Guadalupe Angulo Benítez Coordinación general: Laura Isabel Quiroz Colossio Esta publicación se terminó de imprimir durante el mes de junio de 2016. Diseñada en Dirección Académica del Colegio de Bachilleres del Estado de Sonora. Blvd. Agustín de Vildósola, Sector Sur. Hermosillo, Sonora, México. La edición consta de 1,952 ejemplares.
- 5. PRELIMINARES 3 COMPONENTE: FORMACIÓN PROPEDÉUTICA HORAS SEMANALES: 03 CAMPO DE CONOCIMIENTO: FÍSICO MATEMÁTICO CRÉDITOS: 06 DATOS DEL ALUMNO Nombre: Plantel: Grupo: Turno: Teléfono: E-mail: Domicilio:
- 6. PRELIMINARES 4 El Colegio de Bachilleres del Estado de Sonora (COBACH), desde la implementación de la Reforma Integral de la Educación Media Superior en 2007, de forma socialmente responsable, dio inicio a la adecuación de su Plan de estudios y a sus procesos de enseñanza aprendizaje y de evaluación para reforzar su modelo de Educación Basada en Competencias, y así lograr que pudieran sus jóvenes estudiantes desarrollar tanto las competencias genéricas como las disciplinares, en el marco del Sistema Nacional del Bachillerato. Este modelo por competencias considera que, además de contar con conocimientos, es importante el uso que se hace de ellos en situaciones específicas de la vida personal, social y profesional. Dicho de otra forma, el ser competente se demuestra cuando, de forma voluntaria, se aplican dichos conocimientos a la resolución de situaciones personales o a la adquisición de nuevos conocimientos, habilidades y destrezas, lo que hace que se refuerce la adquisición de nuevas competencias. En ese sentido el COBACH, a través de sus docentes, reestructura la forma de sus contenidos curriculares y lo plasma en sus módulos de aprendizaje, para facilitar el desarrollo de competencias. En el caso del componente de Formación para el Trabajo, además de las competencias genéricas, fortalece el sentido de apreciación hacia procesos productivos, porque aunque el bachillerato que te encuentras cursando es general y te prepara para ir a la universidad, es importante el que aprendas un oficio y poseas una actitud positiva para desempeñarlo. De tal forma que, este módulo de aprendizaje del componente Propedéutico de Temas Selectos de Física 1, es una herramienta valiosa porque con su contenido y estructura propiciará tu desarrollo como persona visionaria, competenteeinnovadora,característicasqueseestablecenenlosobjetivosdelaReformaIntegraldeEducación Media Superior. El módulo de aprendizaje es uno de los apoyos didácticos que el COBACH te ofrece con la finalidad de garantizar la adecuada transmisión de saberes actualizados, acorde a las nuevas políticas educativas, además de lo que demandan los escenarios local, nacional e internacional. En cuanto a su estructura, el módulo se encuentra organizado en bloques de aprendizaje y secuencias didácticas. Una secuencia didáctica es un conjunto de actividades, organizadas en tres momentos: inicio, desarrollo y cierre. En el inicio desarrollarás actividades que te permitirán identificar y recuperar las experiencias, los saberes, las preconcepciones y los conocimientos que ya has adquirido a través de tu formación, mismos que te ayudarán a abordar con facilidad el tema que se presenta en el desarrollo, donde realizarás actividades que introducen nuevos conocimientos dándote la oportunidad de contextualizarlos en situaciones de la vida cotidiana, con la finalidad de que tu aprendizaje sea significativo. Posteriormente se encuentra el momento de cierre de la secuencia didáctica, donde integrarás todos los saberes que realizaste en las actividades de inicio y desarrollo. En todas las actividades de los tres momentos se consideran los saberes conceptuales, procedimentales y actitudinales. De acuerdo a las características y del propósito de las actividades, éstas se desarrollan de forma individual, grupal o equipos. Para el desarrollo de tus actividades deberás utilizar diversos recursos, desde material bibliográfico, videos, investigación de campo, etcétera; así como realizar actividades prácticas de forma individual o en equipo.
- 7. PRELIMINARES 5 La retroalimentación de tus conocimientos es de suma importancia, de ahí que se te invita a participar de forma activa cuando el docente lo indique, de esta forma aclararás dudas o bien fortalecerás lo aprendido; además en este momento, el docente podrá tener una visión general del logro de los aprendizajes del grupo. Recuerda que la evaluación en el enfoque en competencias es un proceso continuo, que permite recabar evidencias a través de tu trabajo, donde se tomarán en cuenta los tres saberes: conceptual, procedimental y actitudinal, con el propósito de que apoyado por tu maestro mejores el aprendizaje. Es necesario que realices la autoevaluación, este ejercicio permite que valores tu actuación y reconozcas tus posibilidades, limitaciones y cambios necesarios para mejorar tu aprendizaje. Así también, es recomendable la coevaluación, proceso donde de manera conjunta valoran su actuación, con la finalidad de fomentar la participación, reflexión y crítica ante situaciones de sus aprendizajes, promoviendo las actitudes de responsabilidad e integración del grupo. Finalmente, se destaca que, en este modelo, tu principal contribución es que adoptes un rol activo y participativo para la construcción de tu propio conocimiento y el desarrollo de tus competencias, a través de lo que podrás dar la respuesta y la contextualización adecuadas para resolver los problemas del entorno a los que te enfrentes, ya sean personales o profesionales.
- 9. PRELIMINARES 7 Se trata de la evaluación que se realizará al inicio de cada secuencia didáctica y que te permitirá estar consciente de tus conocimientos acerca del tema que abordarás. EVALUACIÓN DIAGNÓSTICA Es la relación de palabras nuevas o de las cuales pudieras desconocer su significado. Es útil para conocer nuevos conceptos, ampliar tu vocabulario y comprender mejor las lecturas. GLOSARIO En este espacio realizarás una evaluación de tu propio trabajo, misma que deberá ser honesta para que puedas identificar los conocimientos que has adquirido y las habilidades que has desarrollado, así como las áreas que necesitas reforzar. AUTOEVALUACIÓN En este apartado encontrarás el espacio para calificar tu desempeño, que será por parte de tu profesor, tus compañeros (coevaluación) o tú mismo (autoevaluación). EVALUACIÓN DEACTIVIDADES Durante el semestre, tu profesor te irá indicando qué evidencias (trabajos y ejercicios) debes ir resguardando para integrarlos en un portafolio, mismos que le entregarás cuando te lo indique, a través del cual te evaluará. PORTAFOLIO DE EVIDENCIAS Son reactivos que aparecen al final de un bloque, al realizarlos reforzarás los conocimientos adquiridos durante el bloque y desarrollarás tus habilidades. REACTIVOS DE CIERRE Esta actividad resume los conocimientos adquiridos durante un proceso, ya sea una secuencia didáctica, un bloque o lo visto en un semestre completo. Es la suma teórica y práctica de tus conocimientos y es útil para fortalecer tu aprendizaje. ACTIVIDAD INTEGRADORA Este tipo de evaluación se hace con uno o varios de tus compañeros, en ella tú los evalúas y ellos a ti. Les permite, además de valorar sus aprendizajes, colaborar y aprender unos de otros. COEVALUACIÓN Es el listado de referencias que utilizaron los profesores que elaboraron el módulo de aprendizaje, contiene la bibliografía, las páginas de internet de las cuales se tomó información, los vídeos y otras fuentes que nutrieron los contenidos. Te permite también ampliar la información que te proporcione tu profesor o la del módulo mismo. REFERENCIAS La rúbrica es una tabla que contiene niveles de logro o desempeño especificados en estándares mínimos y máximos de la calidad que deben tener los diversos elementos que componen un trabajo. Sirve como guía para saber qué debe contener un trabajo y cómo debe ser realizado. RÚBRICA DE EVALUACIÓN El glosario icónico es la relación de figuras que encontrarás en diversas partes de tu módulo. Enseguida, se muestran junto con su definición, lo que te orientará sobre las actividades que deberás realizar durante el semestre en cada una de tus asignaturas. ACTIVIDAD 1 SD1-B1 Con este gráfico identificarás la Actividad dentro del texto, incluyendo la indicación y especificando si debe realizarse de manera individual, en equipo o grupal. Individual Equipo Grupal
- 10. PRELIMINARES 8 BLOQUE 1 BLOQUE 2 Aplicaslaestática…………………........................................................................…13 Secuencia didáctica 1. Origen de una fuerza………................................................................….15 ¿Qué es fuerza?.............................................................................................................................16 Fuerza resultante y fuerza equilibrante……..........................................................................………..25 Secuenciadidáctica2.Vectores……..................................................................................………26 Vectores unitarios…...............................................................................................................………27 Operación con vectores………....................................................................................................…..28 Suma y resta de vectores………........................................................................................……………..28 Métododelasortogonales……..................................................................................................……29 Ley de los senos y cosenos……........................................................................................................32 Multiplicación de vectores……................................................................................................……..35 Secuencia didáctica 3. Cuerpo en equilibrio............................................................................42 Cuerpo rígido………...................................................................................................................……43 Resolución de casos de equilibrio estático…………….......................................................................46 Secuencia didáctica 4. Momentos de fuerza............................................................................51 Momento de una fuerza……....................................................................................................…….52 Segunda condición de equilibrio…...........................................................................................…….55 Describes la cinemática en tu entorno……......................................................….71 Secuencia didáctica 1. Movimiento de rotación y traslación….......................................…………73 Movimiento de rotación……...........................................................................................................74 Movimientodetraslación….........................................................................................................….75 DesplazamientoAngular…….......................................................................................................….77 Movimiento Circular Uniforme…...................................................................................................77 Velocidad tangencial……….........................................................................................................…..78 Rapidez angular…......................................................................................................................…..78 Aceleración………...................................................................................................................………79 Presentación del libro ....................................................................................................................... 4 Glosario Icónico ................................................................................................................................ 7 Competencias Genéricas ................................................................................................................... 10 Competencias Disciplinares Básicas ................................................................................................... 11 Mapa de Contenido .......................................................................................................................... 12
- 11. PRELIMINARES 9 BLOQUE 3 Analizas la cinética rotacional……..............................................................……..93 Secuencia didáctica 1: Movimiento de cuerpos rígidos……......................................................95 Movimientodecuerposrígidos…………...........................................................................................96 Movimiento en una trayectoria circular….................................................................................……96 AceleraciónCentrípeta……..........................................................................................................….97 Aceleracióntangencial……………..................................................................................................….97 Dinámica del movimiento circular uniforme……..................................................................……..100 Curvas en las autopistas, peraltadas y sin peralte……...........................................................……..107 Secuencia didáctica 2: Energía cinética rotacional……....................................................……..114 Energía cinética rotacional: momento de inercia….............................................................………115 Torca e inercia de rotación…………................................................................................................116 Energíacinéticaderotación………...............................................................................................….126 Secuencia didáctica 3: Trabajo y potencia rotacionales…................................................…….133 Trabajo y potencia rotacionales……….....................................................................................……134 Cantidad de movimiento angular……...................................................................................……..139 Referencias ……....................................................................................................................158
- 12. PRELIMINARES 10 1 2 3 4 5 6 7 8 9 10 11 Se conoce y valora a sí mismo y aborda problemas y retos teniendo en cuenta los objetivos que persigue. Es sensible al arte y participa en la apreciación e interpretación de sus expresiones en distintos géneros. Elige y practica estilos de vida saludables. Escucha, interpreta y emite mensajes pertinentes en distintos contextos, mediante la utilización de medios, códigos y herramientas apropiados. Desarrolla innovaciones y propone soluciones a problemas a partir de métodos establecidos. Sustenta una postura personal sobre temas de interés y relevancia general, considerando otros puntos de vista de manera crítica y reflexiva. Aprende por iniciativa e interés propio a lo largo de la vida. Participa y colabora de manera efectiva en equipos diversos. Participa con una conciencia cívica y ética en la vida de su comunidad, región, México y el mundo. Mantiene una actitud respetuosa hacia la interculturalidad y la diversidad de creencias, valores, ideas y prácticas sociales. Contribuye al desarrollo sustentable de manera crítica, con acciones responsables.
- 13. PRELIMINARES 11 1 4 5 6 7 8 9 10 2 3 III I III Valora de forma crítica y responsable los beneficios y riesgos que trae consigo el desarrollo de la ciencia y la aplicación de la tecnología en un contexto histórico-social, para dar solución a problemas. Evalúa los factores y elementos de riesgo físico, químico y biológico presentes en la naturaleza que alteran la calidad de vida de una población para proponer medidas preventivas. Aplica la metodología apropiada en la realización de proyectos interdisciplinarios atendiendo problemas relacionados con las ciencias experimentales. Utiliza herramientas y equipos especializados en la búsqueda, selección, análisis y síntesis para la divulgación de la información científica que contribuya a su formación académica. Diseña prototipos o modelos para resolver problemas, satisfacer necesidades o demostrar principios científicos, hechos o fenómenos relacionados con las ciencias experimentales. Confronta las ideas preconcebidas acerca de los fenómenos naturales con el conocimiento científico para explicar y adquirir nuevos conocimientos. Valora el papel fundamental del ser humano como agente modificador de su medio natural proponiendo alternativas que respondan a las necesidades del hombre y la sociedad, cuidando el entorno. Resuelve problemas establecidos o reales de su entorno, utilizando las ciencias experimentales para la comprensión y mejora del mismo. Evalúa las implicaciones del uso de la ciencia y la tecnología, así como los fenómenos relacionados con el origen, continuidad y transformación de la naturaleza para establecer acciones a fin de preservarla en todas sus manifestaciones. Aplica los avances científicos y tecnológicos en el mejoramiento de las condiciones de su entorno social. COMPETENCIAS DISCIPLINARES BÁSICAS DEL CAMPO DE CIENCIAS EXPERIMENTALES BLOQUES DE APRENDIZAJE
- 14. PRELIMINARES 12 Temas Selectos de Física 1 BLOQUE 1. APLICAS LA ESTÁTICA Secuencia didáctica 1. Origen de una fuerza. Secuencia didáctica 2. Vectores. Secuencia didáctica 3. Cuerpo en equilibrio. Secuencia didáctica 4. Momentos de fuerza. BLOQUE 2. DESCRIBES LA CINEMÁTICA EN TU ENTORNO. Secuencia didáctica 1. Movimiento de rotación y traslación. BLOQUE III: ANALIZAS LA CINÉTICA ROTACIONAL Secuencia didáctica 1: Movimiento de cuerpos rígidos. Secuencia didáctica 2: Energía cinética rotacional. Secuencia didáctica 3: Trabajo y potencia rotacionales.
- 15. ■ ■ Evalúa las aplicaciones de la estática, a partir de la construcción de modelos esquemáticos y analíticos de las fuerzas vectoriales en hechos notables de la vida cotidiana; valorando las implicaciones metodológicas. Tiempo asignado: 15 horas ■ ■ Origen de una fuerza. ■ ■ Vectores. ■ ■ Cuerpo en equilibrio. ■ ■ Momentos de fuerza. ■ ■ Valora la estática al aplicar el método analítico y esquemático, en situaciones de su vida cotidiana. ■ ■ Diseña prototipos o modelos para resolver problemas y demostrar principios científicos, hechos o fenómenos relacionados con la estática. ■ ■ Confronta las ideas preconcebidas acerca de los fenómenos naturales con el conocimiento científico, para explicar los elementos relacionados con la estática y adquirir nuevos conocimientos. ■ ■ Evalúa las implicaciones del uso de momentos de fuerza y los relaciona con fenómenos naturales. Desempeño del estudiante al finalizar el bloque Objetos de aprendizaje Competencias a desarrollar Aplicas la estática BLOQUE 1
- 16. 14 C O L E G I O D E B A C H I L L E R E S D E L E S T A D O D E S O N O R A ACTIVIDAD INTEGRADORA Al concluir el presente bloque demostrarás los conocimientos y habilidades adquiridos a través del desarrollo de una actividad experimental, en donde resolverás una situación problemática sobre el equilibrio de los cuerpos. EVALUACIÓN DIAGNÓSTICA De manera individual contesta los siguientes cuestionamientos. 1. ¿A qué se refiere el término estática? __________________________________________________________________________________________ __________________________________________________________________________________________ 2. ¿Qué entiendes por “interacción”? __________________________________________________________________________________________ __________________________________________________________________________________________ 3.¿Qué fuerzas experimenta tu módulo de aprendizaje, al situarlo encima de tu mesabanco? __________________________________________________________________________________________ __________________________________________________________________________________________ 3. ¿A cuánto equivale la magnitud de la fuerza resultante que experimenta un cuerpo en equilibrio? __________________________________________________________________________________________ __________________________________________________________________________________________ 4. ¿Por qué a la fuerza se le clasifica como una cantidad vectorial? __________________________________________________________________________________________ __________________________________________________________________________________________ 5. Menciona y describe brevemente dos métodos utilizados para sumar cantidades vectoriales. __________________________________________________________________________________________ __________________________________________________________________________________________ 6. ¿Qué condición se debe cumplir para que un cuerpo esté en equilibrio? __________________________________________________________________________________________ __________________________________________________________________________________________
- 17. T E M A S S E L E C T O S D E F Í S I C A 1 Aplicas la estática BLOQUE 1 15 7. ¿Cuál es la diferencia entre fuerza resultante y fuerza equilibrante? __________________________________________________________________________________________ __________________________________________________________________________________________ 8. ¿Qué entiendes por momento de una fuerza? __________________________________________________________________________________________ __________________________________________________________________________________________ Menciona tres situaciones de tu entorno, donde apliques la estática. __________________________________________________________________________________________ __________________________________________________________________________________________ Secuencia didáctica 1 Origen de una fuerza Inicio De manera individual responde los siguientes cuestionamientos. 1. ¿Qué entiendes por fuerza? __________________________________________________________________________________________ __________________________________________________________________________________________ 2. Anota cinco tipos de fuerza que experimentan algunos de los cuerpos u objetos presentes en tu entorno. 3. Define qué es un Newton. __________________________________________________________________________________________ __________________________________________________________________________________________ 4. ¿Cómo se denomina el dispositivo o aparato con el que podemos determinar la magnitud de una fuerza? __________________________________________________________________________________________ __________________________________________________________________________________________ 5. ¿Qué efectos podemos observar en un cuerpo que experimenta una fuerza? __________________________________________________________________________________________ __________________________________________________________________________________________ Tipo de fuerza Cuerpos u objetos ACTIVIDAD 1 SD1-B1
- 18. 16 C O L E G I O D E B A C H I L L E R E S D E L E S T A D O D E S O N O R A Desarrollo ¿Qué es fuerza? El concepto de fuerza se originó debido a las actividades o acciones que el hombre ha desarrollado a través del tiempo, con los cuerpos u objetos presentes en su entorno. Todo cuerpo físico en estado de reposo o movimiento ejerce acciones entre todos los cuerpos que le rodean. Por ejemplo, una bola de boliche en movimiento derrumbará los pinos (figura 1); en tanto que un anuncio “jalará” hacia abajo el tirante que le sostiene (figura 2). Las acciones entre los cuerpos siempre son mutuas, por lo que a éstas se les llama interacciones. Es importante señalar que cuando un cuerpo actúa sobre otro, siempre experimentará la acción del cuerpo sobre el cual actúa. Como podemos observar, para poder hablar de la existencia de una fuerza, se debe suponer la presencia de dos cuerpos. Dicho de otra manera, si se observa que sobre un cuerpo actúa una fuerza, entonces se puede decir que en algún lugar, hay otro u otros cuerpos que constituyen el origen de esa fuerza. Un cuerpo no puede ejercer fuerza sobre sí mismo. El concepto físico que explica estas acciones mutuas entre los cuerpos, se denomina fuerza; la cual se define como “todo agente capaz de modificar el estado de reposo o de movimiento de un cuerpo y/o una deformación en éste”. Lo anterior significa, que cuando un cuerpo recibe una fuerza, puede experimentar: Solamente un cambio en su estado de reposo o movimiento. Solamente un cambio físico o deformación. O bien, pueden ocurrir de manera simultánea estos dos efectos antes descritos, como por ejemplo, cuando se golpea un cuerpo sólido, en este caso, se puede adquirir un cambio en su estado de movimiento y también una deformación.
- 19. T E M A S S E L E C T O S D E F Í S I C A 1 Aplicas la estática BLOQUE 1 17 Los cuerpos sólidos se clasifican en dos grupos: deformables y no deformables. Sólidos deformables: Son aquellos que se deforman al aplicarles una fuerza. Se clasifican en dos grupos: a) Cuerpos plásticos: se deforman por la acción de una fuerza y no recuperan su forma inicial al dejar de actuar dicha fuerza, como por ejemplo la plastilina y cera. b) Cuerpos elásticos: se deforman por la acción de una fuerza, pero recuperan su forma inicial cuando deja de actuar la fuerza, como por ejemplo, las gomas elásticas. Sólidos no deformables: se llaman también sólidos rígidos, si las fuerzas que actúan son muy grandes se pueden romper. La magnitud de las fuerzas se miden con un aparato llamado dinamómetro. Este dispositivo, consta de un resorte con una escala graduada, en la cual se registra el valor correspondiente a la deformación producida por el efecto de una fuerza aplicada. Unidades de fuerza: las unidades de medición de la magnitud de la fuerza en cada uno de los sistemas de unidades se presentan a continuación: MKS O SI CGS Inglés Newton (N) Dina Lbf La equivalencia entre estas: 1N=0.225 lb 1Lb=4.45 N 1N=1X105 dn 1Dn=1X10-5 N Existen fuerzas que actúan por contacto entre el cuerpo que produce la fuerza y el que la recibe. Otras veces, las fuerzas se aplican a distancia. Fuerzas de contacto: son aquellas que se presentan cuando dos o más cuerpos, se encuentran en contacto físico. Se identifican porque son de naturaleza electromagnética. Entre estas podemos mencionar las siguientes fuerzas: normal, tensión, fricción y elástica. A continuación se detallan las principales características de cada una de ellas. Fuerza normal: es una fuerza que ejerce una superficie sobre un cuerpo que se encuentra apoyado en ella. Su dirección es perpendicular a la superficie de apoyo y su sentido es hacia afuera.
- 20. 18 C O L E G I O D E B A C H I L L E R E S D E L E S T A D O D E S O N O R A Esta fuerza no tiene una expresión general a partir de la cual podemos calcular directamente su magnitud, sin embargo se puede deducir a partir de la segunda ley de Newton. Es importante que para el cálculo de ésta realices el diagrama de cuerpo libre (DCL), como lo aprendiste en el curso de física 1. Por ejemplo en el esquema anterior, el DCL para los cuerpos A y B, que descansan en una superficie horizontal es: Para el cuerpo C, que descansa sobre una superficie inclinada, el DCL correspondiente es: Fuerza de fricción o de rozamiento: la fuerza de fricción se presenta cuando dos cuerpos están en contacto. Dicha fuerza es paralela o tangente a las dos superficies y, actúa de tal modo, que se opone al movimiento relativo de ambas superficies. La magnitud de la fuerza que actúa sobre la superficie o la fuerza normal en cada caso es igual a la magnitud del peso de los cuerpos que allí se apoyan, pero en sentido contrario. En estos casos la normal se calcula, tomando en cuenta que W=N. El peso del cuerpo se descompone en dos componentes Px y Py. La magnitud y dirección de la fuerza normal, N es igual a Py, pero en sentido contrario.
- 21. T E M A S S E L E C T O S D E F Í S I C A 1 Aplicas la estática BLOQUE 1 19 Las fuerzas de fricción existen no sólo cuando hay un movimiento relativo, sino también cuando uno de los cuerpos tan sólo tiende a deslizarse sobre el otro. Por ejemplo, cuando se aplica una fuerza sobre un cuerpo, que se encuentra en reposo sobre una superficie horizontal; el bloque no se mueve, debido a la acción de la fuerza de fricción estática (Fe); sin embargo, al ir aumentando la magnitud de dicha fuerza, llega un momento en el que el cuerpo se pone en movimiento; a esta fuerza de fricción ejercida por la superficie horizontal que mueve el bloque se le llama fuerza de fricción cinética o dinámica (Fk). Una vez que el cuerpo empieza a moverse, la fuerza de fricción cinética o dinámica es menor que la fuerza de fricción estática. La magnitud de la fuerza de rozamiento entre dos cuerpos en contacto, es proporcional a la normal entre los dos cuerpos, es decir: F = µ·N Donde: µ= coeficiente de fricción. N= Fuerza Normal. Existen dos coeficientes de rozamiento: el estático (µe) y el cinético (µk ), siendo el primero mayor que el segundo: µe > µk Por lo tanto, matemáticamente podemos calcular la fuerza de fricción estática y la fuerza de fricción cinética con las siguientes formulas: Fk = µk·N Fricción cinética Fe = µe·N Fricción estática
- 22. 20 C O L E G I O D E B A C H I L L E R E S D E L E S T A D O D E S O N O R A Las fuerzas de fricción presentan las siguientes características: · Presentan sentido opuesto al movimiento de los cuerpos. · La dirección de la fuerza es paralela a la superficie de contacto. · Es independiente del tamaño del área de contacto entre las superficies. · Dependen de la naturaleza, de las superficies de contacto. Fuerza de Tensión:Es la fuerza aplicada por un cuerpo de masa despreciable e inextensible, sobre otro cuerpo para mantenerlo en equilibrio. Estas fuerzas se originan en objetos, tales como varillas, cables, alambres o cuerdas equilibrando las fuerzas externas aplicadas en sus extremos oponiéndose al alargamiento de los mismos. Las cuerdas, por ejemplo, permiten transmitir fuerzas de un cuerpo a otro. Las fuerzas de tensión son en definitiva, cada una de estas fuerzas que soporta la cuerda sin romperse. Fuerza de Elasticidad: La fuerza elástica es ejercida por objetos tales como resortes que tienen una posición normal, fuera de la cual almacenan energía potencial y ejercen fuerzas. Todo cuerpo elástico (por ejemplo, una cuerda elástica) reacciona contra la fuerza deformadora para recuperar su forma original. Esta fuerza, según la ley de Hooke, es proporcional a la deformación producida, por lo tanto, dicha fuerza deformadora tiene la misma magnitud y dirección, pero su sentido es contrario. Esta ley, matemáticamente se expresa: F= -kx Donde: F= Fuerza elástica. k= Constante elástica (o recuperadora) del resorte. x= deformación.
- 23. T E M A S S E L E C T O S D E F Í S I C A 1 Aplicas la estática BLOQUE 1 21 En equipo de tres integrantes, recuperen del módulo de física 1 u otras fuentes recomendadas por su maestro; información de los temas de fuerza normal y fuerza de fricción, que les refuerce y apoye en la resolución de los siguientes problemas. Esta actividad formará parte de tu Portafolio de Evidencias. 1. Un cuerpo de 4 kg descansa sobre una superficie horizontal. Determinen la fuerza normal que ejerce la superficie sobre este (incluyan DCL). 2. En una superficie horizontal, descansa un baúl de 50 N de peso, para que éste comience a moverse, se necesita una fuerza horizontal de 10 N. Después de que se inicia el movimiento, basta una fuerza de 5 N para que el baúl siga moviéndose con una velocidad constante. Calculen los coeficientes de fricción estática y cinética debidos a la interacción entre la superficie y el baúl. 3. Un cuerpo de 40 lb de peso, es jalado hacia la derecha con velocidad constante, con una fuerza F a 30° respecto al plano horizontal. Calculen la magnitud de la fuerza F, si el coeficiente de fricción cinética es de 0.2 (incluyan DCL). 4. Un bloque de 30 N se desliza sobre una tabla al existir un coeficiente de fricción cinético de 0.4. Determinen el valor de la fuerza que se debe aplicar al bloque, para que se mueva con una velocidad constante cuando la tabla forme un ángulo de 20° respecto al plano horizontal (incluyan DCL). ACTIVIDAD 2 SD1-B1
- 24. 22 C O L E G I O D E B A C H I L L E R E S D E L E S T A D O D E S O N O R A Fuerzas a distancia: Son aquellas que ejercen los cuerpos sin la necesidad de entrar en contacto. En este grupo, encontramos las fuerzas: gravitacional, eléctrica, magnética, nuclear débil y nuclear fuerte, etc. A continuación, se describen las principales características de éstas: Fuerza gravitatoria: Es la fuerza ejercida por la acción entre objetos debido a sus masas. También se le define como la fuerza que ejercen todos los planetas sobre los cuerpos que están en su superficie y que determina su peso. La gravedad es lo que causa que los objetos caigan, que los planetas giren alrededor del sol, que las galaxias se mantengan juntas. La fuerza gravitatoria siempre es atractiva, ya que todos los cuerpos atraen gravitacionalmente a otros. Fuerza eléctrica: Esta fuerza se presenta entre cargas eléctricas. La acción de dichas cargas, provoca una interacción electrostática a partir de la cual, se producen naturalmente fuerzas de atracción o repulsión, dando origen al campo electrostático. La fuerza que mantiene los electrones en órbita alrededor del núcleo, se conoce como eléctrica. La dirección de esta fuerza cuando las cargas interaccionan entre sí, está dado por la ley de las cargas: Cargas iguales se repelen entre sí, y cargas diferentes se atraen entre sí. En la naturaleza constantemente se presentan fuerzas eléctricas repulsivas y atractivas, ya que las partículas eléctricas interaccionan espontáneamente con otros cuerpos eléctricos cercanos. Fuerza magnética: La definición de fuerza magnética,se refiere a la distribuciónde las fuerzas electromagnéticas, debido al movimiento de las cargas que se mantienen en movimiento. Estas fuerzas surgen cuando se mueven partículas cargadas, tal como ocurre con los electrones. En el caso de los imanes, el movimiento produce líneas de campo magnético que salen y vuelven a entrar al cuerpo generando el magnetismo. La fuerza magnética se dirige de un polo hacia otro. Cada polo es un punto donde convergen las líneas de fuerza magnética, y cuando dos imanes se acercan, ésta fuerza genera una atracción entre ambos, siempre que los polos sean opuestos, en cambio, si los polos tienen la misma polaridad, los imanes experimentarán una fuerza de repulsión entre sí. Un ejemplo de fuerza magnética se halla en la brújula, cuya aguja imantada siempre señala el norte magnético.
- 25. T E M A S S E L E C T O S D E F Í S I C A 1 Aplicas la estática BLOQUE 1 23 Fuerza nuclear fuerte: está fuerza mantiene unidos a los protones en el núcleo, a pesar de la fuerza de repulsión eléctrica, se caracteriza por ser un centenar de veces más intensa que la fuerza electromagnética y gracias a ella los nucleones (protones y neutrones) permanecen unidos. Algunas características importantes de estas fuerzas; se mencionan enseguida: a) Presentan un alcance infinito. b) Son de muy corto alcance (radio de acción es menor que una billonésima de milímetro. 10-13 mm, ligeramente menor que el tamaño del núcleo) c) No interactúa con otros núcleos cercanos. Si un núcleo atómico es bombardeado con un haz de neutrones, gana neutrones adicionales y se hace más grande. Llega un momento en que la fuerza nuclear fuerte no tiene el alcance suficiente para mantener al núcleo unido. Como resultado, el núcleo se parte en dos, generando una gran cantidad de energía. Fuerza nuclear débil: Está fuerza es importante en la velocidad de algunas reacciones nucleares, que ocurren en el universo. También, está presente en el origen de las explosiones volcánicas. El radio de acción de esta fuerza es exactamente igual al de la fuerza nuclear fuerte. A una distancia mayor, la intensidad de esta fuerza ya es despreciable. No obstante, aunque es sumamente débil, su existencia hace posible que el sol y las estrellas produzcan luz y energía
- 26. 24 C O L E G I O D E B A C H I L L E R E S D E L E S T A D O D E S O N O R A En equipo de tres integrantes, observen con atención la siguiente figura: Con base a la figura contesten los siguientes cuestionamientos, argumentando claramente cada una de sus respuestas. Fuente: Slisko (2010) 1. ¿Cómo se le llama a la fuerza existente entre los globos? __________________________________________________________________________________________ __________________________________________________________________________________________ 2. Es la fuerza existente entre el hilo y los globos. __________________________________________________________________________________________ __________________________________________________________________________________________ 3. Nombre de la fuerza que la tierra ejerce sobre cada uno de los globos. __________________________________________________________________________________________ __________________________________________________________________________________________ 4. Es la fuerza que el aire ejerce sobre cada uno de los globos. __________________________________________________________________________________________ __________________________________________________________________________________________ Interacción entre dos globos después de ser frotados con un pedazo de tela. ACTIVIDAD 3 SD1-B1
- 27. T E M A S S E L E C T O S D E F Í S I C A 1 Aplicas la estática BLOQUE 1 25 Fuerza resultante y fuerza equilibrante. Cuandodosomásfuerzasactúansobreelmismopuntodeunobjeto(aesteefecto,selellamafuerzasconcurrentes) se ejerce sobre éste finalmente, un efecto neto llamado Fuerza Resultante. Esta fuerza se define como la fuerza única, que produce el mismo efecto tanto en magnitud como en dirección, de las dos o más fuerzas concurrentes que actúan sobre dicho cuerpo. Por otra parte, la fuerza equilibrante, como su nombre lo dice, es la que equilibra a un sistema de fuerzas, tiene la misma magnitud y dirección que la Resultante, pero con sentido contrario. REACTIVOS DE CIERRE Consulta fuentes de información fidedignas o recomendadas por tu maestro e investiga ampliamente sobre las teorías de la unificación de fuerzas, que a continuación se enumeran. Esta actividad formará parte de tu Portafolio de Evidencias. 1. Teoría del campo unificado. __________________________________________________________________________________________ __________________________________________________________________________________________ __________________________________________________________________________________________ 2. Electrodébil. __________________________________________________________________________________________ __________________________________________________________________________________________ __________________________________________________________________________________________ 3. Superfuerza. __________________________________________________________________________________________ __________________________________________________________________________________________ __________________________________________________________________________________________ Cierre
- 28. 26 C O L E G I O D E B A C H I L L E R E S D E L E S T A D O D E S O N O R A Secuencia didáctica 2 Vectores Inicio De manera individual responde los siguientes cuestionamientos. 1. Define con tus propias palabras cantidad vectorial. __________________________________________________________________________________________ __________________________________________________________________________________________ __________________________________________________________________________________________ 2. Describe dos situaciones de tu vida cotidiana, donde hagas uso de cantidades vectoriales. __________________________________________________________________________________________ __________________________________________________________________________________________ __________________________________________________________________________________________ 3. Determina analíticamente las componentes del vector d=20m 37°. Componentes Magnitud Dx Dy 4. Calcula el desplazamiento total de un móvil que se desplaza 10 km al este y posteriormente 12 km al sur. ACTIVIDAD 1 SD2-B1
- 29. T E M A S S E L E C T O S D E F Í S I C A 1 Aplicas la estática BLOQUE 1 27 Desarrollo Un vector es todo segmento de recta dirigido en el espacio, que nos permite representar una magnitud vectorial. En otras palabras, un vector se refiere a aquellas cantidades físicas que para definirse completamente precisan de módulo (valor numérico y unidad de medida), dirección y sentido. A continuación, vamos a recordar los elementos de un vector antes vistos en el curso de física 1. A) Origen o punto de aplicación: es el punto exacto sobre el cual actúa el vector. B) Módulo: corresponde a la magnitud o tamaño del vector. C) Dirección: es el ángulo medido desde el plano horizontal hasta la posición del vector. D) Sentido: se refiere a la orientación del vector. Los vectores se representan gráficamente mediante un segmento de recta a escala en un eje de coordenadas. Vectores unitarios. Un vector unitario es aquel que tiene una magnitud igual a uno y no tiene dimensiones. Se utiliza solamente para especificar una dirección determinada, ya que no tiene ningún otro significado físico. En un sistema de coordenadas rectangulares es común utilizar los símbolos especiales i, j y k^ para representar vectores unitarios en las direcciones y sentidos positivos de los ejes X, Y y Z, respectivamente. Por tanto, los vectores unitarios i^, j^ y k^, forman un conjunto de vectores perpendiculares entre sí, tal como se aprecia en la siguiente figura: Estos vectores i^, j^ y k^, no necesariamente se localizan en el origen del sistema de coordenadas, ya que como todo vector, se pueden trasladar a cualquier lugar en el espacio de las coordenadas, siempre y cuando conserven la misma dirección y sentido respecto a los ejes coordenados. Así pues, las componentes rectangulares de un vector a en función de los vectores unitarios, se expresan de la siguiente manera: Ax = Ax i^ Ay = Ay j^ Az = Az k^ Estos componentes representan respectivamente la magnitud de la componente en X, en Y y en Z, toda vez que como ya señalamos, la magnitud de cada vector unitario es igual a la unidad, es decir: i = j= k= 1.
- 30. 28 C O L E G I O D E B A C H I L L E R E S D E L E S T A D O D E S O N O R A Operación con vectores. Existe una variedad de operaciones que combinan vectores con vectores o vectores con escalares, pero solo a partir de las cuatro operaciones que se presentan en la siguiente tabla, se aplican las Leyes de Newton. Operación Definición Vector + Vector Es sumar componente con componente para obtener un nuevo vector de dos componentes. Vector – Vector Es restar componente con componente para obtener un nuevo vector de dos componentes. Vector * Escalar Es multiplicar cada una de las componentes del vector por el escalar. Vector Escalar Es dividir cada una de las componentes del vector por el escalar. A continuación analizaremos con mayor detalle estas operaciones. Suma y resta de vectores. La suma y resta de vectores se realizan de forma gráfica y analíticamente. Estas operaciones, matemáticamente se resumen de la siguiente manera: a ± b = <a1 ± b1 ,a2 ± b2 > Para sumar o restar gráficamente dos vectores, es necesario primeramente trazarlos a la misma escala. Posteriormente, se realiza la operación correspondiente, a partir del método del triángulo o del método del paralelogramo. El procedimiento en cada caso se muestra en la siguiente figura. Cuando se suman más de dos vectores, igualmente deben trazarse a la misma escala, aplicando el método del polígono, como se observa en la figura que a continuación se muestra. Cuando sumamos vectores analíticamente, se utilizan el método de las ortogonales (también conocido como analítico) y la Ley de los Cosenos.
- 31. T E M A S S E L E C T O S D E F Í S I C A 1 Aplicas la estática BLOQUE 1 29 Método de las ortogonales. A continuación se te presentan de manera resumida los cálculos o procedimientos a desarrollar a partir de este método. Cálculo Fórmula Componentes rectangulares Componente X A * Cos θ Componente Y A * Sen θ Magnitud del vector Resultante (R) R= Rx2 + Ry2 Dirección del vector resultante (θ) Θ= Tan- 1 Ry Rx Ejercicio 1. Un perro que busca un hueso camina 3.5 metros hacia el sur, después 8.2 metros en un ángulo de 30 0 al Noreste y finalmente 15 metros al Oeste. Encontrar la magnitud y dirección del vector de desplazamiento resultante que desarrolla el perro. Los vectores descritos en el texto son: A = 3.5 m 270° B = 8.2 m 30° C= 15 m 180° Desarrollando los cálculos, de acuerdo a la tabla anterior: Vector X (Cos θ ) Y (Sen θ ) A 0 -3.5 B 7.1 4.1 C -15 0 ƩR ƩRx= - 7.9 ƩRy= 0.6
- 32. 30 C O L E G I O D E B A C H I L L E R E S D E L E S T A D O D E S O N O R A R= (-7.9)2 + (0.6)2 R= 7.92 m Θ = Tan- 1 Ry Rx Θ = Tan- 1 0.6 -7.9 R= 7.92 m 4.34° Ejercicio 2. Determinar la magnitud y dirección del vector resultante al sumar los siguientes vectores. Los vectores presentes en el esquema son: A = 3 N 90° B= 3 N 25° C= 4 N 0° D= 2 N 220° Desarrollando los cálculos correspondientes: Vector X (Cos θ ) Y (Sen θ ) A 0 2.5 B 2.7189 1.2678 C 4 0 D -1.532 -1.2856 ƩR ƩRx= 5.1869 ƩRy= 2.4822
- 33. T E M A S S E L E C T O S D E F Í S I C A 1 Aplicas la estática BLOQUE 1 31 De manera individual suma los vectores de los ejercicios anteriores por el método del polígono: Ejercicio 1. Ejercicio 2. Describe los resultados que obtuviste con respecto a los calculados anteriormente: _________________________________________________________________________________________ _________________________________________________________________________________________ _________________________________________________________________________________________ _________________________________________________________________________________________ __________________________________________________________________________________________ R= (5.1869)2 + (2.4822)2 R= 5.75 N Θ = Tan- 1 Ry Rx Θ = Tan- 1 2.4822 5.1869 Θ = 25.6° Por lo tanto R= 5.75 N 25.6° ACTIVIDAD 2 SD2-B1
- 34. 32 C O L E G I O D E B A C H I L L E R E S D E L E S T A D O D E S O N O R A Para la resta de vectores por éste mismo, bastará expresar las componentes de los vectores y luego restarlas en lugar de sumarlas. Como por ejemplo, al restar los vectores A y B R = A – B Por lo que, se obtiene: RX = Ax – Bx Ry= Ay – By La resultante y la dirección se calculan igual que en la operación suma. Ley de los senos y cosenos. A continuación se presentan los cálculos y fórmulas correspondientes a este método. Cálculo Fórmula Resultante R= F1 2 + F2 2 – 2(F1 )(F2 )Cos β Dirección α (respecto al plano horizontal ) F1 = R Sen α Sen β Ejercicio 1. Calcular la magnitud y dirección de la magnitud resultante de los siguientes vectores:
- 35. T E M A S S E L E C T O S D E F Í S I C A 1 Aplicas la estática BLOQUE 1 33 R = 2344 + 1974.48 R 4318. 48 R = 65. 715 N En este caso, considerando que el ángulo β formado por los dos vectores es 150°. Analizando: Aplicamos la ley de los cosenos para encontrar la resultante. R = (F1 )2 + (F2 )2 – 2 (F1 ) (F2 ) cos β R = (30)2 + (38)2 – 2 (30) (38) cos 150° R = 900 + 1444 – 2 (30) (38) (-0.8660) Para calcular el ángulo α, que forma la resultante respecto al ángulo horizontal, aplicamos la ley de los senos. F1 = R Sen α Sen β α=sen-1 F1 *Sen β R α=sen-1 30 N(0.5) 65. 715 N α=13.2° Por lo tanto el valor de la resultante es: R = 65.715 N 13.2°
- 36. 34 C O L E G I O D E B A C H I L L E R E S D E L E S T A D O D E S O N O R A Ejercicio 2. Dos personas jalan, mediante dos cuerdas, un baúl de madera como se observa a continuación: Si una de las personas aplica una F1 de 300N con un ángulo de 18° respecto al este. Determinar la fuerza F2 que debe aplicar la otra persona ,y el ángulo que debe de formar respecto para que el baúl se desplace hacia el este con una fuerza resultante de 450N. Analizando las fuerzas aplicadas sobre el baúl: Por lo tanto aplicando la ley de los cosenos, calculamos la magnitud de la fuerza F2 R = (F1 )2 + (R)2 – 2 (F1 ) (R) cos 18° R = (300)2 + (450)2 – 2 (300) (450) (0.9511) R = 90,000 + 202,500 – 256,797 R = 35,703 R = 188.95 N
- 37. T E M A S S E L E C T O S D E F Í S I C A 1 Aplicas la estática BLOQUE 1 35 Enseguida calcularemos el ángulo α qué forma F2 , aplicando la ley de los senos. Multiplicación de vectores. Producto de un escalar por un vector. El producto de un escalar k por un vector r, se denota k * r, por lo que se define como un nuevo vector con una magnitud k veces mayor que la magnitud de r. Por ejemplo, suponiendo que: k=6 y r= 5N, tenemos, k * r= (6) (5N)= 30 N Como podemos ver el nuevo vector tiene el mismo sentido que r, si k es positivo. Pero, qué sucede si k es negativo: Si k=- 1 y r = 4 N, k * r= (-1) (4N)= - 4N Esto significa que el nuevo vector es opuesto al vector r, con la misma magnitud y dirección, pero con sentido contrario. Veamos a continuación un ejemplo a través de una gráfica. Suponiendo que las coordenadas del vector r = (2,3) y k = 2. Tenemos que: 2 r = (2.2, 2.3); entonces las coordenadas del nuevo vector son (4,6). En el caso de que k = - 2; tenemos: F1 = F2 Sen α Sen β α= sen-1 F1 * Sen 18° α= sen-1 300 N (0.3090) 188.95 N α= sen-1 0.4906 α= 29.4°
- 38. 36 C O L E G I O D E B A C H I L L E R E S D E L E S T A D O D E S O N O R A -2r = (-2.2, -2.3); las coordenadas del nuevo vector son (-4,6) De manera gráfica comprobamos lo antes mencionado. Producto escalar de dos vectores o producto punto. El producto escalar entre dos vectores se obtiene al multiplicar la magnitud de un vector por la componente perpendicular de otro vector en la dirección del primero. Esta operación da como resultado una magnitud escalar, ya que carece de dirección y sentido. a * b = ab Cos Θ El trabajo mecánico, la potencia eléctrica y la densidad de energía electromagnética, son ejemplos de magnitudes físicas que resultan a partir de esta operación. Ejemplo: Calcular el producto escalar de los siguientes vectores.
- 39. T E M A S S E L E C T O S D E F Í S I C A 1 Aplicas la estática BLOQUE 1 37 Producto vectorial de dos vectores o producto cruz. La magnitud del producto vectorial de dos vectores es igual a multiplicar la magnitud de un vector, por la componente perpendicular del otro respecto al primero. Como resultado, se obtiene un vector perpendicular al plano formado por los dos vectores que se multiplican. a * b = c a * b = ab sen Θ La multiplicación ab sen Θ nos proporciona únicamente la magnitud del vector c, por lo que si deseamos conocer su sentido se hará uso de la mano derecha que se describirá más adelante. Algunas magnitudes físicas que resultan de esta operación, son el momento de una fuerza, la fuerza que recibe una carga en movimiento al entrar en un campo magnético y la cantidad de movimiento angular. Ejemplo: calcular el producto vectorial de los siguientes vectores, así como el sentido del vector resultante. Como sabemos, la dirección del vector resultante es perpendicular al plano de F y d, pero el sentido del vector resultante se determina como mencionamos anteriormente, con la regla de la mano derecha, que continuación se explica: para determinar el sentido del vector resultante consideramos la dirección del vector resultante como si fuera un eje, alrededor de él, cerramos los dedos de la mano derecha con el pulgar extendido. Las puntas de los dedos señalarán el sentido de giro por el efecto de la fuerza, mientras que el pulgar indicará el sentido del vector resultante, en este caso hacía arriba, como se muestra en el esquema siguiente.
- 40. 38 C O L E G I O D E B A C H I L L E R E S D E L E S T A D O D E S O N O R A REACTIVOS DE CIERRE Esta actividad formará parte del portafolio de evidencias y se valorará con la rúbrica para evaluar serie de ejercicios, que se presenta al final del bloque. 1. Un avión vuela 200 km rumbo al oeste desde la ciudad A hasta la ciudad B y después 300 km en la dirección de 30 grados al noroeste de la ciudad B hasta la ciudad C. Determinar: a) ¿Qué tan lejos está la ciudad A de la ciudad C? b) ¿Cuál es la dirección de la ciudad C con respecto a la ciudad A? 2. Realizar las operaciones de suma y resta para los siguientes vectores. A= 10 N 0° B= 2 N 45° 3. Aplicando la ley de los cosenos y de los senos, determinar la magnitud y dirección del vector resultante en los ejercicios siguientes. a)
- 41. T E M A S S E L E C T O S D E F Í S I C A 1 Aplicas la estática BLOQUE 1 39 b) c) 4.- Calcula fuerza F2 y el ángulo (α) necesario, para que una lancha se mueva hacia el este con una fuerza resultante de 650 N, como se observa en la siguiente figura.
- 42. 40 C O L E G I O D E B A C H I L L E R E S D E L E S T A D O D E S O N O R A 5. Calcular el producto escalar de los vectores que se muestran a continuación: 6. Calcular el producto escalar de los vectores que se muestran a continuación:
- 43. T E M A S S E L E C T O S D E F Í S I C A 1 Aplicas la estática BLOQUE 1 41 Recursos adicionales para la secuencia didáctica 2 A continuación, se te proporcionan los siguientes recursos disponibles en internet que te permitirán retroalimentar los temas vistos en la secuencia didáctica 2. Tu prepa en videos: http://www.tuprepaenvideos.sep.gob.mx/ Ir a Bachillerato. Dar clic en Materias. Buscar Temas Selectos de Física I. Ir a la pestaña de Lecciones Buscar Bloque 1: Aplicas la estática. Los videos de pueden consultar en el sitio de Tu prepa en videos. Se recomienda los siguientes videos: 1) La importancia de los vectores. 2) Magnitud de vector. 3) Producto cruz entre vectores. 4) Ejemplo de la suma de vectores libres utilizando dos vectores. 5) Vectores por el método de las componentes.
- 44. 42 C O L E G I O D E B A C H I L L E R E S D E L E S T A D O D E S O N O R A Secuencia didáctica 3 Cuerpos en equilibrio Inicio En binas contesten los siguientes cuestionamientos y participen en la dinámica grupal que dirigirá su maestro. 1. ¿Qué significa equilibrio? __________________________________________________________________________________________ __________________________________________________________________________________________ __________________________________________________________________________________________ 2. ¿Qué entiendes por cuerpo rígido? __________________________________________________________________________________________ __________________________________________________________________________________________ __________________________________________________________________________________________ 3. Definan estática, cinemática y dinámica. __________________________________________________________________________________________ __________________________________________________________________________________________ __________________________________________________________________________________________ II. Realizar el diagrama de cuerpo libre de la siguiente figura. ACTIVIDAD 1 SD3-B1
- 45. T E M A S S E L E C T O S D E F Í S I C A 1 Aplicas la estática BLOQUE 1 43 Cuerpo rígido Un cuerpo rígido se define como un cuerpo ideal, cuyas partes (partículas que lo forman) tienen posiciones relativas fijas entre sí cuando se somete a fuerzas externas, es decir, es no deformable. Con esta definición se elimina la posibilidad de que el objeto tenga movimiento de vibración. Este modelo de cuerpo rígido es muy útil en muchas situaciones en las cuales la deformación del objeto es despreciable. El movimiento general de un cuerpo rígido es una combinación de movimiento de traslación y de rotación. En el siguiente bloque se analizarán más profundamente estos tipos de movimiento. A continuación se presenta un esquema de cuerpos que muestra estos movimientos Movimiento de traslación- Movimiento de rotación Para definir equilibrio, debemos recordar que las fuerzas concurrentes son todas las fuerzas cuyas líneas de acción pasan a través de un punto común. Las fuerzas que actúan sobre un objeto puntual son concurrentes porque todas ellas pasan a través del mismo punto u objeto puntual, como se observa en la siguiente figura. Por lo tanto, decimos que un objeto está en equilibrio bajo la acción de fuerzas concurrentes, siempre que esté en reposo o que su centro de masa se mueva con velocidad constante en relación con un observador en un marco de referencia inercial. Por definición, una partícula puede tener sólo movimiento de traslación. Si la resultante de las fuerzas que actúan sobre una partícula es cero, la partícula está moviéndose con velocidad constante o está en reposo; en este último caso se dice que está en equilibrio estático. Desarrollo Una roca de equilibrio es una formación geológica natural con una gran roca o peñasco, a veces de tamaño considerable, que descansa sobre otras rocas que a menudo buscan un equilibrio inestable. La imagen muestra una roca en Balanced Rock Park (EE.UU), una fehaciente prueba del equilibrio en la naturaleza, con más de 15 m de altura y 40 toneladas de peso. Esta roca esculpida por el viento se sostiene por un pedestal de solo un metro y 43 cm de extensión.
- 46. 44 C O L E G I O D E B A C H I L L E R E S D E L E S T A D O D E S O N O R A Pero el movimiento de un cuerpo rígido en general es de traslación y de rotación. En este caso, si la resultante tanto de las fuerzas como de las torcas que actúan sobre el cuerpo rígido es cero éste no tendrá aceleración lineal ni aceleración angular, y sí está en reposo estará en equilibrio estático. La descripción de este último tipo de movimiento es estudiado por la estática. Condiciones de equilibrio. Para que un cuerpo rígido esté en equilibrio estático se deben cumplir dos requisitos simultáneamente, llamados: condiciones de equilibrio. La primera condición de equilibrio, corresponde a la primera ley de Newton; a partir de esta ley se garantiza el equilibrio de traslación. Recordemos que la primera ley de Newton conocida también como ley de inercia, menciona; que si sobre un cuerpo no actúa ningún otro, este permanecerá indefinidamente moviéndose en línea recta con velocidad constante (incluido el estado de reposo, que equivale a velocidad cero). La segunda condición de equilibrio corresponde al equilibrio de rotación la cual se verá en la siguiente secuencia didáctica. Por lo tanto la primera condición de equilibrio se puede representar matemáticamente de la siguiente forma: 1ª condición de equilibrio (equilibrio de traslación): “Si un cuerpo se encuentra en equilibrio, entonces, la fuerza resultante que actúa sobre él es igual a cero”. Centro de gravedad. Cuando se analizan problemas con cuerpos rígidos se debe considerar la fuerza de gravedad o el peso del cuerpo. Debido a que un cuerpo es una distribución continua de masa, en cada una de sus partes actúa la fuerza de gravedad. El centro de gravedad es la posición donde se puede considerar actuando la fuerza de gravedad neta, es el punto ubicado en la posición promedio, donde se concentra el peso total del cuerpo. Para un objeto simétrico homogéneo; el centro de gravedad se encuentra en el centro geométrico, pero no para un objeto irregular. Centro de gravedad en cuerpo regular Centro de gravedad en cuerpo irregular ∑ F = 0 = F1 +F2 +⋯+Fn =0
- 47. T E M A S S E L E C T O S D E F Í S I C A 1 Aplicas la estática BLOQUE 1 45 Centro de masa. Es la posición geométrica de un cuerpo rígido, donde se puede considerar concentrada toda su masa y corresponde a la posición promedio de todas las partículas de masa que forman el cuerpo rígido. El centro de masa de cualquier objeto simétrico homogéneo, se ubica sobre un eje de simetría. Cuando se estudia el movimiento de un cuerpo rígido se puede considerar la fuerza neta aplicada en el centro de masa y analizar el movimiento del centro de masa, como si fuera una partícula. Cuando la fuerza es el peso, entonces se considera aplicado en el centro de gravedad. Para casi todos los cuerpos cerca de la superficie terrestre, el centro de masa es equivalente al centro de gravedad, ya que en éste, la gravedad es prácticamente constante. En otras palabras, si g es constante en toda la masa, el centro de gravedad coincide con el centro de masa como se observa en la figura siguiente. En forma individual realiza los siguientes diagramas de cuerpo libre (DCL). ACTIVIDAD 2 SD3-B1
- 48. 46 C O L E G I O D E B A C H I L L E R E S D E L E S T A D O D E S O N O R A Resolución de casos de equilibrio estático. Los elementos conceptuales y procedimentales analizados anteriormente, nos permiten resolver problemas en los que actúan diversas fuerzas. Mediante la aplicación de las condiciones de equilibrio se establecen diversas ecuaciones, a partir de las cuales se determinan magnitudes y direcciones de las fuerzas presentes en dichos problemas. Ejercicio 1. Una pelota de 200 N cuelga de una cuerda sostenida a otras dos cuerdas, como se observa en la siguiente figura. Con base a la figura, determinar ¿Cuál es la fuerza de tensión ejercida por las cuerdas A, B y C? Para la resolución de este problema es importante realizar primeramente el DCL. Las componentes “x” y “y” de cada vector calculadas a partir de la figura, se presentan en la siguiente tabla. Fuerza Θ Componente en x Componente en y A 120° Ax= A(cos 120°) = - 0.5 A Ax = A(sen 120°)= 0.8660 A B 45° Bx= B (cos 45°) = 0.7071 B Bx = B (sen 45°) = 0.7071 B C 270° Cx = 200 (cos 270°) = 0 Cx = 200 (sen 270°) = -200 Éstas pueden simplificarse por sustitución de funciones trigonométricas conocidas, o sea: - 0.5A + 0.7071 B = 0---------------------- (1) Se necesita más información para resolver esta ecuación. Obtenemos una segunda ecuación sumando las fuerzas a lo largo del eje y, lo que resulta es: 0.866A + 0.7071 B = 200 N --------------- (2) Ahora se resuelven simultáneamente las ecuaciones (1) y (2) para A y B, mediante el proceso de sustitución. Si se despeja A de la ecuación (1) se obtiene: A= (- 0.7071 B )/(- 0.5)=1.4142B -------------- (3) Ahora se sustituye esta igualdad en la ecuación (2) y se obtiene: 0.866 (1.4142 B) + 0.7071 B = 200 N que se utiliza para despejar B como sigue: 1.2247 B + 0.7071 B = 200 N 1.9318 B = 200 N B= (200 N)/1.9318=103.5304 N
- 49. T E M A S S E L E C T O S D E F Í S I C A 1 Aplicas la estática BLOQUE 1 47 Se puede calcular la tensión A sustituyendo B = 103.5304 N en la ecuación (3): A = 1.4142 B = 1.4142 ( 103.5304 N ) o A = 146.4127N Desde luego, la tensión en la cuerda C es 200 N, ya que debe ser igual al peso. Ejercicio 2. Un bloque de 200 N descansa sobre un plano inclinado sin fricción, que tiene una pendiente de 30°. El bloque está atado a una cuerda que pasa sobre una polea sin fricción colocada en el extremo superior del plano y va atada a un segundo bloque. ¿Cuál es el peso del segundo bloque si el sistema se encuentra en equilibrio? Para resolver este problema, es necesario realizar el DCL de cada bloque, como se observa en la siguiente figura: Posteriormente, se aplica la primera condición de equilibrio a cada diagrama para determinar el valor del peso suspendido W2. Para el peso suspendido, ΣFy = 0 O sea: T - W2 = 0 o T = W2 Puesto que la cuerda es continua y el sistema no está afectado por la fricción, la tensión T aplicada para el bloque de 200 N, también debe ser igual a W2. La letra “n” hace referencia a la fuerza normal. Fuerza Θ Componente x Componente y T 0° Tx = T = W2 Ty = 0 N 90° Fn x = 0 Fn y = n W1 240° W1x = 200 N cos 240° W1y = 200 N sen 240° Considerando el DCL para el bloque en un plano inclinado, determinamos las componentes de cada fuerza ejercida sobre él, como en la tabla anterior. Al aplicar la primera condición de equilibrio se obtiene: Σ Fx = 0: T + 200 N cos 240°= 0 -------------------(1) Σ Fy = 0: n + 200 N sen 240°= 0 -------------------(2) De la ecuación (1) obtenemos: T = - 200 N cos 240°= 100 N
- 50. 48 C O L E G I O D E B A C H I L L E R E S D E L E S T A D O D E S O N O R A Como la tensión T en la cuerda es igual al peso W2 se dice que se necesita un peso de 100 N para mantener el equilibrio. La fuerza normal que ejerce el plano sobre el bloque de 200 N se determina a partir de la ecuación (2), aunque este cálculo no fue necesario para determinar el peso W2 . Fn = - 200 N sen 240°= 173.2051 N En binas resuelve los siguientes problemas, incluye el DCL y el procedimiento completo para cada ejercicio. Esta actividad formará parte del portafolio de evidencias, y se valorará con la rúbrica para evaluar serie de ejercicios que se presenta al final del bloque. 1. Determinar las tensiones T1 y T2 , de las cuerdas que sostienen un peso de 600 N, a partir de la siguiente figura. T1 = 503 N, T2 =783 N 2. Suponiendo que W1 en la figura siguiente es de 500 N. Cierre ACTIVIDAD 2 SD3-B1
- 51. T E M A S S E L E C T O S D E F Í S I C A 1 Aplicas la estática BLOQUE 1 49 Calcular la magnitud de W2 y W3 , considerando que el sistema está en equilibrio. W2 =288 N, W3 = 384 N 3. Determinar las tensiones de las cuerdas que sostienen un peso de 600 N en la figura siguiente. R= 346 N, 346 N, 877 N, 877 N, 651 N 4. Se tira una batanga de 200 N con rapidez constante hacia arriba de un plano inclinado que forma un ángulo de 30° con la horizontal, como se observa en la siguiente figura. ¿Qué tan grande debe ser la fuerza paralela (F) al plano inclinado, si se desprecian los efectos de la fricción? F= 100 N
- 52. 50 C O L E G I O D E B A C H I L L E R E S D E L E S T A D O D E S O N O R A Recursos adicionales para la secuencia didáctica 3 A continuación, se te proporcionan los siguientes recursos disponibles en internet que te permitirán retroalimentar los temas vistos en la secuencia didáctica 3. Tu prepa en videos http://www.tuprepaenvideos.sep.gob.mx/ Ir a Bachillerato. Dar clic en Materias. Buscar Temas Selectos de Física I. Ir a la pestaña de Lecciones. Buscar Bloque 1: Aplicas la estática. Los videos de pueden consultar en el sitio de Tu prepa en videos o dando clic derecho sobre el video aparece la opción Obtener la URL del video, la cual es la que compartimos contigo. Se recomienda los siguientes videos: 1) Diagramas de cuerpo libre: Ejercicios resueltos (44:57) https://youtu.be/lmbe7sn39O8 2) Aplicaciones de la Primera Ley de Newton: Problema de equilibrio bidimensional (8:50) https://youtu.be/BCraIavQr0w?t=358
- 53. T E M A S S E L E C T O S D E F Í S I C A 1 Aplicas la estática BLOQUE 1 51 Secuencia didáctica 4 Momento de fuerzas Inicio De manera individual contesta los siguientes cuestionamientos. 1. Una cuerda pasa sobre una polea circular de 6.5 cm de radio. Si la polea da cuatro vueltas sin que la cuerda resbale, ¿qué longitud de cuerda pasará por la polea? __________________________________________________________________________________________ __________________________________________________________________________________________ 2. Supón que un compañero de tu clase de física comenta que un cuerpo rígido puede tener movimiento traslacional y rotacional al mismo tiempo. ¿Estarías de acuerdo? Si lo estás, anota dos ejemplos de estos. __________________________________________________________________________________________ __________________________________________________________________________________________ __________________________________________________________________________________________ __________________________________________________________________________________________ 3. ¿Para qué sirven las poleas y “tecles” (tackle en inglés)? __________________________________________________________________________________________ __________________________________________________________________________________________ 4.¿Qué se gana y qué se pierde cuando se utilizan palancas y poleas? __________________________________________________________________________________________ __________________________________________________________________________________________ __________________________________________________________________________________________ __________________________________________________________________________________________ ACTIVIDAD 1 SD4-B1
- 54. 52 C O L E G I O D E B A C H I L L E R E S D E L E S T A D O D E S O N O R A Desarrollo Momento de una fuerza. Como menciona Wilson y Bufa (2007), siempre es importante mantener el equilibrio, pero en algunas situaciones es imprescindible. Como vemos en la imagen superior, quizá nuestra primera reacción sea asombrarnos de que este acróbata atraviese amplias distancias y no se caiga. Se supone que la garrocha puede ayudarle, pero ¿cómo? Podríamos decir que el acróbata guarda equilibrio, ya que para no caer éste tendería a rotar hacia un lado en torno al alambre. Lo anterior, se explica con la condición de equilibrio rotacional, que estudiaremos en esta secuencia didáctica. El movimiento rotacional es muy importante en física, ya que infinidad de cuerpos experimentan este movimiento, como por ejemplo, las ruedas de automóviles, los engranes, las poleas, los planetas del sistema solar e incluso algunos huesos de nuestro cuerpo. Torca, momento de torsión o momento de fuerza. Bueche F. J. y Hecht E. (2007), definen a la torca como el momento de torsión o momento de fuerza ( ) alrededor de un eje, debida a una fuerza, como una medida de la efectividad de la fuerza para que ésta produzca una rotación alrededor de un eje. Matemáticamente, la torca expresa: Torca = τ = r F sen θ Donde r es la distancia radial desde el eje al punto de aplicación de la fuerza y θ es el ángulo agudo entre las direcciones de r y F, como se muestra en la figura siguiente Con frecuencia, esta definición se escribe en términos del brazo de palanca de la fuerza (a), que es la distancia perpendicular desde el eje a la línea de acción de la fuerza (b). Como el brazo de palanca, es igual a (r) (sen θ); la ecuación de la torca se reescribe como τ = (F) (brazo de palanca) La unidad de medida de la torca en el Sistema Internacional de unidades es metro∙Newton (m∙N), unidad que parece ser igual al Joule (J=N∙m), sin embargo, estas miden cantidades físicas diferentes. El Joule se utiliza para medir las cantidades escalares trabajo y energía; el momento de fuerza es una cantidad vectorial que se mide con las unidades m.N y lb.ft en el SI e inglés respectivamente.
- 55. T E M A S S E L E C T O S D E F Í S I C A 1 Aplicas la estática BLOQUE 1 53 La torca puede tener un valor positivo o negativo: es positivo cuando la rotación alrededor del eje es en sentido opuesto al movimiento de las manecillas del reloj y negativo cuando la rotación es en el mismo sentido en que se mueven las manecillas del reloj, como se muestra a continuación. Para ampliar la información, explicaremos el siguiente esquema, presentado en Harita (2012). Como podemos ver; en este DCL de una tabla de longitud L, que tiene un pivote (puede girar) en O; la tabla tiene su centro de gravedad a la mitad y es allí, donde actúa la fuerza de gravedad de su propio peso W hacia abajo. También actúan otras dos fuerzas hacia arriba, en los puntos A y B. Las tres fuerzas producen momentos de torsión (torcas). Las fuerzas en A y B tienden a hacer girar la tabla en sentido anti horario (contrario a las manecillas del reloj), por lo que sus momentos son positivos. El peso tiende a hacer girar la tabla en sentido horario (a favor de las manecillas del reloj), por lo que su momento es negativo. Se dice que las fuerzas “tienden a hacer girar la tabla” pero, como existe un equilibrio estático, la tabla no se mueve. Los casos en los que los objetos se mueven y giran son estudiados por la dinámica y la cinemática. Ejercicio 1. Considerando que se ejerce una fuerza de 250 N sobre un cable enrollado alrededor de un tambor de 120 mm de diámetro, como se muestra en la figura siguiente. Fuente: Tippens P. (2011). ¿A cuánto equivale el momento de torsión producido aproximadamente al centro del tambor? Como podemos observar, la línea de acción de la fuerza de 250 N es perpendicular al diámetro del tambor; por lo tanto, el brazo de palanca es igual al radio del tambor. Por lo que: r = D / 2 = 120 mm / 2 o r = 60 mm = 0.06 m
- 56. 54 C O L E G I O D E B A C H I L L E R E S D E L E S T A D O D E S O N O R A La magnitud del momento de torsión se obtiene a partir de la ecuación: τ = Fr = (250 N)(0.06 m) = 15.0 m∙N Finalmente, determinamos que el signo del momento de torsión es negativo porque tiende a causar una rotación en el sentido de las manecillas del reloj, por tanto, la respuesta debe escribirse como: τ = - 15.0 m∙N Ejercicio 2. Un mecánico ejerce una fuerza de 20 Ib en el extremo de una llave inglesa de 10 in, como se observa a continuación: Fuente: Tippens P. (2011). Si esta fuerza forma un ángulo de 60° con el mango de la llave, ¿cuál es el momento de torsión producido en la tuerca? Para resolver este problema, te recomendamos primeramente trazar un esquema ordenado, a partir del cual extiendas la línea de acción de la fuerza de 20 lb, después con base a la figura anterior, dibuja el brazo de palanca, tomando en cuenta que el brazo de palanca r es perpendicular tanto a la línea de acción de la fuerza como al eje de rotación. También debes de tener presente que el brazo de palanca es una construcción geométrica y puede estar o no sobre alguna estructura física, como el mango de la llave de tuercas. A partir de la figura, calculamos: r = (10 in) (sen 60°) = 8.66 in τ = Fr = (20 lb) (8.66 in) = 173.2 Ib • in Si se desea, este momento de torsión se puede transformar en 14.43 Ib • ft.
- 57. T E M A S S E L E C T O S D E F Í S I C A 1 Aplicas la estática BLOQUE 1 55 Ejercicio 3. Una pieza angular de hierro gira sobre un punto A, como se observa en la figura contigua. Determinar el momento de torsión resultante en A debido a las fuerzas de 60 N y 80 N, que actúan al mismo tiempo. Primeramente, calculamos la longitud de los brazos de palanca: r1 = (12 cm) (sen 50°) = 9.19 cm r2 = (10 cm) (sen 70°) = 9.40 cm Si se considera A como eje de rotación, el momento de torsión debido a F1 es negativo y el causado por F2 es positivo. El momento de torsión resultante se encuentra así: τ R = τ 1 + τ 2 = F1 r1 + F2 r2 = - (60 N)(9.19 cm) + (80 N)(9.40 cm) = - 551.4 N • cm + 752 N • cm = 200.6 cm∙N El momento de torsión resultante es 200.6 cm∙N , en contrasentido al avance de las manecillas del reloj. En el SI, está magnitud se expresa como 2.006 m∙N. Segunda condición de equilibrio. La segunda condición de equilibrio, corresponde al equilibrio de rotación cuyo enunciado establece: “la suma vectorial de todas las torcas externas que actúan sobre un cuerpo rígido alrededor de cualquier origen es cero”. Esto se resume matemáticamente: “Si un cuerpo se encuentra en equilibrio, entonces el momento de fuerza resultante que actúa sobre él es igual a cero”, como se ilustra a continuación.
- 58. 56 C O L E G I O D E B A C H I L L E R E S D E L E S T A D O D E S O N O R A Ejercicio 4. En la siguiente figura una niña y un niño de 300 N y 400 N de peso respectivamente, están parados sobre una plataforma de 200 N y sostenida por dos soportes A y B. Fuente: Tippens P. (2011). Calcular, qué fuerzas ejercen los soportes sobre la plataforma. Al aplicar la primera condición de equilibrio a las fuerzas verticales, obtenemos: Simplificando esta ecuación se obtiene: A + B = 900 N Puesto que esta ecuación presenta dos incógnitas, es preciso tener más información. Por tanto, aplicamos la segunda condición de equilibrio. Como la rotación no ocurre respecto a ningún punto, podemos elegir un eje de rotación en cualquier parte que deseemos. Una opción lógica sería elegir un punto donde actúe una de las fuerzas desconocidas porque así se tendría un brazo de palanca de cero. Tomemos la suma de los momentos de torsión respecto al soporte B. Por la segunda condición de equilibrio se obtiene: ∑ τ B = 0; - A(12 m) + (300 N)(10 m) + (200 N)(4 m) - (400 N)(4 m) = 0 Observa que la fuerza de 400 N y la fuerza A tienden a producir una rotación en el sentido de avance de las manecillas del reloj con respecto a B. (Sus momentos de torsión fueron negativos). Simplificando, se obtiene: - (12 m)A + 3000 N • m + 800 N • m - 1600 N • m = 0 Al añadir (12 m)A a ambos lados y simplificar queda: 2200 N • m = (12 m)A Al dividir ambos lados entre 12 m, resulta: A = 183.33 N Ahora, para determinar la fuerza ejercida por el soporte B, tomemos en cuenta de nuevo la ecuación obtenida a partir de la primera condición de equilibrio. A + B = 900 N ∑ Fy = 0; A + B - 300 N - 200 N - 400 N = 0
- 59. T E M A S S E L E C T O S D E F Í S I C A 1 Aplicas la estática BLOQUE 1 57 Al despejar B se obtiene: B = 900 N - A = 900 N - 183.33 N = 716.67 N Como comprobación de este resultado podemos elegir, el eje de rotación en A, y luego aplicar la segunda condición de equilibrio para determinar B. Ejercicio 5. Una viga metálica uniforme de longitud L pesa 200 N y sostiene un objeto de 450 N como se muestra en la figura contigua: Fuente: Bueche F. J. y Hecht E. (2007) Calcular la magnitud de las fuerzas que ejercen sobre la viga las columnas de apoyo colocadas en los extremos. Suponer que las longitudes son exactas. Para resolver este ejercicio, debemos tomar en cuenta que como la viga es uniforme, su centro de gravedad se localiza en su centro geométrico. Las fuerzas F1 y F2 son las reacciones de las columnas de apoyo sobre la viga. Como no existen fuerzas en la dirección x que actúen sobre la viga solamente hay que escribir dos ecuaciones para esta condición de equilibrio: Σ Fy = 0 y Σ τ = 0. +↑Σ F= 0 se convierte en F1 +F2 - 200 N - 450 N = 0 Antes de escribir la ecuación de la torca, se debe escoger un eje. Si se escoge en el punto A, de tal forma que la fuerza desconocida F1 pase por éste y no ejerza torca alguna. Entonces la ecuación de la torca es Al dividir la ecuación entre L y resolver para F2 , se encuentra que F2 = 437.5 N. Para calcular el valor de F1 , se sustituye el valor de F2 en la ecuación de las fuerzas y se obtiene F1 = 212.5 N Σ τ = -(L/2)(200 N)(sen 90°)-(3L/4)(450 N)(sen 90°)+(L)(F_2 )(sen 90°)=0
- 60. 58 C O L E G I O D E B A C H I L L E R E S D E L E S T A D O D E S O N O R A Ejercicio 6. Analiza el caso (a) de la siguiente figura. El poste es uniforme y pesa 800 N. Fuente: Bueche F. J. y Hecht E. (2007) Con esta información, calcular las fuerzas FT1 , FT2 y FT3. . Para resolver este problema, es necesario aplicar la condición de equilibrio al punto A. Entonces tenemos: FT2 cos 50.0° - 2 000 N = 0 y FT1 - FT2 sen 50.0° = 0 De la primera ecuación se encuentra FT2 =3.111 kN; y al sustituir en la segunda ecuación se obtiene F T1 = 2.383 kN. Posteriormente, se aplican las condiciones de equilibrio en el poste, para se recomienda analizar el esquema (C). La ecuación de la torca, para las torcas alrededor del punto C, es Al resolver para FT3 , se encuentra que tiene una magnitud de 9.84 kN. · Σ τ = +(L)(FT3 )(sen 20°)-(L)(3110 N)(sen 90°) + (L/2)(800 N)(sen 40°)=0
- 61. T E M A S S E L E C T O S D E F Í S I C A 1 Aplicas la estática BLOQUE 1 59 En equipo de cuatro integrantes respondan los siguientes problemas que se les plantean, anotando el procedimiento completo para cada uno de ellos. Fuente: Tippens P. (2011). Esta actividad formará parte del portafolio de evidencias y se considerará la guía de observación para valorar el trabajo en equipo, que se presenta al final del bloque. 1. Determina el momento de torsión resultante en el puntoAde la figura siguiente. Considerar despreciable el peso de la barra. R= 90 J 2. Una regla graduada de material uniforme se ha equilibrado en su punto medio sobre un solo punto de apoyo. Si una pesa de 60 N se cuelga en la marca de 30 cm. ¿En qué punto será necesario colgar una pesa de 40 N para equilibrar el sistema? R= En la marca de 80 cm 3. Consideren la barra ligera sostenida como se muestra en la siguiente figura. ¿Cuáles son las fuerzas que ejercen los soportes A y B? R: A = 50.9 N, 6 = 49.1 N ACTIVIDAD 2 SD4-B1 Cierre
- 62. 60 C O L E G I O D E B A C H I L L E R E S D E L E S T A D O D E S O N O R A 4. Considerando el esquema de la siguiente barra. ¿Cuáles deben ser las fuerzas F1 y F2 para que la barra permanezca en equilibrio? Considerar despreciable el peso de la barra. 5. Para mantener un hueso de la pierna roto en posición recta mientras sana, algunas veces se requiere tratamiento por extensión, que es el procedimiento mediante el cual se mantiene el hueso bajo fuerzas de tensión de estiramiento en ambos extremos para tenerlo alineado. Imagine una pierna bajo la tensión del tratamiento como en la figura presente. Considerando que el cordel está unido a una masa suspendida de 5.0 kg y pasa por una polea, con un ángulo de 40° respecto a la vertical. Ignorando la masa de la parte inferior de la pierna y de la polea, y suponiendo que todos los cordeles son ideales, determinar la magnitud de la tensión T en el cordel horizontal. T = 41 N
- 63. T E M A S S E L E C T O S D E F Í S I C A 1 Aplicas la estática BLOQUE 1 61 6. Considerando la figura siguiente. Determinar el peso del cuerpo suspendido, si la tensión de la cuerda diagonal es de 20 N. 7. La siguiente barra tiene un peso insignificante. Determinar las fuerzas F y A considerando que el sistema está en equilibrio. R: A = 26.7 N, F= 107 N 5. Determina la intensidad de la fuerza F4 , de la siguiente barra. Fuente:Harita (2012)
- 64. 62 C O L E G I O D E B A C H I L L E R E S D E L E S T A D O D E S O N O R A REACTIVOS DE CIERRE 1. Anota y describe dos situaciones en las que sea necesario disminuir los efectos de la fricción. __________________________________________________________________________________________ __________________________________________________________________________________________ __________________________________________________________________________________________ 2. Por qué las fuerzas de contacto, se les denomina fuerzas electromagnéticas. __________________________________________________________________________________________ __________________________________________________________________________________________ 3. Una pelota de softbol, y una de baloncesto ruedan desde el reposo en un plano inclinado. ¿Cuál llegará primero al punto final? Justifica tu respuesta. __________________________________________________________________________________________ __________________________________________________________________________________________ 4. ¿Cómo se pueden apilar tres ladrillos de manera que el de arriba tenga un desplazamiento horizontal máximo respecto al de abajo? Ejemplo, si los apilas como indican las líneas de puntos parece que quedarían inestables y se caerían. (Sugerencia: comienza por el ladrillo de arriba y avanza hacia abajo. En cada cambio de ladrillo, el centro de gravedad de los ladrillos acomodados arriba, no debe de sobresalir del extremo del ladrillo que los soporta).
- 65. T E M A S S E L E C T O S D E F Í S I C A 1 Aplicas la estática BLOQUE 1 63 Recursos adicionales para la secuencia didáctica 4 A continuación se te proporcionan los siguientes recursos disponibles en internet que te permitirán retroalimentar los temas vistos en la secuencia didáctica 4. Tu prepa en videos http://www.tuprepaenvideos.sep.gob.mx/ Ir a Bachillerato. Dar clic en Materias. Buscar Temas Selectos de Física I. Ir a la pestaña de Lecciones. Buscar Bloque 1: Aplicas la estática. Los videos de pueden consultar en el sitio de Tu prepa en videos o dando clic derecho sobre el video aparece la opción Obtener la URL del video, la cual es la que compartimos contigo. Se recomienda los siguientes videos: 1) Definición de Torque (35:00) https://youtu.be/qDlupqrk14U 2) Persona subiendo en una escalera https://youtu.be/TOyCoRzJRHo 3) Momento de una fuerza(7:27) https://youtu.be/4ltPJXTDLoM
- 66. 64 C O L E G I O D E B A C H I L L E R E S D E L E S T A D O D E S O N O R A ACTIVIDAD INTEGRADORA En equipo de cuatro integrantes aplicarán los conocimientos y habilidades adquiridos, para la resolución de situaciones problémicas de equilibrio estático de los cuerpos, analizados en el presente bloque a partir del desarrollo de la siguiente actividad experimental. El producto a entregar de esta actividad será un reporte de laboratorio, en el formato que tu maestro te indique. Titulo de la actividad: Equilibrio de fuerzas. Objetivo: Comprobar el equilibrio en un sistema de fuerzas. Material: 1. 3 soportes universal. 2. 1 Transportador. 3. 1 Pinzas de sujeción. 4. 1.5 m de hilo. 5. 1 Juego de pesas de diferente magnitud. 6. 2 Poleas fijas. 7. 1 Doble nuez. 8. Regla de 1 m. Procedimiento 1. Montar el diseño experimental como se muestra en el siguiente esquema: Nota: cerciórate utilizando el transportador, cerciórate que los ángulos estén corrcctamente medidos, utilizando el transportador. 1. Plantea el DCL del sistema de fuerzas y comprueba si el sistema está en equilibrio aplicando los métodos, leyes o procedimientos correspondientes. Consideren despreciable la fricción. 2. Varíen el peso de las pesas pueden utilizar los siguientes casos: a) W1 =W2 =W3 b) W1 =W2 W3 c) W1 W2 =W3 b) d) W1 W2 W3 e) W1 W3 =W2
- 67. T E M A S S E L E C T O S D E F Í S I C A 1 Aplicas la estática BLOQUE 1 65 Mediciones F1 F2 F3 FR 1 2 3 4 5 5. Presentación de resultados. Mediciones F1 F3 FR 1 2 3 4 5 Para cada uno de los casos, construir un polígono cerrado y comprobar los resultados por la ley de los senos y ley de los cosenos.
- 68. 66 C O L E G I O D E B A C H I L L E R E S D E L E S T A D O D E S O N O R A Rubrica para evaluar serie de ejercicios ELEMENTOS EXCELENTE BUENO REGULAR DEFICIENTE EJERCICIOS Presenta la totalidad de ejercicios o cuestionamientos a resolver. Entrega más del 80% de los ejercicios o cuestionamientos. Presenta más del 60% de los ejercicios o cuestionamientos a resolver. Presenta menos del 50% de los ejercicios o cuestionamientos. PROCEDIMIENTO Refleja un razonamiento detallado y ordenado, utilizando procesos de análisis y argumentación adecuada, para responder los ejercicios o cuestionamientos de manera correcta. Refleja un razonamiento sin orden puede realizar los ejercicios o cuestionamientos, pero no explica la manera en que los resolvió. Cuando los hace utiliza el proceso adecuado, siguiendo los pasos para resolver los ejercicios de manera correcta. Refleja un razonamiento sin orden puede realizar los ejercicios o cuestionamientos, pero no explica la manera en que los resolvió. Utiliza otro proceso obteniendo un resultado razonable. No refleja ningún razonamiento resuelve los ejercicios o cuestionamientos de manera mecánica o superficial. RESULTADOS Presenta el resultado obtenido a partir del análisis y argumenta de los ejercicios y es correcto. Puede corroborarlo dándole sentido. Presenta 80% ó más resultados correctos, comete algunos errores debido a cálculos o interpretaciones erróneas, utiliza el proceso adecuado y sigue los pasos para resolverlo. Presenta 60 % ó más resultados correctos, comete algunos errores debido a cálculos e interpretaciones erróneas. Presenta 50% o menos resultados correctos, no desarrolla análisis e interpretaciones apropiadas. Total 100% Puntaje 80% Puntaje 60% Puntaje 40% Puntaje
- 69. T E M A S S E L E C T O S D E F Í S I C A 1 Aplicas la estática BLOQUE 1 67 RÚBRICA DE EVALUACIÓN DE ACTIVIDAD INTEGRADORA Niveles de desempeño 5 (Excelente) 3 (Adecuado) 1 (Insuficiente) Introducción Introducción completa y bien escrita proporcionado un buen marco para contextualizar el experimento. Introducción básicamente completa, con omisión solo de algunos aspectos menores. Incorpora cierta información del marco del experimento, omitiendo algunos aspectos importantes. Marco Teórico Las fuentes información excelentemente integradas con el material práctico, coherente y de redacción. Lo presentado argumenta totalmente el tema. La mayoría de los conceptos están sustentados. Presentan alguna desconexión en la redacción y no están del todo claras respecto a lo desarrollado en el laboratorio. Algunos supuestos están evidenciados y justificados. Las citas se integran de modo deficiente, pobre o débil integración de fuentes secundarias. Metodología Se presentan todos los detalles del experimento. Se presentan todos los detalles importantes de la práctica de laboratorio, salvo omisiones menores. Se presentan algunos detalles experimentales importantes, con omisiones relevantes. Resultados Las tablas y esquemas están correctamente diseñados, numerados y titulados. Se comprende fácilmente la actividad desarrollada a partir de la presentación de los resultados. Las tablas y esquemas son en general correctos, aunque presentan algún problema menor que podría ser mejorado. La actividad desarrollada se comprende fácilmente, debido a imprecisiones menores. La mayor parte de las tablas y esquemas presentan errores de diseño, numeración y titulo; además carecen de información importante. Discusión Todos los resultados comparativos han sido interpretados y discutidos correctamente; por lo que se observa una excelente comprensión de la información planteada en los contenidos. Casi todos los resultados han sido interpretados y discutidos correctamente. Se identifican una mediana comprensión de la información planteada en los contenidos. Sólo algunos de los resultados han sido interpretados y discutidos correctamente. No se observa dominio de la información planteada en los contenidos. Conclusiones Se exponen con claridad y de manera coherente, cada uno de los aspectos teóricos relacionados con la actividad experimental. Se exponen con claridad y de manera coherente, solo algunos de los aspectos teóricos relacionados con la actividad experimental. Se exponen con poca claridad y de manera incoherente, la mayoría de los aspectos teóricos relacionados con la actividad experimental, Referencias Referencias bibliográficas completas y correctamente citadas de acuerdo a la metodología APA. Presenta la mayoría de las referencias bibliográficas citadas dentro del marco teórico. Presenta una bibliografía incompleta obviando algunas referencias obligatorias. Entrega El reporte fue entregado en tiempo y la forma solicitada. El reporte fue entregado en tiempo, pero no en la forma solicitada. El reporte no se entregó en tiempo ni en la forma solicitada. Total (Multiplicado por 0.5)
- 70. 68 C O L E G I O D E B A C H I L L E R E S D E L E S T A D O D E S O N O R A Guía de observación para valorar el trabajo en equipo DATOS INSTITUCIONALES GUÍA DE OBSERVACIÓN Unidad de Aprendizaje Nombre de la actividad Coevaluador: Nombre del docente 8. Participa y colabora de manera efectiva en equipos diversos. Atributos: a.1 Propone maneras de solucionar un problema o desarrollar un proyecto en equipo, definiendo un curso de acción con pasos específicos. a.2 Aporta puntos de vista con apertura y considera los de otras personas de manera reflexiva. a.3 Asume una actitud constructiva, congruente con los conocimientos y habilidades con los que cuenta dentro de distintos equipos de trabajo. Antes de iniciar las actividades en el grupo de trabajo, lean íntegramente esta guía de observación. Para cada integrante del equipo se valorarán cuatro aspectos, los integrantes evaluarán a cada uno de sus compañeros y marcarán con una “X” la casilla que consideren más adecuada con base en la siguiente escala: E= Excelente B= Bien NM= Necesita mejorar Nombre estudiante Escucha con respeto a sus compañeros. Se muestra tolerante ante los puntos de vista de sus compañeros. Su participación demuestra conocimientos y habilidades para la solución del problema. Contribuye para que la participación de los integrantes del grupo se dé en un clima de respeto. Integrante 1 E B NM E B NM E B NM E B NM Integrante 2 Integrante 3 Integrante 4 Escala Predomina las E: El estudiante desarrolló los atributos. Predomina las B: El estudiante está en proceso de desarrollo de los atributos. Predomina las NM: El estudiante aún no desarrolla los atributos.
- 71. T E M A S S E L E C T O S D E F Í S I C A 1 Aplicas la estática BLOQUE 1 69 RÚBRICA DE EVALUACIÓN DE PORTAFOLIO DE EVIDENCIAS Criterio/ Puntuación 4 3 2 1 Puntaje Portada Incluye logo y nombre de la institución, autor, curso, fecha y lugar donde fue elaborado. Falta un elemento en la presentación del trabajo. Faltan dos elementos en la presentación del trabajo. Carece de tres o más elementos para la correcta presentación del trabajo Objetivo El objetivo representa el aprendizaje obtenido y la razón por la cual se estructuran de esa forma las evidencias. El objetivo del portafolio considera sólo parcialmente los contenidos estudiados. El objetivo del portafolio no es congruente con los contenidos o lecciones estudiadas. No tiene objetivo explícito Evidencias Incluye todos los tipos de evidencias solicitadas. Las evidencias demuestran los avances en los aprendizajes esperados. Incluye la mayoría de las evidencias solicitadas. Sin embargo no todas las evidencias demuestran claramente el avance en los aprendizajes esperados. Incluye algunas de las evidencias solicitadas. Estas evidencias demuestran mínimamente el avance en los aprendizajes esperados. Incluye sólo uno o ninguna de las evidencias solicitadas, sin demostrar avance en los aprendizajes. Organización Todos los documentos están correctamente presentados. Constan de encabezado, son claros y limpios. A los documentos les falta algún elemento de la presentación. A los documentos les faltan más de dos elementos de presentación. El documento solo tiene un elemento o ninguno de presentación. Ortografía El portafolio de evidencias está elaborado sin errores ortográficos. Se observan hasta cinco errores ortográficos. Se observan de 6 a 10 errores ortográficos en el portafolio Se observan más de 10 errores ortográficos. Total
- 72. 70 C O L E G I O D E B A C H I L L E R E S D E L E S T A D O D E S O N O R A Reflexiones generales relacionados al Bloque I ¿Lograste comunicar tus ideas o puntos de vista al trabajar en equipo o en grupo? Nunca Muy pocas veces Frecuentemente Siempre ¿Tomaste en cuenta la participación de tus compañeros para modificar tus respuestas, tus acercamientos a los problemas, etc.? Nunca Muy pocas veces Frecuentemente Siempre ¿Lograste interpretar las ideas de tus compañeros al realizar alguna tarea o actividad de clase? Nunca Muy pocas veces Frecuentemente Siempre ¿Participaste activamente en las discusiones de equipo o grupales? Nunca Muy pocas veces Frecuentemente Siempre ¿Expresaste alguna forma de resolver los problemas formulados en las actividades a tus compañeros o al profesor? Nunca Muy pocas veces Frecuentemente Siempre ¿Usaste algún recurso tecnológico (software, internet, calculadoras, etc.) para apoyar tus actividades de tarea o de clase? Nunca Muy pocas veces Frecuentemente Siempre ¿Te entusiasma ayudar a tus compañeros o que ellos te ayuden a resolver dudas? Nunca Muy pocas veces Frecuentemente Siempre ¿Qué te pareció más interesante de este bloque? __________________________________________________________________________________________ __________________________________________________________________________________________ _________________________________________________________________________________________ __________________________________________________________________________________________ _________________________________________________________________________________________ __________________________________________________________________________________________ __________________________________________________________________________________________
- 73. ■ ■ Conoce y describe el comportamiento de la cinemática, aplicando los concep- tos de desplazamiento y velocidad an- gular, deduciendo la fuerza centrípeta y centrífuga en su entorno. ■ ■ Aplica los conceptos de movimiento de traslación y rotación, en forma apro- piada en la realización de actividades experimentales, atendiendo problemas relacionados con el movimiento que se efectúe. Tiempo asignado: 8 horas ■ ■ Movimiento de rotación y traslación. ■ ■ Diseña prototipos o modelos para de- mostrar la relación entre cantidades an- gulares y lineales, aplicando principios científicos relacionados con la fuerza centrípeta y centrífuga. ■ ■ Confronta las ideas preconcebidas acer- ca de los fenómenos naturales con el conocimiento científico para explicar las aplicaciones de la cinemática. ■ ■ Resuelve problemas establecidos o rea- les de su entorno, utilizando las ciencias experimentales para la comprensión y mejora del mismo. Desempeño del estudiante al finalizar el bloque Objetos de aprendizaje Competencias a desarrollar Describes la cinemática en tu entorno BLOQUE 2
- 74. 72 C O L E G I O D E B A C H I L L E R E S D E L E S T A D O D E S O N O R A ACTIVIDAD INTEGRADORA EVALUACIÓN DIAGNÓSTICA Alconcluirelpresentebloquedemostraráslosconocimientosyhabilidadespararesolverunasituaciónproblemática sobre el movimiento de rotación de los cuerpos. De manera individual responde los siguientes cuestionamientos. 1. ¿Cuál es la diferencia entre cinemática y dinámica? __________________________________________________________________________________________ __________________________________________________________________________________________ __________________________________________________________________________________________ 2. Menciona cuerpos presentes en tu entorno que experimentan movimientos de rotación y traslación. Rotación:___________________________________________________________________________ Traslación:_________________________________________________________________________________ 3. ¿Qué entiendes por cuerpo rígido? __________________________________________________________________________________________ __________________________________________________________________________________________ __________________________________________________________________________________________ 4. Menciona el beneficio de la aplicación de los movimientos rotación-traslación para nuestra vida cotidiana. __________________________________________________________________________________________ __________________________________________________________________________________________ __________________________________________________________________________________________
- 75. T E M A S S E L E C T O S D E F Í S I C A 1 Describes la cinemática en tu entorno BLOQUE 2 73 Secuencia didáctica 1 Movimiento de rotación y traslación Inicio ACTIVIDAD 1 SD1-B2 Responde de manera individual los siguientes cuestionamientos. 1. ¿Qué significa que un cuerpo ruede, pero no se deslice? __________________________________________________________________________________________ __________________________________________________________________________________________ __________________________________________________________________________________________ 2. Anota dos casos o situaciones de tu entorno en los que se experimenta el movimiento rotacional y traslacional a la vez. __________________________________________________________________________________________ __________________________________________________________________________________________ __________________________________________________________________________________________ 3. Menciona el beneficio para nuestra vida cotidiana, la aplicación de los movimientos rotación-traslación. __________________________________________________________________________________________ __________________________________________________________________________________________ __________________________________________________________________________________________ Desarrollo La cinemática es la parte de la mecánica que describe el movimiento de las partículas, cuerpos y sistema de cuerpos, sin considerar las causas que provocan dicho movimiento. La cinemática de cuerpos rígidos en particular, estudia la trayectoria de los puntos; líneas y otros objetos geométricos; así como las propiedades y relaciones existentes entre el tiempo, posición, velocidad y aceleración de las diferentes partículas que integran a dichos cuerpos.
- 76. 74 C O L E G I O D E B A C H I L L E R E S D E L E S T A D O D E S O N O R A Recordemos que un cuerpo rígido es un modelo idealizado, que considera a un cuerpo indeformable, es decir, con tamaño y forma perfectamente definidos e inmutables. Esto significa, que las posiciones relativas de las partículas que lo componen se mantienen constantes. En realidad los cuerpos no son rígidos, debido a que continuamente experimentan fuerzas que les provocan estiramientos o deformaciones. Sin embargo, el modelo antes descrito es de gran utilidad, en situaciones en las que la deformación es mínima o despreciable. Movimiento de rotación. Resnick, Halliday y Krane (2002), mencionan que un cuerpo rígido se mueve en rotación pura si todos sus puntos lo hacen en una trayectoria circular. El centro de estos puntos ha de estar en una línea recta común eje de rotación. En este movimiento, uno de los puntos se considera fijo, por tanto el único movimiento posible es aquel en el que cada uno de los otros puntos se mueve en la superficie de una esfera, cuyo radio es la distancia del punto móvil al punto fijo. Si se consideran dos puntos fijos, el único movimiento posible, es aquel en que todos los puntos a excepción de aquellos que se encuentran sobre la línea que une a los dos puntos fijos, conocida como eje se mueven paralelamente alrededor de éste.
- 77. T E M A S S E L E C T O S D E F Í S I C A 1 Describes la cinemática en tu entorno BLOQUE 2 75 Movimiento de traslación. Es el movimiento en el que todos los puntos de un cuerpo se mueven en la misma dirección, con la misma velocidad y la misma aceleración en cada instante. Es decir, cuando todas las partículas que forman el cuerpo rígido se mueven a lo largo de trayectorias paralelas. El movimiento de traslación del cuerpo rígido es como si toda su masa estuviera concentrada en el centro de masa y las fuerzas externas actuaran sobre él. Un cuerpo rígido experimenta traslación rectilínea o traslación curvilínea. En la primera se observa que las trayectorias del movimiento de dos partículas determinadas, forman líneas rectas equidistantes; mientras que en la segunda, las trayectorias entre partículas forman líneas curvas equidistantes como se observa en la siguiente figura. Cualquier movimiento en el plano diferente a la rotación y traslación, se denomina movimiento plano general. Muchos casos de este último movimiento, se presentan cuando un cuerpo determinado, exhibe una combinación de la rotación y traslación. La traslación ocurre dentro de un plano de referencia y la rotación sobre un eje perpendicular a dicho plano de referencia, como por ejemplo en los movimientos observados en la rodadura, en el desplazamiento de varillas y en los eslabones de mecanismo. Cuando un sólido rota, a la vez que se traslada realiza lo que se conoce como rodadura, es decir, que gira sin deslizar. En este caso que existe una condición entre la velocidad con la que se
- 78. 76 C O L E G I O D E B A C H I L L E R E S D E L E S T A D O D E S O N O R A traslada el centro de masa y la velocidad angular de rotación del sólido. Lo antes mencionado se explica a través de los siguientes esquemas: En una rodadura el punto de apoyo del sólido (por ejemplo, una esfera apoyada en un suelo horizontal) no sufre desplazamiento con respecto al suelo, o lo que es lo mismo está instantáneamente en reposo. A continuación se esquematiza el caso del desplazamiento de varillas y eslabones de mecanismos.
- 79. T E M A S S E L E C T O S D E F Í S I C A 1 Describes la cinemática en tu entorno BLOQUE 2 77 De manera individual atendiendo las instrucciones de tu maestro (a), realiza un mapa mental con la información que se te presenta en este bloque. Esta actividad formará parte de tu portafolio de evidencias y será valorada con la rúbrica, para evaluar mapa mental que aparece al final del bloque. ACTIVIDAD 2 SD1-B2 Algunos cuerpos que experimentan movimiento rotacional en nuestro entorno son por ejemplo: ruedas, ejes, esferas, cilindros, poleas, giroscopios, entre otros. En cinemática lineal los conceptos desplazamiento (Δx), velocidad (v), y aceleración (a), son de gran relevancia, ya que nos permiten hacer una descripción completa del movimiento de los cuerpos. Análogamente, en el movimiento rotacional esta descripción se da a partir de los conceptos: desplazamiento angular (Δϴ); velocidad angular (ω) y aceleración angular (α). Desplazamiento Angular (ϴ). Con base a la figura, el desplazamiento angular de un cuerpo se define como la cantidad de rotación de un cuerpo. Movimiento Circular Uniforme (MCU). El movimiento circular uniforme es el movimiento de un cuerpo cuando describe una circunferencia con rapidez constante. Periodo (T): Es el tiempo en que se demora un cuerpo en recorrer el perímetro de la circunferencia o en dar una vuelta completa. T = tiempo n° de vueltas
- 80. 78 C O L E G I O D E B A C H I L L E R E S D E L E S T A D O D E S O N O R A Frecuencia (f): Es el inverso del periodo y se define como el numero de vueltas que da el cuerpo en un periodo de tiempo. f = n° de vueltas tiempo Cuando el tiempo empleado es medido en segundos, la unidad de la frecuencia es s-1, el cual es llamado Hertz (Hz). Velocidad tangencial. Cuando un móvil describe un M.C.U. tiene una velocidad lineal que es tangente a la trayectoria. La magnitud de este vector (rapidez tangencial o rapidez lineal) se obtiene del cociente entre longitud o perímetro de la circunferencia y el tiempo que emplea el móvil en recorrerla. vl = longitud = 2πR Tiempo T Cuando tenemos movimientos rectilíneos de un cuerpo solo podemos tener cambios en la magnitud, pero ante un M.C.U., tenemos cambios en la dirección ya que el vector velocidad es siempre tangente a la trayectoria. Rapidez angular. El M.C.U., describirá ángulos iguales en intervalos de tiempo iguales. Podemos decir que ω (omega), es la rapidez angular y que es el ángulo barrido por unidad de tiempo. ω = ángulo tiempo Como el ángulo se mide en radianes, ω queda expresado en radianes/seg. Cuando el ángulo barrido corresponde a un ángulo de giro, es decir un giro completo el tiempo empleado corresponderá al periodo (T).
- 81. T E M A S S E L E C T O S D E F Í S I C A 1 Describes la cinemática en tu entorno BLOQUE 2 79 La velocidad tangencial y la angular se relacionan en forma sencilla: v = ω R Aceleración. Como consecuencia del cambio de dirección del vector velocidad aparece una aceleración. La aceleración media viene dada por Δv (el cambio de velocidad), y apunta hacia el centro de la circunferencia. Esta aceleración es llamada aceleración centrípeta (que busca el centro). Relación matemática para calcular la aceleración centrípeta. Un móvil se encuentra en un punto p1, como se muestra en la figura, cuando t = t1 y su vt será v1. Su posición con respecto al centro de la circunferencia será r1 En el punto p2 será t = t2, v t = v2 y su posición r2
- 82. 80 C O L E G I O D E B A C H I L L E R E S D E L E S T A D O D E S O N O R A Del gráfico podemos deducir que r1, r2 y Δr forman un triángulo isósceles con base en Δr. Al igual que v1, v2 y la base Δv. S la longitud de arco descrito. Si ambos triángulos son isósceles podemos decir que son congruentes y escribir: Si dividimos a ambos lados de la igualdad por Δt, queda: Δv/ Δt es la aceleración centrípeta y s/ Δt modulo de vt cuando P1 y P2 están tan próximos que sea casi igual Δr a S. Por lo tanto se concluye que: ac = v2 R Si el módulo de la velocidad tangencial y r son constantes entonces, para un movimiento circular uniforme, la aceleración centrípeta es constante. Si expresamos T en segundos (S.I.), y se define como el tiempo que demora un móvil en dar un vuelta completa y la frecuencia como el inverso de T entonces: Ejercicios: Un tren eléctrico da vueltas por una pista circular de 50 cm de radio con una velocidad constante de 10 cm/s. Calcula: a) la velocidad angular; b) la aceleración radial; c) el período y la frecuencia; d) número de vueltas que dará en 10 segundos. a)10 cm/s son 0,1 m/s; 50 cm son 0,5 m. Si despejamos ω de la fórmula obtenemos: ω = v/r = 0,1/0,5 ω=0,2 rad/s Vt = 2πR = 2πR * f T ωt = 2π = 2π * f T Vt = ω R ac = V2 = ω2 R R
- 83. T E M A S S E L E C T O S D E F Í S I C A 1 Describes la cinemática en tu entorno BLOQUE 2 81 b) La aceleración radial, o normal, es la fórmula: an = v²/r = 0,1²/0,5 = 0,02 m/s². c) Para el período aplicamos, T = (2 π)/ ω = (2 π)/ 0,2 = 10 π s. La frecuencia es la inversa del período: f = 1/T = 1/10 π = 0,032 ciclos/s. Cierre Resuelve los siguientes ejercicios, anotando el procedimiento desarrollado en cada uno de ellos. 1.¿Cuál es la velocidad angular de un punto dotado de M.C.U. si su período es de 1,4 s? ¿Cuál es la velocidad tangencial si el radio es de 80 cm? 2. Si un motor cumple 8000 R.P.M., determinar: a) ¿Cuál es su velocidad angular? b) ¿Cuál es su período?. 3. Un móvil dotado de M.C.U. da 280 vueltas en 20 minutos, si la circunferencia que describe es de 80 cm de radio hallar: a) ¿Cuál es su velocidad angular? b) ¿Cuál es su velocidad tangencial? c) ¿Cuál es la aceleración centrípeta? ACTIVIDAD 3 SD1-B2
- 84. 82 C O L E G I O D E B A C H I L L E R E S D E L E S T A D O D E S O N O R A Recursos adicionales para la secuencia didáctica 1 A continuación se te proporcionan los siguientes recursos disponibles en internet que te permitirán retroalimentar los temas vistos en la secuencia didáctica 1. Tu prepa en videos http://www.tuprepaenvideos.sep.gob.mx/ Ir a Bachillerato. Dar clic en Materias. Buscar Temas Selectos de Física I. Ir a la pestaña de Lecciones Buscar Bloque 2: Describes la cinemática en tu entorno. Se te recomiendan los siguientes videos: 1) Movimiento de rotación: definición. 2) Movimiento de rotación: cinemática y ejercicio resuelto. 3) Movimiento de rotación: relación entre el movimiento de rotación y movimiento circular uniforme. 4) Movimiento de rotación: aceleración angular constante. 5) Movimiento Circular Uniforme. 6) Movimiento Circular Uniforme: definición. 7) Movimiento Circular Uniforme: parte 1, parte 2 y parte 3. 8) Movimiento Circular Uniforme: aplicaciones a través de ejemplos.
- 85. T E M A S S E L E C T O S D E F Í S I C A 1 Describes la cinemática en tu entorno BLOQUE 2 83 ACTIVIDAD INTEGRADORA A partir de la siguiente actividad experimental, demostrarán sus conocimientos y habilidades para determinar la velocidad angular y periodo de un cuerpo en movimiento de rotación. Esta actividad formará parte del portafolio de evidencias y será valorada con la guía de observación para evaluar el trabajo en equipo. Movimiento de rotación: cálculo de velocidad angular y periodo Tomado de Soto, J. (2014) Material: • Una bicicleta infantil rodado 20. • Una bicicleta de montaña o de carreras. • 1 Cronómetro. • Cinta adhesiva. Procedimiento. 1. Coloque las bicicletas de manera que las llantas delanteras puedan moverse libremente. 2. Señalen con cinta adhesiva un “punto de rotación”, en cada una de las llantas delanteras. 3. Giren las llantas de acuerdo con la frecuencia señalada en la tabla 1. 4. Calculen la velocidad angular (w) y período (T). 5. Completen la tabla con los datos obtenidos. Resultados. Tabla 1. Velocidad angular y período de un cuerpo en rotación. Sentido Frecuencia (Rev/s) W (Rad/s) T (seg) Izquierda 1 2 3 4 Derecha 1 2 3 4
- 86. 84 C O L E G I O D E B A C H I L L E R E S D E L E S T A D O D E S O N O R A Contesten los siguientes cuestionamientos. 1. Expliquen con sus propias palabras qué es lo que sucede con la velocidad angular (W), si se aumenta la frecuencia. _________________________________________________________________________________________ _________________________________________________________________________________________ _________________________________________________________________________________________ 2. Expliquen con sus propias palabras lo que sucede con el período (T), si se disminuye la frecuencia. _________________________________________________________________________________________ _________________________________________________________________________________________ _________________________________________________________________________________________ 3. Expliquen con sus propias palabras lo que sucede con el período (T), si se aumenta la velocidad angular. _________________________________________________________________________________________ _________________________________________________________________________________________ _________________________________________________________________________________________ 4. Expliquen con sus propias palabras lo que sucede con la frecuencia (F), si se aumenta el período. _________________________________________________________________________________________ _________________________________________________________________________________________ _________________________________________________________________________________________
- 87. T E M A S S E L E C T O S D E F Í S I C A 1 Describes la cinemática en tu entorno BLOQUE 2 85 1. Explica cómo controla sus movimientos un clavadista para determinar si va a tocar primero el agua con los pies o con la cabeza. _________________________________________________________________________________________ _________________________________________________________________________________________ _________________________________________________________________________________________ 2. Considerando que una película dura dos horas, durante dicho intervalo, ¿cuál es el desplazamiento angular de la manecilla de las horas de un reloj de pared? ¿Cuál es el correspondiente al minutero y al segundero? _________________________________________________________________________________________ _________________________________________________________________________________________ _________________________________________________________________________________________ 3. La luna rota alrededor de su eje una vez cada 27.3 días y su radio es de 1.74X106 m. Determina: a) El período de rotación de la luna en segundos. _________________________________________________________________________________________ _________________________________________________________________________________________ b) La frecuencia de rotación de la luna en rad/seg. _________________________________________________________________________________________ _________________________________________________________________________________________ 4. Un motor eléctrico gira a 600 rpm. Calcula: a) Su velocidad angular (ω). _________________________________________________________________________________________ _________________________________________________________________________________________ b) Su desplazamiento angular (ϴ) después de 6 segundos. _________________________________________________________________________________________ _________________________________________________________________________________________
- 88. 86 C O L E G I O D E B A C H I L L E R E S D E L E S T A D O D E S O N O R A Rúbrica para evaluar serie de ejercicios Elementos Excelente Bueno Regular Deficiente EJERCICIOS Presenta la totalidad de ejercicios o cuestionamientos a resolver. Entrega más del 80% de los ejercicios a resolver. Presenta más del 60% de los ejercicios a resolver. Presenta menos del 50% de los ejercicios a resolver. PROCEDIMIENTO Refleja un razonamiento detallado y ordenado, utilizando el proceso adecuado, siguiendo los pasos para resolver los ejercicios de manera correcta. Refleja un razonamiento sin orden, puede hacer los ejercicios pero no explica la manera en que los resolvió. Cuando los hace utiliza el proceso adecuado, siguiendo los pasos para resolver los ejercicios de manera correcta. Refleja un razonamiento sin orden, puede hacer los ejercicios pero no explica la manera en que los resolvió. Utiliza otro proceso obteniendo un resultado razonable. No refleja ningún razonamiento, resuelve los ejercicios de manera mecánica. RESULTADOS Presenta el resultado obtenido de los ejercicios y es correcto. Puede corroborarlo dándole sentido Presenta 80% ó más resultados correctos, comete algunos errores debido a cálculos erróneos, utiliza el proceso adecuado y sigue los pasos para resolverlo. Presenta 60 % ó más resultados correctos, comete algunos errores debido a cálculos erróneos, y un proceso inadecuado, se salta los pasos para resolverlo. Presenta 50% o menos resultados correctos, no sigue el procedimiento adecuado. Total 100% Puntaje 80% Puntaje 60% Puntaje 40% Puntaje
- 89. T E M A S S E L E C T O S D E F Í S I C A 1 Describes la cinemática en tu entorno BLOQUE 2 87 Criterio Excelente Muy bien Bueno Regular Insuficiente Puntos 5 4 3 2 1 Enfoque El tema principal se presenta en el centro, de donde se desprenden las demás ramificaciones. El tema principal se presenta en el centro, utilizando una palabra o imagen con poca relación. El tema principal es presentado por una palabra en el centro, es difícil de identificar que se trata del tema principal, ya que no se presenta de forma enfatizada. El tema principal no se presenta en el lugar correcto y exhíbe poca relevancia. El tema principal no se presenta en el lugar correcto ni de forma enfatizada, por lo que no existe representación y organización de la información. Información La información presentada corresponde a la secuencias didáctica que conforma el bloque. La información presentada es completamente clara y precisa. La información presentada corresponde a la secuencia didáctica que conforma el bloque. La mayor parte de la información es clara y precisa. La mayor parte de la información corresponde a la presentada en la secuencia didáctica que conforma el bloque. Solo alguna parte de la información es clara y precisa. Sólo una parte de la información corresponde a la presentada en la secuencia didácticas que conforman el bloque. La información presenta errores y falta de claridad. La información presentada, no corresponde a la mostrada en la secuencia didáctica del bloque. Palabras claves Se manejan conceptos importantes, destacando y diferenciando las ideas principales de las secundarias por medio de colores diferentes, subrayados, recuadros u otras formas. Las palabras clave se destacan por medio de recuadros o colores. Sólo algunas palabras clave aparecen resaltadas para destacar su importancia. No se distinguen los conceptos principales de los secundarios, ya que presentan el mismo formato. Los conceptos no tienen ninguna relación con el tema, por lo que el mapa pierde su concordancia y relación con éste. RÚBRICA PARA EVALUAR EL MAPA MENTAL Alumno:____________________________________________________________ Grupo:_______
- 90. 88 C O L E G I O D E B A C H I L L E R E S D E L E S T A D O D E S O N O R A Organización Los elementos que componen el mapa mental, se encuentran organizados de forma jerárquica, con conectores que hacen fácil su comprensión. Los elementos o imágenes contenidas están organizados de forma jerárquica, pero los conectores no están del todo bien estructurados. Los elementos del mapa están poco dispersos, ya que no aparecen organizados según su relevancia. No hay organización de ideas, por lo que su comprensión es mínima. Los elementos están mal organizados, por lo que el mapa pierde sentido lógico, y no se puede comprender. Imágenes Las imágenes son nítidas y claras, además de que son representativas del concepto a comprender. Éstas aparecen colocadas como el movimiento de las manecillas de un reloj, según su importancia. Las imágenes son nítidas y claras, además de que son representativas del concepto a comprender, pero no están acomodadas correctamente. Las imágenes son nítidas, pero no están relacionadas con el tema y aparecen poco desordenadas. Las imágenes no se perciben completamente, aparecen de forma desordenada y con poca o sin relación con el tema. Las imágenes no presentan nitidez, aparecen de forma desordenada y sin relación con el tema, por lo que no se puede comprender la información que se desea presentar. Creatividad Se utilizan imágenes, trazos y colores diferentes en su elaboración, así como elementos decorativos, que le hacen ser más entendible atractivo y. Son utilizados diferentes imágenes, trazos, colores y elementos decorativos. Se exponen las ideas de forma original, por lo que se observa gran imaginación. Se puede caer en la exageración, evitando comprender la información. Contiene muy pocas imágenes, trazos, colores y elementos decorativos o son casi nulos, por lo que carece de imaginación y no permiten la comprensión total de la información que se desea transmitir. No contiene imágenes, colores, ni elementos decorativos o son casi nulos, por lo que la información que se pretende transmitir, no se comprende. Las imágenes, trazos, colores y elementos decorativos no tienen ninguna relación con el tema, por lo que el mapa pierde su creatividad y el objetivo para el que fue diseñado. Total
- 91. T E M A S S E L E C T O S D E F Í S I C A 1 Describes la cinemática en tu entorno BLOQUE 2 89 Guía de observación para valorar el trabajo en equipo DATOS INSTITUCIONALES GUÍA DE OBSERVACIÓN Unidad de Aprendizaje Nombre de la actividad Coevaluador: Nombre del docente 8. Participa y colabora de manera efectiva en equipos diversos. Atributos: a.1 Propone maneras de solucionar un problema o desarrollar un proyecto en equipo, definiendo un curso de acción con pasos específicos. a.2 Aporta puntos de vista con apertura y considera los de otras personas de manera reflexiva. a.3 Asume una actitud constructiva, congruente con los conocimientos y habilidades con los que cuenta dentro de distintos equipos de trabajo. Antes de iniciar las actividades en el grupo de trabajo, lean íntegramente esta guía de observación. Para cada integrante del equipo se valorarán cuatro aspectos, los integrantes evaluarán a cada uno de sus compañeros y marcarán con una “X” la casilla que consideren más adecuada con base en la siguiente escala: E= Excelente B= Bien NM= Necesita mejorar Nombre estudiante Escucha con respeto a sus compañeros. Se muestra tolerante ante los puntos de vista de sus compañeros. Su participación demuestra conocimientos y habilidades para la solución del problema. Contribuye para que la participación de los integrantes del grupo se dé en un clima de respeto Integrante 1 E B NM E B NM E B NM E B NM Integrante 2 Integrante 3 Integrante 4 Escala Predomina las E: El estudiante desarrolló los atributos. Predomina las B: El estudiante está en proceso de desarrollo de los atributos. Predomina las NM: El estudiante aún no desarrolla los atributos.
- 92. 90 C O L E G I O D E B A C H I L L E R E S D E L E S T A D O D E S O N O R A RÚBRICA DE EVALUACIÓN DE PORTAFOLIO DE EVIDENCIAS Criterio/ Puntuación 4 3 2 1 Puntaje Portada Incluye logo y nombre de la institución, autor, curso, fecha y lugar donde fue elaborado. Falta un elemento en la presentación del trabajo. Faltan dos elementos en la presentación del trabajo. Carece de tres o más elementos para la correcta presentación del trabajo. Objetivo El objetivo representa el aprendizaje obtenido, y la razón por la cual se estructuran de esa forma las evidencias. El objetivo del portafolio, considera sólo parcialmente los contenidos estudiados. El objetivo del portafolio no es congruente con los contenidos o lecciones estudiadas. No tiene objetivo explícito. Evidencias Incluye todos los tipos de evidencias solicitadas. Las evidencias demuestran los avances en los aprendizajes esperados. Incluye la mayoría de las evidencias solicitadas. Sin embargo, no todas las evidencias demuestran claramente el avance en los aprendizajes esperados. Incluye algunas de las evidencias solicitadas. Estas evidencias demuestran mínimamente el avance en los aprendizajes esperados. Incluye sólo uno o ninguna de las evidencias solicitadas, sin demostrar avance en los aprendizajes. Organización Todos los documentos están correctamente presentados: constan de encabezado, son claros y limpios. A los documentos les falta algún elemento de la presentación. A los documentos les faltan más de dos elementos de presentación. El documento solo tiene un elemento o ninguno de presentación. Ortografía El portafolio de evidencias está elaborado sin errores ortográficos. Se observan hasta cinco errores ortográficos. Se observan de 6 a 10 errores ortográficos en el portafolio. Se observan más de 10 errores ortográficos. Total
- 93. T E M A S S E L E C T O S D E F Í S I C A 1 Describes la cinemática en tu entorno BLOQUE 2 91 Reflexiones generales relacionados al Bloque II ¿Lograste comunicar tus ideas o puntos de vista al trabajar en equipo o en grupo? Nunca Muy pocas veces Frecuentemente Siempre ¿Tomaste en cuenta la participación de tus compañeros para modificar tus respuestas, tus acercamientos a los problemas, etc.? Nunca Muy pocas veces Frecuentemente Siempre ¿Lograste interpretar las ideas de tus compañeros al realizar alguna tarea o actividad de clase? Nunca Muy pocas veces Frecuentemente Siempre ¿Participaste activamente en las discusiones de equipo o grupales? Nunca Muy pocas veces Frecuentemente Siempre ¿Expresaste alguna forma de resolver los problemas formulados en las actividades a tus compañeros o al profesor? Nunca Muy pocas veces Frecuentemente Siempre ¿Usaste algún recurso tecnológico (software, internet, calculadoras, etc.) para apoyar tus actividades de tarea o de clase? Nunca Muy pocas veces Frecuentemente Siempre ¿Te entusiasma ayudar a tus compañeros o que ellos te ayuden a resolver dudas? Nunca Muy pocas veces Frecuentemente Siempre ¿Qué te pareció más interesante de este bloque? __________________________________________________________________________________________ __________________________________________________________________________________________ _________________________________________________________________________________________ __________________________________________________________________________________________ _________________________________________________________________________________________ __________________________________________________________________________________________ __________________________________________________________________________________________
- 94. 92 C O L E G I O D E B A C H I L L E R E S D E L E S T A D O D E S O N O R A
- 95. ■ ■ Conoce, identifica y analiza la aplicación de la cinética sobre cuerpos rígidos, re- lacionados con los movimientos de rota- ción y traslación, para resolver proble- mas de trabajo y potencia en diferentes circunstancias. Tiempo asignado: 22 horas ■ ■ Movimiento de cuerpos rígidos. ■ ■ Energía cinética rotacional. ■ ■ Trabajo y potencia rotacionales. ■ ■ Evalúa las implicaciones del uso de la energíacinéticaySegundaLeydeNewton, así como los fenómenos relacionados con los movimientos de rotación y traslación de cuerpos rígidos. ■ ■ Aplicalosavancescientíficosytecnológicos en el mejoramiento de las condiciones de su entorno social. ■ ■ Aplica la metodología apropiada en la solución de problemas relacionados con la cinética rotacional. ■ ■ Emplea prototipos o modelos, para resolver problemas y demostrar principios científicos, hechos o fenómenos relacionados con el movimiento de los cuerpos rígidos. ■ ■ Confrontaslasideaspreconcebidasacercade losfenómenosnaturalesconelconocimiento científico para explicar y adquirir nuestros conocimientos. ■ ■ Resuelve problemas establecidos o reales de su entorno, utilizando las ciencias experimentales para la comprensión y mejora del mismo. Desempeño del estudiante al finalizar el bloque Objetos de aprendizaje Competencias a desarrollar Analizas la cinética rotacional BLOQUE 3
- 96. 94 C O L E G I O D E B A C H I L L E R E S D E L E S T A D O D E S O N O R A ACTIVIDAD INTEGRADORA EVALUACIÓN DIAGNÓSTICA Al concluir el presente bloque mostrarás los conocimientos y habilidades adquiridos, a partir de la demostración de la conservación de energía mecánica en un cuerpo rígido que rueda sin deslizarse. De manera individual responde los siguientes cuestionamientos. Fuente: Hewitt, P. (1996) 1. Se observa que una persona al girar rápidamente una cubeta con agua en un círculo vertical con los brazos extendidos; el agua no se derrama. ¿Por qué? Justifica detalladamente la respuesta. __________________________________________________________________________________________ __________________________________________________________________________________________ __________________________________________________________________________________________ 2. Si vas en un automóvil que toma una curva y no te abrochas el cinturón de seguridad, te deslizarás sobre el asiento y vas a dar contra la puerta. ¿Qué clase de fuerza es la responsable de que suceda esto? ¿Centrípeta, centrífuga o ninguna? Justifica tu respuesta. __________________________________________________________________________________________ __________________________________________________________________________________________ __________________________________________________________________________________________ 3. ¿Quién cree que tendrá mayor aceleración, al rodar bajando de un plano inclinado; un aro o un disco macizo? ¿Por qué? __________________________________________________________________________________________ __________________________________________________________________________________________ __________________________________________________________________________________________
- 97. T E M A S S E L E C T O S D E F Í S I C A 1 Analizas la cinética rotacional BLOQUE 3 95 Secuencia didáctica 1 Movimiento de cuerpos rígidos Inicio ACTIVIDAD 1 SD1-B3 De forma individual resuelve los ejercicios que a continuación se te presentan anotando el procedimiento correspondiente para cada uno de ellos. 1.Realiza las siguientes conversiones de medidas angulares. Fuente: Bueche F. J. y Hecht E. (2007). a) 28° → rev y rad b) 1/4 rev/s → grados /s y rad/s c) 2.18 rad/s2 → rev/s2 y grados /s2 2. Una rueda de 40 cm de radio gira sobre un eje estacionario, si su rapidez aumenta uniformemente desde el reposo hasta una rapidez de 900 rpm en un tiempo de 20 s. Encuentra: a) la aceleración angular constante de la rueda. R= 4.7 rad / s2 b) la aceleración tangencial de un punto que se encuentra en su borde. R= 1.9 m/s2 3. Una polea que forma parte de un motor, tiene 5 cm de radio e inicialmente gira a razón de 30 rev/s, y después de 2 segundos disminuye su velocidad de giro a 20 rev/s. Calcula: a) la aceleración angular. R= -10π rad / s2 b) El desplazamiento angular (θ) con la que gira en ese tiempo. R=100 π rad c) la longitud (L=rθ) de la banda que se enrolla durante este tiempo. R=16 m
- 98. 96 C O L E G I O D E B A C H I L L E R E S D E L E S T A D O D E S O N O R A Movimiento de cuerpos rígidos. Como ya lo hemos visto anteriormente, un cuerpo rígido puede experimentar un movimiento traslacional o rotacional, o bien, ambos a la vez. Cuando un objeto Figura 1. Rodamiento: una combinación de movimiento traslacional y rotacional. Movimiento en una trayectoria circular. Tippens P. (2011), menciona que de acuerdo a la Primera Ley de Newton, todos los cuerpos que se mueven en línea recta con rapidez constante mantendrán inalterada su velocidad a menos que actúe sobre ellos una fuerza externa. La velocidad de un cuerpo es una cantidad vectorial definida por su rapidez y dirección. Esta cantidad, requiere de una fuerza resultante para cambiar tanto la rapidez como la dirección. Siempre que esa fuerza actúa en una dirección diferente a la dirección original del movimiento ocasiona un cambio en la trayectoria de la partícula en movimiento. El movimiento más sencillo en dos dimensiones se produce cuando una fuerza externa constante actúa siempre formando ángulos rectos respecto a la trayectoria de la partícula en movimiento. En este caso, la fuerza resultante producirá una aceleración que sólo cambia la dirección del movimiento y mantiene la rapidez constante. Este tipo de movimiento sencillo se conoce como movimiento circular uniforme (MCU). Un ejemplo de este movimiento es una piedra atada a un cordel, como se muestra en la figura 2. Observamos en (a), que mientras la piedra gira con rapidez constante, la fuerza hacia el centro originado por la tensión en el cordel cambia constantemente la dirección de la piedra, haciendo que ésta se mueva en una trayectoria circular. Sin embargo, en (b), el cordel se rompe y la piedra sale disparada en una dirección tangencial, es decir, perpendicular al radio de su trayectoria circular. únicamente presenta movimiento traslacional, todas sus partículas tienen la misma velocidad instantánea, lo cual implica que el objeto no está girando (figura 1a). En el caso de que un objeto únicamente presente movimiento rotacional, es decir, un movimiento en torno a un eje fijo (figura1b), todas sus partículas tienen la misma velocidad angular instantánea, y viajan en círculos en torno al eje de rotación. Desarrollo Figura 2. a) La tensión que el cordel ejerce sobre la piedra hace que ésta se mueva en una trayectoria circular. (b) Cuando el cordel se rompe, la piedra sale disparada en dirección tangencial al círculo.
- 99. T E M A S S E L E C T O S D E F Í S I C A 1 Analizas la cinética rotacional BLOQUE 3 97 Aceleración Centrípeta (ac): Bueche F. J. y Hecht E. (2007), menciona que una masa puntual m que se mueve con rapidez constante en un círculo de radio r experimenta aceleración. Aunque la magnitud de su velocidad lineal no cambia, la dirección de la velocidad cambia continuamente. Este cambio en la velocidad da origen a una aceleración de la masa, dirigida hacia el centro del círculo. A esta aceleración se le llama aceleración centrípeta (ac) y su magnitud está dada por la expresión: Donde v es la rapidez de la masa en su desplazamiento perimetral en el círculo. Como v=rω, también la aceleración centrípeta, se expresa: ac =rω2 donde ω es la velocidad angular y se mide en rad/s. Tippens P. (2011) define que el término centrípeta significa que la aceleración siempre se dirige hacia el centro. Las unidades de la aceleración centrípeta son las mismas que las de la aceleración lineal. Por ejemplo, en el SI, tendría las unidades siguientes: La aceleración centrípeta también puede encontrarse con la siguiente relación de cantidades físicas: Donde: T = Período f = Frecuencia. R = Radio Aceleración tangencial (a_T): Consideremos una partícula que se mueve en un círculo de radio R y supongamos que la velocidad tangencial cambia de cierto valor inicial vo al valor final vf en un tiempo t. La aceleración tangencial aT , de dicha partícula está dada por: Debido a la estrecha relación entre velocidad tangencial y velocidad angular, podemos expresar también la aceleración tangencial en función de un cambio en la velocidad angular.
- 100. 98 C O L E G I O D E B A C H I L L E R E S D E L E S T A D O D E S O N O R A Donde α representa la aceleración angular. Debemos ser cuidadosos en distinguir entre la aceleración tangencial y la aceleración centrípeta. La aceleración tangencial representa un cambio en la velocidad tangencial, mientras que la aceleración centrípeta representa tan sólo un cambio en la dirección del movimiento. La distinción se muestra gráficamente en la siguiente figura. La aceleración resultante puede determinarse calculando el vector suma de las aceleraciones tangencial y centrípeta. Ejemplo: Una centrífuga de laboratorio como la que se muestra en la figura 3 opera con una rapidez rotacional de 12 000 RPM (revoluciones por minuto). Fuente: Wilson, J; Bufa, A; Lou B. (2007). Figura 3. Centrífuga de laboratorio. a) ¿Cuál es la magnitud de la aceleración centrípeta de un glóbulo rojo, localizado a una distancia de 8 cm, respecto al eje de rotación de una centrífuga? b) Compara esa aceleración con g (Debido a que consideramos el valor de g = 9.80 m/s2 como un valor constante para fines académicos, es por ello que lo tomamos como referencia para conocer qué tan grande o pequeña es la aceleración obtenida con respecto a este valor que consideramos fijo) Razonamiento: Nos dan la rapidez angular y el radio, así que podemos calcular directamente la aceleración centrípeta. El resultado se compara con g utilizando g = 9.80 m/s2 a) Datos: ω= 12000 rpm r=8 cm=0.0800 m Convertimos primeramente a rad/seg:
- 101. T E M A S S E L E C T O S D E F Í S I C A 1 Analizas la cinética rotacional BLOQUE 3 99 ac = rω2 = (0.0800 m) (1.26 x 103 rad/s)2 =1.27 x 105 m/s2 Sustituimos en la fórmula: b) Comparación de ac y g ac =(1.27 x 105 m/s2 )((1 g)/(9.80 m/s2 ))=1.296 x 104 g ≈ 13 000 g ACTIVIDAD 2 SD1-B3 En equipo de tres integrantes resuelvan los siguientes ejercicios. Es necesario que anoten el procedimiento desarrollado para cada uno de ellos. Fuente: Wilson, J; Bufa, A; Lou B. (2007). 1. Se diseña un cilindro giratorio de unos 16 km de longitud y 7.0 km de diámetro para usarse como colonia espacial. ¿Con qué rapidez angular debe girar, para que sus residentes experimenten la misma aceleración debido a la gravedad que en la Tierra? R= 0.053 rad/s=730 rev/día 2. La Luna da una vuelta a la Tierra en 27.3 días, en una órbita casi circular con un radio de 3.8 x 105 km. Suponiendo que el movimiento orbital de la Luna, es un movimiento circular uniforme. ¿Qué aceleración tiene la Luna al “caer” hacia la Tierra? R=2.69x10-3 m/s2 3. Una bola de 150 g al final de una cuerda gira de manera uniforme en un círculo horizontal de 0.600 m de radio. La bola da 2 revoluciones en un segundo. ¿Cuál es su aceleración centrípeta? Fuente: Giancoli, D. (2006) R= 94.7m/s2
- 102. 100 C O L E G I O D E B A C H I L L E R E S D E L E S T A D O D E S O N O R A Ejemplo: La órbita casi circular de la luna alrededor de la tierra, tiene un radio aproximado de 384,000 km y un periodo T de 27.3 días. ¿Qué aceleración ejerce la luna sobre la tierra? Fuente: Giancoli, D. (2006) Razonamiento: se necesita encontrar la velocidad v con la finalidad de encontrar a_c. Debemos primeramente hacer la conversión a unidades SI para obtener v en m/s. Solución: En su órbita alrededor de la tierra, la luna recorre una distancia 2πr, donde r es el radio de su trayectoria circular y equivale a 3.84 x108 m. El tiempo requerido para una órbita completa es el periodo de la luna de 27.3 días. La rapidez de la Luna en su órbita alrededor de la Tierra, se calcula con la siguiente fórmula: v=2πr/T El periodo T en segundos es: Por lo tanto: Esta aceleración se puede expresar en términos la aceleración de la gravedad en la superficie de la tierra, g = 9.80 m/s2 como: Nota: La aceleración centrípeta de la Luna, no es la aceleración de la gravedad para los objetos en la superficie de la luna debido a la gravedad de nuestro satélite. En vez de ello es la aceleración debido a la gravedad de la tierra para cualquier objeto (como la Luna) que está a 384,000 km de la Tierra. Como podemos observar esta magnitud, es sumamente pequeña en comparación con la aceleración de los objetos cerca de la superficie de la Tierra. Dinámica del movimiento circular uniforme De acuerdo a Giancoli, D. (2006), un objeto experimenta aceleración porque hay una fuerza neta que actúa sobre él. Por ejemplo, cuando un objeto se mueve en trayectoria circular, como una bola al final de una cuerda, debe por tanto tener una fuerza aplicada sobre él que lo mantenga en movimiento. Esto es, se necesita una fuerza para proporcionarle aceleración centrípeta. La magnitud de esta fuerza se calcula mediante la segunda ley de Newton para el componente radial, ∑ F =ma Donde a = ac (aceleración centrípeta)
- 103. T E M A S S E L E C T O S D E F Í S I C A 1 Analizas la cinética rotacional BLOQUE 3 101 ∑ F es la fuerza total (o neta) en la dirección radial: Como mencionamos anteriormente en el MCU, la magnitud de la velocidad es constante, la aceleración centrípeta ac , se dirige hacia el centro de la circunferencia en cualquier momento; por lo tanto, la fuerza neta también debe dirigirse hacia el centro de la circunferencia como se muestra en la figura siguiente. Esta fuerza es necesaria, porque de otra manera, el objeto no se movería en un círculo sino en línea recta, como lo establece la primera ley de Newton. La dirección de la fuerza neta cambia continuamente, de modo que siempre se dirige hacia el centro de la circunferencia. A esta fuerza se le llama fuerza centrípeta (“que apunta hacia el centro”). Debemos de tener en cuenta que la “fuerza centrípeta”, no es una nueva fuerza; sino la fuerza neta necesaria para mantener al objeto en una trayectoria circular. Giancoli, D. (2006), señala que existe un error común, cuando se menciona que un objeto que se mueve en trayectoria circular tiene una fuerza hacia fuera que actúa sobre él, una fuerza llamada centrífuga (“que se aleja del centro”). Esto es incorrecto, ya que no existe una fuerza hacia fuera sobre el objeto en movimiento. A continuación explicaremos lo que realmente sucede considerando el siguiente ejemplo: cuando una persona hace girar un cuerpo en el extremo de una cuerda, en la parte superior de su cabeza (figura 4), experimenta un jalón hacia fuera de su mano, denominado erróneamente fuerza “centrífuga”. Tal jalón no es otra cosa que la fuerza que mantiene al cuerpo en una trayectoria circular, ya que cuando la persona ejerce una fuerza sobre la cuerda y ésta sobre el objeto; el objeto ejerce una fuerza igual y opuesta sobre la cuerda (tercera ley de Newton) y ésta es la fuerza hacia fuera que siente en su mano. Figura 4. Giro de un cuerpo en el extremo de una cuerda.
- 104. 102 C O L E G I O D E B A C H I L L E R E S D E L E S T A D O D E S O N O R A Para tener una evidencia todavía más convincente de que una “fuerza centrífuga” no actúa sobre el objeto, consideremos lo que ocurre cuando se suelta la cuerda: si estuviese actuando una fuerza centrífuga, el objeto saldría disparado hacia fuera, como se muestra en la figura 5. Sin embargo podemos observar en la figura 6, que el objeto vuela tangencialmente en la dirección de la velocidad que tenía en el momento en que se liberó, porque la fuerza que lo hace girar ya no actúa más sobre él. Figura 5. Si existiese una fuerza centrífuga, la bola que gira volaría hacia fuera al ser liberada. Figura 6. Vuelo tangencial del objeto al no actuar más la fuerza de giro. Ejemplo (Estimación): Fuerza sobre una bola que gira horizontalmente. Estimar la fuerza que una persona debe ejercer sobre una cuerda unida a una bola de 0.150 kg para que gire en un círculo horizontal de 0.600 m de radio. La bola realiza 2.00 revoluciones por segundo (T= 0.500s). Planteamiento: Primero se necesita dibujar el diagrama de cuerpo libre para la bola. Las fuerzas que actúan sobre ella son la fuerza de gravedad, mg hacia abajo, y la fuerza de tensión FT que la cuerda ejerce sobre la mano en el centro;(porque la persona ejerce esa misma fuerza sobre la cuerda).
- 105. T E M A S S E L E C T O S D E F Í S I C A 1 Analizas la cinética rotacional BLOQUE 3 103 Diagrama de cuerpo libre. El peso de la bola complica las cosas y hace imposible que ésta gire con el cordón perfectamente horizontal. Se supone que el peso es reducido y que ϕ ≈ 0° en el DCL. Por tanto FT actuará casi horizontalmente y en cualquier caso proporcionará la fuerza necesaria para darle a la bola su aceleración centrípeta. Solución: Se aplica la segunda ley de Newton a la dirección radial, que se supone horizontal: Nota: Para incluir el efecto de mg, hay que descomponer FT en el DCL, encontramos entonces, que la componente horizontal de FT es m v^2/r y la componente vertical es mg. Ejemplo: Cuerpos conectados: fuerza centrípeta y segunda ley de Newton. Fuente:Wilson, J; Bufa, A; Lou B. (2007). Supón que dos masas, ml =2.5 kg y m2 = 3.5 kg, están conectadas por cordeles ligeros y están en movimiento circular uniforme sobre una superficie horizontal sin fricción, como se ilustra en la figura siguiente. Calcular: a) La magnitud de la aceleración centrípeta b) La de la rapidez tangencial en las masas m1 y m2 Datos: r1 = 1.0 m r2 = 1.3 m. Tl = 4.5 N T2 = 2.9 N.
- 106. 104 C O L E G I O D E B A C H I L L E R E S D E L E S T A D O D E S O N O R A Razonamiento: Las fuerzas centrípetas que actúan sobre las masas provienen de las tensiones (Tl y T2 ) en los cordeles. Si aislamos las masas, podremos calcular ac para cada una, ya que la fuerza neta sobre una masa es igual a la fuerza centrípeta sobre esa masa (Fc = mac ). Luego se calculan las rapideces tangenciales, pues se conocen los radios (ac = v2 / r). Solución: a) Al aislar m2 en la figura, vemos que la fuerza centrípeta proviene de la tensión en el cordel. (T2 es la única fuerza que actúa sobre m2 hacia el centro de su trayectoria circular). Por lo tanto: T2 = m2 ac2 b) La situación de ml es un poco distinta. En este caso, dos fuerzas radiales actúan sobre la masa m1: las tensiones T1 (hacia adentro) y - T2 (hacia afuera) en los cordeles. También, por la segunda ley de Newton, para tener una aceleración centrípeta, debe haber una fuerza neta, dada por la diferencia entre las dos tensiones, por lo que cabe esperar que Tl >T2, y que: Fneta1 = +T1 + (-T2 ) = m1 ac1 = m1 v1 2 / r Tomamos como positiva la dirección radial (hacia el centro de la trayectoria circular). Entonces; y
- 107. T E M A S S E L E C T O S D E F Í S I C A 1 Analizas la cinética rotacional BLOQUE 3 105 Resuelvan en binas los siguientes ejercicios. Es necesario que anoten el procedimiento desarrollado para cada uno de ellos. Esta actividad formará parte del portafolio de evidencias y se valorará con la lista de cotejo para evaluar serie de ejercicios que aparece al final del bloque. Fuente: Bueche F. J. y Hecht E. (2007) 1. Un objeto de 200 g se amarra al extremo de una cuerda y lo hace girar en un círculo horizontal de 1.20 m de radio a razón de 3 rev/s. Supongan que la cuerda se encuentra en posición horizontal, es decir, el efecto de la gravedad se puede depreciar. Determinar: a) la aceleración del objeto R=426 m/s2 b) la tensión en la cuerda R= 85 N 2. Una pelota de 4 kg se hace girar en un círculo horizontal por medio de una cuerda de 2 m de longitud. ¿Cuál es la tensión en la cuerda; si el periodo es de 0.5 s? Fuente: Tippens P. (2011). R= 1260 N 3. Una bola de 0.500 kg de masa, se une al extremo de una cuerda de 1.50 m de largo y gira en un círculo horizontal como se muestra en la figura 7. Si la cuerda resiste una tensión máxima de 50.0 N. ¿Cuál es la máxima rapidez a la que gira la bola antes de que se rompa la cuerda? Supongan, que la cuerda permanece horizontal durante el movimiento. Fuente: Serway R. y Jewett, J. (2008). R= 12.2 m/s ACTIVIDAD 3 SD1-B3
- 108. 106 C O L E G I O D E B A C H I L L E R E S D E L E S T A D O D E S O N O R A 4. Dos masas de 500 g, giran alrededor de un eje central a 12 rev/s, como se muestra en la figura 7. Fuente: Tippens P. (2011). Figura 7. Objetos que se mueven en una trayectoria circular. La fuerza resultante que ejerce la barra sobre los objetos suministra la fuerza centrípeta necesaria. De acuerdo con la tercera ley de Newton, los objetos ejercen una fuerza de igual magnitud y sentido opuesto llamada “fuerza centrífuga”. Estas fuerzas no se cancelan entre sí porque actúan sobre objetos diferentes. Calcular: a) ¿Cuál es la fuerza constante que actúa sobre cada masa? R= 853 N, hacia el centro. b) ¿Cuál es la tensión en la barra de soporte? R= 853 N, dirigida hacia afuera.
- 109. T E M A S S E L E C T O S D E F Í S I C A 1 Analizas la cinética rotacional BLOQUE 3 107 Curvas en las autopistas, peraltadas y sin peralte. Giancoli, D. (2006) menciona que un ejemplo de dinámica circular ocurre cuando un automóvil toma una curva, por ejemplo, hacia la izquierda. En tal situación, un pasajero quizá sienta que es lanzado hacia la puerta del lado derecho, pero no existe una misteriosa fuerza centrífuga que jale sobre él; lo que ocurre realmente, es que tiende a moverse en una línea recta, mientras que el automóvil ha comenzado a seguir una trayectoria curveada. Paraqueelpasajeroconservelatrayectoriacurvarecibefuerzas,porejemplodefricciónycontacto,específicamente por el asiento y la puerta del automóvil, respectivamente de igual manera sobre el automóvil, se ejercen fuerzas para mantenerlo en la trayectoria curva; como se observa en la figura 8. Igualmente, en un camino plano, un automóvil conserva su trayectoria, gracias a la fuerza de fricción ejercida entre las llantas y la superficie de contacto. Figura 8. El suelo ejerce una fuerza hacia dentro (fricción contra las llantas), sobre un automóvil para mantenerlo en trayectoria curva. El automóvil ejerce una fuerza hacia dentro sobre el pasajero. Si las llantas de un automóvil giran con normalidad, sin derrapar, ni deslizar, la parte inferior de las llantas están en reposo con la superficie a cada instante; por lo que la fuerza de fricción que ejerce la superficie sobre las llantas es fricción estática. Pero si la fuerza de fricción estática no es lo suficientemente grande, como cuando hay hielo, no se puede aplicar suficiente fuerza de fricción y el automóvil derrapará fuera de la trayectoria circular hacia una trayectoria más cercana a una recta. Una vez que un automóvil derrapa o se desliza, la fuerza de fricción se convierte en fricción cinética, que es menor que la fricción estática. Ejemplo: Derrape en una curva. Fuente Giancoli, D. (2006) Un automóvil de 1000 kg toma una curva en una carretera plana de 50 m de radio con una rapidez de 14 m/s. Determinar si el automóvil seguirá la curva o derrapará, en cada uno de los siguientes casos: a) Cuando el pavimento está seco y el coeficiente de fricción estática es µs=0.60
- 110. 108 C O L E G I O D E B A C H I L L E R E S D E L E S T A D O D E S O N O R A b) Cuando el pavimento está cubierto de hielo y µs=0.25 Planteamiento: Las fuerzas sobre el automóvil son la gravedad mg hacia abajo; la fuerza normal FN ejercida hacia arriba por la carretera y una fuerza de fricción horizontal ejercida también por esta última. El DCL correspondiente se muestra a continuación: Figura 9. Fuerzas sobre un automóvil que toma una curva en una carretera plana: a) Vista frontal b) Vista Superior. El automóvil se mantendrá en una trayectoria curva, si la fuerza de fricción estática máxima es mayor que la masa por la aceleración centrípeta. Solución: En la dirección vertical no existe aceleración. De acuerdo a la segunda ley de Newton, la fuerza normal FN, sobre el automóvil es igual al peso mg, pues la carretera es plana: FN = mg = (1000kg) (9.8 m/s2 )=9800 N En el plano horizontal, la única fuerza ejercida es la fricción, por lo tanto, depende de esta producir, en el automóvil, una aceleración centrípeta. La fuerza horizontal neta que se requiere para mantener al automóvil en movimiento circular alrededor de la curva es: El automóvil derrapará, porque el suelo no ejerce suficiente fuerza (se necesitan 3900 N) para mantenerlo en movimiento en una curva de 50 m de radio a una rapidez de 14m/s. La posibilidad de derrapar es mayor aún si las ruedas se bloquean (cuando dejan de girar); al aplicarse los frenos de manera brusca. Cuando las ruedas giran, existe fricción estática, pero si las ruedas se bloquean, las llantas se deslizan y la fuerza de fricción ahora cinética es menor. Algo todavía más importante: la dirección de la fuerza de fricción cambia súbitamente si las ruedas se bloquean. La fricción estática puede apuntar de forma perpendicular a la velocidad, como en la figura 9b, pero si el automóvil Como se necesita una fuerza de sólo 3900 N, y eso es, de hecho, lo que ejercerá la carretera como una fuerza de fricción estática, el auto podrá seguir la curva.
- 111. T E M A S S E L E C T O S D E F Í S I C A 1 Analizas la cinética rotacional BLOQUE 3 109 se desliza, la fricción cinética apuntará en dirección opuesta a la velocidad. La fuerza ya no se ejerce más hacia el centro de la circunferencia y el automóvil no puede continuar en una trayectoria curva. Sucede, incluso algo peor: si la carretera está mojada o cubierta de hielo, el bloqueo de las ruedas ocurre a menor fuerza sobre el pedal del freno pues existe menos fricción de la carretera para mantener a las ruedas girando en lugar de deslizar. El peralte consiste en elevar en las curvas el borde exterior de las vías una cierta cantidad, para que permita que una componente del vehículo se oponga a la fuerza centrífuga (Fc) evitando de esta manera que el vehículo se desvíe radialmente de su trayectoria hacia fuera ocasionando un accidente. El peralte de las curvas reduce la posibilidad de derrape, ya que la fuerza normal ejercida en una superficie con peralte, actúa perpendicularmente a ésta, por lo que tendrá un componente hacia el centro de la circunferencia, con la que se reduce la dependencia de la fricción como se observa en la figura siguiente. Figura 10. Fuerza normal sobre un automóvil que toma una curva peraltada, descompuesta en sus componentes horizontal y vertical (Fuente Giancoli, D, 2006) Para un ángulo de peralte dado θ, habrá una rapidez para la que no se requerirá fricción en absoluto. Éste será el caso cuando la componente horizontal de la fuerza normal (FN sen θ) hacia el centro de la curva (como se observa en la figura anteriormente mostrada), sea justo igual a la fuerza que se requiere para brindar a un vehículo su aceleración centrípeta, es decir cuando: FN *sen θ = m v2 /r [no se requiere fricción]
- 112. 110 C O L E G I O D E B A C H I L L E R E S D E L E S T A D O D E S O N O R A El ángulo de peralte de una superficie, se elige de modo que esta condición se sostenga para una rapidez particular, llamada “rapidez de diseño”, es decir con esa velocidad y con ese ángulo no habrá derrape que puede ocasionar un accidente. Ejercicio: a) Encontrar la expresión matemática que permita calcular el ángulo de peralte para un automóvil que viaja con rapidez alrededor de una curva de radio r, despreciando la fricción. b) ¿Cuál es el ángulo de peralte en una curva de 50 m de radio de una supercarretera, para lograr una rapidez de diseño de 50 km/h? Razonamiento: Es necesario analizar el DCL presentado en la figura 10. Además, es importante señalar que aunque la carretera esté peraltada, el automóvil se mueve a lo largo de un círculo horizontal, de manera que la aceleración centrípeta necesita ser horizontal. Se eligen los ejes x y y como horizontal y vertical respectivamente, de modo que aR, corresponde a la componente del eje x. Las fuerzas sobre el automóvil son la gravedad de la tierra mg hacia abajo y la fuerza normal ejercida por la carretera de forma perpendicular a su superficie. No es necesario considerar la fricción del camino porque como se ha mencionado antes, en una carretera peraltada, no se requieres de fricción. Solución: y se obtiene: :
- 113. T E M A S S E L E C T O S D E F Í S I C A 1 Analizas la cinética rotacional BLOQUE 3 111 En equipo de tres integrantes resuelvan los siguientes ejercicios. Es necesario que anoten el procedimiento desarrollado para cada uno de ellos. Esta actividad formará parte del portafolio de evidencias y se valorará con la rúbrica serie de ejercicios que aparece al final del bloque. Fuente: Bueche F. J. y Hecht E. (2007) . 1. ¿Cuál debe ser el ángulo de peralte, para que un auto se mueva por una curva de 30 m de radio con una rapidez de 13m/s, sin depender de la fricción para evitar un derrape. ¿Cuál debe ser la pendiente de la curva (ángulo de peralte)? R= 30° 2. Un cordel enredado en el borde de una rueda de 20 cm de diámetro se jala a una rapidez de 75 cm/s. ¿Cuántas revoluciones habrá dado la rueda cuando se hayan desenredado 9.0 m de cordel? ¿Cuánto tiempo llevará este proceso? R=14 rev, 12 s. Cierre ACTIVIDAD 4 SD1-B3
- 114. 112 C O L E G I O D E B A C H I L L E R E S D E L E S T A D O D E S O N O R A 3. Una masa de 1.5 kg en el espacio se mueve en un círculo de 25 cm de radio a 2.0 rev/s. Determinar: a) La rapidez tangencial R=3.1 m/s b) La aceleración R= 39 m/s2 radialmente hacia adentro c) la fuerza centrípeta requerida para este movimiento R= 59 N 4. Un carro que se mueve a una rapidez de 5 m/s trata de dar vuelta en una esquina describiendo un arco circular de 8.0 m de radio en un camino plano. ¿Cuál debe ser la magnitud del coeficiente de fricción entre las llantas y el pavimento para que no derrape? R= 0.32 5. Una caja descansa en un punto que se encuentra a 2.0 m del eje de una plataforma circular horizontal. El coeficiente de fricción estática entre la caja y la plataforma es de 0.25. Si la rapidez de rotación de la plataforma aumenta lentamente a partir del reposo, ¿Con qué rapidez angular empezará a resbalar la caja? R= 1.1 rad/s.
- 115. T E M A S S E L E C T O S D E F Í S I C A 1 Analizas la cinética rotacional BLOQUE 3 113 Recursos adicionales para la secuencia didáctica 1 A continuación, se te proporcionan los siguientes recursos disponibles en internet que te permitirán retroalimentar los temas vistos en la secuencia didáctica 1. Tu prepa en videos http://www.tuprepaenvideos.sep.gob.mx/ Ir a Bachillerato Dar clic en Materias Buscar Temas Selectos de Física I Ir a la pestaña de Lecciones Buscar Bloque 3: Analizas la cinética rotacional. Los videos de pueden consultar en el sitio de Tu prepa en videos o dando clic derecho sobre el video aparece la opción Obtener la URL del video, la cual es la que compartimos contigo. Se recomienda los siguientes videos: 1) Dinámica rotacional 1 (40:00) https://youtu.be/4ltPJXTDLoM 2) Momento de torsión y momento de inercia https://youtu.be/8hRtTlj5hLU 3) Movimiento de rotación: Ejercicio # 1 sobre Momento de Inercia (6:33) https://youtu.be/bJ-6PKXqAi8 4) Movimiento de rotación: Ejercicio # 2 sobre Momento de Inercia (6:30) https://youtu.be/DOyRv52j_jo
- 116. 114 C O L E G I O D E B A C H I L L E R E S D E L E S T A D O D E S O N O R A Secuencia didáctica 2 Energía cinética rotacional Inicio De manera individual, lee cuidadosamente los siguientes cuestionamientos, escribe en el paréntesis la opción correcta para cada uno de ellos y escribe un argumento de tu selección. Fuente: Wilson, J; Bufa, A; Lou B. (2007). 1. ( ) De qué depende el cambio de energía potencial gravitacional: a) Solamente de la posición final. b) Del punto de referencia. c) Solamente de la trayectoria. d) De la posición inicial y final. Argumento: __________________________________________________________________________________________ __________________________________________________________________________________________ __________________________________________________________________________________________ 2. ( ) La rapidez de un péndulo es máxima cuando: a) Su energía cinética es mínima. b) Su aceleración es máxima. c) Su energía potencial es mínima. d) Ninguno de los casos anteriores. Argumento: __________________________________________________________________________________________ __________________________________________________________________________________________ __________________________________________________________________________________________ 3. ( ) Dos automóviles idénticos, A y B, que viajan a 55 mi/h chocan de frente. Un tercer auto idéntico, C, choca contra una pared a 55 mi/h. ¿Qué automóvil sufre más daño? a) Auto A . b) Auto B. c) Auto C. d) Sufren el mismo daño los tres. Argumento: __________________________________________________________________________________________ __________________________________________________________________________________________ __________________________________________________________________________________________ 4. ( ) ¿Cuál de los siguientes enunciados hace referencia a un objeto con menor energía cinética? a) Objeto de masa 4m y rapidez v. b) Objeto de masa 3m y rapidez 2v. c) Objeto de masa 2m y rapidez 3v. d) un objeto de masa m y rapidez 4v. Argumento: __________________________________________________________________________________________ __________________________________________________________________________________________ __________________________________________________________________________________________ ACTIVIDAD 1 SD2-B3
- 117. T E M A S S E L E C T O S D E F Í S I C A 1 Analizas la cinética rotacional BLOQUE 3 115 Energía cinética rotacional: momento de inercia. Como ya hemos visto en otros cursos, la energía cinética es aquella que posee un cuerpo debido a su movimiento. Serway R. y Jewett J. (2008) mencionan que un objeto que rota en torno a un eje fijo permanece estacionario en el espacio, por lo que no presenta energía cinética asociada en su movimiento traslacional. Sin embargo, las partículas individuales que conforman el objeto en rotación se mueven a través del espacio siguiendo trayectorias circulares, por lo que en el movimiento rotacional hay energía cinética asociada. La figura 10 muestra al objeto en rotación e identifica una partícula sobre el objeto ubicada a una distancia ri del eje de rotación. Figura 10. Un objeto rígido en rotación en torno al eje z con rapidez angular W. La energía cinética total del objeto se llama energía cinética rotacional. Si la masa de la partícula es mi y su rapidez tangencial es vi, su energía cinética es: Para continuar, recuerda que aunque cada partícula en el objeto rígido tiene la misma rapidez angular ω, la magnitud de la velocidad tangencial en cada una de las partículas depende de la distancia ri , de acuerdo con la ecuación: Por lo tanto, la energía cinética total del objeto rígido en rotación, es la suma de las energías cinéticas de las partículas individuales: Esta expresión se puede escribir en la forma Desarrollo
- 118. 116 C O L E G I O D E B A C H I L L E R E S D E L E S T A D O D E S O N O R A El término ω2 se factoriza en la suma, ya que su magnitud es la misma para cada una de las partículas. A partir de esta ecuación, también se define que la expresión corresponde al momento de inercia (I): I = Por lo tanto, la ecuación de la energía cinética rotacional cuando se tiene o es posible calcular el momento de inercia, es: I La ecuación anterior, nos permite determinar la energía cinética de un cuerpo rígido a partir de suma de energías cinéticas individuales de las partículas que constituyen a dicho cuerpo. Cabe recordar que en el sistema internacional de unidades (SI) cualquier tipo de energía, incluida por supuesto la energía cinética, se mide en Joules (J), que se define como el trabajo realizado por una fuerza de un newton en un desplazamiento de un metro en la dirección de la fuerza, es decir, equivale a multiplicar un Newton por un metro (J=N∙m). Entre sus equivalencias más comunes están: 1 J = 107 erg Acontinuación se te presenta una analogía entre la energía cinética asociada con el movimiento traslacional y la energía cinética rotacional . Las cantidades de I y ω en el movimiento rotacional, son análogas a las cantidades de m y v en el movimiento traslacional, respectivamente; ya que I toma el lugar de m y ω toma el lugar de v cada vez que se compara una ecuación de movimiento traslacional con su contraparte rotacional. El momento de inercia es una medida de la resistencia de un objeto a cambios en su movimiento rotacional, tal como la masa, es una medida de la tendencia de un objeto a resistir cambios en su movimiento traslacional. Torca e inercia de rotación. En el bloque 1 Secuencia didáctica 4 se explicó que Bueche F. J. y Hecht E. (2007) definen a la torca, momento de torsión o momento de fuerza (τ) alrededor de un eje, debida a una fuerza, como una medida de la efectividad de la fuerza para que ésta produzca una rotación alrededor de un eje. La torca se define de la siguiente forma: Torca = τ = r F sen θ Donde r es la distancia radial desde el eje al punto de aplicación de la fuerza y θ es el ángulo agudo entre las direcciones de r y de F. Con frecuencia, esta definición se escribe en términos del brazo de palanca de la fuerza, que es la distancia perpendicular desde el eje a la línea de acción de la fuerza. Como el brazo de palanca, es igual a r sen θ, la ecuación de la torca se reescribe como τ ꞊ (F) (brazo de palanca). Por otro lado, la aceleración angular α de un objeto en rotación, es proporcional a la torca neta τ aplicada (la suma de todas las torcas que actúan sobre el objeto).
- 119. T E M A S S E L E C T O S D E F Í S I C A 1 Analizas la cinética rotacional BLOQUE 3 117 Esto se explica con la segunda ley de Newton para el movimiento de traslación, pero aquí la torca ha tomado el lugar de la fuerza y, en correspondencia la aceleración angular α desempeña el papel de la aceleración lineal a. Por ejemplo, si consideramos una partícula de masa despreciable m, que gira en un círculo de radio r al final de una cuerda o barra, sobre la cual actúa una única fuerza F; la torca que da origen a la aceleración angular es τ=r F. Aplicando la segunda ley de Newton para cantidades lineales y la ecuación que relaciona la aceleración angular con la aceleración lineal tangencial (aT = r α), se obtiene: F = m a = m r α Cuando ambos lados de esta ecuación se multiplican por r, se encuentra que la torca τ=r F, para una sola partícula, está dada por la expresión: τ = m r2 α La expresión anterior relaciona directamente la aceleración angular y la torca aplicada. La cantidad mr2 representa la inercia de rotación de la partícula y se llama su momento de inercia. Giancoli, D. (2006) nos pide que consideremos el caso de un objeto rígido en rotación, como por ejemplo una rueda que gira en torno a un eje. Como sabemos, este cuerpo está constituido por muchas partículas ubicadas en diferentes distancias con respecto al eje de rotación. Para calcular la torca de cada una de las partículas del objeto, se aplica la ecuación τ = m r2 α. La torca total ∑τ, se obtiene a partir de la expresión siguiente: La aceleración angular α, se factoriza porque su magnitud es la misma para todas las partículas que constituyen al objeto. El término ∑ m r2 , representa la suma de las masas de cada partícula en el objeto, multiplicada por el cuadrado de la distancia de dicha partícula a partir del eje de rotación. Sí combinamos: El momento de inercia I, es una medida de la inercia de rotación de un objeto, juega el mismo papel para el movimiento de rotación que desempeña la masa para el movimiento de traslación. Como puede observarse en la ecuación I = ∑ i m i r i 2 , la inercia de rotación de un objeto depende no sólo de su masa, sino también de cómo está distribuida dicha masa con respecto al eje. Por ejemplo, un cilindro de gran diámetro tendrá mayor inercia de rotación que uno de igual masa, pero diámetro más pequeño (y por tanto mayor longitud) como se observa en la figura 11 Será más difícil comenzar a hacer girar al primero, y más difícil de detenerlo. Cuando la masa está concentrada más lejos del eje de rotación, la inercia de rotación es mayor. Para el movimiento de rotación, la masa de un objeto no se puede considerar como concentrada en su centro de masa.
- 120. 118 C O L E G I O D E B A C H I L L E R E S D E L E S T A D O D E S O N O R A Figura 11. Un cilindro de gran diámetro tiene mayor inercia de rotación que uno de diámetro más pequeño pero de igual masa. Ejemplo: Cuerpos rígidos sobre una barra con diferentes ejes y momentos de inercia (I). Dos pequeños “pesos”, de 5.0 kg y 7.0 kg de masa, se colocan separados 4.0 m sobre una barra ligera de masa despreciable, como se muestra a continuación (Referencia Giancoli, D. 2006): Calcula el momento de inercia del sistema, con respecto: Al eje situado a la mitad de los cuerpos En torno al eje situado a 0.50 m a la izquierda de la masa de 5.0 kg Planteamiento: en cada caso, el momento de inercia del sistema se calcula sumando las dos partes. Solución. Ambos pesos están a la misma distancia, 2.0 m, del eje de rotación. Por lo tanto: I=∑mr2 =(5.0 kg) (2.0m)2 +(7.0kg) (2.0m)2 =20 kg∙m2 +28 kg∙m2 =48 kg∙m2
- 121. T E M A S S E L E C T O S D E F Í S I C A 1 Analizas la cinética rotacional BLOQUE 3 119 (b) La masa de 5.0 kg se localiza a 0.50 m del eje, y la masa de 7.0 kg está a 4.50 m del eje. Por lo tanto: I=∑mr2 =(5.0 kg) (0.50m)2 +(7.0kg) (4.5m)2 =1.25 kg∙m2 +141.75 kg∙m2 =143 kg∙m2 Nota: Este ejemplo ilustra dos puntos importantes: Primero, el momento de inercia de un sistema dado es diferente para distintos ejes de rotación. Segundo, en el inciso b) se observa que la masa cercana al eje de rotación contribuye poco al momento de inercia total; ya que, el cuerpo de 5.0 kg contribuyó con menos del 1% del total. Ejemplo: Calcula el momento de inercia para el sistema ilustrado en la figura 12. El peso de las barras que une a las masas es insignificante y el sistema gira con una velocidad angular de 6 rad/s. ¿Cuál es la energía cinética rotacional? Considera que las masas están concentradas en un punto (Referencia Tippens P. 2011). Figura 12. Sistema compuesto de varias masas. Razonamiento: el momento de inercia del sistema es igual a la suma de los momentos de inercia de cada masa respecto del centro de rotación. La energía cinética rotacional, se calcula con la ecuación: I Solución: aplicando la fórmula para el momento de inercia I, tenemos: I = ∑mr2 = m1 r1 2 + m2 r2 2 +m3 r3 2 + m4 r4 2 I = (2 kg) (0.5m)2 +(4 kg) (0.2m)2 + (2 kg)(0.5m)2 + (4 kg)(0.2m)2 I=1.32 kg ∙m2 Usando este resultado y el hecho de que ω = 6 rad/s, la energía cinética rotacional está dada por:
- 122. 120 C O L E G I O D E B A C H I L L E R E S D E L E S T A D O D E S O N O R A Ejemplo: Cualquiera puede bailar ballet. Un ágil profesor de física, se para en el centro de una mesita giratoria con los brazos extendidos horizontalmente y una mancuerna de 5.0 kg en cada mano como se muestra a continuación. Suponiendo que la mesita gira verticalmente, dando una revolución cada 2.0 s. El momento de inercia del profesor sin las mancuernas es de 3 kg∙m2 con los brazos estirados y 2.2 kg∙m2 , cuando pone las manos en el abdomen. Las mancuernas están a 1.0 m del eje al principio y a 0.20 m al final del movimiento que realiza el profesor. Calcula: La velocidad angular del profesor si pega las mancuernas a su abdomen. La energía cinética inicial y final. Sugerencia: considera las mancuernas como partículas. Solución. Identificar: Si despreciamos la fricción en la mesita giratoria, ninguna torca externa actuará alrededor del eje vertical (z), así que el momento angular con respecto a ese eje será constante. Plantear: Usaremos la ecuación I1 ω1Z =I2 ω2Z , para calcular la incógnita (la velocidad angular final ω2Z ). Ejecutar: El momento de inercia del sistema es I = I prof + I manc . Cada mancuerna de masa m aporta mr2 a Imanc. El valor de r, corresponde a la distancia perpendicular del eje de rotación a la mancuerna. Inicialmente tenemos: I1 = 3.0 kg∙m2 + 2(5.0 kg) (1.0m)2 = 13 kg∙m2 El momento de inercia final es: I2 = 2.2 kg∙m2 +2(5.0 kg) (0.20 m)2 = 2.6 kg∙m2 Es decir, la velocidad angular aumenta en un factor de 5, en tanto que el momento angular se mantiene constante. Para calcular la energía cinética debemos expresar ω1 y ω2 en rad/s. Tenemos ω1Z = (0.50 rev/s)(2π rad/rev) = 3.14 rad/s y ω2Z = (2.5 rev/s)(2π rad/rev) = 15.7 rad/s.
- 123. T E M A S S E L E C T O S D E F Í S I C A 1 Analizas la cinética rotacional BLOQUE 3 121 Por lo tanto, la energía cinética inicial es: y la energía cinética final es: La energía cinética adicional proviene del trabajo que el profesor realizó para pegar sus brazos y las mancuernas al abdomen. Para cuerpos que no están compuestos por masas separadas, sino que son en realidad distribuciones continuas de materia, los cálculos del momento de inercia son más difíciles y generalmente requieren conocimientos de cálculo integral. En la figura 13 se muestran algunos casos sencillos, junto con las fórmulas para calcular sus momentos de inercia. Figura 13. Cuerpos sólidos y fórmulas para calcular su momento de inercia.
- 124. 122 C O L E G I O D E B A C H I L L E R E S D E L E S T A D O D E S O N O R A Algunas veces, es conveniente expresar la inercia rotacional de un cuerpo en términos de su radio de giro k. Esta cantidad, se define como la distancia radial del centro de rotación a la circunferencia, en la cual, se puede considerar concentrada la masa total del cuerpo, sin cambiar su momento de inercia. De acuerdo con esta definición el momento de inercia se calcula a partir de la fórmula: I = mk2 Donde m representa la masa total del cuerpo que gira y k es su radio de giro. Ejemplo: Una polea pesada. Fuente: Giancoli, D. (2006). A una cuerda enredada alrededor de una polea de masa m = 4 kg y radio R = 33 cm, se le aplica una fuerza de 15 N (representada por FT), como se ilustra en la figura 14. La polea acelera uniformemente desde el reposo hasta lograr una rapidez angular de 30 rad/s en 3 s, experimentando una torca de fricción τ_Fr= 1.10 m·N en el eje. Determina el momento de inercia de la polea, cuando gira en torno a su centro. Figura 14. Polea pesada Sugerencias para la solución: 1. Analiza la figura anterior, que representa a la polea y el cordón unido a ella. 2. Elije el sistema: la polea. 3. Dibuja un diagrama de cuerpo libre. La fuerza que el cordón ejerce sobre la polea se muestra en la figura 14. La fuerza de fricción también se conoce, pero sólo se proporciona su torca. En el diagrama se podrían incluir otras dos fuerzas: la de gravedad mg hacia abajo y cualquier otra fuerza que mantenga al eje en su lugar. Tales fuerzas no contribuyen con la torca (sus brazos de palanca son cero), así que no se representan. 4. Determina las torcas. La cuerda ejerce una fuerza FT que actúa en el extremo de la polea, así que su brazo de palanca es R. La torca ejercida por la cuerda es igual a RFT y es en sentido contrario a las manecillas del reloj, que se elige como positivo. La torca de fricción está dada como τFr = 1.1 m∙N; es opuesta al movimiento y es negativa.
- 125. T E M A S S E L E C T O S D E F Í S I C A 1 Analizas la cinética rotacional BLOQUE 3 123 Lo anterior, nos permite llegar a los últimos tres pasos, a partir de los cuales se determinarán los valores numéricos que dan respuesta al problema planteado. 5. Aplica la segunda ley de Newton para determinar la torca neta, a partir de la ecuación: A partir de los datos proporcionados, se sabe que la aceleración angular α toma 3 s para acelerar la polea desde el reposo hasta ω = 30 rad/s: 6. Calcular I en la segunda ley de Newton para la rotación, 7. Determinar una estimación aproximada del momento de inercia suponiendo que la polea es un cilindro uniforme: Este último resultado es del mismo orden de magnitud que el obtenido en el punto 6, aunque numéricamente tiene un valor menor. Esta diferencia numérica, se debe precisamente a que la polea, no es un cilindro uniforme, ya que tiene más masa concentrada en el borde exterior. De acuerdo, a lo antes descrito y tomando como referencia la figura 13, un aro delgado, tendrá un momento de inercia mayor que la polea. Para este cuerpo I, se calcula: I = MR2 , por lo tanto I = 0.436 kg ·m2 .
- 126. 124 C O L E G I O D E B A C H I L L E R E S D E L E S T A D O D E S O N O R A Resuelvan en binas los siguientes ejercicios. Es necesario que anoten el procedimiento desarrollado para cada uno de ellos. Esta actividad formará parte del portafolio de evidencias y se valorará con la lista de cotejo para evaluar la serie de ejercicios, que aparece al final del bloque. Fuente: Bueche F. J. y Hecht E. (2007). Una fuerza tangencial de 200 N actúa sobre el borde de una rueda de 25 cm de radio. Calculen: a) la torca (τ). b) la torca (τ), considerando que la fuerza forma un ángulo de 40º con respecto a un rayo de la rueda. R=32 m∙N Cierta rueda de 8.0 kg tiene un radio de giro de 25 cm. Determinar: Su momento de inercia. R= 0.50 kg. m2 ¿De qué magnitud es la torca que se requiere para darle una aceleración angular de 3.0 rads2? R= 1.5 m∙N ACTIVIDAD 2 SD2-B3 R= 50 m∙N
- 127. T E M A S S E L E C T O S D E F Í S I C A 1 Analizas la cinética rotacional BLOQUE 3 125 Una rueda de 4 kg de masa y radio de giro de 20 cm rota a razón de 360 rpm. La torca de fricción retardadora es de 0.12 N.m. Calcular el tiempo que le tomará a la rueda llegar al reposo. R= 50 s Determinar la energía cinética rotacional de una rueda de 25 kg de masa que rota a razón de 6.0 rev/s y su radio de giro es de 22 cm. R= 0.86 kJ Una cuerda de 3 m de longitud se enrolla en el eje de una rueda. Se tira de la cuerda con una fuerza constante de 40 N y cuando esta termina de desenredarse, la rueda sigue girando a razón de 2.0 rev/s. Determinar el momento de inercia de la rueda y del eje. Recomendación: despreciar la fricción (la solución más sencilla es por el método de energía). R=1.5 kg . m2 Una rueda de 500 g que tiene un momento de inercia de 0.015 kg. m2, inicialmente gira a razón de 30 rev/s y después de 163 rev, alcanza el reposo. ¿De qué magnitud es la torca que la frena? R= 0.26 m∙N
- 128. 126 C O L E G I O D E B A C H I L L E R E S D E L E S T A D O D E S O N O R A Energía cinética de rotación (Ec). Como lo mencionamos anteriormente la energía cinética de rotación equivale a: Giancoli, D. (2006), menciona que un objeto que gira mientas su centro de masa (CM) experimenta movimiento de traslación tendrá energía cinética tanto de traslación como de rotación. La ecuación de la EC de rotación nos da la energía cinética de rotación, si el eje de rotación está fijo. Si el objeto se mueve (como una rueda que se dirige colina abajo), esta ecuación todavía es válida en tanto el eje de rotación esté fijo en dirección. En estas condiciones, la energía cinética total es: donde vCM es la velocidad lineal del centro de masa, ICM es el momento de inercia en torno a un eje a través del centro de masa, ω es la velocidad angular en torno a este eje, y M es la masa total del objeto. Ejemplo: Esfera que rueda hacia abajo de un plano inclinado. Fuente: Giancoli, D. (2006). Determinar la rapidez de una esfera sólida de masa M y radio R, al momento de alcanzar el fondo de un plano inclinado, si parte desde el reposo a una altura vertical H y rueda sin deslizamiento, como se observa en la siguiente figura: Planteamiento: se utiliza la ley de la conservación de la energía con energía potencial gravitacional, que ahora incluye energía cinética de rotación y energía cinética de traslación. Solución: la energía total en cualquier punto a una distancia vertical y sobre la base del plano inclinado es: donde v es la rapidez del centro de masa y Mgy es la energía potencial gravitacional. Al aplicar la conservación de la energía, se iguala la energía total en la parte alta (y = H, v = 0, ω = 0) con la energía total en el fondo (y= 0):
- 129. T E M A S S E L E C T O S D E F Í S I C A 1 Analizas la cinética rotacional BLOQUE 3 127 El momento de inercia de la esfera sólida en torno a un eje a través de su centro de masa es . Como la esfera rueda sin deslizar, se tiene Al cancelar M y R se obtiene: O Este resultado, se puede comparar con el caso de un objeto que se desliza hacia abajo de un plano inclinado sin girar y sin fricción, a partir de la ecuación: (de la cual, eliminando el término de rotación). Tenemos que y al sustituir valores, obtenemos un resultado mayor. Por lo tanto, se concluye que un objeto, que se desliza sin fricción o sin rotación transforma por completo su energía potencial inicial en energía cinética de traslación (no en energía cinética de rotación), así que la rapidez de su centro de masa es mayor. Nota: El resultado para la esfera rodante muestra (quizá sorpresivamente) que v es independiente tanto de la masa M como del radio R de la esfera. Ejemplo conceptual. ¿Quién es más rápido? Fuente: Giancoli, D. (2006). Varios objetos ruedan al mismo tiempo, a partir del reposo sin deslizar hacia abajo de un plano inclinado de altura vertical H, como se muestra en la figura 15. Los objetos son: un aro delgado (o un anillo de bodas liso), un canica esférica, un cilindro sólido (una pila D) y una lata vacía de sopa; además, de una caja engrasada que se desliza hacia abajo sin fricción. ¿En qué orden alcanzan el fondo del plano inclinado? Figura 15. Movimiento de objetos en un plano inclinado de altura H.
- 130. 128 C O L E G I O D E B A C H I L L E R E S D E L E S T A D O D E S O N O R A Respuesta: El primer objeto en alcanzar el fondo del plano es la caja, porque la pérdida de energía potencial (MgH) se transforma completamente en EC de traslación, mientras que para los objetos rodantes. La energía potencial inicial se comparte entre la energía cinética de traslación y de rotación, y por tanto, su rapidez lineal es menor. Para cada uno de los objetos rodantes, se puede establecer que la pérdida en energía potencial es igual al incremento en energía cinética: Para todos los objetos que ruedan, el momento de inercia ICM se obtiene multiplicando la masa M y el radio R2 (figura 13). La masa M está en cada término, así que la rapidez de traslación v no depende de la masa M; ni depende del radio R, pues ω = v/R , así que R2 se cancela para todos los objetos que ruedan, igual que en el ejemplo anterior. Por tanto, la rapidez v en el fondo depende solamente de dicho factor numérico en ICM , que expresa cómo está distribuida la masa. El aro, con toda su masa concentrada a un radio R (ICM =MR2 ) tiene el mayor momento de inercia; por tanto, tendrá la menor rapidez y llegará al fondo detrás de la pila D (ICM =1/2 MR2 ), que a su vez estará detrás de la canica ( ICM =2/5 MR2 ). La lata vacía, que es en esencia un aro más un disco pequeño, tiene la mayor parte de su masa concentrada en R; así que será un poco más rápida que el aro delgado, pero más lenta que la pila D, como se observa en la figura 15. Nota: como en el ejemplo de la esfera que rueda hacia abajo de un plano inclinado, la rapidez en el fondo no depende de la masa M del objeto o del radio R, sino sólo de su forma y de la altura H de la colina. Si hubiese existido poca o ninguna fricción estática, entre los objetos rodantes y el plano, los objetos redondos se habrían deslizado en lugar de rodar, o bien, se presentaría una combinación de ambas situaciones. La fricción estática debe estar presente para hacer que un objeto redondo ruede. En la ecuación de energía no se necesitó tomar en cuenta la fricción, porque se trata de fricción estática y no se realiza trabajo. El punto de contacto de la esfera en cada instante no se desliza, sino que se mueve de forma perpendicular al plano, primero hacia abajo y luego hacia arriba, conforme la esfera rueda como se observa en la figura 16. En consecuencia, la fuerza de fricción estática no realiza trabajo porque la fuerza y el movimiento (desplazamiento), son perpendiculares. La razón por la que los objetos que ruedan en los dos ejemplos anteriores se mueven hacia abajo del plano más lentamente que si se estuviesen deslizando, no se debe a que la fricción esté realizando trabajo; más bien, se debe a que parte de la energía potencial gravitacional, se convierte en energía cinética de rotación, y por lo tanto, es menos la conversión a energía cinética de traslación. Figura 16. Una esfera que rueda hacia la derecha sobre una superficie plana. El punto de contacto con el suelo en cualquier momento, el punto P, está momentáneamente en reposo. El punto A hacia la izquierda de P se mueve casi verticalmente hacia arriba en el instante mostrado, y el punto B hacia la derecha se mueve casi verticalmente hacia abajo. Un instante después, el punto B tocará el plano y estará en reposo momentáneamente. Por eso, la fuerza de fricción estática no realiza ningún trabajo.
- 131. T E M A S S E L E C T O S D E F Í S I C A 1 Analizas la cinética rotacional BLOQUE 3 129 Cierre ACTIVIDAD 3 SD2-B3 Resuelvan en binas los siguientes ejercicios. Es necesario que anoten el procedimiento desarrollado para cada uno de ellos. Fuente: Bueche F. J. y Hecht E. (2007). Esta actividad formará parte del portafolio de evidencias y se valorará con la rúbrica para evaluar serie de ejercicios, que aparece al final del bloque. 1. La rueda de un molino es un disco uniforme de 0.90 kg y de 8.0 cm de radio. Si dicha rueda, gira uniformemente a partir del reposo con una rapidez de 1 400 rpm en un tiempo de 35 s. ¿De qué magnitud es la torca de fricción que frena su movimiento? R= -1.2 x 10-2 m∙N 2. Un aro de 20 cm de radio rueda hacia abajo, a partir del reposo desde una colina hasta un punto que se encuentra 5.0 m por debajo del punto inicial. ¿Qué tan rápido rota en ese punto? R= 35 rad/s. 3. Un disco sólido rueda sobre una pista en la parte más alta de una colina con una rapidez es de 80 cm/s. Si las pérdidas por fricción son despreciables. ¿Con qué rapidez se mueve el disco cuando se encuentra a 18 cm por debajo de la cima? R= 1.7 m/s
- 132. 130 C O L E G I O D E B A C H I L L E R E S D E L E S T A D O D E S O N O R A 4. Una esfera sólida uniforme, como se muestra en la figura 17 inicialmente rueda sobre una superficie horizontal a 20 m/s y posteriormente rueda hacia arriba sobre un plano inclinado. Si las pérdidas debidas a la fricción son despreciables, ¿cuál será el valor de h en el lugar donde se detiene la esfera? R= 29 m Figura 17.Esfera sólida uniforme. 5. Un disco uniforme circular como el que se muestra en la figura 18, tiene una masa de 6.5 kg y un diámetro de 80 cm. Calcular el momento de inercia alrededor de un eje perpendicular a esta página que pase: a) a través del punto G. R= 0.52 kg·m2 b) a través del punto A. R= 0.83 kg·m2 Figura 18. Disco uniforme circular. 6. Determinar el momento de inercia de las cuatro masas que se muestran en la figura 19, con relación al eje perpendicular de esta página y que pasa a través de: a) el punto A. R= 27 kg·m2
- 133. T E M A S S E L E C T O S D E F Í S I C A 1 Analizas la cinética rotacional BLOQUE 3 131 b) el punto B. R= 33 kg·m2 Figura 19. Disposición de cuatro masas
- 134. 132 C O L E G I O D E B A C H I L L E R E S D E L E S T A D O D E S O N O R A Recursos adicionales para la secuencia didáctica 2 A continuación, se te proporcionan los siguientes recursos disponibles en internet que te permitirán retroalimentar los temas vistos en la secuencia didáctica 2. Tu prepa en videos. http://www.tuprepaenvideos.sep.gob.mx/ Ir a Bachillerato. Dar clic en Materias. Buscar Temas Selectos de Física I. Ir a la pestaña de Lecciones. Buscar Bloque 3: Analizas la cinética rotacional. Los videos de pueden consultar en el sitio de Tu prepa en videos o dando clic derecho sobre el video aparece la opción Obtener la URL del video, la cual es la que compartimos contigo. Se recomienda los siguientes videos: 1) Movimiento de rotación: Ejercicio # 2 sobre Momento de Torsión (8:49) https://youtu.be/oZBqL2F4Uw4 2) Energía cinética rotacional. Rotación de cuerpos rígidos (8:20) https://youtu.be/I3bH0UFl7CI
- 135. T E M A S S E L E C T O S D E F Í S I C A 1 Analizas la cinética rotacional BLOQUE 3 133 Secuencia didáctica 3 Trabajo y potencial rotacional Inicio ACTIVIDAD 1 SD3-B3 De manera individual contesta los siguientes cuestionamientos. Fuente: Giancoli, D. (2006) 1. ¿En qué formas la palabra “trabajo”, se utiliza igualmente en el lenguaje cotidiano como en su definición física? ¿En qué formas es diferente? Proporciona ejemplos de ambos casos. _________________________________________________________________________________________ _________________________________________________________________________________________ __________________________________________________________________________________________ 2. Una mujer que nada corriente arriba, no se mueve con respecto a la orilla. ¿Ella realiza algún trabajo? Si deja de nadar y simplemente flota; ¿Se realiza trabajo sobre ella? _________________________________________________________________________________________ _________________________________________________________________________________________ __________________________________________________________________________________________ 3. De lo alto de una cascada cae agua hacia un estanque que está debajo. ¿Qué le ocurre a la energía potencial gravitacional del agua de la cascada? _________________________________________________________________________________________ _________________________________________________________________________________________ __________________________________________________________________________________________ 4. ¿Por qué es más fácil escalar una montaña en una ruta en zigzag, que escalarla en línea recta? _________________________________________________________________________________________ _________________________________________________________________________________________ __________________________________________________________________________________________ 5. Suponiendo, que se sube una maleta desde el suelo hasta una mesa. Justifica de cuál de los siguientes factores depende la potencia realizada sobre la maleta: a) si se eleva verticalmente o a lo largo de una trayectoria más complicada; b) del tiempo que toma, c) de la altura de la mesa, d) del peso de la maleta. _________________________________________________________________________________________ _________________________________________________________________________________________ __________________________________________________________________________________________
- 136. 134 C O L E G I O D E B A C H I L L E R E S D E L E S T A D O D E S O N O R A Trabajo y potencia rotacionales. En el curso de Física 1 se definió al trabajo como el producto del desplazamiento por la componente de lafuerzaenladirección del desplazamiento. Acontinuaciónanalizaremos el trabajo realizado en el desplazamiento rotacional bajo la influencia de un momento de torsión resultante. De acuerdo a Tippens P. (2011) consideremos la fuerza F, que actúa al borde de una polea de radio r, como muestra la figura 20. El efecto de dicha fuerza es hacer girar la polea a través de un ángulo θ, mientras el punto en el que se aplica la fuerza se mueve una distancia s. La longitud de arco s se relaciona con θ mediante la expresión: s = r·θ Figura 20. Trabajo y potencia en el movimiento de rotación. El trabajo que realiza esta fuerza F es por definición: Trabajo = F·s = F·r·θ Fr es el momento de torsión debido a la fuerza, por lo que obtenemos: Trabajo= W = τ · θ El ángulo θ debe expresarse en radianes en cualquier sistema de unidades de modo que el trabajo pueda expresarse en libras-pie o Joules (J). La energía mecánica generalmente se transmite en la forma de trabajo rotacional. Cuando hablamos de la potencia de salida que desarrollan las máquinas, lo que nos interesa es la razón de cambio con que se realiza el trabajo rotacional. Acontinuación, deduciremos, la expresión matemática a partir de la cual podremos calcular la potencia rotacional. Potencia = trabajo / t = W / t = (τ · θ) / t Como ( θ)/t representa la velocidad angular media ω escribimos Potencia = τ ω A continuación se presenta la analogía entre las cantidades y ecuaciones traslacionales y rotacionales. Desarrollo
- 137. T E M A S S E L E C T O S D E F Í S I C A 1 Analizas la cinética rotacional BLOQUE 3 135 Ejemplo: Una rueda de 60 cm de radio tiene un momento de inercia de 5 kg∙m2. Se aplica una fuerza constante de 60 N tangente al borde de la misma. Suponiendo que parte del reposo, ¿qué trabajo se realiza en 4 s y qué potencia se desarrolla? Fuente: Tippens, P. (2011). Sugerencia: el trabajo es el producto del momento de torsión por el desplazamiento angular. Primero, se calcula el momento de torsión al multiplicar la fuerza del borde por el radio de la rueda; después se determina la aceleración angular; a partir de la segunda ley de Newton, y una vez que se conoce la aceleración, se puede determinar el desplazamiento lineal el trabajo y la potencia desarrollada por la rueda. Datos: R=0.60 m F=60 N I=5kg∙m2 t= 4 s El momento de torsión aplicado al borde de la rueda es:
- 138. 136 C O L E G I O D E B A C H I L L E R E S D E L E S T A D O D E S O N O R A Ejemplo 2: Un enorme rodillo en forma de cilindro uniforme, es jalado por un tractor para compactar la tierra. Este rodillo tiene 1.80 m de diámetro y un peso de 10 kN. ¿Qué potencia promedio, en caballos de fuerza (HP), debe tener el tractor para acelerar desde el reposo hasta una rapidez de 4.0 m/s en una distancia horizontal de 3.0 m? Nota: la fricción se considera despreciable. Fuente: Bueche F. J. y Hecht E. (2007). La potencia es igual al trabajo realizado por el tractor dividido entre el tiempo que toma hacerlo. El tractor realiza el siguiente trabajo:
- 139. T E M A S S E L E C T O S D E F Í S I C A 1 Analizas la cinética rotacional BLOQUE 3 137 ACTIVIDAD 2 SD3-B3 Resuelvan en binas los siguientes ejercicios. Es necesario que anoten el procedimiento desarrollado para cada uno de ellos. Esta actividad formará parte del portafolio de evidencias y se valorará con la lista de cotejo para evaluar serie de ejercicios, que aparece al final del bloque. Fuente: Bueche F. J. y Hecht E. (2007). 1. Cuando se aplican 100 J de trabajo sobre un volante, su rapidez angular se incrementa de 60 rev/min a 180 rev/ min. ¿Cuál es su momento de inercia? R= 0.63 kg· m2 2. Un motor eléctrico gira a 900 rpm y desarrolla una potencia de 2 HP. ¿De qué magnitud es la torca que produce? R= 16 m∙N 3. La tensión en una banda de transmisión es de 1600 N en el lado tenso y de 500 N en el lado flojo. La banda hace girar una polea de 40 cm de radio a una velocidad de 300 rpm. Si esta polea mueve un dínamo que tiene 90% de eficiencia. ¿Cuántos kilowatts genera el dínamo? R=12 kW
- 140. 138 C O L E G I O D E B A C H I L L E R E S D E L E S T A D O D E S O N O R A 4. Una cuerda enrollada en un disco de 3 kg y 20 cm de diámetro recibe una fuerza de tracción de 40 N, que la desplaza una distancia lineal de 5 m. Determinar: a) ¿Cuál es el trabajo lineal realizado por la fuerza de 40 N? R=200 J b) ¿Cuál es el trabajo rotacional realizado sobre el disco? R= 200 J 5. Un motor de 1.2 kW impulsa durante 8 s, una rueda cuyo momento de inercia es 2 kg·m2. Suponiendo que la rueda estaba inicialmente en reposo. ¿Cuál es su rapidez angular final? R= 98.0 rad/s
- 141. T E M A S S E L E C T O S D E F Í S I C A 1 Analizas la cinética rotacional BLOQUE 3 139 Cantidad de movimiento angular. Tippens, P. (2011) señala que una partícula de masa m, que se mueve en un círculo de radio r, con velocidad tangencial v (figura 21 a) tendrá una cantidad de movimiento rectilíneo p= mv, con respecto a un eje de rotación establecido. La cantidad de movimiento angular (L), para estas partículas, se define como el producto de su cantidad de movimiento rectilíneo por la distancia perpendicular que va del eje de rotación a dicha partícula. L = m∙v∙r En un cuerpo rígido extenso, como el que se muestra en la figura 21 b, cada partícula, tiene una cantidad de movimiento angular dado por la ecuación L= m∙v·r. Figura 21. Cantidad de movimiento angular. a) Partícula de masa m. b) Cuerpo rígido extenso. Sustituyendo v = ω·r, cada partícula tiene una cantidad de movimiento angular dada por: m·v·r = m ( ω · r ) r = ( m r2 ) ω Dado que las partículas que constituyen al cuerpo rígido tienen la misma velocidad angular, la cantidad de movimiento angular del cuerpo es: L = ( ∑ m r2 ) ω Por lo tanto, la cantidad de movimiento angular total es igual al producto de la velocidad angular del cuerpo por su momento de inercia: L = I ω Ejemplo: una varilla uniforme delgada mide 1 m de longitud y tiene una masa de 6 kg; si la varilla se hace girar en su centro y se queda en rotación con una velocidad angular de 16 rad/s, ¿Cuál es la magnitud de su cantidad de movimiento angular? Solución: El momento de inercia de una varilla delgada se calcula a partir de la información presentada en la figura 13.
- 142. 140 C O L E G I O D E B A C H I L L E R E S D E L E S T A D O D E S O N O R A Entonces su cantidad de movimiento angular es Observe que la unidad del SI de la cantidad de movimiento angular es kg • m/s. La unidad del Sistema Usual en Estados Unidos (SUEU) es slug • ft2 /s. Conservación de la cantidad de movimiento angular. Para entender mejor la definición de movimiento angular, recordemos la ecuación básica para el movimiento angular τ = I α, partiendo de la ecuación que define la aceleración angular α= ( ωf - ωo ) t podemos escribir la segunda ley de Newton como τ = I (ωf - ωo ) t Al multiplicar por t, se obtiene la ecuación: τt = Iωf - Iω0 El producto τt, se define como impulso angular o cambio en la cantidad de movimiento angular. Si no se aplica ningún momento de torsión externo a un cuerpo que gira, podemos establecer τ = 0 en la ecuación anterior, y obtener: 0 = Iωf - Iω0 Iωf = Iω0 Cantidad de movimiento angular final = cantidad de movimiento angular inicial De esta manera, llegamos a un enunciado para expresar la conservación de la cantidad de movimiento angular: “Si la suma de los momentos de torsión externos que actúan sobre un cuerpo o sistema de cuerpos es cero, la cantidad de movimiento angular permanece sin cambio.” Este enunciado resulta verdadero aún, en el caso de que el cuerpo que gira no sea rígido, sino que pueda cambiar su forma de tal modo que su momento de inercia cambie. En este caso, la rapidez angular también cambia de tal modo que el producto Iω, siempre es constante. Los patinadores, clavadistas y acróbatas controlan la rapidez con que giran sus cuerpos extendiendo o encogiendo susextremidadesparaaumentarodisminuirsurapidezangular.Un ejemplo interesante que ilustra la conservación de la cantidad de movimiento angular, se muestra en la figura 22, que muestra como una patinadora, al girar con los brazos extendidos (a), experimenta un aumento en su momento de inercia y (b) Al acercar las manos a su cuerpo, disminuye su momento de inercia.
- 143. T E M A S S E L E C T O S D E F Í S I C A 1 Analizas la cinética rotacional BLOQUE 3 141 Dado que la cantidad de su movimiento angular, no puede cambiar notará un aumento considerable en su rapidez angular. Al extender sus brazos podrá disminuir su rapidez angular. Figura 22. La patinadora controla su velocidad de rotación moviendo sus brazos hacia adentro para aumentar su rapidez rotacional o hacia afuera para disminuirla. Ejemplo: Una patinadora como modelo. Fuente:Wilson, J; Bufa, A; Lou B. (2007). Por lo general las situaciones de la vida real son complejas, pero algunas se pueden analizar usando modelos simples. En la figura 23 se ilustra un modelo para analizar el giro de una patinadora, empleando un cilindro y dos varillas para representarlo. En (a), la patinadora inicia el giro con los “brazos” extendidos; mientras que en (b), los “brazos” están sobre la cabeza para lograr un giro más rápido por la conservación de la cantidad de movimiento angular. Si la rapidez de giro inicial es 1 revolución por 1.5 s, ¿cuál será la magnitud de la rapidez angular cuando los brazos están pegados al cuerpo? Figura 23. Modelo de una patinadora: Cambios en el momento de inercia y giro. Razonamiento: la representación de la patinadora a través de un cilindro y dos varillas, nos permite determinar de manera sencilla los momentos de inercia (figura 13). Hay que dar atención especial, al hecho de encontrar el momento de inercia de los brazos alrededor del eje de rotación (a través del cilindro). Esto puede hacerse aplicando el teorema del eje paralelo ( I= ICM +Md2 ).
- 144. 142 C O L E G I O D E B A C H I L L E R E S D E L E S T A D O D E S O N O R A Si se conserva la cantidad de movimiento angular Lf = L0 o Iωf =Iω0 conociendo la rapidez angular inicial y dadas las cantidades para calcular los momentos de inercia es posible determinar la rapidez angular final. Solución. Se listan los datos en la figura 23. Datos Donde el eje paralelo a través del CM de la varilla es una distancia de R + L / 2 a partir del eje de rotación. 1/12 (5 kg) (0.80 m)2 + ( 5 kg) (0.20m+0.40m)2 = 2.067 ≈ 2.1 kg∙m2 Ademas I0 = IC +2I r = 1.5 kg∙m2 + 2 (2.1 kg∙m2 ) = 5.7 kg ∙ m2 Al tratar la masa de un brazo, como si su centro de masa ahora estuviera a sólo unos 20 cm del eje de rotación, el momento de inercia de cada brazo es I = Mr R2 I = Ic + 2(Mr R2 ) =1.5 kg∙m2 + 2 (5 kg∙m2 )(0.20m)2 = 1.9 kg∙m2
- 145. T E M A S S E L E C T O S D E F Í S I C A 1 Analizas la cinética rotacional BLOQUE 3 143 Entonces, con la conservación de la cantidad de movimiento angular, Lf = L0 o Iωf =Iω0 , por lo que: De manera que la rapidez angular se incrementa en un factor de 3. Resuelvan en equipos de tres integrantes los siguientes ejercicios, anotando el procedimiento desarrollado para cada uno de ellos. Esta actividad formará parte del portafolio de evidencias y se valorará con rúbrica para evaluar serie de ejercicios, que aparece al final del bloque. Fuente: Tippens, P. (2011) y Hewitt, P. (1996) 1. Dos masas de 2 kg y 6 kg, están unidas por una barra ligera de 30 cm. Suponiendo que se hace girar el sistema horizontalmente a razón de 300 rpm en torno a un eje localizado a 10 cm de la masa de 6 kg. Determinar: a) ¿Cuál es el momento de inercia en tomo de este eje? R=0.140 kg . m2 b) ¿Cuál es la energía cinética rotacional? R= 69.1 J ACTIVIDAD 2 SD1-B1 Cierre
- 146. 144 C O L E G I O D E B A C H I L L E R E S D E L E S T A D O D E S O N O R A 2. La rueda de una carreta mide 60 cm de diámetro y está montada en un eje central sobre el cual gira a razón de 200 rev/min. Sugerencia: Tomar como modelo de la rueda a una varilla delgada, que gira sobre sus extremos suponiendo que ésta es un aro circular de 2 kg de masa, y cada uno de sus 12 rayos de madera tienen una masa de 500 g. Calcular: a) El momento de inercia de toda la rueda. R= 0.360 kg.m2 b) La energía cinética rotacional. R= 78.9 J 3. Una varilla delgada de 3 kg tiene 40 cm de longitud y oscila sobre su punto medio. ¿Qué momento de torsión se requiere para que la varilla realice 20 revoluciones; para que su rapidez de rotación, se incremente de 200 a 600 rev/min? R= 0.558 m∙N 4. Una masa de 2 kg se balancea en el extremo de una varilla ligera; describiendo un círculo de 50 cm de radio. ¿Qué momento de torsión resultante se requiere para impartir a esa masa, una aceleración angular de 2.5 rad/s2 ? R=1.25 m∙N
- 147. T E M A S S E L E C T O S D E F Í S I C A 1 Analizas la cinética rotacional BLOQUE 3 145 5. Un motor de 1.2 kW impulsa durante 8s una rueda cuyo momento de inercia es 2 kg∙m2 . Suponiendo, que la rueda estaba inicialmente en reposo, ¿a cuánto equivale la magnitud de la rapidez angular final? R= 98.0 rad/s 6. Un motor de 600 W (watts) impulsa a una polea con una velocidad angular media de 20 rad/s. ¿Cuál es el momento de torsión así obtenido? R= 30 m∙N 7. Un cilindro de 2 kg de masa tiene un radio de 20 cm y rueda sin deslizarse a lo largo de una superficie horizontal con una velocidad de 112 m/s. Calcular: a) ¿Cuál es su energía cinética traslacional? R= 144 J (b) ¿Cuál es su energía cinética rotacional? R= 72 J (c) ¿Cuál es la energía cinética total? R= 216 J
- 148. 146 C O L E G I O D E B A C H I L L E R E S D E L E S T A D O D E S O N O R A 8. Suponiendo que, sobre un plano inclinado de 16 m de altura, ruedan los siguientes cuatro objetos, cada uno de 3 kg de masa: un aro circular, un disco, una esfera y una caja. Determinar el orden y la magnitud de las velocidades finales en el cual llegan al punto más bajo del plano. Sugerencia: considerar que la fricción es insignificante para la caja, pero les permite a los otros cuerpos rodar sin deslizarse. R= Vcaja = 17.7 m/s; Vesfera = 14.97 m/s; Vdisco, = 14.46 m/s; Varo = 12.5 m/s 9. El borde de un disco inicialmente en reposo experimenta repentinamente un momento de torsión de 400 N·m. Si la inercia rotacional del disco es de 4 kg • m2 y el momento de torsión actúa durante 0.02 s. Determinar: a) El cambio en la cantidad de movimiento angular. R= 8.00 kg • m2 /s b) La rapidez angular final. R= 2.00 rad/s 10. Una varilla de acero de 500 g de masa y 30 cm de longitud, gira sobre su centro a razón de 300 rev/min. ¿Cuál es la magnitud de su cantidad de movimiento angular? R= 0.118 kg. m/s2
- 149. T E M A S S E L E C T O S D E F Í S I C A 1 Analizas la cinética rotacional BLOQUE 3 147 REACTIVOS DE CIERRE 1. Creemos que nuestra galaxia se formó a partir de una nube gigantesca de gas. Esta nube era mucho más grande que la galaxia actual y de forma más o menos esférica, giraba con mucha más lentitud de la que gira actualmente. En la figura 24, se observa la nube original y la galaxia tal como es hoy. Explica cómo contribuyen la Ley de la Gravitación Universal y la conservación de la cantidad de movimiento angular, para que la galaxia actualmente, tenga esta forma y gire con mayor rapidez. Figura 24. Formación de nuestra galaxia 2. El trompo de la figura 25, inicialmente en reposo, tiene un momento de inercia de 4 x 10-4 kg . m2 y gira libremente sobre un eje inmóvil AA´. Suponiendo que la cuerda enrollada alrededor de la clavija a lo largo del eje del trompo, se tira de tal manera, que se mantiene una tensión constante de 5.57 N en la cuerda evitando que dicha cuerda resbale, al enrollarla alrededor de la clavija. Determinar la rapidez angular del trompo, después de que 80 cm de la cuerda han sido jalados de la clavija, considerando el trabajo que se hace en este movimiento. Figura 25. Trompo en movimiento giratorio en un eje inmóvil AA’
- 150. 148 C O L E G I O D E B A C H I L L E R E S D E L E S T A D O D E S O N O R A 3. Un estudiante se sienta en una silla giratoria sosteniendo dos objetos de 3.0 kg de masa cada uno, como se observa en la siguiente figura: Cuando el estudiante mantiene extendidos sus brazos horizontalmente, los objetos distan a 1.0 m respecto al eje de rotación y éste gira con una rapidez angular de 0.75 rad/s; el momento de inercia del estudiante y la silla, tienen una magnitud constante de 3 kg . m2. Suponiendo que el estudiante jalará los objetos horizontalmente a 0.30 m del eje de rotación, determinar: a) La nueva rapidez angular del estudiante. b) La energía cinética del estudiante antes y después de que los objetos sean aproximados al eje de rotación 4. En un refrigerador hay dos huevos, uno de ellos está crudo y el otro bien cocido. Suponiendo que una persona desea identificar el huevo crudo sin romper los cascarones, para ello decide comparar los movimientos de rotación haciéndolos rodar en el piso. ¿Cuál de los huevos rueda con mayor rapidez? ¿Cuál de los huevos rueda más uniformemente? Explica tu respuesta.
- 151. T E M A S S E L E C T O S D E F Í S I C A 1 Analizas la cinética rotacional BLOQUE 3 149 Actividad experimental: Conservación de la energía mecánica de un cuerpo rígido. Enequipodecuatrointegrantespondránenprácticasusconocimientosyhabilidadesparademostrarlaconservación de la energía mecánica, en un cuerpo rígido que rueda sin deslizarse. El producto a entregar de esta actividad, será un reporte de laboratorio, en el formato que su maestro les indique. Material • 1 Plano inclinado. • 1 Esfera maciza. • 1 Pie de rey o vernier. • 1 Balanza granataria o de triple brazo. Fundamentación teórica. La energía mecánica de un cuerpo rígido (esfera sólida), inicialmente en reposo a una altura h, está dada por la energía potencial y a medida que ésta desciende, dicha energía se transforma en energía cinética de rotación respecto al centro de masa (CM) y en energía cinética de traslación, considerando que rueda sin deslizarse. Para comprobar lo antes descrito, es necesario montar un diseño experimental, como el que se muestra en la siguiente figura: ACTIVIDAD INTEGRADORA La energía cinética que experimenta la esfera sólida, está determinada por la siguiente ecuación: Al llegar a la base del plano, toda la energía potencial de la esfera, se transforma en energía cinética, por lo tanto: Como la esfera es sólida, su momento de Inercia (I) respecto a uno de sus diámetros es:
- 152. 150 C O L E G I O D E B A C H I L L E R E S D E L E S T A D O D E S O N O R A Con base al movimiento de traslación de la esfera, podemos calcular la magnitud de la velocidad, con la que llega a la base del plano utilizando las ecuaciones: Así mismo calcular ω. Deduce a partir de I y ω, la velocidad (V). ¿Qué tan similares o diferentes son estas magnitudes que obtuvieron a partir de procedimientos distintos? Con estos datos, determinarán la magnitud de cada una de las energías involucrados en el movimiento de la esfera sólida y les permitirá comprobar para este sistema, la conservación de la energía mecánica. Nota: Para obtener resultados confiables, se recomienda realizar tres mediciones en los pasos 2, 3 y 4 y utilizar el promedio de estas mediciones en los cálculos correspondientes. Contesten los siguientes cuestionamientos (formarán parte de los anexos del reporte de laboratorio). 1. ¿Cuáles son las fuerzas que actúan sobre la esfera sólida? __________________________________________________________________________________________ __________________________________________________________________________________________ __________________________________________________________________________________________ 2. Planteen la ecuación que describe el movimiento de traslación del centro de masa. __________________________________________________________________________________________ 3. Planteen la ecuación que describe el movimiento de rotación alrededor de un eje que pasa por el centro de masa. __________________________________________________________________________________________ 4. ¿Por qué no es necesario incluir el trabajo de la fuerza de rozamiento en el cálculo de energía de un cuerpo rígido que rueda sin deslizarse? __________________________________________________________________________________________ __________________________________________________________________________________________ __________________________________________________________________________________________ 5. ¿Qué se debe cumplir para que un cuerpo rígido ruede sin deslizarse? __________________________________________________________________________________________ __________________________________________________________________________________________ __________________________________________________________________________________________
- 153. T E M A S S E L E C T O S D E F Í S I C A 1 Analizas la cinética rotacional BLOQUE 3 151 Recursos adicionales para la secuencia didáctica 3 A continuación, se te proporcionan los siguientes recursos disponibles en internet que te permitirán retroalimentar los temas vistos en la secuencia didáctica 3. Tu prepa en videos http://www.tuprepaenvideos.sep.gob.mx/ Ir a Bachillerato. Dar clic en Materias. Buscar Temas Selectos de Física I. Ir a la pestaña de Lecciones. Buscar Bloque 3: Analizas la cinética rotacional. Los videos de pueden consultar en el sitio de Tu prepa en videos o dando clic derecho sobre el video aparece la opción Obtener la URL del video, la cual es la que compartimos contigo. Se recomienda los siguientes videos: SD 3 1) Trabajo rotacional y Potencia rotacional. Ejemplo 1 (13:20) https://youtu.be/wgT2hmy8-Jc 2) Trabajo rotacional y Potencia rotacional. Ejemplo 2 (8:20) https://youtu.be/PRvrd0KGK5A
- 154. 152 C O L E G I O D E B A C H I L L E R E S D E L E S T A D O D E S O N O R A Lista de cotejo para evaluar serie de ejercicios Alumno: _____________________________________________ Grupo: ______ Marque en Sí, si el estudiante muestra el criterio, marque en No, si el estudiante no muestra el criterio. CRITERIO SI NO Plantea correctamente la estrategia elegida para solucionar el problema. Presenta procedimiento (s) correcto (s) de manera ordenada para cada uno de los ejercicios. Resuelve correctamente todos los ejercicios planteados. Señala la respuesta correcta para cada uno de los ejercicios. Anota las unidades correspondientes en cada uno de los datos obtenidos y en el resultado final. Puntos obtenidos
- 155. T E M A S S E L E C T O S D E F Í S I C A 1 Analizas la cinética rotacional BLOQUE 3 153 Rúbrica para evaluar serie de ejercicios Elementos Excelente Bueno Regular Deficiente EJERCICIOS Presenta la totalidad de ejercicios o cuestionamientos a resolver. Entrega más del 80% de los ejercicios a resolver. Presenta más del 60% de los ejercicios a resolver. Presenta menos del 50% de los ejercicios a resolver. PROCEDIMIENTO Refleja un razonamiento detallado y ordenado, utilizando el proceso adecuado, siguiendo los pasos para resolver los ejercicios de manera correcta. Refleja un razonamiento sin orden, puede hacer los ejercicios pero no explica la manera en que los resolvió. Cuando los hace utiliza el proceso adecuado siguiendo los pasos para resolver los ejercicios de manera correcta. Refleja un razonamiento sin orden, puede hacer los ejercicios pero no explica la manera en que los resolvió. Utiliza otro proceso obteniendo un resultado razonable. No refleja ningún razonamiento, resuelve los ejercicios de manera mecánica. RESULTADOS Presenta el resultado obtenido de los ejercicios y es correcto. Puede corroborarlo dándole sentido. Presenta 80% ó más resultados correctos, comete algunos errores, debido a cálculos erróneos, utiliza el proceso adecuado y sigue los pasos para resolverlo. Presenta 60 % ó más resultados correctos, comete algunos errores debido a cálculos erróneos, y un proceso inadecuado, se salta los pasos para resolverlo. Presenta 50% o menos resultados correctos, no sigue el procedimiento adecuado. Total 100% Puntaje 80% Puntaje 60% Puntaje 40% Puntaje Fuente: http://portalacademico.cch.unam.mx/
- 156. 154 C O L E G I O D E B A C H I L L E R E S D E L E S T A D O D E S O N O R A Rúbrica para evaluar la Actividad Integradora Niveles de desempeño 5 (Excelente) 3 (Adecuado) 1 (Insuficiente) Introducción Introducción completa y bien escrita, proporcionado un buen marco para contextualizar el experimento. Introducción básicamente completa, con omisión sólo de algunos aspectos menores. Incorpora cierta información del marco del experimento, omitiendo algunos aspectos importantes. Marco Teórico Las fuentes información excelentemente integradas con el material práctico, coherente redacción. Lo presentado argumenta totalmente el tema. La mayoría de los conceptos están sustentados. Presentan alguna desconexión en la redacción y no están del todo claras respecto a lo desarrollado en el laboratorio. Algunos supuestos están evidenciados y justificados. Las citas se integran de modo deficiente, pobre o débil integración de fuentes secundarias. Metodología Se presentan todos los detalles del experimento. Se presentan todos los detalles importantes de la práctica de laboratorio salvo omisiones menores. Se presentan algunos detalles experimentales importantes, con omisiones relevantes. Resultados Las tablas y esquemas están correctamente diseñados, numerados y titulados. Se comprende fácilmente la actividad desarrollada a partir de la presentación de los resultados. Las tablas y esquemas son en general correctos, aunque presentan algún problema menor que podría ser mejorado. La actividad desarrollada se comprende fácilmente, debido a imprecisiones menores. La mayor parte de las tablas yesquemaspresentanerrores de diseño, numeración y titulo; además carecen de información importante. Discusión Todos los resultados comparativos han sido interpretados y discutidos correctamente; por lo que se observa una excelente comprensión de la información planteada en los contenidos. Casi todos los resultados han sido interpretados y discutidos correctamente. Se identifican una mediana comprensión de la información planteada en los contenidos. Sóloalgunosdelosresultados han sido interpretados y discutidos correctamente. No se observa dominio de la información planteada en los contenidos. Conclusiones Se exponen con claridad y de manera coherente, cada uno de los aspectos teóricos relacionados con la actividad experimental. Se exponen con claridad y de manera coherente, solo algunos de los aspectos teóricos relacionados con la actividad experimental. Seexponenconpocaclaridad y de manera incoherente, la mayoría de los aspectos teóricos relacionados con la actividad experimental,
- 157. T E M A S S E L E C T O S D E F Í S I C A 1 Analizas la cinética rotacional BLOQUE 3 155 Anexos Se responden correctamente y detalladamente los cuestionamientos planteados en este apartado. Se responden correctamente y detalladamente la mayor parte de los cuestionamientos planteados en este apartado. Se responden correctamente y detalladamente solamente dos de los cuestionamientos planteados en este apartado. Referencias Referencias bibliográficas completas y correctamente citadas de acuerdo a la metodología APA. Presenta la mayoría de las referenciasbibliográficacitadas dentro del marco teórico. Presenta una bibliografía incompleta obviando algunas referencias obligatorias. Entrega El reporte fue entregado en tiempo y la forma solicitada. El reporte fue entregado en tiempo, pero no en la forma solicitada. El reporte no se entregó en tiempo ni en la forma solicitada. Alumno: Grupo: Total (Multiplicado por 0.44)
- 158. 156 C O L E G I O D E B A C H I L L E R E S D E L E S T A D O D E S O N O R A RÚBRICA DE EVALUACIÓN DE PORTAFOLIO DE EVIDENCIAS Criterio/ Puntuación 4 3 2 1 Puntaje Portada Incluye logo y nombre de la institución, autor, curso, fecha y lugar donde fue elaborado. Falta un elemento en la presentación del trabajo. Faltan dos elementos en la presentación del trabajo. Carece de tres o más elementos para la correcta presentación del trabajo. Objetivo El objetivo representa el aprendizaje obtenido y la razón por la cual se estructuran de esa forma las evidencias. El objetivo del portafolio considera sólo parcialmente los contenidos estudiados. El objetivo del portafolio no es congruente con los contenidos o lecciones estudiadas. No tiene objetivo explícito. Evidencias Incluye todos los tipos de evidencias solicitadas. Las evidencias demuestran los avances en los aprendizajes esperados. Incluye la mayoría de las evidencias solicitadas. Sin embargo no todas las evidencias demuestran claramente el avance en los aprendizajes esperados. Incluye algunas de las evidencias solicitadas. Estas evidencias demuestran mínimamente el avance en los aprendizajes esperados. Incluye sólo uno o ninguna de las evidencias solicitadas, sin demostrar avance en los aprendizajes. Organización Todos los documentos están correctamente presentados: constan de encabezado, son claros y limpios. A los documentos les falta algún elemento de la presentación. A los documentos les faltan más de dos elementos de presentación. El documento solo tiene un elemento o ninguno de presentación. Ortografía El portafolio de evidencias está elaborado sin errores ortográficos. Se observan hasta cinco errores ortográficos. Se observan de 6 a 10 errores ortográficos en el portafolio. Se observan más de 10 errores ortográficos. Total
- 159. T E M A S S E L E C T O S D E F Í S I C A 1 Analizas la cinética rotacional BLOQUE 3 157 Reflexiones generales relacionados al Bloque Iii ¿Lograste comunicar tus ideas o puntos de vista al trabajar en equipo o en grupo? Nunca Muy pocas veces Frecuentemente Siempre ¿Tomaste en cuenta la participación de tus compañeros para modificar tus respuestas, tus acercamientos a los problemas, etc.? Nunca Muy pocas veces Frecuentemente Siempre ¿Lograste interpretar las ideas de tus compañeros al realizar alguna tarea o actividad de clase? Nunca Muy pocas veces Frecuentemente Siempre ¿Participaste activamente en las discusiones de equipo o grupales? Nunca Muy pocas veces Frecuentemente Siempre ¿Expresaste alguna forma de resolver los problemas formulados en las actividades a tus compañeros o al profesor? Nunca Muy pocas veces Frecuentemente Siempre ¿Usaste algún recurso tecnológico (software, internet, calculadoras, etc.) para apoyar tus actividades de tarea o de clase? Nunca Muy pocas veces Frecuentemente Siempre ¿Te entusiasma ayudar a tus compañeros o que ellos te ayuden a resolver dudas? Nunca Muy pocas veces Frecuentemente Siempre ¿Qué te pareció más interesante de este bloque? __________________________________________________________________________________________ __________________________________________________________________________________________ _________________________________________________________________________________________ __________________________________________________________________________________________ _________________________________________________________________________________________ __________________________________________________________________________________________ __________________________________________________________________________________________
- 160. 158 C O L E G I O D E B A C H I L L E R E S D E L E S T A D O D E S O N O R A BLOQUE 1 Bueche F. J. y Hecht E. (2007). Física General. Colección Schaum. Editorial McGraw-Hill. Décima Edición. Giancoli, D. (2006). FÍSICA. Principios con aplicaciones. Volumen 1. Sexta edición. Pearson Educación, México Harita A. (2012).Temas Selectos de Física 1. Módulo de Aprendizaje. Editorial Cobach Sonora Segunda edición Hewitt, P. (1996). Física Conceptual. Décima edición. Editorial Pearson Addison Wesley Perez H. (2000). Física General. Decima quinta reimpresión. Publicaciones Cultural. México. Serway R. y Jewett, J. (2008). Física para ciencias e ingeniería. Volumen 1. Séptima edición. Cengage Learning. Slisko, J. (2010). Física 1, El GIMNASIO de la MENTE, Competencias para la vida. 2ª edición, Edit. PEARSON, México, D. F. Soto, J. (2014). Vive los Temas Selectos de Física 1. Edit. Progreso, 1ra reimpresión, México, D. F. 112 p. Tippens P. (2011). Física, conceptos y aplicaciones. Editorial McGraw Hill Séptima edición revisada. Vasquez A.(2009).Física 1. Bachillerato General.Pearson Educación. México Wilson, J; Bufa, A; Lou B. (2007). Física. Pearson Educación Sexta edición. Young, H. y Freedman R.( 2009). Física universitaria volumen 1. Decimosegunda edición. Pearson Educación, México. BLOQUE 2 Hewitt, P. (1996). Física Conceptual. Décima edición. Editorial Pearson Addison Wesley Perez H. (2000). Física General. Decima quinta reimpresión. Publicaciones Cultural. México. Serway R. y Jewett, J. (2008). Física para ciencias e ingeniería. Volumen 1. Séptima edición. Cengage Learning. Soto, J. (2014). Vive los Temas Selectos de Física 1. Edit. Progreso, 1ra reimpresión, México, D. F. 112 p. Tippens P. (2011). Física, conceptos y aplicaciones. Editorial McGraw Hill Séptima edición revisada. BLOQUE 3 Bueche F. J. y Hecht E. (2007). Física General. Colección Schaum. Editorial McGraw-Hill. Décima Edición. Giancoli, D. (2006). FÍSICA. Principios con aplicaciones. Volumen 1. Sexta edición. Pearson Educación, México. Harita A. (2012).Temas Selectos de Física 1. Módulo de Aprendizaje. Editorial Cobach Sonora Segunda edición, Hermosillo, sonora. REFERENCIAS
- 161. T E M A S S E L E C T O S D E F Í S I C A 1 Analizas la cinética rotacional BLOQUE 3 159 Hewitt, P. (1996). Física Conceptual. Décima edición. Editorial Pearson Addison Wesley Perez H. (2000). Física General. Decima quinta reimpresión. Publicaciones Cultural. México. Serway R. y Jewett, J. (2008). Física para ciencias e ingeniería. Volumen 1. Séptima edición. Cengage Learning. Tippens P. (2011). Física, conceptos y aplicaciones. Editorial McGraw Hill Séptima edición revisada. Wilson, J; Bufa, A; Lou B. (2007). Física. Pearson Educación Sexta edición. Young, H. y Freedman R. (2009). Física universitaria volumen 1. Decimosegunda edición. Pearson Educación, México.

























































































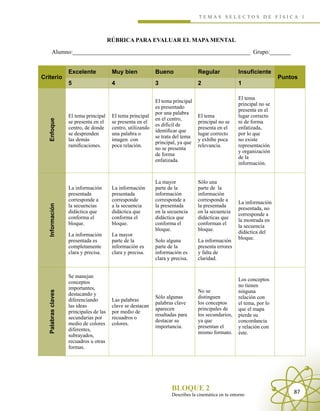





















![T E M A S S E L E C T O S D E F Í S I C A 1
Analizas la cinética rotacional
BLOQUE 3 109
se desliza, la fricción cinética apuntará en dirección opuesta a la velocidad. La fuerza ya no se ejerce más hacia el
centro de la circunferencia y el automóvil no puede continuar en una trayectoria curva.
Sucede, incluso algo peor: si la carretera está mojada o cubierta de hielo, el bloqueo de las ruedas ocurre a menor
fuerza sobre el pedal del freno pues existe menos fricción de la carretera para mantener a las ruedas girando en
lugar de deslizar.
El peralte consiste en elevar en las curvas el borde exterior de las vías una cierta cantidad, para que permita que
una componente del vehículo se oponga a la fuerza centrífuga (Fc) evitando de esta manera que el vehículo se
desvíe radialmente de su trayectoria hacia fuera ocasionando un accidente.
El peralte de las curvas reduce la posibilidad de derrape, ya que la fuerza normal ejercida en una superficie con
peralte, actúa perpendicularmente a ésta, por lo que tendrá un componente hacia el centro de la circunferencia, con
la que se reduce la dependencia de la fricción como se observa en la figura siguiente.
Figura 10. Fuerza normal sobre un automóvil que toma
una curva peraltada, descompuesta en sus componentes
horizontal y vertical (Fuente Giancoli, D, 2006)
Para un ángulo de peralte dado θ, habrá una rapidez para la que no se requerirá fricción en absoluto. Éste será
el caso cuando la componente horizontal de la fuerza normal (FN sen θ) hacia el centro de la curva (como se
observa en la figura anteriormente mostrada), sea justo igual a la fuerza que se requiere para brindar a un vehículo
su aceleración centrípeta, es decir cuando:
FN
*sen θ = m v2
/r [no se requiere fricción]](https://image.slidesharecdn.com/tsf1-210821224735/85/Tsf1-111-320.jpg)



















































