20110522 systems of typed lambda_calculi_moskvin_lecture11

Системы типизации лямбда-исчисления

Лекция 11. Чистые системы типов

Денис Москвин

22.05.2011

CS Club при ПОМИ РАН

1

Чистые системы типов (PTS): введение (1)

Чистые системы типов (Pure Type Systems) задают абстракт-
ную инфраструктуру, позволяющую унифицированно описы-
вать конкретные системы типов:

• интерпретация высказывания-как-типы приобретает про-
стую форму

• легко сравнивать свойства разных систем

• многие свойства доказываются для целых групп систем

Берарди [1989] и Терлов [1989]
2

Чистые системы типов (PTS): введение (2)

Обобщения систем λ-куба, формирующие системы PTS:

• количество сортов становится произвольным
(на кубе их два ∗ и );

• набор аксиом тоже может быть расширен
(на кубе аксиома одна ∗ : );

• сорт Π-типа может отличаться от сорта возвращаемого
значения

3

Определение PTS (1)

Множество (пред)выражений

Λ := V | C | Λ Λ | λV : Λ. Λ | ΠV : Λ. Λ
где V множество переменных, а C констант.

Высказывания M : A, объявления x : A, (пред)контексты Γ
как на λ-кубе.

4

Определение PTS (2)

Спецификация конкретной PTS задаётся тройкой S = (S, A, R)

• S подмножество C, его элементы называют сортами

• A множество аксиом вида c : s, причём c ∈ C и s ∈ S

• R множество правил вида (s1, s2, s3), причём s1, s2, s3 ∈ S

V объединение непересекающихся подмножеств
V = ∪s∈SVs, Vs1 ∩ Vs2 = ∅, Vs = {sx, sy, sz, . . .}
Греко-латинская система: ∗x, ∗y, ∗z, α, β, γ.
5

Аксиомы и правила для Γ λS M : A (1)

Нотация присваивания типов Γ λS M : A задаётся так

Аксиомы , если (c : s) ∈ A
c:s
Γ A:s
Начальное правило , если x ≡ sx ∈ Γ
Γ, x:A x:A

Γ M:A Γ B:s
Правило ослабления , если x ≡ sx ∈ Γ
Γ, x:B M:A

Здесь s ∈ S, c ∈ C, x ∈ V и A, B, M ∈ Λ.

(продолжение далее...)
6


Γ A : s1 Γ , x : A B : s2
Правило произведения , (s1, s2, s3) ∈ R
Γ (Πx : A. B) : s3

Γ M : (Πx : A. B) Γ N : A
Правило применения
Γ M N : B[x := N]

Γ , x : A M : B Γ (Πx : A. B) : s
Правило абстракции
Γ (λx : A. M) : (Πx : A. B)

Здесь s, s1, s2, s3 ∈ S, x ∈ V и A, B, M, N ∈ Λ.

7


Γ A:B Γ B :s B =β B
Правило преобразования
Γ A:B

Здесь s ∈ S и A, B, B ∈ Λ.

Посылка B =β B может быть неразрешима; её можно заме-
нить на
B →β B ∨ B →β B

8

Примеры PTS (1)

Принято обозначение (s1, s2) ≡ (s1, s2, s2).

S ∗, S ∗,
λ→ A ∗: λ2 A ∗:
R (∗, ∗) R (∗, ∗), ( , ∗)

S ∗, S ∗,
λω A ∗: λP A ∗:
R (∗, ∗), ( , ∗), ( , ) R (∗, ∗), (∗, )

9


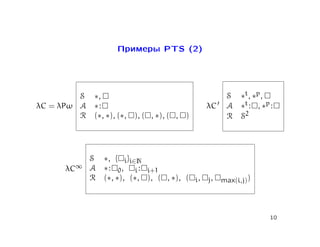
S ∗, S ∗t, ∗p,
λC = λPω A ∗: λC A ∗t : , ∗p :
R (∗, ∗), (∗, ), ( , ∗), ( , ) R S2

S ∗, { i}i∈N
λC∞ A ∗ : 0, i : i+1
R (∗, ∗), (∗, ), ( , ∗), ( i, j, max(i,j))

10


S ∗ S ∗, , ∆
λ∗ A ∗:∗ λU A ∗: , :∆
R (∗, ∗) R (∗, ∗), ( , ∗), ( , ), (∆, ∗), (∆, )

Две последние системы неконсистентны в том смысле,
что в них все типы являются обитаемыми (парадокс Жира-
ра).

11

Свойства PTS (1)

Пусть Γ предконтекст, а A предвыражение.

Γ называется (допустимым) контекстом, если
∃A, B ∈ Λ Γ A : B.

A ∈ Λ называется (допустимым) выражением, если
∃Γ , B ∈ Λ Γ A : B ∨ Γ B : A .

12


Пусть Γ предконтекст, а A предвыражение.

A называется Γ -термом, если
∃B ∈ Λ Γ A : B ∨ Γ B : A .

A называется Γ -типом (сорта s), если
∃s ∈ S Γ A : s.

A называется Γ -элементом (типа B сорта s), если
∃B ∈ Λ ∃s ∈ S Γ A : B : s.

13


Лемма подстановки для PTS
Пусть
Γ , x : A, ∆ M:B
и
Γ N:A
тогда
Γ , ∆[x := N] M[x := N] : B[x := N]

Лемма thinning для PTS
Пусть Γ и ∆ допустимые контексты, причём Γ ⊆ ∆, тогда
Γ M:A ⇒ ∆ M:A
14

Свойства PTS: Лемма генерации (1)

Для Γ P : Q по известной структуре выражения P
Λ := C | V | Λ Λ | λV : Λ. Λ | ΠV : Λ. Λ
представляет свойства Γ и Q.

Лемма генерации для PTS
Γ c : Q ⇒ ∃s ∈ S
Q =β s ∧ (c : s) ∈ A

Γ x : Q ⇒ ∃s ∈ S ∃B =β Q
Γ B : s ∧ (x : B) ∈ Γ ∧ x ≡ sx

15

Свойства PTS: Лемма генерации (2)

Лемма генерации для PTS (продолжение)

Γ (Πx : A. B) : Q ⇒ ∃(s1, s2, s3) ∈ R
Γ A : s1 ∧ Γ , x : A B : s2 ∧ Q =β s3

Γ (λx : A. M) : Q ⇒ ∃s ∈ S ∃B
Γ (Πx : A. B) : s ∧ Γ , x : A M : B ∧ Q =β Πx : A. B

Γ (M N) : Q ⇒ ∃A, B
Γ M : (Πx : A. B) : s ∧ Γ N : A ∧ Q =β B[x := N]

16

Следствия леммы генерации (1)

Γ M : A ⇒ ∃s ∈ S
A≡s ∨ Γ A:s

Γ M : (Πx : B1. B2) ⇒ ∃s1, s2 ∈ S
Γ B1 : s1 ∧ Γ , x : B1 B2 : s2

Если A является Γ -термом, то A это сорт, или Γ -тип или
Γ -элемент.

Если A допустим и B его подтерм, то B допустим.
17

Следствия леммы генерации (2)

Классы сортов, Γ -типов и Γ -элементов могут пересекаться.

Например,

α:∗ (λx : α. x) : (α → α) : ∗
α:∗ (α → α) : ∗ :
Выражение α → α выступает в роли и Γ -типа или Γ -элемента.

Есть здесь ещё смешение ролей?

18

Свойства PTS: редукция субъекта

Теорема о редукции субъекта для PTS

Γ M:A ∧ M βM ⇒ ∆ M :A

Следствия

Γ M:B ∧ B βB ⇒ Γ M:B

(в правиле преобразования ещё требуется B : s!)

Если A является Γ -термом и A β A , то A тоже является
Γ -термом.
19

Свойства PTS: Лемма конденсации

Лемма конденсации для PTS (Condensing, Strengthening)

Γ , x : A, ∆ M : B ∧ x ∈ FV(∆) ∪ FV(M) ∪ FV(B) ⇒ Γ , ∆ M:B

20

Свойства PTS: Теорема единственности типа

Определение. PTS называется функциональной или еди-
носортной (singly sorted), если

1. (c : s1), (c : s2) ∈ A ⇒ s1 ≡ s2;

2. (s1, s2, s3), (s1, s2, s4) ∈ R ⇒ s3 ≡ s4.

Все рассматриваемые нами ранее системы функциональны.

Теорема Для функциональной PTS

Γ M:A ∧ Γ M:A ⇒ A ≡β A

21

Степень терма на λ-кубе

Имеется полезная классификация предтермов, полезная для
анализа допустимых термов в системах λ-куба. Задаётся отоб-
ражение : Λ → {0, 1, 2, 3}:
( ) = 3
(∗) = 2
( x) = 1
(∗x) = 0
(λx : A. B) = (Πx : A. B) = B
(M N) = M
Для M ∈ Λ значение (M) называют степенью M.

Утверждение. Для всех систем λ-куба
Γ M:A ⇒ (M) + 1 = (A)
22

Свойства PTS: нормализуемость.

Определение. PTS называется сильно нормализуемой,
если все её допустимые термы сильно нормализуемы, то есть

Γ M : A ⇒ SN(M) ∧ SN(A)

Утверждение. Все системы λ-куба сильно нормализуемы.

Теорема. Разрешимость TCP и TSP для нормализуе-
мой PTS. Если PTS с конечным числом сортов сильно или
слабо нормализуема, то TCP и TSP разрешимы.

23

Населённость ⊥

Утверждение. Пусть λS это PTS, расширяющая λ2. Тогда

λS M : ⊥ ⇒ M не имеет NF

То есть ⊥ = Πα : ∗. α может быть населён только термами, не
имеющими нормальной формы. Отсюда следует, что если
система нормализуема, то ⊥ не населён.

24

Проверка типов для λP

Одновременно задаются два алгоритма:
OK : PreContext → Bool
TY : PreContext → PreTerm → Term
OK Γ проверяет допустимость контекста Γ
TY Γ M возвращает тип M в контексте Γ
(и ⊥, если M нетипизируемое предвыражение)

Теорема. Алгоритм TY корректен и полон:
∀Γ , M TY Γ M = A ⇒ Γ M : A
∀Γ , M, A Γ M : A ⇒ TY Γ M =βη A
(полнота осмысленна, если имеется единственность типа)
(из полноты следует, что алгоритм завершается на допусти-
мых термах; хотим большего)
25

Проверка типов для λP: алгоритм

OK = TRUE
OK (Γ , x : A) = if TY Γ A ∈ {∗, } then OK Γ else FALSE
TY Γ x = if OK Γ ∧ x : A ∈ Γ then A else ⊥
TY Γ ∗ = if OK Γ then else ⊥
TY Γ (M N) = if TY Γ M = C = ⊥ ∧ TY Γ N = D = ⊥
then if C β Πx : A. B ∧ A =β D
then B[x := N] else ⊥
else ⊥
TY Γ (λx : A. M) = if TY (Γ , x : A) M = B = ⊥
then if TY Γ (Πx : A. B) ∈ {∗, }
then Πx : A. B else ⊥
else ⊥
TY Γ (Πx : A. B) = if TY Γ A = ∗ ∧ TY (Γ , x : A) B = s
then s else ⊥
26

Проверка типов для λP: завершимость (1)

Рекурсивный вызов без уменьшения меры:
TY Γ (λx : A. M) = if TY (Γ , x : A) M = B = ⊥
then if TY Γ (Πx : A. B) ∈ {∗, }
then Πx : A. B else ⊥
else ⊥
Но в λP можно заменить

TY Γ (Πx : A. B) ∈ {∗, }
на
TY Γ A = ∗
(проверьте это!)

27

Проверка типов для λP: завершимость (2)

β-редукция и β-эквивалентность неразрешимы для предтермов!
TY Γ (M N) = if TY Γ M = C = ⊥ ∧ TY Γ N = D = ⊥
then if C β Πx : A. B ∧ A =β D
then B[x := N] else ⊥
else ⊥
К счастью, они вызываются над гарантированно допусти-
мыми термами, и известно, что λP является SN и CR.

Теорема. Aлгоритмы TY Γ M и OK Γ завершаются для любого
предтерма M и предконтекста Γ .

28

Экстенсиональность и интенсиональность

Правило преобразования интенсионально и разрешимо:

Γ A:B Γ B :s B =β B
Γ A:B

Можно ввести в теорию экстенсиональность, добавив пра-
вила

Γ M, N : A → B Γ p : (Πx : A. M x = N x)
Γ (M = N) : A → B

Γ P:A Γ (A = B) : s
Γ P:B

TCP станет неразрешимым, поскольку сведётся к TIP.
29

Литература (1)

ITT2007
Herman Geuvers, Introduction to Type Theory
Types Summer School, August 2007, Bertinoro, Italy

http://typessummerschool07.cs.unibo.it/courses/geuvers-4.pdf

LCWT гл. 5.2, 5.3, 5.5
Henk Barendregt, Lambda calculi with types,
Handbook of logic in computer science (vol. 2), Oxford University
Press, 1993

30

Литература (2)

ATTAPL гл. 2
Benjamin C. Pierce, editor.
Advanced Topics in Types and Programming Languages, MIT,
2005

ITT гл. 6
Herman Geuvers, Introduction to Type Theory
Alfa Lernet Summer school 2008, Uruguay

http://www.cs.ru.nl/H.Geuvers/Uruguay2008SummerSchool.html

31

20110522 systems of typed lambda_calculi_moskvin_lecture11

More Related Content

What's hot (20)

Viewers also liked (20)

Similar to 20110522 systems of typed lambda_calculi_moskvin_lecture11 (20)

More from Computer Science Club (20)

20110522 systems of typed lambda_calculi_moskvin_lecture11