ANOVA.ppt

One-Way ANOVA
Introduction to Analysis of Variance
(ANOVA)

What is ANOVA?
 ANOVA is short for ANalysis Of VAriance
 Used with 3 or more groups to test for MEAN
DIFFS.
 E.g., caffeine study with 3 groups:
 No caffeine
 Mild dose
 Jolt group
 Level is value, kind or amount of IV
 Treatment Group is people who get specific
treatment or level of IV
 Treatment Effect is size of difference in means

Rationale for ANOVA (1)
 We have at least 3 means to test, e.g., H0: 1 = 2
= 3.
 Could take them 2 at a time, but really want to test
all 3 (or more) at once.
 Instead of using a mean difference, we can use the
variance of the group means about the grand mean
over all groups.
 Logic is just the same as for the t-test. Compare the
observed variance among means (observed
difference in means in the t-test) to what we would
expect to get by chance.

Suppose we drew 3 samples from the same population.
Our results might look like this:
10
0
-10
-20
4
3
2
1
0
10
0
-10
-20 10
0
-10
-20
Ra w Sc o re s (X)
10
0
-10
-20
Three Samples fromthe Same Population
M ean 1
M ean 2
M ean 3
Standard Dev Group 3
Note that the
means from the 3
groups are not
exactly the same,
but they are
close, so the
variance among
means will be
small.

Suppose we sample people from 3 different populations.
Our results might look like this:
20
10
0
-10
-20
4
3
2
1
0
Three Samples from3 DiffferentPopulations
20
10
0
-10
-20
20
10
0
-10
-20
20
10
0
-10
-20
Raw Scores (X)
Mean 1
Mean 2
Mean 3
SD Group 1
Note that the
sample means are
far away from one
another, so the
variance among
means will be
large.

Suppose we complete a study and find the following
results (either graph). How would we know or decide
whether there is a real effect or not?
10
0
-10
-20
4
3
2
1
0
10
0
-10
-20 10
0
-10
-20
Ra w Sc o re s (X)
10
0
-10
-20
Three Samples fromthe Same Population
M ean 1
M ean 2
M ean 3
Standard Dev Group 3
20
10
0
-10
-20
4
3
2
1
0
20
10
0
-10
-20
20
10
0
-10
-20
20
10
0
-10
-20
Raw Scores (X)
Mean 1
Mean 2
Mean 3
SD Group 1
To decide, we can compare our observed variance in
means to what we would expect to get on the basis
of chance given no true difference in means.

Review
 When would we use a t-test versus 1-way
ANOVA?
 In ANOVA, what happens to the variance in
means (between cells) if the treatment effect
is large?

Rationale for ANOVA
We can break the total variance in a study into
meaningful pieces that correspond to treatment effects
and error. That’s why we call this Analysis of Variance.
Definitions of Terms Used in ANOVA:
G
X The Grand Mean, taken over all observations.
A
X
1
A
X
The mean of any level of a treatment.
The mean of a specific level (1 in this case)
of a treatment.
i
X The observation or raw data for the ith person.

The ANOVA Model
A treatment effect is the difference between the overall,
grand mean, and the mean of a cell (treatment level).
G
A X
X
Effect
IV 

Error is the difference between a score and a cell
(treatment level) mean.
A
i X
X
Error 

The ANOVA Model:
)
(
)
( A
i
G
A
G
i X
X
X
X
X
X 




An individual’s
score is The grand
mean
+
A treatment
or IV effect + Error

The ANOVA Model
)
(
)
( A
i
G
A
G
i X
X
X
X
X
X 




The grand
mean
A treatment
or IV effect
Error
40
30
20
10
0
Frequency
ANOVA Data by Treatment Level
Grand Mean
Treatment Mean
Error
IV Effect
The graph shows the
terms in the equation.
There are three cells or
levels in this study.
The IV effect and error
for the highest scoring
cell is shown.

ANOVA Calculations
Sums of squares (squared deviations from the mean)
tell the story of variance. The simple ANOVA designs
have 3 sums of squares.
 
 2
)
( G
i
tot X
X
SS
The total sum of squares comes from the
distance of all the scores from the grand
mean. This is the total; it’s all you have.
 
 2
)
( A
i
W X
X
SS The within-group or within-cell sum of
squares comes from the distance of the
observations to the cell means. This
indicates error.
 
 2
)
( G
A
A
B X
X
N
SS The between-cells or between-groups
sum of squares tells of the distance of
the cell means from the grand mean.
This indicates IV effects.
W
B
TOT SS
SS
SS 


Computational Example: Caffeine on
Test Scores
G1: Control G2: Mild G3: Jolt
Test Scores
75=79-4 80=84-4 70=74-4
77=79-2 82=84-2 72=74-2
79=79+0 84=84+0 74=74+0
81=79+2 86=84+2 76=74+2
83=79+4 88=84+4 78=74+4
Means
79 84 74
SDs (N-1)
3.16 3.16 3.16

G1 75 79 16
Control 77 79 4
M=79 79 79 0
SD=3.16 81 79 4
83 79 16
G2 80 79 1
M=84 82 79 9
SD=3.16 84 79 25
86 79 49
88 79 81
G3 70 79 81
M=74 72 79 49
SD=3.16 74 79 25
76 79 9
78 79 1
Sum 370
G
X
i
X 2
)
( G
i X
X 
Total
Sum of
Squares
 
 2
)
( G
i
tot X
X
SS

In the total sum of squares, we are finding the
squared distance from the Grand Mean. If we took
the average, we would have a variance.
 
 2
)
( G
i
tot X
X
SS
Scores on the Dependent Variable by Group
0.5
0.4
0.3
0.1
0.0
Relative
Frequency
Low High
Grand Mean

G1 75 79 16
Control 77 79 4
M=79 79 79 0
SD=3.16 81 79 4
83 79 16
G2 80 84 16
M=84 82 84 4
SD=3.16 84 84 0
86 84 4
88 84 16
G3 70 74 16
M=74 72 74 4
SD=3.16 74 74 0
76 74 4
78 74 16
Sum 120
Within
Sum of
Squares
i
X A
X 2
)
( A
i X
X 
 
 2
)
( A
i
W X
X
SS

Within sum of squares refers to the variance within
cells. That is, the difference between scores and their
cell means. SSW estimates error.
0.5
0.4
0.3
0.1
0.0
Relative
Frequency
Low High
Cell or Treatment Mean
 
 2
)
( A
i
W X
X
SS

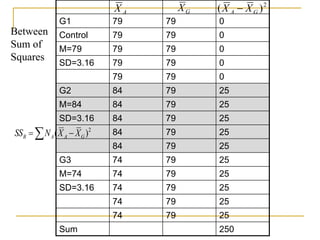
G1 79 79 0
Control 79 79 0
M=79 79 79 0
SD=3.16 79 79 0
79 79 0
G2 84 79 25
M=84 84 79 25
SD=3.16 84 79 25
84 79 25
84 79 25
G3 74 79 25
M=74 74 79 25
SD=3.16 74 79 25
74 79 25
74 79 25
Sum 250
Between
Sum of
Squares
 
 2
)
( G
A
A
B X
X
N
SS
A
X G
X 2
)
( G
A X
X 

The between sum of squares relates the Cell Means to
the Grand Mean. This is related to the variance of the
means.
0.5
0.4
0.3
0.1
0.0
Relative
Frequency
Low High
Cell Mean
Grand Mean
Cell Mean
Cell Mean
 
 2
)
( G
A
A
B X
X
N
SS

ANOVA Source Table (1)
Source SS df MS F
Between
Groups
250 k-1=2 SS/df
250/2=
125
=MSB
F =
MSB/MSW
= 125/10
=12.5
Within
Groups
120 N-k=
15-3=12
120/12 =
10 =
MSW
Total 370 N-1=14

ANOVA Source Table (2)
 df – Degrees of freedom. Divide the sum of
squares by degrees of freedom to get
 MS, Mean Squares, which are population
variance estimates.
 F is the ratio of two mean squares. F is
another distribution like z and t. There are
tables of F used for significance testing.

F Table – Critical Values
Numerator df: dfB
dfW 1 2 3 4 5
5 5%
1%
6.61
16.3
5.79
13.3
5.41
12.1
5.19
11.4
5.05
11.0
10 5%
1%
4.96
10.0
4.10
7.56
3.71
6.55
3.48
5.99
3.33
5.64
12 5%
1%
4.75
9.33
3.89
6.94
3.49
5.95
3.26
5.41
3.11
5.06
14 5%
1%
4.60
8.86
3.74
6.51
3.34
5.56
3.11
5.04
2.96
4.70

Review
 What are critical values of a statistics (e.g.,
critical values of F)?
 What are degrees of freedom?
 What are mean squares?
 What does MSW tell us?

Review 6 Steps
1. Set alpha (.05).
2. State Null &
Alternative
H0:
H1: not all  are =.
3. Calculate test statistic:
F=12.5
4. Determine critical value
F.05(2,12) = 3.89
5. Decision rule: If test
statistic > critical value,
reject H0.
6. Decision: Test is
significant (12.5>3.89).
Means in population are
different.
3
2
1 

 


Post Hoc Tests
 If the t-test is significant, you have a
difference in population means.
 If the F-test is significant, you have a
difference in population means. But you
don’t know where.
 With 3 means, could be A=B>C or A>B>C or
A>B=C.
 We need a test to tell which means are
different. Lots available, we will use 1.

Tukey HSD (1)
HSD means honestly significant difference.
A
W
N
MS
q
HSD 
 
 is the Type I error rate (.05).

q Is a value from a table of the studentized range
statistic based on alpha, dfW (12 in our example)
and k, the number of groups (3 in our example).
W
MS Is the mean square within groups (10).
A
N Is the number of people in each group (5).
33
.
5
5
10
77
.
3
05
. 

HSD
From table
MSW
A
N
Result for our example.
Use with equal sample size per cell.

Tukey HSD (2)
To see which means are significantly different, we
compare the observed differences among our means to
the critical value of the Tukey test.
The differences are:
1-2 is 79-84 = -5 (say 5 to be positive).
1-3 is 79-74 = 5
2-3 is 84-74 = 10. Because 10 is larger than 5.33, this result
is significant (2 is different than 3). The other differences
are not significant. Review 6 steps.

Review
 What is a post hoc test? What is its use?
 Describe the HSD test. What does HSD
stand for?

Test
 Another name for mean square is
_________.
1. standard deviation
2. sum of squares
3. treatment level
4. variance

Test
When do we use post hoc tests?
 a. after a significant overall F test
 b. after a nonsignificant overall F test
 c. in place of an overall F test
 d. when we want to determine the impact of
different factors

ANOVA.ppt

More Related Content

What's hot (20)

Similar to ANOVA.ppt (20)

More from sadiakhan783184 (6)

Recently uploaded (20)

ANOVA.ppt