Calculate Thresholds of Diffusion with Pajek

WANG Chengjun
wangchj04@gmail.com
2010.12.24

 The characteristics of Diffusion
 Diffusion is a special case of brokerage
 Time dimension
 Relationships as channel
 The combination of structural positions &
adoption time

 Empirical data
 Innovations of new mathematics method in
1950, Allegheny County, Pennsylvania, U.S.A.
 School superintendents as gatekeepers
 Nomination method: ask the respondents to
indicate their three best friends
 The social network is named modern math
network

 Read data
 ------------------------------------------------------------------------------
 Reading Network --- E:lingfei
wupajek125ESNAdataChapter8ModMath.net
 ------------------------------------------------------------------------------
 Reading Partition --- E:lingfei
wupajek125ESNAdataChapter8ModMath_adoption.clu
 ------------------------------------------------------------------------------

MODMATH.NET MODMATH_ADOPTION.CLU
 *Vertices 38  *Vertices 38  4
 1  4
 1 "v1" 0.0500 0.5346 0.5000  4
 2 "v2" 0.2300 0.7423 0.5000  2  4
 3 "v3" 0.2300 0.6038 0.5000  2  4
 ...........  2  4
 *Arcs  2  4
 *Edges  3  4
 2 32 1  3  4
 3  4
 2 23 1  5
 2 3 1  3  5
 ……………….  3  5
 3  5
 3  5
 3  5
 3  5
 3  5
 6
 4  6
 4  6

 Two-step flow model
 First phase: Mass media inform and influence
opinion leaders
 Second phase: opinion leaders influence
potential adopters
 Diffusion of innovations
 Opinion leaders use social relations to
influence their contacts
 Advice and friendship relations

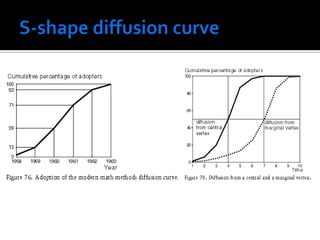
 Personal characteristics
 The type of innovations
 Perceived risk of innovations
 Network structure:
 In a dense network an innovation spreads more easily and
faster than in a sparse network,
 In an unconnected network diffusion will be slower and less
comprehensive than in a connected network,
 In a bi-component diffusion will be faster than in components
with cut-points or bridges,
 The larger the neighborhood of a person within the
network, the earlier s/he will adopt an innovation,
 A central position is likely to lead to early adoption,
 Diffusion from a central vertex is faster than from a vertex in
the margins of the network.

 Dimension: 38
 The lowest value: 1 Diffusion curve
 The highest value: 6
 The highest clusters values: 40
new 38
 Rank Vertex Cluster Id 35 35
 -------------------------------- cummulative

Adoption number
 1 38 6 v38 30
 Frequency distribution of cluster 27
numbers:
25
 Cluster Freq Freq% CumFreq 20
CumFreq% Representative
 ----------------------------------------------- 15 15
---------------- 12
 1 1 2.6316 1 2.6316 v1 10 10
 2 4 10.5263 5 13.1579 v2 5 8
 3 10 26.3158 15 39.4737 v6 5 1 4
 4 12 31.5789 27 71.0526 3
v16
0 1
 5 8 21.0526 35 92.1053 v28
 6 3 7.8947 38 100.0000 v36
 ----------------------------------------------- 1 2 3 4 5 6
----------------
 Sum 38 100.0000 Year

 Create a random network
 Net> Random Network> Vertices Output
Degree
 Out-degree 1 or 2
 No multiple lines
 Pick a vertex as the source of diffusion
process
 Assume a vertex will adopt at the first time
point after it has established direct contact
with an adopter

diffusion curve of random network
40
38
35 35
Adoption number

30 new
25 cummulative 25
20
15 15
10
10 4 10
5 1 6
3 3
0 1
1 2 3 4 5 6
year

 Everyone is unequally susceptible to contagion
 Two approaches to evaluate innovativeness:
 Adoption categories
 Classify people by their adoption time: Innovators, early
adopters, early majority, late adopters, laggards.
 It’s useful to identify the social and demographic characteristics
 Threshold categories:
 The threshold is his or her exposure at the time of adoption
 The exposure of a vertex in a network at a particular moment is
the proportion of its neighbors who have adopted before that
time
 Some people are easily persuaded (more susceptible) than others
 However, individual thresholds are computed after the fact, which
is a hindsight and not informative. They should be validated by
other indicators of innovativeness.

We first choose time 2 (1959), and calculate the exposure at the time 2.
And then, calculate time 3, time4, time 5, time6

 Net> Transform> Arcs->Edges>ALL

 Partition> Binarize (fill in 1-2)
 Adoption time 1 & 2 are assigned a score of
1, and others are assigned a score of 0.

 Operations> Vector> Summing up neighbors

 Because we defined exposure as the
percentage of neighbors who have adopted.
 Vectors> First vector
 Net> Partitions> Degree
There aren’t the
 Partition> Make vector (do not normalize) submenus of first
 Vectors> Second vector vector and second
 Vectors> Divide First by Second vector in
 Options> Read/Write>0/0 PAJEK125 !!!!!!!

Macro> Play
Options> Read/Write>0/0
Making new macro:
Macro> Record----- Macro> Record

Results supplied by the author

 Read Project
 Operations> Transform> Direction> Lower-
Higher

 Threshold=in-degree/ all-degree
 in-degree is the in-degree of network which is directed
and having no multiple lines and no lines within classes
 all-degree is the all-degree of network which is undirected
and having n0 multiple lines
 Because the original network is undirected and having no
multiple lines, so we can calculate all-degree directly.
 To obtain the in-degree, we should re-read original
network and change it into directed one which has no lines
within classes first, and then we can calculate in-degree
directly.
 Using the submenu “divide first by second” in the menu of
“Vectors”, we can get the threshold.
 Draw the vectors, and “mark vertices using” “vector
values”.

 Record macro
 Read project
 Draw partition
 Net> partitions > Degree> ALL
 Vectors> Second vectors
 Read project
 Operations> Transform> Direction
 Net> partitions > Degree> Input
 Vectors> First vectors
 Vectors> Divide First by Second
 Draw> Draw-vector
 Record macro

 NETBEGIN 1
 CLUBEGIN 1
 PERBEGIN 1
 CLSBEGIN 1
 HIEBEGIN 1
 VECBEGIN 1
 Msg Reading Pajek Project File --- E:lingfei wupajek125ESNAdataChapter8ModMath.paj
 Msg Reading Network --- ModMath_directed.net
 Msg Reading Network --- ModMath.net
 Msg Reading Partition --- ModMath_adoption.clu
 N 9999 RDPAJ ?
 N 2 LAYERSNX 2 1
 Msg Optimizing total length of lines ...
 Msg All degree centrality of 2. ModMath.net (38)
 C 2 DEGC 2 [2] (38)
 N 3 ETOAINC 2 1 1 DEL (38)
 Msg Input degree centrality of 3. Directed Network [INC DEL] of N2 according to C1 (38)
 C 3 DEGC 3 [0] (38)
 V 3 DIVV 2 1 (38)

Net> Transform> Arcs->Edges> All
Net> Vector> Centrality> Betweenness
Info > Vector

 A threshold lag is a period in which an actor
does not adopt although he or she is exposed
at the level at which he or she will adopt later.
 The critical mass of a diffusion process is the
minimum number of adopters needed to
sustain a diffusion process.
 V28 and V29 undergoes a threshold
lag, respectively (we can tell that from the pic
of thresholds).

Tools> SPSS> Locate SPSS
Tools> SPSS> Send to SPSS

Diffusion curve
40 38

Adoption number
new 35
30
27
20
15
10 10 12
5 8
1 4 3
0 1
1 2 3 4 5 6
Year

Calculate Thresholds of Diffusion with Pajek

More Related Content

Similar to Calculate Thresholds of Diffusion with Pajek (20)

More from Chengjun Wang (15)

Recently uploaded (20)

Calculate Thresholds of Diffusion with Pajek