DC servomechanism parameter identification a closed loop input error approach

ISA Transactions 51 (2012) 42–49
Contents lists available at SciVerse ScienceDirect
ISA Transactions
journal homepage: www.elsevier.com/locate/isatrans
DC servomechanism parameter identification: A closed loop input error approach
Ruben Garrido∗
, Roger Miranda
Departamento de Control Automático, CINVESTAV-IPN, Av. IPN 2508 San Pedro Zacatenco, México, DF 07360, Mexico
a r t i c l e i n f o
Article history:
Received 17 February 2011
Received in revised form
7 June 2011
Accepted 27 July 2011
Available online 24 August 2011
Keywords:
Closed loop parameter identification
Servomotor
PD control
a b s t r a c t
This paper presents a Closed Loop Input Error (CLIE) approach for on-line parametric estimation of
a continuous-time model of a DC servomechanism functioning in closed loop. A standard Propor-
tional Derivative (PD) position controller stabilizes the loop without requiring knowledge on the ser-
vomechanism parameters. The analysis of the identification algorithm takes into account the control law
employed for closing the loop. The model contains four parameters that depend on the servo inertia,
viscous, and Coulomb friction as well as on a constant disturbance. Lyapunov stability theory permits
assessing boundedness of the signals associated to the identification algorithm. Experiments on a labora-
tory prototype allows evaluating the performance of the approach.
© 2011 ISA. Published by Elsevier Ltd. All rights reserved.
1. Introduction
Direct Current (DC) servomotors are widely employed in in-
dustry; examples of their application include computer-controlled
machines, robots, and process control valves. Modern digital ser-
vodrives used for controlling these actuators perform tuning auto-
matically using real-time data. This procedure is composed of three
sequential steps. In the first step, a parameter estimation algo-
rithm identifies a model of the servomotor. In the second step, the
parameters obtained in the first step, allows computing a control
algorithm. In the third step, the servomotor works using the con-
trol algorithm computed in the second step. Regarding the design
of the control law, there exist a great number of designs includ-
ing Proportional Derivative (PD) and Proportional Integral Deriva-
tive (PID) controllers. On the other hand, even if there exists a
lot of work concerning parameter identification [1,2], most of the
proposed algorithms deal with open loop stable systems. In this re-
gard, note that a second order model of a position-controlled ser-
vomotor is not bounded-input bounded-output stable. Moreover,
if parameter identification is performed when the servomotor is
coupled to a mechanical load, for example to a robot arm, closed-
loop identification with the loop closed around a position sensor
would be desirable for security reasons since open loop techniques
would lead to unbounded motor behavior.
Several papers propose methods for closed-loop identification
of position-controlled servomechanisms [3–11]. In [3], the authors
propose an internal model controller designed from results
obtained using off-line identification algorithms. An off-line least
squares method allows tuning a two degrees-of-freedom linear
∗ Corresponding author. Tel.: +52 55 57 47 37 39; fax: +52 55 57 47 39 82.
E-mail address: garrido@ctrl.cinvestav.mx (R. Garrido).
controller in [4]. In [5], the authors employ a disturbance observer
to obtain discrete-time estimators for the servo inertia and viscous
friction which in turn are employed for obtaining Coulomb friction
estimates. It is worth noting that the authors evaluate performance
of the proposed estimators through experiments. In [6], a recursive
multi-step extended least squares permits identifying a linear
discrete-time model of a servo. The servo input and output feed the
estimation algorithm and a proportional controller closes the loop.
According to the taxonomy given in [12], the approach proposed
in [6] would correspond to a direct approach where the controller
is ignored for identification purposes. It is also worth noting that
the authors do not give a convergence analysis of the identification
algorithm.
Relay-based techniques are widespread for servo identifica-
tion [7–11]. The idea behind these methods, which is similar to
the relay tuning methods in process control [13], is to close the
loop through a relay in order to obtain a sustained oscillation; then,
its amplitude and frequency allow identifying linear and nonlinear
servo models. A drawback of relay-based techniques is the fact that
tuning of the relay controller can be cumbersome and the methods
proposed in the literature do not provide a systematic tuning pro-
cedure of the relay controller.
Refs. [14,15] study several identification algorithms applied
to linear discrete-time plants. These methodologies termed as
the Closed Loop Output Error (CLOE) algorithms have several
advantages with respect to traditional closed loop identification
methodologies. They are able to produce unbiased estimates;
moreover, the controller used for closing the loop has a prime role
in the identification procedure, and iterative tuning procedures
accommodate easily within these methodologies. Moreover, real-
time experiments using laboratory prototypes validate these
approaches.
0019-0578/$ – see front matter © 2011 ISA. Published by Elsevier Ltd. All rights reserved.
doi:10.1016/j.isatra.2011.07.003

R. Garrido, R. Miranda / ISA Transactions 51 (2012) 42–49 43
This work presents an on-line closed loop identification al-
gorithm for estimating the parameters of a DC servomechanism.
The proposed approach, termed as the Closed Loop Input Error
(CLIE) algorithm is based on the same idea used by the CLOE al-
gorithms, i.e., two identical controllers close the loop around the
plant and the identified model. However, instead of using the out-
put error, the algorithm studied here uses the input error and re-
lies on a continuous-time nonlinear model of the servomechanism.
The main features of the proposed approach are as follows. First,
a rigorous parameter convergence result supports the proposed
algorithm; second, it takes explicitly into account the controller
employed for closing the loop as in the case of CLOE algorithms.
However, compared with these algorithms, the CLIE method does
not require values of the parameter estimates obtained previously
under open loop conditions. Furthermore, it does not assume any
prior knowledge on the servomechanism parameters. Finally, a PD
controller, which is tuned straightforwardly, ensures closed loop
stability without knowledge on the servomechanism parameters.
Real-time experiments allow assessing the performance of the pro-
posed approach. The paper outline is as follows. Section 2 presents
the proposed identification algorithm together with its stability
and convergence properties. Section 3 shows the experimental re-
sults obtained in a laboratory prototype using the CLIE algorithm
and a continuous-time least squares algorithm with forgetting fac-
tor. The paper ends with some concluding remarks.
2. Closed loop parameter identification
2.1. Servomechanism dynamics
Consider the following model of a DC servomechanism com-
posed by a brushed servomotor, a servoamplifier, and a position
sensor
J ¨q(t) + f ˙q(t) + fc sign(˙q) = ku(t) + dm (1)
where q, ˙q and ¨q are the angular position, velocity and acceleration
respectively; u the control input voltage, J the motor and load in-
ertia, f and fc are, respectively, the viscous and Coulomb friction
coefficients, k is a parameter related to the amplifier gain and to
the motor torque constant, and the term dm is a constant distur-
bance. This model is widely used in the literature [16–21], and it is
valid for DC and AC brushless servomotors if the amplifier driving
the servomotor works in the current mode.
2.2. Proposed closed loop input error method
The idea behind the proposed Closed Loop Input Error (CLIE)
algorithm is as follows (see Fig. 1). Two identical PD controllers
close the loop around the servomechanism and its model. The
error between the inputs of these closed loop systems feeds
an identification algorithm that subsequently update the model
parameters.
2.3. Stability analysis
Consider Eq. (1) written as follows
¨q = −a˙q − csign(˙q) + bu + d (2)
where parameters a = f /J, b = k/J, c = fc /J, d = dm/J are
positive constants. Let the following PD control law apply to the
servo (2)
u = kpe − kd ˙q + se (3)
Fig. 1. Block diagram of the proposed identification method.
where se is a bounded excitation signal. The terms kp and kd are
positive constants and correspond respectively to the proportional
and derivate gains. The variables
e = qd − q (4)
˙e = −˙q (5)
define the position error and its time derivative with respect to a
reference qd. Substituting (3) into (2) yields
¨q = −a˙q − csign(˙q) + bkpe − bkd ˙q + bse + d. (6)
Note that the term η = −csign(˙q) + bse + d is bounded. The
above notation allows writing
¨q = −c˙q + bkpe + η (7)
with c = a+bkd > 0. The time derivative of the Lyapunov function
candidate
V =
1
2
˙q2
+
1
2

c2
2
+ bkp

e2
+
c
2
e˙q (8)
evaluated along the solutions of (7) is
˙V = −
c
2
˙q2
−
c
2
bkpe2
+ η˙q −
c
2
ηe
which is subsequently upper bounded as
˙V ≤ −
c
2
|˙q|2
−
c
2
bkp |e|2
+ |η| |˙q| +
c
2
|η| |e|
= −zT
Az + |η| BT
z
≤ −λmin(A) ‖z‖
[
‖z‖ −
‖B‖ |η|
λmin(A)
]
with z =

|˙q| |e|
T
, A = c
2
diag

bkp 1

, B =
 c
2
1
T
. The
term λmin(A) stands for the minimum eigenvalue of matrix A.
Hence, ˙V < 0 as long as ‖z‖ ≥ ‖B‖|η|
λmin(A)
and the trajectories of (7)
are uniformly ultimately bounded [22]. This result shows that the
PD controller stabilizes the DC servomechanism model (2) without
explicit knowledge on its parameters.
Consider now the estimated model of the servomechanism with
ˆa, ˆb, ˆc, and ˆd being estimates, respectively, of a, b, c, and d
¨qe = −ˆa˙qe − ˆcsign(˙q) + ˆbue + ˆd (9)

44 R. Garrido, R. Miranda / ISA Transactions 51 (2012) 42–49
in closed loop with the PD control law
ue = kpee − kd ˙qe + se (10)
with
ee = qd − qe. (11)
Note that the same gains are used in (3) and (10). Substituting
(10) into (9) yields
¨qe = −â˙qe − ˆcsign(˙q) + ˆbkpee − ˆbkd ˙qe + ˆbse + ˆd. (12)
Define the error between the plant and the model outputs
ϵ = q − qe. (13)
An expression for the second time derivative of (13) follows by
using (6) and (12); hence
¨ϵ = ¨q − ¨qe
= −c ˙ϵ − bkpϵ +

â − a

˙qe +

ˆc − c

sign(˙q)
+

ˆb − b
 
kd ˙qe − kpee

− (ˆd − d). (14)
Define the error vector ˜θ, the regressor vector φ, and the
disturbance estimation error
˜θ = ˆθ − θ =




â − a
ˆb − b
ˆc − c
ˆd − d



 (15)
φ =



˙qe
kd ˙qe − kpee
sign(˙q)
−1


 =



˙qe
−ue
sign(˙q)
−1


 . (16)
Using these definitions allows writing (14) as
¨ϵ = −c ˙ϵ − bkpϵ + ˜θT
φ. (17)
At this point, it is convenient to define the input error
εu = ue − u. (18)
The following expressions for the input error and its time
derivative result from using (3) and (10)
εu = kpϵ + kd ˙ϵ (19)
˙εu = kp ˙ϵ + kd ¨ϵ. (20)
Consider the following Lyapunov function candidate
V =
1
2kp
ε2
u +
1
2

bk2
d + ckd − 1

kpϵ2
+
1
2
kd
˜θT
Γ −1 ˜θ (21)
with Γ > 0 a constant matrix and κ > 0. The above expression is
positive definite if ckd − 1 > 0. Obtaining the time-derivative of
(21) using (20) leads to
˙V =
1
kp

kp ˙ϵ + kd ¨ϵ

+

bk2
d + ckd − 1

kpϵ˙ϵ + kd
˜θT
Γ −1 ˙˜θ.
Substituting (17) into the above equality yields
˙V = −kd(ckd − 1)˙ϵ2
− bk2
dkpϵ2
+ kd
˜θT

φεu + Γ −1 ˙˜θ

. (22)
Consider the following algorithm for estimating θ
˙ˆθ = −Γ φεu. (23)
Since θ is a constant, then
˙˜θ = ˙ˆθ. Substituting
˙˜θ into (22) gives
˙V = −kd(ckd − 1)˙ϵ2
− bk2
dkpϵ2
. (24)
From the above equality, it is clear that εu, ϵ, and ˜θ are bounded
and V(0) ≥ V if ckd − 1 > 0. Applying Barbalat’s lemma allows
showing that ϵ, ˙ϵ, and εu converge to zero [23]. To this end, note
from (24) that
˙V ≤ −bkdkpϵ2
.
Integrating with respect to time the above inequality yields
V − V(0) ≤ −
∫ t
0
bkdkpϵ2
dρ (25)
from which the following inequality follows
∫ t
0
ϵ2
dρ ≤
V(0)
bkdkp
< ∞. (26)
From the above and the boundedness of ϵ and ˙ϵ, it follows that
ϵ converges to zero. On the other hand, boundedness of ϵ and ˙ϵ
implies boundedness of qe and ˙qe; hence, control signal ue and
consequently, the regressor vector φ are also bounded. The above
results allow concluding that the signal ¨ϵ in (17) is bounded. From
(24) it follows that
˙V ≤ −kd(ckd − 1)˙ϵ2
. (27)
Integrating with respect to time the above inequality leads to
V − V(0) ≤ −
∫ t
0
kd(ckd − 1)˙ϵdρ. (28)
This last results allows writing
∫ t
0
˙ϵ2
dρ ≤
V(0)
kd(ckd − 1)
< ∞. (29)
Applying Barbalat’s lemma permits concluding that ˙ϵ converges
to zero. Finally, from (19) it is clear that εu also converges to zero.
The following proposition resumes the foregoing results.
Proposition 1. Consider the servo model (2) in closed loop with
control law (3) and the estimated model (9) in closed loop with control
law (10). If (23) updates the servo model parameters and ckd − 1 >
0, then, ˜θ, ϵ, ˙ϵ, εu, qe, ˙qe, ¨qe, and φ remain bounded. Moreover, εu
converges to zero.
Note that Proposition 1 only ensures boundedness of ˜θ. Con-
vergence of this vector to zero requires a Persistently Exciting (PE)
condition on the regressor vector φ. The following definition about
a Persistently Exciting (PE) signal [23] establishes a condition for
parameter convergence.
Definition 1. A vector φ : R+ → R2n
is PE if there exist positive
constants α1, α2, δ such that
α2 ≥
∫ t0+δ
t0
vT
φ (τ) φT
(τ) vdτ ≥ α1 (30)
for all t0 ≥ 0, z ∈ R2n
, and ‖v‖ = 1.
The next expressions correspond to the update law (23)
written line-by-line for each parameter estimate assuming Γ =
diag

Γ1 Γ2 Γ3 Γ4

˙â = −Γ1 ˙qeεu
˙ˆb = Γ2ueεu
˙ˆc = −Γ3sign(˙q)εu
˙ˆd = Γ4εu.

Fig. 2. Experimental setup.
3. Experimental results
3.1. Experimental setup
The laboratory prototype consist of a servomotor from Moog,
model C34-L80-W40 (Fig. 2) driven by a Copley Controls power
servoamplifier, model 423, configured in current mode. A BEI
optical encoder, model L15 with 2500 pulses per revolution, allows
measuring the servomotor position. The algorithms are coded
using the MatLab/Simulink software platform under the program
Wincon from Quanser Consulting, and a Quanser Consulting
Q8 board performs data acquisition. The data card electronics
increases four times the optical encoder resolution up to 2500 ×
4 = 10 000 pulses per revolution. The control signal produced by
the Q8 board passes through a galvanic isolation box. The software
runs on a personal computer using an Intel Core 2 quad processor,
and the Q8 board is allocated in a PCI slot inside this computer.
The following transfer function, which is composed of a high-pass
filter in cascade with a low-pass filter, allows obtaining velocity
estimates from position measurements
G(s) =
400s
s + 400
500
s + 500
.
The low pass filter attenuates the high frequency components of
the position signal. The Simulink diagrams use a sampling period of
0.1 ms and the ODE5 solver. Fig. 2 depicts the experimental setup.
3.2. Experiments
3.2.1. Parameter identification
Two Duffing systems generate the signal used for exciting the
servomechanism
˙x1i = x2iωiπ (31)
˙x2i = [−0.25 + x2i + x1i − 1.05x3
1i
+ 0.3 sin(ωiπt)]ωiπ; i = 1, 2
se = 7x11 − 5x12; x1i(0) = 0; x2i(0) = 0;
ω1 = 1 rad/s; ω2 = 2 rad/s.
This type of chaotic excitation was proposed in [24] for pa-
rameter identification of a speed controlled servomotor. Fig. 3
shows the time evolution of se. The gains for the PD controller are
kp = 10 and kd = 0.28, and the update law gains are Γ = diag
12 3000 180 90

.
Fig. 4 shows the time evolution of the parameter estimates
obtained using the proposed approach. Fig. 5 depicts the input
error εu and the evaluation of the PE condition (30) with v =
1
2

1 1 1 1
T
; the values for the PE condition in Fig. 5(b) are
Fig. 3. Chaotic excitation signal.
Fig. 4. Parameter estimates obtained using the CLIE method: ˆa, ˆb, ˆc, and ˆd.
shown every five seconds, i.e. δ = 5 s. Hence, the regressor vector
fulfills the PE condition during the experiment. Table 1 shows the
parameter estimates obtained from the experiment. They were

Fig. 5. Identification error and the PE condition time evolution for the CLIE method.
Table 1
Nominal parameters of the servomechanism and the parameter estimates obtained
using the CLIE method.
â ˆb ˆc ˆd
Nominal parameters 0.193 137.78 – 0
CLIE method 0.1801 139.5 3.475 0.6004
LS method 0.0654 137.1 3.927 0.6519
computed as the mean value of the estimates from the time
period t = 35 s to t = 40 s. This table also depicts the parameter
values computed from the servomotor and servoamplifier data.
Parameters a and b are the only ones available from that data;
Coulomb friction coefficient was unavailable. On the other hand, a
parasitic voltage in the servoamplifier produces a constant voltage
acting as a disturbance. A potentiometer in the servoamplifier
allows compensating for this disturbance voltages; it was set in
such a way that no current flows through the servoamplifier.
Hence, the nominal value of d is set to zero. However, note that
the CLIE algorithm produces a nonzero estimate ˆd. This estimate
would correspond to a constant bias introduced by the galvanic
isolation box. Note also that a value of ˆd = 0.6004 corresponds
to a disturbance voltage of ˆd/ˆb = 4.303 mV. Otherwise, the
parameters â, and ˆb produced by the CLIE algorithm remain close
to the corresponding nominal parameters.
For comparison purposes, the continuous-time least squares
algorithm with forgetting factor [25] allows estimating the
servomechanism parameters; see Appendix for further details.
The forgetting factor is set to β = 1, the initial conditions
and the bound for the gain matrix are set to P(0) = diag
1000 1000 1000

, and R0 = 2(1000)3
. The filters described
in Appendix were implemented using λ1 = 40, and λ2 = 400.
Fig. 6 depicts the estimates obtained using the least squares
algorithm, Fig. 7(a) shows the identification error, and Fig. 7(b) the
PE condition (30) with v = 1
2

1 1 1 1
T
. As in the case of the
CLIE method, Table 1 gives account of the estimates mean value
computed from the time period t = 35 s to t = 40 s.
It is worth remarking that both estimators produce essentially
the same estimate values; however, comparing Figs. 4 and 6,
the time evolution of the parameter estimates produced by the
least squares method exhibits a more oscillatory behavior and,
in the case of the parameter â associated to the viscous friction,
Fig. 6. Parameter estimates obtained using the continuous-time least squares
method: â, ˆb, ˆc, and ˆd.
in some parts of the graph it takes negative values. Concerning
the values presented in Table 1, it is interesting to note that the
parameter estimate â produced by the least squares method is very
different to the nominal value whereas the corresponding estimate
produced by the CLIE method remains closer to this nominal value.
On the other hand, both algorithms produce similar parameter
values ˆb, ˆc, and ˆd.
3.3. Model validation
The estimated model is validated by using the parameter
estimates of Table 1 for computing the following model reference
controller. Fig. 8 depicts a block diagram illustrating the validation
approach. The goal of control law (32)
u =
1
ˆb

−ˆd + â˙q + ˆcsign(˙q) − 2ζωn ˙q + ω2
n(r − q)

(32)

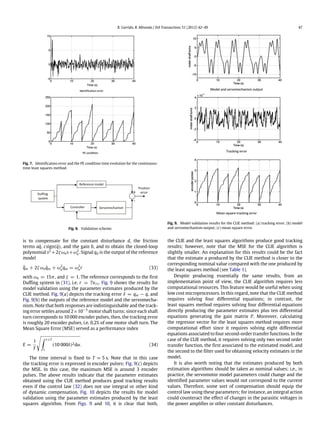
Fig. 7. Identification error and the PE condition time evolution for the continuous-
time least squares method.
Fig. 8. Validation scheme.
is to compensate for the constant disturbance d, the friction
terms a˙q, csign(˙q), and the gain b, and to obtain the closed-loop
polynomial s2
+2ζωns+ω2
n. Signal qd is the output of the reference
model
¨qm + 2ζωn ˙qm + ω2
nqm = ω2
nr (33)
with ωn = 15π, and ζ = 1. The reference corresponds to the first
Duffing system in (31), i.e. r = 7x11. Fig. 9 shows the results for
model validation using the parameter estimates produced by the
CLIE method. Fig. 9(a) depicts the tracking error δ = qm − q, and
Fig. 9(b) the outputs of the reference model and the servomecha-
nism. Note that both responses are indistinguishable and the track-
ing error settles around 2×10−3
motor shaft turns; since each shaft
turn corresponds to 10 000 encoder pulses, then, the tracking error
is roughly 20 encoder pulses, i.e. 0.2% of one motor shaft turn. The
Mean Square Error (MSE) served as a performance index
E =
1
T

∫ t+T
t
(10 000δ)2dα. (34)
The time interval is fixed to T = 5 s. Note that in this case
the tracking error is expressed in encoder pulses; Fig. 9(c) depicts
the MSE. In this case, the maximum MSE is around 3 encoder
pulses. The above results indicate that the parameter estimates
obtained using the CLIE method produces good tracking results
even if the control law (32) does not use integral or other kind
of dynamic compensation. Fig. 10 depicts the results for model
validation using the parameter estimates produced by the least
squares algorithm. From Figs. 9 and 10, it is clear that both,
Fig. 9. Model validation results for the CLIE method: (a) tracking error; (b) model
and servomechanism output; (c) mean square error.
the CLIE and the least squares algorithms produce good tracking
results; however, note that the MSE for the CLIE algorithm is
slightly smaller. An explanation for this results could be the fact
that the estimate a produced by the CLIE method is closer to the
corresponding nominal value compared with the one produced by
the least squares method (see Table 1).
Despite producing essentially the same results, from an
implementation point of view, the CLIE algorithm requires less
computational resources. This feature would be useful when using
low cost microprocessors. In this regard, note that the CLIE method
requires solving four differential equations; in contrast, the
least squares method requires solving four differential equations
directly producing the parameter estimates plus ten differential
equations generating the gain matrix P. Moreover, calculating
the regressor vector for the least squares method requires more
computational effort since it requires solving eight differential
equations associated to four second-order transfer functions. In the
case of the CLIE method, it requires solving only two second order
transfer function, the first associated to the estimated model, and
the second to the filter used for obtaining velocity estimates in the
model.
It is also worth noting that the estimates produced by both
estimation algorithms should be taken as nominal values; i.e., in
practice, the servomotor model parameters could change and the
identified parameter values would not correspond to the current
values. Therefore, some sort of compensation should equip the
control law using these parameters; for instance, an integral action
could counteract the effect of changes in the parasitic voltages in
the power amplifier or other constant disturbances.

Fig. 10. Model validation results for the continuous-time least squares method:
(a) tracking error; (b) model and servomechanism output; (c) mean square error.
4. Conclusion
This paper exposes a Closed Loop Input Error (CLIE) method for
on-line identification of a four-parameter model of a servomecha-
nism. The proposed approach does not rely on relay techniques, it
does not need a priori knowledge about the servo model parame-
ters, and it allows freely choosing the excitation signal. The con-
troller closing the loop is a proportional derivative algorithm. A
rigorous parameter convergence result theoretically supports the
CLIE algorithm. Experiments on a laboratory prototype support the
findings. It is worth remarking that experiments, performed using
a model reference control law designed using the parameter esti-
mates, show a mean square error of 3 encoder pulses using an op-
tical encoder with 2500 × 4 pulses per revolution. Moreover, the
CLIE produces parameter estimates similar to those obtained with
a standard continuous-time least squares algorithm with forget-
ting factor, but with less computational resources.
Acknowledgments
The authors would like to thank Gerardo Castro and Jesús Meza
for their help during the experiments.
Appendix. Model parametrization for applying the on-line
least squares method
This Appendix describes how to apply the on-line continuous-
time LS method for servomechanism identification. Applying this
algorithm requires filtering of both sides of the servomechanism
model (2) (see [23] for further details). Using the second order
linear stable filter λ(s) = s2
+ λ1s + λ2 allows obtaining the
following regression equation
z = θT
φLS
z = L−1

λ2s2
λ(s)

φLS =



φLS1
φLS2
φLS3
1


 =



−h1 ∗ q
−h2 ∗ sign(˙q)
−h2 ∗ u
1



θ =



a
c
b
d



h1 = L−1

λ2s
λ(s)

h2 = L−1

λ2
λ(s)

.
The operators ∗ and L−1
denote, respectively, the convolution
and inverse Laplace transform.
The following continuous-time least squares with forgetting
factor algorithm [25] permits identifying vector θ
ˆz = ˆθT
φLS
ϵLS = z − ˆz = −˜θT
φLS
˙ˆθ = PφLSϵ
˙P =

βP − PφLSφT
LSP, if ‖P(t)‖ ≤ R0
0, otherwise,
P(0) = P0 = PT
0 > 0
β > 0, R0 > 0, ‖P(0)‖ ≤ R0.
Vector ˆθ denotes the estimate of θ, P is the gain matrix, ϵLS is
the identification error and β the forgetting factor.
References
[1] Ljung Lennart. System identification. Prentice Hall; 1987.
[2] Nelles O. Nonlinear system identification. Springer Verlag; 2001.
[3] Adam EJ, Guestrin ED. Identification and robust control for an experimental
servomotor. ISA Transactions 2002;41(2):225–34.
[4] Iwasaki T, Sato T, Morita A, Maruyama M. Autotuning of two degree of freedom
motor control for high accuracy trajectory motion. Control Engineering
Practice 1996;4(4):537–44.
[5] Kobayashi S, Awaya I, Kuromaru H, Oshitani K. Dynamic model based
autotuning digital servo driver. IEEE Transactions on Industrial Electronics
1995;42(5):462–6.
[6] Zhou Y, Han A, Yan S, Chen X. A fast method for online closed loop
system identification. The International Journal of Advanced Manufacturing
Technology 2006;31(1–2):78–84.
[7] Tan KK, Lee TH, Vadakkepat P, Leu FM. Automatic tuning of two degree of
freedom control for DC servomotor system. International Journal of Intelligent
Automation and Soft Computing 2000;6(4):281–9.
[8] Tan KK, Xie Y, Lee TH. Automatic friction identification and compensation with
a self adapting dual relay. International Journal for Intelligent Automation and
Soft Computing 2003;9(2):83–95.
[9] Tan KK, Lee TH, Huang SN, Jiang X. Friction modeling and adaptive
compensation using a relay feedback approach. IEEE Transactions on Industrial
Electronics 2001;48(1):169–76.
[10] Lee TH, Tan KK, Lim SY, Dou HF. Iterative learning control of permanent magnet
linear motor with relay automatic tuning. Mechatronics 2000;10(1):169–90.
[11] Besançon-Voda A, Besançon G. Analysis of a two-relay system configuration
with application to Coulomb friction identification. Automatica 1999;35(8):
1391–9.
[12] Forsell U, Ljung L. Closed loop identification revisited. Automatica 1999;35(7):
1215–41.
[13] Åström KJ, Hagglund T. PID controllers: theory, design and tuning. 2nd ed.
International Society for Measurement and Control; 1994.
[14] Landau ID, Karimi A. An output error recursive algorithm for unbiased
identification in closed loop. Automatica 1997;33(5):933–8.
[15] Landau ID. Identification in closed loop: a powerful design tool (better design
models, simpler controllers). Control Engineering Practice 2001;9:59–65.

[16] Ellis G. Control systems design guide. second ed. Academic Press; 2000.
[17] Kelly R, Moreno J. Learning PID structures in an introductory course of
automatic control. IEEE Transactions on Education 2001;44(4).
[18] Moreno J, Kelly R. On motor velocity control by using only position
measurements: two case study. International Journal of Electrical Engineering
Education 2002;39(2).
[19] Guarino Lo Bianco C, Piazzi A. A servo control system design using dynamic
inversion. Control Engineering Practice 2002;10:847–55.
[20] PI and PID controllers tuning for integral-type servo systems to ensure robust
stability and controller robustness. Electrical Engineering 2006;88:149–56.
[21] Schmidt PB, Lorenz RD. Design principles and implementation of acceleration
feedback to improve performance of DC drives. IEEE Transactions on Industry
Applications 1992;28(3).
[22] Khalil KH. Nonlinear systems. Prentice Hall; 1996.
[23] Sastry S, Bodson M. Adaptive control, stability, convergence and robustness.
Prentice Hall; 1989.
[24] Fuh CC, Tsai HH. Adaptive parameter identification of servo control systems
with noise and high-frequency uncertainties. Mechanical Systems and Signal
Processing 2007;21:1437–51.
[25] Ioannou PA, Sun J. Robust adaptive control. Prentice Hall; 1995.

DC servomechanism parameter identification a closed loop input error approach

More Related Content

What's hot (20)

Viewers also liked (20)

Similar to DC servomechanism parameter identification a closed loop input error approach (20)

More from ISA Interchange (20)

Recently uploaded (20)

DC servomechanism parameter identification a closed loop input error approach