An FPT Algorithm for Maximum Edge Coloring
1 like1,894 views
The document describes research into the maximum edge coloring problem, which involves coloring the edges of a graph such that each vertex sees at most two colors. The goal is to maximize the number of colors used. The problem is known to be NP-complete. The authors present a fixed-parameter tractable algorithm that runs in time O*(20k) by reducing the problem into smaller subproblems involving color palettes, vertex covers, and independent sets. They also discuss some open problems regarding improving the running time and determining whether the problem admits a polynomial kernel.
An FPT Algorithm for Maximum Edge Coloring
- 1. Maximum Edge Coloring Prachi Goyal, Vikram Kamat and Neeldhara Misra Department of Computer Science, Indian Institute of Science
- 2. Maximum Edge Coloring GOAL. Color the edges of a graph so that each vertex “sees” at most two colors. .
- 3. Maximum Edge Coloring GOAL. Color the edges of a graph so that each vertex “sees” at most two colors. ...........
- 4. Maximum Edge Coloring GOAL. Color the edges of a graph so that each vertex “sees” at most two colors. ...........
- 5. Maximum Edge Coloring GOAL. Color the edges of a graph so that each vertex “sees” at most two colors. ..........
- 6. Maximum Edge Coloring GOAL. Color the edges of a graph so that each vertex “sees” at most two colors. ..........
- 7. Maximum Edge Coloring GOAL. Color the edges of a graph so that each vertex “sees” at most two colors. .........
- 8. Maximum Edge Coloring GOAL. Color the edges of a graph so that each vertex “sees” at most two colors. ........
- 9. Maximum Edge Coloring GOAL. Color the edges of a graph so that each vertex “sees” at most two colors. .......
- 10. Maximum Edge Coloring GOAL. Color the edges of a graph so that each vertex “sees” at most two colors. ......
- 11. Maximum Edge Coloring GOAL. Color the edges of a graph so that each vertex “sees” at most two colors. .....
- 12. Maximum Edge Coloring GOAL. Color the edges of a graph so that each vertex “sees” at most two colors. ....
- 13. Maximum Edge Coloring GOAL. Color the edges of a graph so that each vertex “sees” at most two colors. ...
- 14. Maximum Edge Coloring GOAL. Color the edges of a graph so that each vertex “sees” at most two colors. ..
- 15. Maximum Edge Coloring GOAL. Color the edges of a graph so that each vertex “sees” at most two colors. .
- 16. Maximum Edge Coloring GOAL. Color the edges of a graph so that each vertex “sees” at most two colors. .. This is not an optimal coloring yet.
- 17. Maximum Edge Coloring GOAL. Color the edges of a graph so that each vertex “sees” at most two colors. .
- 18. Maximum Edge Coloring GOAL. Color the edges of a graph so that each vertex “sees” at most two colors. .
- 19. Motivation In a network, every system has two interface cards.
- 20. Motivation In a network, every system has two interface cards. The goal is to assign frequency channels so that: ..1 No system is assigned more than two channels. ..2 The number of channels used overall is maximized.
- 21. Motivation In a graph, every system has two interface cards. The goal is to assign frequency channels so that: ..1 No system is assigned more than two channels. ..2 The number of channels used overall is maximized.
- 22. Motivation In a graph, every vertex has two interface cards. The goal is to assign frequency channels so that: ..1 No system is assigned more than two channels. ..2 The number of channels used overall is maximized.
- 23. Motivation In a graph, every vertex has two interface cards. The goal is to assign frequency channels so that: ..1 No vertex sees more than two colors. ..2 The number of channels used overall is maximized.
- 24. Motivation In a graph, every vertex has two interface cards. The goal is to assign frequency channels so that: ..1 No vertex sees more than two colors. ..2 The number of colors used overall is maximimized.
- 25. Past Work Max Edge coloring is known to be NP-Complete and also APX-Hard (Adamaszek and Popa, 2010)
- 26. Past Work Max Edge coloring is known to be NP-Complete and also APX-Hard (Adamaszek and Popa, 2010) A 2-approximation algorithm is known on general graphs (Feng, Zhang and Wang, 2009)
- 27. Past Work Max Edge coloring is known to be NP-Complete and also APX-Hard (Adamaszek and Popa, 2010) A 2-approximation algorithm is known on general graphs (Feng, Zhang and Wang, 2009) The problem is shown to have a polynomial time algorithm for complete graphs and trees (Feng, Zhang and Wang, 2009)
- 28. Past Work Max Edge coloring is known to be NP-Complete and also APX-Hard (Adamaszek and Popa, 2010) A 2-approximation algorithm is known on general graphs (Feng, Zhang and Wang, 2009) The problem is shown to have a polynomial time algorithm for complete graphs and trees (Feng, Zhang and Wang, 2009) There exists a 5 3 -approximation algorithm for graphs with perefect matching (Adamaszek and Popa, 2010)
- 29. Maximum Edge Coloring: The Decision Version Can we color with at least k colors?
- 30. Maximum Edge Coloring: The Decision Version Can we color with at least k colors?
- 31. Maximum Edge Coloring: The Decision Version Can we color with at least k colors? ≡ Can we color with exactly k colors?
- 39. The Maximum Edge Coloring Problem (Parameterized) Input: A graph G and an integer k. Question: Can the edges of G be colored with k colors so that no vertex sees more than two colors? Parameter: k
- 40. The Maximum Edge Coloring Problem (Parameterized) Input: A graph G and an integer k. Question: Can the edges of G be colored with k colors so that no vertex sees more than two colors? Parameter: k
- 41. A parameterized problem is denoted by a pair (Q, k) ⊆ Σ∗ × N.
- 42. A parameterized problem is denoted by a pair (Q, k) ⊆ Σ∗ × N. The first component Q is a classical language, and the number k is called the parameter.
- 43. A parameterized problem is denoted by a pair (Q, k) ⊆ Σ∗ × N. The first component Q is a classical language, and the number k is called the parameter. Such a problem is fixed–parameter tractable or FPT if there exists an algorithm that decides it in time O(f(k)nO(1)) on instances of size n.
- 44. If there are less than k edges ⇒ Say NO.
- 45. If there are less than k edges ⇒ Say NO. A matching of size at least (k − 1) ⇒ Say YES.
- 46. If there are less than k edges ⇒ Say NO. A matching of size at least (k − 1) ⇒ Say YES. ...........
- 47. If there are less than k edges ⇒ Say NO. A matching of size at least (k − 1) ⇒ Say YES. ...........
- 48. If there are less than k edges ⇒ Say NO. A matching of size at least (k − 1) ⇒ Say YES. ...........
- 49. If there are less than k edges ⇒ Say NO. A matching of size at least (k − 1) ⇒ Say YES. ...........
- 50. If there are less than k edges ⇒ Say NO. A matching of size at least (k − 1) ⇒ Say YES. ...........
- 51. If there are less than k edges ⇒ Say NO. A matching of size at least (k − 1) ⇒ Say YES. ...........
- 52. ...
- 53. .....
- 54. .......
- 55. .........
- 56. ...........
- 57. .............
- 58. ...............
- 59. ...............
- 60. ................ We have a vertex cover . of size at most 2k.
- 61. .. We have a vertex cover . of size at most 2k. ..............
- 70. To realize a palette assignment, we must assign colors so that:
- 71. To realize a palette assignment, we must assign colors so that: ..1 Every edge respects the palette. .. VertexCover . IndependentSet
- 72. To realize a palette assignment, we must assign colors so that: ..1 Every edge respects the palette. ..2 Every palette is satisified. ....... VertexCover . IndependentSet
- 73. Sanity Checks
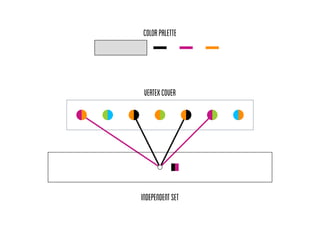
- 79. .. ColorPalette ...... VertexCover . IndependentSet . Every color must be realized in the palettes of the vertex cover vertices.
- 81. Guess a split of the Palette
- 82. .. ColorPalette ...... Guess X: the set of colors assigned to edges within the vertex cover. . VertexCover . IndependentSet
- 83. .. ColorPalette ...... Guess X: the set of colors assigned to edges within the vertex cover. . VertexCover . IndependentSet
- 84. .. ColorPalette ...... Guess X: the set of colors assigned to edges within the vertex cover. . VertexCover . IndependentSet
- 85. .. ColorPalette ...... Guess X: the set of colors assigned to edges within the vertex cover. . VertexCover . IndependentSet
- 87. Assign Colors Within the Vertex Cover
- 88. .. ColorPaletteWithX Fixed ........ VertexCover . IndependentSet . Case 1: The palettes intersect at one color.
- 89. .. ColorPaletteWithX Fixed ....... VertexCover . IndependentSet . Case 1: The palettes intersect at one color.
- 90. .. ColorPaletteWithX Fixed ...... VertexCover . IndependentSet . Case 1: The palettes intersect at one color.
- 91. .. ColorPaletteWithX Fixed ...... VertexCover . IndependentSet . Case 1: The palettes intersect at one color. . The edge gets that color.
- 92. .. ColorPaletteWithX Fixed ...... VertexCover . IndependentSet . Case 2: The palettes are the same.
- 93. .. ColorPaletteWithX Fixed ...... VertexCover . IndependentSet . Case 2: The palettes are the same. . If only one of the colors is in X, assign that color.
- 94. .. ColorPaletteWithX Fixed ...... VertexCover . IndependentSet . Case 2: The palettes are the same. . If both colors are in X, branch.
- 95. Whenever a color in X is assigned to an edge, mark it as used.
- 96. Whenever a color in X is assigned to an edge, mark it as used. Branch only over unused colors.
- 97. Whenever a color in X is assigned to an edge, mark it as used. Branch only over unused colors. Once all colors in X are used, assign colors arbitrarily.
- 98. Assign Colors Outside the Vertex Cover
- 112. As it turns out, there are only two kinds of lists:
- 113. As it turns out, there are only two kinds of lists: ..1 Those with constant size. ..2 Those with a common color.
- 114. As it turns out, there are only two kinds of lists: ..1 Those with constant size. Continue to branch. ..2 Those with a common color.
- 115. As it turns out, there are only two kinds of lists: ..1 Those with constant size. Continue to branch. ..2 Those with a common color. Reduces to a maximum matching problem.
- 116. Running time?
- 117. Palette k2k
- 118. Palette × Guess X k2k · 2k
- 119. Palette × Guess X × Branching k2k · 2k · 10k
- 120. Palette × Guess X × Branching k2k · 2k · 10k Overall: O∗ ((20k)k )
- 121. Other Results
- 122. Other Results ..1 We show an explicit exponential kernel by the application of some simple reduction rules.
- 123. Other Results ..1 We show an explicit exponential kernel by the application of some simple reduction rules. ..2 We also show NP-hardness and polynomial kernels for restricted graph classes (constant maximum degree, and C4-free graphs).
- 124. Other Results ..1 We show an explicit exponential kernel by the application of some simple reduction rules. ..2 We also show NP-hardness and polynomial kernels for restricted graph classes (constant maximum degree, and C4-free graphs). ..3 We consider the dual parameter 1 and show a polynomial kernel in this setting. 1 Can we color with at least (n − k) colors?
- 126. Several Open Problems! ..1 Can the algorithm be improved to a running time of O(ck) for some constant c?
- 127. Several Open Problems! ..1 Can the algorithm be improved to a running time of O(ck) for some constant c? ..2 Does the problem admit a polynomial kernel?
- 128. Several Open Problems! ..1 Can the algorithm be improved to a running time of O(ck) for some constant c? ..2 Does the problem admit a polynomial kernel? ..3 A natural extension would be the above-guarantee version: can we color with at least (t + k) colors, where t is the size of a maximum matching?
- 129. Several Open Problems! ..1 Can the algorithm be improved to a running time of O(ck) for some constant c? ..2 Does the problem admit a polynomial kernel? ..3 A natural extension would be the above-guarantee version: can we color with at least (t + k) colors, where t is the size of a maximum matching? ..4 Is there an explicit FPT algorithm for the dual parameter?
- 130. Thank You.