Scala 初心者が Hom 函手を Scala で考えてみた
0 likes531 views
このスライドは、2020/08/30 に開催された「Pre-ScalaMatsuri」で発表したものです。
![>=> 実際にやってみた
// F[_] が対象の対応関係を，map が射の対応関係を表す
trait EndoFunctor[F[_]] {
def map[A, B](f: A => B): F[A] => F[B]
}
type X = Unit // 固定する型は何でも良いが、今回は Unit 型
type Xto[Y] = X => Y // Hom 函手における、対象の対応関係
implicit val homFunctor = new EndoFunctor[Xto] {
def map[A, B](f: A => B): Xto[A] => Xto[B] = // Hom 函手における、射の対応関係
f compose _
}
// 任意の函手の実装を用いて、射を相手先の圏へ移す(※といいつつ Scala 圏には閉じてるので、Endo = 自己)
def map[F[_], A, B](f: A => B)(implicit functor: EndoFunctor[F]): F[A] => F[B] =
functor.map(f)
19](https://image.slidesharecdn.com/slide-200831023241/85/Scala-Hom-Scala-19-320.jpg)
![>=> 実際につかってみた
val f: Int => String = x => s"String($x)" // Int と String を結ぶ射をピックアップ
val Fa: Xto[Int] = x => 0 // Hom(X, Int) から、要素をピックアップ
// 1. Hom(X, Int) の要素 Fa
// 2. Hom 集合を結ぶ射 map(f)
// これらから、Hom(X, String) の要素 Fb を導出
val Fb: Xto[String] = map(f).apply(Fa)
println(Fb(())) // String(0) と表示される
20
- 実装してみての感想：
- 高階カインドは、やはりあると表現力が高い 🎉
- implicit parameter は、auto capturing default parameter だと思った 🤔
- 本当は map(f).apply(Fa) の部分を、map(f)(Fa) と書けたらかっちょよい](https://image.slidesharecdn.com/slide-200831023241/85/Scala-Hom-Scala-20-320.jpg)
Scala 初心者が Hom 函手を Scala で考えてみた
- 1. Scala 初心者が Hom 函手を Scala で考えてみた Pre-ScalaMatsuri 2020 高瀬 和之 @Guvalif
- 2. >=> 自己紹介 - 名前： 高瀬 和之 (たかせ かずゆき) - 所属： Chatwork 株式会社 @大阪 - 専門： - フロントエンド開発 (React / Redux / TypeScript) - ティーチング (アルゴリズム / 機械学習 / 数学 / 組み込みシステム) - ひとこと： - Scala のイベントは初めてです 💪 2
- 3. >=> アジェンダ 1. ことの発端 2. そもそも函手とは？ 3. Hom 函手 4. Scala での実装例 3
- 4. 01ことの発端
- 5. >=> ある日のひとまく Scala ガチ勢の H 氏 < Haskell 書けるらしいじゃん？ Scala もいけるっしょ 💪 たかせ < えっ？ ～ 数週間後 ～ - 私に送られてきたのは… - State Monad ゴリゴリで， - for 式をいい感じに駆使していて， - Files changed が 18 くらいある， - そんな Pull-Request 😇🎉 5
- 6. >=> とはいえ… - 意外とがんばれば読める - for 式 ⇒ Haskell の do 構文 - Monad ⇒ Haskell の屋台骨 - case class ⇒ Haskell の Record っぽさ - trait ⇒ Haskell の型クラスっぽさ - etc... かくして、”Do Haskell for Scala” という標語が、生まれたとかなんとか… (※フロントエンド開発メンバーとの日常会話にて) 6
- 7. >=> 問題点 🙅♂ - なんとなく読める ≠ 使いこなせる - Scala の言語仕様をきちんと理解した上で、ﾓﾅﾓﾅできるようになりたい！ というわけで… 1. まずはﾌｧﾝｸﾀﾌｧﾝｸﾀできるように、型クラス周りの仕様を知る 2. 何か適当な Functor を実装してみる こうして私は Scala に入門しました 🚪 7
- 9. >=> 圏論ことはじめ (1)：対象と射 - 圏論の材料 - 対象 ⇒ 点 - 射 ⇒ 点から点を結ぶ矢印 (点と点の関連性を表す) - ここまでの事実 ⇒ なんか有向グラフっぽい 9
- 10. >=> 圏論ことはじめ (2)：圏の例 - しりとりの圏 (対象：ひらがな，射：単語) 10 - 型と関数の圏 (対象：型，射：関数) り ご ら ぱ り りんご ごりら らっぱ ぱせり String Int Boolean length isEven isCamelCase
- 11. >=> 圏論ことはじめ (3)：函手 / Functor - ある圏から、グラフ構造を全て抜き出す - 別の圏にて、グラフ構造が一致する箇所に対応づける - 対象と対象の対応関係，および射と射の対応関係，その2つ組と考えてもよい (※実際には公理を満たすように，かつ実用的に必要な性質を盛り込んで考えます) 11 圏 D圏 C
- 12. 03Hom 函手
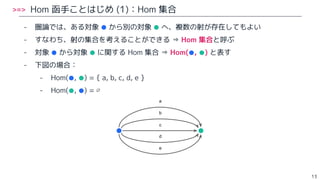
- 13. >=> Hom 函手ことはじめ (1)：Hom 集合 - 圏論では、ある対象 ● から別の対象 ● へ、複数の射が存在してもよい - すなわち、射の集合を考えることができる ⇒ Hom 集合と呼ぶ - 対象 ● から対象 ● に関する Hom 集合 ⇒ Hom(●, ●) と表す - 下図の場合： - Hom(●, ●) = { a, b, c, d, e } - Hom(●, ●) = ∅ 13 a e d b c
- 14. >=> Hom 函手ことはじめ (2)：舞台を集合の圏へ - 圏 C で何か1つ対象を固定する (今回は X) - 固定した対象と、圏 C の任意の対象に関して、Hom 集合を取る 14 X A D C B 圏 C 集合の圏 Hom(X, A) Hom(X, B) Hom(X, C) ※Hom(X, D) は空集合
- 15. >=> Hom 函手ことはじめ (3)：Hom 集合の間に射が存在する条件 - 対象 X から対象 A への任意の射 a - 対象 X から対象 B へのある射 b - これらに対して、b = f ∘ a を満たす射 f が存在すること (※ b を使って X から B へ向かうことと、a と f を使って X から B へ向かうことが等しくなる，の意) 15 X B A 圏 C 集合の圏 Hom(X, A) Hom(X, B) ∀a ∃b ∃f, b = f ∘ a f ∘ _
- 16. >=> Hom 函手ことはじめ (4)：共変 Hom 函手 - 共変 Hom 函手とは： - 任意の圏から集合の圏への函手であって， - 対象 ＊ を対象 Hom(X, ＊) へ移し， - (制約を満たす) 射 f を射 f ∘ _ へ移す，そんな函手 16 X B A 圏 C 集合の圏 Hom(X, A) Hom(X, B) ∀a ∃b ∃f, b = f ∘ a f ∘ _
- 17. 04Scala での実装例
- 18. >=> 共変 Hom 函手 in Scala - 型と関数の圏をベースに、Scala 圏を考えると： - ＊ → Hom(X, ＊) なる対象の対応は、カインド X => ＊ として表現できる (※厳密には、指数対象というものを考えて、Hom 集合を Scala 圏に埋め込むとそうなります) - f → f ∘ _ なる射の対応は、高階関数 f => f compose _ として表現できる 18 X B A Scala 圏 Scala 圏 X => A X => B ∀a ∃b ∃f, b = f compose a f compose _
- 19. >=> 実際にやってみた // F[_] が対象の対応関係を，map が射の対応関係を表す trait EndoFunctor[F[_]] { def map[A, B](f: A => B): F[A] => F[B] } type X = Unit // 固定する型は何でも良いが、今回は Unit 型 type Xto[Y] = X => Y // Hom 函手における、対象の対応関係 implicit val homFunctor = new EndoFunctor[Xto] { def map[A, B](f: A => B): Xto[A] => Xto[B] = // Hom 函手における、射の対応関係 f compose _ } // 任意の函手の実装を用いて、射を相手先の圏へ移す(※といいつつ Scala 圏には閉じてるので、Endo = 自己) def map[F[_], A, B](f: A => B)(implicit functor: EndoFunctor[F]): F[A] => F[B] = functor.map(f) 19
- 20. >=> 実際につかってみた val f: Int => String = x => s"String($x)" // Int と String を結ぶ射をピックアップ val Fa: Xto[Int] = x => 0 // Hom(X, Int) から、要素をピックアップ // 1. Hom(X, Int) の要素 Fa // 2. Hom 集合を結ぶ射 map(f) // これらから、Hom(X, String) の要素 Fb を導出 val Fb: Xto[String] = map(f).apply(Fa) println(Fb(())) // String(0) と表示される 20 - 実装してみての感想： - 高階カインドは、やはりあると表現力が高い 🎉 - implicit parameter は、auto capturing default parameter だと思った 🤔 - 本当は map(f).apply(Fa) の部分を、map(f)(Fa) と書けたらかっちょよい