Sorting method data structure

SORTING METHOD DATA STRUCTURE
PROF. SUNIL D. CHUTE
HEAD DEPT OF COMPUTER SCIENCE
M.G. COLLEGE ARMORI

BUBBLE SORT
• Bubble sort is a simple sorting algorithm. This sorting algorithm
is comparison-based algorithm in which each pair of adjacent
elements is compared and the elements are swapped if they are
not in order. This algorithm is not suitable for large data sets as
its average and worst case complexity are of Ο(n2) where n is
the number of items.

HOW BUBBLE SORT WORKS?
We take an unsorted array for our example. Bubble sort takes Ο(n2) time so we're
keeping it short and precise.
Bubble sort starts with very first two elements, comparing them to check which one is
greater.
In this case, value 33 is greater than 14, so it is already in sorted locations. Next, we
compare 33 with 27.

We find that 27 is smaller than 33 and these two values must be swapped.
The new array should look like this −
Next we compare 33 and 35. We find that both are in already sorted positions.
Then we move to the next two values, 35 and 10.
We know then that 10 is smaller 35. Hence they are not sorted.

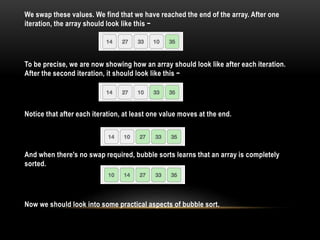
We swap these values. We find that we have reached the end of the array. After one
iteration, the array should look like this −
To be precise, we are now showing how an array should look like after each iteration.
After the second iteration, it should look like this −
Notice that after each iteration, at least one value moves at the end.
And when there's no swap required, bubble sorts learns that an array is completely
sorted.
Now we should look into some practical aspects of bubble sort.

ALGORITHM
• We assume list is an array of n elements. We further assume that swap function
swaps the values of the given array elements.
begin BubbleSort(list)
for all elements of list
if list[i] > list[i+1]
swap(list[i], list[i+1])
end if
end for
return list
end BubbleSort

SELECTION SORT ALGORITHM
• Selection sort is a simple sorting algorithm. This sorting
algorithm is an in-place comparison-based algorithm in which
the list is divided into two parts, the sorted part at the left end
and the unsorted part at the right end. Initially, the sorted part is
empty and the unsorted part is the entire list.
• The smallest element is selected from the unsorted array and
swapped with the leftmost element, and that element becomes a
part of the sorted array. This process continues moving unsorted
array boundary by one element to the right.
• This algorithm is not suitable for large data sets as its average
and worst case complexities are of Ο(n2), where n is the number
of items.

HOW SELECTION SORT WORKS?
• Set the first element as minimum
• Compare minimum with the second element. If the second element is smaller
than minimum, assign the second element as minimum. Compare minimum with the third
element. Again, if the third element is smaller, then assign minimum to the third element
otherwise do nothing. The process goes on until the last element.

• After each iteration, minimum is placed in the front of the unsorted list.
• For each iteration, indexing starts from the first unsorted element. Step 1 to 3 are
repeated until all the elements are placed at their correct positions.

SELECTION SORT ALGORITHM
• selectionSort(array, size)
repeat (size - 1) times
set the first unsorted element as the minimum
for each of the unsorted elements
if element < currentMinimum
set element as new minimum
swap minimum with first unsorted position
end selectionSort

INSERTION SORT
• This is an in-place comparison-based sorting algorithm. Here, a
sub-list is maintained which is always sorted. For example, the
lower part of an array is maintained to be sorted. An element
which is to be 'insert'ed in this sorted sub-list, has to find its
appropriate place and then it has to be inserted there. Hence
the name, insertion sort.
• The array is searched sequentially and unsorted items are
moved and inserted into the sorted sub-list (in the same array).
This algorithm is not suitable for large data sets as its average
and worst case complexity are of Ο(n2), where n is the number
of items.

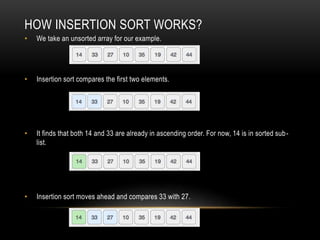
HOW INSERTION SORT WORKS?
• We take an unsorted array for our example.
• Insertion sort compares the first two elements.
• It finds that both 14 and 33 are already in ascending order. For now, 14 is in sorted sub-
list.
• Insertion sort moves ahead and compares 33 with 27.

• And finds that 33 is not in the correct position.
• It swaps 33 with 27. It also checks with all the elements of sorted sub-list. Here we see
that the sorted sub-list has only one element 14, and 27 is greater than 14. Hence, the
sorted sub-list remains sorted after swapping.
• By now we have 14 and 27 in the sorted sub-list. Next, it compares 33 with 10.
• These values are not in a sorted order.

• So we swap them.
• However, swapping makes 27 and 10 unsorted.
• Hence, we swap them too.
• Again we find 14 and 10 in an unsorted order.
• We swap them again. By the end of third iteration, we have a sorted sub-list of 4 items.
• This process goes on until all the unsorted values are covered in a sorted sub-list. Now
we shall see some programming aspects of insertion sort.

INSERTION SORT ALGORITHM
insertionSort(array)
mark first element as sorted
for each unsorted element X
'extract' the element X
for j <- lastSortedIndex down to 0
if current element j > X
move sorted element to the right by 1
break loop and insert X here
end insertionSort

Sorting method data structure

More Related Content

What's hot (20)

Similar to Sorting method data structure (20)

More from sunilchute1 (10)

Recently uploaded (20)

Sorting method data structure