César vallejo 2015

1
2015
• Aptitud Académica
• Matemática
• Ciencias Naturales
• Cultura General
Preguntaspropuestas

Geometría
2
Ángulo, ángulos entre rectas paralelas
y una recta secante
NIVEL BÁSICO
1. Si OM es bisectriz del  AOB, halle x.
x
O B
M
A
25º
A) 170º B) 160º C) 150º
D) 140º E) 130º
2. En el gráfico, halle m AOB.
O
A
α
α
θ
θ
40º
B
A) 80º B) 100º C) 110º
D) 120º E) 140º
3. Del siguiente gráfico, si L L1 2// , ¿qué tipos de
ángulos son a y b?

L 1
L 2
α
β
A) alternos internos
B) alternos externos
C) correspondientes
D) conjugados internos
E) conjugados externos
4. Si L L1 2// , halle x.

L 1
L 280º
5x
A) 9º B) 10º C) 12º
D) 15º E) 16º
5. Si L L1 2// , halle x.

L 1
L 2
8x
60º
A) 5º B) 8º C) 10º
D) 15º E) 20º
6. Si L L1 2// y q=2a, halle a.

L 1
L 2
α
θ
α
A) 20º B)
25
2
º
C) 30º
D) 40º E)
45
2
º

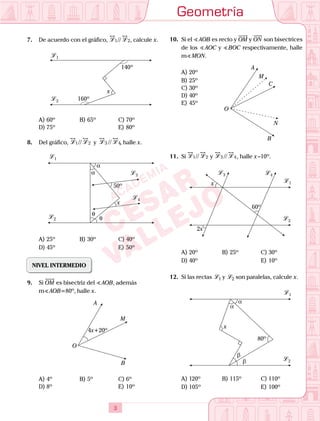
Geometría
3
7. De acuerdo con el gráfico, L L1 2// , calcule x.

L 1
L 2 160º
x
140º
A) 60º B) 65º C) 70º
D) 75º E) 80º
8. Del gráfico, L L1 2// y L L3 4// , halle x.

L 3
L 4
L 1
L 2
θ
θ
α
α
x
50º
A) 25º B) 30º C) 40º
D) 45º E) 50º
NIVEL INTERMEDIO
9. Si OM es bisectriz del  AOB, además
m AOB=80º, halle x.

A
B
M
O
4x+20º
A) 4º B) 5º C) 6º
D) 8º E) 10º
10. Si el  AOB es recto y OM y ON son bisectrices
de los  AOC y  BOC respectivamente, halle
m MON.
A) 20º
A
B
M
C
N
O
B) 25º
C) 30º
D) 40º
E) 45º
11. Si L L1 2// y L L3 4// , halle x –10º.

L 1
L 2
L 4L 3
x
2x
60º
A) 20º B) 25º C) 30º
D) 40º E) 10º
12. Si las rectas L 1 y L 2 son paralelas, calcule x.

L 1
L 2
x
80º
β
β
α
α
A) 120º B) 115º C) 110º
D) 105º E) 100º

Geometría
4
NIVEL AVANZADO
13. En el gráfico mostrado, OM es bisectriz del
 BOC y m AOC=3(m BOM), halle m BOM.

A
B
M
O
C
A) 20º
B) 25º
C) 30º
D) 36º
E) 18º
14. En el gráfico mostrado OB y OC son bisectrices
de los ángulos AOC y AOD respectivamente,
halle q.
A) 10º A
B
O
C
D
100º θ
B) 18º
C) 20º
D) 25º
E) 30º
15. En el gráfico L L1 2// , halle x.

L 1
L 2
β
β
α
α 40º
100º x
A) 110º B) 120º C) 130º
D) 140º E) 150º

Geometría
5
Triángulo I
NIVEL BÁSICO
1. Según el gráfico, calcule 2x.

70º
5x+10º
5x
A) 10º B) 20º C) 30º
D) 24º E) 15º
2. De acuerdo con el gráfico, calcule x.

60º
2x 5x
A) 10º B) 15º C) 20º
D) 25º E) 30º
3. A partir del gráfico, calcule x.
A) 70º
α
α70º
x
30ºB) 75º
C) 80º
D) 85
E) 90º
4. En el gráfico mostrado, m+n=140º. Halle x+y.

x
ym
n
110º
A) 120º B) 130º C) 140º
D) 150º E) 160º
5. En el siguiente gráfico, halle x.

50º
60º α
α
x
A) 60º B) 70º C) 80º
D) 100º E) 110º
6. Del gráfico mostrado, halle a.

70º
40º
θ
θα
2α
A) 10º B) 15º C) 20º
D) 25º E) 30º
7. En el gráfico, calcule x.

4x
2x
θ
θ60º
10º
A) 10º B) 20º C) 25º
D) 30º E) 15º

Geometría
6
8. Según el gráfico, calcule x.
A) 150º
x
120º
2α
β
2β
α
B) 140º
C) 130º
D) 120º
E) 100º
NIVEL INTERMEDIO
9. En el gráfico, a+b+q+f=140º. Calcule m+n.
α
β θ
φm n
A) 200º B) 220º C) 240º
D) 280º E) 110º
10. Del gráfico, calcule x+y.

α
α
θ
θ
x
y
A) 45º B) 60º C) 90º
D) 120º E) 180º
11. En el gráfico, calcule x –y.

160º
y
θ
θ
α
α
x
A) 10º B) 15º C) 25º
D) 20º E) 30º
12. Según el gráfico, m n+ = +180
2
θ
. Calcule x – y.

θ
x
m
n y
A) 2q B)
3
2
q
C)
q
2
D)
5
2
q
E) 3q
NIVEL AVANZADO
13. En un triángulo, los valores numéricos de las
medidas angulares interiores son números
consecutivos. Halle la medida angular inter-
media.
A) 49º B) 58º C) 59º
D) 60º E) 61º
14. Según el gráfico, calcule x+y.

2θ
2α
θ
α β
β
ω
ω
x
y
120º
A) 80º B) 85º C) 90º
D) 70º E) 75º
15. En un triángulo ABC, AB=5, BC=6 y
m ABC > m BAC. Halle la diferencia entre
el mayor y menor valor entero de AC.
A) 1 B) 2 C) 3
D) 4 E) 5

Geometría
7
Triángulo II
NIVEL BÁSICO
1. Si AB=BC=AC=BD, halle x.
A
B
C
D
x
70º
A) 65º B) 70º C) 80º
D) 85º E) 90º
2. Si AB=BC y AC=CD, calcule x.

A
B
C
D
x
100º
A) 50º B) 55º C) 60º
D) 65º E) 70º
3. En el gráfico, BD es bisectriz interior del trián-
gulo ABC, además, AB=BD. Halle m BAC.

30º
A
B
CD
A) 50º B) 60º C) 70º
D) 80º E) 75º
4. En el gráfico, BD es bisectriz exterior del trián-
gulo ABC, halle x.
A
B
C D
30º30º 20º
xx
A) 55º B) 60º C) 65º
D) 70º E) 80º
5. En el gráfico, los triángulos ABC y ADC son
isósceles de bases AC y CD, respectivamente.
Halle x.
A) 10º
A B
C
D
x
40º
B) 15º
C) 20º
D) 5º
E) 25º
6. En un triángulo isósceles, ABC de base AC, se
trazalaalturaCH,talque,m BCH=4(m ACH).
Halle m ABC.
A) 10º B) 15º C) 20º
D) 30º E) 40º
7. Si ABC es un triángulo equilátero, además,
BR=BS, calcule x.

50º
A
B
C
R
x
S
A) 20º B) 30º C) 40º
D) 45º E) 50º

Geometría
8
8. Del gráfico mostrado, si a+b=150º, calcule a.

αα
β
β
θ
θ
a
b
A) 20º B) 30º C) 40º
D) 50º E) 60º
NIVEL INTERMEDIO
9. En un triángulo ABC, se traza la bisectriz interior
BD, tal que m ABD=m ACB. Si m BAC=60º.
Halle m ACB.
A) 20º B) 30º C) 35º
D) 40º E) 25º
10. En un triángulos isósceles ABC de base AC, se
traza la ceviana interior BD, tal que, BD=AD y
m CBD=90º. Halle m BAC.
A) 15º B) 30º C) 36º
D) 45º E) 37º
11. En la región exterior del lado AC de un triángulo
isósceles ABC(AB=BC), se ubica el punto D, tal
que, AD=BC y m BAD=60º. Halle m BCD, si
m ABC=100º.
A) 50º B) 55º C) 60º
D) 65º E) 70º
12. Si L es mediatriz de AC y AB=CM. Halle x en
función de a y b.

βα
L
A
B
M C
x
A) a – b B)
α β−
2
C) a – 2b
D)
α β− 2
2
E)
α β+
2
NIVEL AVANZADO
13. En un triángulo ABC, m ACB=60º y m ABC=70º.
Si se traza la altura BH, halle la medida del ma-
yor ángulo formado por las bisectrices de los
ángulos BAC y HBC.
A) 90º B) 100º C) 110º
D) 120º E) 130º
14. En la región exterior relativa al lado BC de un
triángulo equilátero ABC, se ubica D, tal que
AD ∩ BC = {E} y BE=DE. Halle m CAE, si AC=BD.
A) 10º B) 15º C) 20º
D) 30º E) 40º
15. Del gráfico mostrado, q > a, AB=7 y AC=9.
Halle la cantidad de valores enteros de BC, si
el ABC es acutángulo.

αθ
A
B
C
A) 6 B) 5 C) 4
D) 3 E) 2

Geometría
9
Congruencia de triángulos
NIVEL BÁSICO
1. ¿Cuáles de los siguientes pares de triángulos
son congruentes?
I.
α α
a
b a
b
II.
m
m
n n
III.
a
a
b
m
mb
A) I y III B) solo II C) solo III
D) II y III E) I, II y III
2. En el siguiente gráfico, AB=BC y AM=CN.
Calcule x.

40º
A CM
B
N
x
A) 40º B) 50º C) 60º
D) 70º E) 80º
3. Si AB=BC, CD=2 y DE=3, calcule AE.
A
B
C
D
E
A) 8 B) 7 C) 6
D) 5 E) 4
4. Se muestran los triángulos equiláteros ABC y
CDE. Si AD=6, halle BE.

A
B
C
D E
A) 6 3 B) 6 2 C) 6
D) 3 E) 3 3
5. Si AB=BC, AE=8 y DE=2, halle BE.

α
α
β
β
A
B
C
D
E
A) 10 B) 9 C) 8
D) 7 E) 6
6. En el siguiente gráfico, AB=CE=5, AC=CD=4 y
BD=2, halle DE.

α
α
A
B
C
D
E
A) 5 B) 4 C) 3
D) 6 E) 8

Geometría
10
7. En el siguiente gráfico, AC=CD, AB=6 y DE=4;
halle BE.

A
B C
D
E
A) 12 B) 12,5 C) 10
D) 9 E) 8
8. Del gráfico, las regiones ABC y ECD son con-
gruentes. Halle x.

A
B C
D
E
xx
A) 60º B) 53º C) 45º
D) 37º E) 30º
NIVEL INTERMEDIO
9. Enelgráficomostradolasregionessombreadas
son congruentes. Halle x.

θ
x
A) q B) 2q C) 90º – q
D) 45º+ q E) 45º+ q/2
10. Si el ABC es equilátero, CD=AE, EM=6 y
BD=11; halle MC.
A
B
CD
E
M
A) 2 B) 3 C) 4
D) 5 E) 6
11. En el gráfico mostrado, AB=BC y BD=BE.
Calcule
CM
ME
.
A
B
C
D
E
M
A) 2 B) 1 C)
2
2
D)
1
2
E) 2
12. En el siguiente gráfico, AB=CD y BC=DE.
Halle x.
A) 50º
A
B
C
D
E
100º
70º 70º
x
B) 60º
C) 70º
D) 80º
E) 85º

Geometría
11
NIVEL AVANZADO
13. En un triángulo ABC, se traza la ceviana in-
terior BD, tal que AB=CD, m BAC=30º y
m CBD=75º. Halle m ABD.
A) 30º B) 35º C) 40º
D) 45º E) 50º
14. Indique la secuencia correcta de verdad (V) o
falsedad (F) de las siguientes proposiciones.
I. Si un triángulo presenta solo dos alturas
congruentes, entonces dicho triángulo es
isósceles.
II. En todo triángulo isósceles, la altura relativa
a la base biseca a dicha base.
III. En un triángulo equilátero, las tres alturas
son congruentes entre sí.
A) VVV B) VFV C) VVF
D) FVV E) FFV
15. Indique la secuencia correcta de verdad (V) o
falsedad (F) de los siguientes enunciados.
I. Si las longitudes de los tres lados de un
triángulo son iguales a las longitudes de los
lados de otro triángulo, entonces dichos
triángulos son congruentes.
II. Todos los triángulos equiláteros isoperimé-
tricos son congruentes entre sí.
III. Si dos triángulos rectángulos isósceles pre-
sentan un lado común, entonces dichos trián-
gulos son congruentes.
A) VVV B) VFV C) VVF
D) VFF E) FVV

Geometría
12
Aplicaciones de la congruencia
NIVEL BÁSICO
1. En el gráfico mostrado, BD=3 y AC=AB+4.
Halle x.
A) 45º
θ
θ
A B
C
D
x
B) 53º
C) 60º
D) 37º
E) 30º
2. En un triángulo ABC, se traza la altura BH (H en AC),
tal que HC=10 y m HBC=m BAC+m ACB.
Halle la distancia de C hacia AB.
A) 5 B) 5 2 C) 10
D) 10 2 E) 20
3. En el gráfico mostrado, L es mediatriz de AC,
además AB=BD. Halle x.

40º
L
A
B
C
D
x
120º
A) 60º B) 65º C) 70º
D) 75º E) 80º
4. En el gráfico mostrado, AD es bisectriz del
 BAC y L es mediatriz de BC. Si AB=6 y
DE=1, halle AC.

A
D
E
B
C
L
A) 12 B) 7 C) 8
D) 9 E) 10
5. En el gráfico, M, N, P y Q son los puntos medios
de AC, AB, NR y MR. Si BP=9 y QC=3, halle PQ.
A
B
Q
CM
N
P
R
A) 2 B) 3 C) 4
D) 5 E) 3,5
6. En el gráfico, AB = 6 2. Halle AC+BC.

α
α
θ
θ
A
B
C
A) 6 2 B) 12 C) 3
D) 6 E) 12 2
7. En el siguiente gráfico, BC=CD y AB=CE.
Halle x.
A
B
C
DE
x53º
A) 37º B) 53º C) 30º
D) 45º E) 60º

Geometría
13
8. En un triángulo ABC, se traza la mediana BM, y
en su prolongación se ubica el punto P, tal que
la m APB=90º, además BC=2(AP).
Halle m MBC.
A) 15º B) 30º C) 37º
D) 45º E) 60º
NIVEL INTERMEDIO
9. En un triángulo rectángulo ABC, recto en
B, se traza la ceviana interior AD, tal que
m ACB=2(m BAD). Si BD=a y CD=b, halle AC.
A) 2a+b B) a+2b C) 2(a+b)
D) 2 a b+( ) E) 2a+3b
10. Se tiene un triángulo rectángulo ABC, recto
en B, se traza la ceviana interior AD, tal que
m DAC=2(m BAD), además AC=AD+2(BD).
Halle m BAD.
A) 15º B) 16º C) 18º
D) 20º E) 24º
11. Se muestra un triángulo equilátero ABC.
Halle
DN
CL
.

45º
A
B
C
D
L
N
A)
1
4
B)
3
2
C)
3
4
D)
6
4
E)
6
8
12. En el triángulo rectángulo ABC, recto en B, se
ubicaPenlaregióninterior,demodoquePB=3,
PA=5, m PAC=2(m PBC)=2(m ACB).
Calcule la m ACB.
A) 15º B) 30º C) 37º
D)
37
2
º
E)
53
2
º
NIVEL AVANZADO
13. Se tiene un triángulo rectángulo ABC, recto en
B, se traza la bisectriz interior CD, y en AD y CD
se ubican M y N tal que BD=DM y CD=2(MN).
Calcule m MNC, si m BAC=60º
A) 106º B) 120º C) 135º
D) 143º E) 150º
14. En la prolongación de AC de un triángulo rec-
tángulo ABC, recto en B se ubica D, tal que
m CBD=2(m BAC) y AB=DM (M: punto me-
dio de AC). Calcule m BAC.
A) 10º B) 15º C) 20º
D) 25º E) 30º
15. Se tiene un triángulo ABC isósceles de base AC,
tal que m ABC=20º, AB=10, además, se traza
la bisectriz interior AI. Halle el perímetro de la
región triangular AIC.
A) 20 B) 15 C) 10
D) 5 E) 5 2

Geometría
14
Anual UNI
01 - E
02 - C
03 - C
04 - E
05 - D
06 - E
07 - C
08 - C
09 - B
10 - E
11 - C
12 - C
13 - E
14 - C
15 - B
01 - E
02 - C
03 - C
04 - E
05 - D
06 - E
07 - C
08 - C
09 - B
10 - E
11 - C
12 - C
13 - E
14 - C
15 - B
01 - B
02 - C
03 - C
04 - D
05 - E
06 - E
07 - C
08 - E
09 - B
10 - E
11 - D
12 - C
13 - D
14 - A
15 - C
01 - B
02 - C
03 - C
04 - D
05 - E
06 - E
07 - C
08 - E
09 - B
10 - E
11 - D
12 - C
13 - D
14 - A
15 - C
01 - C
02 - D
03 - C
04 - E
05 - B
06 - D
07 - C
08 - C
09 - D
10 - B
11 - E
12 - D
13 - B
14 - C
15 - C
01 - C
02 - D
03 - C
04 - E
05 - B
06 - D
07 - C
08 - C
09 - D
10 - B
11 - E
12 - D
13 - B
14 - C
15 - C
01 - E
02 - D
03 - D
04 - C
05 - E
06 - D
07 - C
08 - C
09 - E
10 - D
11 - B
12 - B
13 - D
14 - A
15 - C
01 - E
02 - D
03 - D
04 - C
05 - E
06 - D
07 - C
08 - C
09 - E
10 - D
11 - B
12 - B
13 - D
14 - A
15 - C
Ángulo, ángulos entre rectas paralelas y una secante
Triángulo I
Triángulo II
Congruencia de triángulos
Aplicaciones de la congruencia
01 - D
02 - C
03 - C
04 - C
05 - C
06 - B
07 - C
08 - B
09 - A
10 - C
11 - E
12 - D
13 - E
14 - C
15 - C
01 - D
02 - C
03 - C
04 - C
05 - C
06 - B
07 - C
08 - B
09 - A
10 - C
11 - E
12 - D
13 - E
14 - C
15 - C

César vallejo 2015

Más contenido relacionado

La actualidad más candente (20)

Destacado (20)

Similar a César vallejo 2015 (20)

Último (20)

César vallejo 2015