Masejerazonamientologico1
- 1. Ejercicio 1:Torre de Hanoi Se requiere mover todos los discos de la pila de la izquierda a la pila de la derecha. Solo puede moverse un disco a la vez y no puede colocarse un disco de mayor tamaño sobre otro más chico. Si el número de discos es n=3 ¿Cuántos movimientos deben realizarse? Respuesta
- 2. El número de movimientos para la torre de hanoi es donde n= número de discos. Entonces Ejercicio 2: Se coloca 5 dados en pila ¿cuánto vale la suma de los puntos de cada cara oculta por arriba y por debajo de cada dado, debido a la apilación? En un dado normal (común/balanceado), la suma de las caras opuestas valen 7. Entonces las caras ocultas de los 1ros 4 dados es: y como en el dado de hasta arriba, se le ve los puntos de su cara de arriba (2 puntos) y Entonces la suma total es
- 3. Ejercicio 3: Se requiere medir exactamente 7 litros, pero solo se cuenta con cubetas de 3 y 5 litro. ¿Cuantos transvases deben de hacerse como mínimo? F Respuesta
- 4. Es decir son 5 transvases los que deben hacerse Ejercicio 4: ¿Cuántas fichas se deben de mover para pasar de la figura a laa ? Se requiereb mover el mínimo número de fichas. Respuesta R= Se deben mover solo 4 fichas, las dos de adelante hacia atrás y viceversa
- 5. Ejercicio 5: Cuatro sospechosas fueron interrogadas, por el atropellamiento de un peatón. Las siguientes afirmaciones, las hicieron ellas cuando fueron interrogadas: Lucia: “Fue Leticia” Maria: “Fue Lucia” Ana: “Yo no fui” Leticia “Lucia miente” Si solo una de ellas miente, ¿Quién atropello al peatón? Respuesta Para que se cumpla la condición de: 3 verdades y una mentira, Lucia tiene que ser la que atropello al peatón: Lucia y Leticia se contradicen, implica que una de ellas está mintiendo, pero María dice que “fue Lucia” y como solo una de ellas está mintiendo, entonces significa que María dice la verdad y la que atropello al peatón fue Lucia.
- 6. Ejercicio 6: De acuerdo a la siguiente figura y tomando los números del 1 al 9. Se quiere que la suma de los números de cada lado sea la misma y que sea la menor posible. Escribe los números del 1 al 9 en cada círculo, de tal forma que se cumpla la condición anterior. Respuesta Los números que afectarían a 2 lados al mismo tiempo, serían los que están en las esquinas (vértices). Así que se tiene: Y la suma sería: La suma de los 3 lados, menos la suma de los números que se repiten (los que afecta a dos lados al mismo tiempo IGUAL a la suma de los números del 1 al 9 Pero la suma del Como se quiere la menor suma, entonces es conveniente que a, b, c valgan 1,2 y 3
- 7. A cada lado le falta: 17-(1+2) =17-3=14 17-(1+3) = 17-4=13 17-(3+2) = 17-5=12 Se escriben los números que faltan de tal manera que cada lado sume 17 y ningún número se repita. Ejercicio 7: completa la serie Respuesta
- 8. Ejercicio 8: completa los siguientes cuadrados mágicos Respuesta Los cuadrados mágicos son cuadrados que cada una de sus columnas, filas y diagonales suman un mismo número. Resolviendo el inciso a 15-(8+6)=15-14=1 15-(8+4)=15-12=3 15-(4+2)=15-6=9
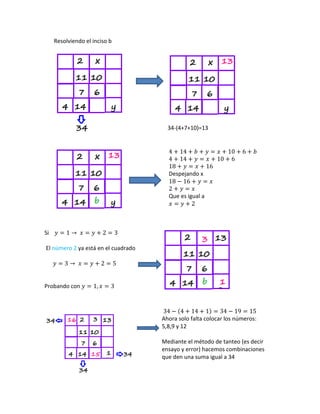
- 9. Resolviendo el inciso b 34-(4+7+10)=13 Despejando x Que es igual a Si El número 2 ya está en el cuadrado Probando con Ahora solo falta colocar los números: 5,8,9 y 12 Mediante el método de tanteo (es decir ensayo y error) hacemos combinaciones que den una suma igual a 34
- 10. Ejercicio 9: completa los cuadrados Respuesta Analizando los cuadrados: Por lo tanto 𝟐
- 11. Por lo tanto 𝟖 Por lo tanto la respuesta es: De hecho: