OLIMPAMER - JOSE A. ENCINAS

23.er
gr. – JOSÉ ANTONIO ENCINAS
01. Pertenencia:
Si:     x
xA ,5 x 9n
Colocar verdadero o falso según
corresponda:
I. 5  A ( )
II. 10  A ( )
III. 7  A ( )
IV. 6  A ( )
A. VVFV B. FVVF C. VVFF
D. FVFV E. VVVV
02. Observar el gráfico y hallarA B.
A B
.1 .3
.4
.5
.6
A. {3; 4; 5; 6} B. {1; 3; 4; 5; 6}
C. {1; 5; 6} D. {1;3;4;5;6;7;8;9}
E. {1; 7}
03. Descomponer polinomicamente cada
numeral
I. 108(9) = ______ II. 210(3) = _____
A. 81, 20 B. 90, 25 C. 89, 21
D. 89, 25 E. 108, 21
04. Si:     x
xA ,par; 5 x 10n
    x 1
xB ,impar; 3 x 8n
entonces, hallarAB.
A. { } B. {10} C. {4; 6}
D. {6; 8} E. {1}
05. Tengo 21 años. ¿Hace cuántos años tuve
la tercera parte de la edad que tendré
dentro de 15 años?
A. 9 B. 10 C. 11
D. 12 E. 15
06. Resolver: A = 5 + 8 + 9 – 7
A. 12 B 15 C. 9
D. 11 E. 8
07. Resolver: x + 5 = 17
A. 9 B. 10 C. 12
D. 22 E. 17
08. Un número aumentado en 5 da como
resultado 13. Hallar dicho número.
A. 18 B. 5 C. 6
D. 7 E. 8
09. Resolver: C = [(19 – 11) + 7] – 2
A. 12 B. 13 C. 11
D. 9 E. 5
10. Resolver:       2 1x 1 2x 3 2
3 6
A.
12
7
B.
13
6
C.
15
4
D.
7
8
E.
11
6
11. El ángulo formado por las manecillas del
reloj es:
A. agudo
B. recto
C. obtuso
D. negativo
E. lineal
12. Si reemplazamos "" por el valor de 40°.
Indicar que ángulos son agudos.
-31° +11°
(I) (II) (III)
A. III B. II C. I y II
D. I y III E. I

33.er
13. Según el gráfico, la mAOB= 79°. Calcular
el valor de "x".
A. 64°
B. 50°
A
BO
x+15°
C. 60°
D. 54°
E. 74°
14. En el plano cartesiano se ubican las
siguientes figuras:
1
2
3
4
1 2 3 4 5 6
Al verificar las ubicaciones se obtiene:
I. ...........(1;1) II. ........(3;3)
III. ..............(4;6)
¿Cuántas proposiciones son verdaderas?
A. 3 B. 1 C. 4
D. 2 E. 0
15. En la figura se tiene la recta L, calcular la
medida del mayor ángulo mostrado.
A. 80º
3x 7º
4x 3º
7x+10º
B. 90º
C. 99,7º
D. 100º
E. 101º
16. Si: a * b = a + b
Calcular: 5 * 2
A. 3 B. 7 C. 10
D. 15 E. 52
17. Determinar el término que continúa:
5; 9; 13; 17; 21; ________
A. 22 B. 24 C. 25
D. 26 E. 27
18. ¿Cuántos triángulos hay en total en la
siguiente figura?
A. 3
B. 4
C. 5
D. 6
E. 7
19. Determinar el valor de "x"
5 (12) 7
8 (10) 2
9 (x) 5
A. 45 B. 4 C. 15
D. 14 E. 41
20. Calcular: A + B + C
A. 8
B. 10
A52
2B6
79C

C. 14
D. 12
E. 17
21. Calcular el valor de "x"
3
2
4
9
6
2
2
11
3
2
1
x
A. 5 B. 4 C. 8
D. 6 E. 10
22. Si: a = a  a.Calcular 8
A. 16 B. 64 C. 32
D. 36 E. 8

224.to
07. Reducir
A = 12x + 5y – 40x + 9y + 8x
A. 20x + 4y B. 36x + 14y
C. 20x + 14y D. 14y – 20x
E. 18x + 4y
08. Si se sabe que:
t1 = 7x10
yb
; t2 = 9xa
y7
son términos semejantes, calcular a + b
A. 7 B. 17 C. 10
D. 3 E. 16
09. Sea la expresión algebraica:
A = 9x3
y4
+ 7x11
y – 4x5
y2
Hallar la suma de coeficientes.
A. 18 B. 12 C. 20
D. 14 E. 21
10. Resolver: 2(x – 3) + 3x – 1 = 8
A. 1 B. 2 C. 5
D. 3 E. 8
11. Sea el conjunto:
A = {20°; 80°; 120°; 90°; 140°; 2°; 91°}
¿Cuántas medidas corresponden a ángulos
agudos?
A. 5 B. 4 C. 3
D. 6 E. 2
12. ¿Cuántos ángulos obtusos hay en la figura?
A. 1
B. 2
A
B
C
DA
20° 100°
10°
C. 3
D. 4
E. 5
01. Dado el conjunto:
A = {e; d; w; i; n; d; u; l; a; n; t; o}
Calcular: n(A)
A. 12 B. 11 C. 7
D. 9 E. 10
02. Si: n(A) = 22, n(B) = 30 y n(A B) = 10
Calcular: n(A B)
A. 42 B. 30 C. 22
D. 32 E. 40
03. Del gráfico mostrado:
A B
.1
.9
.5
.11
.13
U
.3
.7
.17 .15
Hallar A  B
A. {1; 3} B. {9; 7} C. {5; 7; 9}
D. {11; 13} E. {1; 3; 11; 13}
04. Descomponer polinomicamentey efectúar:
mama
A. 1010m + 201a B. 1100m + 11a
C. 1010m + 10a D. 1010m +101a
E. 1001m + 11a
05. Viviana va de compras a "Gamarra" con
420 soles y se compra 10 shorts a 10 soles
cada uno y con el resto se compró 16
minifaldas. ¿Cuánto costó cada minifalda?
A. S/.18 B. S/.20 C. S/.19
D. S/.21 E. S/.25
06. Resolver:
(–2)(–5)(3)  6 + (–3)(4) – 9
A. 20 B. –16 C. 18
D. 26 E. 13

334.to
13. Un gato se encuentra en la posición inicial
(1;1) y realiza la traslación (3; 4). ¿Cuál
es la posición final?
1
2
3
4
1 2 3 4 5 6
3
4
7 8 9
A. (4; 4) B. (5; 4) C. (4; 5)
D. (3; 5) E. (5; 5)
14. El triángulo mostrado es isóscelesAB = BC
A
C
B
x+5
16
Calcular el perímetro de la región:
x-5
5
x
x+1
A. 41 B. 35 C. 34
D. 38 E. 33
15. En la figura, mAOC = 80º, mBOD = 70º y
mAOD = 120º. Calcular mBOC.
A. 10
A
B
C
DO
B. 20
C. 30
D. 40
E. 50
16. Determinar el término que continúa:
7; 9; 12; 16; 21; ______
A. 22 B. 25 C. 26
D. 28 E. 27
17. ¿Cuántostriánguloshayentotalenlasiguiente
figura?
A. 9
B. 10
C. 12
D. 8
E. 4
18. Si: a * b = 2a + 3b.Calcular 2 * 3
A. 55 B. 13 C. 9
D. 4 E. 5
19. ¿Cuál es el gráfico que continúa?
?
A. B. C.
D. E.
20. Calcular a + b + c, si cada casilla es el
resultado de sumar las dos inferiores.
A. 15
B. 22
a
b 7
c 5
6 1
C. 47
D. 37
E. 27
5 (10) 2
4 (12) 3
9 (x) 4
A. 15 B. 22 C. 13
D. 36 E. 26

444.to
A. 88
B. 26
14
2 4
3 5
12
3 2
4 3
x
6 7
2 1
C. 36
D. 68
E. 16
23. Determinar losvalores que faltan:
A; 5; C; 7; E; 9; G;11; ________; ______
A. 12; 13 B. H; 13 C. I;J
D. I; 13 E. 12; H
24. Si: * a b c
a a b c
b b c a
c c a b
Calcular: (a * b) * c
A. b B. a C. 2a
D. c E. a/b
5 3 6
4 2 4
9 5 x
A. 24 B. 2 C. 14
D. 10 E. 45
26. Si: a = 2a y b 3b
Calcular: 2 + 3
A. 13 B. 5 C. 55
D. 23 E. 12
27. Señalar la fracción de la parte no sombreada
A.
2
6
B.
3
6
C.
4
6
D.
1
6
E.
1
2
28. ¿Cuántostriánguloshayenla siguiente figura?
A. 8
B. 10
C. 12
D. 13
E. 14
29. Si:   

a #b
a b ;a b
a b
, además m # n = m +
2n
Hallar el valor de


8 4E
2 1
A. 6 B. 5 C. 1
D. 12 E. 13
30. Indicar cuántos triángulos contienen por lo
menos un asterisco:
A. 4
* *
B. 6
C. 8
D. 9
D. 10

25.to
07. Dados los conjuntos:
A = {a, m, c};
B = {a, b, c, d};
C = {a, m, c, d, e}
Indicar verdadero (V) o falso (F) según
corresponda:
i) A  C ii) A  B iii)B  C
A. VVF B. VFF C. FFF
D. VFV E. VVF
08. ¿Cuántosnúmeros de3 cifras son múltiplos
de 17?
A. 48 B. 53 C. 63
D. 42 E. 50
09. Resolver:       
0 2 10
R (40 2) 4 (5 6) .
A. 16 B. 17 C. –17
D. 1 E. 18
10. Resolver:  
 
   
 
3
1 11
G 5 (13)
5
A. 10 B. 117 C. 5
D. –10 E. 143
11. Resolver: A = 52
 5–4
 57
 5–2
.
A. 25 B. 125 C. 5
D. 1 E. –5
12. Resolver:
 
  


8 3 5 1
2
5 7 5 7
C
5 7
A. 5 B. 7 C. 14
D. 35 E. 25
13. Simplificar:  
  
2 12
5 3 2
E a a a
A. a B. a11
C. a–2
D. a18
E. a12
01. Si:     A (12 36) (4 7) y
    B (17 14) (7 9) .
Calcular B–A.
A. 84 B. 10 C. 22
D. 15 E. 39
02. Sean los conjuntosA= {x/x es un día de la
semana}
B = {lunes, martes, miércoles, viernes}.
¿Cuántos elementos tiene A B ?
A. 7 B. 6 C. 5
D. 4 E. 3
03. Si A = 2 + 3 × 5 – 1
B = 3 + 3 + 5 × 2 + 1. Calcular B + A.
A. 17 B. 30 C. 23
D. 48 E. 33
04. Carlos y Pepe tienen entre los dos S/.600,
si Pepe tiene S/.40 más que Carlos.
¿Cuánto dinero tiene Pepe?
A. S/.280 B. S/.340 C. S/.300
D. S/.310 E. S/.320
05. Descomponer la suma de 584675 y
216234
A. 7CM + 8DM + 9C
B. 7UM + 9D
C. 8DM + 7UM + 9D
D. 7UM + 9C + 8
E. 8CM + 9C + 9U
06. Las edades de Pepe y Pepo suman 47, si
la edad de Pepo es la suma de los valores
absolutos del número 96354. ¿Cuál es la
edad de Pepe?
A. 27 B. 16 C. 15
D. 20 E. 17

35.to
14. Resolver:   
     
7
3
03
2 1
B (2) 2
A. 2 B. 6 C. 3
D. 4 E. 5
15. Resolver: 2(x – 3) + 3 (2x + 8) = 5(x + 4)
A. 1/3 B. 4/3 C. 2/3
D. 1/5 E. 3/5
16. Resolver:           
   
x 1 x 2 x 23 5 3
4 8 2
A. 1/2 B. 3/4 C. 12/11
D. 12/7 E. 13/7
17. A un hilo bien estirado de 7 m. de longitud,
se le dobla en forma de "S", ¿Cuál es la
longitud de la línea curva?
SA. 7 m2
B. 7m3
C. 7 m
D. 7 cm E. 14 m
18. De la figura, calcular el perímetro de la
región sombreada.
A. 30 cm
B. 28 cm
10cm
6cm
2cm
3cm
6cm
C. 25 cm
D. 27 cm
E. 32 cm
19. Según la figura,calcular el área dela región
sombreada.
A. 80 u2
B. 40 u2
C. 50 u2
D. 60 u2
2u
3u
5u
8uE. 70 u2
20. Según la figura, la recta
L es eje de
simetría, calcular "x".
A. 5 cm
B. 10 cm
A
B
A'
B'
C. 15 cm
D. 18 cm
E. 20 cm
21. La figura muestra tres cuadradosA, B y C.
Si las áreas de los cuadrados B y C son
25 y 49, calcular el área del cuadradoA.
A. 121
A
C
BB. 144
C. 74
D. 256
E. 100
22. La figura muestra un triángulo equilátero y
un rectángulo. Si el perímetro de la figura
sombreada es 60, calcular el valor de x.
A. 6
B. 7
C. 8
D. 9
E. 10
23. Hallar el máximo total de triángulos que hay
en la siguiente figura:
A. 18
B. 27
C. 9
D. 12
E. 21
24. Hallar el valor de "x" en la siguiente
distribución:
4 5 6 1
7 2 3 4
1 2 x 6
A. 9 B. 5 C. 6
D. 8 E. 7

45.to
25. Hallar el gráfico que sigue en la siguiente
analogía gráfica:
es a como es a:
A. B. C.
D. E.
26. Hallar que números continúan en la
siguiente sucesión:
21
; 33
; 59
; 727
; 1181
; 13243
; ______
A. 17327
B. 15729
C. 17729
D. 19729
E. 19327
27. En un taller hay 15 timones entre bicicletas
y triciclos, y hay 36 ruedas en total.
¿Cuántas bicicletas hay?
A. 10 B. 4 C. 8
D. 6 E. 9
28. Sea la operación matemática:
3 2 3
a b c a b c**    .
Hallar el valor de 5 * 36 * 64
A. 4 B. 3 C. 2
D. 5 E. 6
29. Dada la sucesión:
1, 2, 3, 4, 5, 8, x, y, z. Calcular x – y + z
A. –1 B. 0 C. 1
D. 2 E. 3
30. ¿Cuántos triángulos se cuentan en total en
la siguiente figura?
A. 6
B. 8
C. 9
D. 10
E. 13

26.to
07. Con 24 obreros pueden terminarse una
obra en 63 días. ¿Cuántos obreros se de-
ben agregar si se quiere terminar la obra
en 18 días?
A. 90 B. 70 C. 84
D. 77 E. 60
08. Se parte en dos una varilla de 180 cm. Si
comparamos ambos pedazos, resulta que
la más grande contiene dos veces a la más
pequeña, con un sobrante de 30 cm.
¿Cuánto mide la parte más pequeña?
A. 45 cm B. 48 cm C. 50 cm
D. 51 cm E. 52
09. Resolver:
3 2 2 0 113 6 9 1  
A. 2 B. 0 C. 1
D. –1 E. 5
10. Resolver: 5 3432 81 64   
A. –5 B. 5 C. 9
D. –9 E. 7
11. Resolver:
1
2 3 618 12
9 2 5 
A. –46 B. 92 C. 32
D. 46 E. –92
12. Resolver:
3 4 8
7 7 5 
A. 12 B. 35 C. 7
D. 5 E. 49
13. Resolver:
3 3 442 4 3 27  
A. 1 B. –1 C. –5
D. 5 E. 6
01. Si Ángel tiene S/.50 menos que Beto.
¿Cuánto dinero tiene Beto si se sabe que
juntos tienen S/.300?
A. S/.185 B. S/.165 C. S/.125
D. S/.175 E. S/.250
02. En una multiplicación de tres enteros, si se
triplica cadauno deellos. ¿Qué sucede con
el producto?
A. Se mantiene B. Disminuye
C. Aumentó D. Se duplicó
E. Ninguna de las anteriores
03. Calcular el dividendo de una división
inexacta si se sabe que el divisor es 30 y
el cociente 20; además, el residuo es máxi-
mo
A. 601 B. 59 C. 79
D. 619 E. 629
04. SeanA y B dos conjuntos si se cumple:
g n(A) + n(B) = 26
g n(A  B) = 20
Hallar  n P(A B)
A. 8 B. 64 C. 32
D. 63 E. 16
05. Si: A= {x – 2, 12, y2
+ 3} es unitario, hallar
"x + y".
A. 42 B. 11 C. 13
D. 18 E. 17
06. Si el número a3a es múltiplo de 5, hallar
a2
.
A. 16 B. 0 C. 25
D. 81 E. 9

36.to
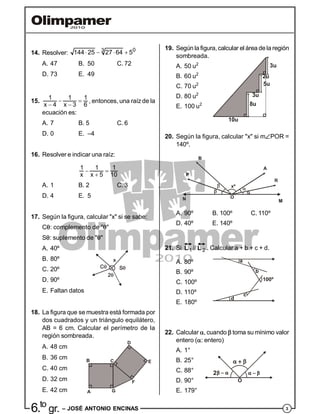
14. Resolver:
03
144 25 27 64 5   
A. 47 B. 50 C. 72
D. 73 E. 49
15.
1 1 1
x 4 x 3 6
 
 
, entonces, una raíz de la
ecuación es:
A. 7 B. 5 C. 6
D. 0 E. –4
16. Resolver e indicar una raíz:
1 1 1
x x 5 10
 

A. 1 B. 2 C. 3
D. 4 E. 5
17. Según la figura, calcular "x" si se sabe:
C: complemento de ""
S: suplemento de ""
A. 40º
B. 80º
C. 20º
D. 90º
E. Faltan datos
18. La figura que se muestra está formada por
dos cuadrados y un triángulo equilátero,
AB = 6 cm. Calcular el perímetro de la
región sombreada.
A. 48 cm
B. 36 cm
C. 40 cm
A
B C
D
E
F
G
D. 32 cm
E. 42 cm
19. Según la figura,calcular el área dela región
sombreada.
A. 50 u2
3u
2u
5u
8u
10u
3u
B. 60 u2
C. 70 u2
D. 80 u2
E. 100 u2
20. Según la figura, calcular "x" si mPOR =
140º.
A. 90º B. 100º C. 110º
D. 40º E. 140º
21. Si 1 2//
 L L . Calcular a + b + c + d.
A. 80º
d
c
100º
b
a
B. 90º
C. 100º
D. 110º
E. 180º
22. Calcular , cuando  toma su mínimo valor
entero (: entero)
A. 1°
2
O
B. 25°
C. 88°
D. 90°
E. 179°

46.to
28. Si
ba #b 3a
4
  . Hallar 5 # 16
A. 20 B. 32 C. 19
D. 21 E. 30
29. Un guardián para saber que no le falta
ningún triciclo, ni bicicleta que están a su
cuidado, contaba siempre 84 ruedas y 60
pedales. ¿Cuántos triciclos tenía a su
cuidado el guardían?
A. 23 B. 24 C. 18
D. 31 E. 12
30. Identificar la alternativa que continúa
correctamente la secuencia.
A. B. C.
D. E.
23. Indicar el número total de triángulos que se
pueden contar en la siguiente figura:
A. 110
B. 50
C. 100
...
1 2 3 4 9 10
D. 55
E. 11
24. Hallar (A + B) × (C – D) si:
4 C 6 A +
D A B 8
A 8 9 3
A. 24 B. 14 C. 10
D. 22 E. 16
25. Indicar el valor de 2x – y en:
3 ; 7 ; 11 ; 15 ; x ; y
A. 15 B. 27 C. 44
D. 98 E. 20
26. Hallar el valor de "x" en:
5 6 30
7 9 63
10 15 x
A. 210 B. 120 C. 18
D. 20 E. 150
27. Hallar el valor de "x"
A. 12
B. 27
C. 14
8
3
2
16
2
4
x
3
3
D. 9
E. 38

21.er
año – JOSÉ ANTONIO ENCINAS
07. Hallar la suma de los divisores primos de
1200.
A. 5 B. 7 C. 8
D. 10 E. 12
08. Un grupo A de profesores se reúne en el
colegio cada 12 días, otro grupo B cada 8
días y otro grupo C cada 9 días. Si hoy día
asistieron los 3 grupos al colegio para su
respectiva reunión. ¿Cuántos días deben
transcurrir paraque vuelvana encontrarse?
A. 75 B. 71 C. 47
D. 149 E. 111
09. Si lossiguientes términosse reducen a uno
solo: 3ax7
– 2bx2+a
+ 2axb+5
¿Cuál es el coeficiente de dicho número?
A. 20 B. 18 C. 21
D. 19 E. 22
10. Si T1 = 6x2b+2a
y13
 T2 = 2x10
y2a–b
son
términos semejantes, calcular: ab
.
A. 0 B. 6 C. 2
D. 1 E. 3
11. Si Q(x) = 2x – 1, calcular: Q(Q(Q(2)))
A. 3 B. 5 C. 7
D. 9 E. 10
12. P(x) = mx + b; además P(2) = –5 y P(4) = 1,
calcular: "m – b".
A. –9 B. –10 C. 14
D. –14 E. 9
13. P(x,y) = 2y4k–4
z3m–2
; además G.R(y) = 12 
G.R(z) = 25, hallar "k + m".
A. 14 B. 12 C. 13
D. 15 E. 11
01. Un barco que llevaba 150 pasajeros sufrió
un naufragio. Si de los sobrevivientes los
2/5 perdieron sus celulares, los 3/7 son
matemáticos; 1/3 son deportistas.
¿Cuántas personas murieron en dicho
naufragio?
A. 65 B. 75 C. 85
D. 105 E. 45
02. El cociente de dos números es 15 y su
MCD es 18. Calcular el mayor de dichos
números.
A. 180 B. 150 C. 200
D. 270 E. 240
03. Se tienen 3 barriles de 60 lt., 90 lt. y 150 lt.,
y sequiere distribuir en recipientes de igual
cantidad. ¿Cuál es la mínima cantidad de
envases que se pueden utilizar?
A. 5 B. 8 C. 7
D. 9 E. 10
04. Si n(A C) =f;A B,n(B  C)=3; n(C)= 2n
(A);n(B –A)=8;n(B)= 10.Calcularn(C– B).
A. 1 B. 2 C. 3
D. 4 E. 5
05. Pedrito va al cine cada 5 días, al gimnasio
cada 7 días y a visitar a su hijita cada 2
días; si el 23 de mayo realizó las tres acti-
vidades. ¿En qué fecha volverá a realizar
las tres actividades por primera vez?
A. 1 agosto B. 2 agosto
C. 30 julio D. 31 julio
E. 30 agosto
06. Si N = 3210
× 27n
posee 2190 divisores
compuestos. Hallar "n".
A. 10 B. 12 C. 14
D. 17 E. 21

31.er
14. Q(x)= (m+ 6)x+ (n– 4)x3
+ (m+ 2)x2
+ n– 1,
es un polinomiocuadrático y mónico, hallar
Q(4).
A. 36 B. 37 C. 38
D. 39 E. 35
15. Resolver y dar una raíz:
2
2
4x 3x 5
2
x 2x 13
 

 
A. 7/2 B. –8 C. –7/2
D. 2 E. 1
16. Hallar: x
x 1 x 1 x 3 5
3 7 11
    
A. 2 B. 3 C. 4
D. 6 E. 8
17. De la figura, las rectas L1 y L2 son
paralelas, calcular " x
y
".
A. 8
B. 3
C. 6
60º
25º
yºxº
130º
30º
D. 5
E. 2
18. Del gráfico, calcular "x".
A. 150º
B. 140º
C. 155º
A
B
C
xD. 120º
E. 118º
19. Según la figura, calcular "x".
50º
30º
-10
20º
x
A. 10 B. 20 C. 30
D. 40 E. 50
20. Según la figura, AB = 7 – a, BC = 2a y
CD = a – 5. Si "a" es una cantidad entera,
calcularAD.
A. 6 u
B. 12 u
C. 13 u A B C D
D. 14 u
E. 15 u
21. En la figura 3 m2
, 4 m2
, 6 m2
y S son las
áreas de las regiones. Calcular "S".
A. 5 m2
3
4
6
S
B. 6 m2
C. 7 m2
D. 8 m2
E. 9 m2
22. Si ABC y DEF son equiláteros, calcular
"x", si AM = MB.
A. 40º
C
D
F B
E
M
40º
x
A
B. 50º
C. 60º
D. 75º
E. 90º

41.er
23. ¿Cuántos paralelepípedos se pueden
contar en la siguiente figura?
20
3
2
1
12
152 3 1
2
3
A. 400 B. 308 C. 408
D. 410 E. 500
24. Hallarel término10enlasiguiente sucesión:
3 ; 11 ; 22 ; 37 ; ...
A. 98 B. 110 C. 240
D. 211 E. 120
25. Hallar el valor de "x" en:
8 (39) 5
7 (45) 2
4 ( x ) 3
A. 24 B. 12 C. 36
D. 7 E. 25
26. Hallar el valor de 10 =
Si:  x 2x 1  y-1 =
5
y
2
A. 110 B. 50,5 C. 55
D. 45 E. 50
27. En una granja de patos, gallinas y conejos
se cuentan 70 cabezas y 220 patas, si la
cantidad de gallinas es el doble de patos.
¿Cuál es la cantidad de conejos?
A. 15 B. 40 C. 20
D. 30 E. 35
28. Si PAMER AMOR 57634  . Hallar
PAPA MAMA .
A. 25432 B. 67382 C. 13736
D. 12743 E. 23542
29. ¿Qué número continúa en la siguiente
sucesión?
147; 144; 12; 9; 3; _____
A. 1 B. 0 C. –1
D. –3 E. 6
30. Se define en Z+
la operación:
x = 1 + 2 + 3 + ... + x
Simplificar: k =
x - 1 · x
x - 1
2
; x 1
A. 1 B. 2 C. 1/2
D. x E. 1/x

22.do
08. SeanAy B magnitudes tales que:
Para B 6: A DP B
Para B 6: A IP B
Se sabe que para B = x,A = 5; x < 6 y para
B = 2x + 6, A = z.
Además al hacer la gráfica se observa que
el valor máximo deAes 10. Hallar la suma
de las cifras de z4
.
A. 10 B. 11 C. 12
D. 13 E. 14
09. Si P(x) = 2x – 3. Hallar P(x + 1).
A. 2x – 3 B. 2x – 2 C. 2x – 1
D. 0 E. –1
10. Si xx
= 2. Calcular:
x 1
x
x

A. 5 B. 4 C. 3
D. 2 E. 1
11. Resolver:
2x 3y 27
5x y 8
 

 
, indica el valor de
yx
.
A. 289 B. 729 C. 343
D. 81 E. 225
12. Resolver:
2(x – 3) + 3(x + 2) = 7(x – 1) – 2(x + 1) + 9
A. 0 B. 1 C. 2
D. R E. 
13. Reducir: 3 6
x x x 
A. 1 B. x C. x2
D. 6 5
x E. 10 3
x
14. Si a + b = 3  ab = 1. Calcular: a2
+ b2
.
A. 2 B. 3 C. 5
D. 7 E. 9
01. Si a43ba 45

 . Hallar: a × b.
A. 15 B. 5 C. 6
D. 8 E. 10
02. Con "n" obreros se termina una obra en 10
días, pero con 5 obreros más, la obra ter-
minaría 2 días antes, hallar "n".
A. 12 B. 10 C. 16
D. 18 E. 20
03. Hallar la cantidad de divisores de 2500.
A. 18 B. 20 C. 15
D. 12 E. 10
04. La razón de las edades de un padre y la
de su hijo es de 5 a 2. Dentro de cuatro
años estarán en la relación de 13 a 6. Ha-
llar la edad del padre.
A. 30 B. 35 C. 40
D. 45 E. 25
05. Si:n(A)=21;n(B)=18;n(A')=9;n(A–B)=7.
Hallar: n(U) + n(B – A) + n(A B)
A. 48 B. 42 C. 36
D. 30 E. 12
06. Se reparte 600 DP a los números 4, 5 y 6.
Hallar la menor parte.
A. 40 B. 200 C. 240
D. 160 E. 120
07. Sean A, B y C magnitudes tales que:
Ap
DP Bq
(cuando C = cte.)
A IP Cr
(cuando B = cte.)
C IP Bn
(cuando A = cte.)
Hallar: n.
A.
rp
q
B. –
p
qr C.
p
qr
D.
q
pr E. –
q
pr

32.do
15. Simplificar:
   
   
3 33 2
3 33 2
a b 2b 6ab a b
a b 2a 6a b a b
    
    
A. –2 B. 1 C. 0
D. –1 E. 2
16. Reducir al máximo:
   
b x b xx b b x1 bx 1 bx :
x bx b x b b x
1 1
1 bx 1 bx
           
      
  
A. b
b 1
B. x
1 x
C. bx
b x
D. x
b x
E. 2x
b x
17. Según la figura, los cuadriláteros ABCD,
CEFG son cuadrados, la región sombrea-
da ABCD tiene área 9 u2
y DE = 4 u. Cal-
cular el área de la región cuadrada CEFG.
A. 16 u2
B. 9 u2
C. 36 u2
A
B C
D E
F
G
D. 25 u2
E. 49 u2
18. En un polígono se cumple, cien veces el
número de lados es igual a quinientas ve-
ces el número primo par. ¿Cómo se lla-
ma el polígono?
A. Triángulo B. Pentágono
C. Icoságono D.Cuadrilátero
E. Decágono
19. Según la figura, calcular "x".
A. 30°
B. 40°
y
y
x
y
2
C. 50°
D. 20°
E. 45°
20. Según la figura, las rectas L1 y L2 son pa-
ralelas, calcular " x
y
".
xy
A. 5 B.
2
5
C.
3
5
D.
5
2
E.
5
3
21. En un triángulo rectángulo las medidas de
los ángulos agudos están en la relación de
1 a 3. Calcular la menor medida angular.
A. 23º B. 22º C. 22º 30'
D. 23º 30' E. 24º
22. En la figura calcular "x".
x
80º
60º
70º
x
x
A. 40º B. 50º C. 60º
D. 70º E. 45º

42.do
23. ¿Qué letra continua?
0 ; S ; S ; O ; O ; S
A. A B. B C. C
D. D E. E
24. Indicar: "U + N + I"
Si: UU NN UN  II I
A. 10 B. 18 C. 15
D. 16 E. 20
25. Indicar el número que falta:
12 (18) 24
21 (12) 13
23 ( ) 15
A. 30 B. 33 C. 39
D. 40 E. 20
26. Hallar el total de triángulos que contengan
por lo menos un (
*)
A. 24
B. 27
C. 25
D. 23
E. 20
27. Sea
 2
b a
a b
a

  , señalar 8  1.
A. 1 B. 2 C. 3
D. 4 E. 5
28. Hallar un número tal que al sumarle 3,
multiplicarle por 5, restarle 4, extraer la raíz
cuadrada y luego elevarlo al cubo, se
obtiene 216.
A. 1 B. 2 C. 5
D. 4 E. 3
29. Como mínimo una araña emplea 5 minutos
en recorrer todas las aristas de un cubo
construido de alambre de 60 cms de
longitud. El tiempo que emplea en recorrer
una arista es:
A. 18,75 s B. 20 s C. 25 s
D. 30 s E. 17, 50 s
30. La hermana de Juan, tiene una hermana
más que hermanos. ¿Cuántas hermanas
más que hermanos tiene Juan?
A. 1 B. 2 C. 3
D. 4 E. 5

3.er
año – JOSÉ ANTONIO ENCINAS 1
07. Tres socios A, B y C formaron una empre-
sa que duró 10 meses, los cuales aporta-
ron S/.4000, S/.5000 y S/.6000 respecti-
vamente,Aestuvo los 10 meses, B estuvo
los 4 primeros meses, C estuvo los 6 pri-
meros meses y hubo una utilidad total de
S/.12000. Si el socio C hubiera retornado
faltando dos meses (para el cierre de la
empresa) con una aportación de S/.7000,
entonces este socio hubiera ganado un

33,3% más que en el primer caso. Hallar la
suma de las cifras de la utilidad total del
segundo caso.
A. 2 B. 3 C. 4
D. 5 E. 6
08. Se deposita un capital a interés simple. Si
el monto a los 12 meses es S/.2660 y el
monto a los 10 meses es S/.2550. Hallar
la suma de las cifras del capital.
A. 1 B. 2 C. 3
D. 4 E. 5
09. Factorizar:
P(x,y) = 2x2
+ 4xy + 2y2
+ 7x + 7y + 5
Indicar el factor primo con mayor suma de
coeficientes.
A. 2x + y + 5 B. x + 2y + 1
C. 2x + 2y + 5 D. x + y + 1
E. x + y + 5
10. Factorizar: P(x) = x3
– x2
– 4x + 4
Indicar la suma de factores primos.
A. 3x B. 3x – 5 C. 3x + 5
D. 3x + 1 E. 3x – 1
11. Resolver: x2
– 5x + 6 = 0 e indicar la mayor
raíz.
A. 3 B. 2 C. 1
D. 4 E. 6
01. ¿Cuántos múltiplos de 8 existen del 1 al
72?
A. 8 B. 7 C. 9
D. 10 E. 11
02. Si:A = {a, b, c, d, e}  B = {c, a, r, m, e, n}.
Hallar
n(A) n(A B)
4
 
A. 1 B. 4 C. 2
D. 6 E. 5
03. Si:P = 27
× 35
× 5
Q = 23
× 34
× 53
Calcular el MCD y MCM de P y Q.
A. 23
× 34
y 27
× 35
B. 23
× 34
× 5 y 27
× 35
× 53
C. 1 y 27
× 35
× 53
D. 22
× 32
y 2 7
× 53
E. N. A
04. De un grupo de 70 personas, se desea
saber cuántos varones hay, si la sexta par-
te usan camisa y la séptima parte usan
zapatos.
A. 42 B. 43 C. 84
D. 0 E. 126
05. Si con "a" obreros se termina una obra en
5 días pero con 3 obreros más la obra ter-
mina en tres días menos. Hallar "a".
A. 2 B. 8 C. 4
D. 6 E. 7
06. Si 24x
tiene 21 divisores. ¿Cuántos divi-
sores tiene 6x
?
A. 9 B. 10 C. 4
D. 8 E. 110

3.er
12. Si el discriminante de ax2
+ ax + 1 = 0;
es –4. Determinar "a".
A. 1 B. 2 C. –2
D. –1 E. 3
13. Resolver x2
+ 5x + 1 = 0 e indicar la menor
raíz.
A.
5 21
2

B. 5 21
2
 
C. 5 21
2
 D. 5 21
4
 
E. 5 21
2
 
14. Construye la ecuación cuadrática cuyas
raíces son 3 y –1.
A. x2
+ 2x – 3 = 0 B. x2
– 2x – 3 = 0
C. x2
+ 2x + 3 = 0 D. x2
– 3x + 2 = 0
E. x2
+ 3x + 2 = 0
15. El primer término de una P.A. es 2, y el
primero, tercero y séptimo forman una P.G.
Hallar la suma de los siete primeros
términos de la P.A.
A. 32 B. 64 C. 35
D. 47 E. 82
16. Resolver el siguiente sistema e indicar el
conjunto de soluciones.
3x2
+ 5xy – 2y2
= 0
7x2
+ 9xy – 3y2
= 7
A. (2; –1) (–2; 1)
B. (2; –1) (–2; 1) (1; 1)
C. (2; –1) (–2; –1) (–1; 3) (1; 3)
D. (1; 1) (2; 2) (3; 3)
E. (2; –1) (–2; 1) (–1; – 3) (1; 3)
17. Según la figura, AN = 10 u, BT = 4 u y
ABCD es un trapecio isósceles, calcular
la longitud de la media MN.
A. 6 u
A
B C
D
M N
60º 80º
20º
80º
T
B. 7 u
C. 8 u
D. 5 u
E. 9 u
18. Según la figura, mABE = mDBC, cal-
cular "x".
A. 80º
A B
C
D
E
x
80º
B. 60º
C. 70º
D. 50º
E. 90º
19. Según la figura, calcular "x + y".
A. 140°
B. 110°
A
B
C
L
T y
30º
x
C. 100°
D. 150°
E. 180°
20. En la figura, calcular "x" si se sabe que ""
asume el mínimo valor entero.
A. 45º
B. 91º
C. 46º
x
D. 47º
E. 48º
21. En la figura, las rectas
 1 2yL L son parale-
las. Calcular "x".
A. 120º
B. 40º
C. 60º
D. 80º
E. 70º

3.er
22. En la figura, el ABC es congruente con el
ATC,AD = a y CD – BC = a. Calcular "x".
A. 60º
B. 40º
C. 45º A
B
C
D
T
2x
2x
D. 30º
E. 37º
23. ¿Qué número continua en la siguiente su-
cesión:
1 ; 3 ; 0 ; 0 ; 7 ; –4 ; –52; ___
A. 18 B. –40 C. 40
D. –35 E. 35
24. Calcular el valor de x:
2 3 17
5 2 57
10 1 x
A. 11 B. 12 C. 21
D. 22 E. 361
25. Si x = x
Además: x = 64x + 105. Calcular 3
A. 18 B. 14 C. 17
D. 15 E. 10
26. Calcular el valor de "x"
28
26 31
23 42
9
102 12
18 75
x
11 21
42 25
A. 4 B. –4 C. 8
D. –8 E. 16
27. Si abc
cba
3mz

Calcular el máximo valor de R = a × c × m.
A. 288 B. 320 C. 405
D. 810 E. 205
28. Calcular el número total de triángulos en:
A. 40
B. 60
C. 120
D. 130
E. 180
29. Francisco es un vendedor de bolsas. Una
mañana vendiósus bolsasde unmodo muy
especial; cada hora vendió 3/4 de las bol-
sas que tenía en esa hora y media bolsa
más, quedándose al final de 3 horas úni-
camente con 2 bolsas. Luego:
I. Vendió 170 bolsas
II. Si cada bolsa lo vendía a S/.3 obtiene
S/.504.
III. Después de la segunda hora le queda-
ron 10 bolsas.
Son ciertas:
A. Solo III B. IIyIII C. IyIII
D. IyII E. N. A.
30. ¿Cuál es el mínimo número de soldados
que se necesitan para formar 4 filas de 3
soldados cada fila?
A. 12 B. 10 C. 8
D. 6 E. 5

24.to
01. Si 4aa13 9

y 4b125 11

, hallar (a + b).
A. 9 B. 10 C. 11
D. 12 E. 13
02. Si
A 3 B 5
;
B 4 C 6
  . Si A+ C = 78, hallar "B".
A. 10 B. 20 C. 30
D. 40 E. 50
03. Si n(A  B) = 2; n(A B) = 14; n(A – B) = 7.
Hallar: n(A) – n(B)
A. 2 B. 4 C. 6
D. 8 E. 14
04. Si doce máquinas pueden producir 35 000
lapiceros en 21 horas, ¿Cuántos lapiceros
podránproducir en18 horas,24 máquinas?
A. 60 000 B. 45 000 C. 48 000
D. 30 000 E. 120 000
05. Un comerciante tiene lapiceros rojos y
azules en razón de 7 a 4; si se venden los
2/5 del total de lapiceros de los cuales 3/5
son rojos y el resto azules, ¿Cuál es la
nueva relación de lapiceros rojos y azules?
A. 3/2 B. 5/7 C. 109/56
D. 4/11 E. 7/11
06. Se distribuyeron 240 litros de aceite en 2
recipientes "A" y "B", luego se le agrega
80 litros a cada uno de ellos y sus conteni-
dos son ahora como 3 es a 5, para "A" y
"B", en ese orden. ¿Cuántos litros tenía "A"
inicialmente?
A. 70 B. 170 C. 200
D. 100 E. 90
07. ¿Cuántos números ab0ab son divisibles
entre 2, 7, 11 y 13 a la vez?
A. 45 B. 46 C. 47
D. 48 E. 49
08. Hallar el mayor número de 3cifras abc que
al dividirlo entre 32 el residuo es 11 y al
dividirlo entre 26 el residuo es 5. Dar como
respuesta a + b + c.
A. 7 B. 8 C. 9
D. 10 E. 11
09. Si la ecuación x3
+ ax2
+ bx + 8 = 0 tiene
una raíz de multiplicidad 3. Hallar "a + b"
A. 14 B. 6 C. 12
D. 18 E. 20
10. Si"x"esunnúmeroreal quetal queeltérmino
central en el desarrollo de  
12
2 3x
3 2
 es
294. hallar el valor de 1+ x2
+ x4
+ x6
.
A. 4 B. 8 C. 6
D. 16 E. 2
11. Sea f y g dos funciones: f(x) = ax + 3;
g(x) = bx + a.
Si f(2) = 13  g(1) = 13. Hallar "ab".
A. 5 B. 8 C. 13
D. 20 E. 40
12. Resolver: 2
2
x 5x 6
0
x x 56
 

 
A. x 8;2 3;7  
B.  x ; 8 7;     
C. x ; 8 7;    
D.  x ; 8 2;3 7;     
E. 
13. Un lápiz y su borrador cuestan S/.2,30, si
el lápiz cuesta S/.2 más que el borrador.
¿Cuántos soles vale el lápiz?
A. S/.2 B. S/.2,15 C. S/.2,05
D. S/.2,20 E. S/.3

34.to
14. Hallar los valores de "k" para que la
ecuación x2
+kx+1 =0 notenga soluciones
reales.
A. ;4 B. ;2 C. 2;2
D. 2;2 E.  2;2
15. Si a, b, c y r son números reales tal que:
a2
+b2
+c2
=2y(a+b+c)(1+ab+ac+bc)=4r3
entonces el valor de a + b + c es igual a:
A. r/2 B. r C. 2r
D. 4r E. 6r
16. Si el polinomio: P1 (x, y, z) = x8
+ (y2
– z2
)2
–
mx4
(y2
+ z2
) tiene como divisor al polinomio
P2 (x, y, z) = x2
– y – z, entonces el valor de
m3
+ m + 1 es igual a:
A. –9 B. –1 C. 1
D. 11 E. 31
17. Si mADB 20º x  ; m ACB = x – 80°.
Calcular "x"
A. 115°
B. 90°
C. 110°
A
B
CD
D. 100°
E. 120°
18. Si AB = BC = AD, calcular "x".
A. 78º
B. 80º
C. 85º
A
B
C
D
60º
x
x
D. 90º
E. 95º
19. El segmento perpendicular, desdeun punto
de la circunferencia a su diámetro, mide
12 cm y determina sobre el mismo un
segmento de 4 cm, entonces, el radio de
la circunferencia mide:
A. 10 cm
B. 5 cm
C. 20 cm
R
12
4
D. 12 cm
E. 25 cm
20. En la figura mostrada NM es mediatriz de
AC , si AB 20m . Hallar DC.
A. 10 u
B. 7,5 u
C. 5 u
A
B
CD
N
M
60º
D. 2,5 u
E. 2 u
21. Los lados de un octógono circunscrito a
una circunferencia están en progresión
geométrica de razón "r" y de perímetro "k".
Entonces el valor dela diferenciadel mayor
y menor lado es:
A. kr
8
B. kr
4
C. 0
D.
k
r
E.
7
kr k
8

22. Se tiene un octaedro regular P – ABCD –
Q, cuya arista mide "k". Si M PB tal que
2(BM) = 3(PM). Calcular la distancia entre
AM y QD.
A. k B. k 6
6
C. k 6
3
D. k 15
4
E.
2
k 3
3

44.to
23. ¿Qué hora es según el gráfico?
A. 1 : 50
B. 1 : 49 : 3/13
C. 1 : 48
12
1
2
3
4
5
6
7
8
9
10
11
D. 1 : 50 : 1/11
E. 1 : 45
24. Según el gráfico, ¿Quéhora indica el reloj?
Si
39º
2
   
A. 7 : 56
B. 7 : 53
C. 7 : 57
12
1
2
3
4
5
6
7
8
9
10
11
D. 7 : 54
E. 7 : 59
25. En una heladería se tiene disponible 8
sabores de helado diferentes, ¿Cuántas
posibilidades paraservir un pedido trisabor
hay?
A. 54 C. 64 E. 48
B. 60 D. 56
26. Cinco personas rinden un examen, si se
sabe que:
g B obtuvo un punto más que D.
g D obtuvo un punto más que C.
g E obtuvo dos puntos menos que D.
g B obtuvo dos puntos menos queA.
Ordénar los de manera creciente.
A. ABCDE B. ECDBA C. ABDCE
D. EDCBA E. ECDAB
27. Si la suma de dos números es cinco, y
cuatro veces su producto es 21, ¿Cuál es
la menor diferencia de los cuadrados de
dichos números?
A. –10 B. –8 C. 2
D. 4 E. 10
28. Cierta persona participa en un juego de
azar,el cual pagael doblede loque apuesta
el ganador, arriesgando sucesivamente:
S/.1; 2; 3; 4; ... de tal forma que gana todos
los juegos en que interviene excepto el
último. Retirándose entonces con una
ganancia de S/.65. ¿Cuántosjuegos ganó?
A. 15 B. 14 C. 13
D. 12 E. 11
29. Calcular el valor de la siguiente expresión:
1
E Sec 80º 2Sen70º
2
 
A. Tg10º B. Ctg10º C. –1
D. 1 E. 1/2Ctg10º
30. Calcular:
3E Tg Arc Sec 2 Arc Tg
3
 
  
 
A. 1/4 B. 2 – 3 C. 2 + 3
D. 2 E. 4

25.to
01. Calcular el valor de la expresión:
9 9 9 9
k cifras
N 8 88 888 ... 88...88     
A.
k 1
9 8k 9
8

  B.
k 1
9 8k 9
8

 
C.
k 1
9 8k 9
8

  D.
k 1
9 8k 9
8

 
E.
k 1
9 8k 8
8

 
02. Si  MCD a5a;7b7 11 , hallar "a + b".
A. 9 B. 11 C. 13
D. 15 E. 17
03. La razón de dos números es 5/8, si el
menor es 40. ¿Cuánto vale el mayor?
A. 21 B. 22 C. 23
D. 64 E. 15
04. Hallar el promedio de 1, 2, 3, 4, ..., 38, 39,
40.
A. 20,5 B. 31 C. 20
D. 19 E. 21,5
05. Si:
a b
2,13
5 3
  , hallar el mayor valor de
"a + b".
A. 11 B. 10 C. 9
D. 12 E. 8
06. Se tiene 4 varillas de metal cuyo promedio
de longitudes es 65, si cada una tiene una
medida que a lo más es 70. ¿Cuál puede
ser la mínima longitud de una de ellas.
A. 50 B. 40 C. 46
D. 45 E. 51
07. Si: N = 2ab al extraer N , deja como
residuo un residuo máximo, determinar el
mayor valor de a + b.
A. 10 B. 12 C. 14
D. 16 E. 11
08. Indicar verdadero (V) o falso (F) en las
siguientes proposiciones:
I. Si cuatro números enteros positivos son
PESI entonces también son PESI 2 a 2.
II. Si la cantidad de divisores de un
número entero positivo es impar,
entonces, dicho número esun cuadrado
perfecto.
III. Si 2
k 7 2 

entonces necesariamente
k 7 4 

IV. Todo número cubo perfecto múltiplo de
4 también será múltiplo de 64.
A. FFFF B. FFVF C. FVFF
D. VFFV E. FVFV
09. Si f(x) = ax + b; a < 0; f(0) = 2; f(f(1)) = 5.
Halla f(+2)
A. –8 B. –4 C. 0
D. 2 E. 8
10. Hallar:
2 2
x 4Ln
2
 
 
 
Si Lnx 36
Ln(xy) 12
y e



A. 3 B. 4 C. 6
D. 12 E. 36
11. Hallar el dominio de la función:
2
(x)F 4 x 
A.  2;2 B.  3;7
C.  4;2 D.    ; 2 2;   
E. 

35.to
12. Si 2;5 , halla el intervalo de variación de
 2x 1
x 6


A. 11;3 / 8 B.  11;3 / 8
C. 3 / 8;11 D.  3 / 8;11
E. N. A
13. Si a, b, c son las raíces de: 3x3
+ 6x+ 1 = 0,
hallar:
3 3 3
ab ac bcE
a b c
 
 
A. –2 B. –4 C. –5
D. –8 E. 3
14. Las raíces de la ecuación polimonial:
2x3
+ 9x2
+ 9x + b = 0 están en proporción:
1 : 2 : 6. Halla: b2
–b
A. 3 B. 6 C. 9
D. 12 E. 15
15. Si el polinomio P(x) = x4
+ ax3
+ bx2
+ cx + 1
tiene raíz cuadrada exacta, entonces 4b –
c2
es igual a:
A. 0 B. 2 C. 6
D. 8 E. 12
16. Simplificar:  4 4
E 6 4 3 27 3  
A. 3 2
2
B. 6 C. 3 3
2
D. 2 3 E. 3 3
17. En la figura, hallar el valor del arco "x".
A. 80º
B. 90º
C. 100º
20º 40º x 80º
D. 110º
E. 120º
18. En el gráfico, AM = 2(MN). Calcular mAM
A. 37º
B. 40º
C. 60º
A
B
M
N
O
D. 30º
E. 53º
19. En el trapezoide simétrico, calcular
x
y , si
BC EC .
A. 1/2
B. 1/3
C. 1/4 E
B
C
D
x
y
D. 1/5
E. 1
20. Si AE = EM y EH = 1 m. Hallar AB
A. 6 m
B. 7 m
C. 5 m
A
B
C
E
H
M
D. 10 m
E. 8 m
21. En un triánguloABC se trazan las cevianas
AR y BD que se intersectan en K, tal que
 CK DR P  , AD = DB, mDBC = 90°
y mBCA = 40°. Calcular la mPBC.
A. 40 B. 65 C. 45
D. 80 E. 50
22. En un tetraedro regular "r" medida del radio
de la esfera inscrita y "k" medida del radio
de laesfera ex-inscrita,entonces el valor de
"
k
r
"
A. 1 B. 2 C. 3/2
D. 4/3 E. 3

45.to
23. Efectuar:
T = 2(3) + 6(4) + 12(5) + ... + 272(18)
A. 23356 B. 23256 C. 23756
D. 23852 E. 23842
24. Hallar: M – N si:
52 términos
50 términos
M 2 4 6 8 ...
N 1 3 5 7 ...
    
    


A. 250 B. 265 C. 256
D. 331 E. 337
25. Definidas las operaciones:
2n - 1 = 4n + 1
2n + 1 = 16n + 9
Calcular: E = 3 + 4
A. 81 B. 64 C. 225
D. 188 E. 125
26. De 8 amigos y 5 mujeres se va a formar
grupos mixtos de 6 personas. ¿De cuántas
maneras diferentes se podría formar el
grupo, si en él hay por lo menos 4 mujeres?
A. 124 B. 112 C. 148
D. 96 E. 216
27. Hallar la suma de las cifras del resultado
de efectuar:
 2
121cifras
1000......005

A. 14 B. 12 C. 9
D. 7 E. 525
28. Si: abc a 975
b abc 650
abc c 1625
 
 
 
Indicar la suma de las cifras del resultado
de efectuar: abc cba
A. 32 B. 34 C. 35
D. 37 E. 40
29. Simplificar: E = Sen4
x – Cos4
x + Cos2
x
A. Cos2
x B. Cos4
x C. Sen4
x
D. Sen2
x E. Senx + Cosx
30. Dada la ecuación polinomial:
x3
– x2
– 2x + 1 = 0
Señalar cual de las alternativas representa
una de sus raíces.
A. Sen
9

B. Cos
9

C. 2Cos
9

D. 2Cos
7

E. Sen
7


OLIMPAMER - JOSE A. ENCINAS

Más contenido relacionado

La actualidad más candente (20)

Similar a OLIMPAMER - JOSE A. ENCINAS (20)

Más de Edinsson R. Javier Villanueva (17)

Último (20)

OLIMPAMER - JOSE A. ENCINAS