Robert hernandez 25563571

Universidad Fermín Toro
Vicerrectorado Académico
Facultad de Ingeniería
APLICACIÓN DE LA INTEGRAL DEFINIDA
Integrante:
Robert Hernández
C.I:25.563.571
Saia :A
Cabudare 04 de septiembre de 2018

La integral definida es una herramienta u´til en las ciencias f´ısicas y sociales, ya que muchas cantidades de interés
en dichas ciencias pueden definirse medianteel tipo de suma que se presenta en la integral definida.
Antes de estudiar casos espec´ıficos en que se utiliza la integral definida, daremos las siguientes definiciones:
Deftnición 1
Recibe el nombre de partición de un intervalo cerrado [a, b] un conjunto de intervalos cerrados:
{[x0, x1], [x1, x2], [x2, x3], . . . , [xn−2, xn−1], [xn−1, xn]}
que posee las propiedades:
1. [x0,x1] ∪ [x1,x2] ∪ . . . ∪ [xn−2,xn−1],[xn−1,xn]} = [a, b]
2. [xi−1 , xi] ∩ [xi, xi+1 ] = xi con i ∈ {1, 2, . .. , n}
3. [xj−1 , xj] ∩ [xk , xk+1 ] = ∅ a menos que k = j o j − 1 = k + 1.
Deftnición 2
Cada intervalo en una partición de [a, b] se llama subintervalo [a, b]. Una partición está determinada por los
nu´meros que son puntos externos de los subintervalos de la partición. As´ı, una partición que contenga n
subintervalos queda determinada por un conjunto de n + 1 nu´meros.
{x0, x1, x2, . . . , xn−1, xn},
donde x0 = a, xn = b, xi−1 < xi para i ∈ {1, 2, 3, . . . , n}.
Denotaremos con Pn la partición determinada por este conjunto de n + 1 nu´meros, as´ı:
Deftnición 3
Pn = {[x0, x1], [x1, x2], . . . , [xn−2, xn−1], [xn−1, xn]}
Si Pn es una partición de un intervalo [a, b], la norma Np de Pn es el mayor de los n nu´meros
donde
(x1 − x0), (x2 − x1), (x3 − x2), . . . , (xn − xn−1),
∆x1 = x1 − x0, ∆x2 = x2 − x1, . . . , ∆xn = xn − xn−1,
o sea ∆xi = xi − xi−1 para i ∈ {1, 2, . . . , n}.
La norma Np de una partición Pn es la longitud del más grande de los subintervalos en la gráfica de Pn que se
muestra a continuacion:

5
≥ ∈
Figura 7 .1:
Deftnición 4
Si Pn es una partición en un intervalo [a, b], un aumento Tn de la partición es un conjunto de nu´meros
{t1, t2, . . . , tn} tales que
x0 ≤ t1 ≤ x1, x1 ≤ t2 ≤ x2, x2 ≤ t3 ≤ x3, . . . , xn−1 ≤ tn ≤ xn,
o sea, xi−1 ≤ ti ≤ xi con i ∈ {1, 2, . . . , n}.
Gráficamente:
Figura 7 .2:
7.1 Cálculo de áreas
Sea f una función cuyo dominio está en el intervalo cerrado [a, b], tal que f(x) 0 para x [a, b].
Sea R la región plana limitada por las gráficas de las ecuaciones: y = f (x), y = 0 (eje x), x = a, x = b.
Figura 7 .3:
Sea Pn una partición de [a, b] en n subintervalos determinados por el conjunto {x0 , x1 , x2 , . . ., xn−1 , xn}, con
∆xi = xi − xi−1 , i ∈ {1, 2, . . ., n}.
Sea Tn = {t1, t2,. . . , tn} un aumento de Pn.

Σ
n
.
.
Σ
Construimos n rectángulos cuyas bases sean los n intervalos de la partición Pn cuyas alturas sean
f(t1), f(t2), . . . , f(ti), . . . , f(tn−1), f(tn).
Figura 7 .4:
El área del i–ésimo rectángulo está dada por f (ti) · ∆xi; y la suma
n
f(ti)∆xi
i=n
de las áreas de los n rectángulos será una aproximación al área de R.
Si aumentamos el nu´mero de subintervalos, entonces decrece la longitud de cada subintervalo de la partición
Pn, obteniéndose una nueva suma que dará una mayor aproximación al área de R.
Demos ahora la siguiente definición:
Deftnición 5
Si f (x) ≥ 0 para x ∈ [a, b], y si existe un nu´mero A tal que dada una s > 0, exista δ > 0 tal que
.
Σ
i=1
f(ti) ∆xi − A. < s
para toda partición Pn de [a, b], y todo aumento de Pn en que Np < δ, entonces este nu´mero A es el área de la
región limitada por las gráficas de la ecuación y = f(x), y = 0, x = a, x = b.
Note que de esta definición se tiene que:
y si A existe, entonces:
lim
max ∆xi →0
n
i=1
f (ti) ∆xi
Σ
= A
A =
a
f(x)
Ejemplo 1
Calculemos el área de la región R limitada por las gráficas de = 1 +
6x − x2
,
9
y = 0, x = 5, x = 0.
∫
y

7
i
n
i −i
Σ
x +
9
x2 −
27 .
−
0
Solución
La representación gráfica es la siguiente:
( ) = 1 +
6ti − t2
f ti
9
i
El área del i−ésimo rectángulo es:
1 +
6ti − t2
9
∆xi
Figura 7 .5:
La suma de aproximacion para el área de R es:
Σ
i=1
.
1 +
6 2
9
· ∆xi
(En la gráfica anterior se muestra el i−ésimo rectángulo de la aproximación). Luego
de la definición ?? se tiene que:
=
∫ 5 .
1 +
6x x2
9
dx
.
3 x3 Σ
.5
3
= 5 +
9
(25) −
=
235
(u.l.)2
27
125
27
− 0
Ejemplo 2
Calculemos el área de la región R limitada por las gráficas de y = ln x, y = 0, x = e.
Solución
Graficamente se tiene:
0
0
·
=
Σ
A

⇐⇒
∫
.
≥ ∈
Figura 7 .6:
Como ln x = 0 x = 1, entonces la curva interseca al eje x en el punto (1,0). El área de la región R está
dada por:
e
A = ln x dx
1
= (x ln x − x)
. Se utilizó el método de
integracion “por partes”.
1
= e ln e − e − ln 1 + 1
= 1 (u.l.)2
7.2 A´ rea de una región comprendida entre dos curvas
Sean f y g dos funciones con dominio en el intervalo [a,b], tales que f(x) g(x) para x [a, b].
Vamos a determinar cuál es el área de la región R limitada por las gráficas de y = f (x), y = g(x), x = a, x = b
que se muestra a continuacion:
Figura 7 .7 :
Construimos un conjunto de rectángulos tales que la suma de sus áreas sea una aproximación al área de R.
e

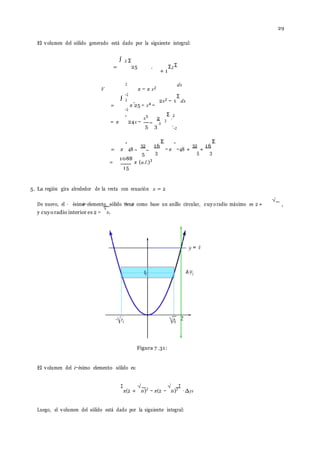
9
{ }
− −
·
Σ
n
.
n
Figura 7 .8:
Sea Pn una partición de [a, b] en n subintervalos determinados por el conjunto
{x0 , x1 , x2 ,. . . , xi−1 , xi, . .. , xn−1 , xn},
donde ∆xi = xi − xi−1 , i ∈ {1, 2, .. . , n}.
Sea Tn = t1 , t2 , . . . , ti−1 , ti, .. . , tn−1 , tn un aumento de Pn. Construim os n rectángulos cuyos anchos sean los
n subintervalos de la partición Pn, y cuyas alturas sean:
f(t1) − g(t1), f (t2) − g(t2), . . . , f(ti) − g(ti), . . . , f(tn) − g(tn).
El área del i ésimo rectángulo es: [f (ti) g(ti)] ∆xi, y la suma de aproximación para el área de R está dada
por:
n
[f (ti) − g(ti)] · ∆xi
i=1
Si aumentamos el nu´mero de subintervalos, entonces decrece la longitud de cada subintervalo de la partición
Pn, obteniéndose una nueva suma que dará una mayor aproximación al área de R.
Se tiene entonces la siguiente definición:
Deftnición 6
Si f (x) ≥ g(x) para x ∈ [a, b], y si existe un nu´mero A, tal que dada una s > 0 exista una δ > 0 para lo cual
.
Σ
i=1
[f (ti) − g(ti)] · ∆xi − A. < s
para toda partición Pn de [a, b] y todo aumento de Pn con Np < δ, entonces dicho nu´mero A es el área de la
región limitada por las gráficas de las ecuaciones y = f (x), y = g(x), x = a y x = b.
De esta definición se tiene que:
A = lim
Σ
[f (ti) − g(ti)] · ∆xi
Np→0
i=1

∫
n
5
ti +
5
−
9
− 1
5
x +
5
−
9
+ 1
5
+
5
x −
27
+ x
−
Σ
Si h es la función definida por h(x) = f (x) − g(x) para x ∈ [a, b], y si A existe, entonces:
b
A = h(x) dx =
a
b
[f (x) g(x)]dx
a
Ejemplo 3
Hallar el área de la región R
Solución
limitada por las gráficas de las ecuaciones: =
(x − 2)2
9
1, y =
2
x
5
+
2
, x = 4
5
Figura 7 .9:
Note que las gráficas de =
(x − 2)2
9 1, y =
2
x
5
+
2
se intersecan en el punto (
5
−1,0).
En este caso, el área del i−ésimo rectángulo es:
Σ.
2 2
Σ .
(ti − 2)2
ΣΣ
y la suma de aproximacion está dada por:
Σ
i=1
2
5
ti +
2 (ti
5
−
− 2)2
9
−1
ΣΣ
· ∆xi
Seguń la definición ?? se tiene que:
∫ 4 Σ
2 2 (x − 2)2
Σ
Σ
x2 2 (x − 2)3
Σ
.4
−1
.
−1
−1
∫
−
−
.
· ∆xi
A =
dx
=
y
y

11
2
∫ .
4
x
5 5 27 5 5 27
=
16
+
8
−
8
+ 4 −
.
1
−
2
+
27
− 1
Σ
=
235
(u.l.)2
27
Ejemplo 4
Hallar el área de la región R limitada por las gráficas de las ecuaciones y =
−x
+ 1, x = −2, x = 4, y = 0.
Solución
Figura 7 .10:
La recta con ecuación y =
−x
+ 1 interseca al eje x en el punto (2, 0).
2
Note que la región R está formada por dos partes, las regiones R1 y R2 , por lo que el área de R = área de R1
+ área de R2 .
La región R1
está limitada superiormente por la gráfica de y =
−x
+ 1, inferiormente por la de y = 0, lateral-
2
mente por la de x = −2 y x = 2.
Luego:
área de R1
=
2
−x
+ 1
−2 2 − 0
Σ
dx
=
.
−x2
+
Σ
.2
La región R2
está limitada superiormente por la gráfica de y = 0, inferiormente por la de y =
−x
+ 1, lateral-
2
mente por la de x = 2 y x = 4.
−2
= 4 (u.l.)2
−2
.

2
−
2
3
3
∫ Σ
4
− x
2
2
Luego:
área de R2 =
∫ 4 Σ
0
.
−x
+ 1
ΣΣ
dx
=
∫ 4 . x
1
Σ
dx
2
.
x2
Σ
.4
= 1 (u.l.)2
Por tanto, el área de R es igual a: 4 + 1 = 5 (u.l.)2
.
Ejemplo 5
Hallar el área de la región R senãlada en la figura adjunta, que está limitada por las gráficas de las ecuaciones:
x2 x
y =
2
− 2x + 1, y =
3
+ 1, y = −x + 5.
Figura 7 .11:
Solución
R puede dividirse en dos regiones R1 y R2.
Las rectas con ecuaciones y =
x
+ 1, y = −x + 5 se intersecan en el punto (3, 2) (¡compruébelo!). La
recta con ecuación y = −x + 5 y la parábola se intersecan en el punto (4, 1).
La recta con ecuación y = x
+ 1 y la parábola se intersecan en el punto (0, 1)
Luego: área de R = área de R1 + área de R2
área de R1
=
3
x
+ 1
0 3
x
−2x + 1
ΣΣ
dx
2
2
2
.
=
.
−
−

13
−x
.
Σ
6
x2 −
4x +
2
−
x −
2
2
x −
2
=
∫ 3 Σ Σ
dx
.
7 x3 Σ
.3
área de R2
= 6 (u.l.)2
=
∫ 4 Σ
+ 5 −
x
−2x + 1
ΣΣ
dx
=
∫ 4 .
4 +
x2
.
x2
x3 Σ
.4
Entonces: área de R = 6 +
31
(u.l.)2
.
3
=
31
(u.l.)2
3
Ejemplo 6
Hallar el área de la región R limitada por las gráficas de las ecuaciones y2 = x, y = −x + 2.
Solución
Figura 7 .12:
Las gráficas se intersecan en los puntos (1, 1) y (4, −2) (Verif´ıquelo algebraicamente).
En esta caso podemos tomar“y” como variableindependientey x como la variable dependiente, es decir,
x = g(y) = 2 − y.
As´ı el área de la región R está dada por:
3
6
3
6
3
0
6
0
6 0
3
= .
=
.
dx

∫
0
x −
xdx
.
− −
3
( x)3
1
(2
−2
− y − y )dy
.
y2
y3 Σ
.1
= 2y −
9
2
−
3 .
−2
=
2
(u.l.)2
Otra forma de obtener el área de la región R es la siguiente:
y =
√
x y = −
√
x y = 2 − x
Figura 7 .13:
Dividimos la región R en dos regiones R1 y R2 . La región R1 está limitada superiormente por la gráfica de
y =
√
x, inferiormente por la de y = −
√
x, lateralmente por la de x = 1 y x = 0.
As´ı:
área de R1 =
∫ 1 Σ√
=
∫ 1
2
√
(−
√
x)
Σ
dx
0
4 √ .
=
4
(u.l.)2
3
La región R2 está limitada superiormente por la gráfica de y = x + 2, inferiormente por la de y =
√
x,
lateralmente por la de x = 1.
Luego:
área de R2 =
∫ 4
Σ
+ 2 − (−
√
x)
Σ
dx
1
1
0
0
1
−x
=
2

15
∫
2x −
2
+
=
4
(2
1
− x +
√
x)dx
.
x2
2x3/2
Σ
.4
Por tanto:
=
19
(u.l.)2
6
área de R = área de R1 + área de R2
=
4
+
19
3 6
=
27
(u.l.)2
.
6
7.3 Volu´menes de sólidos de revolución
Sea f una función definida en el intervalo [a, b].
Recibe el nombre de sólido de revolución, el sólido generado al girar alrededor del eje x, la región limitada por
la gráfica de y = f (x), el eje x y las gráficas de x = a y x = b. El eje x es un eje de simetr´ıa de dicho sólido y
una sección recta perpendicular al eje x es un c´ırculo.
Figura 7 .14:
Para determinar el volumen de este tipo de sólidos, seguiremos un procedimiento similar al utilizado para el
área de una región, aproximando el “volumen” de un sólido de revolución por medio de una suma de volu´menes
de sólidos más elementales, en los que el volumen ya ha sido definido.
Vamos a considerar discos o cilindros circulares como los sólidos elementales, asumiendo que el volumen de un
disco circular es, por definición, el producto del área A de la base por el espesor h (o altura).
1
3
1
3= .

16
Σ
h
Figura 7 .15:
Consideremos una partición Pn del intervalo [a, b] determinada por el conjunto de nu´meros
{x0 , x1 , x2 ,. . . , xi−1 , xi, . .. , xn−1 , xn},
donde ∆xi = xi−1 − xi, con i ∈ {1, 2, 3, . . . , n}.
Sea Tn = {t1, t2,. . . , tn} un aumento de Pn.
Consideremos ahora los ndiscos circulares, cuyos sensores son ∆x1,∆x2,...,∆xi, ...,∆xn, y cuyas bases tienen
radios f(t1),f(t2),.. . ,f(ti), . . . ,f(tn).
Figura 7 .16:
El volumen del i−ésimo disco es:
La suma
π[f (ti)]2
· ∆xi
n
π[f (ti)]2
· ∆xi
i=1
de los volu´menes de los n discos nos da una aproximación al volumen del sólido de revolución.
Podemos suponer que mientras más delgados sean los discos, mayor será la aproximación de la suma anterior
al volumen del sólido.
Se tiene entonces la siguiente definición:
Deftnición 7

17
n
.
Σ
Σ
∈
≥
h x
π f x
Si existe un nu´mero V tal que dada s > 0 exista δ > 0 para la cual
.
Σ
i=1
π[f (ti)]2
· ∆xi − V . < s
para toda partición Pn de [a, b] y todo aumento Tn de Pn, y con Np < δ, este nu´mero V es el volumen del sólido
obtenido por revolución del área limitada por las gráficas de y = f (x), y = 0, x = a, x = b alrededor del eje x.
Si h es la función dada por h(x) = π[f (x)]2
para x ∈ [a, b], entonces la suma de aproximación:
n
π[f (ti)]2
· ∆xi
i=1
utilizada en la definición del volumen del sólido de revolución, puede escribirse como:
donde ti ∈ [xi−1 , xi], ∆xi = xi−1 − xi.
n
h(ti) · ∆xi
i=1
Luego, de la definición de integral y de la definición de V dada, se tiene que
=
∫ b
( ) =
∫ b
[ ( )]
Consideremos ahora dos funciones f y g continuas en el intervalo cerrado [a, b], tales que f (x) g(x) para
x [a, b]. Sea R la región del plano limitada por las curvas con ecuaciones y = f (x), y = g(x) y las rectas con
ecuaciones x = a, x = b.
Figura 7 .17 :
Deseamos determinar el volumen V del sólido de revolución generado al girar la región R alrededor del eje x
(note que en este caso no giramos la región R alrededor de una de sus fronteras).
El sólido generado se muestra en la siguiente figura:
aa
aa
V dx 2
dx

18
− −
Figura 7 .18:
Sea Pn una partición del intervalo [a, b] determinada por el conjunto de nu´meros {x0 , x1 ,x2 , . . . , xi−1 , xi, . . . , xn}
con ∆xi = xi − xi−1 para i ∈ {1, 2, . . . , n}, y sea Tn = {t1 , t2 , . .. , ti, . .. , tn} un aumento de Pn.
En este caso, los sólidos elementales usados para obtener una suma de aproximación del volumen del sólido de
revolución, serán anillos circulares.
Se muestra a continuacion el i ésimo rectángulo y el i ésimo anillo circular generado al rotar aquel alrededor del
eje x.
Figura 7 .19:
Figura 7.20:
Luego, el área del anillo circular es:

19
Σ . Σ
n
Σ . Σ
Σ
h x f x − g x 2
π[f (ti)]2
− π[g(ti)]2
por lo que el volumen del i−ésimo elemento sólido será:
∆Vi = π
.
[f (ti)]2
− [g(ti)]2
Σ
· ∆xi
Entonces, la suma de aproximacion para el volumen del sólido de revolución es:
n
π [f (ti)]2
− [g(ti)]2
· ∆xi
i=1
Puede suponerse que mientras más delgados sean los anillos circulares, mayor será la aproximación de la suma
anterior al volumen del sólido.
Deftnición 8
Si existe un nu´mero V tal que dada s > 0 exista δ > 0 para la cual
.
Σ
i=1
π
.
[f (ti)]2
− [g(ti)]2
Σ
∆xi − V
.
< s
para toda partición Pn de [a, b] y todo aumento Tn de Pn, y con Np < δ, este nu´mero de V es el volumen del sólido
obtenido por revolución del área limitada por las gráficas de y = f (x), y = g(x), x = a, x = b, alrededor del eje x.
Si h es la función dada por h = π
.
[f (x)]2
− [g(x)]2
Σ
para x ∈ [a, b], entonces la suma de aproximación
π [f (ti)]2
− [g(ti)]2
· ∆xi
i=1
utilizada en la definición ??, puede escribirse como:
donde ti ∈ [xi−1, xi], ∆xi = xi − xi−1.
Luego se tiene que:
n
h(ti) ∆xi
i=1
=
∫ b
( ) =
∫ b
.
[ ( )] [ ( )]
Σ
Ejemplo 7
Hallar el volumen del sólido de revolución generado al girar alrededor del eje x, la región limitada por la gráfica de
y =
√
x, y = 0, x = 1, x = 4.
aa
aa
n
2
V dx π dx

20
−
Σ √
∫
.2 1
2
2 4
−
Solución
Figura 7 .21:
Observe, en la figura de la derecha, i ésimo rectángulo que al rotar alrededor del eje x genera un disco circular en
forma de cilindro circularrecto.
El volumen del i−ésimo disco circular es:
π[f (ti)]2
· ∆xi = π(
√
ti)2
· ∆xi
La suma de aproximacion del volumen:
El volumen del sólido está dado por:
n
π( ti)2
· ∆xi
i=1
4
V = πx dx
1
= π
x .
= 8π −
π
=
15
π (u.l.)3
2
Ejemplo 8
Hallar el volumen del sólido generado cuando la región limitada por las gráficas de y = 2 x, x = 0, y = 0 gira
alrededor del eje x.
Solución
La representación gráfica del sólido de revolución es la siguiente:
El volumen del i−ésimo disco circular es:
π[f (ti)]2
· ∆xi = π[2 − ti]2
· ∆xi
1 4

21
Σ
2
Σ
f x
π − x dx
3
(2 − x)3
.
Figura 7 .22:
La suma de aproximacion del volumen es:
n
π(2 − ti)2
· ∆xi
i=1
Luego, si f (x) = 2 − x, entonces el volumen del sólido está dado por:
∫ 2
[ ( )] =
∫ 2
(2 )
−π .
=
8π
(u.l.)3
3
Ejemplo 9
Hallar el volumen engendrado cuando la superficie limitada por la curva y = sen x, y las rectas con ecuaciones
y = 0, x = 0, x = π, gira en torno al eje x.
Solución
Si f (x) = sen x entonces:
1. El volumen del i−ésimo rectángulo es:
π[f (ti)]2
· ∆xi = π(sen ti)2
· ∆xi
2. La suma de aproximacion del volumen es:
n
π(sen ti)2
· ∆xi
i1
0
00
00
0
2
2
dx
=

22
0
∫
−
x −
2
sen 2x
Figura 7 .23:
3. El volumen del sólido está dado por:
π
π(sen
0
x)2
dx = π
π
1 cos 2x
2
dx
π
.
1 Σ
.π
=
π2
( )3
2
u.l.
Ejemplo 10
Hallar el volumen del cuerpo engendrado al girar alrededordel eje x, la superficie comprendida entrelas
parábolas con ecuaciones y = x2 , y =
√
x.
Solución
La representación gráfica de la región y del i−ésimo rectángulo es la siguiente:
Figura 7 .24:
El volumen del i−ésimo anillo circular es:
0
2
2 0
∫
=
.

23
i
Σ . Σ√
π [ t ]
− [t ] · ∆xi
i
x 2 − x2 2
2
− .
2 5
π
.
[
√
ti]2
− [t2 ]2
Σ
· ∆xi
La suma de aproximacion del volumen es:
n
2 2 2
i
i=1
Luego, el volumen del sólido de revolución está dado por:
=
∫ 1
Σ
(
√
) ( )
Σ
= π
∫
.
x − x4
Σ
dx
.
x2
x5 Σ
.1
= π
.
1
−
1
Σ
− 0
=
3
π (u.l.)3
10
Ejemplo 11
Determinar el volumen del sólido obtenido al girar la región del ejemplo anterior, alrededor del eje y.
Solución
Figura 7 .25:
El anillo circular tiene como radio máximo g(ti), y como radio m´ınimo f (ti).
0
2 0
V
π dx
= π

24
∫
g y − f y 2
π y −y4
2
−
En este caso tomamos x como la variable dependiente, y se tiene que el volumen del sólido está dado por:
=
∫ 1
.
[ ( )] [ ( )]
Σ
=
1
0
=
∫ 1
π
Σ
(
√
.
y)2
−
Σ
(y2)2
Σ
dy
.
y2
y5 Σ
.1
=
3
π (u.l.)3
10
Ejemplo 12
Hallar el volumen del cuerpo engendrado al girar, alrededor del eje y, la parte de la parábola y2 = 4ax, a > 0, que
intercepta la recta x = a
Solución
La representación gráfica de la región y del i−ésimo rectángulo es la siguiente:
Figura 7 .26:
El anillo circular tiene como radio máximo x = a, y como radio interior =
y2
.
4a
0
0
0
2 0
2 0
2
V π
dy
dx
= π .
x

25
∫
a2
π a2 −
16
a2y −
80
π a −
80a2 − a
80a2
Tomamos x como la variable dependiente.
V =
2a
−2a
π
Σ
a2 −
.
y2 Σ2
Σ
=
∫ 2a .
y4 Σ
.
y5 Σ
.2a
=
.
2 3 32a5
Σ .
2 3
+
32a5
Σ
=
16
a3π (u.l.)3
5
Ejemplo 13
Determinar el volumen del sólido de revolución generado cuando la región limitada por las gráficas de las ecua-
ciones y = x2, y = 4, gira alrededor de:
1. el eje y
2. la recta con ecuación y = 4
3. el eje x
4. la recta con ecuación y = −1
5. la recta con ecuación x = 2
Solución
1. La región en el plano xy que gira alrededor del eje y es la siguiente:
Figura 7 .27 :
a2
−2a
4a
−2a
dx
= π .
− π
dy

26
∫
.y
= π
0
= 8π (u.l.)3
Se tiene que el radio del sólido generado es:
x =
√
y
El volumen del i−ésimo elemento sólido es:
π[
√
ti]2
· ∆yi
4
V
0
=
∫ 4
π[
√
y]2
dy
2 4
2 .
2. La región gira alrededor de la recta con ecuación y = 4
Figura 7 .28:
El radio del i−ésimo disco circular es:
0
0
π y dy
=

27
i
∫
∫
.
i
i
16x −
3
x3 + .
− x
16x −
.
=
.
π −
4 − t2
π
Σ
4 − t2
Σ2
· ∆x
En general, el radio del sólido generado es:
Luego, el volumen del sólido está dado por:
4 − y = 4 − x2
V π 4 −x
−2
Σ2
dx
=
2
16
−2
8x2 + x4
Σ
dx
.
8 x5 Σ
.2
= π
.
32 −
64
+
32
Σ
− π
.
−32 +
64
−
32
Σ
3 5 3 5
=
512
π (u.l.)3
15
3. Note que al girar la región alrededor del eje x, el i−ésimo elemento sólido tiene como base un anillo circular.
Σ
π(4)2
− π(t2)2
Σ
· ∆xi
Luego, el volumen del sólido generado está dado por la siguiente integral:
=
∫ 2
Σ
16 ( )
Σ
V
2
=
∫ 2
π −
.
16
x2 2 dx
Σ
.
x5 Σ
.2
= π
.
32 −
32
Σ
− π
.
−32 +
32
Σ
5 5
=
256
π (u.l.)3
5
−2
−
2
5 −2
5 −2
2
4
i
= π
π dx
= π

28
i
Figura 7 .29:
4. La región gira alrededor de la recta con ecuación y = −1
El radio máximo del anillo circular es y = 5 = 4 + | − 1|
El radio interior del anillo es y = x2 + | − 1| = x2 + 1
Figura 7 .30:
Σ
π(5)2
− π
.
t2 + 1
Σ2
Σ
· ∆xi

29
∫
3
. .i− − ti
24x −
5
−
3
x .
−
5
− 3 5 3
.
El volumen del sólido generado está dado por la siguiente integral:
=
∫ 2 Σ
25 .
+ 1
Σ2
Σ
V π − π x2
−2
= π 25 − x4 −
−2
2x2 −
dx
1
Σ
dx
.
x5
2
Σ
.2
= π
.
48
32 16
Σ
− π
.
−48 +
32
+
16
Σ
=
1088
π (u.l.)3
15
5. La región gira alrededor de la recta con ecuación x = 2
De nuevo, el ésimo elemento sólido tiene como base un anillo circular, cuyo radio máximo es 2+
√
,
y cuyo radio interior es 2 −
√
ti.
Figura 7 .31:
Σ
π(2 +
√
ti)2
− π(2 −
√
ti)2
Σ
· ∆yi
Luego, el volumen del sólido está dado por la siguiente integral:
2
2
−2
= π

30
∫
Σ
=
∫
√
8
.y
.
y
3
π
3
.
4
V π(2 +
√
0
y)2
− π(2−
√
y)2
Σ
dy
4
= π y dy
0
3/2 4
16 √ .
=
128
π (u.l.)3
3
7.4 Longitud de una curvaplana
Vamos a determinar la longitud s del arco de una curva con ecuación y = f (x), comprendida entre los puntos
A(a, f (a)), B(b, f(b)).
Figura 7 .32:
Como se muestra en la figura anterior, dividimos el arco AB en n partes, uniendo luego los sucesivos puntosde
división por segmentos rectil´ıneos.
Por ejemplo, el segmento DE tendrá como longitud
√
(∆xi)2 + (∆yi)2 .
0
0
= 8π
3/2
0
4
=

31
Σ √
n
n
.
∗j(∆x ) +
[f (x ) · ∆x ]i i
. Σ
∫
. . Σ
Luego, tendremos una aproximaxion de la longitud de la curva AB, mediantela suma:
n
(∆xi)2 + (∆yi)2.
i=1
Si aumentamos indefinidamente el nu´mero de puntos de división, entonces las longitudes de los segmentos tien-
den a cero, por lo que:
lim
Σ √
(∆xi)2 + (∆yi)2
nos da el arco AB, siempre que el l´ımite exista.
Para expresar el l´ımite como una integral tenemos lo siguiente: supongamos que la función con ecuación y = f (x)
es continua y posee derivada continua en cada punto de la curva, donde A(a, f (a)) hasta B(b, f (b)). Luego,
por el teorema del valor medio para derivadas, existe un punto D∗ (x∗
i , yi
∗
) entre los puntos D y E de la curva,
donde la tangente es paralela a la cuerda DE, esto es:
fj(x∗ ) =
∆yi
o sea ∆y = fj(x∗ ) · ∆x
i
∆xi
i i i
Luego
lim
Σ √
(∆xi)2 + (∆yi)2
n→∞
i=1
puede expresarse como:
lim
n→∞
2 2
i
i=1
.
Σn . Σ
= lim
max ∆xi →0
que por definición corresponde a la integral:
i=1 1 + [f j(x∗
)]2 · ∆x
∫ b
.
1 +
dy 2
dx
dx
(hemos expresado f j(x) como dy/dx).
Como la longitud de una curva no depende de la elección de los ejes coordenados, si x puede expresarse como
función de y, entonces la longitud del arco está dada por
f(b)
1 +
f (a)
dx 2
dy
dy
a
n
i
n→+∞
i=1
Σ

32
. Σ
x2 x2
En cada caso calcular la longitud del arco de curva que se indica.
Ejemplo 14
y
1 2 3/2
=
3
(x + 2) , desde x = 0 hasta x = 3.
Solución
Designemos con Lla longitud del arco.
Como y
1
x2 + 2)3/2
, entonces
dy
= x
√
x2 + 2
Luego:
=
3
(
dx
=
∫ 3
.
1 +
Σ √
+ 2
Σ2
L
0
=
∫ 3 √
1 +
x x2 dx
( + 2)
=
∫ 3 √
+ 2x2 + 1 dx
0
=
∫ 3 √
( + 1)2 dx
0
=
∫ 3
( + 1) dx
0
.
x3
Σ
.3
=
= 12
3
+ x .
Ejemplo 15
9x2 = 4y3, desde (0,0) hasta (2
√
3,3)
Solución
En este caso, tomemos x como variable dependiente y obtengamos
dx
por medio de derivación impl´ıcita:
dy
18x
dx
dy
= 12y2 de donde
dx
=
dy
2y2
3x
Luego, la longitud L del arco está dada por:
L =
∫ 3
.
1 +
2y2 2
3x
dy
0
0
0
x4
x2
x2
dx

33
∫ .
= 1 +
∫ .
= 1 +
. Σ
∫ .
−
=
∫ √
=
∫ √
=
∫
=
∫ .
=
(1 + y) 2
3
4
−
8y2
.
1
Σ
3
4y4
9x2
dy
0
3
4y4
4y3
dy
0
=
∫ 3 √
1 + y dy
3 .
=
16
−
2
3 3
=
14
3
Ejemplo 16
y4
x =
4
+
1
8y2
, desde y = 1 hasta y = 2
Soluci´on
Obtenemos de nuevo
dx
, pues x = h(y)
dy
dx
=
dy
3 1
y −
4y3
=
4y6 − 1
4y3
Luego: L =
∫ 2
.
1 +
4y6 − 1 2
4y3
2
16y6 + 16y12 8y6 + 1
16y6
dy
1
2
16y12 + 8y6 + 1
4y3
dy
1
2
(4y6 + 1)2
4y3
dy
1
2
4y6 + 1
4y3
dy
1
2
y3 + y−3 dx
41
.
y4 1
Σ
.2
= 4
1
.
1
−
1
Σ
−
32
−
4 8
=
123
32
1
0
0
0
3
0
1
.=
=
2

34
∫ .
= 1 +
∫ .
= 1 +
∫
.
−
(1 + 9x) 2
27
27 27
Σ
Ejemplo 17
(y + 1)2
= 4x3, desde x = 0 hasta x = 1
Solución
Obtengamos
dy
dx
por medio de derivación impl´ıcita:
Luego:
2(y + 1)
dx
dy
= 12x2 de donde
dy
=
dx
6x2
y + 1
=
∫ 1
.
1 +
6x2 2
y + 1
dx
1
36x4
(y + 1)2
dx
0
1
36x4
4x3
dx
0
=
1 √
1 + 9
0
2
x dx
3 .
=
2
(10)3/2
−
2
=
2
(10
√
10 1)
27
7.5 Cálculo de trabajo con ayuda de la integral definida
Vamos a estudiar la aplicación de la integral definida al concepto de “trabajo”.
Si una fuerza constante F actuá sobre un objeto desplazándolo una distancia x, a lo largo de una l´ınea recta, y la
dirección de la fuerza coincide con la del movimiento, entonces el trabajo realizado W se expresa como el
producto de la fuerza F por el camino recorrido.
Es decir: W = F · x.
Cuando la fuerza no es constante,por ejemplo, cuando se contraeo estira un resorte, el trabajo no se puede
expresar en forma tan simple.
Consideremos una part´ıculaP que se desplaza sobreel eje x, desde el punto (a,0) al punto (b,0) por medio de
una fuerza f = F (x), x ∈ [a, b].
Dividamos el segmento [a,b] en n partes arbitrarias de longitudes ∆x1,∆x2,...,∆xi, ...,∆xn, y tomemos en
cada subintervalo [xi−1 , xi] un punto arbitrario ti como se muestra a continuación.
0
0
0
.
1
=
L

35
Σ
Σ
n
n ∫
Figura 7 .33:
Cuando la part´ıcula se mueve de xi−1 a xi, el trabajo realizado es aproximadamente igual al producto F (ti)·∆xi.
Luego, la suma:
n
F (ti) · ∆xi
i=1
nos dará la expresión aproximada del trabajo de la fuerza F en todo el segmento [a, b].
La suma
n
F (ti) · ∆xi
i=1
representa una suma integral, por lo que si
lim
Σ
F (ti) · ∆xi
existe, entonces este expresa el trabajo realizado por la fuerza f = F(x) al mover una part´ıcula de a a b, a lo
largo del eje x.
Se tiene entonces que
W = lim
Σ
F (ti) · ∆xi = ( )b
F x dx
max ∆xi →0
i=1 a
siendo F (x) la fuerza aplicada a la part´ıcula cuando ésta se encuentra en el punto cuya coordenada es x.
Si la unidad de fuerza es el kilogramo, y si la unidad de distancia es el metro, entonces la unidad de trabajo es
el kilográmetro. También pueden utilizarse como unidades de trabajo la libra-pie y el gramo-cent´ımetro.
El alargamiento o la compresión de un resorte helicoidal, nos proporciona un ejemplo del trabajo realizado
por una fuerza variable. La ley de Hooke afirma que la fuerza necesaria para estirar un resorte helicoidal, es
proporcional a la elongación del resorte. As´ı, la fuerza necesaria para producir una elongación de x unidades,
está dada por la expresión F = kx, donde k es la constante de proporcionalidad, que depende del material, del
grosor del alambre, de la temperatura, etc.
max ∆xi →0
i=1

36
∫
.
Ejemplo 18
Un resorte tiene una longitud natural de 8 pulgadas. Si una fuerza de 20 libras estira el resorte 1/2 pulgada,
determinar el trabajo realizado al estirar el resorte de 8 pulgadas a 11 pulgadas.
Solución
Consideremos el resorteubicado a lo largo del eje x, con su extremo fijo en el origen:
Figura 7 .34:
Por la ley de Hooke se sabe que F = kx.
Como x = 0, 5 pulgadas cuando F = 20 libras, entonces 20 = k(0,5) de donde k = 40.
Luego, F = 40x. Se desea calcular el trabajo realizado por esta fuerza si aumenta la extensión de 8 a 11
pulgadas. Luego:
3
W = 40x dx
0
.
= 180 pulgadas-libras.
Ejemplo 19
Un resorte tieneuna longitudnaturalde 10 pulgadas,y una fuerza de 30 libras lo estira 11,5 pulgadas. Determi-
nar el trabajo realizado al estirarel resorte de 10 pulgadas a 12 pulgadas. Luego encontrarel trabajo realizado
al estirar el resorte de 12 pulgadas a 14 pulgadas.
Solución
Como F = kx, y x = 11,5 pulgadas, cuando F = 30 libras, entonces 30 = 11,5k, por lo que k = 60/23.
0
0
3
= 20x2

37
2
x
x
∫ 2
60
=
2
23 .
∫ 4
60
2
23 .
23 23
0
.
2
.
Figura 7 .35:
El trabajo realizado para estirar el resorte de 10 a 12 pulgadas está dado por:
W =
23
x dx
30
=
120
pulgadas-libras
23
El trabajo realizado para estirar el resorte de 12 a 14 pulgadas está dado por:
W =
23
x dx
30
=
480
−
120
=
360
pulgadas-libras
23
Ejemplo 20
Una fuerza de 25 kg alarga un resorte 3 cm. Determine el trabajo requerido para alargar el resorte 2 cm más.
Solución
Como F = kx y x = 0, 03 m, cuando F = 25 kg, entonces k = 2500/3.
El trabajo requerido para alargar el resorte 2 cm más (es decir, hasta 5 cm), está dado por:
2
00
2
4
=

38
∫
3
.
x
.
.
2
3 .
∫ 0,06
Figura 7 .36:
0,05
2500
W = x dx
0,03
1250
0,05
=
3, 125
−
1,125
3 3
=
2
kgm
3
Ejemplo 21
Determinar el trabajo efectuado al alargar un resorte 6 cm, sabiendo que se necesita una fuerza de 15 kg para
alargarlo 1 cm.
Solución
Seguń la ley de Hooke F = kx, por lo que 15 = k · 0, 01, de donde k = 1500.
Luego, F = 1500x y el trabajo efectuado para alargar el resorte 0,06 m está dado por:
W = 1500 xdx
0
0,06
= 2, 7 kgm
Ejemplo 22
0
0,03
= 7 50 x2
=

39
·
.
.
.
∫ 1,5
Un resorte tiene unalongitud natural de 6cm. Si 1200 dinas lo comprimen 0,5 cm, calcular el trabajo efectuado
al comprimirlo desde 0,6 cm hasta 4,5 cm. ¿Qué trabajo se requiere para hacer que el resorte llegue a 9 cm,
partiendo de su estado comprimido de 4,5 cm?
Solución
1.
Figura 7 .37 :
Como F = kx y x = 0, 5 cm cuando F = 1200, entonces k = 2400. Luego F = 2400 x. El trabajo
necesario para comprimir el resorte desde 6 hasta 4,5 cm está dado por:
W = 2400 xdx
0
1,5
= 1200(1,5)2
= 27 00 ergs
2. dib sno281
El trabajo que se requiere para hacerque el resorte lleguea 9 cm, partiendo de su estado comprimido de
4,5 cm, está dado por:
3
W =
1,5
2400 xdx
.
= 1200 · 9 − 1200 · (1, 5)2
= 8100 ergs
1,5
0
= 1200 x2
1,5
∫
3
= 1200 x2

Robert hernandez 25563571

Más contenido relacionado

La actualidad más candente (20)

Similar a Robert hernandez 25563571 (20)

Más de robert eleasther hernandez escobar (10)

Último (20)

Robert hernandez 25563571