線形代数の視覚的理解のためのノート
3 likes1,717 views
線形代数の視覚的理解のためのノート Graphic Notes on Prof. Gilbert Strang's "Linear Algebra for Everyone" Gilbert 先生の線形代数の講義に惚れて作りました。 コンタクト頂ければ、PowerPoint 版をお配りします。 また、マトリックスワールド、も是非ご覧ください。 https://qiita.com/kenjihiranabe/items/854dbe1f6d9fca9df85c
線形代数の視覚的理解のためのノート
- 1. 線形代数の視覚視的理解 のためのノート Graphic notes on “Linear Algebra for Everyone” by Gilbert Strang Kenji Hiranabe Version 1.0 = 1
- 2. これは何? • Gilbert Strang 著 『Linear Algebra for Everyone』 は線形代数を直感理解するのに とてもいい本です。 • 定理と証明の連鎖ではなく、マトリックス語法と例⽰で直感的な理解と実⽤的な 応⽤法を得ることができます。 • YouTube の MIT Open Courseware、 先⽣の講義プレイリストである 18.06 と 18.065 には、200万⼈の購読者がいます。（ぼくもその⼀⼈です） • この本のハイライトは、 • AB=C の4つの⾒⽅ • 基本的な4つの部分空間 • 5つのマトリックス分解 • 通常の線形代数の教科書はジョルダン標準形がクライマックスですが、この 本では、SVD です。そして、 • 機械学習を含むデータサイエンスへの⼊⾨につながっています。 • この1と2のコンセプトをグラフィック表現できないか、というアイディアです。 By Kenji Hiranabe with the kindest help of Prof. Gilbert Strang 2 1 2
- 3. なぜこの ノートを 読む? • ⾏列とベクトルの掛け算には、複数の⾒⽅ があります。 • このノートは、それらを可視化し、教育⽤ コンテンツとする試みです。 • それによって ... • ⾏列とベクトルの演算を直感的に⾏えるよう になります。 • その直感を、5つの⾏列分解法、などのコンセ プトの理解につなげることができます。 By Kenji Hiranabe with the kindest help of Prof. Gilbert Strang 3
- 4. ⽬次 • 4つの⾏列の⾒⽅ • 2つのベクトルの積 • ⾏列のベクトルの積 – 2つの⾒⽅ • ⾏列と⾏列の積 – 4つの⾒⽅ • 便利な応⽤パターン • 5つの⾏列分解 • 𝐶𝑅, 𝐿𝑈, 𝑄𝑅, 𝑄Λ𝑄!, 𝑈Σ𝑉! By Kenji Hiranabe with the kindest help of Prof. Gilbert Strang 4
- 5. = = = 3つの数からなる 2つの列ベクトル 2つの数からなる 3つの⾏ベクトル 6つの数1 つの⾏列 4つの⾏列の⾒⽅ 𝐴 = 𝑎!! 𝑎!" 𝑎"! 𝑎"" 𝑎#! 𝑎#" = | 𝒂 𝟏 | | 𝒂 𝟐 | = −𝒂! ∗ − −𝒂" ∗ − −𝒂# ∗ − 以降、太字で列ベクトル𝒂 𝟏、*を付けて⾏ベクトル𝒂" ∗ 、を表現する。 また、右肩にTをつけて転置ベクトル𝒂 𝑻や転置⾏列𝑨 𝑻を表現する。 𝐴 = 1 4 2 5 3 6 = 1 4 2 5 3 6 = 1 4 2 5 3 6 By Kenji Hiranabe with the kindest help of Prof. Gilbert Strang 5
- 6. = = =内積(スカラー) Rank1の⾏列 v1 = 1 2 3 𝑥 𝑦 = 𝑥 𝑦 2𝑥 2𝑦 3𝑥 3𝑦 2つのベクトルの積 1 2 3 𝑥! 𝑥" 𝑥# = 1 2 3 , 𝑥! 𝑥" 𝑥# = 𝑥! + 2𝑥" + 3𝑥# ２つの列ベクトル𝑎, 𝑏を𝑎𝑏! の順に掛けると、⾏ 列 (𝐴 = 𝑎𝑏! ) になる。 𝑎, 𝑏どちらも0でなければ、 この⾏列はRankが1になることが分かる。（各 ⾏は定数倍であり、各列も定数倍である） ２つの列ベクトルの内積(𝑎 ) 𝑏)は⾏列形 式では、𝑎! 𝑏 と表現され、1つのスカ ラーになる。 v2 By Kenji Hiranabe with the kindest help of Prof. Gilbert Strang 6
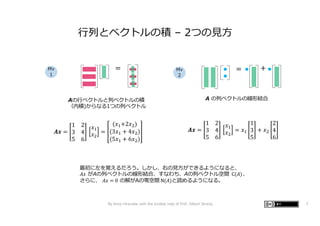
- 7. = = + ⾏列とベクトルの積 – 2つの⾒⽅ Aの⾏ベクトルと列ベクトルの積 （内積)からなる1つの列ベクトル A の列ベクトルの線形結合 𝑨𝒙 = 1 2 3 4 5 6 𝑥! 𝑥" = (𝑥!+2𝑥") (3𝑥! + 4𝑥") (5𝑥! + 6𝑥") 𝑨𝒙 = 1 2 3 4 5 6 𝑥! 𝑥" = 𝑥! 1 3 5 + 𝑥" 2 4 6 最初に左を覚えるだろう。しかし、右の⾒⽅ができるようになると、 𝐴𝑥 がAの列ベクトルの線形結合、すなわち、Aの列ベクトル空間 C(𝐴)、 さらに、 𝐴𝑥 = 0 の解がAの零空間 N(𝐴)と読めるようになる。 Mv 1 Mv 2 By Kenji Hiranabe with the kindest help of Prof. Gilbert Strang 7
- 8. ⾏列と⾏列の積 – 4つの⾒⽅ = = + 1 2 3 4 5 6 𝑥" 𝑦" 𝑥# 𝑦# = (𝑥"+2𝑥#) (𝑦"+2𝑦#) (3𝑥"+4𝑥#) (3𝑦"+4𝑦#) (5𝑥"+6𝑥#) (5𝑦"+6𝑦#) 1 2 3 4 5 6 𝑥" 𝑦" 𝑥# 𝑦# = 𝑨 𝒙 𝒚 = 𝑨 𝒙 𝑨𝒚 = = = = 1 2 3 4 5 6 𝑏"" 𝑏"# 𝑏#" 𝑏## = 𝒂 𝟏 𝒂 𝟐 𝒃 𝟏 ∗ 𝒃 𝟐 ∗ = 𝒂 𝟏 𝒃 𝟏 ∗ + 𝒂 𝟐 𝒃 𝟐 ∗ = 1 3 5 𝑏"" 𝑏"# + 2 4 6 𝑏#" 𝑏## = 𝑏"" 𝑏"# 3𝑏"" 3𝑏"# 5𝑏"" 5𝑏"# + 2𝑏#" 2𝑏## 4𝑏#" 4𝑏## 6𝑏#" 6𝑏## 結果の各列 𝑨𝒙, 𝑨𝒚 は、それぞれA の列ベクトルの線形結合 1 2 3 4 5 6 𝑥" 𝑦" 𝑥# 𝑦# = 𝒂 𝟏 ∗ 𝒂 𝟐 ∗ 𝒂 𝟑 ∗ 𝑿 = 𝒂 𝟏 ∗ 𝑿 𝒂 𝟐 ∗ 𝑿 𝒂 𝟑 ∗ 𝑿 ⾏列の積は、rank1の⾏列の和に分解される。 結果の各⾏は、⾏ベクトルの線形結合 結果の各要素は、⾏ベクトルと列ベクトルの内積 MM 1 MM 2 MM 3 MM 4 By Kenji Hiranabe with the kindest help of Prof. Gilbert Strang 8
- 9. 便利な応⽤パターン(1/3) 2 3 = 1 2 31 1 = 21 + 3 + 2 = 21 + 3 + 3 = 21 + 3 + 1 2 3 = 1 2 3 1 = +1 2 3+ 2 = +1 2 3+ 3 = +1 2 3+ MM 2 Mv 2 MM 3 右からの操作は、列に作⽤する。 この表現は、右の3つの線形結合を 1つの⾏列表現で表したものだとも ⾔える。 左からの操作は、⾏に作⽤する。 この表現は、右の3つの線形結合を 1つの⾏列表現で表したものだとも ⾔える。 P1 P2 using using By Kenji Hiranabe with the kindest help of Prof. Gilbert Strang 9
- 10. 便利な応⽤パターン(2/3) = = 𝐴𝐷 = 𝒂 𝟏 𝒂 𝟐 𝒂 𝟑 𝑑! 𝑑" 𝑑# = 𝑑! 𝒂 𝟏 𝑑" 𝒂 𝟐 𝑑" 𝒂 𝟐 𝐷𝐵 = 𝑑! 𝑑" 𝑑# 𝒃! ∗ 𝒃! ∗ 𝒃! ∗ = 𝑑! 𝒃! ∗ 𝑑! 𝒃! ∗ 𝑑! 𝒃! ∗ 対⾓⾏列を右から掛けると各列がスカラー倍 対⾓⾏列を左から掛けると各⾏がスカラー倍 これらを⽬に焼き付けると、さらに、、、、 P1ʼ P2ʼ By Kenji Hiranabe with the kindest help of Prof. Gilbert Strang 10
- 11. 便利な応⽤パターン(3/3) = + + スカラー倍された列ベクトルの線形結合(ベクトル漸化式やベクトル線形微分⽅程式で活⽤) = 𝑿𝑫𝒄 = 𝒙 𝟏 𝒙 𝟐 𝒙 𝟑 𝑑! 𝑑" 𝑑# 𝑐! 𝑐" 𝑐# = 𝑐! 𝑑! 𝒙 𝟏 + 𝑐" 𝑑" 𝒙 𝟐+ 𝑐# 𝑑# 𝒙 𝟑 𝑼𝚺𝑽 𝑻 = 𝒖 𝟏 𝒖 𝟐 𝒖 𝟑 𝜎! 𝜎" 𝜎# 𝒗! + 𝒗" + 𝒗# + = 𝜎! 𝒖! 𝒗! + + 𝜎" 𝒖" 𝒗" + + 𝜎# 𝒖# 𝒗# + + + Rank1⾏列の和(SVDや対称⾏列のスペクトル分解で活⽤) P3 P4 By Kenji Hiranabe with the kindest help of Prof. Gilbert Strang 11
- 12. 5つの⾏列分解 𝐴 = 𝐶𝑅 𝐴 = 𝐿𝑈 𝐴 = 𝑄𝑅 𝑆 = 𝑄Λ𝑄! 𝐴 = 𝑈Σ𝑉! By Kenji Hiranabe with the kindest help of Prof. Gilbert Strang 12 独⽴列⾏列と⾏簡約⾏列の積 (⾏ランク=列ランクを⽰す) LU分解=ガウスの消去法 QR分解=Gram-Schmidtの直⾏化 対称⾏列の固有値分解 どんな⻑⽅⾏列にも使える 特異値分解
- 13. 𝐴 = 𝐶𝑅 Aの列ベクトルを左から順に⾒て、独⽴なもののみ選び出していく。1,2列⽬は⽣き残り、3列⽬は1列⽬+2列 ⽬なので捨てる。残った２つの列ベクトルCを使ってAを復元すると、Rには階段⾏列が現れる。 これを、よく⾒て、⼆つの表現で表すと… ⻑⽅⾏列Aの⾏ランクと、Aの列ランクが等しいことを最も直感的に⽰す分解。 CはAの線形独⽴な列ベクトル。Rは⾏簡約階段⾏列(row reduced echelon form)となる。 2 = 1 2 3 2 3 5 = 1 2 2 3 1 0 1 0 1 1 1 | 𝒂 𝟏 | | 𝒂 𝟐 | | 𝒂 𝟑 | = | 𝒄 𝟏 | | 𝒄 𝟐 | 1 0 1 0 1 1 𝒂 𝟏 = 𝒄 𝟏, 𝒂 𝟐= 𝒄 𝟐, 𝒂 𝟑 = 𝒄 𝟏 + 𝒄 𝟐 −𝒂" ∗ − −𝒂# ∗ − = 1 2 2 3 −𝒓" ∗ − −𝒓# ∗ − 𝒂" ∗ = 𝒓" ∗ + 2𝒓# ∗ , 𝒂# ∗ = 2𝒓" ∗ + 3𝒓# ∗ 213 = 1 + 2 1 + 2 1 + 2 すべての列ベクトルはc1,c2の線形結合。すなわち、列ランク=dim C(A)=2。 = +1 2 1 2 1 2+ = すべての⾏ベクトルはr1,r2の線形結合。すなわち、⾏ランク=dim C(AT)=2。 𝑨 = 𝑪𝑹 P1 P2 using using By Kenji Hiranabe with the kindest help of Prof. Gilbert Strang 13
- 14. == + + 𝑨 = | 𝒍 𝟏 | −𝒖! ∗ − + 𝟎 𝟎 𝟎 𝟎 𝟎 𝑨 𝟐 ＝ | 𝒍 𝟏 | −𝒖! ∗ − + | 𝒍 𝟐 | −𝒖" ∗ − + 𝟎 𝟎 𝟎 𝟎 𝟎 𝟎 𝟎 𝟎 𝑨 𝟑 = 𝑳𝑼 𝐴 = 𝐿𝑈 Aの⾏1ベクトルと列1ベクトルでできるrank1⾏列を取り出し、サイズが1つ減った⾏列をA1とする。 この操作を再帰的に繰り返して、rank1の和に分解する。 = + + LU を逆向きに計算してAに戻すのは容易。 MM 4 ガウスの消去法は、⾏基本変形をAの左から掛けていくが、その逆⾏列がLである。 𝐿 𝑈 using By Kenji Hiranabe with the kindest help of Prof. Gilbert Strang 14 𝐴
- 15. == 𝐴 = 𝑄𝑅 Aの各列ベクトルを、Gram-Schmidtの直⾏化によってQの列ベクトルに直⾏化する。 その際の係数を逆にすることで、Rに上三⾓⾏列が作られる。 Gram-Schmidt の直⾏化。 2 31 | 𝒂 𝟏 | | 𝒂 𝟐 | | 𝒂 𝟑 | = | 𝒒 𝟏 | | 𝒒 𝟐 | | 𝒒 𝟑 | 𝑟"" 𝑟"# 𝑟"( 𝑟## 𝑟#( 𝑟(( 31 + 1 2 + 1 2 + 𝒂 𝟏 = 𝑟"" 𝒒 𝟏 𝒂 𝟐 = 𝑟"# 𝒒 𝟏 + 𝑟## 𝒒 𝟐 𝒂 𝟐 = 𝑟"( 𝒒 𝟏 + 𝑟#( 𝒒 𝟐 + 𝑟(( 𝒒 𝟑 𝑨 = 𝑸𝑹 P1 using By Kenji Hiranabe with the kindest help of Prof. Gilbert Strang 15 𝑄 𝑅𝐴 𝒂 𝟏 𝒂 𝟐 𝒂 𝟑
- 16. 𝑺 = 𝑸𝜦𝑸+= | 𝒒 𝟏 | | 𝒒 𝟐 | | 𝒒 𝟑 | 𝜆! 𝜆" 𝜆# −𝒒! + − −𝒒" + − −𝒒# + − =𝜆! | 𝒒 𝟏 | −𝒒! + − + 𝜆" | 𝒒 𝟐 | −𝒒" + − + 𝜆# | 𝒒 𝟑 | −𝒒# + − 𝑆 = 𝑄𝛬𝑄3 対称⾏列Sは、直⾏⾏列Qによって固有値の対⾓⾏列Λに対⾓化される。 さらに、これをRank1の射影⾏列の和に分解できる。（スペクトル分解） = 𝜆! 𝑷! + 𝜆" 𝑷 𝟐 + 𝜆# 𝑷 𝟑 対称⾏列Sの固有値分解。固有値はすべて実数であり、固有ベクトルは必ず互いに直⾏したものが取れる。 2 31 = + += 1 2 3 1 1 2 2 3 3 𝑺 = 𝑺 𝑻, 𝑸 𝑻 = 𝑸,𝟏 𝑷 𝟏 𝟐 = 𝑷 𝟐 𝟐 = 𝑷 𝟏 𝟐 = 𝑰 𝑷 𝟏 𝑷 𝟐 = 𝑷 𝟐 𝑷 𝟑 = 𝑷 𝟑 𝑷 𝟏 = 𝑶 P4 using By Kenji Hiranabe with the kindest help of Prof. Gilbert Strang 16 𝑄 𝛬𝑆 𝑄+ 𝜆! 𝒒 𝟏 𝒒! + 𝜆" 𝒒 𝟐 𝒒" + 𝜆# 𝒒 𝟑 𝒒# +
- 17. 𝐴 = 𝑈Σ𝑉+= | 𝒖 𝟏 | | 𝒖 𝟐 | | 𝒖 𝟑 | 𝜎! 𝜎" −𝒗! + − −𝒗" + − =𝜎! | 𝒖 𝟏 | −𝒗! + − + 𝜎" | 𝒖 𝟐 | −𝒗" + − 𝐴 = 𝑈Σ𝑉3 Aの⾏空間ℝ) の正規直交基底としてV、列空間 ℝ* の正規直交規定としてUをそれぞれうまく取ると、対 ⾓化される。これを特異値分解という。さらに、これをRank1の射影⾏列の和に分解できる。 = 𝜎! 𝒖 𝟏 𝒗! + + 𝜎" 𝒖 𝟐 𝒗" + Aが⼀般の⻑⽅⾏列の場合でも、特異値分解は必ず可能。 = += 1 1 2 2 2 31 1 2 𝑼,𝟏 = 𝑼 𝑻, 𝑽,𝟏 = 𝑽 𝑻 P4 using By Kenji Hiranabe with the kindest help of Prof. Gilbert Strang 17 𝑈 Σ𝐴 𝑉+ 𝜎! 𝒖 𝟏 𝒗! + 𝜎" 𝒖 𝟐 𝒗" +
- 18. 参照⽂献と 謝辞 • Linear Algebra for Everyone (⽇本語 来年期待) http://math.mit.edu/everyone/ • MIT OpenCourseWare 18.06 http://web.mit.edu/18.06/www/vi deos.shtml • A 2020 Vision of Linear Algebra https://ocw.mit.edu/resources/res -18-010-a-2020-vision-of-linear- algebra-spring-2020/ • マトリックスワールド https://anagileway.com/2020/09/ 29/matrix-world-in-linear-algebra- for-everyone/ • 4つの部分空間 Tシャツ https://anagileway.com/2020/06/ 04/prof-gilbert-strang-linear- algebra/ This work is inspired by Prof. Strangʼs books and lecture videos. I deeply appreciate his work, passion and personality. By Kenji Hiranabe with the kindest help of Prof. Gilbert Strang 18
- 19. Thank you for reading! Any comments or feedbacks are welcome to: Kenji Hiranabe (hiranabe@gmail.com) = 19