線形代数の視覚的理解 V1.1-Gストラング勉強会
- 2. ⽬次 • ⾏列の⾒⽅ – 4つ • ベクトルの積 – 2つ • ⾏列のベクトルの積 – 2つ • ⾏列と⾏列の積 – 4つ By Kenji Hiranabe with the kindest help of Prof. Gilbert Strang 2
- 3. = = = 3つの数からなる 2つの列ベクトル 2つの数からなる 3つの⾏ベクトル 6つの数 1 つの⾏列 ⾏列の⾒⽅ – 4つ 𝐴 = 𝑎!!𝑎!" 𝑎"!𝑎"" 𝑎#!𝑎#" = | 𝒂𝟏 | | 𝒂𝟐 | = −𝒂! ∗ − −𝒂" ∗ − −𝒂# ∗ − 以降、太字で列ベクトル𝒂𝟏、*を付けて⾏ベクトル𝒂" ∗ 、を表現する。 また、右肩にTをつけて転置ベクトル𝒂𝐓や転置⾏列𝑨𝐓を表現する。 𝐴 = 1 4 2 5 3 6 = 1 4 2 5 3 6 = 1 4 2 5 3 6 By Kenji Hiranabe with the kindest help of Prof. Gilbert Strang 3
- 4. = = = 内積(スカラー) Rank1の⾏列 v1 = 1 2 3 𝑥 𝑦 = 𝑥 𝑦 2𝑥 2𝑦 3𝑥 3𝑦 ベクトルの積 – 2つ 1 2 3 𝑥! 𝑥" 𝑥# = 1 2 3 , 𝑥! 𝑥" 𝑥# = 𝑥! + 2𝑥" + 3𝑥# 2つの列ベクトル𝒂, 𝒃を𝒂𝒃! の順に掛けると、⾏ 列 (𝐴 = 𝒂𝒃! ) になる。 𝒂, 𝒃どちらも0でなければ、 この⾏列はRankが1になることが分かる。(各 ⾏は定数倍であり、各列も定数倍である) 2つの列ベクトルの内積(𝒂 ) 𝒃)は⾏列形 式では、𝒂! 𝒃 と表現され、1つのスカ ラーになる。 v2 By Kenji Hiranabe with the kindest help of Prof. Gilbert Strang 4
- 5. 練習問題-1 By Kenji Hiranabe with the kindest help of Prof. Gilbert Strang 5 4 5 6 1 2 3 について v2 で計算し,Rank 1 (各列および各⾏が線形従属)を確かめよ.
- 6. = = + ⾏列とベクトルの積 – 2つ 𝐴 の⾏ベクトルと列ベクトルの積 (内積)からなる1つの列ベクトル 𝐴 の列ベクトルの線形結合 𝐴𝒙 = 1 2 3 4 5 6 𝑥! 𝑥" = (𝑥!+2𝑥") (3𝑥! + 4𝑥") (5𝑥! + 6𝑥") 𝐴𝒙 = 1 2 3 4 5 6 𝑥! 𝑥" = 𝑥! 1 3 5 + 𝑥" 2 4 6 最初に左を覚えるだろう。しかし、右の⾒⽅ができるようになると、 𝐴𝒙 が𝐴の列ベクトルの線形結合、すなわち、 𝐴の列ベクトル空間 𝐂(𝐴)、 さらに、 𝐴𝒙 = 0 の解がAの零空間 𝐍(𝐴)と読めるようになる。 Mv 1 Mv 2 By Kenji Hiranabe with the kindest help of Prof. Gilbert Strang 6
- 7. 練習問題-2 By Kenji Hiranabe with the kindest help of Prof. Gilbert Strang 7 𝐴𝒙 = 1 2 3 4 5 6 1 2 について,Mv1, Mv2 のやり⽅でそれぞれ計算し,同じ結果を確認せよ. Mv 1 1 2 3 4 5 6 1 2 Mv 2 1 2 3 4 5 6 1 2
- 8. By Kenji Hiranabe with the kindest help of Prof. Gilbert Strang 8
- 9. ⾏列と⾏列の積 – 4つ = 1 2 3 4 5 6 𝑥" 𝑦" 𝑥# 𝑦# = (𝑥"+2𝑥#) (𝑦"+2𝑦#) (3𝑥"+4𝑥#) (3𝑦"+4𝑦#) (5𝑥"+6𝑥#) (5𝑦"+6𝑦#) 1 2 3 4 5 6 𝑥" 𝑦" 𝑥# 𝑦# = 𝐴 𝒙 𝒚 = 𝐴𝒙 𝐴𝒚 = = 結果の各列 𝐴𝒙, 𝐴𝒚 は、それぞれ𝐴 の列ベクトルの線形結合 結果の各要素は、⾏ベクトルと列ベクトルの内積 MM 1 MM 2 By Kenji Hiranabe with the kindest help of Prof. Gilbert Strang 9
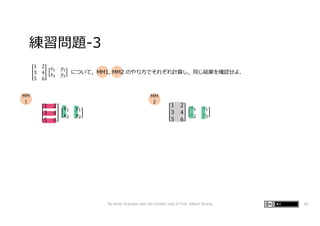
- 10. 練習問題-3 By Kenji Hiranabe with the kindest help of Prof. Gilbert Strang 10 1 2 3 4 5 6 𝑥" 𝑦" 𝑥# 𝑦# について,MM1, MM2 のやり⽅でそれぞれ計算し,同じ結果を確認せよ. MM 1 1 2 3 4 5 6 𝑥! 𝑦! 𝑥" 𝑦" 1 2 3 4 5 6 𝑥! 𝑦! 𝑥" 𝑦" MM 2
- 11. ⾏列と⾏列の積 – 4つ = + = = 1 2 3 4 5 6 𝑏"" 𝑏"# 𝑏#" 𝑏## = 𝒂𝟏 𝒂𝟐 𝒃𝟏 ∗ 𝒃𝟐 ∗ = 𝒂𝟏𝒃𝟏 ∗ + 𝒂𝟐𝒃𝟐 ∗ = 1 3 5 𝑏"" 𝑏"# + 2 4 6 𝑏#" 𝑏## = 𝑏"" 𝑏"# 3𝑏"" 3𝑏"# 5𝑏"" 5𝑏"# + 2𝑏#" 2𝑏## 4𝑏#" 4𝑏## 6𝑏#" 6𝑏## 1 2 3 4 5 6 𝑥" 𝑦" 𝑥# 𝑦# = 𝒂𝟏 ∗ 𝒂𝟐 ∗ 𝒂𝟑 ∗ 𝑋 = 𝒂𝟏 ∗ 𝑋 𝒂𝟐 ∗ 𝑋 𝒂𝟑 ∗ 𝑋 ⾏列の積は、rank 1の⾏列の和に分解される。 結果の各⾏は、⾏ベクトルの線形結合 MM 3 MM 4 By Kenji Hiranabe with the kindest help of Prof. Gilbert Strang 11
- 12. 練習問題-4 By Kenji Hiranabe with the kindest help of Prof. Gilbert Strang 12 1 2 3 4 5 6 1 1 1 2 について,MM4 のやり⽅で計算し,通常の計算(MM1)と同じ結果を確認せよ.
- 13. 便利な応⽤パターン – 3つ 2 3 = 1 2 3 1 1 = 2 1 + 3 + 2 = 2 1 + 3 + 3 = 2 1 + 3 + MM 2 Mv 2 右からの操作は、列に作⽤する。 この表現は、右の3つの線形結合を 1つの⾏列表現で表したものだとも ⾔える。 P1 using By Kenji Hiranabe with the kindest help of Prof. Gilbert Strang 13
- 14. 練習問題-4 By Kenji Hiranabe with the kindest help of Prof. Gilbert Strang 14 1 4 7 2 5 8 3 6 9 1 0 1 0 1 1 0 0 1 を P1 に従って計算し,各列の変化を観察せよ.
- 15. 1 2 3 = 1 2 3 1 = + 1 2 3 + 2 = + 1 2 3 + 3 = + 1 2 3 + MM 3 左からの操作は、⾏に作⽤する。 この表現は、右の3つの線形結合を 1つの⾏列表現で表したものだとも ⾔える。 P2 using By Kenji Hiranabe with the kindest help of Prof. Gilbert Strang 15 便利な応⽤パターン – 3つ
- 16. 練習問題-4 By Kenji Hiranabe with the kindest help of Prof. Gilbert Strang 16 1 0 0 0 1 0 1 1 1 1 4 7 2 5 8 3 6 9 を P2 に従って計算し,各⾏の変化を観察せよ.