Lesson 24: The Definite Integral (Section 4 version)

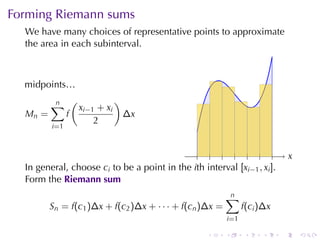
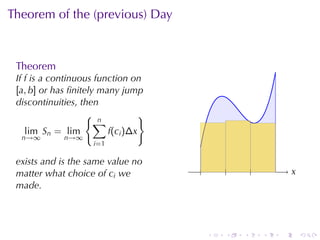
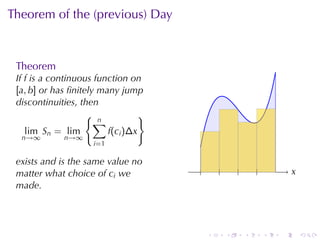
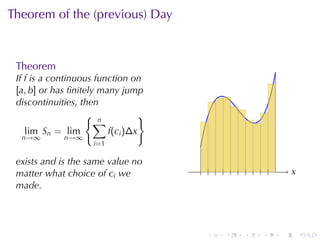
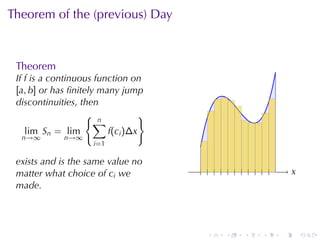
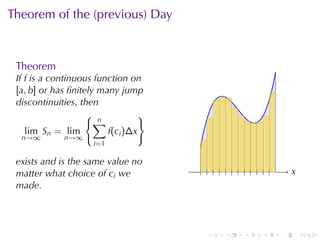
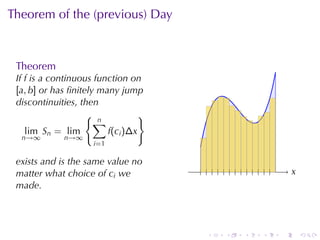
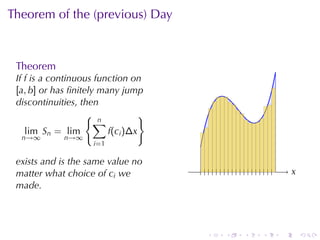
The document discusses the concept of the definite integral in calculus, emphasizing its definition as a limit and various properties. It describes methods to estimate the definite integral using Riemann sums with different choices of representative points, such as left endpoints, right endpoints, and midpoints. Additionally, it presents the theorem stating that if a function is continuous or has finitely many jump discontinuities on an interval, the limit of the Riemann sums will converge to the same value regardless of the chosen representative points.