Regularized Principal Component Analysis for Spatial Data
- 1. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Regularized Principal Component Analysis for Spatial Data Wen-Ting Wang Institute of Statistics, National Chiao Tung University January 25, 2017 Joint work with Hsin-Cheng Huang, Academia Sinica 1
- 2. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Outline 1 Background 2 Regularized Principal Component Analysis 3 Computation algorithm 4 Numerical Example 5 Summary 2
- 3. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Outline 1 Background 2 Regularized Principal Component Analysis 3 Computation algorithm 4 Numerical Example 5 Summary 3
- 4. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Background • Spatial processes of interest: {ηi(s); s ∈ D} ; i = 1, . . . , n – D ⊂ Rd – mean zero – common covariance function: Cη(s∗ , s) = Cov(ηi(s∗ ), ηi(s)) – η1(·), . . . , ηn(·): uncorrelated 4
- 5. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Background • Spatial processes of interest: {ηi(s); s ∈ D} ; i = 1, . . . , n – D ⊂ Rd – mean zero – common covariance function: Cη(s∗ , s) = Cov(ηi(s∗ ), ηi(s)) – η1(·), . . . , ηn(·): uncorrelated • Observed data at locations s1, . . . , sp ∈ D, Yi(sj) = ηi(sj) + ϵij; i = 1, . . . , n, j = 1, . . . , p – ϵij ∼ (0, σ2 ): white noise – ϵij and ηi(sj) are uncorrelated for any i, j 4
- 6. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Targets 1 Detect the dominant patterns (modes) of η1(·), . . . , ηn(·) – interpret the variability of spatial data physically 2 Estimate spatial covariance function Cη(·, ·) – no specific assumption (e.g., parametric form or stationarity) – spatial prediction (kriging) of {ηi(s); s ∈ D} 5
- 7. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Example: dominant patterns • Two dominant patterns (Deser, 2009) Basin-wide mode East-west dipole mode −0.04 −0.02 0.00 0.02 0.04 – Data: Indian Ocean sea surface temperature anomalies (Monthly average) – related to El Ninõ–Southern Oscillation (ENSO) 6
- 8. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Rank-K spatial model • Data: Yi(sj) = ηi(sj) + ϵij; i = 1, . . . , n, j = 1 . . . , p 7
- 9. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Rank-K spatial model • Data: Yi(sj) = K∑ k=1 ξikφk(sj) + ϵij; i = 1, . . . , n, j = 1 . . . , p – ξi1, . . . , ξiK ∼ (0, Λ); ΛK×K is positive-definite – φ1(·) . . . , φK (·): K unknown orthonormal functions – ξik uncorrelated with ϵij 8
- 10. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Rank-K spatial model • Data: Yi(sj) = K∑ k=1 ξikφk(sj) + ϵij; i = 1, . . . , n, j = 1 . . . , p – ξi1, . . . , ξiK ∼ (0, Λ); ΛK×K is positive-definite – φ1(·) . . . , φK (·): K unknown orthonormal functions – ξik uncorrelated with ϵij • Spatial covariance function: Cη(s∗ , s) = K∑ k=1 K∑ k′=1 λkk′ φk(s∗ )φk′ (s) – λkk′ : (k, k′ ) entry of Λ 8
- 11. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Goal • Find φ1(·), . . . , φK(·) to represent the dominant patterns. 9
- 12. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Goal • Find φ1(·), . . . , φK(·) to represent the dominant patterns. • Standard approach: Principal component analysis (PCA) 9
- 13. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Principal Component Analysis • p-dimensional data vector: Yi = (Yi(s1), . . . , Yi(sp))′ ∼ (0, Σ) • Idea: Find ϕ ∈ Rp with ϕ′ϕ = 1,which maximizes Var(ϕ′Yi) 10
- 14. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Principal Component Analysis • p-dimensional data vector: Yi = (Yi(s1), . . . , Yi(sp))′ ∼ (0, Σ) • Idea: Find ϕ ∈ Rp with ϕ′ϕ = 1,which maximizes Var(ϕ′Yi) • Spectral decomposition: Σ – eigenvalues: λ1 ≥ · · · ≥ λp – eigenvectors: ϕ1, . . . , ϕp 10
- 15. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Principal Component Analysis • p-dimensional data vector: Yi = (Yi(s1), . . . , Yi(sp))′ ∼ (0, Σ) • Idea: Find ϕ ∈ Rp with ϕ′ϕ = 1,which maximizes Var(ϕ′Yi) • Spectral decomposition: Σ – eigenvalues: λ1 ≥ · · · ≥ λp – eigenvectors: ϕ1, . . . , ϕp • Dominant patterns: ϕ1, . . . , ϕK (with λ1, . . . , λK large) 10
- 16. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Principal Component Analysis • Data matrix: Yn×p = (Y1, . . . , Yn)′ • Sample covariance matrix: S = Y ′Y /n • Spectral decomposition: S – sample eigenvalues: ˜λ1 ≥ · · · ≥ ˜λp – sample eigenvectors: ˜ϕ1, . . . , ˜ϕp • ˜ϕ1, . . . , ˜ϕK are estimates of ϕ1, . . . , ϕK 11
- 17. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Principal Component Analysis • Data matrix: Yn×p = (Y1, . . . , Yn)′ • Sample covariance matrix: S = Y ′Y /n • Spectral decomposition: S – sample eigenvalues: ˜λ1 ≥ · · · ≥ ˜λp – sample eigenvectors: ˜ϕ1, . . . , ˜ϕp • ˜ϕ1, . . . , ˜ϕK are estimates of ϕ1, . . . , ϕK • Problems: – high estimation variability: n is small or p is large → unstable and noisy patterns → weak physical interpretation – without spatial structure of ϕ 11
- 18. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Example: PCA : φ ~ −0.2 0.0 0.2 0.4 0.6 0.8 1.0 12
- 19. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Example: True : φ PCA : φ ~ −0.2 0.0 0.2 0.4 0.6 0.8 1.0 12
- 20. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Motivation To enhance the interpretablity, we implement PCA by incorporating 13
- 21. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Motivation To enhance the interpretablity, we implement PCA by incorporating 1 spatial structure of eigenvectors 13
- 22. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Motivation To enhance the interpretablity, we implement PCA by incorporating 1 spatial structure of eigenvectors 2 sparsity of eigenvectors 13
- 23. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Motivation To enhance the interpretablity, we implement PCA by incorporating 1 spatial structure of eigenvectors 2 sparsity of eigenvectors 3 orthogonality of eigenvectors 13
- 24. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Outline 1 Background 2 Regularized Principal Component Analysis 3 Computation algorithm 4 Numerical Example 5 Summary 14
- 25. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Quick review • Data Yi = (Yi(s1), . . . , Yi(sp))′; i = 1, . . . , n – Yi(sj) = K∑ k=1 ξikφk(sj) + ϵij; j = 1 . . . , p • φ1(·) . . . , φK (·): K unknown orthonormal functions • ξi1, . . . , ξiK ∼ (0, Λ); ΛK×K ≻ 0 • ϵij ∼ (0, σ2 ); ϵij: uncorrelated with ξik 15
- 26. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Quick review • Data Yi = (Yi(s1), . . . , Yi(sp))′; i = 1, . . . , n – Yi(sj) = K∑ k=1 ξikφk(sj) + ϵij; j = 1 . . . , p • φ1(·) . . . , φK (·): K unknown orthonormal functions • ξi1, . . . , ξiK ∼ (0, Λ); ΛK×K ≻ 0 • ϵij ∼ (0, σ2 ); ϵij: uncorrelated with ξik • Spatial covariance function: Cη(s∗ , s) = K∑ k=1 K∑ k′=1 λkk′ φk(s∗ )φk′ (s) – λkk′ : (k, k′ ) entry of Λ 15
- 27. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Quick review • Data Yi = (Yi(s1), . . . , Yi(sp))′; i = 1, . . . , n – Yi(sj) = K∑ k=1 ξikφk(sj) + ϵij; j = 1 . . . , p • φ1(·) . . . , φK (·): K unknown orthonormal functions • ξi1, . . . , ξiK ∼ (0, Λ); ΛK×K ≻ 0 • ϵij ∼ (0, σ2 ); ϵij: uncorrelated with ξik • Spatial covariance function: Cη(s∗ , s) = K∑ k=1 K∑ k′=1 λkk′ φk(s∗ )φk′ (s) – λkk′ : (k, k′ ) entry of Λ • Unknown parameters: φ1(·), . . . , φK(·), Λ, σ2 15
- 28. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary PCA (alternative version) • Data matrix: Yn×p = (Y1, . . . , Yn)′ • PCA : ˜Φ = arg min Φ:Φ′ Φ=IK ∥Y − Y ΦΦ′ ∥2 F – Φp×K = (ϕ1, . . . , ϕK ) with ϕjk = φj(sk) – ∥M∥2 F = n∑ i=1 p ∑ j=1 m2 ij 16
- 29. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Regularized PCA • Data matrix: Yn×p = (Y1, . . . , Yn)′ • Φp×K = (ϕ1, . . . , ϕK) with ϕjk = φj(sk) • Objective function ∥Y − Y ΦΦ′ ∥2 F subject to Φ′ Φ = IK 17
- 30. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Regularized PCA • Data matrix: Yn×p = (Y1, . . . , Yn)′ • Φp×K = (ϕ1, . . . , ϕK) • Objective function ∥Y − Y ΦΦ′ ∥2 F +τ1 K∑ k=1 J(φk) + τ2 K∑ k=1 p∑ j=1 |φk(sj)| subject to Φ′ Φ = IK – J(φk) = ∑ z1+···+zd=2 ∫ Rd ( ∂2 φk(s) ∂xz1 1 . . . ∂x zd d )2 ds • s = (x1, . . . , xd)′ 17
- 31. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Regularized PCA • Data matrix: Yn×p = (Y1, . . . , Yn)′ • Φp×K = (ϕ1, . . . , ϕK) • Objective function ∥Y − Y ΦΦ′ ∥2 F +τ1 K∑ k=1 J(φk) + τ2 K∑ k=1 p∑ j=1 |φk(sj)| subject to Φ′ Φ = IK – J(φk) = ∑ z1+···+zd=2 ∫ Rd ( ∂2 φk(s) ∂xz1 1 . . . ∂x zd d )2 ds • s = (x1, . . . , xd)′ – τ1: smoothness parameter – τ2: sparseness parameter 17
- 32. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Spatial PCA (SpatPCA) • J(φk) = ϕ′ kΩϕk – Ωp×p: determined only by s1, . . . , sp – Ref: Green and Silverman (1994) 18
- 33. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Spatial PCA (SpatPCA) • J(φk) = ϕ′ kΩϕk – Ωp×p: determined only by s1, . . . , sp – Ref: Green and Silverman (1994) • Proposal: SpatPCA ˆΦ = arg min Φ:Φ′ Φ=IK ∥Y − Y ΦΦ′ ∥2 F + τ1 K∑ k=1 ϕ′ kΩϕk + τ2 K∑ k=1 p∑ j=1 |ϕjk| 18
- 34. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Spatial PCA (SpatPCA) • J(φk) = ϕ′ kΩϕk – Ωp×p: determined only by s1, . . . , sp – Ref: Green and Silverman (1994) • Proposal: SpatPCA ˆΦ = arg min Φ:Φ′ Φ=IK ∥Y − Y ΦΦ′ ∥2 F + τ1 K∑ k=1 ϕ′ kΩϕk + τ2 K∑ k=1 p∑ j=1 |ϕjk| • As τ1 = τ2 = 0, ˆϕk is the k-th eigenvector of S. 18
- 35. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary SpatPCA: ˆφ1(·), . . . , ˆφK(·) • ( ˆφ1(·), . . . , ˆφK(·)) minimizes ∥Y − Y ΦΦ′ ∥2 F +τ1 K∑ k=1 J(φk) + τ2 K∑ k=1 p∑ j=1 |φk(sj)|, subject to Φ′ Φ = IK • ˆφk(·): smoothing spline based on ˆϕk ˆφk(s) = p∑ i=1 aig(∥s − si∥) + b0 + d∑ j=1 bjxj – s = (x1, . . . , xd)′ – g(r) = 1 16π r2 log r; if d = 2, Γ(d/2 − 2) 16πd/2 r4−d ; if d = 1, 3, – a = (a1, . . . , ap)′ and b = (b0, b1, . . . , bd)′ depend on ˆϕk 19
- 36. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Why considering two penalties? 20
- 37. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary 1D Example τ1 = 0 True PCA SpatPCA 21
- 38. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Case 1: ˆϕ as τ2 = 0 (only smoothness) τ1 = 0 True PCA SpatPCA 22
- 39. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Case 1: ˆϕ as τ2 = 0 (only smoothness) τ1 = 0.03 True PCA SpatPCA 23
- 40. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Case 1: ˆϕ as τ2 = 0 (only smoothness) τ1 = 0.09 True PCA SpatPCA 24
- 41. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Case 1: ˆϕ as τ2 = 0 (only smoothness) τ1 = 0.32 True PCA SpatPCA 25
- 42. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Case 1: ˆϕ as τ2 = 0 (only smoothness) τ1 = 3.81 True PCA SpatPCA 26
- 43. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Case 1: ˆϕ as τ2 = 0 (only smoothness) τ1 = 156.17 True PCA SpatPCA 27
- 44. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Case 1: ˆϕ as τ2 = 0 (only smoothness) τ1 = 6405.22 True PCA SpatPCA 28
- 45. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Case 1: ˆϕ as τ2 = 0 (only smoothness) τ1 = 25000 True PCA SpatPCA 29
- 46. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Case 2: ˆϕ as τ1 = 0 (only sparseness) τ2 = 0 True PCA SpatPCA 30
- 47. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Case 2: ˆϕ as τ1 = 0 (only sparseness) τ2 = 39 True PCA SpatPCA 31
- 48. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Case 2: ˆϕ as τ1 = 0 (only sparseness) τ2 = 82 True PCA SpatPCA 32
- 49. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Case 2: ˆϕ as τ1 = 0 (only sparseness) τ2 = 126 True PCA SpatPCA 33
- 50. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Case 2: ˆϕ as τ1 = 0 (only sparseness) τ2 = 212 True PCA SpatPCA 34
- 51. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Case 2: ˆϕ as τ1 = 0 (only sparseness) τ2 = 342 True PCA SpatPCA 35
- 52. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Case 2: ˆϕ as τ1 = 0 (only sparseness) τ2 = 472 True PCA SpatPCA 36
- 53. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Case 2: ˆϕ as τ1 = 0 (only sparseness) τ2 = 520 True PCA SpatPCA 37
- 54. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Case 3: ˆϕ as τ1 = τ2 τ1 = τ2 = 0 True PCA SpatPCA 38
- 55. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Case 3: ˆϕ as τ1 = τ2 τ1 = τ2 = 0.02 True PCA SpatPCA 39
- 56. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Case 3: ˆϕ as τ1 = τ2 τ1 = τ2 = 0.04 True PCA SpatPCA 40
- 57. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Case 3: ˆϕ as τ1 = τ2 τ1 = τ2 = 0.09 True PCA SpatPCA 41
- 58. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Case 3: ˆϕ as τ1 = τ2 τ1 = τ2 = 0.41 True PCA SpatPCA 42
- 59. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Case 3: ˆϕ as τ1 = τ2 τ1 = τ2 = 4.19 True PCA SpatPCA 43
- 60. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Case 3: ˆϕ as τ1 = τ2 τ1 = τ2 = 42.68 True PCA SpatPCA 44
- 61. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Case 3: ˆϕ as τ1 = τ2 τ1 = τ2 = 100 True PCA SpatPCA 45
- 62. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary 2D Example True : φ PCA : φ ~ −0.2 0.0 0.2 0.4 0.6 0.8 1.0 46
- 63. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Case 1: ˆϕ as τ2 = 0 (only smoothness) True : φ τ1 = 0 −0.2 0.0 0.2 0.4 0.6 0.8 1.0 47
- 64. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Case 1: ˆϕ as τ2 = 0 (only smoothness) True : φ τ1 = 0 −0.2 0.0 0.2 0.4 0.6 0.8 1.0 48
- 65. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Case 1: ˆϕ as τ2 = 0 (only smoothness) True : φ τ1 = 93 −0.2 0.0 0.2 0.4 0.6 0.8 1.0 49
- 66. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Case 1: ˆϕ as τ2 = 0 (only smoothness) True : φ τ1 = 201 −0.2 0.0 0.2 0.4 0.6 0.8 1.0 50
- 67. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Case 1: ˆϕ as τ2 = 0 (only smoothness) True : φ τ1 = 437 −0.2 0.0 0.2 0.4 0.6 0.8 1.0 51
- 68. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Case 1: ˆϕ as τ2 = 0 (only smoothness) True : φ τ1 = 2053 −0.2 0.0 0.2 0.4 0.6 0.8 1.0 52
- 69. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Case 1: ˆϕ as τ2 = 0 (only smoothness) True : φ τ1 = 20932 −0.2 0.0 0.2 0.4 0.6 0.8 1.0 53
- 70. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Case 1: ˆϕ as τ2 = 0 (only smoothness) True : φ τ1 = 213414 −0.2 0.0 0.2 0.4 0.6 0.8 1.0 54
- 71. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Case 1: ˆϕ as τ2 = 0 (only smoothness) True : φ τ1 = 5e+05 −0.2 0.0 0.2 0.4 0.6 0.8 1.0 55
- 72. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Case 2: ˆϕ as τ2 = 0 (only sparseness) True : φ τ2 = 0 −0.2 0.0 0.2 0.4 0.6 0.8 1.0 56
- 73. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Case 2: ˆϕ as τ2 = 0 (only sparseness) True : φ τ2 = 35 −0.2 0.0 0.2 0.4 0.6 0.8 1.0 57
- 74. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Case 2: ˆϕ as τ2 = 0 (only sparseness) True : φ τ2 = 42 −0.2 0.0 0.2 0.4 0.6 0.8 1.0 58
- 75. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Case 2: ˆϕ as τ2 = 0 (only sparseness) True : φ τ2 = 50 −0.2 0.0 0.2 0.4 0.6 0.8 1.0 59
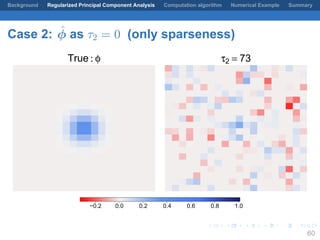
- 76. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Case 2: ˆϕ as τ2 = 0 (only sparseness) True : φ τ2 = 73 −0.2 0.0 0.2 0.4 0.6 0.8 1.0 60
- 77. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Case 2: ˆϕ as τ2 = 0 (only sparseness) True : φ τ2 = 127 −0.2 0.0 0.2 0.4 0.6 0.8 1.0 61
- 78. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Case 2: ˆϕ as τ2 = 0 (only sparseness) True : φ τ2 = 220 −0.2 0.0 0.2 0.4 0.6 0.8 1.0 62
- 79. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Case 2: ˆϕ as τ2 = 0 (only sparseness) True : φ τ2 = 270 −0.2 0.0 0.2 0.4 0.6 0.8 1.0 63
- 80. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Case 3: ˆϕ as τ1 = τ2 True : φ τ1 = τ2 = 0 −0.2 0.0 0.2 0.4 0.6 0.8 1.0 64
- 81. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Case 3: ˆϕ as τ1 = τ2 True : φ τ1 = τ2 = 33 −0.2 0.0 0.2 0.4 0.6 0.8 1.0 65
- 82. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Case 3: ˆϕ as τ1 = τ2 True : φ τ1 = τ2 = 38 −0.2 0.0 0.2 0.4 0.6 0.8 1.0 66
- 83. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Case 3: ˆϕ as τ1 = τ2 True : φ τ1 = τ2 = 43 −0.2 0.0 0.2 0.4 0.6 0.8 1.0 67
- 84. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Case 3: ˆϕ as τ1 = τ2 True : φ τ1 = τ2 = 55 −0.2 0.0 0.2 0.4 0.6 0.8 1.0 68
- 85. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Case 3: ˆϕ as τ1 = τ2 True : φ τ1 = τ2 = 81 −0.2 0.0 0.2 0.4 0.6 0.8 1.0 69
- 86. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Case 3: ˆϕ as τ1 = τ2 True : φ τ1 = τ2 = 118 −0.2 0.0 0.2 0.4 0.6 0.8 1.0 70
- 87. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Case 3: ˆϕ as τ1 = τ2 True : φ τ1 = τ2 = 136 −0.2 0.0 0.2 0.4 0.6 0.8 1.0 71
- 88. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary (τ1, τ2) selection • M-fold cross-validation: CV(τ1, τ2) = 1 M M∑ m=1 ∥Y (m) − Y (m) ˆΦ (−m) τ1,τ2 ( ˆΦ (−m) τ1,τ2 )′ ∥2 F 72
- 89. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary (τ1, τ2) selection • M-fold cross-validation: CV(τ1, τ2) = 1 M M∑ m=1 ∥Y (m) − Y (m) ˆΦ (−m) τ1,τ2 ( ˆΦ (−m) τ1,τ2 )′ ∥2 F – Partition {Y1, . . . , Yn} into M parts with equal (or roughly) size – Y (m) : the sub-matrix of Y corresponding to the m-th part – ˆΦ (−m) τ1,τ2 : the estimate of Φ for (τ1, τ2) based on Y (−m) • Y (−m) : remaining data, i.e., Y excluding Y (m) 72
- 90. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary (τ1, τ2) selection • M-fold cross-validation: CV(τ1, τ2) = 1 M M∑ m=1 ∥Y (m) − Y (m) ˆΦ (−m) τ1,τ2 ( ˆΦ (−m) τ1,τ2 )′ ∥2 F – Partition {Y1, . . . , Yn} into M parts with equal (or roughly) size – Y (m) : the sub-matrix of Y corresponding to the m-th part – ˆΦ (−m) τ1,τ2 : the estimate of Φ for (τ1, τ2) based on Y (−m) • Y (−m) : remaining data, i.e., Y excluding Y (m) • Find τ1 and τ2 which minimize CV(τ1, τ2) 72
- 91. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Estimation of spatial covariance function • Spatial covariance function: Cη(s∗ , s) = K∑ k=1 K∑ k′=1 λkk′ φk(s∗ )φk′ (s) • Till now, σ2 and Λ are unknown • Λ has K(K + 1)/2 unknown elements 73
- 92. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Estimation of spatial covariance function • Spatial covariance function: Cη(s∗ , s) = K∑ k=1 K∑ k′=1 λkk′ φk(s∗ )φk′ (s) • Λ has K(K + 1)/2 unknown elements • Apply the regularized method (Tzeng and Huang (2015)): ( ˆσ2 , ˆΛ ) = arg min (σ2,Λ):σ2≥0, Λ⪰0 { 1 2 S − ( ˆΦΛ ˆΦ ′ + σ2 I) 2 F + γ∥ ˆΦΛ ˆΦ ′ ∥∗ } – 1st term : goodness of fit based on var(Yi) = ΦΛΦ′ + σ2 I – ˆΦ: given SpatPCA estimate – γ ≥ 0 – ∥M∥∗ = tr((M′ M)1/2 ) 73
- 93. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Estimation of spatial covariance function • Spatial covariance function: Cη(s∗ , s) = K∑ k=1 K∑ k′=1 λkk′ φk(s∗ )φk′ (s) • Λ has K(K + 1)/2 unknown elements • Apply the regularized method (Tzeng and Huang (2015)): ( ˆσ2 , ˆΛ ) = arg min (σ2,Λ):σ2≥0, Λ⪰0 { 1 2 S − ( ˆΦΛ ˆΦ ′ + σ2 I) 2 F + γ∥ ˆΦΛ ˆΦ ′ ∥∗ } – 1st term : goodness of fit based on var(Yi) = ΦΛΦ′ + σ2 I – ˆΦ: given SpatPCA estimate – γ ≥ 0 – ∥M∥∗ = tr((M′ M)1/2 ) • Proposed estimate: ˆCη(s∗ , s) = K∑ k=1 K∑ k′=1 ˆλkk′ ˆφk(s∗ ) ˆφk′ (s) 73
- 94. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Solution of (σ2 , Λ) Closed-form solutions : • ˆΛ = ˆV diag ( ˆλ∗ 1, . . . , ˆλ∗ K ) ˆV ′ • ˆσ2 = 1 p − ˆL ( tr(S) − ˆL∑ k=1 ( ˆdk − γ ) ) ; if ˆd1 > γ, 1 p (tr(S)) ; if ˆd1 ≤ γ , – ˆV diag( ˆd1, . . . , ˆdK ) ˆV ′ is the eigen-decomposition of ˆΦ ′ S ˆΦ with ˆd1 ≥ · · · ≥ ˆdK – ˆL = max { L : ˆdL − γ > 1 p−L ( tr(S) − ∑L k=1( ˆdk − γ) ) , L = 1, . . . , K } – ˆλ∗ k = max( ˆdk − ˆσ2 − γ, 0); k = 1, . . . , K. 74
- 95. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary γ selection Selection of γ by minimizing the CV criterion: CV2(γ) = 1 M M∑ m=1 S(m) − ˆΦ ˆΛ (−m) γ ˆΦ ′ − (ˆσ2 γ)(−m) I 2 F • Partition Y into M parts, Y (1), . . . , Y (M) • S(m): sample covariance matrix associated with Y (m) • Y (−m): remaining data • (( ˆσ2 γ )(−m) , ˆΛ (−m) γ ) : estimate of (σ2, Λ) based on Y (−m) 75
- 96. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Outline 1 Background 2 Regularized Principal Component Analysis 3 Computation algorithm 4 Numerical Example 5 Summary 76
- 97. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Computation • Original optimization problem min Φ ∥Y − Y ΦΦ′ ∥2 F + τ1 K∑ k=1 ϕ′ iΩϕk + τ2 K∑ k=1 p∑ j=1 |ϕjk|, subject to Φ′ Φ = IK • Difficulties: orthogonal constraint and ℓ1 norm penalty 77
- 98. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Computation • Original optimization problem min Φ ∥Y − Y ΦΦ′ ∥2 F + τ1 K∑ k=1 ϕ′ iΩϕk + τ2 K∑ k=1 p∑ j=1 |ϕjk|, subject to Φ′ Φ = IK • Difficulties: orthogonal constraint and ℓ1 norm penalty • Alternating direction method of multipliers (ADMM) – Gabay and Mercier (1976), Boyd, et. al. (2010). – Idea: original optimization problem → several easy subproblems 77
- 99. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Alternating direction method of multipliers • Equivalent problem (ADMM form): min Φ,Q,R ∥Y − Y ΦΦ′ ∥2 F + τ1 K∑ k=1 ϕ′ iΩϕk + τ2 K∑ k=1 p∑ j=1 |rjk| , subject to Q′Q = IK and Φ = Q = R 78
- 100. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Alternating direction method of multipliers • Equivalent problem (ADMM form): min Φ,Q,R ∥Y − Y ΦΦ′ ∥2 F + τ1 K∑ k=1 ϕ′ iΩϕk + τ2 K∑ k=1 p∑ j=1 |rjk| , subject to Q′Q = IK and Φ = Q = R • Augmented Lagrangian function: L(Φ, Q, R, Γ1, Γ2) =∥Y − Y ΦΦ′ ∥2 F + τ1 K∑ k=1 ϕ′ iΩϕk + τ2 K∑ k=1 p∑ j=1 |rjk| + tr(Γ′ 2(Φ − R)) + ρ 2 ∥Φ − R∥2 F + tr(Γ′ 1(Φ − Q)) + ρ 2 ∥Φ − Q∥2 F subject to Q′Q = IK – Γ1, Γ2:Lagrange multipliers; some ρ > 0 78
- 101. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Algorithm:at the ℓ-th iteration Φ(ℓ+1) = arg min Φ L ( Φ, Q(ℓ) , R(ℓ) , Γ (ℓ) 1 , Γ (ℓ) 2 ) Q(ℓ+1) = arg min Q:Q′Q=IK L ( Φ(ℓ+1) , Q, R(ℓ) Γ (ℓ) 1 , Γ (ℓ) 2 ) R(ℓ+1) = arg min R L ( Φ(ℓ+1) , Q(ℓ+1) , R, Γ (ℓ) 1 , Γ (ℓ) 2 ) Γ (ℓ+1) 1 = Γ (ℓ) 1 + ρ ( Φ(ℓ+1) − Q(ℓ+1) ) Γ (ℓ+1) 2 = Γ (ℓ) 2 + ρ ( Φ(ℓ+1) − R(ℓ+1) ) 79
- 102. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Algorithm:at the ℓ-th iteration Φ(ℓ+1) = 1 2 (τ1Ω + ρIp − Y ′ Y )−1 { ρ ( Q(ℓ) + R(ℓ) ) − Γ1 − Γ2 } Q(ℓ+1) = U(ℓ) ( V (ℓ) )′ R(ℓ+1) = 1 ρ Sτ2 ( ρΦ(ℓ+1) + Γ (ℓ) 1 ) Γ (ℓ+1) 1 = Γ (ℓ) 1 + ρ ( Φ(ℓ+1) − Q(ℓ+1) ) Γ (ℓ+1) 2 = Γ (ℓ) 2 + ρ ( Φ(ℓ+1) − R(ℓ+1) ) • U(ℓ)D(ℓ) ( V (ℓ) )′ = Φ(ℓ+1) + 1 ρ Γ (ℓ) 2 (SVD) • Sτ (S) = {sign(sik) max(|sik| − τ, 0)} 80
- 103. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Algorithm:at the ℓ-th iteration Φ(ℓ+1) = 1 2 (τ1Ω + ρIp − Y ′ Y )−1 { ρ ( Q(ℓ) + R(ℓ) ) − Γ1 − Γ2 } Q(ℓ+1) = U(ℓ) ( V (ℓ) )′ R(ℓ+1) = 1 ρ Sτ2 ( ρΦ(ℓ+1) + Γ (ℓ) 1 ) Γ (ℓ+1) 1 = Γ (ℓ) 1 + ρ ( Φ(ℓ+1) − Q(ℓ+1) ) Γ (ℓ+1) 2 = Γ (ℓ) 2 + ρ ( Φ(ℓ+1) − R(ℓ+1) ) • U(ℓ)D(ℓ) ( V (ℓ) )′ = Φ(ℓ+1) + 1 ρ Γ (ℓ) 2 (SVD) • Sτ (S) = {sign(sik) max(|sik| − τ, 0)} • All subproblems have closed-form solutions. 80
- 104. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Outline 1 Background 2 Regularized Principal Component Analysis 3 Computation algorithm 4 Numerical Example 5 Summary 81
- 105. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Example: Artificial Sea Surface Temperature Data • Data settings: Yi(sj) = ξi1φ1(sj) + ξi2φ2(sj) + ϵij; – j = 1, . . . , p = 2780, i = 1, . . . , n = 60 – s1, . . . , s2780: located in the Indian Ocean – ξi1 ∼ N(0, 101.7), ξi2 ∼ N(0, 17.1), cov(ξi1, ξi2) = 0 – ϵij ∼ N(0, 1) – (τ1, τ2): selected by 5-fold CV φ1(s) φ2(s) −0.04 −0.02 0.00 0.02 0.04 82
- 106. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Result I: φ1(s) True PCA SpatPCA −0.04 −0.02 0.00 0.02 0.04 83
- 107. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Result I: φ2(s) True PCA SpatPCA −0.04 −0.02 0.00 0.02 0.04 84
- 108. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Result II: Performance • Loss function: Loss( ˆCη) = p∑ i=1 p∑ j=1 ( ˆCη(si, sj) − Cη(si, sj) )2 • 50 replications – γ: selected by 5-fold CV 85
- 109. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Result II: Performance • Loss function: Loss( ˆCη) = p∑ i=1 p∑ j=1 ( ˆCη(si, sj) − Cη(si, sj) )2 • 50 replications – γ: selected by 5-fold CV • Boxplot: q q q 0 5000 10000 15000 PCA SpatPCA 85
- 110. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Example: 8-hour average ozone data • Region: midwestern US • Number of effective sites: 67 (irregular locations) • Number of time points: 89 days (June 3 through August 31, 1987) • At each sites, time-series is linearly detrended −93 −83 3744 longitude latitude illinois indiana iowa kentucky michigan:south missouri ohio wisconsin 86
- 111. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Result I: φ1(s) PCA + interpolation SpatPCA 0.00 0.05 0.10 0.15 0.20 87
- 112. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Outline 1 Background 2 Regularized Principal Component Analysis 3 Computation algorithm 4 Numerical Example 5 Summary 88
- 113. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Summary SpatPCA: • higher-dimensional analysis → (low-dimensional) structure • with the smoothness and sparseness penalties • enhance physical interpretation 89
- 114. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Summary SpatPCA: • higher-dimensional analysis → (low-dimensional) structure • with the smoothness and sparseness penalties • enhance physical interpretation • non-stationary spatial covariance function • can cope with irregular locations 89
- 115. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Summary SpatPCA: • higher-dimensional analysis → (low-dimensional) structure • with the smoothness and sparseness penalties • enhance physical interpretation • non-stationary spatial covariance function • can cope with irregular locations • simple and efficient algorithm • R package: SpatPCA – CRAN: https://cran.r-project.org/web/packages/SpatPCA/index.html – GitHub: https://github.com/egpivo/SpatPCA 89
- 116. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Background Regularized Principal Component Analysis Computation algorithm Numerical Example Summary Thanks for your attention! 90