Stat prob07 probabilitytheory_counting
Download as PPT, PDF3 likes1,371 views
Dokumen tersebut membahas tentang konsep-konsep dasar probabilitas seperti populasi dan sampel, ruang sampel dan titik sampel, keluaran dan kejadian, variabel acak, serta metode penghitungan probabilitas menggunakan permutasi, kombinasi, dan contoh-contoh penerapannya seperti dadu dan poker.
Stat prob07 probabilitytheory_counting
- 1. PROBABILITAS : Permutasi & Kombinasi ARIF RAHMAN 1
- 2. Populasi dan Sampel Populasi atau semesta (universe) adalah set lengkap observasi yang menjadi perhatian peneliti. Sampel (sample) adalah sejumlah observasi yang diambil dari populasi Sebaran sampel mengikuti pola distribusi populasi. 2
- 4. Ruang Sampel dan Titik Sampel Ruang sampel (sample space) adalah satu set lengkap semua keluaran yang mungkin terjadi dalam populasi. Titik sampel (sample point) adalah setiap keluaran yang menjadi elemen atau anggota ruang sampel. Ruang sampel dapat dirinci titik sampelnya, atau menggunakan interval atau pernyataan (statement / rule) jika terlalu banyak. 4
- 5. Ruang Sampel dan Titik Sampel Berdasarkan prinsip kesempatan yang sama (equally likely) bagi setiap anggota populasi untuk terpilih sebagai sampel, maka dalam ruang sampel S dengan anggota sejumlah n, probabilitas setiap titik sampel adalah sama yaitu : p1= p2= ... = pn= 1/n 5
- 6. Ruang Sampel dan Titik Sampel Dengan setiap anggota populasi mempunyai peluang yang sama terpilih sebagai sampel, secara acak pengambilan sampel sejumlah n dari populasi sejumlah N, mempunyai ragam ruang sampel sebanyak : N! / (n.(N-n)!) Sehingga probabilitas memperoleh ruang sampel tertentu adalah : (n.(N-n)!) / N! 6
- 7. Ruang Sampel dan Titik Sampel Untuk memprediksikan ruang sampel dan probabilitas titik sampel perlu memperhatikan metode pengambilan sampel berdasarkan : Banyaknya populasi Populasi terbatas Populasi tak hingga (sangat besar) Status sampel setelah diambil Pengambilan dengan pengembalian Pengambilan tanpa pengembalian 7
- 8. Ruang Sampel dan Titik Sampel 8 -1 -1 -1 N-n+2 N-n+1N-n+3N N-1 N-2 -1 -1 -1 p1(x) ≠ p2(x) ≠ p3(x) ≠ ... ≠ pn-2(x) ≠ pn-1(x) ≠ pn(x) -1 -1 -1 N NNN N N -1 -1 -1 p1(x) = p2(x) = p3(x) = ... = pn-2(x) = pn-1(x) = pn(x) Tanpa Pengembalian (without replacement) Dengan Pengembalian (with replacement)
- 9. Keluaran dan Kejadian Keluaran (outcome) adalah fakta hasil pengumpulan data dalam observasi ataupun eksperimen Kejadian (event) adalah peristiwa yang termasuk dalam keluaran-keluaran yang mungkin (possible outcomes) terjadi saat pengumpulan data. 9
- 10. Keluaran dan Kejadian Kejadian E menjadi himpunan bagian dari ruang sampel S. Probabilitas kejadian E dalam ruang sampel S adalah sebanding dengan banyaknya titik sampel dalam kejadian E. P(E) = N(E) / n 10
- 11. Variabel Acak Variabel acak (random variable) adalah suatu nilai bersifat acak dalam numerik (format angka diskrit atau kontinyu) atau nonnumerik yang menandai keluaran dalam ruang sampel tertentu (finite atau infinite). Variabel acak dinotasikan dengan huruf kapital miring (misal : X). Sedangkan nilai variabel acak dinotasikan dengan huruf kecil miring (misal : x). 11
- 12. Variabel Acak Probabilitas variabel acak adalah frekuensi relatif titik sampel elemen kejadian E dalam ruang sampel S. Aproksimasi penghitungan banyaknya anggota dari keluaran-keluaran yang mungkin (possible outcomes) baik dalam ruang sampel dan kejadian berkaitan dengan permutasi dan kombinasi. 12
- 13. Metode Penghitungan Diagram pohon (tree diagram) dan Prinsip multiplikasi (multiplication rule) Permutasi dan Kombinasi 13
- 14. Prinsip Multiplikasi Jika operasi pertama dapat dilakukan dengan n1 cara, dan untuk setiap cara tersebut berkaitan (dilanjutkan) dengan operasi kedua yang dapat dilakukan dengan n2 cara, maka kedua operasi tersebut dapat dilakukan dalam n1.n2 cara. ... 14
- 15. Prinsip Multiplikasi ... Jika operasi pertama dapat dilakukan dengan n1 cara, dan operasi kedua dapat dilakukan dengan n2 cara, dan seterusnya hingga operasi ke-k dapat dilakukan dengan nk cara, sehingga secara simultan rangkaian k operasi tersebut dapat dilakukan dengan n1.n2.···.nk cara. 15
- 16. Diagram Pohon Pelemparan Koin Tiga Trial Ruang sampel S = {GGG, GGA, GAG, GAA, AGG, AGA, AAG, AAA} 16 Lemparan ke-1 Lemparan ke-2 Lemparan ke-3 G G G A A G A A G G A A G A
- 17. Diagram Pohon Tiga Operasi (Atribut) Berbeda n1.n2.n3 = 2 x 2 x 3 = 12 17 X A α XAα β XAβ γ XAγ B α XBα β XBβ γ XBγ Y A α YAα β YAβ γ YAγ B α YBα β YBβ γ YBγ
- 18. Permutasi Permutasi (permutation) adalah susunan seluruh atau sebagian elemen himpunan objek yang berbeda-beda. Permutasi mengestimasi banyaknya susunan dengan r anggota yang diambil dari n objek yang berbeda dengan memperhatikan urutannya. 18
- 19. Permutasi Menggunakan notasi nPr atau Pr n di mana : n : banyaknya macam objek r : banyaknya tempat dalam susunan. dengan r < n. 19 )!( ! rn n Pn r − =
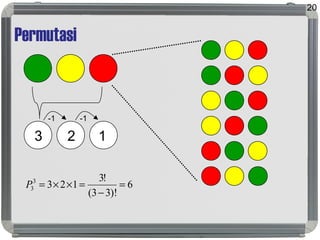
- 20. Permutasi 20 6 )!33( !3 1233 3 = − =××=P 3 2 1 -1 -1
- 21. Permutasi 21 60 )!35( !5 3455 3 = − =××=P 5 4 3 -1 -1
- 22. 22
- 23. Kombinasi Kombinasi (combination) adalah susunan seluruh atau sebagian elemen himpunan objek yang berbeda-beda dengan pembedaan susunan hanya berdasarkan perbedaan isinya paling tidak satu objek. Kombinasi mengestimasi banyaknya susunan dengan r anggota yang diambil dari n objek yang berbeda tanpa memperhatikan urutan 23
- 24. Kombinasi Menggunakan notasi nCr , Cr n atau (r n ) di mana : n : banyaknya macam objek r : banyaknya tempat dalam susunan. dengan r < n. 24 ! )!(! ! r P P P rnr n r n n r r r n r == − =
- 25. Kombinasi 25 1 )!33(!3 !3 6 123 3 3 = − = ×× = 3 2 1 -1 -1 Dianggap sama tak berbeda 6
- 27. 27
- 28. Permutasi Siklik Permutasi siklik atau lingkar (circular permutation) adalah susunan seluruh elemen himpunan objek yang berbeda- beda dalam bentuk melingkar. di mana : n : banyaknya macam objek dan banyaknya tempat dalam susunan melingkar. 28 )!1( ! −== n n n Pn n
- 30. Permutasi Objek Sama Permutasi objek sama (distinct permutation) adalah susunan seluruh elemen himpunan objek yang terdiri dari beberapa kelompok objek yang sama. di mana : n : banyaknya macam objek n1,...nk : banyaknya objek dalam masing-masing kelompok. dengan Σni = n. 30 ∏= == k i i k n n n n nnn n P 1 21 ! ! !.!.!. !
- 31. Permutasi Objek Sama 31 20 !1!1!3 !55 5 = ⋅⋅ =P 1 1 1 G1 G2 G3 Y1 R1 2 3 1 1 13 2 2 1 11 3 2 1 13 1 3 1 11 2 3 1 12 1
- 32. Kombinasi Partisi Kombinasi partisi (partition combination) adalah susunan seluruh elemen himpunan objek yang dipecah menjadi beberapa bagian (cell). di mana : n : banyaknya macam objek n1,...nk : banyaknya objek dalam setiap bagian. dengan Σni = n. 32 ∏= == k i i kk n n nnn n nnn n 1 2121 ! ! !.!.!. ! ,,
- 34. Kombinasi Objek Sama Kombinasi objek sama (distinct combination) adalah susunan seluruh elemen himpunan objek yang diambil dari bagian beberapa kelompok objek yang sama di mana : N1,...Nk : banyaknya seluruh objek di setiap kelompok. n1,...nk : banyaknya objek bagian setiap kelompok. dengan Σni = n, ΣNi = N, dan ni < Ni 34 = k k k k n N n N n N nnn NNN 2 2 1 1 21 21 . ,, ,,
- 35. Probabilitas Dadu 35 P(1)=P(2)=P(3)=P(4)=P(5)=P(6)=1/6 1 2 3 4 5 6 1 2 3 4 5 6 7 2 3 4 5 6 7 8 3 4 5 6 7 8 9 4 5 6 7 8 9 10 5 6 7 8 9 10 11 6 7 8 9 10 11 12
- 36. Probabilitas Dadu 36 P(1)=P(2)=P(3)=P(4)=P(5)=P(6)=1/6 P(1)=P(6)=1/36 P(2)=P(5)=3/36 P(3)=P(4)=5/36 P(1)=P(6)= 1/216 P(2)=P(5)=10/216 P(3)=P(4)=25/216 P(1)=P(6)= 1/7776 P(2)=P(5)=126/7776 P(3)=P(4)=651/7776
- 37. Probabilitas Poker 37 Royal Flush – Top 5 cards in a suit Straight Flush – 5 sequential cards in the same suit suit 4 of a kind – plus any other card Full House – 3 of one kind, 2 of another. (Also called a “boat.”) Flush – 5 cards in a suit, not sequential Straight – 5 cards in a numerical row, not the same suit P(2)=P(3)=...=P(J)=P(Q)=P(K)=P(A)=4/52 P(♠)=P(♣)=P(♥)=P(♦)=13/52 P(2♠)=...=P(A♦)=1/52
- 38. Probabilitas Poker 38 -------------------------------------------------------------------------- Poker Hand Different Combinations Probability Odds Against Royal Straight Flush 4 .0000015391 649,729:1 Other Straight Flush 36 .0000138517 72,193:1 Four of a kind 624 .0002400960 4,164:1 Full House 3,744 .0014405762 693:1 Flush 5,108 .0019654015 508:1 Straight 10,200 .0039246468 254:1 Three of a kind 54,912 .0211284514 46:1 Two Pairs 123,552 .0475390156 20:1 One Pair 1,098,240 .4225690276 1.4:1 High card only (None of above) 1,302,540 .5011773940 1:1 Total 2,598,960 1.0000000000 -------------------------------------------------------------------------- 000000385,0 1084769,3 960.598.2 1 5 52 1 )poker( 7 = ×= = = − P
- 39. Probabilitas Poker 39 960.598.2 5 52 )sampelruang( = =N 4sama}jenis);AK,Q,J,10,{()FlushRoyal( ==N 3649sama}jenis);KQ,J,,10,9(),...,A,2,3,4,5{()FlushStraight( =×==N 108.5)FlushStraight()FlushRoyal( !5 )910111213(4 )Flush( =−− ××××× = NNN ( ) 200.10)FlushStraight()FlushRoyal()44444(10)Straight( =−−×××××= NNN 540.302.1200.10108.5364888.317.1 )Straight()Flush()FlushStraight()FlushRoyal( !5 )1652()1252()852()452(52 )CardHigh( =−−−−= −−−− −×−×−×−× = NNNN N S RF Straight Flush Straight Flush different numbers
- 40. Probabilitas Poker 40 960.598.2 5 52 )sampelruang( = =N 624)452( 4 4 13)kindaofFour( = −× ×=N 912.54 !2 )852()452( 3 4 13)kindaofThree( = −×− × ×=N 240.098.1 !3 )1252()852()452( 2 4 13)pairOne( = −×−×− × ×=N
- 41. Probabilitas Poker 41 960.598.2 5 52 )sampelruang( = =N 552.123)852( !2 2 4 12 2 4 13 )pairsTwo( = −× ×× × =N 744.3 2 4 12 3 4 13)HouseFull( = ×× ×=N
- 42. Roulette Wheel 42 18 Red numbers 18 Black numbers 2 Green numbers (0,00) P(Black)=P(Red)=18/38 P(1)=P(2)=...=P(36)=P(0)=P(00) =1/38
- 44. Roulette Wheel 44 Bet name Winning spaces Payout 0 0 37 to 1 00 00 37 to 1 Straight up Any single number 37 to 1 Row 00 0, 00 36 to 2 Split any two adjoining numbers vertical or horizontal 36 to 2 Basket 0, 1, 2 or 00, 2, 3 or 0, 00, 2 35 to 3 Street any three numbers horizontal 35 to 3 Corner any four adjoining numbers in a block 34 to 4 Top line 0, 00, 1, 2, 3 33 to 5 Six line any six numbers from two horizontal rows 32 to 6 1st column 1, 4, 7, 10, 13, 16, 19, 22, 25, 28, 31, 34 26 to 12 2nd column 2, 5, 8, 11, 14, 17, 20, 23, 26, 29, 32, 35 26 to 12 3rd column 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36 26 to 12 1st dozen 1 through 12 26 to 12 2nd dozen 13 through 24 26 to 12 3rd dozen 25 through 36 26 to 12 Snake 1, 5, 9, 12, 14, 16, 19, 23, 27, 30, 32, 34 26 to 12 Odd 1, 3, 5, ..., 35 20 to 18 Even 2, 4, 6, ..., 36 20 to 18 Red 1, 3, 5, 7, 9, 12, 14, 16, 18, 19, 21, 23, 25, 27, 30, 32, 34, 36 20 to 18 Black 2, 4, 6, 8, 10, 11, 13, 15, 17, 20, 22, 24, 26, 28, 29, 31, 33, 35 20 to 18 1 to 18 (Low) 1, 2, 3, ..., 18 20 to 18 19 to 36 (High) 19, 20, 21, ..., 36 20 to 18
- 45. Formasi Barisan 45 A B C D E F G H I J K A B C D E F G H I J K A B C D E F G H I J K D C B A G F E K J I H D C B A G F E K J I H
- 46. Formasi Barisan Banyaknya susunan = (Permutasi 11 orang diambil 11 orang) / (Kombinasi susunan yang sebenarnya sama) 46 4 !11 =S
- 47. Permainan Bola Voli 47 A B C D E F G H I J K L M N O P Q R 1 6 5 2 3 4 5 6 1 4 3 2
- 48. Permainan Bola Voli Banyaknya susunan = (Kombinasi 18 orang diambil 12 pemain) X (Kombinasi Partisi 12 pemain menjadi dua tim) X (Permutasi siklik 6 pemain di tim 1) X (Permutasi siklik 6 pemain di tim 2) 48 )!16)!.(16.( 6,6 12 . 12 18 −− =S
- 49. Permainan Bridge Patkawan 49 1 2 3 4 1 4 3 2 A B C D E F G H Closed Room Open Room U
- 50. Permainan Bridge Patkawan Banyaknya susunan = (Permutasi 8 orang diambil 8 orang) 50 !8=S
- 51. 51 Terima kasih ...Terima kasih ... ... Ada pertanyaan ???... Ada pertanyaan ???