![Solution (continued):
2
2
2
3.80 4.00
1271.20 1261.50 4.00 4.00 1.5 1.5
2 2 2 2
0.975 9.85 8.775 0
4
2
0.975
9.85
8.775
9.1152 911.52'
L L L
L
L L
b b ac
x
a
a
b
c
L stations
+
= + + − + + +
− + =
− ± −
=
=
= −
=
= =
Check by substituting x = [(9.1152/2)+1.5] stations into the
elevation equation to see if it matches a value of 1271.20’](https://image.slidesharecdn.com/31430049-vertical-curves-190131144620/85/vertical-curves-23-320.jpg)
vertical-curves
- 2. Profiles: Curve a: Crest Vertical Curve (concave downward) Curve b: Sag Vertical Curve (concave upward) Tangents: Constant Grade (Slope)
- 4. Terms: BVC: Beginning of Vertical Curve aka PVC V: Vertex aka PVI EVC: End of Vertical Curve aka PVT g1: percent grade of back tangent g2: percent grade of forward tangent L: curve length (horizontal distance) in feet or stations x: horizontal distance from any point on the curve to the BVC
- 5. Equations: r = (g2 – g1)/L where: g2 & g1 - in percent (%) L – in stations and Y = YBVC + g1x + (r/2)x2 where: YBVC – elevation of the BVC in feet
- 6. Example: Equal-Tangent Vertical Curve Given the information show below, compute and tabulate the curve for stakeout at full 100’ stations.
- 7. Solution: L = STAEVC – STABVC L = 4970 – 4370 = 600’ or 6 full stations r = (g2 – g1) / L r = (-2.4 – 3) / 6 r = -0.90 r/2 = -0.45 % per station STABVC = STAVertex – L / 2 = 4670 – 600/2 = STABVC = STA 43 + 70 STAEVC = STAVertex + L / 2 = 4670 + 600/2 = STAEVC = STA 49 + 70 Elev = Elev – g (L/2) = 853.48 – 3.00 (3) =
- 8. Solution: (continued) r/2 = -0.45 % per station Elevx = ElevBVC + g1x + (r/2)x2 Elev44+00 = 844.48 + 3.00(0.30) –0.45(0.30)2 = 845.34’ Elev45+00 = 844.48 + 3.00(1.30) –0.45(1.30)2 = 847.62’ Elev46+00 = 844.48 + 3.00(2.30) –0.45(2.30)2 = 849.00’ etc. Elev49+00 = 844.48 + 3.00(5.30) –0.45(5.30)2 = 847.74’
- 9. Solution: (continued) Station x (station s) g1x r/2 x2 Curve Elevatio n 43 + 70 BVC 0.0 0.00 0.00 844.48 44 + 00 0.3 .90 - 0.04 845.34 45 + 00 1.3 3.90 - 0.76 847.62 46 + 00 2.3 6.90 - 849.00
- 10. High and Low Points on Vertical Curves Sag Curves: Low Point defines location of catch basin for drainage. Crest Curves: High Point defines limits of drainage area for roadways. Also used to determine or set elevations based on minimum clearance requirements.
- 11. Equation for High or Low Point on a Vertical Curve: y = yBVC + g1x + (r/2)x2 Set dy/dx = 0 and solve for x to locate turning point 0 = 0 + g1 + r x Substitute (g2 – g1) / L for r -g1 = x (g2 – g1) / L -g1 L = x (g2 – g1) x = (-g1 L) / (g2 – g1) or
- 12. Example: High Point on a Crest Vertical Curve From previous example: g1 = + 3 %, g2 = - 2.4%, L = 600’ = 6 full stations, r/2 = - 0.45, ElevBVC = 844.48’ x = (g1 L) / (g1 – g2) x = (3)(6) / (3 + 2.4) = 3.3333 stations or 333.33’ HP STA = BVC STA + x HP STA = 4370 + 333.33 = HP STA 47 + 03.33 ELEVHP = 844.48 + 3.00(3.3333) – 0.45(3.3333)2 = 849.48’
- 13. Unequal-Tangent Parabolic Curve A grade g1of -2% intersects g2 of +1.6% at a vertex whose station and elevation are 87+00 and 743.24, respectively. A 400’ vertical curve is to be extended back from the vertex, and a 600’ vertical curve forward to closely fit ground conditions. Compute and tabulate the curve for stakeout at full stations.
- 14. The CVC is defined as a point of compound vertical curvature. We can determine the station and elevation of points A and B by reducing this unequal tangent problem to two equal tangent problems. Point A is located 200’ from the BVC and Point B is located 300’ from the EVC. Knowing this we can compute the elevation of points A and B. Once A and B are known we can compute the grade from A to B thus allowing us to solve this problem as two equal tangent curves. Pt. A STA 85 + 00, Elev. = 743.24 + 2 (2) = 747.24’ Pt. B STA 90 + 00, Elev. = 743.24 + 1.6 (3) = 748.04’ Solution:
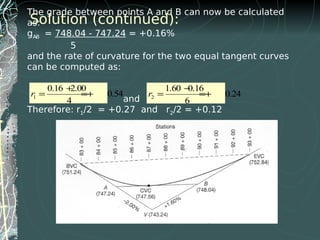
- 15. The grade between points A and B can now be calculated as: gA-B = 748.04 - 747.24 = +0.16% 5 and the rate of curvature for the two equal tangent curves can be computed as: and Therefore: r1/2 = +0.27 and r2/2 = +0.12 1 0.16 2.0 0.54 4 r + = = + Solution (continued): 1 0.16 2.00 0.54 4 r + = =+ 2 1.60 0.16 0.24 6 r − = =+
- 16. The station and elevations of the BVC, CVC and EVC are computed as: BVC STA 83 + 00, Elev. 743.24 + 2 (4) = 751.24’ EVC STA 93 + 00, Elev. 743.24 + 1.6 (6) = 752.84’ CVC STA 87 + 00, Elev. 747.24 + 0.16 (2) = 747.56’ Please note that the CVC is the EVC for the first equal tangent curve and the BVC for the second equal tangent curve. Solution (continued):
- 17. STATION x g1x (r/2)x 2 CurveElevation BVC 83+00 0 0 0 751.24' 84+00 1 -2.00 85+00 2 86+00 3 CVC 87+00 4 747.56' 88+00 1 0.16 89+00 2 90+00 3 91+00 4 92+00 5 EVC 93+00 6 g1x=-2(1) =-2.00 g2x=.16(1) =0.16 Computation of values for g1x and g2x
- 18. STATION x g1x (r/2)x 2 CurveElevation BVC 83+00 0 0 0 751.24' 84+00 1 -2.00 0.27 85+00 2 -4.00 86+00 3 -6.00 CVC 87+00 4 -8.00 747.56' 88+00 1 0.16 0.12 89+00 2 0.32 90+00 3 0.48 91+00 4 0.64 92+00 5 0.80 EVC 93+00 6 0.96 (r1/2)x 2 =(0.27)(1) 2 =0.27 (r2/2)x 2 =(0.12)(1) 2 =0.12 Computation of values for (r1/2)x2 and (r2/2)x2
- 19. STATION x g1x (r/2)x 2 CurveElevation BVC 83+00 0 0 0 751.24' 84+00 1 -2.00 0.27 85+00 2 -4.00 1.08 86+00 3 -6.00 2.43 CVC 87+00 4 -8.00 4.32 747.56' 88+00 1 0.16 0.12 89+00 2 0.32 0.48 90+00 3 0.48 1.08 91+00 4 0.64 1.92 92+00 5 0.80 3.00 EVC 93+00 6 0.96 4.32 Y1 =751.24-2.00+0.27=749.51' Y2 =747.56+0.16+0.12=747.84' Elevation Computations for both Vertical Curves
- 20. STATION x g1x (r/2)x 2 CurveElevation BVC 83+00 0 0 0 751.24' 84+00 1 -2.00 0.27 749.51' 85+00 2 -4.00 1.08 748.32' 86+00 3 -6.00 2.43 747.67' CVC 87+00 4 -8.00 4.32 747.56' 88+00 1 0.16 0.12 747.84' 89+00 2 0.32 0.48 748.36' 90+00 3 0.48 1.08 749.12' 91+00 4 0.64 1.92 750.12 92+00 5 0.80 3.00 751.36' EVC 93+00 6 0.96 4.32 752.84' Computed Elevations for Stakeout at Full Stations (OK)
- 21. Designing a Curve to Pass Through a Fixed Point Design a equal-tangent vertical curve to meet a railroad crossing which exists at STA 53 + 50 and elevation 1271.20’. The back grade of -4% meets the forward grade of +3.8% at PVI STA 52 + 00 with elevation 1261.50.
- 22. Solution: 2 1 2 1 1 2 2 (5350 5200) 150' 1.5 2 2 2 2 1261.50 4.00 2 4.00 4.00 1.5 2 3.80 4.00 3.80 4.00 1.5 2 2 2 BVC BVC L L L x stations r y y g x x g g r L L Y L g x x r L r L x L = + − = + = + = + + − = = + = − = − + + = + = +
- 23. Solution (continued): 2 2 2 3.80 4.00 1271.20 1261.50 4.00 4.00 1.5 1.5 2 2 2 2 0.975 9.85 8.775 0 4 2 0.975 9.85 8.775 9.1152 911.52' L L L L L L b b ac x a a b c L stations + = + + − + + + − + = − ± − = = = − = = = Check by substituting x = [(9.1152/2)+1.5] stations into the elevation equation to see if it matches a value of 1271.20’
- 24. Sight Distance Defined as “the distance required, for a given design speed to safely stop a vehicle thus avoiding a collision with an unexpected stationary object in the roadway ahead” by AASHTO (American Association of State Highway and Transportation Officials) Types Stopping Sight Distance Passing Sight Distance Decision Sight Distance Horizontal Sight Distance
- 25. Sight Distance Equations For Crest Curves For Sag Curves ( ) ( ) ( ) 2 1 2 1 2 2 1 2 1 2 2 2 2 S L S g g L h h S L h h L S g g ≤ − = + ≥ + = − − ( )2 2 1 1 2 4 3.5 4 3.5 2 S L S g g L S S L S L S g g ≤ − = + ≥ + = − − h1: height of the driver’s eye above the roadway h2: height of an object sighted on the roadway AASHTO recommendations: h1 = 3.5 ft, h2 = 0.50 ft (stopping), h2 = 4.25 ft (passing) Lengths of sag vertical curves are based upon headlight criteria for nighttime driving conditions.