2 primera ley
0 recomendaciones5,896 vistas
La Primera Ley de la Termodinámica establece que la energía total de un sistema aislado se conserva. Define conceptos clave como trabajo (W), calor (Q) y energía interna (U), y establece que los cambios en la energía interna de un sistema son iguales a la suma del calor y el trabajo transferidos al sistema.
2 primera ley
- 1. Primera Ley de la Termodinámica
- 2. Componentes fundamentales. La Primera Ley de la Termodinámica es uno de los principios fundamentales de la Naturaleza y puede resumirse de una manera muy simple: entradas iguales a salidas. Al día de hoy, no existe absolutamente nada que haya podido cuestionar su observancia. Para definirla rigurosamente es necesario tener clara la definición y los alcances de algunos conceptos fundamentales involucrados en su estudio que discutiremos en esta sección: Trabajo (W), Calor (Q), Energía Interna (U) y Entalpía (H).
- 3. El trabajo en Termodinámica posee un significado idéntico en lo conceptual al que se desarrolla en los cursos de Física (fuerza por distancia): con él, algo cambia en un sistema. Ejemplos de tipos de trabajo que resultan de interés en Termodinámica son: el que se desarrolla sobre la superficie de un líquido (γdA, γ = tensión superficial, A = área), en una batería (Edq, E = voltaje, q = carga eléctrica) o el que experimenta un gas en expansión al interior de un cilindro (PdV), etc. Centraremos nuestra atención en este último. TRABAJO, W.
- 4. Considera un experimento imaginario (al estilo Einstein) donde un gas contenido dentro de un cilindro se expande isotérmicamente desarrollando un cierto trabajo W gracias al cual se logra que una pesa con peso mg colocada sobre un pistón sin peso ascienda a la posición final que se indica. Expansión isotérmica de un gas. P1, V1, T P2, V2, T mg mg pistón
- 5. Todo lo anterior transcurre asumiendo que la presión atmosférica exterior es igual a cero y que el pistón no ejerce fricción sobre las paredes del cilindro. Bajo tales condiciones, el gas dentro del cilindro deja de expandirse hasta que la presión que ejerce iguala a la del exterior, mg/A. Expansión isotérmica de un gas. P1, V1, T P2, V2, T mg mg
- 6. donde Pop = presión que se opone a la expansión del gas = peso de la pesa (mg) / área del pistón (A); Δx = distancia que se mueve en vertical el pistón hasta que las presiones interior y exterior se igualan. Expansión isotérmica de un gas. P1, V1, T P2, V2, T mg mg Pop = mg A Definamos a la p r e s i ó n d e l exterior como se muestra en la Ecuación 1: u
- 7. W = trabajo realizado por el sistema; F = fuerza; d = distancia. El signo (–) indica que el sistema está haciendo trabajo sobre los alrededores. Expansión isotérmica de un gas. P1, V1, T P2, V2, T mg mg Definamos ahora a l t r a b a j o m e d i a n t e l a Ecuación 2: W = – F x d W = – mg x Δx v
- 8. Pero A x Δx = ΔV = incremento de volumen que ganó el gas en su trabajo de expansión. Con esto llegamos a la Ecuación 3 que define el trabajo desarrollado durante la expansión del gas: W = – Pop ΔV Expansión isotérmica de un gas. P1, V1, T P2, V2, T mg mg Al combinar las ecuaciones 1 y 2 igualando ambas a mg se obtiene: W = – Pop x A x Δx w
- 9. Expansión isotérmica de un gas. P V P1,V1 P2,V2 La magnitud del trabajo desarrollado por el gas queda expresada a partir de la Ecuación 3, pero puede expresarse también de manera gráfica: da- do que W está en función de Pop y que, al final del experimento, Pop = P2, el área en a z u l r e p r e s e n t a g r á f i c a m e n t e a l trabajo: advierte que las aristas de este rectángulo resultan ser (P2) y (V2–V1).
- 10. Expansión isotérmica de un gas. P V P1,V1 P2,V2 La expansión del gas efectuada de esta manera, en una sola etapa, procede en un tiempo finito (el menor posible) dado que se trata de un sistema que no se encuentra en equilibrio y que no se d e t i e n e h a s t a a l c a n z a r l o . A u n p r o c e s o c o n t a l e s características se le define como un proceso termodinámicamen- te irreversible.
- 11. Expansión isotérmica de un gas. ¿A que se le se le puede denominar entonces proceso reversible? Un proceso reversible es aquél al que se le impone (teóricamente) que proceda a través de una serie de cambios infinitesimales sucesivos (en este caso, expansiones de un gas) entre dos estados, lo que implica disponer para él de un tiempo infinito para que pueda completarse. A partir de esto, queda claro que los procesos puramente reversibles no existen, no obstante, resulta trascendente examinar los resultados que se obtendrían con respecto a la producción de trabajo si uno de ellos pudiese tener lugar.
- 12. Expansión isotérmica de un gas. Primer punto. Para entender que ocurre en el caso de la expansión reversible de un gas, consideremos al mismo sistema que analizamos antes, salvo que ahora al inicio, en lugar una única pesa mg, sobre el pistón se encontrará colocada una cantidad infinita de pequeñas pesas que ejercen en conjunto una presión sobre el gas tal que igualan el valor de P1. De esta manera, y a diferencia del proceso anterior en donde asumimos que desde un principio el gas se expande espontáneamente, ahora consideraremos que no podrá hacerlo hasta que no sea removida la primera de esas pequeñas pesas infinitesimales.
- 13. Expansión isotérmica de un gas. Segundo punto. Suponte que ahora remueves la primera de las pesas y a continuación la siguiente, y a s í s u c e s i v a m e n t e . A l m o d i f i c a r s e infintesimalmente la presión externa conforme las pesas se remueven, nuestro gas dentro del cilindro comenzará a expandirse aumentando en dV su volumen en cada una de las etapas. Esta sucesión infinita de etapas continuará hasta llegar al estado final (idéntico al del primer ejemplo), de tal manera que si queremos determinar el trabajo total desarrollado por el sistema, una buena estrategia a seguir sería calcular el trabajo desarrollado en cada una de estas etapas y, al final, realizar una sumatoria de todos estos valores.
- 14. Expansión isotérmica de un gas. Tercer punto. Para expresar formalmente esta sumatoria, será necesario plantear una expresión que incluya una integral definida para calcular el trabajo. Ésta se muestra en la Ecuación 4. A diferencia de la expansión en una etapa, la remoción continuada de las pesas infinitesimales estará asociada a una variación apenas mínima en las posiciones de equilibrio de dos etapas consecutivas, lo que define a un proceso reversible. V2 V1 W = – PopdV x
- 15. Expansión isotérmica de un gas. Cuarto punto. ¡Cuidado!: la Pop en este caso, estrictamente hablando, no fue constante durante todo el experimento, por lo que la expresión anterior no es completamente válida. No obstante, hagamos lo siguiente: en cada cambio, Pin – Pop = dP (Pin = presión del gas; dP = cambio de presión infinitesimal originado por la remoción de cada pesa). Despejando Pop obtenemos Pop = Pin – dP, expresión gracias a la cual podemos transformar la Ecuación 4 en: W = – (Pin – dP) dV V2 V1
- 16. Expansión isotérmica de un gas. Cuarto punto. Y como el producto de dos diferenciales se puede aproximar a cero, la ecuación se reduce a: W = – Pin dV Pin depende sólo de nuestro gas (y su comportamiento está en función de V2 y V1). Es más: si asumimos que nuestro gas es ideal (para simplificar nuestra discusión, mas nunca para invalidarla) llegamos a: W = – dV V2 V1 nRT V V2 V1
- 17. Expansión isotérmica de un gas. Quinto punto. Finalmente, luego de integrar, se obtiene el trabajo realizado por un sistema reversible (Ecuación 5). W = – nRT ln Una forma alterna para esta ecuación es la siguiente: W = – nRT ln P1 P2 V2 V1 y y
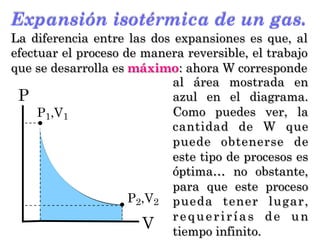
- 18. P P1,V1 V P2,V2 Expansión isotérmica de un gas. La diferencia entre las dos expansiones es que, al efectuar el proceso de manera reversible, el trabajo que se desarrolla es máximo: ahora W corresponde al área mostrada en azul en el diagrama. Como puedes ver, la cantidad de W que puede obtenerse de este tipo de procesos es óptima… no obstante, para que este proceso pueda tener lugar, requerirías de un tiempo infinito.
- 19. Expansión isotérmica de un gas. Los procesos a tiempo infinito no pueden tener lugar en la realidad. Sin embargo, ahora ya tienes p r e s e n t e u n a i d e a fundamental de lo que persigue la Ingeniería en términos termodinámicos: que la la optimización de los procesos que son de su interés busca para ellos tendencias de optimización reversibles.
- 20. ¤ 1 julio (J, joule, SI!) = 1 Nm ¤ 1 litro-atmósfera (L-atm) = 101.325 J ¤ 1 ergio (erg, dina-cm) = 1 x 10-7 J ¤ 1 caloría = 4.184 J ¤ 1 british thermal unit (BTU) = 1055.06 J ¤ 1 kilowatt-hora = 3.6 x 106 J ¤ 1 libra fuerza-pie (lb-ft) = 1.355 J Unidades importantes de W.
- 21. W no es una función de estado. A partir de lo revisado, debe ser claro que la magnitud de W depende de la trayectoria que haya seguido un experimento y que no es una función de estado (no se calculó un “–ΔW” ni puede afirmarse que un sistema posea una cierta cantidad de trabajo). En contraste, la magnitud del cambio en una función de estado sólo depende de los estados inicial y final del sistema: el incremento en volumen ΔV en ambos casos analizados, a pesar de que uno fue reversible y el otro irreversible y siguieron trayectorias disímbolas, fue idéntico (se empleó el mismo equipo y se le permitió recorrer al pistón la misma distancia Δx.
- 22. El calor es la transferencia de energía entre dos cuerpos que se encuentran a diferente temperatura. Al igual que W, sólo aparece en el contorno del sistema y no es una propiedad del sistema ni una función de estado: sólo se trata de una medida de la transferencia de energía cuyos cambios dependen de la trayectoria seguida en ese cambio de estado e igualmente sólo puede definirse a partir de un proceso. CALOR, Q.
- 23. El cambio de energía Q transferido desde los alrededores al sistema se cuantifica a partir de Q = msΔT donde m = masa de la muestra; s = calor específico de una sustancia = cantidad de calor que hay que suministrar a una unidad de masa de una sustancia o sistema termodinámico para elevar su temperatura en una unidad. Nuevamente, si el sistema trasnfiere calor, Q poseerá un valor negativo. Cuantificación de Q.
- 24. La energía interna es la energía total de un sistema asociada a la suma de las energías potencial y cinética de todas las moléculas que lo componen (energía rotacional, vibracional, traslacional, etc.). Es una función de estado. ENERGÍA INTERNA, U.
- 25. PRIMERA LEY DE LA TERMODINÁMICA. La Primera Ley de la Termodinámica establece que la energía puede ser convertida de una forma a otra pero jamás creada o destruida, o lo que es lo mismo, la energía del Universo permanece siempre constante.