Gauss method 2019

Método de Gauss
G. Edgar Mata Ortiz

Las ecuaciones lineales
Una ecuación lineal se caracteriza porque sus incógnitas
están elevadas a una potencia unitaria.
No contiene funciones trascendentes como logaritmo,
seno o coseno, entre otras.
Un sistema de ecuaciones lineales consta de dos o más
ecuaciones, generalmente con el mismo número de
incógnitas.
𝟐𝒙 𝟏 + 𝟑𝒙 𝟐 − 𝟒𝒙 𝟑 = 𝟓
𝟑𝒙 𝟏 − 𝟒𝒙 𝟐 − 𝟐𝒙 𝟑 = −𝟏
−𝒙 𝟏 + 𝟐𝒙 𝟐 − 𝟑𝒙 𝟑 = 𝟐

Solución de un sistema de ecuaciones lineales
La solución de un sistema de ecuaciones
lineales está formada por los valores de
las incógnitas que, al mismo tiempo,
hacen verdaderas a todas las ecuaciones
que forman el sistema.
Se puede comprobar si la solución
obtenida es correcta sustituyendo los
valores obtenidos en todas las ecuaciones:
Si se obtienen identidades, la solución es
correcta.
𝟑𝒙 − 𝟔𝒚 + 𝟗𝒛 = 𝟏𝟖
𝟐𝒙 − 𝟒𝒚 + 𝟓𝒛 = 𝟏𝟏
−𝟑𝒙 − 𝟒𝒚 + 𝟔𝒛 = 𝟏𝟕
𝒙 = −𝟏
𝒚 = −𝟐
𝒛 = 𝟏
Soluciones
𝟑(−𝟏) − 𝟔(−𝟐) + 𝟗(𝟏) = 𝟏𝟖
𝟐(−𝟏) − 𝟒(−𝟐) + 𝟓(𝟏) = 𝟏𝟏
−𝟑(−𝟏) − 𝟒(−𝟐) + 𝟔(𝟏) = 𝟏𝟕

No todos los sistemas de
ecuaciones tiene solución, y
cuando la tienen, no siempre es
solución única.
Existen diferentes métodos de
solución de sistemas de ecuaciones
lineales:
Método gráfico
Métodos algebraicos
Métodos lineales
𝒙 − 𝟐𝒚 + 𝟑𝒛 = 𝟏𝟎
𝟐𝒙 − 𝟒𝒚 + 𝟔𝒛 = 𝟐𝟎
−𝟓𝒙 + 𝟒𝒚 + 𝟔𝒛 = 𝟏𝟕
EL sistema no tiene solución
porque las ecuaciones uno y dos
son múltiplo una de la otra
𝒙 − 𝟐𝒚 + 𝟑𝒛 = 𝟏𝟎
por dos es igual a:
𝟐𝒙 − 𝟒𝒚 + 𝟔𝒛 = 𝟐𝟎

Sin importar cuál método se
elija para resolver un sistema de
ecuaciones, la solución será la
misma.
Método gráfico
Métodos algebraicos
Métodos lineales
A veces es preferible un método
de solución, en otras ocasiones
no es posible emplear algún
método en particular, por ello,
es necesario conocer diferentes
métodos y elegir el que mejor
responde a las necesidades
específicas de cada problema.
En este material estudiaremos
el método de Cramer o método
por determinantes.

El método de Gauss
El método de Gauss presenta importantes ventajas cuando
los sistemas de ecuaciones son grandes, de tres o más
incógnitas.
+ 3 x 1 - 9 x 2 + 5 x 3 + 2 x 4 + 2 x 5 = - 15
+ 9 x 1 - 3 x 2 - 8 x 3 - 2 x 4 + 4 x 5 = + 69
- 5 x 1 + 4 x 2 + 4 x 3 + 2 x 4 + 6 x 5 = - 80
+ 4 x 1 + 7 x 2 + 7 x 3 + 5 x 4 + 8 x 5 = - 112
+ 4 x 1 + 4 x 2 + 5 x 3 + 1 x 4 + 5 x 5 = - 59

Ejemplo: Resolver el siguiente sistema de
ecuaciones por el método de Gauss
2𝑥 + 5𝑦 + 6𝑧 = −10
5𝑥 + 13𝑦 − 9𝑧 = 48
4𝑥 − 12𝑦 − 5𝑧 = −13

Inicio del proceso: obtener la Matriz
aumentada del sistema
En forma similar a lo que ocurre en el método de Cramer, vamos a omitir las
incógnitas y concentraremos nuestra atención en los coeficientes.
EL arreglo rectangular de los coeficientes de las incógnitas y los términos
independientes forman la matriz aumentada del sistema de ecuaciones.

Matriz aumentada del sistema
Los elementos de la matriz se identifican mediante el nombre de dicha
matriz, por ejemplo matriz A, con dos subíndices que hacen referencia
al renglón y columna en la que se encuentra.
2 5 6 10
5 13 9 48
4 12 5 13
− 
 − 
 − − − 
A11
A21
A31
A12
A34
A14

El método de Gauss
El objetivo central de este método es la obtención de una matriz
simplificada que recibe el nombre de forma escalonada por renglones
de la matriz del sistema.
2 5 6 10
5 13 9 48
4 12 5 13
− 
 − 
 − − − 
1
0 1
0 0 1
a b c
d e
f
 
 
 
  
Forma escalonada por renglonesMatriz aumentada del sistema
Método de
Gauss

El método de Gauss
Para obtener la forma escalonada por renglones de la matriz del
sistema se emplean operaciones fundamentales con renglones:
1. Intercambiar dos renglones
2. Multiplicar o dividir un renglón por una constante
3. Sumar o restar dos renglones
4. Y la combinación de ellas

Obtener 1 en la posición A11
El elemento A11 tiene un valor de dos, y para el método de Gauss
debemos efectuar operaciones en el renglón uno para que su valor sea
uno
2 5 6 10
5 13 9 48
4 12 5 13
− 
 − 
 − − − 
A11
Debe ser igual a uno

Para conseguir el uno en esta posición, casi siempre se
va a dividir el renglón uno entre el valor de A11, en este
caso, entre 2.
2 5 6 10
5 13 9 48
4 12 5 13
− 
 − 
 − − − 
A11
Debe ser igual a uno

Para conseguir el uno en esta posición, siempre se va a
dividir el renglón uno entre el valor de A11, en este
caso, entre 2.
2 5 6 10
5 13 9 48
4 12 5 13
− 
 − 
 − − − 
A11 Dividir el renglón
uno, entre dos

Se divide el renglón uno entre el valor del elemento A11, que en este
caso es 2.
2 5 6 10
5 13 9 48
4 12 5 13
− 
 − 
 − − − 
5
1 3 5
2
5 13 9 48
4 12 5 13
 
− 
 
− 
 − − −
 
 
𝑅1
2

Se obtuvo el uno en la posición señalada y el resto del renglón se ve
afectado, es parte del proceso.
2 5 6 10
5 13 9 48
4 12 5 13
− 
 − 
 − − − 
5
1 3 5
2
5 13 9 48
4 12 5 13
 
− 
 
− 
 − − −
 
 
𝑅1
2

Obtener ceros debajo del uno que se obtuvo
en la posición A11
Una vez que se ha obtenido en el uno en la posición A11, el siguiente
paso es obtener ceros debajo de dicho elemento.
5
1 3 5
2
5 13 9 48
4 12 5 13
 
− 
 
− 
 − − −
 
 
Ceros

en la posición A11
Para obtener ceros se efectúan operaciones con renglones
5
1 3 5
2
5 13 9 48
4 12 5 13
 
− 
 
− 
 − − −
 
 
Multiplicar el renglón uno por
una cantidad adecuada de modo
que al sumarse con cada renglón
(R2 y R3), se elimine el valor
indicado.

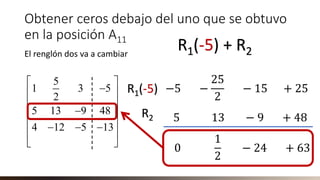
en la posición A11
La cantidad por la que se multiplica es el propio número que se desea
convertir en cero, con el signo contrario
5
1 3 5
2
5 13 9 48
4 12 5 13
 
− 
 
− 
 − − −
 
 
R1(-5) + R2
−5 −
25
2
− 15 + 25

en la posición A11
El resultado de la multiplicación, se suma con el renglón dos.
5
1 3 5
2
5 13 9 48
4 12 5 13
 
− 
 
− 
 − − −
 
 
R1(-5) + R2
−5 −
25
2
− 15 + 25
5 13 − 9 + 48

en la posición A11
Al efectuar la suma se obtendrá el cero en la posición A21.
5
1 3 5
2
5 13 9 48
4 12 5 13
 
− 
 
− 
 − − −
 
 
R1(-5) + R2
−5 −
25
2
− 15 + 25
5 13 − 9 + 48
R1(-5)
R2

en la posición A11
Se ha obtenido el cero
5
1 3 5
2
5 13 9 48
4 12 5 13
 
− 
 
− 
 − − −
 
 
R1(-5) + R2
−5 −
25
2
− 15 + 25
5 13 − 9 + 48
R1(-5)
R2
0
1
2
− 24 + 63

en la posición A11
El renglón dos va a cambiar
5
1 3 5
2
5 13 9 48
4 12 5 13
 
− 
 
− 
 − − −
 
 
R1(-5) + R2
−5 −
25
2
− 15 + 25
5 13 − 9 + 48
R1(-5)
R2
0
1
2
− 24 + 63

Obtener ceros debajo del 1 que se obtuvo en A11
Se multiplica el renglón uno, por el valor que se desea convertir en cero, con el
signo contrario; estos valores se suman con el renglón dos, y el resultado se escribe
como un nuevo renglón dos.
El renglón uno no va a cambiar en este paso, solamente el renglón dos, y
posteriormente el renglón tres.
𝑅1 −5 + 𝑅2
5
1 3 5
2
5 13 9 48
4 12 5 13
 
− 
 
− 
 − − −
 
 
5
1 3 5
2
1
0 24 73
2
4 12 5 13
 
− 
 
 −
 
 − − − 
  

La nueva matriz ha sido modificada, el renglón uno ahora presenta un
uno en la posición A11 y un cero en la posición A21
5
1 3 5
2
1
0 24 73
2
4 12 5 13
 
− 
 
 −
 
 − − − 
  
Sólo nos interesaba obtener el uno y el
cero señalados pero, dado que se
efectúan operaciones con renglones, el
resto de dichos renglones sufre cambios
que no tienen importancia para el
procedimiento.

Ahora se va a modificar el renglón tres, se multiplica el renglón uno, por el
valor que se desea convertir en cero, con el signo contrario; estos resultados
se suman con el renglón tres. Es similar a lo ya realizado con el renglón dos.
5
1 3 5
2
1
0 24 73
2
4 12 5 13
 
− 
 
 −
 
 − − − 
  
R1(-4) + R3
−4 − 10 − 12 + 20R1(-4)

Al multiplicar el renglón uno por menos cuatro se obtiene un menos cuatro
que servirá para obtener el cero en la posición A31.
5
1 3 5
2
1
0 24 73
2
4 12 5 13
 
− 
 
 −
 
 − − − 
  
R1(-4) + R3
−4 − 10 − 12 + 20R1(-4)
R3 4 − 12 − 5 − 13

Se ha obtenido el cero al restar cuatro menos cuatro
5
1 3 5
2
1
0 24 73
2
4 12 5 13
 
− 
 
 −
 
 − − − 
  
R1(-4) + R3
−4 − 10 − 12 + 20R1(-4)
R3 4 − 12 − 5 − 13
0 − 22 − 17 + 7

El renglón tres se sustituirá con los resultados de este procedimiento.
5
1 3 5
2
1
0 24 73
2
4 12 5 13
 
− 
 
 −
 
 − − − 
  
R1(-4) + R3
−4 − 10 − 12 − 20R1(-4)
R3 4 − 12 − 5 − 13
0 − 22 − 17 + 7

Se multiplica el renglón uno, por el valor que se desea convertir en cero, con el
signo contrario; estos resultados se suman con el renglón tres.
El renglón uno no va a cambiar en este paso, solamente el renglón dos, y
posteriormente el renglón tres.
𝑅1 −4 + 𝑅3
5
1 3 5
2
5 13 9 48
4 12 5 13
 
− 
 
− 
 − − −
 
 
5
1 3 5
2
1
0 24 73
2
0 22 17 7
 
− 
 
 −
 
 − − 
  

uno en la posición A11 y ceros en las posiciones A21 y A31.
5
1 3 5
2
1
0 24 73
2
0 22 7 7
 
− 
 
 −
 
 − − 
  
Sólo nos interesaba obtener el uno y los
ceros señalados pero, dado que se
procedimiento.

El siguiente elemento que debe modificarse es el A22, debe ser igual a
uno.
5
1 3 5
2
1
0 24 73
2
0 22 17 7
 
− 
 
 −
 
 − − 
  
A22
Uno

Para obtener el uno en la posición indicada debemos dividir el renglón
dos entre el valor de A22, en este caso, entre
1
2
.
5
1 3 5
2
1
0 24 73
2
0 22 17 7
 
− 
 
 −
 
 − − 
  
A22
Uno

Al dividir el renglón dos entre el valor de A22, (en este caso, entre
1
2
), se
obtienen los resultados anotados a la derecha.
5
1 3 5
2
1
0 24 73
2
0 22 17 7
 
− 
 
 −
 
 − − 
  
A22
Debe ser igual
a uno
𝑅2 ÷
1
2
0 1 − 48 146

Pendiente
El resultado de esta división será el nuevo renglón dos.
𝑅2
1
2
5
1 3 5
2
0 1 48 146
0 22 17 7
 
− 
 
− 
 − −
 
 
5
1 3 5
2
1
0 24 73
2
0 22 17 7
 
− 
 
 −
 
 − − 
  

Obtener uno en la posición A22
uno en la posición A11, ceros en las posiciones A21 y A31; y un uno en la
posición A22.
5
1 3 5
2
0 1 48 146
0 22 7 7
 
− 
 
− 
 − −
 
 
Sólo nos interesaba obtener los unos y
ceros señalados pero, dado que se
procedimiento.

Obtener ceros debajo de A22.
El uno obtenido en la posición A22 será utilizado para obtener ceros
debajo de él.
5
1 3 5
2
0 1 48 146
0 22 17 7
 
− 
 
− 
 − −
 
 
Debe ser
cero

Como se llevó a cabo anteriormente para obtener ceros debajo de A11, vamos a
multiplicar el renglón dos por una cantidad adecuada de modo que, al sumar estos
valores con el renglón tres, el elemento A32 se convierta en cero.
5
1 3 5
2
0 1 48 146
0 22 17 7
 
− 
 
− 
 − −
 
 
𝑅2 +22 + 𝑅3
Debe ser
cero
0 22 − 1056 3212R2(+22)
R3
0 − 22 − 17 7

Como se llevó a cabo anteriormente para obtener ceros debajo de A11, vamos a
multiplicar el renglón dos por una cantidad adecuada de modo que, al sumar estos
valores con el renglón tres, el elemento A32 se convierta en cero.
5
1 3 5
2
0 1 48 146
0 22 17 7
 
− 
 
− 
 − −
 
 
𝑅2 +22 + 𝑅3
Debe ser
cero
0 22 − 1056 3212R2(+22)
R3
0 − 22 − 17 7
0 0 − 1073 3219

El renglón tres se sustituirá por el resultado del proceso anteriormente explicado,
obteniéndose así el cero (A32) debajo del uno (A22).
5
1 3 5
2
0 1 48 146
0 22 17 7
 
− 
 
− 
 − −
 
 
𝑅2 +22 + 𝑅3
0 22 − 1056 3212R2(+22)
R3
0 − 22 − 17 7
0 0 − 1073 3219

El renglón tres se sustituirá por el resultado del proceso anteriormente explicado,
obteniéndose así el cero (A32) debajo del uno (A22).
5
1 3 5
2
0 1 48 146
0 0 1073 3219
 
− 
 
− 
 −
 
 
𝑅2 +22 + 𝑅3
0 22 − 1056 3212R2(+22)
R3
0 − 22 − 17 7
0 0 − 1073 3219

Obtener cero debajo del 1 que se obtuvo en A22
Se multiplica el renglón dos, por el valor que se desea convertir en cero, con
el signo contrario; estos resultados se suman con el renglón tres.
El renglón uno y dos no van a cambiar en este paso, solamente el renglón
tres.
5
1 3 5
2
0 1 48 146
0 22 17 7
 
− 
 
− 
 − −
 
 
𝑅2 22 + 𝑅3
5
1 3 5
2
0 1 48 146
0 0 1073 3219
 
− 
 
− 
 −
 
 

Se divide el renglón tres entre el valor del elemento en la posición
A33, en este caso – 1073.
Los renglones uno y dos ya no vana cambiar, solamente el renglón
tres será modificado.
5
1 3 5
2
0 1 48 146
0 0 1073 3219
 
− 
 
− 
 −
 
 
𝑅3
−1073
5
1 3 5
2
0 1 48 146
0 0 1 3
 
− 
 
− 
 −
 
 

Al obtener este último uno, termina la parte matricial del método de
Gauss, se ha conseguido una matriz diagonal.
La matriz representa el sistema de ecuaciones pero se ha simplificado.
5
1 3 5
2
0 1 48 146
0 0 1073 3219
 
− 
 
− 
 −
 
 
𝑅3
−1073
5
1 3 5
2
0 1 48 146
0 0 1 3
 
− 
 
− 
 −
 
 

5
1 3 5
2
0 1 48 146
0 0 1 3
 
− 
 
− 
 −
 
 
1𝑥 +
5
2
𝑦 + 3𝑧 = −5
1𝑦 − 48𝑧 = 146
𝑧 = −3
EL sistema de ecuaciones del lado derecho es equivalente al sistema de
ecuaciones original, pero ha sido simplificado mediante operaciones
con renglones.

5
1 3 5
2
0 1 48 146
0 0 1 3
 
− 
 
− 
 −
 
 
1𝑥 +
5
2
𝑦 + 3𝑧 = −5
1𝑦 − 48𝑧 = 146
𝑧 = −3
1𝑦 − 48 −3 = 146
𝑦 + 144 = 146
𝑦 = 146 − 144
𝑦 = 2
El valor de la incógnita x3 se lee directamente de la matriz final del
método de Gauss, las demás incógnitas se obtienen sustituyendo en las
ecuaciones de abajo hacia arriba.

5
1 3 5
2
0 1 48 146
0 0 1 3
 
− 
 
− 
 −
 
 
1𝑥 +
5
2
𝑦 + 3𝑧 = −5
1𝑦 − 48𝑧 = 146
𝑧 = −3
1𝑦 − 48 −3 = 146
𝑦 + 144 = 146
𝑦 = 146 − 144
𝑦 = 2
1𝑥 +
5
2
2 + 3 −3 = −5
𝑥 + 5 − 9 = −5
𝑥 − 4 = −5
𝑥 = −5 + 4
𝑥 = −1
Las soluciones son:

Método de Gauss
En resumen, se siguió el proceso:
5
1 3 5
2
0 1 48 146
0 0 1 3
 
− 
 
− 
 −
 
 
2𝑥 + 5𝑦 + 6𝑧 = −10
5𝑥 + 13𝑦 − 9𝑧 = 48
4𝑥 − 12𝑦 − 5𝑧 = −13
2 5 6 10
5 13 9 48
4 12 5 13
− 
 − 
 − − − 
1𝑥 +
5
2
𝑦 + 3𝑧 = −5
1𝑦 − 48𝑧 = 146
𝑧 = −3
𝒙 = −𝟏
𝒚 = 𝟐
𝒛 = −𝟑

Comprobación
Para comprobar que los valores de las incógnitas son correctos, se deben sustituir en
las ecuaciones originales. Al efectuar operaciones deben obtenerse valores iguales en
ambos lados de las ecuaciones.
2𝑥 + 5𝑦 + 6𝑧 = −10
5𝑥 + 13𝑦 − 9𝑧 = 48
4𝑥 − 12𝑦 − 5𝑧 = −13
𝒙 = −𝟏, 𝒚 = 𝟐, 𝒛 = −𝟑
2(−𝟏) + 5(𝟐) + 6(−𝟑) = −10
5(−𝟏) + 13(𝟐) − 9(−𝟑) = 48
4(−𝟏) − 12(𝟐) − 5(−𝟑) = −13

Comprobación
Para comprobar que los valores de las incógnitas son correctos, se deben sustituir en
las ecuaciones originales. Al efectuar operaciones deben obtenerse valores iguales en
ambos lados de las ecuaciones.
2𝑥 + 5𝑦 + 6𝑧 = −10
5𝑥 + 13𝑦 − 9𝑧 = 48
4𝑥 − 12𝑦 − 5𝑧 = −13
𝒙 = −𝟏, 𝒚 = 𝟐, 𝒛 = −𝟑
2(−𝟏) + 5(𝟐) + 6(−𝟑) = −10
5(−𝟏) + 13(𝟐) − 9(−𝟑) = 48
4(−𝟏) − 12(𝟐) − 5(−𝟑) = −13
−2 + 10 − 18 = −10
−5 + 26 + 27 = 48
−4 − 24 + 15 = −13

Por su atención
Gracias
Fuentes de información en línea:
http://licmata-math.blogspot.mx/
https://www.facebook.com/licemata
https://www.linkedin.com/in/licmata
http://www.slideshare.net/licmata
Twitter @licemata

Gauss method 2019

Más contenido relacionado

La actualidad más candente (20)

Similar a Gauss method 2019 (20)

Más de Edgar Mata (20)

Último (20)

Gauss method 2019