20110204 quantum algorithms_vyali_lecture02
- 1. Квантовые алгоритмы: возможности и ограничения. Лекция 2: Квантовые запросы к «черному ящику» М. Вялый Вычислительный центр им. А.А.Дородницына Российской Академии наук Санкт-Петербург, 2011 М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 1 / 36
- 2. План 1 Введение 2 Квантовый запрос 3 Моделирование классических действий квантовыми 4 Фазовый запрос 5 Задача Дойча 6 Задача Дойча – Джоза 7 Алгоритм Гровера: поиск иголки в стоге сена М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 2 / 36
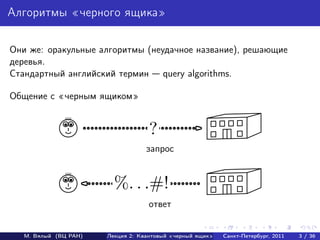
- 3. Алгоритмы «черного ящика» Они же: оракульные алгоритмы (неудачное название), решающие деревья. Стандартный английский термин query algorithms. Общение с черным ящиком ? запрос %. . .#! ответ М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 3 / 36
- 4. Сложность алгоритмов «черного ящика» Чем меньше запросов, тем лучше. На сложность обработки запросов внимания не обращаем лишнее обращение к черному ящику стоит дороже. М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 4 / 36
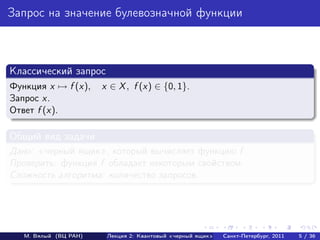
- 5. Запрос на значение булевозначной функции Классический запрос Функция x → f (x), x ∈ X , f (x) ∈ {0, 1}. Запрос x. Ответ f (x). Общий вид задачи Дано: черный ящик , который вычисляет функцию f . Проверить: функция f обладает некоторым свойством. Сложность алгоритма: количество запросов. М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 5 / 36
- 6. Запрос на значение булевозначной функции Классический запрос Функция x → f (x), x ∈ X , f (x) ∈ {0, 1}. Запрос x. Ответ f (x). Общий вид задачи Дано: черный ящик , который вычисляет функцию f . Проверить: функция f обладает некоторым свойством. Сложность алгоритма: количество запросов. М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 5 / 36
- 7. План 1 Введение 2 Квантовый запрос 3 Моделирование классических действий квантовыми 4 Фазовый запрос 5 Задача Дойча 6 Задача Дойча – Джоза 7 Алгоритм Гровера: поиск иголки в стоге сена М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 6 / 36
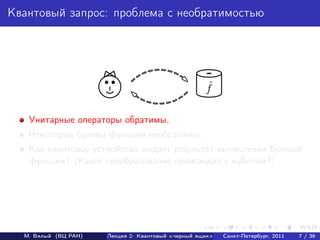
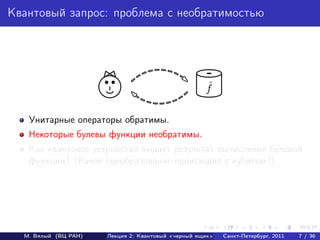
- 8. Квантовый запрос: проблема с необратимостью ˆ f Унитарные операторы обратимы. Некоторые булевы функции необратимы. Как квантовое устройство выдает результат вычисления булевой функции? (Какое преобразование происходит с кубитом?) М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 7 / 36
- 9. Квантовый запрос: проблема с необратимостью ˆ f Унитарные операторы обратимы. Некоторые булевы функции необратимы. Как квантовое устройство выдает результат вычисления булевой функции? (Какое преобразование происходит с кубитом?) М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 7 / 36
- 10. Квантовый запрос: проблема с необратимостью ˆ f Унитарные операторы обратимы. Некоторые булевы функции необратимы. Как квантовое устройство выдает результат вычисления булевой функции? (Какое преобразование происходит с кубитом?) М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 7 / 36
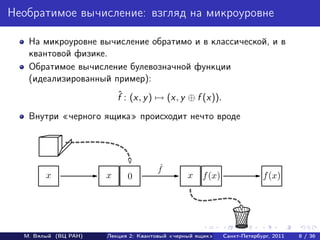
- 11. Необратимое вычисление: взгляд на микроуровне На микроуровне вычисление обратимо и в классической, и в квантовой физике. Обратимое вычисление булевозначной функции (идеализированный пример): ˆ f : (x, y ) → (x, y ⊕ f (x)). Внутри черного ящика происходит нечто вроде М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 8 / 36
- 12. Необратимое вычисление: взгляд на микроуровне На микроуровне вычисление обратимо и в классической, и в квантовой физике. Обратимое вычисление булевозначной функции (идеализированный пример): ˆ f : (x, y ) → (x, y ⊕ f (x)). Внутри черного ящика происходит нечто вроде М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 8 / 36
- 13. Необратимое вычисление: взгляд на микроуровне На микроуровне вычисление обратимо и в классической, и в квантовой физике. Обратимое вычисление булевозначной функции (идеализированный пример): ˆ f : (x, y ) → (x, y ⊕ f (x)). Внутри черного ящика происходит нечто вроде ˆ f x x 0 x f (x) f (x) М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 8 / 36
- 14. Обратимый (квантовый) запрос ˆ f продолжается до унитарного оператора (перестановочного). Пример с функцией f : {0, 1} → {0, 1}, f (x) = x: 1 0 0 0 0 1 0 0 ˆ f = 0 0 0 1 , 0 0 1 0 (При записи матриц в вычислительном базисе мы упорядочиваем битовые строки в лексикографическом порядке.) Будем считать оператор ˆ f : |x, b → |x, b ⊕ f (x) квантовым запросом общего вида. М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 9 / 36
- 15. Обратимый (квантовый) запрос ˆ f продолжается до унитарного оператора (перестановочного). Пример с функцией f : {0, 1} → {0, 1}, f (x) = x: 1 0 0 0 0 1 0 0 ˆ f = 0 0 0 1 , 0 0 1 0 (При записи матриц в вычислительном базисе мы упорядочиваем битовые строки в лексикографическом порядке.) Будем считать оператор ˆ f : |x, b → |x, b ⊕ f (x) квантовым запросом общего вида. М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 9 / 36
- 16. Посылаем и получаем и регистр аргумента, и регистр значения |x, b ˆ f |x, b ⊕ f (x) М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 10 / 36
- 17. План 1 Введение 2 Квантовый запрос 3 Моделирование классических действий квантовыми 4 Фазовый запрос 5 Задача Дойча 6 Задача Дойча – Джоза 7 Алгоритм Гровера: поиск иголки в стоге сена М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 11 / 36
- 18. Имитация детерминированного запроса Квантовый алгоритм может реализовать любую перестановку векторов вычислительного базиса. Этому соответствует обратимое классическое преобразование. Избавление от необратимости: использование свежей памяти, как в уже рассмотренном случае ˆ f : |x, b → |x, b ⊕ f (x) . В общем случае необратимое отображение f : A → A можно ˜ имитировать подходящим обратимым f со свежей копией памяти A в фиксированном состоянии a0 : ˜ f : (a, a0 ) → (a, f (a)) продолжается до перестановки на A × A. М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 12 / 36
- 19. Имитация детерминированного запроса Квантовый алгоритм может реализовать любую перестановку векторов вычислительного базиса. Этому соответствует обратимое классическое преобразование. Избавление от необратимости: использование свежей памяти, как в уже рассмотренном случае ˆ f : |x, b → |x, b ⊕ f (x) . В общем случае необратимое отображение f : A → A можно ˜ имитировать подходящим обратимым f со свежей копией памяти A в фиксированном состоянии a0 : ˜ f : (a, a0 ) → (a, f (a)) продолжается до перестановки на A × A. М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 12 / 36
- 20. Имитация детерминированного запроса Квантовый алгоритм может реализовать любую перестановку векторов вычислительного базиса. Этому соответствует обратимое классическое преобразование. Избавление от необратимости: использование свежей памяти, как в уже рассмотренном случае ˆ f : |x, b → |x, b ⊕ f (x) . В общем случае необратимое отображение f : A → A можно ˜ имитировать подходящим обратимым f со свежей копией памяти A в фиксированном состоянии a0 : ˜ f : (a, a0 ) → (a, f (a)) продолжается до перестановки на A × A. М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 12 / 36
- 21. Имитация детерминированного запроса Квантовый алгоритм может реализовать любую перестановку векторов вычислительного базиса. Этому соответствует обратимое классическое преобразование. Избавление от необратимости: использование свежей памяти, как в уже рассмотренном случае ˆ f : |x, b → |x, b ⊕ f (x) . В общем случае необратимое отображение f : A → A можно ˜ имитировать подходящим обратимым f со свежей копией памяти A в фиксированном состоянии a0 : ˜ f : (a, a0 ) → (a, f (a)) продолжается до перестановки на A × A. М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 12 / 36
- 22. Имитация вероятностного запроса Запрос по распределению pk имитируем приготовлением вектора √ |p = pk |k k в регистре аргумента и применением квантового запроса к |p, 0 . Получится √ pk |k, f (k) k Если в этот момент провести измерение, получится запрос по распределению pk . М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 13 / 36
- 23. Имитация вероятностного запроса Запрос по распределению pk имитируем приготовлением вектора √ |p = pk |k k в регистре аргумента и применением квантового запроса к |p, 0 . Получится √ pk |k, f (k) k Если в этот момент провести измерение, получится запрос по распределению pk . М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 13 / 36
- 24. Имитация вероятностного запроса Запрос по распределению pk имитируем приготовлением вектора √ |p = pk |k k в регистре аргумента и применением квантового запроса к |p, 0 . Получится √ pk |k, f (k) k Если в этот момент провести измерение, получится запрос по распределению pk . М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 13 / 36
- 25. Как избавиться от промежуточных измерений? Использовать каждый раз свежую копию регистра аргумента, выполняя обратимое копирование. Тогда распределение исходов после финального измерения в точности совпадает с распределением, порождаемым вероятностным алгоритмом. Вычисление в случае двух запросов по распределениям p (1) , p (2,k) (второе распределение зависит от результатов первого). Вектор состояния перед измерением (1) (2,k1 ) pk |k1 ⊗ pk2 |k2 , F (k1 , k2 ) = k1 k2 (1) (2,k1 ) = pk pk2 |k1 , k2 , F (k1 , k2 ) k1 ,k2 М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 14 / 36
- 26. Как избавиться от промежуточных измерений? Использовать каждый раз свежую копию регистра аргумента, выполняя обратимое копирование. Тогда распределение исходов после финального измерения в точности совпадает с распределением, порождаемым вероятностным алгоритмом. Вычисление в случае двух запросов по распределениям p (1) , p (2,k) (второе распределение зависит от результатов первого). Вектор состояния перед измерением (1) (2,k1 ) pk |k1 ⊗ pk2 |k2 , F (k1 , k2 ) = k1 k2 (1) (2,k1 ) = pk pk2 |k1 , k2 , F (k1 , k2 ) k1 ,k2 М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 14 / 36
- 27. Как избавиться от промежуточных измерений? Использовать каждый раз свежую копию регистра аргумента, выполняя обратимое копирование. Тогда распределение исходов после финального измерения в точности совпадает с распределением, порождаемым вероятностным алгоритмом. Вычисление в случае двух запросов по распределениям p (1) , p (2,k) (второе распределение зависит от результатов первого). Вектор состояния перед измерением (1) (2,k1 ) pk |k1 ⊗ pk2 |k2 , F (k1 , k2 ) = k1 k2 (1) (2,k1 ) = pk pk2 |k1 , k2 , F (k1 , k2 ) k1 ,k2 М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 14 / 36
- 28. Как избавиться от промежуточных измерений? Вычисление в случае двух запросов по распределениям p (1) , p (2,k) (второе распределение зависит от результатов первого). Вектор состояния перед измерением (1) (2,k1 ) pk1 |k1 ⊗ pk2 |k2 , F (k1 , k2 ) = k1 k2 (1) (2,k1 ) = pk1 pk2 |k1 , k2 , F (k1 , k2 ) k1 ,k2 Вероятность исхода (k1 , k2 , F (k1 , k2 )) равна (1) (2,k1 ) pk1 pk2 , как и случае вероятностного алгоритма. Для нескольких запросов вычисление аналогично. М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 15 / 36
- 29. Как избавиться от промежуточных измерений? Вычисление в случае двух запросов по распределениям p (1) , p (2,k) (второе распределение зависит от результатов первого). Вектор состояния перед измерением (1) (2,k1 ) pk1 |k1 ⊗ pk2 |k2 , F (k1 , k2 ) = k1 k2 (1) (2,k1 ) = pk1 pk2 |k1 , k2 , F (k1 , k2 ) k1 ,k2 Вероятность исхода (k1 , k2 , F (k1 , k2 )) равна (1) (2,k1 ) pk1 pk2 , как и случае вероятностного алгоритма. Для нескольких запросов вычисление аналогично. М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 15 / 36
- 30. План 1 Введение 2 Квантовый запрос 3 Моделирование классических действий квантовыми 4 Фазовый запрос 5 Задача Дойча 6 Задача Дойча – Джоза 7 Алгоритм Гровера: поиск иголки в стоге сена М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 16 / 36
- 31. Пример использования квантового «черного ящика» 1 Магическое состояние |ψ = √ (|0 2 − |1 ). М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 17 / 36
- 32. Пример использования квантового «черного ящика» 1 Магическое состояние |ψ = √ (|0 2 − |1 ). |x ⊗ |ψ Запрос и ответ: ˆ f (−1)f (x) |x ⊗ |ψ М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 17 / 36
- 33. Пример использования квантового «черного ящика» 1 Магическое состояние |ψ = √ (|0 2 − |1 ). |x ⊗ |ψ Запрос и ответ: ˆ f (−1)f (x) |x ⊗ |ψ Фазовый запрос Of : |x → (−1)f (x) |x (вспомогательный кубит не пишем его состояние не меняется). М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 17 / 36
- 34. Проверка работы фазового запроса ˆ Рассмотрим применение f к |x ⊗ |ψ : 1 ˆ f 1 |x ⊗ √ |0 − |1 − √ |x ⊗ |f (x) − |x ⊗ |1 ⊕ f (x) = → 2 2 1 |x ⊗ √ |0 − |1 , если f (x) = 0, 2 = = 1 −|x ⊗ √ |0 − |1 , если f (x) = 1, 2 1 = (−1)f (x) |x ⊗ √ |0 − |1 . 2 Упражнение ˆ Проверьте, что собственные числа оператора f равны ±1. Найдите соответствующие им собственные пространства. М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 18 / 36
- 35. Проверка работы фазового запроса ˆ Рассмотрим применение f к |x ⊗ |ψ : 1 ˆ f 1 |x ⊗ √ |0 − |1 − √ |x ⊗ |f (x) − |x ⊗ |1 ⊕ f (x) = → 2 2 1 |x ⊗ √ |0 − |1 , если f (x) = 0, 2 = = 1 −|x ⊗ √ |0 − |1 , если f (x) = 1, 2 1 = (−1)f (x) |x ⊗ √ |0 − |1 . 2 Упражнение ˆ Проверьте, что собственные числа оператора f равны ±1. Найдите соответствующие им собственные пространства. М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 18 / 36
- 36. Проверка работы фазового запроса ˆ Рассмотрим применение f к |x ⊗ |ψ : 1 ˆ f 1 |x ⊗ √ |0 − |1 − √ |x ⊗ |f (x) − |x ⊗ |1 ⊕ f (x) = → 2 2 1 |x ⊗ √ |0 − |1 , если f (x) = 0, 2 = = 1 −|x ⊗ √ |0 − |1 , если f (x) = 1, 2 1 = (−1)f (x) |x ⊗ √ |0 − |1 . 2 Упражнение ˆ Проверьте, что собственные числа оператора f равны ±1. Найдите соответствующие им собственные пространства. М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 18 / 36
- 37. Проверка работы фазового запроса ˆ Рассмотрим применение f к |x ⊗ |ψ : 1 ˆ f 1 |x ⊗ √ |0 − |1 − √ |x ⊗ |f (x) − |x ⊗ |1 ⊕ f (x) = → 2 2 1 |x ⊗ √ |0 − |1 , если f (x) = 0, 2 = = 1 −|x ⊗ √ |0 − |1 , если f (x) = 1, 2 1 = (−1)f (x) |x ⊗ √ |0 − |1 . 2 Упражнение ˆ Проверьте, что собственные числа оператора f равны ±1. Найдите соответствующие им собственные пространства. М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 18 / 36
- 38. Проверка работы фазового запроса ˆ Рассмотрим применение f к |x ⊗ |ψ : 1 ˆ f 1 |x ⊗ √ |0 − |1 − √ |x ⊗ |f (x) − |x ⊗ |1 ⊕ f (x) = → 2 2 1 |x ⊗ √ |0 − |1 , если f (x) = 0, 2 = = 1 −|x ⊗ √ |0 − |1 , если f (x) = 1, 2 1 = (−1)f (x) |x ⊗ √ |0 − |1 . 2 Упражнение ˆ Проверьте, что собственные числа оператора f равны ±1. Найдите соответствующие им собственные пространства. М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 18 / 36
- 39. План 1 Введение 2 Квантовый запрос 3 Моделирование классических действий квантовыми 4 Фазовый запрос 5 Задача Дойча 6 Задача Дойча – Джоза 7 Алгоритм Гровера: поиск иголки в стоге сена М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 19 / 36
- 40. Задача Дойча Булевых функций от одной переменной ровно 4: 0, 1, x, ¬x. Первые две из них константы, вторые две нет. Задача Дойча Определить, является ли функция, вычисляемая черным ящиком , константой. Одного запроса для решения задачи Дойча в классическом случае недостаточно: по значению в одной точке нельзя понять, является ли функция константой. М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 20 / 36
- 41. Задача Дойча Булевых функций от одной переменной ровно 4: 0, 1, x, ¬x. Первые две из них константы, вторые две нет. Задача Дойча Определить, является ли функция, вычисляемая черным ящиком , константой. Одного запроса для решения задачи Дойча в классическом случае недостаточно: по значению в одной точке нельзя понять, является ли функция константой. М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 20 / 36
- 42. Задача Дойча Булевых функций от одной переменной ровно 4: 0, 1, x, ¬x. Первые две из них константы, вторые две нет. Задача Дойча Определить, является ли функция, вычисляемая черным ящиком , константой. Одного запроса для решения задачи Дойча в классическом случае недостаточно: по значению в одной точке нельзя понять, является ли функция константой. М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 20 / 36
- 43. Квантовое решение задачи Дойча за один запрос 1 Применим к состоянию |0 унитарный оператор HOf H, где 1 1 1 H=√ (преобразование Адамара). 2 1 −1 2 Произведем измерение в вычислительном базисе. 3 Ответ 0 будет означать, что функция константа. М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 21 / 36
- 44. Квантовое решение задачи Дойча за один запрос 1 Применим к состоянию |0 унитарный оператор HOf H, где 1 1 1 H=√ (преобразование Адамара). 2 1 −1 2 Произведем измерение в вычислительном базисе. 3 Ответ 0 будет означать, что функция константа. М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 21 / 36
- 45. Квантовое решение задачи Дойча за один запрос 1 Применим к состоянию |0 унитарный оператор HOf H, где 1 1 1 H=√ (преобразование Адамара). 2 1 −1 2 Произведем измерение в вычислительном базисе. 3 Ответ 0 будет означать, что функция константа. М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 21 / 36
- 46. Проверка корректности H 1 1 O 1 1 H |0 − √ |0 + √ |1 − f √ (−1)f (0) |0 + √ (−1)f (1) |1 − → → → 2 2 2 2 1 f (0) 1 f (1) (−1) (|0 + |1 ) + (−1) (|0 − |1 ) = 2 2 1 1 = (−1)f (0) + (−1)f (1) |0 + (−1)f (0) − (−1)f (1) |1 = 2 2 ± |0 , если f константа, = . ± |1 , в противном случае. М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 22 / 36
- 47. Проверка корректности 1 1 1 H=√ 2 1 −1 H 1 1 O 1 1 H |0 − √ |0 + √ |1 − f √ (−1)f (0) |0 + √ (−1)f (1) |1 − → → → 2 2 2 2 1 f (0) 1 f (1) (−1) (|0 + |1 ) + (−1) (|0 − |1 ) = 2 2 1 1 = (−1)f (0) + (−1)f (1) |0 + (−1)f (0) − (−1)f (1) |1 = 2 2 ± |0 , если f константа, = . ± |1 , в противном случае. М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 22 / 36
- 48. Проверка корректности H 1 1 O 1 1 H |0 − √ |0 + √ |1 − f √ (−1)f (0) |0 + √ (−1)f (1) |1 − → → → 2 2 2 2 1 f (0) 1 f (1) (−1) (|0 + |1 ) + (−1) (|0 − |1 ) = 2 2 1 1 = (−1)f (0) + (−1)f (1) |0 + (−1)f (0) − (−1)f (1) |1 = 2 2 ± |0 , если f константа, = . ± |1 , в противном случае. М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 22 / 36
- 49. Проверка корректности 1 1 1 H=√ 2 1 −1 O H 1 1 O 1 1 H |0 − f− √ |0 + √ |1 − f √ (−1)f (0) |0 + √ (−1)f (1) |1 − −→ → → 2 2 2 2 1 f (0) 1 f (1) (−1) (|0 + |1 ) + (−1) (|0 − |1 ) = 2 2 1 1 = (−1)f (0) + (−1)f (1) |0 + (−1)f (0) − (−1)f (1) |1 = 2 2 ± |0 , если f константа, = . ± |1 , в противном случае. М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 22 / 36
- 50. Проверка корректности HOf H 1 1 O 1 1 H |0 − − → √ |0 + √ |1 − f √ (−1)f (0) |0 + √ (−1)f (1) |1 − −− → → 2 2 2 2 1 f (0) 1 f (1) (−1) (|0 + |1 ) + (−1) (|0 − |1 ) = 2 2 1 1 = (−1)f (0) + (−1)f (1) |0 + (−1)f (0) − (−1)f (1) |1 = 2 2 ± |0 , если f константа, = . ± |1 , в противном случае. М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 22 / 36
- 51. Проверка корректности HOf H 1 1 O 1 1 H |0 − − → √ |0 + √ |1 − f √ (−1)f (0) |0 + √ (−1)f (1) |1 − −− → → 2 2 2 2 1 f (0) 1 f (1) (−1) (|0 + |1 ) + (−1) (|0 − |1 ) = 2 2 1 1 = (−1)f (0) + (−1)f (1) |0 + (−1)f (0) − (−1)f (1) |1 = 2 2 ± |0 , если f константа, = . ± |1 , в противном случае. М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 22 / 36
- 52. План 1 Введение 2 Квантовый запрос 3 Моделирование классических действий квантовыми 4 Фазовый запрос 5 Задача Дойча 6 Задача Дойча – Джоза 7 Алгоритм Гровера: поиск иголки в стоге сена М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 23 / 36
- 53. Формулировка Задача Дойча – Джоза Дано: черный ящик , который вычисляет функцию f : {0, 1}n → {0, 1}. Заранее известно: выполняется одно из двух: (к) функция f константа; (б) функция f сбалансирована, т. е. число нулей и единиц у нее одинаково. Выяснить: какой из случаев имеет место. Это пример задачи с априорными ограничениями на входные данные (promise problem). М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 24 / 36
- 54. Формулировка Задача Дойча – Джоза Дано: черный ящик , который вычисляет функцию f : {0, 1}n → {0, 1}. Заранее известно: выполняется одно из двух: (к) функция f константа; (б) функция f сбалансирована, т. е. число нулей и единиц у нее одинаково. Выяснить: какой из случаев имеет место. Это пример задачи с априорными ограничениями на входные данные (promise problem). М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 24 / 36
- 55. Решение задачи Дойча – Джоза за один квантовый запрос 1 Применим к состоянию |0n унитарный оператор J = H ⊗n Of H ⊗n . 2 Произведем измерение в вычислительном базисе. 3 Если результат измерения |0n , то f константа, т. е. имеет место случай (к). В противном случае имеет место случай (б). М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 25 / 36
- 56. Решение задачи Дойча – Джоза за один квантовый запрос 1 Применим к состоянию |0n унитарный оператор J = H ⊗n Of H ⊗n . 2 Произведем измерение в вычислительном базисе. 3 Если результат измерения |0n , то f константа, т. е. имеет место случай (к). В противном случае имеет место случай (б). М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 25 / 36
- 57. Решение задачи Дойча – Джоза за один квантовый запрос 1 Применим к состоянию |0n унитарный оператор J = H ⊗n Of H ⊗n . 2 Произведем измерение в вычислительном базисе. 3 Если результат измерения |0n , то f константа, т. е. имеет место случай (к). В противном случае имеет место случай (б). М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 25 / 36
- 58. Действие H ⊗n на базисных векторах 1 1 1 H= √ 2 1 −1 1 H|α = √ (−1)α·β |β . 2 β∈{0,1} n H ⊗n |α = H ⊗n |α1 , . . . , αn = H|αk = k=1 n 1 = (−1)αk ·βk |βk = 2n/2 k=1 βk ∈{0,1} 1 = (−1)α1 β1 ⊕α2 β2 ⊕...⊕αn βn |β1 β2 . . . βn = 2n/2 (β1 ,...,βk )∈{0,1}n 1 = (−1)(α,β) |β . 2n/2 β∈{0,1}n М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 26 / 36
- 59. Действие H ⊗n на базисных векторах 1 H|α = √ (−1)α·β |β . 2 β∈{0,1} n H ⊗n |α = H ⊗n |α1 , . . . , αn = H|αk = k=1 n 1 = (−1)αk ·βk |βk = 2n/2 k=1 βk ∈{0,1} 1 = (−1)α1 β1 ⊕α2 β2 ⊕...⊕αn βn |β1 β2 . . . βn = 2n/2 (β1 ,...,βk )∈{0,1}n 1 = (−1)(α,β) |β . 2n/2 β∈{0,1}n М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 26 / 36
- 60. Действие H ⊗n на базисных векторах 1 H|α = √ (−1)α·β |β . 2 β∈{0,1} n H ⊗n |α = H ⊗n |α1 , . . . , αn = H|αk = k=1 n 1 = (−1)αk ·βk |βk = 2n/2 k=1 βk ∈{0,1} 1 = (−1)α1 β1 ⊕α2 β2 ⊕...⊕αn βn |β1 β2 . . . βn = 2n/2 (β1 ,...,βk )∈{0,1}n 1 = (−1)(α,β) |β . 2n/2 β∈{0,1}n М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 26 / 36
- 61. Действие H ⊗n на базисных векторах 1 H|α = √ (−1)α·β |β . 2 β∈{0,1} n H ⊗n |α = H ⊗n |α1 , . . . , αn = H|αk = k=1 n 1 = (−1)αk ·βk |βk = 2n/2 k=1 βk ∈{0,1} 1 = (−1)α1 β1 ⊕α2 β2 ⊕...⊕αn βn |β1 β2 . . . βn = 2n/2 (β1 ,...,βk )∈{0,1}n 1 = (−1)(α,β) |β . 2n/2 β∈{0,1}n М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 26 / 36
- 62. Действие H ⊗n на базисных векторах 1 H|α = √ (−1)α·β |β . 2 β∈{0,1} n H ⊗n |α = H ⊗n |α1 , . . . , αn = H|αk = k=1 n 1 = (−1)αk ·βk |βk = 2n/2 k=1 βk ∈{0,1} 1 = (−1)α1 β1 ⊕α2 β2 ⊕...⊕αn βn |β1 β2 . . . βn = 2n/2 (β1 ,...,βk )∈{0,1}n 1 = (−1)(α,β) |β . 2n/2 β∈{0,1}n М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 26 / 36
- 63. Действие H ⊗n на базисных векторах 1 H|α = √ (−1)α·β |β . 2 β∈{0,1} n H ⊗n |α = H ⊗n |α1 , . . . , αn = H|αk = k=1 n 1 = (−1)αk ·βk |βk = 2n/2 k=1 βk ∈{0,1} 1 = (−1)α1 β1 ⊕α2 β2 ⊕...⊕αn βn |β1 β2 . . . βn = 2n/2 (β1 ,...,βk )∈{0,1}n 1 = (−1)(α,β) |β . 2n/2 β∈{0,1}n М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 26 / 36
- 64. Действие H ⊗n на базисных векторах 1 H|α = √ (−1)α·β |β . 2 β∈{0,1} n H ⊗n |α = H ⊗n |α1 , . . . , αn = H|αk = k=1 n 1 = (−1)αk ·βk |βk = 2n/2 k=1 βk ∈{0,1} 1 = (−1)α1 β1 ⊕α2 β2 ⊕...⊕αn βn |β1 β2 . . . βn = 2n/2 (β1 ,...,βk )∈{0,1}n 1 = (−1)(α,β) |β . 2n/2 β∈{0,1}n М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 26 / 36
- 65. Действие J на векторе |0n H ⊗n 1 O 1 H ⊗n |0n − − −→ |α − f → (−1)f (α) |α − − −→ 2n/2 2n/2 α∈{0,1}n α∈{0,1}n 1 (−1)f (α)+(α·β) |β = 2n α∈{0,1}n β∈{0,1}n 1 = n (−1)f (α)+(α,β) |β . 2 β∈{0,1}n α∈{0,1}n М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 27 / 36
- 66. Действие J на векторе |0n H ⊗n 1 O 1 H ⊗n |0n − − −→ |α − f → (−1)f (α) |α − − −→ 2n/2 2n/2 α∈{0,1}n α∈{0,1}n 1 (−1)f (α)+(α·β) |β = 2n α∈{0,1}n β∈{0,1}n 1 = n (−1)f (α)+(α,β) |β . 2 β∈{0,1}n α∈{0,1}n М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 27 / 36
- 67. Действие J на векторе |0n H ⊗n 1 O 1 H ⊗n |0n − − −→ |α − f → (−1)f (α) |α − − −→ 2n/2 2n/2 α∈{0,1}n α∈{0,1}n 1 (−1)f (α)+(α·β) |β = 2n α∈{0,1}n β∈{0,1}n 1 = n (−1)f (α)+(α,β) |β . 2 β∈{0,1}n α∈{0,1}n М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 27 / 36
- 68. Действие J на векторе |0n O H ⊗n 1 O 1 H ⊗n |0n − f− → −− |α − f → (−1)f (α) |α − − −→ 2n/2 2n/2 α∈{0,1}n α∈{0,1}n 1 (−1)f (α)+(α·β) |β = 2n α∈{0,1}n β∈{0,1}n 1 = n (−1)f (α)+(α,β) |β . 2 β∈{0,1}n α∈{0,1}n М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 27 / 36
- 69. Действие J на векторе |0n H ⊗n O H ⊗n 1 O 1 H ⊗n |0n − − − − − −f − → |α − f → (−1)f (α) |α − − −→ 2n/2 2n/2 α∈{0,1}n α∈{0,1}n 1 (−1)f (α)+(α·β) |β = 2n α∈{0,1}n β∈{0,1}n 1 = n (−1)f (α)+(α,β) |β . 2 β∈{0,1}n α∈{0,1}n М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 27 / 36
- 70. Действие J на векторе |0n H ⊗n O H ⊗n 1 O 1 H ⊗n |0n − − − − − −f − → |α − f → (−1)f (α) |α − − −→ 2n/2 2n/2 α∈{0,1}n α∈{0,1}n 1 (−1)f (α)+(α·β) |β = 2n α∈{0,1}n β∈{0,1}n 1 = n (−1)f (α)+(α,β) |β . 2 β∈{0,1}n α∈{0,1}n М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 27 / 36
- 71. Проверка корректности решения задачи Дойча – Джоза 1 H ⊗n Of H ⊗n |0n −− − − − − −→ n (−1)f (α)+(α,β) |β 2 β∈{0,1}n α∈{0,1}n Так как (α, 0n ) = 0, то вероятность наблюдения исхода 0n равна 2 1, в случае (к), 1 (−1)f (α) = 2n 0, в случае (б). α∈{0,1}n М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 28 / 36
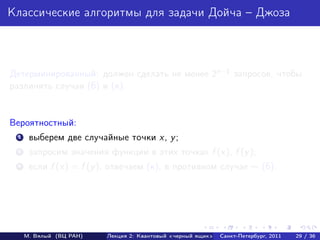
- 72. Классические алгоритмы для задачи Дойча – Джоза Детерминированный: должен сделать не менее 2n−1 запросов, чтобы различить случаи (б) и (к). Вероятностный: 1 выберем две случайные точки x, y ; 2 запросим значения функции в этих точках f (x), f (y ); 3 если f (x) = f (y ), отвечаем (к), в противном случае (б). М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 29 / 36
- 73. Классические алгоритмы для задачи Дойча – Джоза Детерминированный: должен сделать не менее 2n−1 запросов, чтобы различить случаи (б) и (к). Вероятностный: 1 выберем две случайные точки x, y ; 2 запросим значения функции в этих точках f (x), f (y ); 3 если f (x) = f (y ), отвечаем (к), в противном случае (б). М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 29 / 36
- 74. Классические алгоритмы для задачи Дойча – Джоза Детерминированный: должен сделать не менее 2n−1 запросов, чтобы различить случаи (б) и (к). Вероятностный: 1 выберем две случайные точки x, y ; 2 запросим значения функции в этих точках f (x), f (y ); 3 если f (x) = f (y ), отвечаем (к), в противном случае (б). М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 29 / 36
- 75. Классические алгоритмы для задачи Дойча – Джоза Детерминированный: должен сделать не менее 2n−1 запросов, чтобы различить случаи (б) и (к). Вероятностный: 1 выберем две случайные точки x, y ; 2 запросим значения функции в этих точках f (x), f (y ); 3 если f (x) = f (y ), отвечаем (к), в противном случае (б). М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 29 / 36
- 76. Классические алгоритмы для задачи Дойча – Джоза Детерминированный: должен сделать не менее 2n−1 запросов, чтобы различить случаи (б) и (к). Вероятностный: 1 выберем две случайные точки x, y ; 2 запросим значения функции в этих точках f (x), f (y ); 3 если f (x) = f (y ), отвечаем (к), в противном случае (б). М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 29 / 36
- 77. Вероятность ошибки Ошибка односторонняя: (к) 0 (ответ всегда правильный); (б) 1/2 (вероятность того, что f (x) = f (y )). Вероятность ошибки можно уменьшить до 2−k , повторив алгоритм k раз. Вывод Для любого ε > 0 существует вероятностный алгоритм, который решает задачу Дойча – Джоза с вероятностью ошибки < ε за O(1) запросов. М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 30 / 36
- 78. Вероятность ошибки Ошибка односторонняя: (к) 0 (ответ всегда правильный); (б) 1/2 (вероятность того, что f (x) = f (y )). Вероятность ошибки можно уменьшить до 2−k , повторив алгоритм k раз. Вывод Для любого ε > 0 существует вероятностный алгоритм, который решает задачу Дойча – Джоза с вероятностью ошибки < ε за O(1) запросов. М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 30 / 36
- 79. Вероятность ошибки Ошибка односторонняя: (к) 0 (ответ всегда правильный); (б) 1/2 (вероятность того, что f (x) = f (y )). Вероятность ошибки можно уменьшить до 2−k , повторив алгоритм k раз. Вывод Для любого ε > 0 существует вероятностный алгоритм, который решает задачу Дойча – Джоза с вероятностью ошибки < ε за O(1) запросов. М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 30 / 36
- 80. План 1 Введение 2 Квантовый запрос 3 Моделирование классических действий квантовыми 4 Фазовый запрос 5 Задача Дойча 6 Задача Дойча – Джоза 7 Алгоритм Гровера: поиск иголки в стоге сена М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 31 / 36
- 81. Задача поиска Формулировка Дано: черный ящик , который вычисляет функцию f : M → {0, 1}, где M некоторое конечное множество размера m. Заранее известно: функция равна 1 ровно в одной точке y множества M. Найти: точку y . М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 32 / 36
- 82. Нижняя оценка для вероятностных алгоритмов поиска Теорема Любой вероятностный алгоритм, решающий задачу поиска с вероятностью ошибки < ε, делает Ω(m) запросов. Доказательство М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 33 / 36
- 83. Нижняя оценка для вероятностных алгоритмов поиска Теорема Любой вероятностный алгоритм, решающий задачу поиска с вероятностью ошибки < ε, делает Ω(m) запросов. Доказательство Предполагаем, что алгоритм делает ровно k запросов и смотрит на ответы после выполнения всех запросов. (Неадаптивный алгоритм.) Это не ограничивает общности, поскольку до момента, когда найдена точка y , все ответы одинаковы и любой алгоритм ведет себя так же, как некоторый неадаптивный. М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 33 / 36
- 84. Нижняя оценка для вероятностных алгоритмов поиска Теорема Любой вероятностный алгоритм, решающий задачу поиска с вероятностью ошибки < ε, делает Ω(m) запросов. Доказательство Предполагаем, что алгоритм делает ровно k запросов и смотрит на ответы после выполнения всех запросов. (Неадаптивный алгоритм.) Это не ограничивает общности, поскольку до момента, когда найдена точка y , все ответы одинаковы и любой алгоритм ведет себя так же, как некоторый неадаптивный. Оценка в худшем случае . Ответы готовит противник , который стремится минимизировать вероятность успеха. М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 33 / 36
- 85. Нижняя оценка для вероятностных алгоритмов поиска Теорема Любой вероятностный алгоритм, решающий задачу поиска с вероятностью ошибки < ε, делает Ω(m) запросов. Доказательство Пусть pS вероятность того, что алгоритм запросил точки из множества S ⊂ M, |S| = k. М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 33 / 36
- 86. Нижняя оценка для вероятностных алгоритмов поиска Теорема Любой вероятностный алгоритм, решающий задачу поиска с вероятностью ошибки < ε, делает Ω(m) запросов. Доказательство Пусть pS вероятность того, что алгоритм запросил точки из множества S ⊂ M, |S| = k. Успех алгоритма означает, что y ∈ S. М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 33 / 36
- 87. Нижняя оценка для вероятностных алгоритмов поиска Теорема Любой вероятностный алгоритм, решающий задачу поиска с вероятностью ошибки < ε, делает Ω(m) запросов. Доказательство Пусть pS вероятность того, что алгоритм запросил точки из множества S ⊂ M, |S| = k. Успех алгоритма означает, что y ∈ S. Вероятность успеха: p(y ) = pS . S y М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 33 / 36
- 88. Нижняя оценка для вероятностных алгоритмов поиска Теорема Любой вероятностный алгоритм, решающий задачу поиска с вероятностью ошибки < ε, делает Ω(m) запросов. Доказательство Пусть pS вероятность того, что алгоритм запросил точки из множества S ⊂ M, |S| = k. Успех алгоритма означает, что y ∈ S. Вероятность успеха: p(y ) = pS . S y Существует такое y , что p(y ) k/m. Действительно, 1 1 k pS k p(y ) = pS = = . m y m y m m S y М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 33 / 36
- 89. Нижняя оценка для вероятностных алгоритмов поиска Теорема Любой вероятностный алгоритм, решающий задачу поиска с вероятностью ошибки < ε, делает Ω(m) запросов. Доказательство Вероятность успеха в худшем случае k p∗ . m Если p ∗ > 1 − ε, то k 1 − ε < p∗ , m значит, k > (1 − ε)m, т. е. k = Ω(m). М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 33 / 36
- 90. Составляющие для алгоритма Гровера фазовый запрос Oy : |x → (−1)δ(y ,x) |x ; Oy отражение относительно гиперплоскости, ортогональной |y ; 1 еще один оператор Rψ = 2|ψ ψ| − I , где |ψ = √ m x |x ; Rψ |ψ = |ψ . Если ψ|ξ = 0, то Rψ |ξ = −ξ; Rψ симметрия относительно прямой, содержащей |ψ ; итерация Гровера G = Rψ Oy . М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 34 / 36
- 91. Составляющие для алгоритма Гровера фазовый запрос Oy : |x → (−1)δ(y ,x) |x ; Oy отражение относительно гиперплоскости, ортогональной |y ; 1 еще один оператор Rψ = 2|ψ ψ| − I , где |ψ = √ m x |x ; Rψ |ψ = |ψ . Если ψ|ξ = 0, то Rψ |ξ = −ξ; Rψ симметрия относительно прямой, содержащей |ψ ; итерация Гровера G = Rψ Oy . М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 34 / 36
- 92. Составляющие для алгоритма Гровера фазовый запрос Oy : |x → (−1)δ(y ,x) |x ; Oy отражение относительно гиперплоскости, ортогональной |y ; 1 еще один оператор Rψ = 2|ψ ψ| − I , где |ψ = √ m x |x ; Rψ |ψ = |ψ . Если ψ|ξ = 0, то Rψ |ξ = −ξ; Rψ симметрия относительно прямой, содержащей |ψ ; итерация Гровера G = Rψ Oy . М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 34 / 36
- 93. Составляющие для алгоритма Гровера фазовый запрос Oy : |x → (−1)δ(y ,x) |x ; Oy отражение относительно гиперплоскости, ортогональной |y ; 1 еще один оператор Rψ = 2|ψ ψ| − I , где |ψ = √ m x |x ; Rψ |ψ = |ψ . Если ψ|ξ = 0, то Rψ |ξ = −ξ; Rψ симметрия относительно прямой, содержащей |ψ ; итерация Гровера G = Rψ Oy . М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 34 / 36
- 94. Составляющие для алгоритма Гровера фазовый запрос Oy : |x → (−1)δ(y ,x) |x ; Oy отражение относительно гиперплоскости, ортогональной |y ; 1 еще один оператор Rψ = 2|ψ ψ| − I , где |ψ = √ m x |x ; Rψ |ψ = |ψ . Если ψ|ξ = 0, то Rψ |ξ = −ξ; Rψ симметрия относительно прямой, содержащей |ψ ; итерация Гровера G = Rψ Oy . М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 34 / 36
- 95. Составляющие для алгоритма Гровера фазовый запрос Oy : |x → (−1)δ(y ,x) |x ; Oy отражение относительно гиперплоскости, ортогональной |y ; 1 еще один оператор Rψ = 2|ψ ψ| − I , где |ψ = √ m x |x ; Rψ |ψ = |ψ . Если ψ|ξ = 0, то Rψ |ξ = −ξ; Rψ симметрия относительно прямой, содержащей |ψ ; итерация Гровера G = Rψ Oy . М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 34 / 36
- 96. Квантовый алгоритм для решения задачи поиска Алгоритм Гровера 1 Приготавливаем состояние |0 . 1 2 Преобразуем состояние |0 в |ψ = √m x |x . √ 3 Применяем (π/4) m раз оператор G . 4 Измеряем полученное состояние в классическом базисе. 5 Ответ: результат измерения. Теорема √ Число запросов в алгоритме Гровера O( m). Вероятность ошибки O(1/m). М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 35 / 36
- 97. Квантовый алгоритм для решения задачи поиска Алгоритм Гровера 1 Приготавливаем состояние |0 . 1 2 Преобразуем состояние |0 в |ψ = √m x |x . √ 3 Применяем (π/4) m раз оператор G . 4 Измеряем полученное состояние в классическом базисе. 5 Ответ: результат измерения. Теорема √ Число запросов в алгоритме Гровера O( m). Вероятность ошибки O(1/m). М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 35 / 36
- 98. Квантовый алгоритм для решения задачи поиска Алгоритм Гровера 1 Приготавливаем состояние |0 . 1 2 Преобразуем состояние |0 в |ψ = √m x |x . √ 3 Применяем (π/4) m раз оператор G . 4 Измеряем полученное состояние в классическом базисе. 5 Ответ: результат измерения. Теорема √ Число запросов в алгоритме Гровера O( m). Вероятность ошибки O(1/m). М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 35 / 36
- 99. Квантовый алгоритм для решения задачи поиска Алгоритм Гровера 1 Приготавливаем состояние |0 . 1 2 Преобразуем состояние |0 в |ψ = √m x |x . √ 3 Применяем (π/4) m раз оператор G . 4 Измеряем полученное состояние в классическом базисе. 5 Ответ: результат измерения. Теорема √ Число запросов в алгоритме Гровера O( m). Вероятность ошибки O(1/m). М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 35 / 36
- 100. Квантовый алгоритм для решения задачи поиска Алгоритм Гровера 1 Приготавливаем состояние |0 . 1 2 Преобразуем состояние |0 в |ψ = √m x |x . √ 3 Применяем (π/4) m раз оператор G . 4 Измеряем полученное состояние в классическом базисе. 5 Ответ: результат измерения. Теорема √ Число запросов в алгоритме Гровера O( m). Вероятность ошибки O(1/m). М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 35 / 36
- 101. Квантовый алгоритм для решения задачи поиска Алгоритм Гровера 1 Приготавливаем состояние |0 . 1 2 Преобразуем состояние |0 в |ψ = √m x |x . √ 3 Применяем (π/4) m раз оператор G . 4 Измеряем полученное состояние в классическом базисе. 5 Ответ: результат измерения. Теорема √ Число запросов в алгоритме Гровера O( m). Вероятность ошибки O(1/m). М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 35 / 36
- 102. Итерация Гровера как поворот в плоскости G : C(|y , |ψ ) → C(|y , |ψ ) 1 |y sin ϑ = ψ|y = √ , m 1 ϑ = √ + o(m−1 ). 2ϑ m |ψ Вектор состояния поворачивается √ ϑ в направлении |y на угол ∼ 2/ m за итерацию. Начальный угол почти прямой. √ После k = (π/4) m итераций √ угол станет O(1/ m). Вероятность ошибки: квадрат сину- са угла, т. е. O(1/m). М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 36 / 36
- 103. Итерация Гровера как поворот в плоскости G : C(|y , |ψ ) → C(|y , |ψ ) 1 |y sin ϑ = ψ|y = √ , m 1 ϑ = √ + o(m−1 ). 2ϑ m |ψ Вектор состояния поворачивается √ ϑ в направлении |y на угол ∼ 2/ m за итерацию. Начальный угол почти прямой. √ После k = (π/4) m итераций √ угол станет O(1/ m). Вероятность ошибки: квадрат сину- са угла, т. е. O(1/m). М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 36 / 36
- 104. Итерация Гровера как поворот в плоскости G : C(|y , |ψ ) → C(|y , |ψ ) 1 |y sin ϑ = ψ|y = √ , m 1 ϑ = √ + o(m−1 ). 2ϑ m |ψ Вектор состояния поворачивается √ ϑ в направлении |y на угол ∼ 2/ m за итерацию. Начальный угол почти прямой. √ После k = (π/4) m итераций √ угол станет O(1/ m). Вероятность ошибки: квадрат сину- са угла, т. е. O(1/m). М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 36 / 36
- 105. Итерация Гровера как поворот в плоскости G : C(|y , |ψ ) → C(|y , |ψ ) 1 |y sin ϑ = ψ|y = √ , m 1 ϑ = √ + o(m−1 ). 2ϑ m |ψ Вектор состояния поворачивается √ ϑ в направлении |y на угол ∼ 2/ m за итерацию. Начальный угол почти прямой. √ После k = (π/4) m итераций √ угол станет O(1/ m). Вероятность ошибки: квадрат сину- са угла, т. е. O(1/m). М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 36 / 36
- 106. Итерация Гровера как поворот в плоскости G : C(|y , |ψ ) → C(|y , |ψ ) 1 |y sin ϑ = ψ|y = √ , m 1 ϑ = √ + o(m−1 ). 2ϑ m |ψ Вектор состояния поворачивается √ ϑ в направлении |y на угол ∼ 2/ m за итерацию. Начальный угол почти прямой. √ После k = (π/4) m итераций √ угол станет O(1/ m). Вероятность ошибки: квадрат сину- са угла, т. е. O(1/m). М. Вялый (ВЦ РАН) Лекция 2: Квантовый «черный ящик» Санкт-Петербург, 2011 36 / 36