20110409 quantum algorithms_vyali_lecture08
- 1. Квантовые алгоритмы: возможности и ограничения. Лекция 8: Факторизация чисел М. Вялый Вычислительный центр им. А.А.Дородницына Российской Академии наук Санкт-Петербург, 2011 М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 1 / 33
- 2. План 1 Алгоритмы оценки фазы (собственного числа) 2 Алгоритм нахождения периода 3 Сводимость задачи факторизации к задаче нахождения периода М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 2 / 33
- 3. Основная схема (схема для косинуса) U унитарный оператор, |ψ его собственный вектор с собственным числом λ = exp(2πiϕ): U|ψ = λ|ψ . Как определить собственное число? Рассмотрим такую схему: М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 3 / 33
- 4. Основная схема (схема для косинуса) U унитарный оператор, |ψ его собственный вектор с собственным числом λ = exp(2πiϕ): U|ψ = λ|ψ . Как определить собственное число? Рассмотрим такую схему: |0 H H |ξ |ψ U |ψ М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 3 / 33
- 5. Действие на управляющем кубите |0 H H |ξ |ψ U |ψ 1 1 1 1 0 1 1 1 |ξ = √ √ |0 = 2 1 −1 0 λ 2 1 −1 1 1+λ 1−λ 1 1+λ = |0 = . 2 1−λ 1+λ 2 1−λ ∗) U|ψ = λ|ψ . М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 4 / 33
- 6. Действие на управляющем кубите |0 H H |ξ |ψ U |ψ 1 1 1 1 0 1 1 1 |ξ = √ √ |0 = 2 1 −1 0 λ 2 1 −1 1 1+λ 1−λ 1 1+λ = |0 = . 2 1−λ 1+λ 2 1−λ ∗) U|ψ = λ|ψ . М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 4 / 33
- 7. Действие на управляющем кубите |0 H H |ξ |ψ U |ψ 1 1 1 1 0 1 1 1 |ξ = √ √ |0 = 2 1 −1 0 λ 2 1 −1 1 1+λ 1−λ 1 1+λ = |0 = . 2 1−λ 1+λ 2 1−λ ∗) U|ψ = λ|ψ . М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 4 / 33
- 8. Измерение управляющего кубита Вероятность исхода 0: 2 1+λ 1 Pr(|ξ , 0) = = (1 + cos(2πϕ))2 + sin(2πϕ)2 = 2 4 1 + cos(2πϕ) = 2 1 1+λ |ξ = 2 ; 1−λ λ = exp(2πiϕ); раскрываем скобки; приводим подобные. М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 5 / 33
- 9. Измерение управляющего кубита Вероятность исхода 0: 2 1+λ 1 Pr(|ξ , 0) = = (1 + cos(2πϕ))2 + sin(2πϕ)2 = 2 4 1 + cos(2πϕ) = 2 1 1+λ |ξ = 2 ; 1−λ λ = exp(2πiϕ); раскрываем скобки; приводим подобные. М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 5 / 33
- 10. Измерение управляющего кубита Вероятность исхода 0: 2 1+λ 1 Pr(|ξ , 0) = = (1 + cos(2πϕ))2 + sin(2πϕ)2 = 2 4 1 + cos(2πϕ) = 2 1 1+λ |ξ = 2 ; 1−λ λ = exp(2πiϕ); раскрываем скобки; приводим подобные. М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 5 / 33
- 11. Измерение управляющего кубита Вероятность исхода 0: 2 1+λ 1 Pr(|ξ , 0) = = (1 + cos(2πϕ))2 + sin(2πϕ)2 = 2 4 1 + cos(2πϕ) = 2 1 1+λ |ξ = 2 ; 1−λ λ = exp(2πiϕ); раскрываем скобки; приводим подобные. М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 5 / 33
- 12. Серия измерений Последовательно применяем основную схему к s различным управляющим кубитам. Измеряем каждый из s управляющих кубитов. Поскольку состояние управляющих кубитов после применения основной схемы |ξ ⊗s , результаты измерений независимы, вероятность 0 в каждом кубите равна p = (1 + cos(2πϕ))/2. Отношение числа нулей среди исходов измерения к s дает приближенное значение p. Оценка Чернова Пусть проведена серия из s испытаний Бернулли с вероятностью успеха p. Вероятность отклонения частоты ν = (число успехов)/s от вероятности оценивается как 2 Pr [|ν − p| > δ] < 2e −2δ s . М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 6 / 33
- 13. Серия измерений Последовательно применяем основную схему к s различным управляющим кубитам. Измеряем каждый из s управляющих кубитов. Поскольку состояние управляющих кубитов после применения основной схемы |ξ ⊗s , результаты измерений независимы, вероятность 0 в каждом кубите равна p = (1 + cos(2πϕ))/2. Отношение числа нулей среди исходов измерения к s дает приближенное значение p. Оценка Чернова Пусть проведена серия из s испытаний Бернулли с вероятностью успеха p. Вероятность отклонения частоты ν = (число успехов)/s от вероятности оценивается как 2 Pr [|ν − p| > δ] < 2e −2δ s . М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 6 / 33
- 14. Серия измерений Последовательно применяем основную схему к s различным управляющим кубитам. Измеряем каждый из s управляющих кубитов. Поскольку состояние управляющих кубитов после применения основной схемы |ξ ⊗s , результаты измерений независимы, вероятность 0 в каждом кубите равна p = (1 + cos(2πϕ))/2. Отношение числа нулей среди исходов измерения к s дает приближенное значение p. Оценка Чернова Пусть проведена серия из s испытаний Бернулли с вероятностью успеха p. Вероятность отклонения частоты ν = (число успехов)/s от вероятности оценивается как 2 Pr [|ν − p| > δ] < 2e −2δ s . М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 6 / 33
- 15. Серия измерений Последовательно применяем основную схему к s различным управляющим кубитам. Измеряем каждый из s управляющих кубитов. Поскольку состояние управляющих кубитов после применения основной схемы |ξ ⊗s , результаты измерений независимы, вероятность 0 в каждом кубите равна p = (1 + cos(2πϕ))/2. Отношение числа нулей среди исходов измерения к s дает приближенное значение p. Оценка Чернова Пусть проведена серия из s испытаний Бернулли с вероятностью успеха p. Вероятность отклонения частоты ν = (число успехов)/s от вероятности оценивается как 2 Pr [|ν − p| > δ] < 2e −2δ s . М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 6 / 33
- 16. Серия измерений Последовательно применяем основную схему к s различным управляющим кубитам. Измеряем каждый из s управляющих кубитов. Поскольку состояние управляющих кубитов после применения основной схемы |ξ ⊗s , результаты измерений независимы, вероятность 0 в каждом кубите равна p = (1 + cos(2πϕ))/2. Отношение числа нулей среди исходов измерения к s дает приближенное значение p. Оценка Чернова Пусть проведена серия из s испытаний Бернулли с вероятностью успеха p. Вероятность отклонения частоты ν = (число успехов)/s от вероятности оценивается как 2 Pr [|ν − p| > δ] < 2e −2δ s . М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 6 / 33
- 17. Схема для синуса Основная схема позволяет оценивать косинус фазы ϕ. Для оценки синуса нужно поменять местами действительную и мнимую части λ: |0 H H |ξ |ψ U i |ψ 2 1 + iλ 1 − sin(2πϕ) Pr(|ξ , 0) = = 2 2 М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 7 / 33
- 18. Схема для синуса Основная схема позволяет оценивать косинус фазы ϕ. Для оценки синуса нужно поменять местами действительную и мнимую части λ: |0 H H |ξ |ψ U i |ψ 2 1 + iλ 1 − sin(2πϕ) Pr(|ξ , 0) = = 2 2 М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 7 / 33
- 19. Точность оценки фазы Утверждение Фаза ϕ собственного числа λ оценивается с точностью δ и вероятностью ошибки < ε за 2s применений схем косинуса и синуса, где s = O(δ −2 log(1/ε)). Вероятность ошибки уменьшается очень быстро. Но точность уменьшается медленно: оценка с точностью 2−n требует экспоненциального времени (размера схемы). М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 8 / 33
- 20. Точность оценки фазы Утверждение Фаза ϕ собственного числа λ оценивается с точностью δ и вероятностью ошибки < ε за 2s применений схем косинуса и синуса, где s = O(δ −2 log(1/ε)). Вероятность ошибки уменьшается очень быстро. Но точность уменьшается медленно: оценка с точностью 2−n требует экспоненциального времени (размера схемы). М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 8 / 33
- 21. Уточнение значения: алгоритм экспонент Если U|ψ = λ|ψ , то U k |ψ = λk |ψ . k Оценим с точностью δ < π/8 фазы ϕk = 2k ϕ степеней U 2 при k = 0, . . . , n. Утверждение. По этим данным можно оценить фазу ϕ = ϕ1 с точностью π/2n+3 . Лемма Если |y − 2ϕ| < δ < π, то либо |y − ϕ| < δ/2, либо |y − ϕ| < δ/2, где y , y решения уравнения 2x ≡ y (mod 2π). Одно из двух решений выбирается исходя из δ-приближения ϕ. М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 9 / 33
- 22. Уточнение значения: алгоритм экспонент Если U|ψ = λ|ψ , то U k |ψ = λk |ψ . k Оценим с точностью δ < π/8 фазы ϕk = 2k ϕ степеней U 2 при k = 0, . . . , n. Утверждение. По этим данным можно оценить фазу ϕ = ϕ1 с точностью π/2n+3 . Лемма Если |y − 2ϕ| < δ < π, то либо |y − ϕ| < δ/2, либо |y − ϕ| < δ/2, где y , y решения уравнения 2x ≡ y (mod 2π). Одно из двух решений выбирается исходя из δ-приближения ϕ. М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 9 / 33
- 23. Уточнение значения: алгоритм экспонент Если U|ψ = λ|ψ , то U k |ψ = λk |ψ . k Оценим с точностью δ < π/8 фазы ϕk = 2k ϕ степеней U 2 при k = 0, . . . , n. Утверждение. По этим данным можно оценить фазу ϕ = ϕ1 с точностью π/2n+3 . Лемма Если |y − 2ϕ| < δ < π, то либо |y − ϕ| < δ/2, либо |y − ϕ| < δ/2, где y , y решения уравнения 2x ≡ y (mod 2π). Одно из двух решений выбирается исходя из δ-приближения ϕ. М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 9 / 33
- 24. Уточнение значения: алгоритм экспонент Если U|ψ = λ|ψ , то U k |ψ = λk |ψ . k Оценим с точностью δ < π/8 фазы ϕk = 2k ϕ степеней U 2 при k = 0, . . . , n. Утверждение. По этим данным можно оценить фазу ϕ = ϕ1 с точностью π/2n+3 . Лемма Если |y − 2ϕ| < δ < π, то либо |y − ϕ| < δ/2, либо |y − ϕ| < δ/2, где y , y решения уравнения 2x ≡ y (mod 2π). Одно из двух решений выбирается исходя из δ-приближения ϕ. М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 9 / 33
- 25. Уточнение значения: алгоритм экспонент Если U|ψ = λ|ψ , то U k |ψ = λk |ψ . k Оценим с точностью δ < π/8 фазы ϕk = 2k ϕ степеней U 2 при k = 0, . . . , n. Утверждение. По этим данным можно оценить фазу ϕ = ϕ1 с точностью π/2n+3 . y Лемма y Если |y − 2ϕ| < δ < π, то 2ϕ либо |y − ϕ| < δ/2, либо |y − ϕ| < δ/2, где y , y решения уравнения 2x ≡ y (mod 2π). Одно из двух решений выбирается исходя из δ-приближения ϕ. y М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 9 / 33
- 26. Уточнение значения: алгоритм экспонент Если U|ψ = λ|ψ , то U k |ψ = λk |ψ . k Оценим с точностью δ < π/8 фазы ϕk = 2k ϕ степеней U 2 при k = 0, . . . , n. Утверждение. По этим данным можно оценить фазу ϕ = ϕ1 с точностью π/2n+3 . y Лемма ϕ y Если |y − 2ϕ| < δ < π, то 2ϕ либо |y − ϕ| < δ/2, либо |y − ϕ| < δ/2, где y , y решения уравнения 2x ≡ y (mod 2π). Одно из двух решений выбирается исходя из δ-приближения ϕ. y М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 9 / 33
- 27. Работа алгоритма на произвольном входе Вопрос Что будет, если на ход алгоритма оценки фазы подать не собственный вектор? Пусть |ψ = N ck |ψk , где |ψk k=1 собственные вектора оператора U единичной длины: U|ψk = exp(2πiϕk )|ψk . Утверждение. Алгоритм оценки фазы с вероятностью |ck |2 выдает оценку фазы собственного числа λk . Собственные векторы унитарного оператора ортогональны, а амплитуды складываются. Поэтому амплитуда нулевого исхода k ck (1 + λk )/2 и 1 + cos(2πϕk ) Pr(|ψ , 0) = |ck |2 . 2 k М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 10 / 33
- 28. Работа алгоритма на произвольном входе Вопрос Что будет, если на ход алгоритма оценки фазы подать не собственный вектор? Пусть |ψ = N ck |ψk , где |ψk k=1 собственные вектора оператора U единичной длины: U|ψk = exp(2πiϕk )|ψk . Утверждение. Алгоритм оценки фазы с вероятностью |ck |2 выдает оценку фазы собственного числа λk . Собственные векторы унитарного оператора ортогональны, а амплитуды складываются. Поэтому амплитуда нулевого исхода k ck (1 + λk )/2 и 1 + cos(2πϕk ) Pr(|ψ , 0) = |ck |2 . 2 k М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 10 / 33
- 29. Работа алгоритма на произвольном входе Вопрос Что будет, если на ход алгоритма оценки фазы подать не собственный вектор? Пусть |ψ = N ck |ψk , где |ψk k=1 собственные вектора оператора U единичной длины: U|ψk = exp(2πiϕk )|ψk . Утверждение. Алгоритм оценки фазы с вероятностью |ck |2 выдает оценку фазы собственного числа λk . Собственные векторы унитарного оператора ортогональны, а амплитуды складываются. Поэтому амплитуда нулевого исхода k ck (1 + λk )/2 и 1 + cos(2πϕk ) Pr(|ψ , 0) = |ck |2 . 2 k М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 10 / 33
- 30. Работа алгоритма на произвольном входе Вопрос Что будет, если на ход алгоритма оценки фазы подать не собственный вектор? Пусть |ψ = N ck |ψk , где |ψk k=1 собственные вектора оператора U единичной длины: U|ψk = exp(2πiϕk )|ψk . Утверждение. Алгоритм оценки фазы с вероятностью |ck |2 выдает оценку фазы собственного числа λk . Собственные векторы унитарного оператора ортогональны, а амплитуды складываются. Поэтому амплитуда нулевого исхода k ck (1 + λk )/2 и 1 + cos(2πϕk ) Pr(|ψ , 0) = |ck |2 . 2 k М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 10 / 33
- 31. Работа алгоритма на произвольном входе Вопрос Что будет, если на ход алгоритма оценки фазы подать не собственный вектор? Пусть |ψ = N ck |ψk , где |ψk k=1 собственные вектора оператора U единичной длины: U|ψk = exp(2πiϕk )|ψk . Утверждение. Алгоритм оценки фазы с вероятностью |ck |2 выдает оценку фазы собственного числа λk . Собственные векторы унитарного оператора ортогональны, а амплитуды складываются. Поэтому амплитуда нулевого исхода k ck (1 + λk )/2 и 1 + cos(2πϕk ) Pr(|ψ , 0) = |ck |2 . 2 k М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 10 / 33
- 32. Работа на произвольном входе (продолжение) Что происходит при серии измерений? Раскладывая по ортогональной системе собственных векторов, убеждаемся, что амплитуда для набора исходов x1 , . . . , xs равна s ck (1 + (−1)xj λk )/2 k j=1 (для каждого собственного вектора в управляющих кубитах получаем разложимое состояние |ξk ⊗s ). Вероятность наблюдения набора исходов x1 , . . . , xs s 1 + (−1)xj cos(2πϕk ) Pr(|ψ , (x1 , . . . , xs )) = |ck |2 . 2 k j=1 Такую же вероятность дает классический процесс: выбрать с вероятностью |ck |2 параметр pk = 1+cos(2πϕk ) и провести s 2 испытаний Бернулли с этим параметром. М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 11 / 33
- 33. Работа на произвольном входе (продолжение) Что происходит при серии измерений? Раскладывая по ортогональной системе собственных векторов, убеждаемся, что амплитуда для набора исходов x1 , . . . , xs равна s ck (1 + (−1)xj λk )/2 k j=1 (для каждого собственного вектора в управляющих кубитах получаем разложимое состояние |ξk ⊗s ). Вероятность наблюдения набора исходов x1 , . . . , xs s 1 + (−1)xj cos(2πϕk ) Pr(|ψ , (x1 , . . . , xs )) = |ck |2 . 2 k j=1 Такую же вероятность дает классический процесс: выбрать с вероятностью |ck |2 параметр pk = 1+cos(2πϕk ) и провести s 2 испытаний Бернулли с этим параметром. М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 11 / 33
- 34. Работа на произвольном входе (продолжение) Что происходит при серии измерений? Раскладывая по ортогональной системе собственных векторов, убеждаемся, что амплитуда для набора исходов x1 , . . . , xs равна s ck (1 + (−1)xj λk )/2 k j=1 (для каждого собственного вектора в управляющих кубитах получаем разложимое состояние |ξk ⊗s ). Вероятность наблюдения набора исходов x1 , . . . , xs s 1 + (−1)xj cos(2πϕk ) Pr(|ψ , (x1 , . . . , xs )) = |ck |2 . 2 k j=1 Такую же вероятность дает классический процесс: выбрать с вероятностью |ck |2 параметр pk = 1+cos(2πϕk ) и провести s 2 испытаний Бернулли с этим параметром. М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 11 / 33
- 35. Алгоритмы оценки фазы: основные свойства Используя только оператор U можно оценить фазу собственного числа с точностью δ и вероятностью ошибки ε за время O(δ −2 log(1/ε). k Используя операторы U 2 , k = 0, . . . , n = O(log(1/δ)), можно оценить фазу собственного числа с точностью δ и вероятностью ошибки ε за время O(log(1/δ) log log(1/δ) log(1/ε)) (повторный логарифм возникает из-за необходимости оценивать фазу для k каждого U 2 с вероятностью ошибки < ε/n). Если применять алгоритм оценки фазы к линейной комбинации собственных векторов |ψ = N ck |ψk , то в результате работы k=1 алгоритма с вероятностью |ck |2 получается оценка фазы ϕk . М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 12 / 33
- 36. Алгоритмы оценки фазы: основные свойства Используя только оператор U можно оценить фазу собственного числа с точностью δ и вероятностью ошибки ε за время O(δ −2 log(1/ε). k Используя операторы U 2 , k = 0, . . . , n = O(log(1/δ)), можно оценить фазу собственного числа с точностью δ и вероятностью ошибки ε за время O(log(1/δ) log log(1/δ) log(1/ε)) (повторный логарифм возникает из-за необходимости оценивать фазу для k каждого U 2 с вероятностью ошибки < ε/n). Если применять алгоритм оценки фазы к линейной комбинации собственных векторов |ψ = N ck |ψk , то в результате работы k=1 алгоритма с вероятностью |ck |2 получается оценка фазы ϕk . М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 12 / 33
- 37. Алгоритмы оценки фазы: основные свойства Используя только оператор U можно оценить фазу собственного числа с точностью δ и вероятностью ошибки ε за время O(δ −2 log(1/ε). k Используя операторы U 2 , k = 0, . . . , n = O(log(1/δ)), можно оценить фазу собственного числа с точностью δ и вероятностью ошибки ε за время O(log(1/δ) log log(1/δ) log(1/ε)) (повторный логарифм возникает из-за необходимости оценивать фазу для k каждого U 2 с вероятностью ошибки < ε/n). Если применять алгоритм оценки фазы к линейной комбинации собственных векторов |ψ = N ck |ψk , то в результате работы k=1 алгоритма с вероятностью |ck |2 получается оценка фазы ϕk . М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 12 / 33
- 38. План 1 Алгоритмы оценки фазы (собственного числа) 2 Алгоритм нахождения периода 3 Сводимость задачи факторизации к задаче нахождения периода М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 13 / 33
- 39. Задача нахождения периода Формулировка задачи нахождения периода Даны: двоичные записи чисел q, a, где a < q, (a, q) = 1 ((a, q) обозначает наибольший общий делитель). Найти: период a относительно q, т. е. такое наименьшее неотрицательное число t, что at ≡ 1 (mod q). Другими словами, период это порядок числа a в мультипликативной группе вычетов (Z/qZ)∗ . Будем обозначать период числа a относительно q как perq (a). Нас интересует время работы алгоритмов, решающих задачу нахождения периода в зависимости от длины записи входа. Вместо длины записи входа будем использовать n = 1 + log q . М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 14 / 33
- 40. Задача нахождения периода Формулировка задачи нахождения периода Даны: двоичные записи чисел q, a, где a < q, (a, q) = 1 ((a, q) обозначает наибольший общий делитель). Найти: период a относительно q, т. е. такое наименьшее неотрицательное число t, что at ≡ 1 (mod q). Другими словами, период это порядок числа a в мультипликативной группе вычетов (Z/qZ)∗ . Будем обозначать период числа a относительно q как perq (a). Нас интересует время работы алгоритмов, решающих задачу нахождения периода в зависимости от длины записи входа. Вместо длины записи входа будем использовать n = 1 + log q . М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 14 / 33
- 41. Задача нахождения периода Формулировка задачи нахождения периода Даны: двоичные записи чисел q, a, где a < q, (a, q) = 1 ((a, q) обозначает наибольший общий делитель). Найти: период a относительно q, т. е. такое наименьшее неотрицательное число t, что at ≡ 1 (mod q). Другими словами, период это порядок числа a в мультипликативной группе вычетов (Z/qZ)∗ . Будем обозначать период числа a относительно q как perq (a). Нас интересует время работы алгоритмов, решающих задачу нахождения периода в зависимости от длины записи входа. Вместо длины записи входа будем использовать n = 1 + log q . М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 14 / 33
- 42. Теоретико-числовые алгоритмы Напомним, что существуют эффективные (работающие за полиномиальное время) классические алгоритмы для решения следующих задач (числа заданы двоичными записями): Найти значения арифметических операций над целыми числами. По x, q найти x mod q. По x, n, q найти x n mod q. Проверить, является ли x точной степенью (т. е., что существует y и k 2 такие, что x = y k ). По x, y найти наибольший общий делитель (x, y ). М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 15 / 33
- 43. Теоретико-числовые алгоритмы Напомним, что существуют эффективные (работающие за полиномиальное время) классические алгоритмы для решения следующих задач (числа заданы двоичными записями): Найти значения арифметических операций над целыми числами. По x, q найти x mod q. По x, n, q найти x n mod q. Проверить, является ли x точной степенью (т. е., что существует y и k 2 такие, что x = y k ). По x, y найти наибольший общий делитель (x, y ). М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 15 / 33
- 44. Теоретико-числовые алгоритмы Напомним, что существуют эффективные (работающие за полиномиальное время) классические алгоритмы для решения следующих задач (числа заданы двоичными записями): Найти значения арифметических операций над целыми числами. По x, q найти x mod q. По x, n, q найти x n mod q. Проверить, является ли x точной степенью (т. е., что существует y и k 2 такие, что x = y k ). По x, y найти наибольший общий делитель (x, y ). М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 15 / 33
- 45. Теоретико-числовые алгоритмы Напомним, что существуют эффективные (работающие за полиномиальное время) классические алгоритмы для решения следующих задач (числа заданы двоичными записями): Найти значения арифметических операций над целыми числами. По x, q найти x mod q. По x, n, q найти x n mod q. Проверить, является ли x точной степенью (т. е., что существует y и k 2 такие, что x = y k ). По x, y найти наибольший общий делитель (x, y ). М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 15 / 33
- 46. Теоретико-числовые алгоритмы Напомним, что существуют эффективные (работающие за полиномиальное время) классические алгоритмы для решения следующих задач (числа заданы двоичными записями): Найти значения арифметических операций над целыми числами. По x, q найти x mod q. По x, n, q найти x n mod q. Проверить, является ли x точной степенью (т. е., что существует y и k 2 такие, что x = y k ). По x, y найти наибольший общий делитель (x, y ). М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 15 / 33
- 47. Собственные числа циклической перестановки Рассмотрим (классический) оператор на n кубитах Ua : |x → |ax mod q . Как было сказано, для Ua существует схема полиномиального размера. Более того, существует схема полиномиального от m, n размера для 2m 2m m Ua , так как Ua : |x → |a2 x mod q . Пространство, натянутое на |1 , |a , |a2 , . . . , |at−1 , является инвариантным пространством Ua , который циклически переставляет указанные векторы. Утверждение Собственные числа циклической перестановки Ct : |j → |j + 1 mod t равны exp(2πik/t). t−1 1 Собственные векторы: |ξk = √ exp(−2πikj/t)|j . t j=0 М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 16 / 33
- 48. Собственные числа циклической перестановки Рассмотрим (классический) оператор на n кубитах Ua : |x → |ax mod q . Как было сказано, для Ua существует схема полиномиального размера. Более того, существует схема полиномиального от m, n размера для 2m 2m m Ua , так как Ua : |x → |a2 x mod q . Пространство, натянутое на |1 , |a , |a2 , . . . , |at−1 , является инвариантным пространством Ua , который циклически переставляет указанные векторы. Утверждение Собственные числа циклической перестановки Ct : |j → |j + 1 mod t равны exp(2πik/t). t−1 1 Собственные векторы: |ξk = √ exp(−2πikj/t)|j . t j=0 М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 16 / 33
- 49. Собственные числа циклической перестановки Рассмотрим (классический) оператор на n кубитах Ua : |x → |ax mod q . Как было сказано, для Ua существует схема полиномиального размера. Более того, существует схема полиномиального от m, n размера для 2m 2m m Ua , так как Ua : |x → |a2 x mod q . Пространство, натянутое на |1 , |a , |a2 , . . . , |at−1 , является инвариантным пространством Ua , который циклически переставляет указанные векторы. Утверждение Собственные числа циклической перестановки Ct : |j → |j + 1 mod t равны exp(2πik/t). t−1 1 Собственные векторы: |ξk = √ exp(−2πikj/t)|j . t j=0 М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 16 / 33
- 50. Собственные числа циклической перестановки Рассмотрим (классический) оператор на n кубитах Ua : |x → |ax mod q . Как было сказано, для Ua существует схема полиномиального размера. Более того, существует схема полиномиального от m, n размера для 2m 2m m Ua , так как Ua : |x → |a2 x mod q . Пространство, натянутое на |1 , |a , |a2 , . . . , |at−1 , является инвариантным пространством Ua , который циклически переставляет указанные векторы. Утверждение Собственные числа циклической перестановки Ct : |j → |j + 1 mod t равны exp(2πik/t). t−1 1 Собственные векторы: |ξk = √ exp(−2πikj/t)|j . t j=0 М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 16 / 33
- 51. Собственные числа циклической перестановки Рассмотрим (классический) оператор на n кубитах Ua : |x → |ax mod q . Как было сказано, для Ua существует схема полиномиального размера. Более того, существует схема полиномиального от m, n размера для 2m 2m m Ua , так как Ua : |x → |a2 x mod q . Пространство, натянутое на |1 , |a , |a2 , . . . , |at−1 , является инвариантным пространством Ua , который циклически переставляет указанные векторы. Утверждение Собственные числа циклической перестановки Ct : |j → |j + 1 mod t равны exp(2πik/t). t−1 1 Собственные векторы: |ξk = √ exp(−2πikj/t)|j . t j=0 М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 16 / 33
- 52. Доказательство утверждения Каждый из указанных векторов собственный с указанным собственным числом: t−1 1 Ct |ξk =√ exp(−2πikj/t)Ct |j = t j=0 t−1 t−1 1 1 =√ exp(−2πikj/t)|j + 1 mod t = √ exp(−2πik(j − 1)/t)|j = t j=0 t j=0 t−1 1 = exp(2πik/t) · √ exp(−2πikj/t)|j = exp(2πik/t)|ξk t j=0 Поскольку найдены t собственных чисел (вида exp(2πik/t)), то других собственных чисел нет. М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 17 / 33
- 53. Доказательство утверждения Каждый из указанных векторов собственный с указанным собственным числом: t−1 1 Ct |ξk =√ exp(−2πikj/t)Ct |j = t j=0 t−1 t−1 1 1 =√ exp(−2πikj/t)|j + 1 mod t = √ exp(−2πik(j − 1)/t)|j = t j=0 t j=0 t−1 1 = exp(2πik/t) · √ exp(−2πikj/t)|j = exp(2πik/t)|ξk t j=0 Поскольку найдены t собственных чисел (вида exp(2πik/t)), то других собственных чисел нет. М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 17 / 33
- 54. Доказательство утверждения Каждый из указанных векторов собственный с указанным собственным числом: t−1 1 Ct |ξk =√ exp(−2πikj/t)Ct |j = t j=0 t−1 t−1 1 1 =√ exp(−2πikj/t)|j + 1 mod t = √ exp(−2πik(j − 1)/t)|j = t j=0 t j=0 t−1 1 = exp(2πik/t) · √ exp(−2πikj/t)|j = exp(2πik/t)|ξk t j=0 Поскольку найдены t собственных чисел (вида exp(2πik/t)), то других собственных чисел нет. М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 17 / 33
- 55. Доказательство утверждения Каждый из указанных векторов собственный с указанным собственным числом: t−1 1 Ct |ξk =√ exp(−2πikj/t)Ct |j = t j=0 t−1 t−1 1 1 =√ exp(−2πikj/t)|j + 1 mod t = √ exp(−2πik(j − 1)/t)|j = t j=0 t j=0 t−1 1 = exp(2πik/t) · √ exp(−2πikj/t)|j = exp(2πik/t)|ξk t j=0 Поскольку найдены t собственных чисел (вида exp(2πik/t)), то других собственных чисел нет. М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 17 / 33
- 56. Доказательство утверждения Каждый из указанных векторов собственный с указанным собственным числом: t−1 1 Ct |ξk =√ exp(−2πikj/t)Ct |j = t j=0 t−1 t−1 1 1 =√ exp(−2πikj/t)|j + 1 mod t = √ exp(−2πik(j − 1)/t)|j = t j=0 t j=0 t−1 1 = exp(2πik/t) · √ exp(−2πikj/t)|j = exp(2πik/t)|ξk t j=0 Поскольку найдены t собственных чисел (вида exp(2πik/t)), то других собственных чисел нет. М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 17 / 33
- 57. Описание алгоритма нахождения периода 1 = 5 раз применим алгоритм оценки фазы с точностью 2−2n−2 и вероятностью ошибки < 1/32 к оператору Ua и вектору |1 . В ответе получим некоторые дроби pj /qj , j = 1, . . . , . 2 Для каждой дроби pj /qj найдем ближайшую дробь kj /tj со знаменателем < 2n (используя разложение в цепную дробь). 3 Выдадим в качестве ответа наименьшее общее кратное чисел tj . М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 18 / 33
- 58. Первый шаг алгоритма В силу анализа алгоритма оценки фазы и возможности вычислять m U 2 за полиномиальное от m, n время первый шаг алгоритма выполняется за полиномиальное от длины входа время. Упражнение Проверьте, что для циклической перестановки Ct t−1 1 |0 = √ |ξk t k=0 Для оператора Ua вектор |1 играет такую же роль, как вектор |0 для циклической перестановки (по циклу переставляются показатели). Значит, результаты измерений в п. 1 с вероятностью ошибки < 5/32 дают приближения с точностью 2−2n+2 к числам kj /t, где каждое kj распределено равномерно на множестве {0, . . . , t − 1}. М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 19 / 33
- 59. Первый шаг алгоритма В силу анализа алгоритма оценки фазы и возможности вычислять m U 2 за полиномиальное от m, n время первый шаг алгоритма выполняется за полиномиальное от длины входа время. Упражнение Проверьте, что для циклической перестановки Ct t−1 1 |0 = √ |ξk t k=0 Для оператора Ua вектор |1 играет такую же роль, как вектор |0 для циклической перестановки (по циклу переставляются показатели). Значит, результаты измерений в п. 1 с вероятностью ошибки < 5/32 дают приближения с точностью 2−2n+2 к числам kj /t, где каждое kj распределено равномерно на множестве {0, . . . , t − 1}. М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 19 / 33
- 60. Первый шаг алгоритма В силу анализа алгоритма оценки фазы и возможности вычислять m U 2 за полиномиальное от m, n время первый шаг алгоритма выполняется за полиномиальное от длины входа время. Упражнение Проверьте, что для циклической перестановки Ct t−1 1 |0 = √ |ξk t k=0 Для оператора Ua вектор |1 играет такую же роль, как вектор |0 для циклической перестановки (по циклу переставляются показатели). Значит, результаты измерений в п. 1 с вероятностью ошибки < 5/32 дают приближения с точностью 2−2n+2 к числам kj /t, где каждое kj распределено равномерно на множестве {0, . . . , t − 1}. М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 19 / 33
- 61. Цепные дроби Напомним факты о цепных дробях. Утверждение Каждое действительное число α раскладывается в цепную дробь 1 α = a0 + , 1 a1 + a2 + . . . подходящие дроби имеют вид pk 1 = a0 + . qk 1 a1 + 1 a2 + 1 ··· + ak М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 20 / 33
- 62. Неравенства с подходящими дробями Теорема Для подходящих дробей выполняются неравенства p0 p2 p3 p1 pk pk−1 1 < < ··· < α < ··· < < и − = . q0 q2 q3 q1 qk qk−1 qk qk−1 Следствие pk−1 1 α− < 2 . qk−1 qk−1 Теорема 1 Если |α − p/q| < , то p/q подходящая дробь для α. 2q 2 М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 21 / 33
- 63. Неравенства с подходящими дробями Теорема Для подходящих дробей выполняются неравенства p0 p2 p3 p1 pk pk−1 1 < < ··· < α < ··· < < и − = . q0 q2 q3 q1 qk qk−1 qk qk−1 Следствие pk−1 1 α− < 2 . qk−1 qk−1 Теорема 1 Если |α − p/q| < , то p/q подходящая дробь для α. 2q 2 М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 21 / 33
- 64. Неравенства с подходящими дробями Теорема Для подходящих дробей выполняются неравенства p0 p2 p3 p1 pk pk−1 1 < < ··· < α < ··· < < и − = . q0 q2 q3 q1 qk qk−1 qk qk−1 Следствие pk−1 1 α− < 2 . qk−1 qk−1 Теорема 1 Если |α − p/q| < , то p/q подходящая дробь для α. 2q 2 М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 21 / 33
- 65. Алгоритмические следствия Утверждение Подходящие дроби для рационального α вычисляются за полиномиальное от длины записи α время (как в алгоритме Евклида). Анализ шага 2 алгоритма нахождения периода Поскольку число pj /qj отличается от фазы kj /t не более, чем на 2−2n+2 , а t < 2n , то разложение в цепную дробь даст несократимую дробь kj /tj = kj /t, где kj случайный (равномерно распределенный числитель). Выполняется за полиномиальное время. М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 22 / 33
- 66. Алгоритмические следствия Утверждение Подходящие дроби для рационального α вычисляются за полиномиальное от длины записи α время (как в алгоритме Евклида). Анализ шага 2 алгоритма нахождения периода Поскольку число pj /qj отличается от фазы kj /t не более, чем на 2−2n+2 , а t < 2n , то разложение в цепную дробь даст несократимую дробь kj /tj = kj /t, где kj случайный (равномерно распределенный числитель). Выполняется за полиномиальное время. М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 22 / 33
- 67. Шаг 3 алгоритма нахождения периода Лемма Пусть по равномерному распределению независимо выбраны числа 0 kj < t, 1 j , 2. Тогда вероятность того, что наименьшее общее кратное знаменателей 2 несократимых дробей, равных kj /t, отлично от t, меньше π · 2− . 3 Доказательство Вероятность того, что k1 , . . . , k имеют общий простой делитель p, не больше, чем 1/p . Поэтому вероятность того, что k1 , . . . , k не взаимно просты в совокупности (равносильно тому, что НОК не равен t), не выше ∞ 1 π2 − < ·2 . k 3 k=2 М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 23 / 33
- 68. Шаг 3 алгоритма нахождения периода Лемма Пусть по равномерному распределению независимо выбраны числа 0 kj < t, 1 j , 2. Тогда вероятность того, что наименьшее общее кратное знаменателей 2 несократимых дробей, равных kj /t, отлично от t, меньше π · 2− . 3 Доказательство Вероятность того, что k1 , . . . , k имеют общий простой делитель p, не больше, чем 1/p . Поэтому вероятность того, что k1 , . . . , k не взаимно просты в совокупности (равносильно тому, что НОК не равен t), не выше ∞ 1 π2 − < ·2 . k 3 k=2 М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 23 / 33
- 69. Шаг 3 алгоритма нахождения периода Лемма Пусть по равномерному распределению независимо выбраны числа 0 kj < t, 1 j , 2. Тогда вероятность того, что наименьшее общее кратное знаменателей 2 несократимых дробей, равных kj /t, отлично от t, меньше π · 2− . 3 Доказательство Вероятность того, что k1 , . . . , k имеют общий простой делитель p, не больше, чем 1/p . Поэтому вероятность того, что k1 , . . . , k не взаимно просты в совокупности (равносильно тому, что НОК не равен t), не выше ∞ 1 π2 − < ·2 . k 3 k=2 М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 23 / 33
- 70. Анализ алгоритма нахождения периода Алгоритм работает за полиномиальное от длины входа время (НОК находится с помощью алгоритма Евклида и формулы (x, y ) · [x, y ] = xy ). Вероятность ошибки не превосходит π2 1 1 +5 · < . 3 32 3 Теорема Существует полиномиальный квантовый алгоритм нахождения периода, вероятность ошибки которого < 1/3. М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 24 / 33
- 71. Анализ алгоритма нахождения периода Алгоритм работает за полиномиальное от длины входа время (НОК находится с помощью алгоритма Евклида и формулы (x, y ) · [x, y ] = xy ). Вероятность ошибки не превосходит π2 1 1 +5 · < . 3 32 3 Теорема Существует полиномиальный квантовый алгоритм нахождения периода, вероятность ошибки которого < 1/3. М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 24 / 33
- 72. Анализ алгоритма нахождения периода Алгоритм работает за полиномиальное от длины входа время (НОК находится с помощью алгоритма Евклида и формулы (x, y ) · [x, y ] = xy ). Вероятность ошибки не превосходит π2 1 1 +5 · < . 3 32 3 Теорема Существует полиномиальный квантовый алгоритм нахождения периода, вероятность ошибки которого < 1/3. М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 24 / 33
- 73. План 1 Алгоритмы оценки фазы (собственного числа) 2 Алгоритм нахождения периода 3 Сводимость задачи факторизации к задаче нахождения периода М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 25 / 33
- 74. Задача факторизации Задача факторизации числа Дано: натуральное число y в двоичной записи. Найти: разложение y на простые множители α α α y = p1 1 p2 2 · . . . · pk k . Прагматическое свидетельство трудности факторизации На предположении о трудности задачи факторизации основаны практические алгоритмы криптографии (шифрование с открытым ключом, например). Если бы существовал нетрудоемкий алгоритм ее решения, кто-нибудь уже взломал бы RSA. М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 26 / 33
- 75. Задача факторизации Задача факторизации числа Дано: натуральное число y в двоичной записи. Найти: разложение y на простые множители α α α y = p1 1 p2 2 · . . . · pk k . Прагматическое свидетельство трудности факторизации На предположении о трудности задачи факторизации основаны практические алгоритмы криптографии (шифрование с открытым ключом, например). Если бы существовал нетрудоемкий алгоритм ее решения, кто-нибудь уже взломал бы RSA. М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 26 / 33
- 76. Полиномиальный квантовый алгоритм для задачи факторизации Теорема Существует полиномиальная вероятностная сводимость задачи факторизации к задаче нахождения периода. Следствие Существует полиномиальный квантовый алгоритм факторизации числа. Замечания Исходный квантовый алгоритм Шора также использовал эту сводимость. Квантовая часть (нахождение периода) была устроена иначе и основывалась на преобразовании Фурье (переход к базису собственных векторов для циклического сдвига). Алгоритм Шора также включает использование цепных дробей. М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 27 / 33
- 77. Полиномиальный квантовый алгоритм для задачи факторизации Теорема Существует полиномиальная вероятностная сводимость задачи факторизации к задаче нахождения периода. Следствие Существует полиномиальный квантовый алгоритм факторизации числа. Замечания Исходный квантовый алгоритм Шора также использовал эту сводимость. Квантовая часть (нахождение периода) была устроена иначе и основывалась на преобразовании Фурье (переход к базису собственных векторов для циклического сдвига). Алгоритм Шора также включает использование цепных дробей. М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 27 / 33
- 78. Полиномиальный квантовый алгоритм для задачи факторизации Теорема Существует полиномиальная вероятностная сводимость задачи факторизации к задаче нахождения периода. Следствие Существует полиномиальный квантовый алгоритм факторизации числа. Замечания Исходный квантовый алгоритм Шора также использовал эту сводимость. Квантовая часть (нахождение периода) была устроена иначе и основывалась на преобразовании Фурье (переход к базису собственных векторов для циклического сдвига). Алгоритм Шора также включает использование цепных дробей. М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 27 / 33
- 79. Описание сводимости Мы построим процедуру, которая использует подпрограмму вычисления периода и находит некоторый нетривиальный делитель числа y с вероятностью 1/2 или сообщает, что y простое. Из этой процедуры уже легко получить полиномиальный алгоритм факторизации: 1 Повторяя процедуру нахождения делителя s раз, уменьшаем вероятность ошибки до 2−s . 2 Применяем такую усиленную процедуру O(log y ) раз, вероятность ошибки ухудшается до O(log y /2s ), но этого достаточно. М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 28 / 33
- 80. Описание сводимости Мы построим процедуру, которая использует подпрограмму вычисления периода и находит некоторый нетривиальный делитель числа y с вероятностью 1/2 или сообщает, что y простое. Из этой процедуры уже легко получить полиномиальный алгоритм факторизации: 1 Повторяя процедуру нахождения делителя s раз, уменьшаем вероятность ошибки до 2−s . 2 Применяем такую усиленную процедуру O(log y ) раз, вероятность ошибки ухудшается до O(log y /2s ), но этого достаточно. М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 28 / 33
- 81. Описание сводимости Мы построим процедуру, которая использует подпрограмму вычисления периода и находит некоторый нетривиальный делитель числа y с вероятностью 1/2 или сообщает, что y простое. Из этой процедуры уже легко получить полиномиальный алгоритм факторизации: 1 Повторяя процедуру нахождения делителя s раз, уменьшаем вероятность ошибки до 2−s . 2 Применяем такую усиленную процедуру O(log y ) раз, вероятность ошибки ухудшается до O(log y /2s ), но этого достаточно. М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 28 / 33
- 82. Описание сводимости Мы построим процедуру, которая использует подпрограмму вычисления периода и находит некоторый нетривиальный делитель числа y с вероятностью 1/2 или сообщает, что y простое. Из этой процедуры уже легко получить полиномиальный алгоритм факторизации: 1 Повторяя процедуру нахождения делителя s раз, уменьшаем вероятность ошибки до 2−s . 2 Применяем такую усиленную процедуру O(log y ) раз, вероятность ошибки ухудшается до O(log y /2s ), но этого достаточно. М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 28 / 33
- 83. Процедура нахождения делителя 1 Проверяем четность y . Если y четное, то выдаем ответ 2 . 2 Проверяем, извлекается ли из y нацело корень k-й степени при k = 2, . . . , log2 y . Если y = mk , то ответ m . 3 Выбираем случайно и равновероятно a среди чисел от 1 до y , вычисляем r = pery (a) (используя имеющийся по предположению алгоритм нахождения периода) и, если r нечетное, то ответ y простое . 4 Если же r четное, то находим d = (ar /2 − 1, y ) алгоритмом Евклида и если d > 1, то ответ d , иначе ответ y простое . Из построения ясно, что алгоритм работает полиномиальное время. Ясно также, что неправильным может быть лишь ответ y простое . М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 29 / 33
- 84. Процедура нахождения делителя 1 Проверяем четность y . Если y четное, то выдаем ответ 2 . 2 Проверяем, извлекается ли из y нацело корень k-й степени при k = 2, . . . , log2 y . Если y = mk , то ответ m . 3 Выбираем случайно и равновероятно a среди чисел от 1 до y , вычисляем r = pery (a) (используя имеющийся по предположению алгоритм нахождения периода) и, если r нечетное, то ответ y простое . 4 Если же r четное, то находим d = (ar /2 − 1, y ) алгоритмом Евклида и если d > 1, то ответ d , иначе ответ y простое . Из построения ясно, что алгоритм работает полиномиальное время. Ясно также, что неправильным может быть лишь ответ y простое . М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 29 / 33
- 85. Процедура нахождения делителя 1 Проверяем четность y . Если y четное, то выдаем ответ 2 . 2 Проверяем, извлекается ли из y нацело корень k-й степени при k = 2, . . . , log2 y . Если y = mk , то ответ m . 3 Выбираем случайно и равновероятно a среди чисел от 1 до y , вычисляем r = pery (a) (используя имеющийся по предположению алгоритм нахождения периода) и, если r нечетное, то ответ y простое . 4 Если же r четное, то находим d = (ar /2 − 1, y ) алгоритмом Евклида и если d > 1, то ответ d , иначе ответ y простое . Из построения ясно, что алгоритм работает полиномиальное время. Ясно также, что неправильным может быть лишь ответ y простое . М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 29 / 33
- 86. Процедура нахождения делителя 1 Проверяем четность y . Если y четное, то выдаем ответ 2 . 2 Проверяем, извлекается ли из y нацело корень k-й степени при k = 2, . . . , log2 y . Если y = mk , то ответ m . 3 Выбираем случайно и равновероятно a среди чисел от 1 до y , вычисляем r = pery (a) (используя имеющийся по предположению алгоритм нахождения периода) и, если r нечетное, то ответ y простое . 4 Если же r четное, то находим d = (ar /2 − 1, y ) алгоритмом Евклида и если d > 1, то ответ d , иначе ответ y простое . Из построения ясно, что алгоритм работает полиномиальное время. Ясно также, что неправильным может быть лишь ответ y простое . М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 29 / 33
- 87. Процедура нахождения делителя 1 Проверяем четность y . Если y четное, то выдаем ответ 2 . 2 Проверяем, извлекается ли из y нацело корень k-й степени при k = 2, . . . , log2 y . Если y = mk , то ответ m . 3 Выбираем случайно и равновероятно a среди чисел от 1 до y , вычисляем r = pery (a) (используя имеющийся по предположению алгоритм нахождения периода) и, если r нечетное, то ответ y простое . 4 Если же r четное, то находим d = (ar /2 − 1, y ) алгоритмом Евклида и если d > 1, то ответ d , иначе ответ y простое . Из построения ясно, что алгоритм работает полиномиальное время. Ясно также, что неправильным может быть лишь ответ y простое . М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 29 / 33
- 88. Анализ процедуры нахождения делителя Лемма Процедура нахождения делителя выдает собственный делитель y с вероятностью не меньше 1 − 1/2k−1 , где k число различных простых делителей y . (Для простого y эта вероятность равна 0.) Китайская теорема об остатках k αj Если y = j=1 pj разложение на простые, то k α (Z/y Z) ∼ ∗ = (Z/pj j )∗ . j=1 Цикличность мультипликативной группы вычетов по модулю p α Группа (Z/p α Z)∗ циклическая, т. е. существует такой вычет g , что (Z/p α Z)∗ = {g s : 0 s < p α − p α−1 }. М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 30 / 33
- 89. Анализ процедуры нахождения делителя Лемма Процедура нахождения делителя выдает собственный делитель y с вероятностью не меньше 1 − 1/2k−1 , где k число различных простых делителей y . (Для простого y эта вероятность равна 0.) Китайская теорема об остатках k αj Если y = j=1 pj разложение на простые, то k α (Z/y Z) ∼ ∗ = (Z/pj j )∗ . j=1 Цикличность мультипликативной группы вычетов по модулю p α Группа (Z/p α Z)∗ циклическая, т. е. существует такой вычет g , что (Z/p α Z)∗ = {g s : 0 s < p α − p α−1 }. М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 30 / 33
- 90. Анализ процедуры нахождения делителя Лемма Процедура нахождения делителя выдает собственный делитель y с вероятностью не меньше 1 − 1/2k−1 , где k число различных простых делителей y . (Для простого y эта вероятность равна 0.) Китайская теорема об остатках k αj Если y = j=1 pj разложение на простые, то k α (Z/y Z) ∼ ∗ = (Z/pj j )∗ . j=1 Цикличность мультипликативной группы вычетов по модулю p α Группа (Z/p α Z)∗ циклическая, т. е. существует такой вычет g , что (Z/p α Z)∗ = {g s : 0 s < p α − p α−1 }. М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 30 / 33
- 91. Когда процедура отвечает «y — простое» Пусть rj = per(pαj ) a = 2sj rj , где rj нечетноe. j Утверждение. Ответ y простое равносилен s1 = s2 = · · · = sk . Если r = pery (a) нечетное, то rj нечетное для каждого j, поскольку r равен НОК rj для всех j (китайская теорема). Это случай s1 = s2 = · · · = sk = 0. Если r = pery (a) четное, то (ar /2 + 1)(ar /2 − 1) ≡ 0 (mod y ). Так как ar /2 ≡ 1 (mod y ), в этом случае процедура выдаст ответ y простое только тогда, когда ar /2 ≡ −1 (mod y ). α α arj /2 ≡ −1 (mod pj j ) (используем цикличность (Z/pj j Z)∗ ). Если s1 = s2 = . . . = sk 1, то и ar /2 ≡ −1 (mod y ) (используем китайскую теорему об остатках). М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 31 / 33
- 92. Когда процедура отвечает «y — простое» Пусть rj = per(pαj ) a = 2sj rj , где rj нечетноe. j Утверждение. Ответ y простое равносилен s1 = s2 = · · · = sk . Если r = pery (a) нечетное, то rj нечетное для каждого j, поскольку r равен НОК rj для всех j (китайская теорема). Это случай s1 = s2 = · · · = sk = 0. Если r = pery (a) четное, то (ar /2 + 1)(ar /2 − 1) ≡ 0 (mod y ). Так как ar /2 ≡ 1 (mod y ), в этом случае процедура выдаст ответ y простое только тогда, когда ar /2 ≡ −1 (mod y ). α α arj /2 ≡ −1 (mod pj j ) (используем цикличность (Z/pj j Z)∗ ). Если s1 = s2 = . . . = sk 1, то и ar /2 ≡ −1 (mod y ) (используем китайскую теорему об остатках). М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 31 / 33
- 93. Когда процедура отвечает «y — простое» Пусть rj = per(pαj ) a = 2sj rj , где rj нечетноe. j Утверждение. Ответ y простое равносилен s1 = s2 = · · · = sk . Если r = pery (a) нечетное, то rj нечетное для каждого j, поскольку r равен НОК rj для всех j (китайская теорема). Это случай s1 = s2 = · · · = sk = 0. Если r = pery (a) четное, то (ar /2 + 1)(ar /2 − 1) ≡ 0 (mod y ). Так как ar /2 ≡ 1 (mod y ), в этом случае процедура выдаст ответ y простое только тогда, когда ar /2 ≡ −1 (mod y ). α α arj /2 ≡ −1 (mod pj j ) (используем цикличность (Z/pj j Z)∗ ). Если s1 = s2 = . . . = sk 1, то и ar /2 ≡ −1 (mod y ) (используем китайскую теорему об остатках). М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 31 / 33
- 94. Когда процедура отвечает «y — простое» Пусть rj = per(pαj ) a = 2sj rj , где rj нечетноe. j Утверждение. Ответ y простое равносилен s1 = s2 = · · · = sk . Если r = pery (a) нечетное, то rj нечетное для каждого j, поскольку r равен НОК rj для всех j (китайская теорема). Это случай s1 = s2 = · · · = sk = 0. Если r = pery (a) четное, то (ar /2 + 1)(ar /2 − 1) ≡ 0 (mod y ). Так как ar /2 ≡ 1 (mod y ), в этом случае процедура выдаст ответ y простое только тогда, когда ar /2 ≡ −1 (mod y ). α α arj /2 ≡ −1 (mod pj j ) (используем цикличность (Z/pj j Z)∗ ). Если s1 = s2 = . . . = sk 1, то и ar /2 ≡ −1 (mod y ) (используем китайскую теорему об остатках). М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 31 / 33
- 95. Когда процедура отвечает «y — простое» Пусть rj = per(pαj ) a = 2sj rj , где rj нечетноe. j Утверждение. Ответ y простое равносилен s1 = s2 = · · · = sk . Если r = pery (a) нечетное, то rj нечетное для каждого j, поскольку r равен НОК rj для всех j (китайская теорема). Это случай s1 = s2 = · · · = sk = 0. Если r = pery (a) четное, то (ar /2 + 1)(ar /2 − 1) ≡ 0 (mod y ). Так как ar /2 ≡ 1 (mod y ), в этом случае процедура выдаст ответ y простое только тогда, когда ar /2 ≡ −1 (mod y ). α α arj /2 ≡ −1 (mod pj j ) (используем цикличность (Z/pj j Z)∗ ). Если s1 = s2 = . . . = sk 1, то и ar /2 ≡ −1 (mod y ) (используем китайскую теорему об остатках). М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 31 / 33
- 96. Завершение доказательства утверждения Если не все sj равны, то при некотором m получим arm /2 ≡ 1 (mod pmm ), т. е. ar /2 ≡ −1 (mod y ). α Действительно, r делится на 2s , где s = maxj sj . Если не все sm < s, то 2sm rm | r /2, что и означает arm /2 ≡ 1 (mod pmm ). α М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 32 / 33
- 97. Завершение доказательства утверждения Если не все sj равны, то при некотором m получим arm /2 ≡ 1 (mod pmm ), т. е. ar /2 ≡ −1 (mod y ). α Действительно, r делится на 2s , где s = maxj sj . Если не все sm < s, то 2sm rm | r /2, что и означает arm /2 ≡ 1 (mod pmm ). α М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 32 / 33
- 98. Оценка вероятности события s1 = s2 = . . . = sk По китайской теореме об остатках случайный равномерный выбор a есть то же самое, что независимый случайный равномерный α выбор всех aj ≡ a (mod pj j ). Оценим вероятность события s1 = s при независимом выборе a1 . α α Пусть p1 1 − 1 = 2t q, q нечетное, g образующая (Z/p1 1 Z)∗ . Тогда t−s |{a1 : s1 = s}| = |{g 2 m : m нечетное}| = q, если s = 0, = 1 s−1 1 t (2s − 2s−1 )q = 2 q < 2 q, если s > 0, 2 2 поэтому вероятность s1 = s не больше 1/2. Отсюда получаем, что вероятность события s1 = s2 = . . . = sk не выше 1/2k−1 . Лемма доказана. Значит, вероятность ошибки процедуры нахождения делителя < 1/2. М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 33 / 33
- 99. Оценка вероятности события s1 = s2 = . . . = sk По китайской теореме об остатках случайный равномерный выбор a есть то же самое, что независимый случайный равномерный α выбор всех aj ≡ a (mod pj j ). Оценим вероятность события s1 = s при независимом выборе a1 . α α Пусть p1 1 − 1 = 2t q, q нечетное, g образующая (Z/p1 1 Z)∗ . Тогда t−s |{a1 : s1 = s}| = |{g 2 m : m нечетное}| = q, если s = 0, = 1 s−1 1 t (2s − 2s−1 )q = 2 q < 2 q, если s > 0, 2 2 поэтому вероятность s1 = s не больше 1/2. Отсюда получаем, что вероятность события s1 = s2 = . . . = sk не выше 1/2k−1 . Лемма доказана. Значит, вероятность ошибки процедуры нахождения делителя < 1/2. М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 33 / 33
- 100. Оценка вероятности события s1 = s2 = . . . = sk По китайской теореме об остатках случайный равномерный выбор a есть то же самое, что независимый случайный равномерный α выбор всех aj ≡ a (mod pj j ). Оценим вероятность события s1 = s при независимом выборе a1 . α α Пусть p1 1 − 1 = 2t q, q нечетное, g образующая (Z/p1 1 Z)∗ . Тогда t−s |{a1 : s1 = s}| = |{g 2 m : m нечетное}| = q, если s = 0, = 1 s−1 1 t (2s − 2s−1 )q = 2 q < 2 q, если s > 0, 2 2 поэтому вероятность s1 = s не больше 1/2. Отсюда получаем, что вероятность события s1 = s2 = . . . = sk не выше 1/2k−1 . Лемма доказана. Значит, вероятность ошибки процедуры нахождения делителя < 1/2. М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 33 / 33
- 101. Оценка вероятности события s1 = s2 = . . . = sk По китайской теореме об остатках случайный равномерный выбор a есть то же самое, что независимый случайный равномерный α выбор всех aj ≡ a (mod pj j ). Оценим вероятность события s1 = s при независимом выборе a1 . α α Пусть p1 1 − 1 = 2t q, q нечетное, g образующая (Z/p1 1 Z)∗ . Тогда t−s |{a1 : s1 = s}| = |{g 2 m : m нечетное}| = q, если s = 0, = 1 s−1 1 t (2s − 2s−1 )q = 2 q < 2 q, если s > 0, 2 2 поэтому вероятность s1 = s не больше 1/2. Отсюда получаем, что вероятность события s1 = s2 = . . . = sk не выше 1/2k−1 . Лемма доказана. Значит, вероятность ошибки процедуры нахождения делителя < 1/2. М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 33 / 33
- 102. Оценка вероятности события s1 = s2 = . . . = sk По китайской теореме об остатках случайный равномерный выбор a есть то же самое, что независимый случайный равномерный α выбор всех aj ≡ a (mod pj j ). Оценим вероятность события s1 = s при независимом выборе a1 . α α Пусть p1 1 − 1 = 2t q, q нечетное, g образующая (Z/p1 1 Z)∗ . Тогда t−s |{a1 : s1 = s}| = |{g 2 m : m нечетное}| = q, если s = 0, = 1 s−1 1 t (2s − 2s−1 )q = 2 q < 2 q, если s > 0, 2 2 поэтому вероятность s1 = s не больше 1/2. Отсюда получаем, что вероятность события s1 = s2 = . . . = sk не выше 1/2k−1 . Лемма доказана. Значит, вероятность ошибки процедуры нахождения делителя < 1/2. М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 33 / 33
- 103. Оценка вероятности события s1 = s2 = . . . = sk По китайской теореме об остатках случайный равномерный выбор a есть то же самое, что независимый случайный равномерный α выбор всех aj ≡ a (mod pj j ). Оценим вероятность события s1 = s при независимом выборе a1 . α α Пусть p1 1 − 1 = 2t q, q нечетное, g образующая (Z/p1 1 Z)∗ . Тогда t−s |{a1 : s1 = s}| = |{g 2 m : m нечетное}| = q, если s = 0, = 1 s−1 1 t (2s − 2s−1 )q = 2 q < 2 q, если s > 0, 2 2 поэтому вероятность s1 = s не больше 1/2. Отсюда получаем, что вероятность события s1 = s2 = . . . = sk не выше 1/2k−1 . Лемма доказана. Значит, вероятность ошибки процедуры нахождения делителя < 1/2. М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 33 / 33


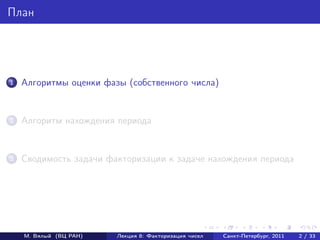









![Серия измерений
Последовательно применяем основную схему к s различным
управляющим кубитам.
Измеряем каждый из s управляющих кубитов.
Поскольку состояние управляющих кубитов после применения
основной схемы |ξ ⊗s , результаты измерений независимы,
вероятность 0 в каждом кубите равна p = (1 + cos(2πϕ))/2.
Отношение числа нулей среди исходов измерения к s дает
приближенное значение p.
Оценка Чернова
Пусть проведена серия из s испытаний Бернулли с вероятностью
успеха p. Вероятность отклонения частоты ν = (число успехов)/s
от вероятности оценивается как
2
Pr [|ν − p| > δ] < 2e −2δ s .
М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 6 / 33](https://image.slidesharecdn.com/20110409quantumalgorithmsvyalilecture08-110410105446-phpapp02/85/20110409-quantum-algorithms_vyali_lecture08-12-320.jpg)
![Серия измерений
Последовательно применяем основную схему к s различным
управляющим кубитам.
Измеряем каждый из s управляющих кубитов.
Поскольку состояние управляющих кубитов после применения
основной схемы |ξ ⊗s , результаты измерений независимы,
вероятность 0 в каждом кубите равна p = (1 + cos(2πϕ))/2.
Отношение числа нулей среди исходов измерения к s дает
приближенное значение p.
Оценка Чернова
Пусть проведена серия из s испытаний Бернулли с вероятностью
успеха p. Вероятность отклонения частоты ν = (число успехов)/s
от вероятности оценивается как
2
Pr [|ν − p| > δ] < 2e −2δ s .
М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 6 / 33](https://image.slidesharecdn.com/20110409quantumalgorithmsvyalilecture08-110410105446-phpapp02/85/20110409-quantum-algorithms_vyali_lecture08-13-320.jpg)
![Серия измерений
Последовательно применяем основную схему к s различным
управляющим кубитам.
Измеряем каждый из s управляющих кубитов.
Поскольку состояние управляющих кубитов после применения
основной схемы |ξ ⊗s , результаты измерений независимы,
вероятность 0 в каждом кубите равна p = (1 + cos(2πϕ))/2.
Отношение числа нулей среди исходов измерения к s дает
приближенное значение p.
Оценка Чернова
Пусть проведена серия из s испытаний Бернулли с вероятностью
успеха p. Вероятность отклонения частоты ν = (число успехов)/s
от вероятности оценивается как
2
Pr [|ν − p| > δ] < 2e −2δ s .
М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 6 / 33](https://image.slidesharecdn.com/20110409quantumalgorithmsvyalilecture08-110410105446-phpapp02/85/20110409-quantum-algorithms_vyali_lecture08-14-320.jpg)
![Серия измерений
Последовательно применяем основную схему к s различным
управляющим кубитам.
Измеряем каждый из s управляющих кубитов.
Поскольку состояние управляющих кубитов после применения
основной схемы |ξ ⊗s , результаты измерений независимы,
вероятность 0 в каждом кубите равна p = (1 + cos(2πϕ))/2.
Отношение числа нулей среди исходов измерения к s дает
приближенное значение p.
Оценка Чернова
Пусть проведена серия из s испытаний Бернулли с вероятностью
успеха p. Вероятность отклонения частоты ν = (число успехов)/s
от вероятности оценивается как
2
Pr [|ν − p| > δ] < 2e −2δ s .
М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 6 / 33](https://image.slidesharecdn.com/20110409quantumalgorithmsvyalilecture08-110410105446-phpapp02/85/20110409-quantum-algorithms_vyali_lecture08-15-320.jpg)
![Серия измерений
Последовательно применяем основную схему к s различным
управляющим кубитам.
Измеряем каждый из s управляющих кубитов.
Поскольку состояние управляющих кубитов после применения
основной схемы |ξ ⊗s , результаты измерений независимы,
вероятность 0 в каждом кубите равна p = (1 + cos(2πϕ))/2.
Отношение числа нулей среди исходов измерения к s дает
приближенное значение p.
Оценка Чернова
Пусть проведена серия из s испытаний Бернулли с вероятностью
успеха p. Вероятность отклонения частоты ν = (число успехов)/s
от вероятности оценивается как
2
Pr [|ν − p| > δ] < 2e −2δ s .
М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 6 / 33](https://image.slidesharecdn.com/20110409quantumalgorithmsvyalilecture08-110410105446-phpapp02/85/20110409-quantum-algorithms_vyali_lecture08-16-320.jpg)





















































![Анализ алгоритма нахождения периода
Алгоритм работает за полиномиальное от длины входа время
(НОК находится с помощью алгоритма Евклида и формулы
(x, y ) · [x, y ] = xy ).
Вероятность ошибки не превосходит
π2 1 1
+5 · < .
3 32 3
Теорема
Существует полиномиальный квантовый алгоритм нахождения
периода, вероятность ошибки которого < 1/3.
М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 24 / 33](https://image.slidesharecdn.com/20110409quantumalgorithmsvyalilecture08-110410105446-phpapp02/85/20110409-quantum-algorithms_vyali_lecture08-70-320.jpg)
![Анализ алгоритма нахождения периода
Алгоритм работает за полиномиальное от длины входа время
(НОК находится с помощью алгоритма Евклида и формулы
(x, y ) · [x, y ] = xy ).
Вероятность ошибки не превосходит
π2 1 1
+5 · < .
3 32 3
Теорема
Существует полиномиальный квантовый алгоритм нахождения
периода, вероятность ошибки которого < 1/3.
М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 24 / 33](https://image.slidesharecdn.com/20110409quantumalgorithmsvyalilecture08-110410105446-phpapp02/85/20110409-quantum-algorithms_vyali_lecture08-71-320.jpg)
![Анализ алгоритма нахождения периода
Алгоритм работает за полиномиальное от длины входа время
(НОК находится с помощью алгоритма Евклида и формулы
(x, y ) · [x, y ] = xy ).
Вероятность ошибки не превосходит
π2 1 1
+5 · < .
3 32 3
Теорема
Существует полиномиальный квантовый алгоритм нахождения
периода, вероятность ошибки которого < 1/3.
М. Вялый (ВЦ РАН) Лекция 8: Факторизация чисел Санкт-Петербург, 2011 24 / 33](https://image.slidesharecdn.com/20110409quantumalgorithmsvyalilecture08-110410105446-phpapp02/85/20110409-quantum-algorithms_vyali_lecture08-72-320.jpg)






























