Peer instructions questions for basic quantum mechanics
- 1. Planck/Einstein: E = hν = ω De Broglie: h p = = k λ Classical wave equa3on: ∂ 2 Ψ(x,t) 2 ∂ Ψ(x,t) 2 =v ∂t 2 ∂x 2 Schrödinger Ψ(x,t) = Aei(kx − ω t ) ∂ ∂ ∂ ax Ψ = −iωΨ ⇒ i Ψ = EΨ e = aeax ∂t ∂t ∂x ∂2 2 ∂2 ⎛ p2 ⎞ Ψ = −k Ψ ⇒ − 2 Ψ=⎜ Ψ ∂x 2 2m ∂x 2 ⎝ 2m ⎟ ⎠
- 2. Time dependent Schrödinger equa3on ∂ ⎛ p2 ⎞ i Ψ = EΨ = ⎜ +V⎟ Ψ ∂t ⎝ 2m ⎠ ∂ ⎛ 2 ∂2 ⎞ i Ψ = ⎜ − +V⎟ Ψ ∂t ⎝ 2m ∂x 2 ⎠ ∂ ˆ i Ψ = HΨ ∂t Time independent Schrödinger equa3on (standing wave solu0on) Ψ(x,t) = Ψ(x)e−iEt / ∂ i Ψ = EΨ ∂t ˆ H Ψ(x) = EΨ(x)
- 3. Par3cle in a box H atom 0 0<x<L V= 1 C x < 0 or x > L V =− r ⎛ 2 2 ⎞ − ⎜ 2m ∇ + V ⎟ Ψ n = En Ψ n ⎝ ⎠ Rigid Rotor Harmonic oscillator (rota0onal spectroscopy) (vibra0onal spectroscopy) 1⎛ 1 ∂ ∂ 1 ∂2 ⎞ V = kx 1 2 ∇ = 2⎜ 2 sin θ + 2 2 r ⎝ sin θ ∂θ ∂θ sin θ ∂φ 2 ⎟ ⎠ V =0
- 4. ⎛ 2 2 1 ⎞ ⎜ − 2m ∇ − r ⎟ Ψ n = En Ψ n ⎝ ⎠ −me4 13.6 eV En = =− n = 1, 2, 3,... 2 ( 4πε 0 ) n 2 2 2 n2 1 −r Ψ1 = e 1s π 1 ⎛ r⎞ Ψ 2,0 = ⎜ 1 − ⎟ e− r /2 2s 8π ⎝ 2⎠ 1 Ψ 2,1 = xe− r /2 2 p 4 2π Probability P(x) = Ψ(x) dx 2 Probability density (amplitude) Ψ(x) 2
- 5. Par3cle in a box H atom 0 0<x<L V= 1 C x < 0 or x > L V =− r ⎛ 2 2 ⎞ − ⎜ 2m ∇ + V ⎟ Ψ n = En Ψ n ⎝ ⎠ Harmonic oscillator Probability density (vibra0onal spectroscopy) (amplitude) Ψ(x) 2 V = 1 kx 2 2
- 6. ⎛ 2 2 1 ⎞ ⎜ − 2m ∇ − r ⎟ Ψ n = En Ψ n ⎝ ⎠ −me4 13.6 eV En = =− n = 1, 2, 3,... 2 ( 4πε 0 ) n 2 2 2 n2 1 −r Ψ1 = e 1s π 1 ⎛ r⎞ Ψ 2,0 = ⎜ 1 − ⎟ e− r /2 2s 8π ⎝ 2⎠ 1 Ψ 2,1 = xe− r /2 2 p 4 2π Probability P(x) = Ψ(x) dx 2 Probability density Ψ(x) 2
- 8. End of video slides
- 9. Please start your Socra0ve app or go to m.socra3ve.com in your browser Room number 9076
- 10. ⎛ 2 2 1 ⎞ ⎜ − 2m ∇ − r ⎟ Ψ n = En Ψ n ⎝ ⎠ −me4 13.6 eV En = =− n = 1, 2, 3,... 2 ( 4πε 0 ) n 2 2 2 n2 1 −r Ψ1 = e 1s π What is the most probable posi0on of an electron in the 1s orbital of H atom? A inside the nucleus B outside the nucleus C don’t know
- 11. ⎛ 2 2 1 ⎞ ⎜ − 2m ∇ − r ⎟ Ψ n = En Ψ n ⎝ ⎠ −me4 13.6 eV En = =− n = 1, 2, 3,... 2 ( 4πε 0 ) n 2 2 2 n2 1 −r Ψ1 = e 1s π What is the most probable posi0on of an electron in the 1s orbital of H atom? A inside the nucleus B outside the nucleus C don’t know
- 12. ⎛ 2 2 1 ⎞ ⎜ − 2m ∇ − r ⎟ Ψ n = En Ψ n ⎝ ⎠ −me4 13.6 eV En = =− n = 1, 2, 3,... 2 ( 4πε 0 ) n 2 2 2 n2 1 −r Ψ1 = e 1s π What is the most probable posi0on of an electron in the 1s orbital of H atom? Probability P(x) = Ψ(x) dx 2 Very small for nucleus
- 13. Par0cle in a box Harmonic oscillator Why is the probability density higher at the edges than in the middle for high energy solu0ons to the Schrödinger equa0on for the harmonic oscillator? Enter your answer on Socra0ve
- 14. ⎛ 2 2 1 ⎞ ⎜ − 2m ∇ − r ⎟ Ψ n = En Ψ n ⎝ ⎠ −me4 13.6 eV En = =− n = 1, 2, 3,... 2 ( 4πε 0 ) n 2 2 2 n2 1 −r Ψ1 = e 1s π 1 ⎛ r⎞ Ψ 2,0 = ⎜ 1 − ⎟ e− r /2 2s 8π ⎝ 2⎠ What is the lowest excita3on energy of the H atom? A 13.6 eV B 10.2 eV C 6.8 eV D don’t know
- 15. ⎛ 2 2 1 ⎞ ⎜ − 2m ∇ − r ⎟ Ψ n = En Ψ n ⎝ ⎠ −me4 13.6 eV En = =− n = 1, 2, 3,... 2 ( 4πε 0 ) n 2 2 2 n2 1 −r Ψ1 = e 1s π 1 ⎛ r⎞ Ψ 2,0 = ⎜ 1 − ⎟ e− r /2 2s 8π ⎝ 2⎠ What is the lowest excita3on energy of the H atom? A 13.6 eV B 10.2 eV C 6.8 eV D don’t know
- 16. ⎛ 2 2 1 ⎞ ⎜ − 2m ∇ − r ⎟ Ψ n = En Ψ n ⎝ ⎠ ΔE = E2 − E1 −me4 13.6 eV −13.6 −13.6 En = =− n = 1, 2, 3,... = − 2 ( 4πε 0 ) n 4 1 2 2 2 n2 = 10.2 eV 1 −r Ψ1 = e 1s π 1 ⎛ r⎞ Ψ 2,0 = ⎜ 1 − ⎟ e− r /2 2s 8π ⎝ 2⎠ What is the lowest excita3on energy of the H atom? A 13.6 eV B 10.2 eV C 6.8 eV D don’t know
- 17. +4.2 eV -‐4.5 eV
- 18. Par3cle in a box L = 2.94 nm ⎛ 2 ⎞ 0 0<x<L h2n2 ⎜ − ∇ + V ⎟ Ψ n = En Ψ n V= En = n = 1, 2, 3... ⎝ 2m ⎠ C x < 0 or x > L 8mL2 h2 E12 − E11 = (12 − 11 ) 2 = 1.60 × 10 −19 J (1.0 eV) 2 +4.2 eV 2 8mL -‐4.5 eV Experiment = 2.5 eV (497 nm / blue green)
- 19. ⎛ 2π x ⎞ 1/2 ⎛ 2⎞ Ψ(x) = ⎜ ⎟ sin ⎜ ⎝ L⎠ ⎝ L ⎟ ⎠
- 20. Par3cle in a box: some useful predic3ons for nano sized systems h2 ΔE = En +1 − En = (2n + 1) 8mL2 Excita0on energy (band gap) Increases with n Decreases faster with L ΔE decreases with molecular size Absorp0on wave length (λ) increases hc λ= with molecular size ΔE 8mc L2 λ= h (2n + 1) L2 ( = 3.30 × 10 m 12 −1 ) (2n + 1) ⎛ −1 1 m ⎞ L2 = ⎜ 3.30 × 10 m × 9 12 ⎟ ⎝ 10 nm ⎠ (2n + 1) L2 ( = 3300 nm −1 ) (2n + 1)
- 21. Based on L2 λ = ( 3300 nm −1 ) (2n + 1) Where does 1,3,5-‐hexatriene absorb light? (you can use h[p://dgu.ki.ku.dk/molcalc/editor to es0mate length) A ca 50 nm B ca 100 nm C ca 300 nm D don’t know
- 22. Based on L2 λ = ( 3300 nm −1 ) (2n + 1) Where does 1,3,5-‐hexatriene absorb light? (you can use h[p://dgu.ki.ku.dk/molcalc/editor to es0mate length) L2 A ca 50 nm λ = ( 3300 nm −1 ) (2n + 1) 0.8 2 B ca 100 nm ( = 3300 nm ) −1 7 C ca 300 nm = ( 3300 nm ) −1 ( 0.09 ) D don’t know = 302 nm
- 23. Based on L2 λ = ( 3300 nm −1 ) (2n + 1) Where does 1,3,5-‐hexatriene absorb light? (you can use h[p://dgu.ki.ku.dk/molcalc/editor to es0mate length) L2 λ = ( 3300 nm −1 ) (2n + 1) 0.8 2 ( = 3300 nm ) −1 7 Experiment: 258 nm = ( 3300 nm ) −1 ( 0.09 ) = 302 nm
- 24. Based on Orbital theory Where does 1,3,5-‐hexatriene absorb light? (you can use h[p://dgu.ki.ku.dk/molcalc/editor to compute orbital energies) A ca 50 nm B ca 100 nm C ca 300 nm D don’t know
- 25. Based on Orbital theory Where does 1,3,5-‐hexatriene absorb light? (you can use h[p://dgu.ki.ku.dk/molcalc/editor to compute orbital energies) hc λ= ΔE A ca 50 nm 1240 eV nm = B ca 100 nm (5.72 − (−6.28)) eV = 103 nm C ca 300 nm D don’t know Experiment: 258 nm
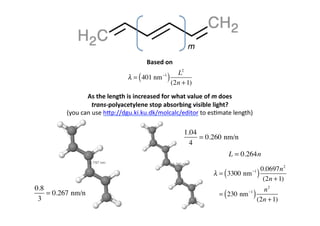
- 26. m Based on L2 λ = ( 3300 nm −1 ) (2n + 1) As the length is increased for what value of m does trans-‐polyacetylene stop absorbing visible light? (you can use h[p://dgu.ki.ku.dk/molcalc/editor to es0mate length)
- 27. m Based on L2 λ = ( 401 nm −1 ) (2n + 1) As the length is increased for what value of m does trans-‐polyacetylene stop absorbing visible light? (you can use h[p://dgu.ki.ku.dk/molcalc/editor to es0mate length) 1.04 = 0.260 nm/n 4 L = 0.264n 0.0697n 2 λ = ( 3300 nm −1 ) (2n + 1) 0.8 n2 3 = 0.267 nm/n ( = 230 nm −1 ) (2n + 1)
- 28. m Based on L2 λ = ( 401 nm −1 ) (2n + 1) As the length is increased for what value of m does trans-‐polyacetylene stop absorbing visible light? (you can use h[p://dgu.ki.ku.dk/molcalc/editor to es0mate length) n2 λ = ( 230 nm −1 ) (2n + 1) λ Visible light stops at about 800 nm n2 ( 800 = 230 nm −1 ) (2n + 1) ⇒ n ≈ 7 or 8 m ≈ 5 or 6 n