Oblique triangles 02
15 recomendaciones3,152 vistas
Este documento explica cómo resolver problemas de triángulos que no son rectángulos usando la ley de los senos y la ley de los cosenos. Explica que en un triángulo cualquiera existen seis magnitudes básicas (tres lados y tres ángulos) y que si se conocen tres de estas magnitudes, se pueden determinar las tres restantes usando las leyes trigonométricas. Proporciona ejemplos numéricos para ilustrar cómo aplicar estas leyes.
Oblique triangles 02
- 2. El triángulo rectángulo La resolución de problemas en los que se presentan triángulos rectángulos es sencilla; se aplica el Teorema de Pitágoras o cualquiera de las funciones trigonométricas básicas para determinar los lados y ángulos que sea necesario.
- 3. El triángulo rectángulo La resolución de problemas en los que se presentan triángulos rectángulos es sencilla; se aplica el Teorema de Pitágoras o cualquiera de las funciones trigonométricas básicas para determinar los lados y ángulos que sea necesario.
- 4. Problemas diferentes ¿Cómo resolvemos problemas en los que los triángulos que se presentan, no tienen ningún ángulo recto?
- 5. Problemas diferentes ¿Cómo resolvemos problemas en los que los triángulos que se presentan, no tienen ningún ángulo recto? ¿Cómo determinamos las medidas faltantes de un triángulo si ninguno de sus ángulos mide 90°?
- 6. ¿Cómo determinamos las medidas faltantes de un triángulo si ninguno de sus ángulos mide 90°? Problemas diferentes
- 7. Disponemos de dos herramientas: Problemas diferentes Ley de los cosenos Ley de los senos
- 8. Ley de los senos y ley de los cosenos. En un triángulo cualquiera, existen seis magnitudes básicas: tres lados y tres ángulos.
- 9. Ley de los senos y ley de los cosenos. En un triángulo cualquiera, existen seis magnitudes básicas: tres lados y tres ángulos. Si se conocen tres de estas magnitudes, se pueden determinar las tres restantes.
- 10. Ley de los senos y ley de los cosenos. En un triángulo cualquiera, existen seis magnitudes básicas: tres lados y tres ángulos. Si se conocen tres de estas magnitudes, se pueden determinar las tres restantes. Dependiendo de las magnitudes que se conozcan, se aplica la ley de los senos o la ley de los cosenos.
- 13. Resolución de problemas Como ya vimos, es necesario conocer, al menos, tres datos para poder aplicar la fórmula de la ley de los cosenos.
- 14. Resolución de problemas Se toma la fórmula que contiene los tres datos conocidos. Si se conocen a, b, y el ángulo C, entonces se toma esa fórmula:
- 15. Resolución de problemas Se toma la fórmula que contiene los tres datos conocidos. Si se conocen a, b, y el ángulo C, entonces se toma esa fórmula:
- 16. Resolución de problemas Como ya vimos, es necesario conocer, al menos, tres datos para poder aplicar la fórmula de la ley de los cosenos. ¿Pueden ser 3 datos cualesquiera?
- 17. Resolución de problemas Como ya vimos, es necesario conocer, al menos, tres datos para poder aplicar la fórmula de la ley de los cosenos. ¿Pueden ser 3 datos cualesquiera? Para aplicar la ley de los senos, no pueden ser tres datos cualesquiera, pero en este caso, ¿Qué piensas?
- 18. Resolución de problemas Por ejemplo: Si se conocen a, b, y el ángulo A, resulta Se genera una ecuación de segundo grado, pero no estamos seguros si tiene solución. Resuelve el siguiente ejemplo y determina si pueden ser tres datos cualesquiera.
- 19. Con referencia a la figura adjunta, resuelve el siguiente problema aplicando la ley de los cosenos: 1. A= 36°, a = NL ×12, b = NL ×17
- 20. Después de resolver el problema, realiza una investigación y determina si la ley de los cosenos puede aplicarse a cualquier grupo de tres datos. En caso de que sea así, busca y publica un ejemplo de cada combinación de datos y sus restricciones.
- 21. En el triángulo de la figura el lado a mide 5 cm; el lado b, 6 cm, y el ángulo C, 56°. Ejemplo 1 (Tomado de la parte 1) La primera parte de este material se encuentra en el enlace: http://licmata-math.blogspot.mx/2016/01/learn-to-solve-easily-oblique-triangles.html
- 22. En el triángulo de la figura el lado a mide 5 cm; el lado b, 6 cm, y el ángulo C, 56°. Ejemplo 1 (Tomado de la parte 1) En la parte 1 de esta presentación, se pedía resolver este problema aplicando la ley de los senos y no fue posible, tal como se muestra a continuación.
- 23. En el triángulo de la figura el lado a mide 5 cm; el lado b, 6 cm, y el ángulo C, 56°. Al sustituir en la fórmula obtenemos: Ejemplo 1 (Aplicando ley de los senos)
- 24. Al sustituir en la fórmula obtenemos: No es posible despejar ninguna de las magnitudes desconocidas. Ejemplo 1 (Aplicando ley de los senos)
- 25. Al sustituir en la fórmula obtenemos: No es posible despejar ninguna de las magnitudes desconocidas. Este problema no puede ser resuelto mediante la ley de los senos, debemos buscar una estrategia diferente. Ejemplo 1 (Aplicando ley de los senos)
- 26. Al sustituir en la fórmula obtenemos: No es posible despejar ninguna de las magnitudes desconocidas. Ahora veremos cómo resolver este problema mediante la ley de los cosenos. Ejemplo 1 (Aplicando ley de los senos)
- 27. Ejemplo 1 (Aplicando ley de los cosenos) En el triángulo de la figura el lado a mide 5 cm; el lado b, 6 cm, y el ángulo C, 56°.
- 28. Ejemplo 1 (Aplicando ley de los cosenos) En el triángulo de la figura el lado a mide 5 cm; el lado b, 6 cm, y el ángulo C, 56°.
- 29. Ejemplo 1 (Aplicando ley de los cosenos) En el triángulo de la figura el lado a mide 5 cm; el lado b, 6 cm, y el ángulo C, 56°. Esta fórmula es la que podemos emplear porque contiene los datos disponibles.
- 30. Ejemplo 1 (Aplicando ley de los cosenos) En el triángulo de la figura el lado a mide 5 cm; el lado b, 6 cm, y el ángulo C, 56°. Sólo es necesario despejar y sustituir para determinar el valor de c.
- 31. Ejemplo 1 (Aplicando ley de los cosenos) En el triángulo de la figura el lado a mide 5 cm; el lado b, 6 cm, y el ángulo C, 56°.
- 32. Ejemplo 1 (Aplicando ley de los cosenos) En el triángulo de la figura el lado a mide 5 cm; el lado b, 6 cm, y el ángulo C, 56°.
- 33. Ejemplo 1 (Aplicando ley de los cosenos) En el triángulo de la figura el lado a mide 5 cm; el lado b, 6 cm, y el ángulo C, 56°.
- 34. Ejemplo 1 (Aplicando ley de los cosenos) En el triángulo de la figura el lado a mide 5 cm; el lado b, 6 cm, y el ángulo C, 56°.
- 35. Ejemplo 1 (Aplicando ley de los cosenos) En el triángulo de la figura el lado a mide 5 cm; el lado b, 6 cm, y el ángulo C, 56°. Se ha avanzado en la solución del problema, ahora conocemos los tres lados del triángulo y un ángulo. Falta determinar los ángulos A y B.
- 36. Para terminar el problema, despeja las otras dos fórmulas para determinar los ángulos faltantes y verifica que la suma de A, B y C, sea 180°.
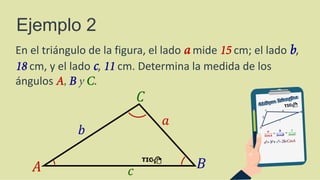
- 37. En el triángulo de la figura, el lado a mide 15 cm; el lado b, 18 cm, y el lado c, 11 cm. Determina la medida de los ángulos A, B y C. Ejemplo 2
- 38. En el triángulo de la figura, el lado a mide 15 cm; el lado b, 18 cm, y el lado c, 11 cm. Determina la medida de los ángulos A, B y C. Ejemplo 2 Se conocen los tres lados, por lo tanto deben despejarse los tres cosenos de los ángulos.
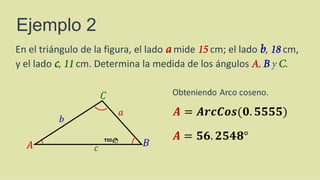
- 39. En el triángulo de la figura, el lado a mide 15 cm; el lado b, 18 cm, y el lado c, 11 cm. Determina la medida de los ángulos A, B y C. Ejemplo 2 Se conocen los tres lados, por lo tanto deben despejarse los tres cosenos de los ángulos. Comenzaremos por determinar el valor del ángulo A.
- 40. En el triángulo de la figura, el lado a mide 15 cm; el lado b, 18 cm, y el lado c, 11 cm. Determina la medida de los ángulos A, B y C. Ejemplo 2
- 41. En el triángulo de la figura, el lado a mide 15 cm; el lado b, 18 cm, y el lado c, 11 cm. Determina la medida de los ángulos A, B y C. Ejemplo 2
- 42. En el triángulo de la figura, el lado a mide 15 cm; el lado b, 18 cm, y el lado c, 11 cm. Determina la medida de los ángulos A, B y C. Ejemplo 2
- 43. En el triángulo de la figura, el lado a mide 15 cm; el lado b, 18 cm, y el lado c, 11 cm. Determina la medida de los ángulos A, B y C. Ejemplo 2
- 44. En el triángulo de la figura, el lado a mide 15 cm; el lado b, 18 cm, y el lado c, 11 cm. Determina la medida de los ángulos A, B y C. Ejemplo 2 Se ha avanzado en la solución del problema, ahora conocemos los tres lados del triángulo y un ángulo. Falta determinar los ángulos B y C.
- 45. Para terminar el problema, despeja las otras dos fórmulas para determinar los ángulos faltantes y verifica que la suma de A, B y C, sea 180°.
- 46. Se dice que la matemática no es un deporte de espectadores, es decir, no podemos afirmar que hemos aprendido matemáticas en tanto no hayamos resuelto, en forma autónoma, algunos problemas. La siguiente diapositiva contiene ejercicios que deberás resolver para comprender el tema. La primera parte de este material se encuentra en el enlace: http://licmata-math.blogspot.mx/2016/01/learn-to-solve-easily-oblique-triangles.html
- 48. Gracias Por su atención Fuentes de información en línea http://licmata-math.blogspot.mx/ http://www.scoop.it/t/mathematics-learning https://www.facebook.com/licemata https://www.linkedin.com/in/licmata http://www.slideshare.net/licmata Twitter @licemata