Prop inv blog
- 1. Tipos de funciones. Interpretación de fenómenos sociales y económicos ©Abel Martín & Marta Martín Sierra www.aulamatematica.com Dadas las siguientes funciones, (a) ¿Qué tipo de función se trata? Indica las asíntotas verticales y el dominio de la función (b) Calcula los puntos de corte con el eje OX por métodos algebraicos y haz un esbozo de su representación gráfica, señalando el nombre de las asíntotas en el caso de que las tenga. 02. y = x 1− RESOLUCIÓN Es una función de proporcionalidad inversa. Asíntotas verticales Comprobamos los valores que hacen cero el denominador: x = 0 Dominio: Dom (y) = ℜ – {0} Puntos de corte con el eje OX x 1− = 0 – 1 = 0 Imposible No corta en ningún punto al eje OX (A) TABLA REALIZADA CON CALCULADORA 0 ℜ Estudio del comportamiento de la función respecto a x = 0 por la izquierda Tiende a (+ ∞) Estudio del comportamiento de la función respecto a x = 0 por la derecha Tiende a (– ∞)
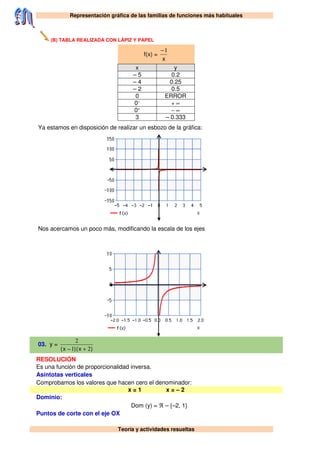
- 2. Representación gráfica de las familias de funciones más habituales Teoría y actividades resueltas (B) TABLA REALIZADA CON LÁPIZ Y PAPEL f(x) = x 1− x y – 5 0.2 – 4 0.25 – 2 0.5 0 ERROR 0– + ∞ 0+ – ∞ 3 – 0.333 Ya estamos en disposición de realizar un esbozo de la gráfica: Nos acercamos un poco más, modificando la escala de los ejes 03. y = )x()x( 21 2 +− RESOLUCIÓN Es una función de proporcionalidad inversa. Asíntotas verticales Comprobamos los valores que hacen cero el denominador: x = 1 x = – 2 Dominio: Dom (y) = ℜ – {–2, 1} Puntos de corte con el eje OX
- 3. Tipos de funciones. Interpretación de fenómenos sociales y económicos ©Abel Martín & Marta Martín Sierra www.aulamatematica.com )x()x( 21 2 +− = 0 2 = 0 Imposible No corta en ningún punto al eje OX (A) TABLA REALIZADA CON CALCULADORA - 2 ℜ Estudio del comportamiento de la función respecto a x = – 2 por la izquierda Tiende a (+ ∞) Estudio del comportamiento de la función respecto a x = – 2 por la derecha Tiende a (– ∞) 1 ℜ Estudio del comportamiento de la función respecto a x = 1 por la izquierda Tiende a (– ∞) Estudio del comportamiento de la función respecto a x = 1 por la derecha
- 4. Representación gráfica de las familias de funciones más habituales Teoría y actividades resueltas Tiende a (+ ∞) (B) TABLA REALIZADA CON LÁPIZ Y PAPEL y = )x()x( 21 2 +− x y – 5 0.11 – 4 0.20 – 3 0.50 – 2 Asíntota – 2– + ∞ – 2+ – ∞ – 1.5 – 1.6 – 1 – 1 – 0.5 - 0.888 0 – 1 1 Asíntota 1– – ∞ 1+ + ∞ 2 0.50 3 0.20 Asíntota horizontal Con la tabla de valores podríamos intuir cuál la asíntota horizontal, observando valores muy alejados... x y – 200 0.00005 200 0.00005 Asíntota horizontal y = 0 Ya estamos en disposición de realizar un esbozo de la gráfica: 04. y = )x()x( 23 2 −+ − RESOLUCIÓN Es una función de proporcionalidad inversa. Asíntotas verticales Comprobamos los valores que hacen cero el denominador: x = – 3 x = – 2 Dominio:
- 5. Tipos de funciones. Interpretación de fenómenos sociales y económicos ©Abel Martín & Marta Martín Sierra www.aulamatematica.com Dom (y) = ℜ – {– 3, 2} Puntos de corte con el eje OX )x()x( 23 2 −+ − = 0 – 2 = 0 Imposible No corta en ningún punto al eje OX (A) TABLA REALIZADA CON CALCULADORA - 3 ℜ Estudio del comportamiento de la función respecto a x = – 3 por la izquierda Tiende a (- ∞) Estudio del comportamiento de la función respecto a x = 2 por la derecha Tiende a (+ ∞) (B) TABLA REALIZADA CON LÁPIZ Y PAPEL y = )x()x( 23 2 −+ − x y – 5 – 0.142 – 4 – 0.333 – 3 Asíntota – 3– - ∞ – 3+ + ∞ – 2 0.50 – 1.5 0.38 – 1 0.333
- 6. Representación gráfica de las familias de funciones más habituales Teoría y actividades resueltas – 0.5 0.32 0 0.333 0.50 0.38 1 0.50 2 Asíntota 2– - ∞ 2+ + ∞ 2.5 – 0.727 3 – 0.333 Asíntota horizontal Con la tabla de valores podríamos intuir cuál la asíntota horizontal, observando valores muy alejados... x y – 200 0.00005 200 0.00004 Asíntota horizontal y = 0 Ya estamos en disposición de realizar un esbozo de la gráfica: