Lecture 14 modulacion digital parte 2

Universidad Nacional de Ingeniería
Comunicaciones II
Conferencia 14: Modulación Digital Parte 2
UNIDAD V: TRANSMISIÓN PASABANDA DE SEÑALES
DIGITALES
Instructor: Israel M. Zamora, MS Telecommunications Management
Profesor Titular, Departamento de Sistemas Digitales y Telecomunicaciones.
Universidad Nacional de Ingeniería
2S 2009- I. Zamora UniV-Conf14: Tx Pasabanda de Señ Dig. 1

Outline
• Esquema de modulación QPSK
Coherente
• Esquema MSK Coherente
• Espectro de Potencia para QPSK y
MSK Coherente
• Esquema de modulación QAM
Coherente
• Esquema BFSK No coherente
• PSK Diferencial (DPSK)

Outline
• Otros esquemas M-arios
– Caso: Esquema M-ario PSK
– Caso: Esquema M-ario FSK
–Modulación multiportador y OFDM
• Eficiencia de ancho de banda en
sistemas M-arios
• Capacidad de Canal de Shannon con
AWGN
• Aplicaciones en módems

Esquema de modulación QPSK Coherente
QPSK: Quadrature Phase Shift Keying
ì
2E
= + £ £
cos(2π f t θ ); 0 t T
T
c i
0; Otra parte
s (t)
con θ (2i 1) π
4
; i 1, 2, 3, 4.
i
E =
Energía de señal transmitida por símbolo
T =
Periodo de duración de Símbolo
f n
; n E para número entero de ciclos
T
= c
Î
c c
Aplicando la siguiente
identidad tendremos:
ì
ù
cos ( i ) cos( π f t ) E
- é - p úû
E
é - p =
s (t) c c
i
j (t) = 2
2 j (t) =
2
sen( 2 π f t )
1 c 2 c 2S 2009- I. Zamora UniV-Conf14: Tx Pasabanda de Señ Dig. 4
i
= -
=
ïî
ïí
de onda portadora.
cos (A+B) =cos Acos B-senAsenB
ïî
ïí
£ £ úû
êë
ù
êë
; Otra parte
sen ( i ) sen( π f t ); t T
T
T
0
2 0
4
2 2 2 1
4
2 2 1
De allí que las funciones ortonormales corresponden a:
cos( π f t )
T
T

i ij = j + j = j =å=
s (t) s ( t ) s ( t ) s ( t ), i , , , j i i
1 1 2 2 1 2 3 4
úû
ì é p úû
j - - j £ £ é - p =
s (t) E cos ( 2 i 1 ) ( t ) Esen ( i ) ( t ); t T 1 2
i
= - é - p úû
= é - p
2 1 1 2 s E cos ( i ) , s Esen ( i ) i i
é
- é - p úû
= = é - p
2 1 1 2 s s ,s E cos ( i ) , Esen ( i ) i i i
2S 2009- I. Zamora UniV-Conf14: Tx Pasabanda de Señ
Dig.
5
QPSK: Quadrature Phase Shift Keying Coherente
ïî
ïí
ù
êë
ù
êë
; Otra parte
0
0
4
2 1
4
ù
úû
êë
ù
êë
4
2 1
4
ù
ù
[ ] úû
êë
úû
êë
ù
êë
4
2 1
4
2
1
j

Relación de fases y señales QPSK Coherente
θ (2i 1 ) π i = -
4
La siguiente tabla lista las fases, los puntos y los mensajes.
Observe que la tercera y cuarta columna representan los dibits
Para los cuatro mensajes en código Gray.
Símbolo i qi Si1 (en fase) Si2
(cuadratura)
Código Gray (bits)
Fase Cuadratura
1 p/4 E/2
1 0
2 3p/4 - E/2
0 0
3 5p/4 - E/2
0 1
4 7p/4 1 1
E/2
- E/2
- E/2
E/2
E/2
[ ] [ ]
[ E/2 , E/2] [ E/2 , E/2]
s s
E/2 , E/2 E/2 , E/2
= - = - -
1 2
s s
= - =
3 4
Las cuatro señales
vectoriales de la
constelación.

QPSK: Quadrature Phase Shift Keying Coherente
Z3 Z4
q4
q3
( t ) 2 j
E
2
- E
2
11 4 s «
E
2
01 3 s «
- E
2
10 1s «
00 2 s «
q2 q1
( t ) 1 j
Z1
Z2
Recuerde: Esta es la misma constelación de señales que se definen para QAM.

Esquema QPSK Coherente
TTrraannssmmiissoorr QQPPSSKK
X
( ) 1 j t
X
( ) 2 j t
+
å
+
Onda QPSK
(impares) b1(t)
Demultiplexor
Serie binaria
de entrada
b ± E
= 2 = 1
(pares) b2(t) b QPSK PSK T T BW BW
2
RReecceeppttoorr QQPPSSKK
X
r(t)
( ) 1 j t
T
ò
dt
0
Dispositivo
de
Decisión
X
( ) 2 j t
T
ò
dt
0
Dispositivo
de
Decisión
si r
1 0
î í ì
1
si r
0 0
Mux 2-1
>
<
1
r1
r si r 2
1 0
î í ì
>
<
2
si r
0 0
2

Esquema CPFSK y MSK Coherente
Consideremos una señal CPFSK, expresada como:
ì
ï ï
í
ï ï
î
CPFSK: Continuos Phase Shift Keying
E
MSK: Minimum Shift Keying
2 cos ( 2 π f t + θ( 0 )); 0 £ t £
T para un '
1
1
T
b
E
b
b
2 cos ( 2 π f t + θ( 0 )); 0 £ t £
T para un '
0
=
2
T
s(t)
b
b
b
Donde:
Eb es la energía de bit de la señal transmitida,
Tb es la duración del bit
q(0) es el valor de la fase en t=0

Esquema MSK Coherente
s(t) E c
= 2 b cos 2 +
[ π f t θ(t)]
T
b
Puede escribirse como
Donde q(t) es la fase de s(t) dado por
θ(t) θ( ) πh b
= 0 ± t, 0 £t £T +«1 y -«0
f 1
f f h
= - = +
h T (f f )
f f h
πh 1
El caso h=1/2, es el mínimo número de modo que son
Ortonormales.
D = 1
Es decir que es el mínimo espaciamiento en frecuencia para
que las dos señales de arriba sean ortonormales. Note que:
ì
ï ïî
ï ïí
= + = -
2T
(f f )
2
2T
b 2 1
b
2 c
c 1 2
b
1 c
De donde tenemos que:
î í ì
«
- «
- =
πh 0
θ(T ) θ(0) b
( πf t) ( πf t) 1 2 cos 2 y cos 2
b T
f
2
2 1 Df = f - f
T
b

æ
cos π
(t) £ £ ÷ ÷ø
t cos ( πf t), -T t T
T
T
æ
2
sen π
T
2 £ £ ÷ ÷ø
(t) 2 0 2
t sen( πf t), t T
T
2
Dig.
11
Una señal CPFSK para h=1/2 se denomina enllavamiento por
desplazamiento mínimo (MSK)!!!
Similarmente, tal como lo hicimos con QPSK, usando identidad trigonométrica,
tendremos:
s( t ) = s j ( t )+ s j ( t ), 0 £ t £Tb 1 1 2 2
donde las funciones básicas ortonormales están dadas por:
c b b
b b
ö
ç çè
j = 2
2
2
1
c b
b b
ö
ç çè
j =
y además: [ (0)] 1 s E cos θ b = [ ( )] b b s = - E sen θ T 2
donde q(0) puede tomar solo valores 0 y p. Por tanto, q(Tb) toma valores + p/2 y - p/2.

La relación correspondiente con los símbolos son como sigue:
s s
E , E E , E
= - = - -
1 2
s s
Dig.
12
q(0) q(Tb) bit
0 p/2 1
p p/2 0
p -p/2 1
0 -p/2 0
[ ] [ ]
[ b b E , E ] [ b b
E , E
]
b b b b = - =
3 4
si1 si2
b E b - E
b - E
b - E
b - E
b E
b E
b E

Z3 Z4
s3 :1 E
b s4 :0
b E
b - E
s2 :0 s1: 1
b - E
Z2 Z1
El resultado es una constelación de señales idénticas a la de QPSK para el
Caso de un canal AWGN.

Secuencia de entrada binaria
Escala de tiempo
( )
kTb
q
polaridad de
s ( t )
1 1 j
( )
kTb
q
polaridad de
s ( t )
2 2 j
s( t )
Forma de onda
de la función de
tiempo escalada
s1j1(t)
Forma de onda
de la función de
tiempo escalada
s2j2(t)
Forma de onda de la señal
MSK s(t) obtenida al sumar
s1j1(t) y s2j2(t) sobre un
esquema bit por bit.

Diagrama de bloque Tx y Rx MSK Coherente
Señal
MSK
S
+
+
+
+
Filtro de
banda
angosta
(t) 1 j
a (t) 1
X S
-
S
X
X
BPF
(f1)
BPF
(f1)
+
(t) 2 j
s(t)
cos( f t ) c 2p
ö
÷ ÷ø
æ
cos πt
ç çè
b T
2
a (t) 2
Tx MSK
Circuito
lógico para
intercalar
decisiones
de fase
Secuencia
binaria de
salida
Canal en fase
Dispostivo
de
decisión
Umbral=0
Dispostivo
de
decisión
X
(t) 1 j
X
Canal en cuadratura
Umbral=0
T
T
ò-
b
b
dt
ò 2
Tb dt 0
r1
r2
Estimación
de fase
( ) 0 θˆ
Estimación
de fase ( ) b T θˆ
Rx MSK
Entrada
r(t)
(t) 2 j

Espectro de Potencia para QPSK y MSK Coherente
Las componentes en fase y en cuadratura tienen una densidad espectral de potencia
común, a saber:
2
S f =
Esenc Tf
( ) 2 ( )
2
E senc T f
4 (2 )
b b
QPSK
=
ù
úû
é
S f E p
T f
( ) 32 cos(2 ) b b
2 T 2 f 2
êë
-
=
16 1
b
MSK
p

Esquema de modulación QAM Coherente
QAM: Quadrature Amplitude Modulation
Introduciremos directamente la modulación en amplitud en cuadratura M-aria o
QAM-M para M=2k y donde k > 1.
Esquema QAM: Sea un conjunto con dos funciones ortonormales dado por
(t) c c j = 2 2 j = 2 2 0 £ £
1 2
sen( π f t) t T
T
cos ( π f t) y (t)
T
Sea EO la energía de la señal con la amplitud mas baja, la señal QAM M-aria que
se transmite para el símbolo i, estará definida entonces por:
= j - j
1 2
2 2 2 2
B sen( π f t)
T
s ( t ) A (t) B (t)
i i i
A cos ( π f t)
T
s (t)
= -
i i c i c
t T
0 1 2
0
£ £
= ± ±
i , , ,...
A ,B a, a,..., ( M )a, M k con k par
Donde: i i = ± ±3 ± -1 = 2

La energía transmitida en la QAM M-aria es variable en cuanto que su valor
instantáneo depende del símbolo particular que se transmite. Por tanto, resulta mas
lógico expresar la probabilidad de error Pe en términos del valor promedio de la
energía transmitida y no en los de EO. Suponiendo que los N niveles de amplitud de
la componente en fase o en cuadratura son igualmente probables, tenemos:
ù
E E
2 2 0 (2 1)2
é - = å=
S i
Dig.
20
Debe notarse que se considerado que: mín O a = E
En las constelaciones anteriores se observa que amín es igual a a.
úû
êë
/ 2
1
N
i
N

Donde el factor multiplicador 2 fuera de los corchetes toma en cuenta las contribuciones
iguales hechas de las componentes en fase y cuadratura. Los límites de la sumatoria y
el factor multiplicador 2 dentro de los corchetes explican la naturaleza simétrica de los
niveles de amplitud pertinentes alrededor del cero. Al efectuar la sumatoria en la
ecuación anterior obtenemos:
2( 2 1)
E = N -
E
3
M E
= -
2( 1)
3
O
O
S
E 3
ES
O 2 -
1
(M )
o =
en el cual a es un parámetro que corresponde a la raíz cuadrada de la energía de
la señal con la amplitud mas baja. Sea ES la energía media (promedio) por
símbolo asumiendo que todas las amplitudes ocurren con igual probabilidad,
entonces tendremos:
a = E =
3
Es
O 2 1
(M -
)

Constelaciones cuadradas QAM
Con un número par de bits por símbolos, podemos escribir N = M
donde N es un entero positivo. Bajo esta condición, una constelación cuadrada QAM M-aria
puede considerarse siempre como el producto cartesiano de una constelación PAM N-aria
unidimensional consigo misma.
0000 0001 0011 0010
a
1000 1001 1011 1010
-a a
-a
1100 1101 1111 1110
1 j
2 j
3a
-3a 3a
-3a
0100 0101 0111 0110
1 j
-3a -a 0 a 3a
Diagrama del espacio de señales de la
señal PAM-4 correspondiente (N=4 ó
cuaternaria).
QAM M-aria para M=16; los puntos
mensaje en cada cuadrante se identifican
con los cuadribits de codificación Gray.

1 j
2 j
a
00 01
-a a
-a
10 11
QAM M-aria para M=4; los puntos mensaje
en cada cuadrante se identifican con los
dibits de codificación Gray.
1. Para QAM 4-ario, tiene constelación de
señales idéntica a la de QPSK, por tanto tiene
la misma probabilidad de error para un canal
AWGN. Así, no hay ventaja de QAM 4-ario
sobre QPSK.
2. Para QAM 16-ario, se ha asociado una representación binaria a cada punto al rotular las
ubicaciones en-fase (I) en cuadratura (Q) de conformidad con el código Gray con los
primeros dos dígitos denotando “I” los segundos dos “Q”. Esto garantiza que un error de
un solo bit ocurre si un error del “vecino mas cercano” ocurre. El cálculo de la
probabilidad de error se omite aquí (se insta intentar esto al notar que hay tres diferentes
formas de las regiones de decisión.

Dispositivo
de
Decisión
Decisión
X
(t) 1 j
X
òT dt
0
òT dt
0
r1
Canal en fase
r2
Estimación
de fase
I
Estimación
de fase
Q
Canal en cuadratura
Entrada
r(t)
(t) 2 j
Estructura de detector para QAM 16-ario.
Nota:
QPSK (o QPSK offset), MASK y QAM-16 son esquemas de modulación comúnmente usados
en la práctica. Todos ellos tienen un espacio de señal bidimensional.

Esquema BFSK No coherente
Para FSK, la señal transmitida es:
s (t) E
2 cos 2 0
i ( π f t) t T
= £ £ i b
T
b
b
i = = + =
, n : entero, i 1,2
i 1,2 f n i
c
t
c
b
1 s (t) usando frecuencia f
«
1 1
«
0 s (t) usando frecuencia f
2 2
Así, el esquema BFSK No Coherente es un caso especial del la modulación
ortogonal no cohernte con T=Tb y E=Eb, donde Tb es la duración del bit y Eb
es la energía por bit de la señal.

Esquema BPSK
Receptor BBPPSSKK NNoo ccoohheerreennttee
1
si r r
î í ì
1 2
Acoplado a
2/T cos(2π f t)
b 1
0 t T
Acoplado a
2/T cos(2π f t)
b 1
0 t T
Muestra en t=Tb
1 r
Dispositivo de
Comparación
>
<
1 2
0
si r r
b
£ £
b
£ £
Detector
de envolvente
Detector
de envolvente
Muestra en t=Tb
2 r
r(t)

PSK Diferencial (DPSK)
En la DPSK (Differential Phase-shift Keying), el transmisor tiene
dos operaciones sobresalientes:
1. Codificación diferencial de la secuencia binaria de entrada y
2. Enllavamiento por desplazamiento de fase (PSK)
Generación de DPSK:
Para una secuencia binaria de entrada {bk}, se determina una secuencia
codificada diferencialmente {dk} dada por:
k k k d d b 1= Å - k k k d d b 1= Å o -
Donde Å denota la operación en módulo o suma booleana exor y las barras
encima denotan complemento.
( ) 1 f t
q (k)
1 s 2 s 0

PSK Diferencial (DPSK)
0 1 2 3 4 5 6 7 8 9 10
1 1 0 1 0 1 1 0 0 1
1 1 0 0 1 1 1 0 1 1
k k k d d b 1= Å -
π π 0 0 π π π 0 π π
Índice k:
{ } k b
{ } k d
{q (k)}
Secuencia
diferencial
codificada
Desplazamiento
de fase
correspondiente
Bit ref
1
ò Tb dt
r(t) Ä k b
Retardo
Tb
Dispositivo
De
Decisión
0
Receptor DPSK (detección diferencial)

Otros esquemas M-arios: M- PSK
Caso: Esquema M-ario PSK
La fase de la señal portadora toma uno de los M posibles valores de los
símbolos o pulsos, es decir:
θ (2i 1)π /M i 1,..,M i = - =
Una señal M-aria se representa como:
s (t) 2E i c = + = £ £
), i 1,...,M, 0 t T
cos(2π f t (2i -1)π
T
M
Donde T es la duración del símbolo y E es la energía de la señal por símbolo o
pulso. La frecuencia fc portadora donde nc es un entero fijo es:
f nc
c =
T

Otros esquemas M-arios: M- PSK
De forma similar como hicimos con QPSK, cada señal si(t) puede
representarse por las siguientes funciones ortonormales (ortogonales de
energía unitaria):
(t) 2 c 2
1 j = sen( π f t )
cos( π f t )
T
(t) 2 c 2
2 j =
T
o
Las coordenadas de la señal recibida dado que si(t) fue transmitida son:
x E ( i )π + ÷ø
x E ( i )π + ÷ø
= cosæ 2 -1 o Q Q n
ö çè
I I n
M
= - cosæ 2 -1
ö M
çè
Donde nI y nQ son variables aleatorias Gaussianas con media cero y varianza No/2.

Otros esquemas M-arios: M-FSK
Caso: Esquema M-ario FSK
En el esquema FSK M-aria, la señal transmitida son definidas por:
s (t) E i o = 2 cos 2 + -1
π[ f (i ) Δf ] t
T
para 0 £ t £ T, i =1,...,M
Donde foT se toma como un entero por conveniencia y (Dfmín)=1/2T es el mínimo
espaciamiento espectral (en frecuencia) de modo que las señales adyacentes
sean ortogonales (recordar los resultados a partir de MSK).

0 BW f
Dig.
36
Modulación multiportador y OFDM
Las aplicaciones de FSK M-aria: modulación multiportador y OFDM.
Modulación multiportador:
Es la forma de transmitir datos digitales a través de canales de banda limitada.
Para tal fin, uno puede subdividir el ancho de banda de canal en un número de
subcanales de igual ancho de banda, donde el ancho de banda del subcanal son
casi ideales.
C( f )
Df
Subdivisión del canal de ancho de banda BW en subcanales de
banda angosta de igual anchura Df.

Modulación por división ortogonal de Frecuencia - OFDM
f f (i ) Δf, i , ,...,K i o = + -1 =1 2
Dig.
37
Ortogonalidad: Cada subcanal se asocia a una portadora dada por:
El cual es la frecuencia media en el subcanal i-ésimo. Al seleccionar la
tasa de transmisión de símbolos (pulsos) R=1/Ts, en cada uno de los
subcanales, de modo que sea igual a la separación Df de las
subportadoras adyacentes, las subportadoras son ortogonales sobre el
intervalo de símbolo Ts, independientemente de la relación de las fases
relativas entre subportadoras. En este caso, lo llamamos Orthogonal
Frequency-Division Multiplexing o simplemente OFDM.
Reducción ISI: El intervalo de símbolo en el sistema OFDM es T=KTs donde
Ts es el intervalo de símbolo en un sistema de portadora única. Así que,
seleccionando K para que sea suficientemente grande, el intervalo de símbolo
T puede hacerse significativamente mas grande que el tiempo de duración de la
dispersión de canal en el tiempo. De este modo, ISI puede hacerse
arbitrariamente pequeña al seleccionar un valor adecuado de K.

Modulación por división ortogonal de Frecuencia - OFDM
Implementación:
Puede realizarse con el uso de bancos paralelos de filtros basados en la
transformada discreta de Fourier.
Desventaja:
Se manifiesta una alta razón de potencia pico a potencia media (PAR).

Eficiencia de ancho de banda en sistemas M-arios
En la diapositiva 14 de la conferencia 16 se introdujo el concepto de eficiencia
de ancho de banda, r, expresado como bits por segundo por hertz (bps/Hz). En
este caso el objetivo es considerar el valor de r de varios esquemas de
modulación digital, i.e., (bps Hz)
R
Tx X
BW
b /
,
r =
Donde T x X representa el ancho de banda de modulaciónd el esquema X. BW ,
Para un DCS tipo M-ario, sea
Rb la tasa de bits y R la tasa de
símbolos. Sabemos que:
R R M b 2 = ×log
(1) Para esquemas M-ario PSK, QAM, DPSK,
el ancho nulo-a-nulo, es:
BW Rb
M
Tx X
2
= 2
, log
0.5 (log ) bps/Hz 2 r = × M

Eficiencia de ancho de banda en sistemas M-arios
(2) Para FSK M-ario coherente, considere que el espaciamiento entre frecuencias
es mínimo. Entonces el ancho de banda es:
BW (M )Rb
Eficiencias de ancho de banda para señales M-arias
Dig.
40
(bps Hz)
M
M /
3
2log2+
r =
M
Tx,MFSK
= +3
2 2log
M 2 4 8 16 32 64
r
PSK
DPSK
0.5 1 1.5 2 2.5 3
QAM
FSK 1 1 0.75 0.5 0.3125 0.1875
(1) Tanto PSK M-ario y QAM M-ario tienen un espacio de señales bidimensionales y ambas
son eficientes en ancho de banda (o eficiencia espectral).
(2) FSK M-aria, tiene un espacio de señales M-dimensional y es ineficiente en ancho de
banda.

Aplicaciones en módems

Velocidades a lo largo del tiempo
 300 Bits/segundo: 1960 hasta 197... y muchos.
 600 Bits/segundo: A finales de los 70.
 1200 Bits/segundo: Ganó popularidad en 1984 y 1985.
En esta época ya se notaba mas la influencia del mercado. A partir de aquí
los aumentos son impresionantes, debido sobretodo a una mejora de los
componentes electrónicos, mayor escala de integración, microchips mas
veloces, etc.
 2400 Bits/segundo: Finales de los 80.
 9600 Bits/segundo: Aparecieron a finales de 1990 y principios de 1991.
 19.2 Kbits/segundo.
 56 Kbits por segundo -se convirtió en el estándar en 1998.
 ASDL, Cable Modems, ISDN.

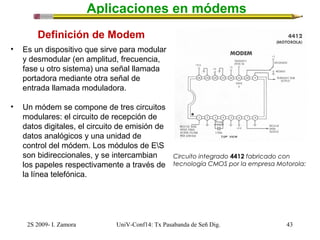
Definición de Modem
• Es un dispositivo que sirve para modular
y desmodular (en amplitud, frecuencia,
fase u otro sistema) una señal llamada
portadora mediante otra señal de
entrada llamada moduladora.
• Un módem se compone de tres circuitos
modulares: el circuito de recepción de
datos digitales, el circuito de emisión de
datos analógicos y una unidad de
control del módem. Los módulos de ES
son bidireccionales, y se intercambian
los papeles respectivamente a través de
la línea telefónica.
Circuito integrado 4412 fabricado con
tecnología CMOS por la empresa Motorola:

Definición de Modem
UART es la sigla "Universal Asynchronous Receiver - Transmitter" (Transmisor-
Receptor Asincrónico Universal). Todos los dispositivos seriales, tales como los
módems seriales, usan un chip de interfase UART (o emulan a UART) para
comunicarse con su PC. El componente más importante de un módem es este
chip.

Definición de Modem  Las distorsiones físicas de la señal las
trata el ETCD y los problemas a nivel
de bit los trata el ETTD.
 ETCD Equipo terminal del circuito de
datos, también conocido como ECD
(Equipo de Comunicación de datos, en
inglés DCE).
Un ETCD es todo dispositivo que
participa en la comunicación entre dos
dispositivos pero que no es receptor
final ni emisor original de los datos que
forman parte de esa comunicación. Es
el componente del circuito de datos
que que transforma o adecua las
señales para poder utilizar el canal de
comunicaciones.

Tipos de Modem
Analógicos
• Modems Externos
- Puerto serie
- Puerto USB
Modems Internos
- Ranura ISA
- Ranura PCI
- Ranura AMR
• Módems Software
o HSP
• Módems PC-Card

Tipos de Modem
ISDN Digitales
Los módems digitales, como su nombre lo indica, necesitan
una línea telefónica digital, llamada RDSI o ISDN (en
inglés), permitiendo velocidades hasta de 128 kbps. La
Red Digital de Servicios Integrados (RDSI) no es sino la
evolución natural de las líneas telefónicas
convencionales descrita anteriormente.
El Acceso Básico (BRI) es el tipo de conexión más común
a la RDSI. Se compone de dos canales B de 64 Kbps
cada uno y un canal D de 16kps. Los canales B son
utilizados para la transmisión de información del
usuario (voz, datos, fax, etc.), mientras que el canal D
se utiliza para señalización.
Los Accesos Primarios (PRI) son conexiones a la RDSI
para grandes centrales telefónicas o grandes
servidores de acceso remoto a redes de área local
principalmente. Se componen de 30 canales B de 64
Kbps cada uno y un canal D de 64 Kbps.

Tipos de Modem
Cable
Módems coaxiales de Fibra Óptica (HFC, Hybrid
Fiber-coax).
Son dispositivos bidireccionales que operan por
cable HFC. Ofrecen velocidades de carga en el
rango de 3 a 30 Mb, con velocidades de descarga
que van de 128Kb hasta 10Mb, aunque actualmente
los usuarios pueden esperar velocidades alrededor
de 4Mb.
Módems Unidireccionales.
Son más antiguos que los anteriores que operan por
los cables de televisión coaxiales tradicionales.
Permiten velocidades de carga de hasta 2Mb, y
requieren un módem convencional de marcación
para completar la conexión.

Tipos de Modem
ADSL
ADSL (Asymmetric Digital Subscriber Line o Línea
de Abonado Digital Asimétrica) es una tecnología
que, basada en el par de cobre de la línea telefónica
normal, la convierte en un línea de alta velocidad.
Emplea los espectros de frecuencia que no son
utilizados para el transporte de la voz, y que por lo
tanto, hasta ahora, no se utilizaban, abriendo de esta
forma un canal de datos a alta velocidad,
permitiendo a su vez (gracias a esa separación
datos / voz), poder aplicar una tarifa plana para ese
transporte de datos (los de Internet).
Dos canales de alta velocidad (uno de recepción de
datos y otro de envío de datos).
Un canal para la comunicación normal de voz
(servicio telefónico básico).

Velocidades
Si consideramos la transferencia de un archivo de 10 Mb

Selección de estándares de módem de banda de voz (línea telefónica) ITU

Selección de estándares de módem de banda de voz (línea telefónica) ITU
Estándar ITU Tipo de modulación
Tasa de
bits/seg
(bps)
Tasa de
símbolos
(baudios)
a) Módems simétricos V.21
V.22 bis
V.22bis, V.26
V.23, V.27
V.32
V.32bis
V.34
V.34 Alta velocidad
BFSK
QPSK
QPSK
PSK 8
QAM 16
QAM 1024
Constelación anidada de
cuatro constelaciones
QAM 960
300
1200
2400
4800
9600
14,400
28800
33600
300
600
1200
2400
2400
3429
b) Módems asimétricos V.90: Sentido directo
Sentido inverso
Digital
Alta Velocidad
56000
33600
Varias entre
57,333 y
34,666
El sufijo “bis” designa la segunda versión de un estándar particular.

Estándard
V.92
• Mayor Velocidad: Ahora es posible
enviar datos vía Internet con
velocidades hasta 48.000 bps. Para
enviar e-mail con gran contenido o
cargar nuestras páginas web en el
servidor, el beneficio es la alta
velocidad del V.92 .
• Acceso Online más rápido: Un click
y estas conectado. Porque el
módem memoriza automáticamente
todos los parámetros de conexión,
permite un procedimiento
considerablemente más rápido para
todas las conexiones sucesivas. En
términos V.92, esto se define "Quick
Connect".
Aumento de la compresión hasta el
160%: Los datos estrechamente
comprimidos permiten mayor
velocidad y divertimiento. La
compresión automática de los datos
V.44 hace los datos Internet más
compactos hasta el 160%, permitiendo
divertirnos con complejas
animaciones, Internet video y telefonía
Internet.
Módem-on-Hold: Puedes ser
localizado en el teléfono también
cuando estas en Internet. V.92 pone
fin a todas las señales frustrantes de
ocupado. Con el módem-on-hold,
respondes simplemente al teléfono y el
módem retarda la conexión Internet
hasta que la línea no se utiliza más.
No es más necesario desconectarse y
conectarse de nuevo.

Lecture 14 modulacion digital parte 2

Más contenido relacionado

La actualidad más candente (20)

Destacado (11)

Similar a Lecture 14 modulacion digital parte 2 (20)

Más de nica2009 (20)

Último (20)

Lecture 14 modulacion digital parte 2